Risk Model Validation: An Intraday VaR and ES Approach Using the Multiplicative Component GARCH
Abstract
:1. Introduction
- (1)
- A rigorous model validation, both in terms of in-sample fit and out-sample performance for the Multiplicative Component Generalised Autoregressive Heteroskedasticity (MC-GARCH) model under five error distributions is provided. Statistical and graphical tests are conducted to validate the models.
- (2)
- One component of the MC-GARCH model is the daily variance forecast. For this purpose, the GARCH(1,1) and EGARCH(1,1) under the five error distributions are compared and the best model among the 10 GARCH models is used to forecast the daily variance.
- (3)
- The modelling and forecasting performance of the MC-GARCH model under different distributional assumptions is assessed in this study.
- (4)
- The 99% intraday VaR is forecasted and three backtesting procedures are used. This is the first study to assess the VaR predictive ability of the MC-GARCH models by using an asymmetric VaR loss function.
- (5)
- This is the first study to forecast the intraday expected shortfall under different distributional assumptions for the MC-GARCH model. Again, three backtests are used including the recently proposed ES regression backtest of Bayer and Dimitriadis (2018).
2. Past Studies on MC-GARCH Model
3. Methodology
3.1. Model Specification
3.1.1. Models for the Daily Variance Component
3.1.2. Model for Intraday Returns
- denotes the daily variance component
- denotes the diurnal/calendar variance component in each intraday period
- denotes the intraday variance component
- is an error term following a specified distribution
3.2. Parameter Estimation
3.3. Value-at-Risk and Expected Shortfall Evaluation
3.4. Backtesting
3.4.1. Value-at-Risk Backtesting
3.4.2. Expected Shortfall Backtesting
4. Estimation Results
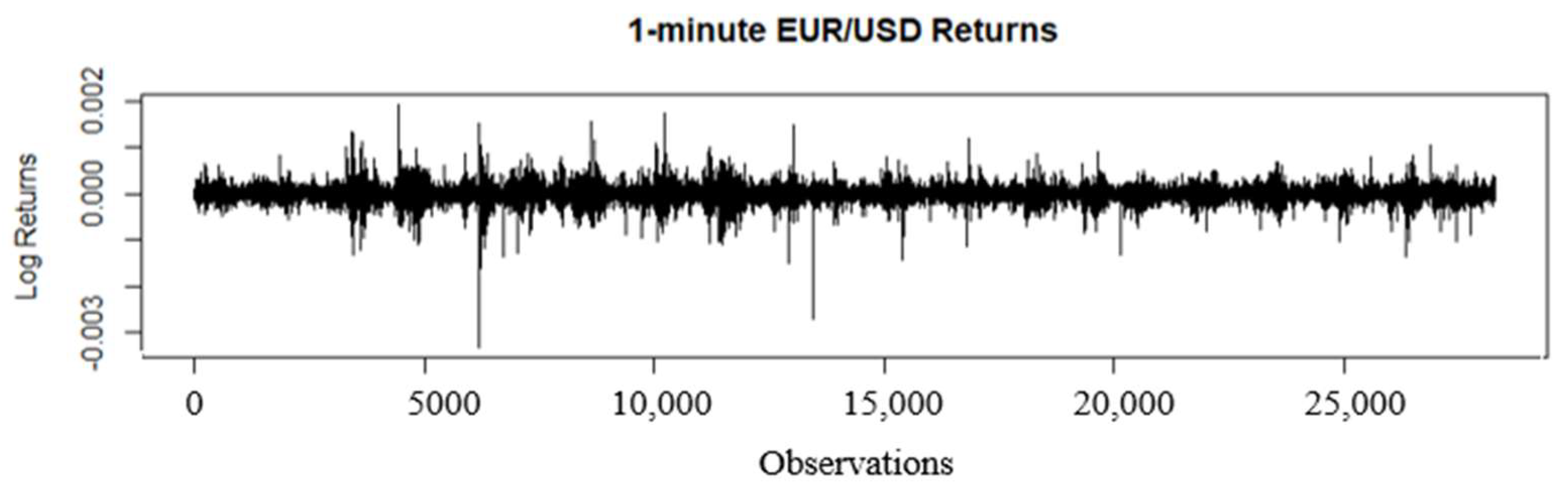
4.1. Data Description
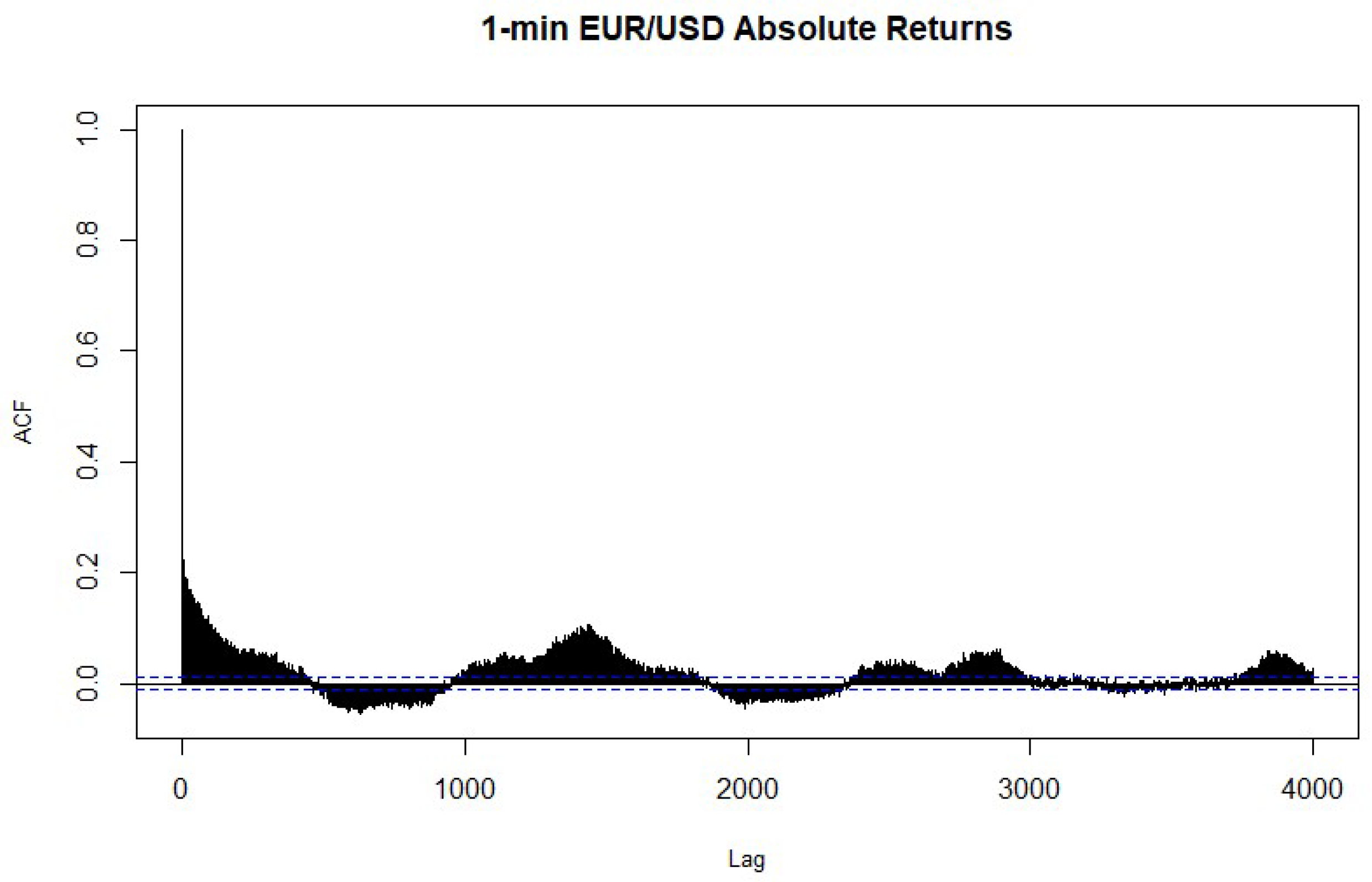
4.2. Heteroskedasticity and Normality Tests of the Return Series
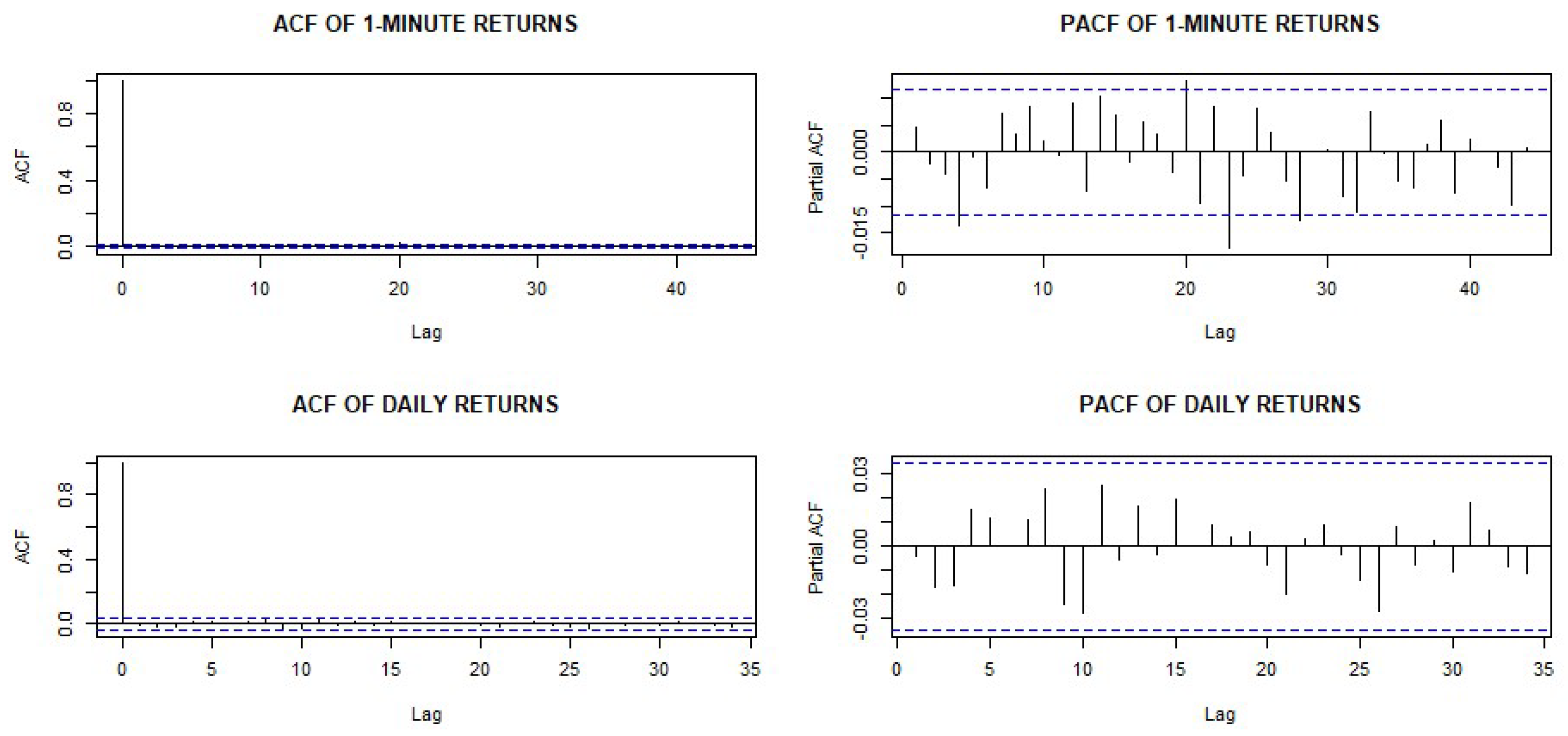
4.3. Identifying the Conditional Mean Equation
4.4. Model Checking for the Mean Equation
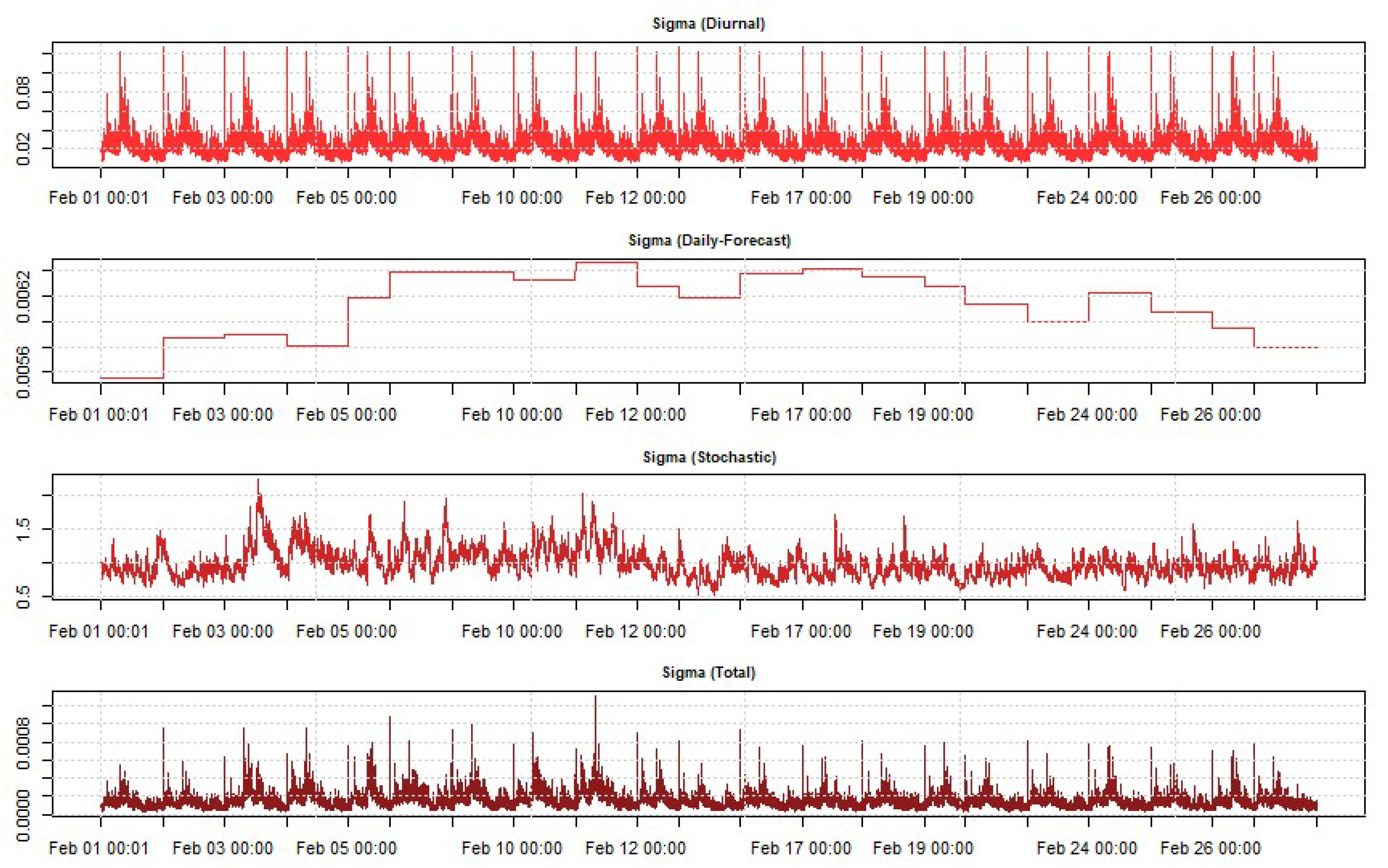
4.5. Estimation of Daily Variance Forecast
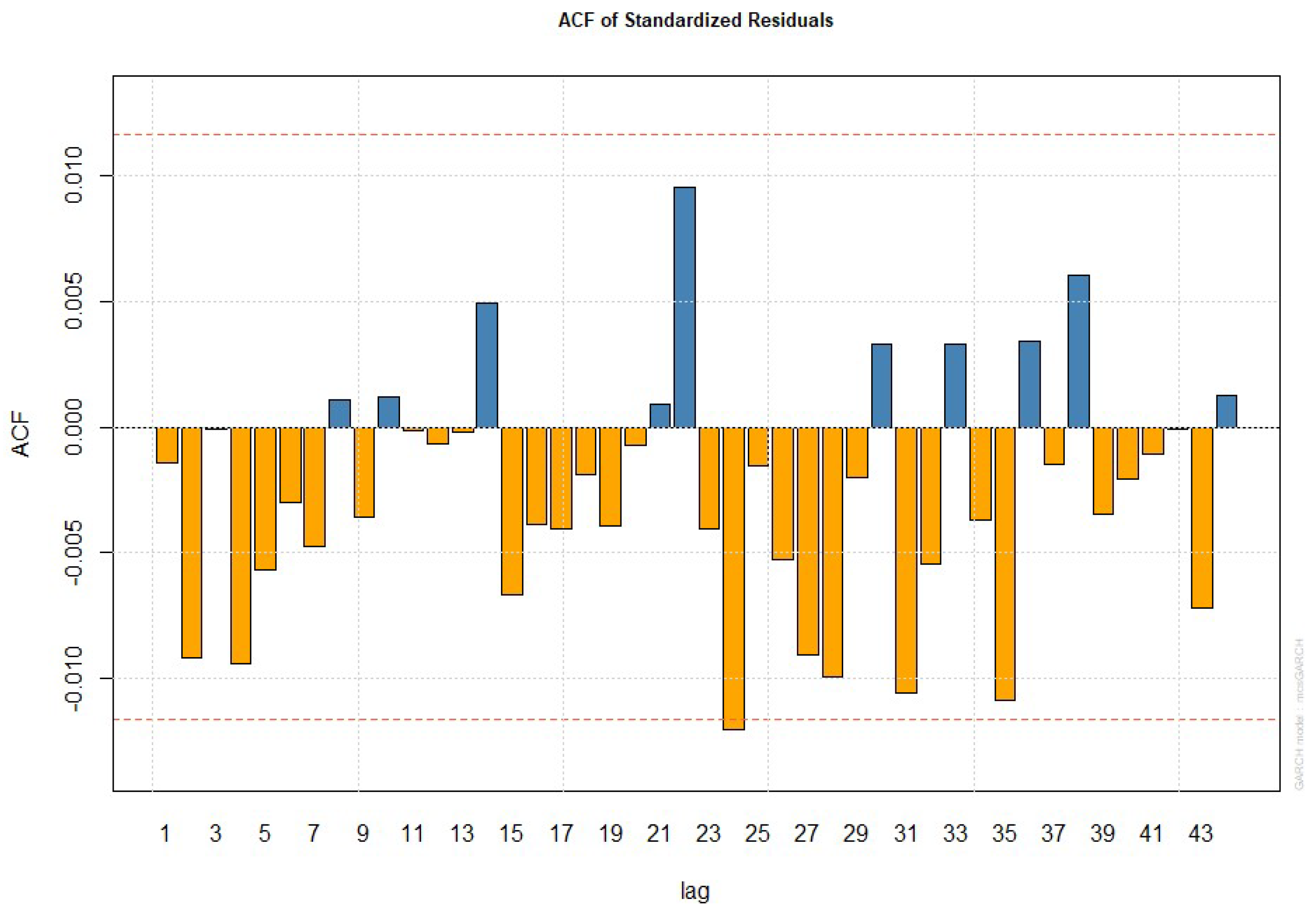
4.6. Fitting Performance
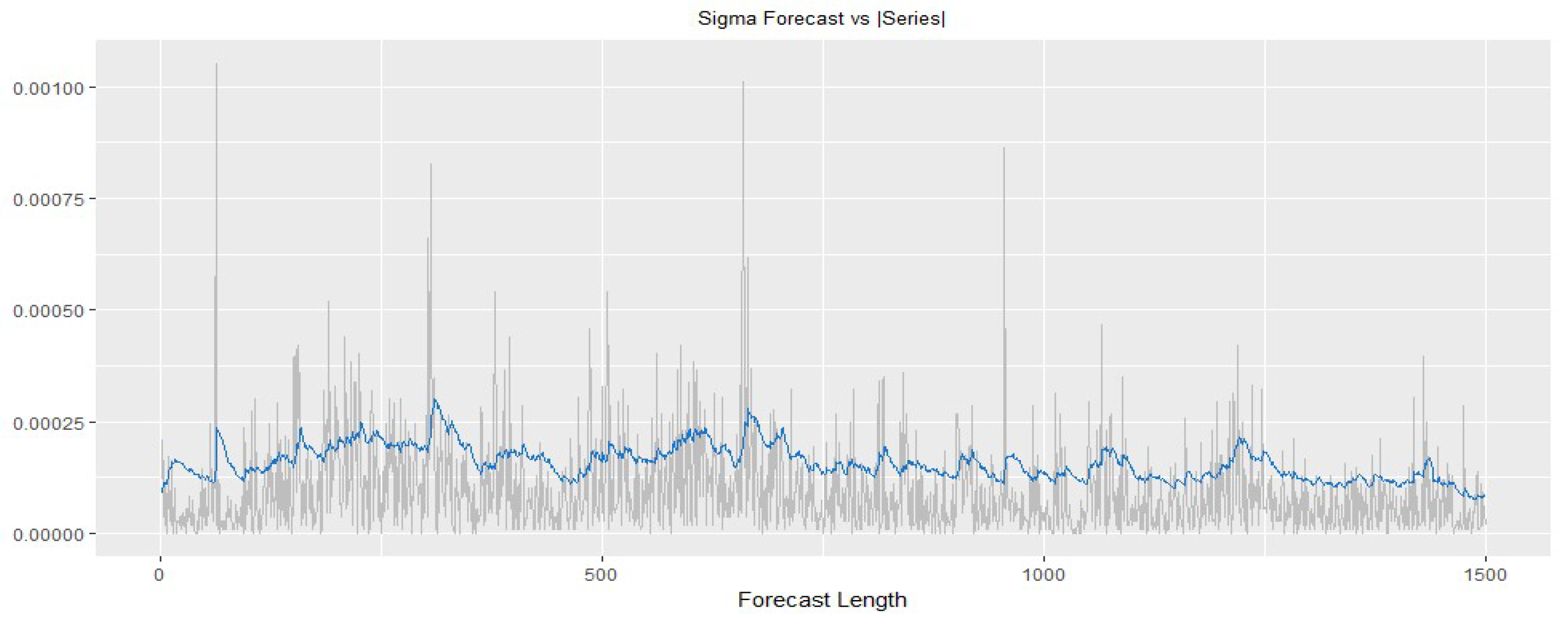
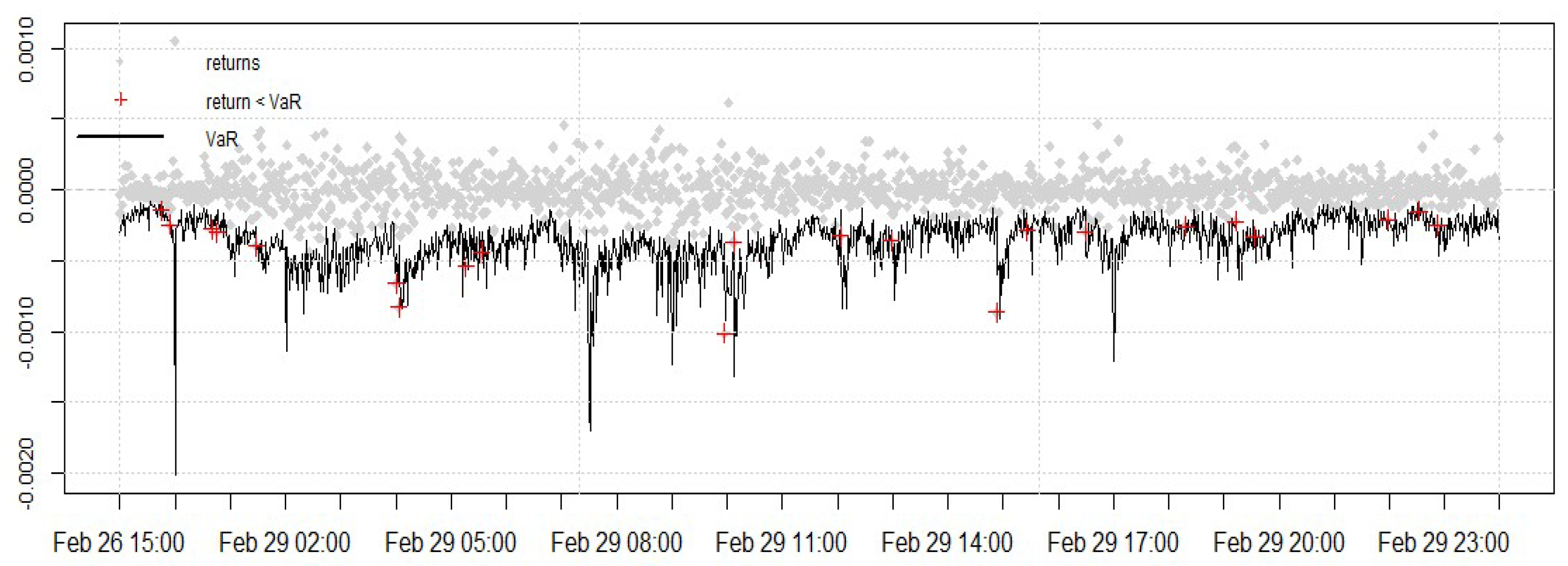
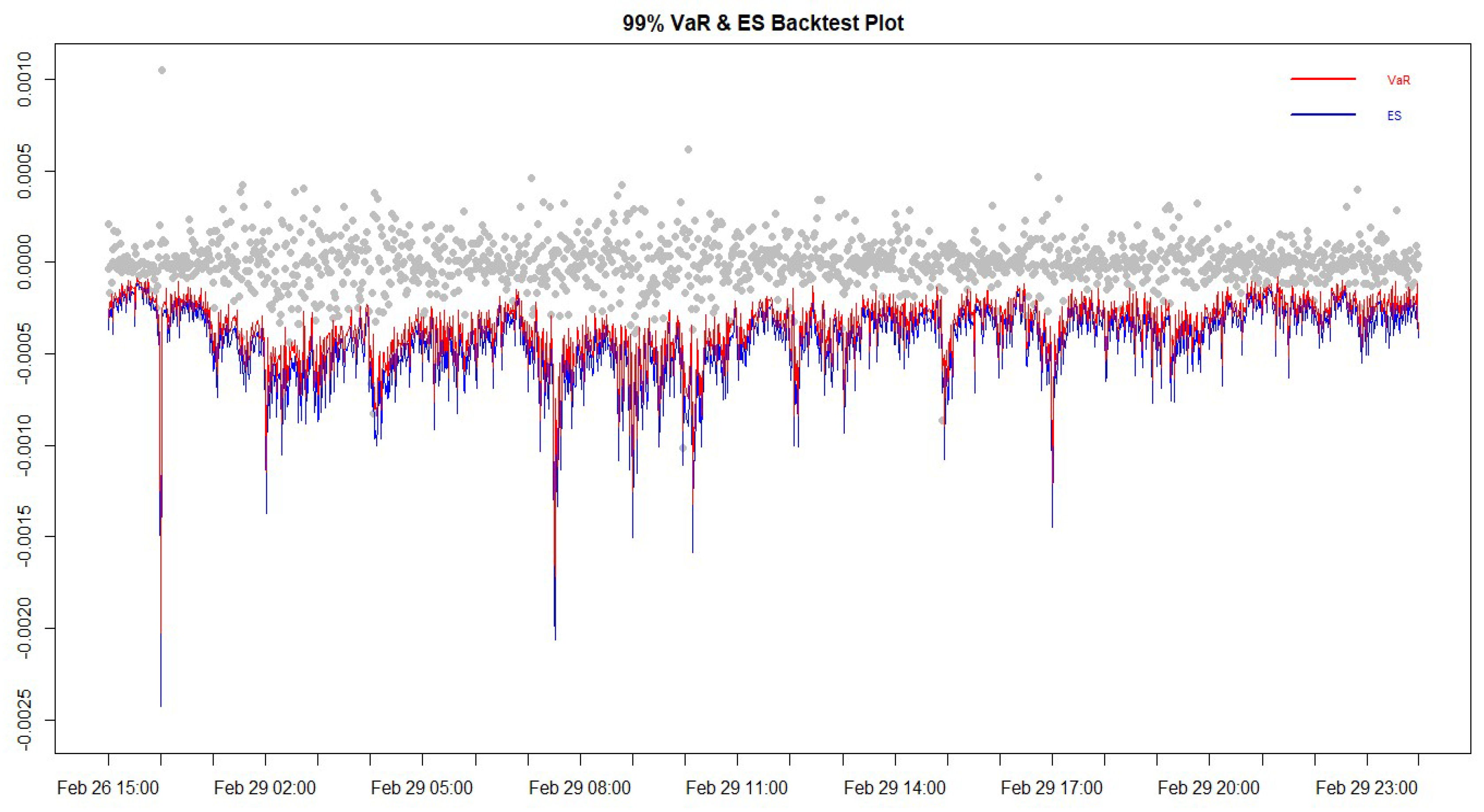
4.7. Intraday VaR Forecast
4.7.1. Kupiec’s Test
4.7.2. VaR Duration Test
4.7.3. Backtesting VaR Using an Asymmetric Loss Function
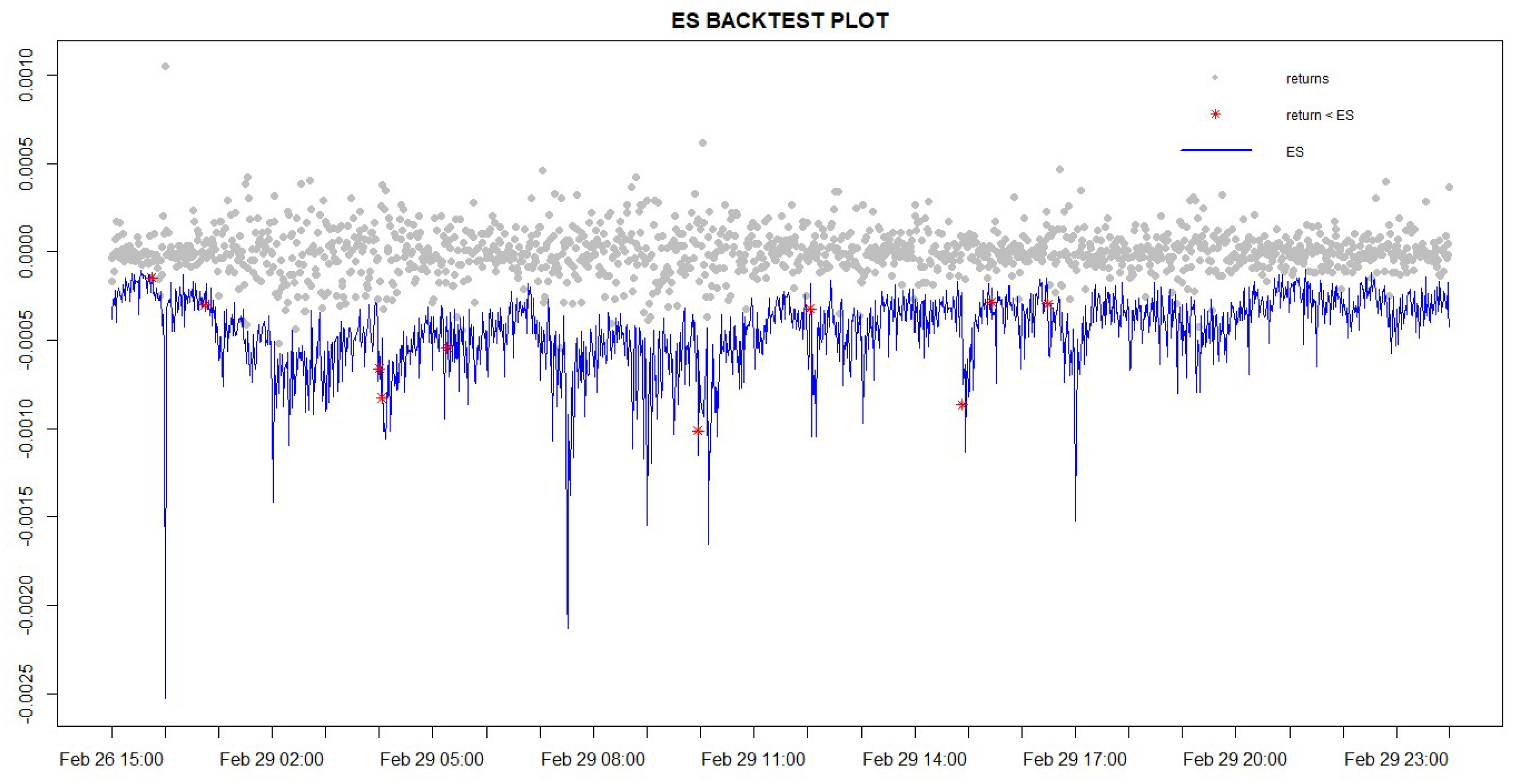
4.8. Intraday ES Forecast
4.8.1. A Regression-Based ES Backtesting Procedure: the Bivariate ES Regression Backtest
4.8.2. Exceedance Residual (ER) Backtest
4.8.3. V-Tests
5. Conclusions
5.1. Recommendations for Practitioners
5.2. Further Studies
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 1-min Returns | Daily Returns | |
|---|---|---|
| Mean | 1.23 × 10−7 | 4.62 × 10−5 |
| Standard deviation | 0.00017 | 0.00633 |
| Maximum | 0.00193 | 0.02781 |
| Minimum | −0.00332 | −0.03733 |
| Skewness | −0.38839 | −0.08208 |
| Kurtosis | 18.31108 | 4.90965 |
| Observations | 28,289 | 3159 |
| Test Statistic | p-Value | Decision | |
|---|---|---|---|
| 1-min returns | 277,030 | 0 | Reject |
| Daily returns | 483.55 | 0 | Reject |
| Test Statistic | Lag Order | p-Value | |
|---|---|---|---|
| 1-min returns | −30.596 | 30 | 0.01 |
| Daily returns | −14.03 | 14 | 0.01 |

References
- Andersen, Torben G., and Tim Bollerslev. 1997. Intraday periodicity and volatility persistence in financial markets. Journal of Empirical Finance 4: 115–58. [Google Scholar] [CrossRef]
- Andersen, Torben G., and Tim Bollerslev. 1998. Answering the Skeptics: Yes, Standard Volatility Models do Provide Accurate Forecasts. International Economic Review 39: 885. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Steve Lange. 1999. Forecasting financial market volatility: Sample frequency vis-à-vis forecast horizon. Journal of Empirical Finance 6: 457–77. [Google Scholar] [CrossRef]
- Bayer, Sebastian, and Timo Dimitriadis. 2018. Regression Based Expected Shortfall Backtesting. arXiv, arXiv:1801.04112. [Google Scholar]
- Basel Committee on Banking Supervision. 2010. Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems. Basel: Bank for International Settlements. [Google Scholar]
- Basel Committee on Banking Supervision. 2012. Fundamental Review of the Trading Book. Basel: Bank for International Settlements. [Google Scholar]
- Basel Committee on Banking Supervision. 2016. Minimum Capital Requirements for Market Risk. Basel: Bank for International Settlements. [Google Scholar]
- Bernardi, Mauro, Leopoldo Catania, and Lea Petrella. 2014. Are news important to predict large losses? arXiv, arXiv:1410.6898. [Google Scholar]
- Bollerslev, Tim. 1987. A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return. The Review of Economics and Statistics 69: 542. [Google Scholar] [CrossRef]
- Christoffersen, Peter, and Denis Pelletier. 2003. Backtesting Value-at-Risk: A Duration-Based Approach. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Culp, Christopher L., Merton H. Miller, and Andrea M. P. Neves. 1998. Value at Risk: Uses and Abuses. Journal of Applied Corporate Finance 10: 26–38. [Google Scholar] [CrossRef]
- Diao, Xundi, and Bin Tong. 2015. Forecasting intraday volatility and VaR using multiplicative component GARCH model. Applied Economics Letters 22: 1457–64. [Google Scholar] [CrossRef]
- Efron, Bradley, and Robert J. Tibshirani. 1994. An Introduction to the Bootstrap. Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Engle, Robert F. 1982. A general approach to lagrange multiplier model diagnostics. Journal of Econometrics 20: 83–104. [Google Scholar] [CrossRef]
- Engle, Robert Fry, and Jeffrey Russell. 2004. Analysis of High Frequency Financial Data. In Handbook of Financial Econometrics. Edited by Yacine Ait-Sahalia and Lars Hansen. Amsterdam: North Holland Press. [Google Scholar]
- Engle, Robert F., and Magdalena E. Sokalska. 2011. Forecasting intraday volatility in the US equity market. Multiplicative component GARCH. Journal of Financial Econometrics 10: 54–83. [Google Scholar] [CrossRef]
- García Jorcano, Laura. 2018. Sample Size, Skewness and Leverage Effects in Value at Risk and Expected Shortfall Estimation. Ph.D. Dissertation, Universidad Complutense de Madrid, Madrid, Spain. [Google Scholar]
- Giot, Pierre. 2000. Time transformations, intraday data, and volatility models. The Journal of Computational Finance 4: 31–62. [Google Scholar] [CrossRef]
- González-Rivera, Gloria, Tae-Hwy Lee, and Santosh Mishra. 2004. Forecasting volatility: A reality check based on option pricing, utility function, value-at-risk, and predictive likelihood. International Journal of Forecasting 20: 629–45. [Google Scholar] [CrossRef]
- Hansen, Peter R., Asger Lunde, and James M. Nason. 2011. The Model Confidence Set. Econometrica 79: 453–97. [Google Scholar] [CrossRef]
- Kupiec, Paul. 1995. Techniques for Verifying the Accuracy of Risk Measurement Models. The Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Lopez, Jose A. 1998. Methods for Evaluating Value-at-Risk Estimates. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- McNeil, Alexander J., and Rüdiger Frey. 2000. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach. Journal of Empirical Finance 7: 271–300. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press. [Google Scholar]
- Mondal, Prapanna, Labani Shit, and Saptarsi Goswami. 2014. Study of Effectiveness of Time Series Modeling (Arima) in Forecasting Stock Prices. International Journal of Computer Science, Engineering and Applications 4: 13–29. [Google Scholar] [CrossRef]
- Müller, Ulrich A. 2000. Volatility Computed by Time Series Operators at High Frequency. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Narsoo, Jason. 2016. High Frequency Exchange Rate Volatility Modelling Using the Multiplicative Component GARCH. International Journal of Statistics and Applications 6: 8–14. [Google Scholar]
- Nelson, Daniel B. 1991. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 59: 347. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and C. Granger. 2001. Forecasting Financial Market Volatility: A Review. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Singh, Abhay Kumar, David E. Allen, and Robert J. Powell. 2013. Intraday Volatility Forecast in Australian Equity Market. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Tsay, Ruey S. 2005. Analysis of Financial Time Series. New York: Wiley. [Google Scholar]
- Zivot, Eric. 2005. Analysis of High Frequency Financial Data: Models, Methods and Software. Part I: Descriptive Analysis of High Frequency Financial Data with S-PLUS. Available online: https://faculty.washington.edu/ezivot/research/hflectures.pdf (accessed on 15 January 2019).
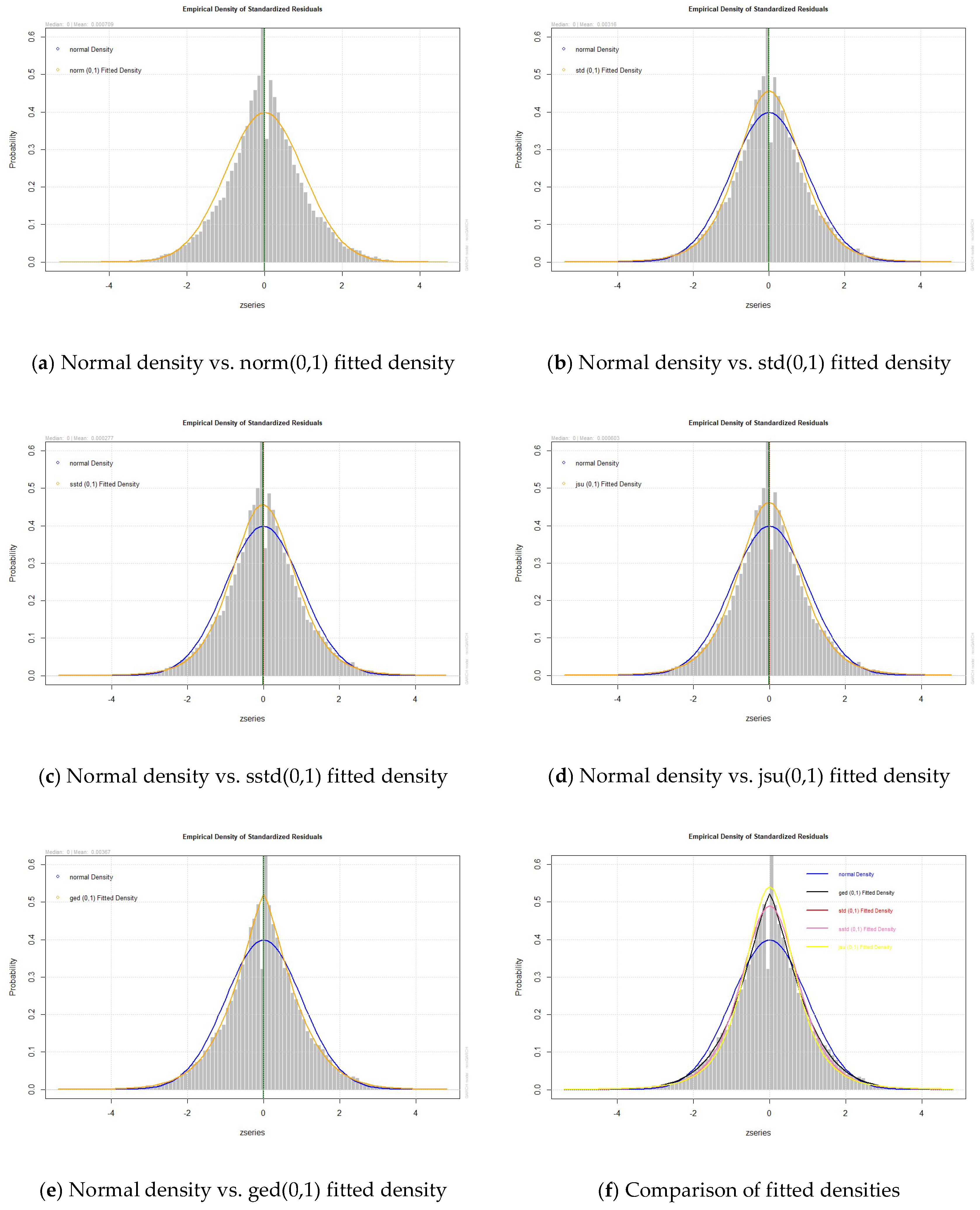
| GARCH(1,1) | |||||
|---|---|---|---|---|---|
| Normal | Student’s-t | Skewed Student’s-t | JSU | GED | |
| AIC | −7.4566 | −7.4665 | −7.4659 | −7.4662 | −7.4704 |
| BIC | −7.449 | −7.4569 | −7.4543 | −7.4547 | −7.4608 |
| Log-likelihood | 11,781.8 | 11,798.33 | 11,798.32 | 11,798.9 | 11,804.5 |
| EGARCH(1,1) | |||||
|---|---|---|---|---|---|
| Normal | Student’s-t | Skewed Student’s-t | JSU | GED | |
| AIC | −7.4602 | −7.4695 | −7.4689 | −7.4693 | −7.4734 |
| BIC | −7.4506 | −7.458 | −7.4555 | −7.4559 | −7.4619 |
| Log-likelihood | 11,788.4 | 11,804.14 | 11,804.15 | 11,804.8 | 11,810.2 |
| MC-GARCH(1,1) | |||||
|---|---|---|---|---|---|
| Normal | Student’s-t | Skewed Student’s-t | JSU | GED | |
| 0 (0.62316) | 0 (0.94151) | 0 (0.53047) | 0 (0.59145) | 0 (0.98539) | |
| 0.011999 (0) | 0.008613 (0) | 0.008651 (0) | 0.008727 (0) | 0.009911 (0) | |
| 0.037484 (0) | 0.043874 (0) | 0.043774 (0) | 0.043762 (0) | 0.041275 (0) | |
| 0.950441 (0) | 0.949255 (0) | 0.949335 (0) | 0.949197 (0) | 0.949529 (0) | |
| shape, | - | 6.893944 (0) | 6.894106 (0) | 1.878735 (0) | 1.340094 (0) |
| skewness | - | - | 1.012434 (0) | 0.037765 (0) | - |
| MC-GARCH(1,1) | |||||
|---|---|---|---|---|---|
| Normal | Student’s-t | Skewed Student’s-t | JSU | GED | |
| AIC | −15.021 | −15.046 | −15.046 | −15.048 | −15.057 |
| BIC | −15.019 | −15.045 | −15.044 | −15.046 | −15.055 |
| Log-Likelihood | 212,463 | 212,826 | 212,827.4 | 212,849.3 | 212,976.5 |
| Rank | 5 | 4 | 3 | 2 | 1 |
| Normal | Student’s-t | Skewed Student’s-t | JSU | GED | |
|---|---|---|---|---|---|
| Expected VaR Exceedances | 15 | 15 | 15 | 15 | 15 |
| Actual VaR Exceedances | 27 | 21 | 22 | 21 | 20 |
| Actual % | 1.80% | 1.40% | 1.50% | 1.40% | 1.30% |
| p-value | 0.005 | 0.142 | 0.089 | 0.142 | 0.217 |
| Model | b | p-Value |
|---|---|---|
| MC-GARCH_norm | 0.877439 | 0.397975 |
| MC-GARCH_std | 0.85151 | 0.392917 |
| MC-GARCH_sstd | 0.85151 | 0.392917 |
| MC-GARCH_jsu | 0.85151 | 0.392917 |
| MC-GARCH_ged | 0.85151 | 0.392917 |
| Superior Set of Model | ||
|---|---|---|
| Model | Rank | Loss (× 10−6) |
| MC-GARCH_std | 2 | 4.61995 |
| MC-GARCH_sstd | 1 | 4.615442 |
| MC-GARCH_jsu | 4 | 4.744222 |
| MC-GARCH_ged | 3 | 4.639826 |
| Model | p-Value | Boot p-Value |
|---|---|---|
| MC-GARCH_std | 0.806 | 0.580 |
| MC-GARCH_sstd | 0.763 | 0.527 |
| MC-GARCH_jsu | 0.755 | 0.492 |
| MC-GARCH_ged | 0.868 | 0.664 |
| Model | Expected Exceedances | Actual Exceedances | p-Value |
|---|---|---|---|
| MC-GARCH_std | 15 | 21 | 0.1845 |
| MC-GARCH_sstd | 15 | 22 | 0.1322 |
| MC-GARCH_jsu | 15 | 21 | 0.1302 |
| MC-GARCH_ged | 15 | 20 | 0.1077 |
| Model | V | ||
|---|---|---|---|
| MC-GARCH_std | 0.0004419 | 0.0015778 | 0.0010099 |
| MC-GARCH_sstd | 0.0004391 | 0.0015690 | 0.0010041 |
| MC-GARCH_jsu | 0.0004383 | 0.0015667 | 0.0010025 |
| MC-GARCH_ged | 0.0004243 | 0.0015206 | 0.0009724 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Summinga-Sonagadu, R.; Narsoo, J. Risk Model Validation: An Intraday VaR and ES Approach Using the Multiplicative Component GARCH. Risks 2019, 7, 10. https://doi.org/10.3390/risks7010010
Summinga-Sonagadu R, Narsoo J. Risk Model Validation: An Intraday VaR and ES Approach Using the Multiplicative Component GARCH. Risks. 2019; 7(1):10. https://doi.org/10.3390/risks7010010
Chicago/Turabian StyleSumminga-Sonagadu, Ravi, and Jason Narsoo. 2019. "Risk Model Validation: An Intraday VaR and ES Approach Using the Multiplicative Component GARCH" Risks 7, no. 1: 10. https://doi.org/10.3390/risks7010010
APA StyleSumminga-Sonagadu, R., & Narsoo, J. (2019). Risk Model Validation: An Intraday VaR and ES Approach Using the Multiplicative Component GARCH. Risks, 7(1), 10. https://doi.org/10.3390/risks7010010





