The W,Z/ν,δ Paradigm for the First Passage of Strong Markov Processes without Positive Jumps
Abstract
:1. A Brief Review of First Passage Theory for Strong Markov Processes without Positive Jumps and Their Draw-Downs
- The function may be obtained by integrating the fundamental law (Mijatovic and Pistorius 2012, Thm 1), (Landriault et al. 2017a, Thm 3.1)2where is given by (11). Integrating yields
2. Geometric Considerations Concerning the Joint Evolution of a Lévy Process and Its Draw-Down in a Rectangle
- If , it is impossible for the process to leave R through the upper boundary of and for these parameter values reduces to . Here it suffices to know the functions (1) to obtain the Laplace transform of .
- If , it is impossible for the process to leave R through the left boundary of , and reduces to . Here it suffices to apply the spectrally negative drawdown formulas provided in Landriault et al. (2017a); Mijatovic and Pistorius (2012).
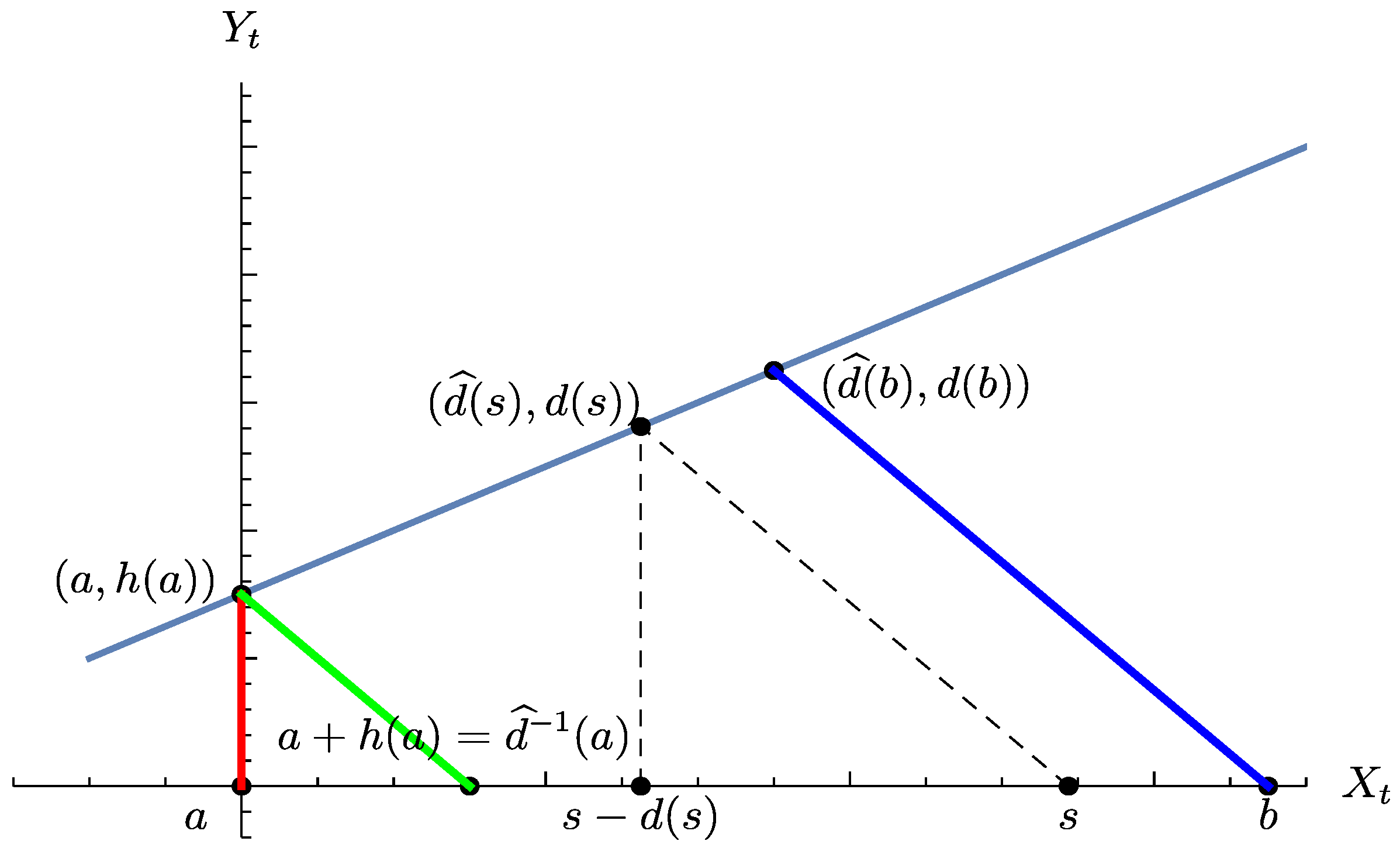
- In the remaining case , both drawdown and classic exits are possible. For the latter case, see Figure 1. The key observation here is that drawdown [classic] exits occur iff does [does not] cross the line . The final answers will combine these two cases.
3. The Three Laplace Transforms of the Exit Time out of a Rectangle for Lévy Processes without Positive Jumps
- the middle case may happen only if visits a before ;
- the first case (exit through b) and the third case (drawdown exit) may happen only if visits first , with the drawdown barrier being invisible, and that subsequently the lower first passage barrier a becomes invisible.
4. Generalized Draw-Down Stopping for Processes without Positive Jumps
- 1.
- Due to creeping, is a product of infinitesimal eventsTaking product, with , yields (24).
- 2.
- Informally, we condition on the density . The integrand of is obtained multiplying survival infinitesimal events up to level y by an infinitesimal termination event in . The probability of this event, conditioned on survival up to y, is given by the deficit formulaFor a rigorous (rather intricate) proof, see Avram et al. (2018b).
5. The Three Laplace Transforms of the Exit Time out of a Curved Trapezoid, for Processes without Positive Jumps
6. de Finetti’s Optimal Dividends for Spectrally Negative Markov Processes with Generalized Draw-Down Stopping
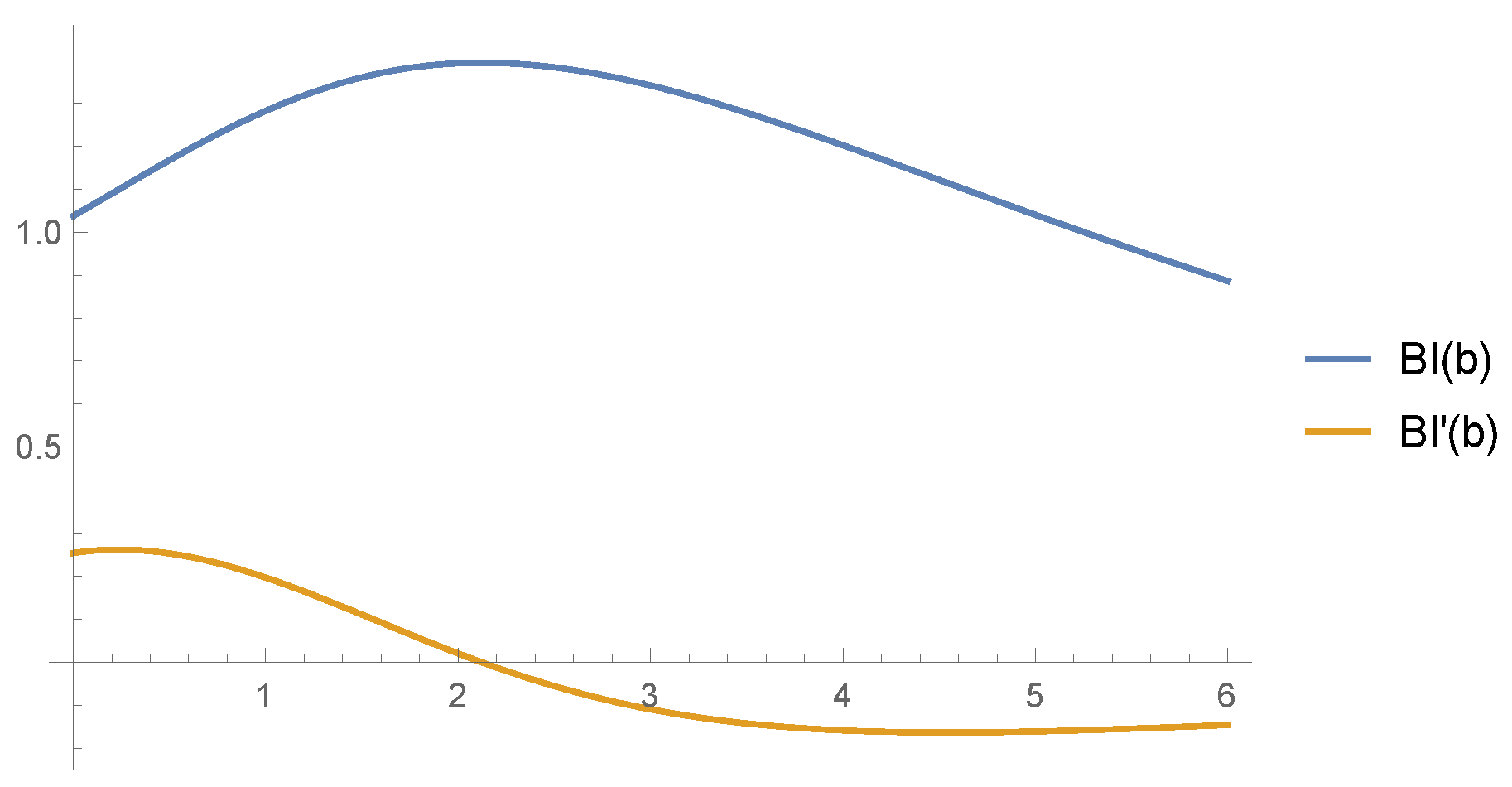
7. Example: Affine Draw-Down Stopping for Brownian Motion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Albrecher, Hansjörg, and Sören Asmussen. 2010. Ruin Probabilities. Singapore: World Scientific, vol. 14. [Google Scholar]
- Albrecher, Hansjörg, Florin Avram, Corina Constantinescu, and Jevgenijs Ivanovs. 2014. The tax identity for Markov additive risk processes. Methodology and Computing in Applied Probability 16: 245–58. [Google Scholar] [CrossRef]
- Albrecher, Hansjörg, Jevgenijs Ivanovs, and Xiaowen Zhou. 2016. Exit identities for Lévy processes observed at Poisson arrival times. Bernoulli 22: 1364–82. [Google Scholar] [CrossRef]
- Avram, Florin, and J. P. Garmendia. 2019. Some first passage theory for the Segerdahl-Tichy risk process, and open problems. Forthcoming. [Google Scholar]
- Avram, Florin, and Dan Goreac. 2018. A pontryaghin maximum principle approach for the optimization of dividends/consumption of spectrally negative Markov processes, until a generalized draw-down time. arXiv, arXiv:1812.08438. [Google Scholar]
- Avram, Florin, Andreas E. Kyprianou, and Martijn R. Pistorius. 2004. Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. The Annals of Applied Probability 14: 215–38. [Google Scholar]
- Avram, Florin, Zbigniew Palmowski, and Martijn R. Pistorius. 2007. On the optimal dividend problem for a spectrally negative Lévy process. The Annals of Applied Probability 17: 156–80. [Google Scholar] [CrossRef]
- Avram, Florin, Zbigniew Palmowski, and Martijn R. Pistorius. 2015. On Gerber–Shiu functions and optimal dividend distribution for a Lévy risk process in the presence of a penalty function. The Annals of Applied Probability 25: 1868–935. [Google Scholar] [CrossRef]
- Avram, Florin, Danijel Grahovac, and Ceren Vardar-Acar. 2017a. The W,Z scale functions kit for first passage problems of spectrally negative Lévy processes, and applications to the optimization of dividends. arXiv, arXiv:1706.06841. [Google Scholar]
- Avram, Florin, Nhat Linh Vu, and Xiaowen Zhou. 2017b. On taxed spectrally negative Lévy processes with draw-down stopping. Insurance: Mathematics and Economics 76: 69–74. [Google Scholar] [CrossRef]
- Avram, Florin, José-Luis Pérez, and Kazutoshi Yamazaki. 2018a. Spectrally negative Lévy processes with Parisian reflection below and classical reflection above. Stochastic Processes and Their Applications 128: 255–90. [Google Scholar] [CrossRef]
- Avram, Florin, Bin Li, and Shu Li. 2018b. A unified analysis of taxed draw-down spectrally negative Markov processes. Forthcoming. [Google Scholar]
- Avram, Florin, and Matija Vidmar. 2017. First passage problems for upwards skip-free random walks via the Φ,W,Z paradigm. arXiv, arXiv:1708.06080. [Google Scholar]
- Avram, Florin, and Xiaowen Zhou. 2017. On fluctuation theory for spectrally negative Lévy processes with parisian reflection below, and applications. Theory of Probability and Mathematical Statistics 95: 17–40. [Google Scholar] [CrossRef]
- Azéma, Jacques, and Marc Yor. 1979. Une solution simple au probleme de Skorokhod. In Séminaire de Probabilités XIII. Berlin: Springer, pp. 90–115. [Google Scholar]
- Bertoin, Jean. 1997. Exponential decay and ergodicity of completely asymmetric Lévy processes in a finite interval. The Annals of Applied Probability 7: 156–69. [Google Scholar] [CrossRef]
- Bertoin, Jean. 1998. Lévy Processes. Cambridge: Cambridge University Press, vol.121. [Google Scholar]
- Borovkov, Alexandr. 2012. Stochastic Processes in Queueing Theory. Berlin: Springer Science & Business Media, vol. 4. [Google Scholar]
- Carr, Peter. 2014. First-order calculus and option pricing. Journal of Financial Engineering 1: 1450009. [Google Scholar] [CrossRef]
- Chan, Terence, Andreas E. Kyprianou, and Mladen Savov. 2011. Smoothness of scale functions for spectrally negative Lévy processes. Probability Theory and Related Fields 150: 691–708. [Google Scholar] [CrossRef]
- Czarna, Irmina, José-Luis Pérez, Tomasz Rolski, and Kazutoshi Yamazaki. 2017. Fluctuation theory for level-dependent Lévy risk processes. arXiv, arXiv:1712.00050. [Google Scholar]
- Czarna, Irmina, Adam Kaszubowski, Shu Li, and Zbigniew Palmowski. 2018. Fluctuation identities for omega-killed Markov additive processes and dividend problem. arXiv, arXiv:1806.08102. [Google Scholar]
- Dubins, Lester E., Larry A. Shepp, and Albert Nikolaevich Shiryaev. 1994. Optimal stopping rules and maximal inequalities for Bessel processes. Theory of Probability & Its Applications 38: 226–61. [Google Scholar]
- Egami, Masahiko, and Tadao Oryu. 2015. An excursion-theoretic approach to regulator’s bank reorganization problem. Operations Research 63: 527–39. [Google Scholar] [CrossRef]
- Hobson, David. 2007. Optimal stopping of the maximum process: A converse to the results of Peskir. Stochastics An International Journal of Probability and Stochastic Processes 79: 85–102. [Google Scholar] [CrossRef]
- Ivanovs, Jevgenijs, and Zbigniew Palmowski. 2012. Occupation densities in solving exit problems for Markov additive processes and their reflections. Stochastic Processes and Their Applications 122: 3342–60. [Google Scholar] [CrossRef]
- Jacobsen, Martin, and Anders Tolver Jensen. 2007. Exit times for a class of piecewise exponential Markov processes with two-sided jumps. Stochastic Processes and Their Applications 117: 1330–56. [Google Scholar] [CrossRef]
- Kyprianou, Andreas. 2014. Fluctuations of Lévy Processes with Applications: Introductory Lectures. Berlin: Springer Science & Business Media. [Google Scholar]
- Landriault, David, Bin Li, and Shu Li. 2015. Analysis of a drawdown-based regime-switching Lévy insurance model. Insurance: Mathematics and Economics 60: 98–107. [Google Scholar] [CrossRef]
- Landriault, David, Bin Li, and Hongzhong Zhang. 2017a. On magnitude, asymptotics and duration of drawdowns for Lévy models. Bernoulli 23: 432–58. [Google Scholar] [CrossRef]
- Landriault, David, Bin Li, and Hongzhong Zhang. 2017b. A unified approach for drawdown (drawup) of time-homogeneous Markov processes. Journal of Applied Probability 54: 603–26. [Google Scholar] [CrossRef]
- Lehoczky, John P. 1977. Formulas for stopped diffusion processes with stopping times based on the maximum. The Annals of Probability 5: 601–7. [Google Scholar] [CrossRef]
- Li, Bo, Linh Vu, and Xiaowen Zhou. 2017. Exit problems for general draw-down times of spectrally negative Lévy processes. arXiv, arXiv:1702.07259. [Google Scholar]
- Li, Bo, and Xiaowen Zhou. 2018. On weighted occupation times for refracted spectrally negative Lévy processes. Journal of Mathematical Analysis and Applications 466: 215–37. [Google Scholar] [CrossRef]
- Mijatovic, Aleksandar, and Martijn R Pistorius. 2012. On the drawdown of completely asymmetric Lévy processes. Stochastic Processes and Their Applications 122: 3812–36. [Google Scholar] [CrossRef]
- Page, Ewan S. 1954. Continuous inspection schemes. Biometrika 41: 100–15. [Google Scholar] [CrossRef]
- Peskir, Goran. 1998. Optimal stopping of the maximum process: The maximality principle. Annals of Probability 26: 1614–40. [Google Scholar] [CrossRef]
- Pistorius, Martijn R. 2004. On exit and ergodicity of the spectrally one-sided Lévy process reflected at its infimum. Journal of Theoretical Probability 17: 183–220. [Google Scholar] [CrossRef]
- Shepp, Larry, and Albert N. Shiryaev. 1993. The Russian option: Reduced regret. The Annals of Applied Probability 3: 631–40. [Google Scholar] [CrossRef]
- Suprun, V. N. 1976. Problem of destruction and resolvent of a terminating process with independent increments. Ukrainian Mathematical Journal 28: 39–51. [Google Scholar] [CrossRef]
- Taylor, Howard M. 1975. A stopped Brownian motion formula. The Annals of Probability 3: 234–46. [Google Scholar] [CrossRef]
- Wang, Wenyuan, and Xiaowen Zhou. 2018. General drawdown-based de Finetti optimization for spectrally negative Lévy risk processes. Journal of Applied Probability 55: 513–42. [Google Scholar] [CrossRef]
| 1 | The fact that the survival probability has the multiplicative structure (2) is equivalent to the absence of positive jumps, by the strong Markov property. |
| 2 | Please note that (Mijatovic and Pistorius 2012, Thm. 1) give a more complicated “sextuple law” with two cases, and that (Landriault et al. 2017a, Thm 3.1) use an alternative to the function , so that some computing is required to get (11) and (14). |
| 3 | Choosing optimally in various control problems involving optimal dividends and capital injections should be of interest, and will be pursued in further work. |

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avram, F.; Grahovac, D.; Vardar-Acar, C. The W,Z/ν,δ Paradigm for the First Passage of Strong Markov Processes without Positive Jumps. Risks 2019, 7, 18. https://doi.org/10.3390/risks7010018
Avram F, Grahovac D, Vardar-Acar C. The W,Z/ν,δ Paradigm for the First Passage of Strong Markov Processes without Positive Jumps. Risks. 2019; 7(1):18. https://doi.org/10.3390/risks7010018
Chicago/Turabian StyleAvram, Florin, Danijel Grahovac, and Ceren Vardar-Acar. 2019. "The W,Z/ν,δ Paradigm for the First Passage of Strong Markov Processes without Positive Jumps" Risks 7, no. 1: 18. https://doi.org/10.3390/risks7010018
APA StyleAvram, F., Grahovac, D., & Vardar-Acar, C. (2019). The W,Z/ν,δ Paradigm for the First Passage of Strong Markov Processes without Positive Jumps. Risks, 7(1), 18. https://doi.org/10.3390/risks7010018




