Abstract
Based on a rich dataset of recoveries donated by a debt collection business, recovery rates for non-performing loans taken from a single European country are modelled using linear regression, linear regression with Lasso, beta regression and inflated beta regression. We also propose a two-stage model: beta mixture model combined with a logistic regression model. The proposed model allowed us to model the multimodal distribution we found for these recovery rates. All models were built using loan characteristics, default data and collections data prior to purchase by the debt collection business. The intended use of the models was to estimate future recovery rates for improved risk assessment, capital requirement calculations and bad debt management. They were compared using a range of quantitative performance measures under K-fold cross validation. Among all the models, we found that the proposed two-stage beta mixture model performs best.
1. Introduction
In Basel II, an internal ratings-based (IRB) approach was proposed by the Basel Committee in 2001 to determine capital requirements for credit risk (Bank for International Settlements 2001). This IRB approach grants banks permission to use their own risk models or assessments to calculate regulatory capital. Under the IRB approach, banks are required to estimate the following risk components: probability of default (PD), loss given default (LGD), exposure at default (EAD) and maturity (M) (Bank for International Settlements 2001). Since Basel II’s capital requirement calculation depends heavily on LGD, financial institutions have put more emphasis on modelling LGD in recent years. Unlike the estimation of PD, which is well-established, LGD is not so well-understood and still subject to research. Improving LGD modelling can help financial institutions assess their risk and regulatory capital requirement more precisely, as well as improving debt management.
LGD is defined as the proportion of money financial institutions fail to collect during the collection period, given the borrower has already defaulted. Conversely, Recovery Rate (RR) is defined as the proportion of money financial institutions successfully collected minus the administration fees during the collection period, given the borrower has already defaulted. Equations (1) and (2) give formal definitions of RR and LGD, respectively:
- Suppose individual i has already defaulted on a loan, let be the exposure at default for this individual i.
- Let be the administration costs (e.g., letters, phone calls, visits, lawyers and legal work) incurred for individual i.
- Let be the amount recovered for individual i.
Then,
and
RR mainly lies in the interval [0, 1] and typically has high concentrations at the boundary points 0 and 1. It is possible for RR to be negative if recoveries are less than administration costs, , and greater than 1 if recoveries exceed exposure plus administration costs, . Typically, however, RR is truncated within the interval [0, 1] when developing LGD models.
The main challenge in estimating LGD is the bimodal property with high concentrations at 0 and 1 typically present in LGD empirical distributions, where people either repay in full or repay nothing. For the dataset we used in this study, we found our LGD distribution is actually tri-modal. Therefore, regression models have been studied that specifically deal with this problem. For example, Bellotti and Crook (2012) built Tobit and decision tree models along with beta and fractional logit transformation of the RR response variable to forecast the LGD based on a dataset of 55,000 defaulted credit cards in the UK from 1999 to 2005. They concluded that ordinary least squares regression with macroeconomic variables performed the best in terms of forecast performance. Calabrese (2012) proposed a mixed continuous-discrete model, where the boundary values 0 and 1 are modelled by Bernoulli random variables and the continuous part of the RR is modelled by a Beta random variable. This model is then applied to predict RR of Bank of Italy’s loans from 1985 to 1999. The result is compared with Papke and Wooldrige’s fractional response model with log-log, logistic and complementary log-log link functions (Papke and Wooldridge 1996) and linear regression. The mixed continuous and discrete model achieves the best performance. Qi and Zhao (2011) applied four linear models, namely ordinary least squares regression, fractional response regression, inverse Gaussian regression, and inverse Gaussian regression with beta transformation, and two non-linear models, namely regression tree and neural network, to model the LGD of 3751 defaulted bank loans and bonds in the US from 1985 to 2008. They concluded that fractional response regression is slightly better than the ordinary least squares regression. Moreover, they reported that non-linear models perform best. Loterman et al. (2012) performed a benchmark study of LGD by comparing twenty-four different models using six datasets extracted from international banks. They concluded that non-linear models, such as neural network, support vector machine and mixture models perform better than linear models.
For this project, we specifically modelled and predicted RR for data from a single European country provided by a debt collection company. Due to reasons of commercial confidentiality and data protection, the debt collection company will remain anonymous and some aspects of the data were also anonymised, including the country of origin. Consequently, the data cannot be made publicly available. We applied some of the models that have already been studied previously and also extended the existing models, proposing a new beta mixture model to improve the accuracy of RR prediction. A good prediction of RR would help the debt collection company to determine collection policy for new debt portfolios. It is important to note that the RR we modelled is different from most RR, as the data only contain positive repayments and no administration fee was recorded. Therefore, all the RRs in our data lie in the range (0, 1] instead of [0, 1]. Figure 1 shows a histogram of RR for the data. We can clearly see that there are modes at 0, 0.55 (approximately) and a high spike at boundary value 1. Since the shape of the empirical RR distribution demonstrates a trimodal feature, it is reasonable to assume that the recovery rate is a mixed type random variable. The multi-modality of RR is a natural consequence of different groups of bad debts being serviced using different strategies; e.g., one strategy may be that some bad debts are allowed to be written off if the debtor paid back some agreed fixed percentage of the outstanding balance. Having outcome RR within motivated the use of the beta regression model and the multi-modal nature of RR motivates the use of a mixture model within this context.
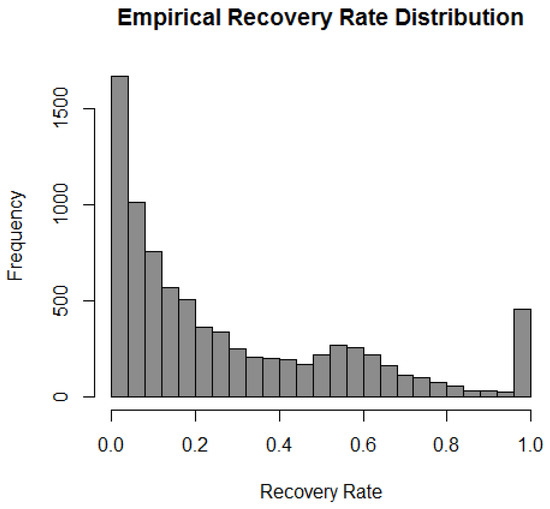
Figure 1.
Histogram of recovery rates for 8237 loans after pre-preprocessing described in Section 2. The stack of 1s shows frequency of , but the stack at 0 shows frequency for small .
The beta mixture model has been applied successfully within several other application domains. Ji et al. (2005) showed how to apply the beta mixture regression model in several bioinformatics applications such as meta-analysis of gene expression data and to cluster correlation coefficients between gene expressions. Laurila et al. (2011) used a beta mixture model to describe DNA methylation patterns, helping to reduce the dimensionality of microarray data. Moustafa et al. (2018) used a beta mixture model as the basis of an anomaly detection system. Their network data are typically bounded, which suggests a beta distribution, and the use of the beta mixture allowed them to identify latent clusters in normal network use.
Inspired by Calabrese’s mixed continuous-discrete model (Calabrese 2012), we propose a two-stage model composed of:
- A beta mixture model is parameterised by mean and precision based on two sets of predictor variables on the interval of (0, 1) in order to model the two modes located at just after 0 and around 0.55.
- A logistic regression model is used for the mode at boundary value 1.
The above proposed model allows representation of the trimodal feature of the data. The beta mixture component groups the clients into two clusters for RR < 1, based on their personal information, debt conditions and repayment history, which may become useful information for other business analysis and decision-making, and then uses logistic regression to model the third case RR = 1. In addition, we also used linear regression, linear regression with Lasso, beta regression and inflated beta regression to model RR. Model performance was measured by mean squared error, mean absolute error and mean aggregate absolute error under K-fold cross validation.
To our knowledge, this is the first study for estimating RR for portfolios of non-performing loans using a statistical model, and the first use of a beta mixture model for LGD. We also developed a novel procedure for predicting an expected value of outcome from a beta mixture model based on assigning a new observation to one of the clusters in the mixture. The remainder of the article is organised as follows: Section 2 provides a detailed data overview. Section 3 introduces the modelling methodology with great emphasis on the proposed beta mixture model combined with logistic regression model. Section 4 analyses some important features of the models and reports the model performance and Section 5 concludes with key findings and future recommendations.
2. Data
Three datasets were provided by the debt collection company:
- Dataset 1
- provides 48 predictor variables of personal information including socio-demographic variables, Credit Bureau Score and debt status for 120,699 individuals for loans originating between January 1998 and May 2014 from several different financial institutions. Overall, 97.5% of them have credit card debt and only 2.5% are refinanced credit cards (product = “R”). Partial information was extracted from a Bad Debt Bureau. Each record corresponds to a bad loan and has a unique key Loan.Ref.
- Dataset 2
- records all the recoveries made by the bank before the debt collection company purchased the debt portfolio. It contains 15 predictor variables about historical collection information, which includes number of calls, contacts and visits made by the bank to collect the debt. It also includes repayments in the format of monthly summary. In total, there are 42,832 individuals’ records in Dataset 2, among which only 34,807 individuals can be matched to Dataset 1 by Loan.Ref. Numbers of calls, contacts, visits, repayment and some other monthly activities are aggregated by summing for each loan identified by Loan.Ref.
- Dataset 3
- records all the recoveries made by the debt collection company after they purchased the debt portfolio from the bank. It includes 12 predictor variables about the ongoing collection information. There are 8281 individuals in total, among which only 8237 individuals are from Dataset 1. Since only positive repayments are recorded, all the recovery rates we calculated are strictly greater than 0. Therefore, in the modelling section, we only focus on the recovery modelling in the interval (0, 1], which is slightly different from the usual RR defined in [0, 1]. The debt collection period recorded in this dataset is from January 2015 to end of November 2016.
Figure 2 shows how the data were joined. There are 8237 data points presented in Dataset 3, but only 7161 individual historical collection information are recorded in Dataset 2. In these cases, there are no historical recoveries by bank, i.e., no calls, contacts, visits or payments for the remaining 1076 individuals. Therefore, a value of 0 was assigned to aggregate recoveries in Dataset 2 for the remaining 1076 individuals. The modified Dataset 2 was then joined to Datasets 1 and 3 by the unique key Loan.Ref and we obtained a table of 8237 data points with 61 variables.
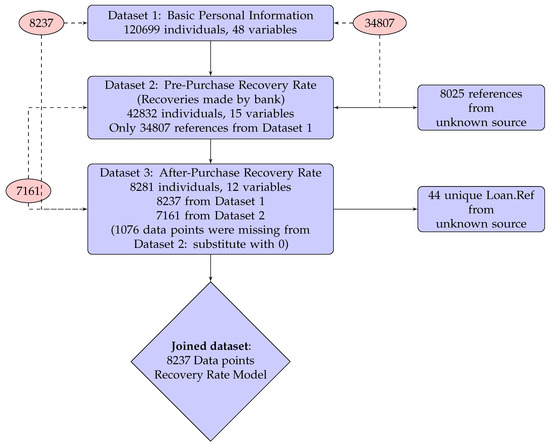
Figure 2.
Joining the three datasets.
Table A1 gives descriptive statistics for each of the variables in the joined dataset used in the statistical modelling. The predictor variable Pre-Recovery Rate is the bank’s RR before the debt portfolio was purchased. The minimum value is −0.130, which is negative due to the substantial amount of administration fee exceeding repayments incurred during the collection period. The predictor variable Credit Bureau Score is a generic credit score provided by a credit bureau.
Recovery Rate Calculation
Since the repayments in Datasets 2 and 3 were recorded in the format of monthly activity summaries, each individual may have several repayments for the same loan. Therefore, we defined the recovery rate as the sum of repayments minus the administration fee (if available) over the original balance of the loan, which is also equivalent to the difference between original balance and ending balance over the original balance. For each individual i, RR is calculated using:
Figure 1 is the empirical RR histogram calculated based on Equation (3), for the 8237 data points after pre-processing. The remaining 112,462 data points not included in the analysis essentially have RR = 0, but we do not know whether they have been serviced or not, thus they were not included in the analysis. Essentially, the goal of our model is to estimate RR computed from Dataset 3 (post-purchase), based on pre-purchase information given in Datasets 1 and 2.
3. Modelling Methodology
We applied various models to estimate RR. In all cases, model performance was measured within a K-fold cross validation framework. We first tried using ordinary least squares linear regression, with and without stepwise backward variable selection using the AIC criterion. In the following sub-sections, we list the other modelling approaches we explored. Let y indicate the outcome variable, recovery rate, and X is a corresponding vector of predictor variables.
3.1. Linear Regression with Lasso
We applied linear regression with a Lasso (Least Absolute Shrinkage and Selection Operator) penalty. The model structure is
where and are intercept and coefficients to be estimated and is the error term. Then, estimation using least squares error with Lasso is given by the optimisation problem on a training dataset of N observations:
where is a tuning parameter controlling the size of regularisation. Regression with Lasso will tend to shrink coefficient estimates to zero and hence is a form of variable selection (Friedman et al. 2010). The value of is chosen using K-fold cross validation. For this project, the R packages “lars” (Hastie and Efron 2013) and “glmnet” (Friedman et al. 2010) were used to estimate linear regression with Lasso.
3.2. Multivariate Beta Regression
The problem with linear regression is that it does not take account of the particular distribution of RR, which is between 0 and 1. The beta distribution, with two shape parameters and , allows us to model RR in the open interval :
where , > 0 are the shape parameters and is the Gamma function. The beta distribution is reparameterised by mean and precision parameters, denoting by and , respectively, following Ferrari and Cribari-Neto (2004), since this parameterisation meaningfully express the expected value and variance:
The reparameterised beta distribution is then
with and . Figure 3a demonstrates three examples of the beta distribution with fixed and different . The variance is maximised at . Figure 3b demonstrates another three examples of beta distribution with fixed and different .
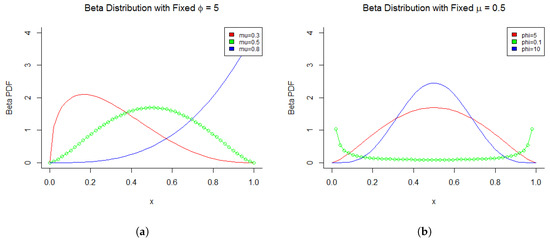
Figure 3.
Beta distribution. (a) Beta Distribution with Fixed ; (b) Beta Distribution with Fixed .
The precision parameter is negatively correlated with , given a fixed . Furthermore, the variance of Y is a function of , which enables the regression to model heteroskedasticity. RR is modelled as ∼ B(,) for for sample size N. The multivariate beta regression model (Cribari-Neto and Zeileis 2010) is defined as:
where is a vector of parameters which needs to be estimated corresponding to predictor variables X and is a vector of parameters which needs to be estimated corresponding to predictor variables W.
The predictor variables in W may be the same as in X, or a subset, or contain different variables. For this study, W will have a subset of predictor variables determined using stepwise variable selection. The link function ensures that and . We applied Logit and Log link function to and , respectively:
With this multivariate beta regression model, and can be estimated by maximum likelihood estimation, where the log-likelihood function is
By substituting and into Equation (8), the log-likelihood is obtained as a function of and . The parameters can be estimated using Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton method, which is considered to be the most appropriate method (Mittelhammer et al. 2000; Nocedal and Wright 1999).
3.3. Inflated Beta Regression
The disadvantage of beta regression is that it does not include the boundary values 0 or 1. Therefore, a modification is required before fitting the model. To better represent RR on the boundaries 0 and 1, Calabrese (2012) suggested considering RR as a mixture of Bernoulli random variables for the boundary 0 and 1, and a Beta random variable for the open interval (0, 1). The distribution for this inflated beta regression on [0, 1] is then defined as
for y ∈ [0, 1], , , and is the beta distribution defined in Section 3.2. Moreover, if RR (0, 1], i.e., it only inflates at one, as our data do, then the distribution is just
We used maximum likelihood estimation to estimate parameters for Bernoulli random variable and Beta random variables, parameterising the discrete part in the following way (Calabrese 2012):
The log-likelihood function is then
The continuous beta random variables can be parameterised in the same way as described in Section 3.2.
3.4. Beta Mixture Model combined with Logistic Regression
Examining the distribution of RR shown in Figure 1, it can be seen that the distribution between 0 and 1 is bimodal. For this reason, we consider a beta mixture model to deal with what appears to be two different groups of recoveries. We propose a two-stage model: beta mixture model combined with logistic regression. The beta mixture model allows us to model the multimodality of RR in the interval (0, 1). This is similar to the two-stage (decision tree) model used by Bellotti and Crook (2012), but with a beta mixture used for regression.
Firstly, RR is classified into ones and non-ones using logistic regression. Secondly, within the non-ones group, a mixture of beta distributions is used to model RR in the range (0, 1). In general, a mixture of beta distribution consists of m components where each component follows a parametric beta distribution. The prior probability of component j is denoted as , where . Let denote the jth component/cluster in the beta mixture model. The beta mixture model with m components is defined as:
where is the beta distribution corresponding to the jth component with separate parameter vectors and . The same link functions are used as in Section 3.2. The prior probabilities, , need to satisfy the following conditions:
The iterative Expectation-Maximisation (EM) algorithm was used to estimate the parameters of the beta mixture model, as described by (Leisch 2004). In particular, R package “flexmix” (Leisch 2004; Gruen and Leisch 2007, 2008) embedded in R package “betareg” (Cribari-Neto and Zeileis 2010; Gruen et al. 2012) was applied to estimate the model. Figure 4 illustrates the two-stage mixture model as a decision tree.
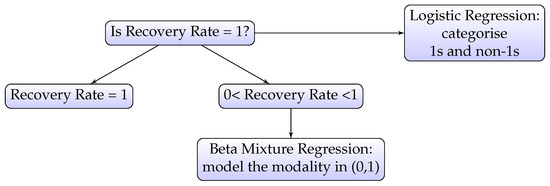
Figure 4.
Estimate the expected value of RR using two-stage decision tree model.
The choice of m in the model depends on the number of clusters expected in the data. Based on our analysis of the recoveries for the dataset we used, was used since this corresponded to the two modes we see in the RR distribution for RR < 1, as shown in Figure 1. If it is not clear how many clusters may exist, approaches based on AIC can be used.
Predictions Using the Beta Mixture Model
Given the beta mixture model, we need to predict the RR for new clients based on their information, i.e., and . Figure 5 shows a flowchart explaining how to calculate the estimated RR from the beta mixture model. This gives an expected value of RR y conditional on the cluster . Therefore, we need to first identify which cluster the new observation belongs to. Even though the R package “betareg” (Cribari-Neto and Zeileis 2010; Gruen et al. 2012) can compute the conditional expectation for us, it does not identify which cluster the new points should be assigned to. Therefore, we propose a method to do this. In general, there are two feasible approaches to assign a new observation to :
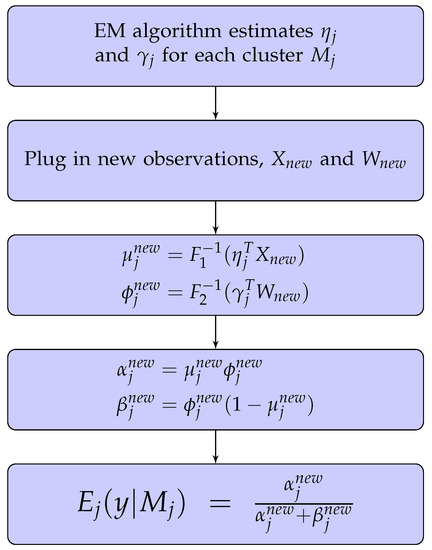
Figure 5.
Prediction of RR conditional on each cluster .
- Assign the new observation to the cluster that achieves the highest log-likelihood. This is a hard clustering approach, which assigns the observation to exactly one cluster (Fraley and Raftery. 2002).
- Assign the new observation to each cluster j with probability . This is a soft clustering approach, which assigns the observation to a percentage weighted cluster (Leisch 2004).
Decomposing the expected value of y using the Law of Total Expectation, we get
where is calculated from the beta mixture model prediction (refer to Figure 5). We can replace where , to get
where is the prior probability of belonging to cluster . The density is estimated using kernel density estimation,
where is the Gaussian kernel (Azzalini and Menardi 2014) and d is the number of dimensions in data x. In addition, may be high-dimensional, which makes the kernel density estimation computationally expensive. As a remedy, we applied Principal Component Analysis (PCA) to reduce the dimension of , and then kernel density estimation was performed in the reduced dimension space.
Approach 1: Maximum log-likelihood.
Given a new observation , choose j that maximises the density:
which is computed using the log-likelihood function. If the objective function is maximised with respect to Cluster , then set
and hence, from Equation (12), the expected value of y is given by .
Approach 2: Prior Probability.
Treat as a prior estimated using methods given in Table 1 and use in Equation (13) for soft clustering. By substituting given in Table 1 into Equation (13), we can compute for .

Table 1.
Determining in Approach 2.
After calculating for the interval (0, 1) using the beta mixture model, the boundary 1 needs to be taken into consideration using a logistic regression model. From the decision tree defined in Figure 4, the logistic regression can provide the estimates at the first leaf node: . Then, the overall expectation of RR y∈ (0, 1] is
where is the predicted RR from the beta mixture model using Approach 1 or 2.
4. Results
The linear model had an adjusted of 0.69, which was considerably higher than most models of RR (e.g., see Bellotti and Crook (2012); Loterman et al. (2012)), which could be explained by the richness of data, especially collections information. We expected that the linear regression model was misspecified, due to the range of the outcome variable and this is confirmed in the residual vs. fitted plot for the model and a Breusch-Pagan test for heteroscedasticity ().
For the beta mixture model, we used all variables for X, but variable selection for W based firstly on the output of stepwise selection using AIC in linear regression and then on a series of likelihood ratio tests. The result was the selection of four variables for W: pre-recovery rate, post balance, customer payment frequency and credit bureau score. Table 2 shows parameter estimates for and for the two clusters, along with coefficient estimates under standard beta regression in the interval (0, 1) for comparison.

Table 2.
and estimated by EM algorithm. M1 and M2 represent Clusters 1 and 2.
In Table 2, there are “NA” values for some of the p-values in the beta mixture model. This is because the estimation algorithm could not produce reliable standard errors in these cases. We can see that the significance of variables was diluted by the two clusters. For instance, credit bureau score was significant in the standard beta regression with a p-value of 0.0022, but in the beta mixture model, it was not significant for either of the clusters, taking a significance level of 5%. The direction of association of coefficient estimates in beta mixture model for both clusters were mostly consistent, where the estimates were significant (at 5% level), although magnitude of association differed. Pre-Recovery Rate for component was the only exception to this observation. The model also demonstrated some interesting significant associations between some variables and RR: taking insurance showed higher recoveries and having a record at the bad debt bureau was associated with lower recovery rates. In addition, the recoveries, pre-purchase, were positively correlated with future RR, although total number of calls to customer had a negative association, perhaps because these were difficult customers from whom to collect, hence requiring more intervention.
Following the procedure in Figure 5, the expected value of RR conditional on Cluster was calculated based on the parameters and estimated in Table 2. Since it was too time consuming to perform kernel density estimation on 29 variables, we reduced the dimension to six by employing PCA analysis, which greatly shortened the running time for two clusters’ density estimations. Nevertheless, it is inevitable that information is lost during the dimension reduction process, which may result in weaker estimates. Figure 6 shows histograms of expected value of RR conditional on each jth cluster for the test dataset. The shapes of the two clusters are similar, except Cluster 2 has more estimates in the range 0.2 to 0.6.
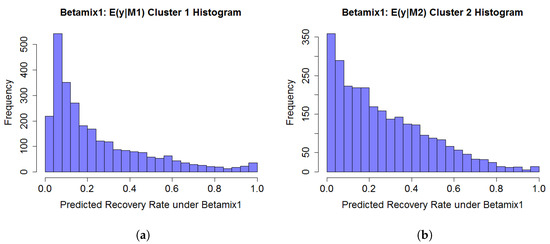
Figure 6.
based on the Test dataset, for the two clusters (). (a) ; (b) .
Figure 7 shows four histograms of predicted RR corresponding to the four different priors defined in Table 1, in contrast to the true RR. The predicted value of beta mixture model combined with logistic regression model was calculated by applying the formula derived in Equation (14). Models with the different priors performed in a similar way. Importantly, they were all able to model the bimodal nature of the RR. The figure shows that none of the models ewre good at predicting the extreme values of RR close to 0 or 1, but this naturally follows from the fact that these predictions are estimates of expected values of RR, through Equation (12), albeit conditional on predictor variables, and thus do not represent the extremes in the distribution well. Further detail can be seen in Figure 8, which shows predicted RR against true RR. The strong correlation between predicted and true RR is clear. However, it is noticeable that, when true RR was around 0.6, the model tended to under-estimate for some observations. This was because the model was not perfect at detecting observations in Cluster 2. This suggests future improvements to the model to enhance its capacity to predict the correct latent cluster.
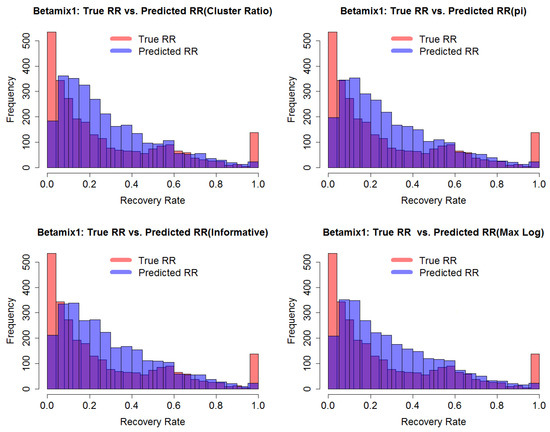
Figure 7.
Predicted RR on test data () using beta mixture with four different priors, combined with logistic regression.
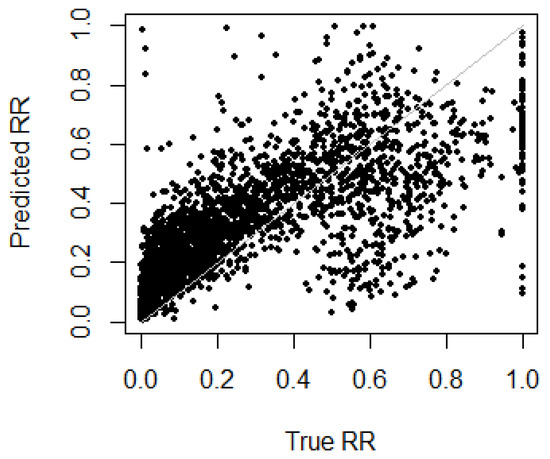
Figure 8.
Predicted RR against true RR on test data () using beta mixture with the indifferent prior, combined with logistic regression.
Model Performance
Predictive performance was measured using K-fold cross validation with three performance measures popular in the literature on RR estimation: mean squared error (MSE), mean absolute error (MAE) and mean aggregate absolute error (MAAE). Since the sample size (8237) was relatively large and model estimation time was long, was chosen. Let n be the sample size. Then,
MAAE is the MAE at segment level (Thomas and Bijak 2015) and defined here as
where V is the number of segments expressed as disjoint index sets . The segments could express different characteristics, e.g., risk bands. However, for this study, each segment was a different random sample from the test data with approximately the same sample size and jointly exhaustive. We used since this gave a balance of number of segments approximately equal to number of observations in each segment. MSE, MAE and MAAE are all penalty measures, thus the smaller the value, the better the model. Since the RR is a financial ratio between 0 and 1, the MAE can reflect the size of the error in a more intuitive and direct way. If one is interested in the segment portfolio level, then the MAAE should be used.
All models were trained on the same partitions of data into cross validation folds, to avoid bias being introduced due to different samples. Table 3 shows the results. There was little difference between results for the various linear regressions, with or without variable selection or Lasso penalty, in terms of predictive performance. The last linear model, “excluding Dataset 2”, was built without predictor variables from Dataset 2. This showed noticeably worse performance than the other linear models, especially for MAE, which demonstrates that including past recoveries data (i.e., Dataset 2) improved performance. The standard beta regression model, with and without zero-inflation, performed much worse than linear regression, but the beta mixture model with logistic regression gave the best performance on all three measures. The different priors gave slightly different performances but are not very much different, although Approach 1 method for selecting cluster assignment (max log-likelihood) was slightly worse than Approach 2, soft clustering methods.

Table 3.
Predictive results using three-fold cross validation.
5. Conclusions
Linear regression, beta regression, inflated beta regression, and a beta mixture model combined with logistic regression were applied to model the recovery rate of non-performing loans. The models’ predictive performances were measured using mean squared error, mean absolute error and mean aggregate absolute error under three-fold cross validation. To produce predictions from the beta mixture model, methods of hard and soft clustering were developed and the soft clustering approaches gave marginally better predictive performance. Theoretically, the proposed model, beta mixture model combined with logistic regression model, should be a suitable model to predict recovery rate for this data since it allows us to model the multimodality in the dataset and takes extra consideration of the boundary value. Indeed, we found that it achieved the best results amongst the models. Stepwise linear regression also achieved relatively good performance; however, the normality and homoscedasticity assumptions did not hold. In our experiments, we also found that inclusion of previous collections data boosted predictive performance.
We believe the beta mixture model is useful for modelling RR because it is explaining different servicing strategies. In the case of our study, the cluster with mode around 0.55 is likely expressing those loans for which the debt servicer has agreed with the borrower to repay just a proportion of the outstanding debt. There may be servicing strategies in other bad debt portfolios that could be discovered using a similar mixture model or clustering approach. We developed a technique to predict the correct latent cluster for new observations and this works well. However, results suggest that further work to refine this aspect of the use of the model could yield improved performance.
Author Contributions
Conceptualisation, H.Y. and T.B.; methodology, H.Y. and T.B.; validation, T.B.; investigation and statistical modelling, H.Y.; data analysis, H.Y.; writing—original draft preparation, H.Y..; writing—review and editing, T.B.; and supervision, T.B.
Funding
This research received no external funding.
Acknowledgments
We wish to thank the anonymous debt collection company for use of their data and their expertise, which was essential to understand the meaning and context of the data. We would also like to thank Tommaso Pappagallo who did preliminary data analysis as part of his MSci project, which was useful in taking this project work forward.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IRB | Internal ratings based |
| RR | Recovery rate |
| LGD | Loss given default |
| PD | Probability of default |
| EAD | Exposure at default |
| EM | Expectation-Maximisation (algorithm) |
| MSE | Mean square error |
| MAE | Mean absolute error |
| MAAE | Mean absolute aggregate error |
Appendix A

Table A1.
Descriptive statistics. . For numeric variables: min, mean (standard deviation), max. For factors, frequency (%age) for each level. All predictive data is collected prior to servicing.
Table A1.
Descriptive statistics. . For numeric variables: min, mean (standard deviation), max. For factors, frequency (%age) for each level. All predictive data is collected prior to servicing.
| Variable | Type | Description | Statistics |
|---|---|---|---|
| RR post | numeric | Recovery rate (outcome variable) | 0.000508, 0.280 (0.283), 1 |
| Product | factor | Type of loan | C:7468 (90.7%), R:769 (9.3%) |
| Principal | numeric | Original loan amount | 0, 3120 (2330), 15000 |
| Interest | numeric | Interest payments | 0, 551 (439), 3380 |
| Insurance | numeric | Insurance fees | 0, 42 (84.6), 953 |
| Late charges | numeric | Late charge fees | 0, 269 (109), 1470 |
| Overlimit fees | numeric | Over credit limit fees | 0, 13.3 (24.6), 315 |
| Creditlimit | numeric | Credit limit | 0, 4560 (2660), 13800 |
| Sex | factor | Sex | F:3196 (38.8%), M:5041 (61.2%) |
| Married | factor | Marriage status | 0:1201 (14.6%), D:518 (6.3%), M:3929 (47.7%), O:217 (2.6%), S:2230 (27.1%), W:142 (1.7%) |
| Age | numeric | Age | 1, 48.7 (11.1), 87 |
| DelphiScore | integer | Credit bureau score | 0, 298 (138), 443 |
| Bureau Sub 1 | factor | Loan is in the servicer’s bureau (1 = True) | 0: 1520 (18.5%), 1: 6717 (81.5%) |
| CustPaymentFreq | integer | Customer repayment frequency | 1, 7.56 (5.59), 29 |
| Post Balance | numeric | Exposure amount at start of servicing | 0, 3130 (2630), 15900 |
| Total paid amount | numeric | Total net paid amount | −275, 1200 (1100), 11200 |
| Total calls | numeric | Total number of calls | 0, 104 (106), 911 |
| Total contacts | numeric | Total number of contacts (except calls) | 0, 28.5 (26.5), 196 |
| Bankreport Freq | numeric | Bank reporting frequency | 0, 11.6 (7.92), 26 |
| Pre recovery rate | numeric | Recovery rate | −0.130, 0.258 (0.217), 2.89 |
| Employer | factor | Employer known | EmployerProvided:8053 (97.8%), NoInfo:184 (2.2%) |
| Total number | integer | Total number of loan accounts | 0, 2.3 (2.43), 68 |
References
- Azzalini, Adelchi, and Giovanna Menardi. 2014. Clustering via nonparametric density estimation: The R package pdfCluster. Journal of Statistical Software 57: 1–26. [Google Scholar] [CrossRef]
- Bank for International Settlements. 2001. The Internal Ratings-based Approach. Basel: Bank for International Settlements. [Google Scholar]
- Bellotti, Tony, and Jonathan Crook. 2012. Loss given default models incorporating macroeconomic variables for credit cards. International Journal of Forecasting 28: 171–82. [Google Scholar] [CrossRef]
- Calabrese, Raffaella. 2012. Predicting bank loan recovery rates with a mixed continuous-discrete model. Applied Stochastic Models in Business and Industry 30: 99–114. [Google Scholar] [CrossRef]
- Cribari-Neto, Francisco, and Achim Zeileis. 2010. Beta regression in R. Journal of Statistical Software 34: 1–24. [Google Scholar] [CrossRef]
- Ferrari, Silvia, and Francisco Cribari-Neto. 2004. Beta regression for modelling rates and proportions. Journal of Applied Statistics 31: 799–815. [Google Scholar] [CrossRef]
- Fraley, Chris, and Adrian E Raftery. 2002. Model-based clustering, discriminant analysis, and density estimation. Journal of the American Statistical Association 97: 611–31. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2010. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33: 1–22. [Google Scholar] [CrossRef] [PubMed]
- Gruen, Bettina, Ioannis Kosmidis, and Achim Zeileis. 2012. Extended beta regression in R: Shaken, stirred, mixed, and partitioned. Journal of Statistical Software 48: 1–25. [Google Scholar] [CrossRef]
- Gruen, Bettina, and Friedrich Leisch. 2007. Fitting finite mixtures of generalized linear regressions in R. Computational Statistics & Data Analysis 51: 5247–52. [Google Scholar]
- Gruen, Bettina, and Friedrich Leisch. 2008. Flexmix version 2: Finite mixtures with concomitant variables and varying and constant parameters. Journal of Statistical Software 28: 1–35. [Google Scholar] [CrossRef]
- Hastie, Trevor, and Brad Efron. 2013. lars: Least Angle Regression, Lasso and Forward Stagewise, R package version 1.2; Available online: https://cran.r-project.org/web/packages/lars/lars.pdf (accessed on 18 February 2019).
- Ji, Yuan, Chunlei Wu, Ping Liu, Jing Wang, and Kevin R. Coombes. 2005. Applications of beta-mixture models in bioinformatics. Bioinformatics 21: 2118–22. [Google Scholar] [CrossRef] [PubMed]
- Laurila, Kirsti, Bodil Oster, Claus L. Andersen, Philippe Lamy, Torben Orntoft, Olli Yli-Harja, and Carsten Wiuf. 2011. A beta-mixture model for dimensionality reduction, sample classification and analysis. BMC Bioinformatics 12: 215. [Google Scholar] [CrossRef] [PubMed]
- Leisch, Friedrich. 2004. Flexmix: A general framework for finite mixture models and latent class regression in R. Journal of Statistical Software 11: 1–38. [Google Scholar] [CrossRef]
- Loterman, Gert, Iain Brown, David Martens, Christophe Mues, and Bart Baesens. 2012. Benchmarking regression algorithms for loss given default modeling. International Journal of Forecasting 28: 161–70. [Google Scholar] [CrossRef]
- Mittelhammer, Ron C., George Judge, and Douglas Miller. 2000. Econometric Foundations, 1st ed.Cambridge: Cambridge University Press. [Google Scholar]
- Moustafa, Nour, Gideon Creech, and Jill Slay. 2018. Anomaly Detection System using Beta Mixture Models and Outlier Detection. In Progress in Computing, Analytics and Networking. Advances in Intelligent Systems and Computing. Edited by Prasant Kumar Pattnaik, Siddharth Swarup Rautaray, Himansu Das and Janmenjoy Nayak. Singapore: Springer, vol. 710. [Google Scholar] [CrossRef]
- Nocedal, Jorge, and Stephen J. Wright. 1999. Numerical Optimization, 1st ed.Berlin: Springer. [Google Scholar]
- Papke, Leslie, and Jeffrey Wooldridge. Econometric methods for fractional response variables with an application to 401(k) plan participation rates. Journal of Applied Econometrics 11: 619–32. [CrossRef]
- Qi, Min, and Xinlei Zhao. 2011. Comparison of modeling methods for loss given default. Journal of Banking & Finance 35: 2842–55. [Google Scholar]
- Thomas, Lyn, and Katarzyna Bijak. 2015. Impact of Segmentation on the Performance Measures of LGD Models. Available online: https://crc.business-school.ed.ac.uk/wp-content/uploads/sites/55/2017/02/Impact-of-Segmentation-on-the-Performance-Measures-of-LGD-Models-Lyn-Thomas-and-Katarzyna-Bijak.pdf (accessed on 18 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).