Abstract
Policymakers in developing and emerging countries are facing higher risk that is related to natural disasters in comparison to developed ones because of persistent problem of supply-side bottleneck for disaster insurance. Additionally, lower insurance consumption, higher disaster risk, and high income elasticity of insurance demand have worsened the loss consequences of natural disaster in these markets. In this context, current study for the first time argues that the supply side bottleneck problem has its origin in peculiar pattern of disaster consumption owing to memory cues. The study finds that relatively higher frequency of natural disasters acts as a negative memory cue and positively impacts insurance consumption. On the other hand, a relatively lower frequency of natural disasters adversely impacts insurance consumption in the background of variation in risk aversion behavior. For this purpose, current study has based its work on Mullainathan (2002), which builds its argument around memory cues.
1. Introduction
The scholars on the subject of climate change have predicted that 21st century will be characterized by more severe losses in cities than the rural areas due to increasing proximity of dwellings and irreversible migration towards cities (Jha et al. 2012; Pelling 2012). On the similar lines, United Nations Conference on Trade and Development (UNCTAD) has stated in paragraph 55 of Doha Mandate—“developing countries need, inter alia, support to develop capacities that would enable greater use of catastrophic insurance risk coverage.”
Added to it, globally over 1.7 million are killed, and 5.1 billion people are affected from 1991 to 2014 (Centre for Research on the Epidemiology of Disasters 2015). These constant warnings over the future repercussions of natural disasters losses have been reinforcing the need to search insurance solutions especially in developing & emerging countries (Outreville 1990; Nell and Richter 2004; Swiss Reinsurance Company 2017). The recent pattern of natural disaster losses, and occurrences has intensified this discussion in industry as well as in academic domain. For instance, Munich Reinsurance Company Report (2007) estimated that the average economic losses due to natural disasters in relation to the national income are twice as high as in developing countries when compared to the losses in developed countries. Linnerooth-Bayer et al. (2009) found that over 95 percent of deaths and about US$ 100 billion per annum losses occurred in developing countries only.
The existing literature focusing on disaster insurance in developing and emerging countries has covered merely few aspects, such as the post disaster government policies, agriculture insurance, and micro insurance (Linnerooth-Bayer et al. 2009; Krishna 2005; Sawada and Takasaki 2017; Fusco et al. 2018). The reason for having such a narrow academic contribution on this subject in the context of developing and emerging countries can be attributed to policy orientation in these countries. The policymakers and firms in most of the developing and emerging countries have held the view that high-risk premium and low affordability creates the problem of supply side bottle-neck. Whereas, the recent pattern on income, education, and urbanization in these countries contradicts the widely held view of policymakers and firms on underdeveloped disaster insurance markets. Additionally, theoretical arguments on risk aversion behavior provide us sufficient backing to believe increased consumption of disaster insurance products in the background of rising magnitude and frequency of natural disasters in developing and emerging countries. Nonetheless, the supply side bottleneck problem still persists for disaster insurance covers in these countries. Therefore, there still remains a gap that this study aims to address.
In this context, the current study argues that problem of supply side bottleneck is an outcome of cyclic pattern exists in occurrences of natural disaster. The pattern of natural disaster acts memory cues, which in turn increases/decreases the tendency of people to protect themselves against low probability severe nature risks (Mullainathan 2002).
Thus, the current study is extending the work of two existing studies. The first study is Kunreuther et al. (1978) who argue that property owners’ more likely buy disaster insurance if their homes have been damaged in the recent past. The second one is Bjerge and Trifkovic (2018) who have found that the past rainfall has positive impact on demand of index link weather insurance in India. Despite, partially similar findings, these studies have provided little guidance to firms and policymakers on which specific variable they should focus for improving disaster insurance supply. The current study has uniquely tested the frequency of natural disasters and found that the pattern of these frequencies is major source of supply side problem in disaster insurance markets in developing and emerging markets.
The remaining paper is organized as follows. Section 2 surveyed the past literature on the subject in terms of its contribution and the gap. Section 3 provides details of the theoretical framework used in the current study. Section 4 discusses the data and estimation methods. Section 5 discusses the estimation results. Section 6 is about conclusion, limitation, and future research direction.
2. Literature Review
The previously available literature on the subject, in the context of developing countries has focused mainly on weather insurance demand, crop insurance, government policies, and economic vulnerability of population living in rural and coastal areas (Mirza 2003; Toya and Skidmore 2007; Ghesquiere and Mahul 2007; Levine et al. 2000; Liu and Neilson 2006; Linnerooth-Bayer et al. 2009; Elango and Jones 2011; Hellin et al. 2017; Sawada and Takasaki 2017; Bjerge and Trifkovic 2018; Yuzva et al. 2018; Klomp and Hoogezand 2018). In the context, Linnerooth-Bayer et al. (2009) have provided a comprehensive discussion over the need of disaster insurance markets in developing countries. Mirza (2003) has focused on model development for risk capacities in developing countries. Toya and Skidmore (2007) have presented comparative analysis. They find that precautionary measures for disaster risk are less prevalent in the countries that have higher educational levels, more open economies, sound financial systems, and smaller governments. Ghesquiere and Mahul (2007) show that sovereign insurance should only focus on short term liquidity. Whereas, Hellin et al. (2017) have focused on bundling of weather insurance products with agriculture finance, and agriculture inputs to expand the insurance consumption. Elango and Jones (2011) have focused on the factors that affect insurance demand. In this context, although Bjerge and Trifkovic (2018) have found that the past rainfall has positive impact on the demand of index link weather insurance in India. But, Yuzva et al. (2018) have shown that due to basis risk, the demand for index link weather insurance remains low in low income group countries. Klomp and Hoogezand (2018) have studied the impact of natural disasters on the agriculture protection and found significant positive causal relation which again supports earlier research findings. Sawada and Takasaki (2017) explained the complimentary nature of three actors namely, government, insurance markets, and local communities.
However, extant literature in the context of developed countries on disaster insurance has covered broad spectrum of variables in empirical research framework, such as climate change, economic impact of disaster losses, charity, and vulnerability of people to natural disasters risk, compulsory insurance, and infrastructure deficiencies charity hazard (post disaster aid, low interest loans, and tax exemption during the rehabilitation and restoration), income, risk perception, price elasticity of flood insurance, education, etc. (Anderson 1974; Kunreuther et al. 1978; Kunreuther 1984; Lewis and Nickerson 1989; Kunreuther 1996; Levmore 1996; Pasterick 1998; Browne and Hoyt 2000; Kriesel and Landry 2004; Lai and Hsieh 2007; Pielke et al. 2008; Barthel and Neumayer 2012; Pešta and Okhrin 2014; Kousky et al. 2018; Luke et al. 2018).
Therefore, on the one hand, the current study is trying to find the type of insurance solution in general. On other hand, it is making an effort to find a solution for the supply-side problem that persists in developing and emerging countries. Therefore, this paper fills crucial gap in existing literature.
3. Theoretical Framework
The theoretical framework for the current study has been taken from two groups of theories, namely risk aversion and memory cues (Kahneman and Tversky 1979; Tversky and Kahneman 1992; Mullainathan 2002). We are using these theories for the first time to study insurance solution against natural disasters.
The earlier literature in the domain of natural disaster insurance consumption has majorly focused on the theoretical framework of the Samaritan’s Dilemma which says that charity has dual effect. In some context, it can improve situation while in other context, it can worsen some situations. The argument of this theory is that outcome of charity depends upon the way people use it and not on the charity itself (Buchanan 1975; Raschky and Weck-Hannemann 2007). The some of the reasons for such theoretical focus of earlier works can be attributed to the previous policy orientation of governments in these countries.
Different from the previous literature, the current study has used the frameworks of Tversky and Kahneman (1992) and Mullainathan (2002) because of the following reasons:
- (i)
- unlike previous empirical work in developing and emerging economies on natural disasters insurance, the current study is focusing on overall disaster insurance markets, which are barely studied in previous studies;
- (ii)
- the current study has drawn its logic from Prospect Theory (Tversky and Kahneman 1992). The argument of current study is based on weighing function and value functions (Kahneman and Tversky 1979). This framework is better than earlier deterministic theoretical arguments because insurance buying behavior is an outcome of perceived risk; and,
- (iii)
- both frequency and magnitude (losses) of natural disaster are cyclic in nature (see Figure 1 and Figure 2), which has provided authors an opportunity to test the impact of memory on risk aversion behavior (Mullainathan 2002).
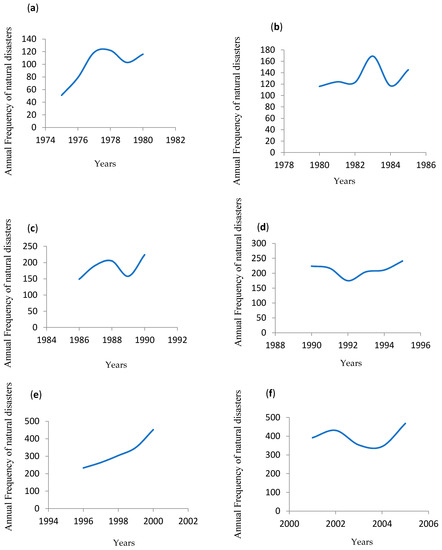
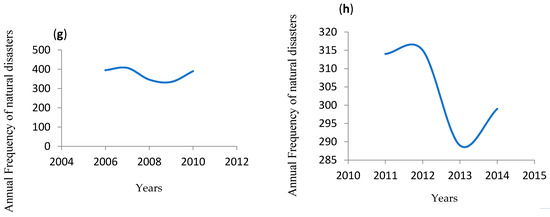 Figure 1. Average Cycle Period is shown in above figures (source: Author created based on International Disaster Database—Centre for Research on the Epidemiology of Disasters). Note: In the above figures; (a–h) authors show annual frequency of natural disasters on y axis. Years are plotted on X axis. In this figure author showed that average period for one complete cycle is nearly five years.
Figure 1. Average Cycle Period is shown in above figures (source: Author created based on International Disaster Database—Centre for Research on the Epidemiology of Disasters). Note: In the above figures; (a–h) authors show annual frequency of natural disasters on y axis. Years are plotted on X axis. In this figure author showed that average period for one complete cycle is nearly five years.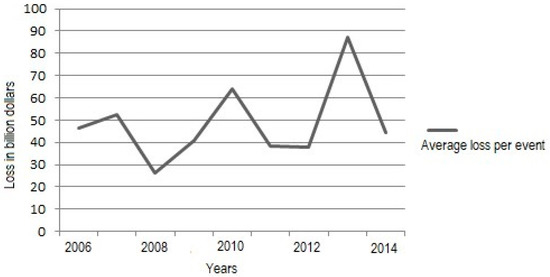 Figure 2. This Figure Shows that average loss per event is increasing every year. Note: In the Figure 2, Y axis shows per annum average loss, whereas, years are depicted on X axis (Source: Author created based on EM-Dat database).
Figure 2. This Figure Shows that average loss per event is increasing every year. Note: In the Figure 2, Y axis shows per annum average loss, whereas, years are depicted on X axis (Source: Author created based on EM-Dat database).
Hypothesis Development: In Cumulative Prospect Theory (Tversky and Kahneman 1992), risk aversion and risk seeking are determined by the joint effect of value function and capacity function. Whereas, earlier theories on risk aversion had used probabilities as they are given. This joint analysis provides authors an opportunity to explore disaster insurance in new light. In the present context, we are focusing on Reflection Effect discussed in the Cumulative Prospect Theory (Tversky and Kahneman 1992).
Let us assume that x represents the large loss with very low probability p, whereas y represents certainty equivalent, i.e., .
Also, v represents value function and represents decision weight function.
As per Cumulative Prospect Theory (Tversky and Kahneman 1992), if p is near zero (which is similar in case of natural disasters), we can write:
As v is convex for losses, we can write:
Cumulative Prospect Theory also suggests that people are more risk averse over small probability losses i.e., they prefer sure small losses over uncertain large losses (Reflection Effect). Therefore, we can write:
Though, the earlier theoretical evidences suggest that insurance purchase is often prevalent in mid-range risk probabilities but, later on Cumulative Prospect Theory presented its argument that people tend to become more risk averse for the losses of low probabilities (Kunreuther et al. 1978; Slovic et al. 1977; Tversky and Kahneman 1992). Under this theoretical argument, we can support our hypothesis that people have greater tendency to buy low probability insurance (Tversky and Kahneman 1992). However, the argument of Cumulative Prospect Theory is not sufficient to study the context of disaster insurance consumption because in current study there is time lapse between the occurrences of natural disasters and insurance buying. Therefore, apart from the argument that is proposed in Equation (3), we need to incorporate the memory effect. To assimilate the role of memory, we tested the role of memory cues in the current study.
For this purpose, we have plotted the annual frequency of natural disasters on Y axis, and years on X axis in various sub parts of Figure 1. Similarly, we have also plotted annual average loss per disaster on Y axis, and years on X axis in Figure 2. The eight sub-parts of Figure 1 shows that there is a cyclic behavior in annual frequencies of natural disasters. Additionally, Figure 1 shows that average period of one complete cycle is converging to four to five years. In context of disaster insurance Kunreuther et al. (1978) and (MacDonald et al. 1987), argued in one of their qualitative findings that property owners are more likely buy disaster insurance if their homes have been damaged in the recent past by a disaster. Mullainathan (2002) argues that cues help people to recall certain events. In this context, the present study argues that frequency of extreme events acts as a memory cues that can increase/decrease disaster insurance consumption.
We know that cyclic trend has two components namely, mean and deviations depicted in Figure 3.
Figure 3.
Shows Components Extreme Events cycles. Note: Figure shows yearly frequency trend of disaster events in developing and emerging economies (Source: EM-Dat).
However, in our analysis, we have considered only vertical components because the current study is intended to focus on in insurance solutions, which is possible only if outcomes are applicable in short term i.e., few years. Based on the outcomes of various parts of Figure 1, we can conclude that one cycle completes on an average in range of four to five years.
where is total effect of memory cues (disaster frequency) of country i in year t.
and are the mean frequency and mean deviation of natural disaster for country i in year t. Whereas, represents noise and a, b, and c are constants. Nevertheless, we also know from our analysis in Figure 1 that average period of complete cycle is four to five years, and we have collected nine years data for each country. Therefore, we can only calculate mean of five years frequencies.
From Equations (3) and (4)
where E() = 0
Since here we are focusing on within the cycle c variation of frequencies, and in each year of one complete frequency cycle, the mean frequency will remain same.
Now, if = +ve, it will act as positive memory cue and increase the disaster insurance consumption. Whereas, if = −ve, acts as a negative cue and will reduce the disaster insurance consumption.
Therefore, we have proposed following hypotheses:
Hypothesis 1 (H1).
Ceteris Paribas, the mean deviation of frequency of natural disasters positively impacts premium density.
Hypothesis 1a (H1a).
Ceteris Paribas, relatively higher mean deviation of natural disaster acts as positive memory cue and positively impacts nonlife premium density.
Hypothesis 1b (H1b).
Ceteris Paribas, relatively lower mean deviation of natural disaster acts as negative memory cue and negatively impacts nonlife premium density.
4. Data and Methodology
Similar to previous literature in the domain of nonlife, the definition of property and casualty insurance (PCI) consumption that is used in this work is equal to the sum of the individual firm and household annual consumption. This macroeconomic industry consumption analysis is done assuming that, within the country, all of the individuals are homogeneous in comparison to those in other countries. We have tested two models with a two-different-proxy-variables (secondary education and tertiary education) for the same specification in order for the current work to more robust. For the present study, we have gathered data from sources like Em-Dat, World Bank and, Swiss Re. The total number of developing and emerging countries taken into the consideration for this study are 111. However, we could find the data on our study variables only for 88 countries for the period 2006 to 2014 (sample are listed in Table A1).
The definition and list of developing countries and emerging countries are taken from World Economic Outlook Report, April 2015. Total of nine years data starting from 2006 to 2014 has been taken into consideration for this work. This time frame is suitable for current work, because, during this period, the frequency of natural disasters has increased significantly in developing and emerging countries.
Control Variables: Our primary focus of this study is to empirically test the impact of relatively higher and lower frequencies of natural disasters on nonlife insurance consumption in order to understand the role of memory in changing risk aversion behavior. In this work, all of the other variables except for frequency of extreme events are taken as the control variables. Here, for the simplicity of current models, the study has used only three control variables. These control variables are common in all of the nonlife insurance studies in which the panel data estimation method is used (Esho et al. 2004; Kriesel and Landry 2004; Trinh et al. 2016). For per person income, the study has used per capita GDP in US $ at a constant price of 2010 (Trinh et al. 2016). The current study has proxied risk exposure with urbanization. To control the individual risk aversion, secondary and tertiary levels education are used.
In order to test the hypothesis, and, constructing the models, we have used panel data. The advantage of using panel data is that it controls country-specific and period-specific effects (Greene 2011), such as cyclic business fluctuations or difference in across the country culture, and risk management practices. Thus, panel data provides more consistent, reliable, and robust results. Additionally, panel data estimation is widely used in the domain of non-life insurance (Pešta and Okhrin 2014; Peštová and Pešta 2017).
Since, in panel studies of nonlife insurance consumption, the problem of endogeneity is prevalent. Therefore, we have used two techniques for estimation of this panel data study. The first technique is OLS with dynamic panel data, and the other one is GMM with lag term and difference method to examine the dynamic adjustments in the PCI consumption equation (Peštová and Pešta 2015; Peštová and Pešta 2017).
To deal with the non-stationarity issue, we have tested panel unit root test and found that four of the variables have a unit root. However, in our final form of study variable i.e., mean deviation from the average of five-year period (period of complete cycle), there is not a non-stationarity issue. Within the OLS panel data estimation, there are three types of estimation models, namely pooled effect, fixed effect, and random effects. To find out the most appropriate model among three, we have conducted the Wald Test as well as the Lagrange Multiplier (LM) test to check the relative efficiency of heterogeneous fixed and random effect estimation against the estimation of homogeneous pooled OLS. The values of LM chi-square, the Wald F-statistics, and Hausman specification test are summarized in Appendix B1. The test in most of the models found the computed F value and found it to be statistically significant at (one tailed). We infer from these results that the null hypothesis of zero correlation between the observable country specific effects and the explanatory variables in the model can be rejected. In this case, the fixed effect model can still derive consistent estimates but the random effect model cannot; therefore, we used a fixed effect model in the current study. For random effect study, data need be drawn from a large population (Baltagi and Li 1995).
The Specification of Model for Estimation Methods:
From (3) and (6)
Provided . Else, people will not buy disaster insurance cover.
Now if is nonlife insurance consumption against disaster, then we can write:
Here, the subscript i denotes the number of countries i = 1, 2, 3, …, 88; and subscript t denotes the years t = 1, 2, 3, …, 9 (our data interval is 2006–2014); denotes premium density; denotes country specific intercepts, , , , … and , … are country specific slopes parameters; and is the random error terms. is dependent variable i.e., premium density and, is lag dependent variable. are column vectors for other variables such as education, income, and urbanization.
Estimation Method: LSDV with the small time period (T < 30) produces at least 20% biased estimates (Judson and Owen 1999). Therefore, we used GMM system estimator.
Since in the simple OLS model with dynamic term, there is an issue of endogeneity as the same error term enters the equation for every observation in group i (Greene 2011, p. 308). Therefore, difference estimator method is the method that can address the issue.
This method uses first difference of Equation (8)
Moment generating condition (where s ≥ 2; t = 3, 4, 5, … T; ).
However, this method may also have biased and imprecise results in case the variance of permanent effects increases relative to the transitory shocks (Blundell and Bond 1999). Therefore, independent variables and country specific correlation is time invariant, results in additional moment conditions such that
where t = 3 and s = 1.
In this r, dependent variable is premium density = Total Premium (nonlife) consumed in country/Total population in country. control independent variables are GDP/capita, secondary education, tertiary education, and urbanization. main variable is mean deviation of disaster frequency with five years mean.
This additional condition along with difference estimator is known as a GMM system estimator and this provides better estimation results. The GMM dynamic system estimator is developed by Arellano and Bond (1991).
The consistency of GMM depends upon the number of assumptions, specifically the assumption of serial correlation in error terms and validity of instruments. Therefore, along with model results, diagnostic results have also been provided.
5. Result and Discussion
Table 1 and Table 2 provide panel data results. There are two regression models in each table. Table 1 has OLS estimation results. Whereas, Table 2 has GMM estimation results. We have used two proxies for the individual tendency of risk aversion used in earlier studies i.e., secondary enrollment and tertiary enrollment. However, we have not used a third widely used proxy i.e., uncertainty avoidance index. It is not included because more than one country has the same index value, and at the same time, there is only one value for all the years. This in turn would limit our ability to include lag independent variables. Additionally, it creates problem of singular matrix. Regression model 1 in Table 1 shows the dynamic panel results. In model 1, the lag term of premium density and GDP per capita at the 2010 constant price is significant at the 1% significance level. Other than these, no other control variable is found to be significant.

Table 1.
Determinant of property and casualty insurance (PCI) with frequency of extreme events as memory cues: panel data results (OLS).

Table 2.
Determinant of PCI with frequency of extreme events as memory cues: panel data results (GMM).
Similarly, in model 2 of Table 1, other than GDP at 2010 constant prices and lag term of premium density, no other term is found to be significant. The both the terms are significant at 1% level.
In our regression model 1, and 2, we have tested four terms i.e., level term and three lag terms of main variables of our hypothesis. In model 1, one-year lag term, and three years lag term of mean deviation of frequency are found significant at the 5% significance level. In model 2 of Table 1, we have found that one-year lag term and three years lag term of mean deviations of frequency variable are found to be significant at the 10% significance level.
In Table 2, GMM of two model outcomes are presented. In model 1 of Table 2, the lag term of premium density, and GDP at 2010 constant prices are found to be significant at the 10% significance level. Other than these, no other control variable is found to be significant. However, in terms of our main variable, there are certain different results in model 1. Except the level term of mean deviation frequency, one year, two year, and three-year lag terms are found to be significant at the 10%, 5%, and 10% significance levels. However, other than three-year lag term, other two terms are negative in sign.
In this table, the dependent variable is premium density = Total Premium (nonlife) consumed in country/Total population in country. Control Independent Variables are GDP/capita, secondary education, tertiary education, and urbanization. Main Variable is mean deviation of disaster frequency with five years mean.
In model 2 of Table 2, other than lag term of the dependent variable i.e., premium density and GDP, no other control variable is found to be significant. These two terms are found to be significant at the 1% significance level, which is higher than the significance level of model 2 in Table 1.
In terms of main variable level term all the lag terms are significant at 1% significance levels with similar signs.
In all these four models, neither primary nor secondary education is found significant. This may be due to relatively higher risk aversion tendency that is caused by natural disasters. Similarly, urbanization is also not found to be significant due to the fact that natural disasters impact rural and urban population alike.
Coming to the outcomes of our main hypothesis, except third year lag term, other lag terms are either not significant or significant with negative magnitude. Therefore, the current study failed to accept our first hypothesis directly. However, the study has further put the element of memory to test the hypotheses i.e., effect of memory. Having considered memory element, we found our hypothesis true in the current context. Here, every third year, lag term produces a positive impact on insurance consumption. Whereas, level term is producing a negative effect on the insurance consumption. The negative impact of level term indicates that year we are considering here level term has relatively lower frequency in comparison to previous years. Whereas, the positive impact of third year lag term shows that, in our study, three year back, average frequency of disaster events was higher than the previous years. This in turn provides an extension in the findings of risk aversion behavior. This study has proposed the similar impact of memory on risk aversion behavior at initial phase of current study. The current study has argued that positive memory cues positively impact risk aversion behavior, whereas relatively lower frequency acts as a deterrent to recall negative event and it adversely impacts insurance consumption. Both hypotheses are proved true in the context of developing and emerging countries.
6. Conclusions
In developing countries, there is low insurance consumption. However, the current study found that supply side bottleneck for disaster insurance consumption is not the outcome of overall low insurance consumption. The current study finds that supply side bottleneck has its origin in demand pattern. It further adds that, due to cyclic nature of demand pattern of disaster insurance, markets do not function well (see it in Figure 4). Figure 5 shows that at some point of time at t = 1 (we can assume that it is second period immediately following starting point, t = 0) if, there is demand and supply . Now, if a cyclic pattern exists, there may be two cases, namely relatively lower frequency and relatively high frequency. In the case that the disaster frequency is not relatively high, people will demand less. However, it is difficult for insurance firms to maintain same price. This happens due to the reduced diversification opportunities and uncertainty in the markets. Therefore, firms will increase price. This in turn reduces price elasticity of supply (shown in Figure 4 and Figure 5). Inappropriate increases in risk premium further puts down side pressure on disaster insurance demand (though, the consumer cannot observe reduced diversification opportunities for firms, but he can observe increased risk premium). Now, if at time t = 1, there is relatively higher frequency, demand will increase, but there are chances of demand being not reached up to the previous levels (t = 0) because of new price levels, i.e., < . In this way, in every cycle, risk premium will increase and demand will decrease. This vicious cycle will continue until the supply of disaster risk cover stops.
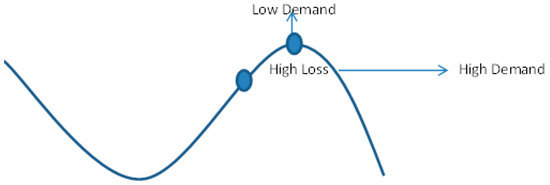
Figure 4.
Cycle of demand and supply.

Figure 5.
Vicious cycle of market failure.
In order to avoid the adverse repercussions of vicious cycle of disaster insurance demand, the firms should increase the period of disaster insurance policies from a one-year period to an average 3–5-year period. In this way, firms can have temporal diversification opportunities, which in turn resolve the problem of the limitation of diversification opportunities across the larger group. Policy makers can use the findings of current study in developing countercyclical policies for disaster insurance market. For instance, policy makers should give the subsidies and tax exemption in the years of relatively lower frequency of disaster risk. The study has also extended the theory of risk aversion behavior described by advances in prospect theory for lower probability higher magnitude risk by adding memory element. According to this, lower probability risk does not always increase the individual risk aversion tendency, rather it can vary within the lower probability risks. The study finds that people give more weight to those low probability risks that they can recall easily. Thus, risk aversion behavior depends upon the recalling capacity of an individual. The limitation of the current study lies in the economic setting that it has chosen. Future studies can be carried out in more specific geographical settings. For example, the similar studies can provide more refined results in the context of one country, specific economic, and strategic group of countries. Other than this, the current study has taken selected limited control variables, which in turn create limited applicability. Therefore, future research may study the context of culture, institution, and society.
Author Contributions
The current work is combined efforts of A.T., and A.P. The specific contribution is made in following manner, conceptualization A.T., and A.P.; methodology, A.T.; software, A.T., and A.P.; validation, A.T., and A.P.; formal analysis, A.T.; investigation, A.P.; resources, A.P.; data curation, A.T.; writing—original draft preparation, A.T.; writing—review and editing, A.P.; visualization, A.P.; supervision, A.P.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
List of developing and emerging economies.
Table A1.
List of developing and emerging economies.
| Albania | Ecuador | Mali | Russia |
| Algeria | Egypt | Mauritania | Rwanda |
| Angola | El Salvador | Mexico | Saudi Arabia |
| Argentina | Ethiopia | Moldova | Senegal |
| Azerbaijan | Gabon | Mongolia | Serbia Montenegro |
| Bahamas | Gambia | Montenegro | Sierra Leone |
| Bahrain | Georgia | Morocco | South Africa |
| Bangladesh | Ghana | Mozambique | Sri Lanka |
| Benin | Guatemala | Namibia | Syrian Arab Republic |
| Bolivia | Guinea | Nepal | Tanzania |
| Bosnia and Herzegovina | Honduras | Nicaragua | Thailand |
| Brazil | Hungary | Niger | Togo |
| Burkina Faso | India | Nigeria | Tunisia |
| Burundi | Iran | Oman | Turkey |
| Cambodia | Iraq | Pakistan | Uganda |
| Cameroon | Jordan | Panama | Ukraine |
| Central African Republic | Kazakhstan | Paraguay | United Arab Emirates |
| China | Kenya | Peru | Uzbekistan |
| Colombia | Lebanon | Philippines | Venezuela |
| Democratic Republic of the Congo | Libya | Poland | Viet Nam |
| Costa Rica | Malawi | Qatar | Zambia |
| Dominican Republic | Malaysia | Romania | Zimbabwe |

Table A2.
Data definitions.
Table A2.
Data definitions.
| Variable | Description | Source |
|---|---|---|
| PCI | Ratio of property casualty gross premium to population in US $ | Swiss Re |
| GDP/Capita | GDP per capita in constant 2010 US $ | World Bank |
| Urbanization | The portion of population living in urban areas | World Bank |
| Secondary Education | The portion of population enrolled in secondary education within prospective age group | World Bank |
| Tertiary Education | The portion of population enrolled in tertiary education within prospective age group | World Bank |
| Frequency | Annual frequency of natural disasters | EM-DAT |

Table A3.
Data sources.
Table A3.
Data sources.
| Data | Sources | Publishers |
|---|---|---|
| Premium Density | International Insurance Fact Book (2007–2017) | Axco Insurance Information Services/Swiss Re |
| GDP | World Bank national accounts data, and OECD National Accounts data files | The World Bank |
| Secondary Level Education | United Nations Educational, Scientific and Cultural Organization Statistical Year Book | UNESCO |
| Third Level Education | United Nation Educational, Scientific and Cultural Organization Statistical Year Book | UNESCO |
| Urbanization | World Tables | The World Bank |
| Frequency | EM-DAT | Centre For Research on the Epidemiology of Disaster |

Table A4.
Summary statistics.
Table A4.
Summary statistics.
| Measure | Premium Density | Per Capita GDP | Secondary Education | Tertiary Education | Urbanization | Annual Frequency (Natural Disaster) |
|---|---|---|---|---|---|---|
| Mean | 55.18266 | 5720.561 | 70.55974 | 1.058573 | 27.68619 | 6.222951 |
| Median | 23.73345 | 3264.450 | 79.33659 | 1.040420 | 25.79282 | 3.000000 |
| Maximum | 716.3261 | 96732.53 | 120.2947 | 6.315640 | 63.87144 | 64.00000 |
| Minimum | 0.000000 | 0.000000 | 10.73256 | 0.269630 | 3.021368 | 0.000000 |
| Std. Dev. | 79.35052 | 9424.676 | 27.05183 | 0.633586 | 13.94163 | 8.776246 |
| Observations | 305 | 305 | 305 | 305 | 305 | 305 |

Table A5.
Correlation table.
Table A5.
Correlation table.
| Variables | Per Capita GDP | Secondary Education | Tertiary Education | Urbanization | Annual Frequency |
|---|---|---|---|---|---|
| Per Capita GDP | 1 | ||||
| Secondary Education | 0.411056 | 1 | |||
| Tertiary Education | 0.865859 | 0.520748 | 1 | ||
| Urbanization | −0.098128 | −0.273754 | −0.054524 | 1 | |
| Annual Frequency | −0.065811 | 0.074825 | −0.070033 | −0.371366 | 1 |
Appendix B
Appendix B1

Table A6.
Diagnostic tests for Table 1.
Table A6.
Diagnostic tests for Table 1.
| Test | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Wald Test | (0.000) | (0.000) | Fixed Effect Model is superior to Pooled OLS |
| LM Test | (0.000) | (0.000) | Random Effect Model is superior to Pooled OLS |
| Hausman Test | (0.000) | (0.000) | Fixed Effect Model is superior to Random Effect Model |
| Jaraque Bera | JB = 2116.682 (0.000) | JB = 2449.586 (0.000) | Normality is rejected in error term |
| Ramsey’s Test | (0.131) | (0.213) | No, misspecification cannot be rejected |
Note: In brackets there are p-values.
Appendix B2
Let us assume that p is actual probability of any loss x.
Then insurance company will charge premium y = . where includes various administrative expenses. It is used in a specific way in above expression to keep the discussion simple.
From Cumulative Prospect Theory, we know p is very small probability,
From convexity of losses assumption and Equation (A1), we can write,
Again, we know that insurance sale can happen only when,
From Equations (A3) and (A4):
References
- Anderson, Dan R. 1974. The national flood insurance program. Problems and potential. Journal of Risk and Insurance 41: 579–99. [Google Scholar] [CrossRef]
- Arellano, Manuel, and Stephen Bond. 1991. Some Test of Specification for Panel Data: Monte Carlo Evidence and An Application to Employment Equations. Review of Economic Studies 58: 277–97. [Google Scholar] [CrossRef]
- Baltagi, Badi H., and Qi Li. 1995. Testing AR (1) against MA (1) disturbances in an error component model. Journal of Econometrics 68: 133–51. [Google Scholar] [CrossRef]
- Barthel, Fabian, and Eric Neumayer. 2012. A trend analysis of normalized insured damage from natural disasters. Climatic Change 113: 215–37. [Google Scholar] [CrossRef]
- Bjerge, Benedikte, and Neda Trifkovic. 2018. Extreme weather and demand for index insurance in rural India. European Review of Agricultural Economics 45: 397–431. [Google Scholar] [CrossRef]
- Blundell, Richard, and Stephen Bond. 1999. GMM estimation with persistent panel data: An application to production functions. Econometric Reviews 19: 321–40. [Google Scholar] [CrossRef]
- Browne, Mark J., and Robert E. Hoyt. 2000. The demand for flood insurance: Empirical evidence. Journal of Risk and Uncertainty 20: 291–306. [Google Scholar] [CrossRef]
- Buchanan, James M. 1975. The Samaritan’s Dilemma. In Altruism, Morality and Economic Theory. Edited by Edmund S. Phelps. New York: Russel Sage Foundation. [Google Scholar]
- Centre for Research on the Epidemiology of Disasters. 2015. Disasters in Numbers. Brussels: Centre for Research on the Epidemiology of Disasters, pp. 1–2. [Google Scholar]
- Elango, B., and James Jones. 2011. Drivers of insurance demand in emerging markets. Journal of Service Science Research 3: 185–204. [Google Scholar]
- Esho, Neil, Anatoly Kirievsky, Damian Ward, and Ralf Zurbruegg. 2004. Law and the determinants of property-casualty insurance. Journal of Risk and Insurance 71: 265–83. [Google Scholar] [CrossRef]
- Fusco, Giulio, Pier Paolo Miglietta, and Donatella Porrini. 2018. How Drought Affects Agricultural Insurance Policies: The Case of Italy. Journal of Sustainable Development 11: 1. [Google Scholar] [CrossRef]
- Ghesquiere, Francis, and Olivier Mahul. 2007. Sovereign natural disaster insurance for developing countries: A paradigm shift in catastrophe risk financing. Washington: The World Bank. [Google Scholar]
- Greene, William H. 2011. Econometric Analysis, 5th ed. New Delhi: Dorling Kindersley (India) Pvt. Ltd./licensees of Pearson Education in South Asia, pp. 283–93. [Google Scholar]
- Hellin, Jon, James W. Hansen, Alison Rose, and Melody Braun. 2017. Scaling up Agricultural Adaptation through Insurance: Bringing Together Insurance, Big Data and Agricultural Innovation. Wageningen: CGIAR Research Program on Climate Change, Agriculture and Food Security (CCAFS), CCAFS Policy Briefs 385. [Google Scholar]
- Jha, Abhas K., Robin Bloch, and Jessica Lamond. 2012. Cities and Flooding: A Guide to Integrated Urban Flood Risk Management for the 21st Century. World Bank © World Bank. License: CC BY 3.0 IGO. Available online: https://openknowledge.worldbank.org/handle/10986/2241 (accessed on 21 August 2018).
- Judson, Ruth A., and Ann L. Owen. 1999. Estimating dynamic panel data models: A guide for macroeconomists. Economics Letters 65: 9–15. [Google Scholar] [CrossRef]
- Liu, Liqun, and William S. Neilson. 2006. Endogenous private safety investment and the willingness to pay for mortality risk reductions. European Economic Review 50: 2074. [Google Scholar] [CrossRef]
- Levmore, Saul. 1996. Coalitions and Quakes: Disaster Relief and Its Prevention. Roundtable: University of Chicago Law School 3: 1–34. [Google Scholar]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 278. [Google Scholar] [CrossRef]
- Klomp, Jeroen, and Barry Hoogezand. 2018. Natural disasters and agricultural protection: A panel data analysis. World Development 104: 404–17. [Google Scholar] [CrossRef]
- Kousky, Carolyn, Erwann O. Michel-Kerjan, and Paul A. Raschky. 2018. Does federal disaster assistance crowd out flood insurance? Journal of Environmental Economics and Management 87: 150–64. [Google Scholar] [CrossRef]
- Kriesel, Warren, and Craig Landry. 2004. Participation in the National Flood Insurance Program: An empirical analysis for coastal properties. Journal of Risk and Insurance 71: 405–20. [Google Scholar] [CrossRef]
- Krishna, H. 2005. Insurance for Vulnerability Reduction: Oxfam’s Experience of Using Insurance as a Strategy for DISASTER Risk Reduction in Coastal Andhra Pradesh-South of India. Background Paper for World Bank Institute online training course for India, Financial Strategies for Managing the Economic Impacts of Natural Disasters. Washington, DC: The World Bank. [Google Scholar]
- Kunreuther, Howard. 1984. Causes of underinsurance against natural disasters. Geneva Papers on Risk and Insurance 9: 206–20. [Google Scholar] [CrossRef]
- Kunreuther, Howard. 1996. Mitigating disaster losses through insurance. Journal of Risk and Uncertainty 12: 171–87. [Google Scholar] [CrossRef]
- Kunreuther, Howard, R. Ginsberg, L. Miller, P. Sagi, P. Slovic, B. Borkan, and N. Katz. 1978. Disaster Insurance Protection: Public Policy Lessons. New York: Wiley. [Google Scholar]
- Lai, Li-Hua, and Hsiu-Yi Hsieh. 2007. Assessing the demand factors for residential earthquake insurance in Taiwan: Empirical evidence on spatial econometrics. Contemporary Management Research 3. [Google Scholar] [CrossRef]
- Levine, Ross, Norman Loayza, and Thorsten Beck. 2000. Financial intermediation and growth: Causality and causes. Journal of Monetary Economics 46: 31–77. [Google Scholar] [CrossRef]
- Lewis, Tracy, and David Nickerson. 1989. Self-insurance against natural disasters. Journal of Environmental Economics and Management 16: 209–23. [Google Scholar] [CrossRef]
- Linnerooth-Bayer, Joanne, Koko Warner, Christoph Bals, Peter Höppe, Ian Burton, Thomas Loster, and Armin Haas. 2009. Insurance, developing countries, and climate change. The Geneva Papers on Risk and Insurance-Issues and Practice 34: 381–400. [Google Scholar] [CrossRef]
- Luke, Adam, Brett F. Sanders, Kristen A. Goodrich, David L. Feldman, Danielle Boudreau, Ana Eguiarte, Kimberly Serrano, Abigail Reyes, Jochen E. Schubert, Amir AghaKouchak, and et al. 2018. Going beyond the flood insurance rate map: Insights from flood hazard map co-production. Natural Hazards and Earth System Sciences 18: 1097–120. [Google Scholar] [CrossRef]
- MacDonald, Don N., James C. Murdoch, and Harry L. White. 1987. Uncertain hazards, insurance, and consumer choice: Evidence from housing markets. Land Economics 63: 361–71. [Google Scholar] [CrossRef]
- Mirza, M. Monirul. 2003. Climate change and extreme weather events: Can developing countries adapt? Climate Policy 3: 233–48. [Google Scholar] [CrossRef]
- Mullainathan, Sendhil. 2002. A memory-based model of bounded rationality. The Quarterly Journal of Economics 117: 735–74. [Google Scholar] [CrossRef]
- Munich Reinsurance Company Report. 2007. Munich Re Group Annual Report. Munich: Munich Reinsurance Group, Geoscience Research Group, pp. 224–89. [Google Scholar]
- Nell, Martin, and Andreas Richter. 2004. Improving risk allocation through indexed cat bonds. The Geneva Papers on Risk and Insurance. Issues and Practice 29: 183–201. [Google Scholar] [CrossRef]
- Outreville, J. Francois. 1990. The economic significance of insurance markets in developing countries. Journal of Risk and Insurance 57: 487–98. [Google Scholar] [CrossRef]
- Pasterick, Edward T. 1998. The national flood insurance program. In Paying the Price: The Status and Role of Insurance Against Natural Disasters in the United States. Washington, DC: The National Academies Press, pp. 125–54. [Google Scholar]
- Pelling, Mark. 2012. The Vulnerability of Cities: Natural Disasters and Social Resilience. New York: Routledge. [Google Scholar]
- Pešta, Michal, and Ostap Okhrin. 2014. Conditional least squares and copulae in claims reserving for a single line of business. Insurance: Mathematics and Economics 56: 28–37. [Google Scholar] [CrossRef]
- Peštová, Barbora, and Michal Pešta. 2015. Testing structural changes in panel data with small fixed panel size and bootstrap. Metrika 78: 665–89. [Google Scholar] [CrossRef]
- Peštová, Barbora, and Michal Pešta. 2017. Change point estimation in panel data without boundary issue. Risks 5: 7. [Google Scholar] [CrossRef]
- Pielke, Roger A., Jr., Joel Gratz, Christopher W. Landsea, Douglas Collins, Mark A. Saunders, and Rade Musulin. 2008. Normalized hurricane damage in the United States: 1900–2005. Natural Hazards Review 9: 29–42. [Google Scholar] [CrossRef]
- Raschky, Paul A., and Hannelore Weck-Hannemann. 2007. Charity hazard—A real hazard to natural disaster insurance? Environmental Hazards 7: 321–29. [Google Scholar] [CrossRef]
- Sawada, Yasuyuki, and Yoshito Takasaki. 2017. Natural disaster, poverty, and development: An introduction. World Development 94: 2–15. [Google Scholar] [CrossRef]
- Slovic, Paul, Baruch Fischhoff, Sarah Lichtenstein, Bernard Corrigan, and Barbara Combs. 1977. Preference for insuring against probable small losses: Insurance implications. Journal of Risk and insurance 44: 237–58. [Google Scholar] [CrossRef]
- Swiss Reinsurance Company. 2017. Sigma, Natural Catastrophe, and Man-Made Disasters in 2016: A Year of Widespread Damage, No 2/2017. Zurich: Swiss Reinsurance Company. [Google Scholar]
- Toya, Hideki, and Mark Skidmore. 2007. Economic development and the impacts of natural disasters. Economics Letters 94: 20–25. [Google Scholar] [CrossRef]
- Trinh, Tam, Xuan Nguyen, and Pasquale Sgro. 2016. Determinants of non-life insurance expenditure in developed and developing countries: An empirical investigation. Applied Economics 48: 5639–53. [Google Scholar] [CrossRef]
- Tversky, Amos, and Daniel Kahneman. 1992. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty 5: 297–323. [Google Scholar] [CrossRef]
- Yuzva, Kristina, WJ Wouter Botzen, Jeroen Aerts, and Roy Brouwer. 2018. A global review of the impact of basis risk on the functioning of and demand for index insurance. International Journal of Disaster Risk Reduction 28: 845–53. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).