1. Introduction
We are interested in modeling interaction between utility-maximizing private actors (which for simplicity we call private banks or simply banks) and a central bank, which regulates borrowing activity via an interest rate. Private banks exchange (exogenous) cash flows, and borrow from the non-banking financial sector to invest in profitable but risky assets. This central bank can lower interest rate to stimulate financial activity by private actors, or increase this rate to cool this activity down. Sometimes, however, there are not many profitable investments. Then, the private actors do not borrow at all, while the central bank is not able to remedy this even by lowering the rate to zero; this is called the liquidity trap.
We mention the concept of
systemic risk, which can be informally described as the probability of a large number of banks defaulting or getting into financial trouble. We understand
default or
failure of a bank as its net worth (assets minus liabilities) going below a given threshold. We are interested in probability of this undesirable event; of the mechanism of such failure; and of the
financial contagion, when failure of a few banks leads to many more failures. We refer the reader to the handbook (
Fouque and Langsam 2013) containing many different approaches to systemic risk. Our work is inspired by the model introduced in (
Carmona et al. 2013) and also described in (
Carmona 2016, sct. 5.5).
If
is the wealth and
, authors in (
Carmona et al. 2013) model the banking system as a system of
N continuous-time stochastic processes
, with multidimensional Ornstein–Uhlenbeck dynamics. The stochastic differential equations are given by:
with i.i.d. (independent identically distributed) Brownian motions
, constants
, and
The constant
a is referred to as the
interbank flow rate. In (
Carmona et al. 2013), these mean-reverting drifts are generated by the decisions of banks to borrow money from one another. Their decisions are done by minimizing a certain cost functional, which measures, roughly speaking, the preference of a bank to borrow from other banks, as opposed to borrowing from the central bank. The authors discuss both the finite player solution and the mean-field limit of the problem in the context of systemic risk.
Remark 1. Apply Itô’s formula to rewrite Equation (1) in terms of(the actual net worth of the ith bank) instead of. Then, the interbank flows derived from Ornstein–Uhlenbeck-type termsdo not add up to 0. One can think that the remainder comes from (or to, depending on the sign) the real economy or non-banking financial sector. Nevertheless, the model in Equation (1) attracted a lot of attention because of its simplicity and analytical tractability. We further explore the individual decision-making of the private banks and extend the role of the central bank. Furthermore, we analyze how this decision-making affects the stability of the system. More specifically, we extend the model by assuming that each private bank invests in a risky portfolio of assets, borrows money from the non-banking financial sector to invest in this portfolio (with interest rate controlled by the central bank), pockets the profit, and pays back the interest. Private banks want to maximize the terminal logarithmic wealth:
by borrowing and investing in a portfolio of risky assets. For simplicity, we assume the portfolios of private banks are correlated geometric Brownian motions. The choice of logarithmic utility function allows us to solve the corresponding Hamilton–Jacobi–Bellman (HJB) equation explicitly. Logarithmic utility, as shown in (
Feldman 1992), corresponds to myopic decision-making; in other words, private actors are short-sighted.
Unlike (
Carmona et al. 2013), where the decision making of the central bank is not analyzed, in our model the central bank uses
interest rate as a monetary policy instrument (to govern the behavior of the private banks). This is a solution of the control problem solved by the central bank:
As we see later, the central bank is more risk-averse than private banks. Sometimes it needs to reduce overall risk by increasing the interest rate, which controls the overall size of the system, measured by
from Equation (
2). This is
not the average net worth of banks; this is the average of the logarithms of net worth. This measure is somewhat non-standard; however, it is more appropriate for our model, when dynamics in Equation (
1) is written in terms of logarithms
of net worth
. This measure is used in (
Carmona et al. 2013) and subsequent papers, so we feel justified in using it here. Similar to the problem in Equation (
3), we can solve Equation (
4) explicitly, because of the choice of exponential utility. (Sometimes it is called CARA: constant absolute risk aversion utility function.) For other choices of utility functions, it is probably impossible to solve these optimal control problems explicitly. Then, one could possibly try to use mean-field limits, as in (
Carmona et al. 2016;
Carmona and Lacker 2015;
Lacker 2016).
Remark 2. This setup resembles the principal–agent problem: the principal (now the central bank) allows private banks to borrow from the non-banking financial sector, and private banks (agents) maximize their expected logarithmic terminal utility (their contract).
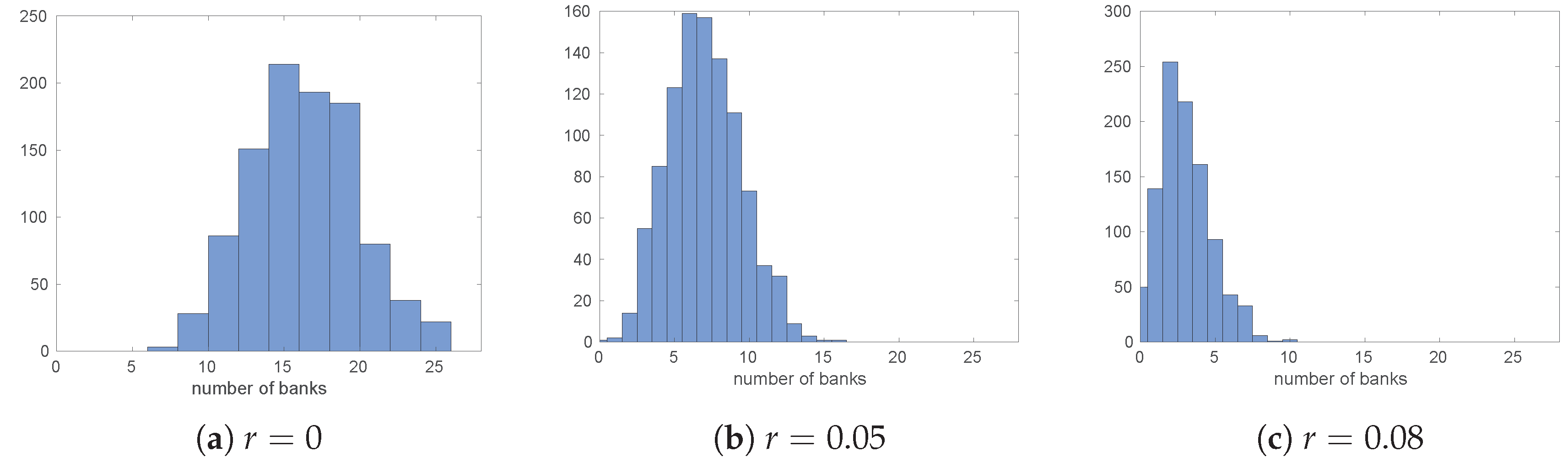
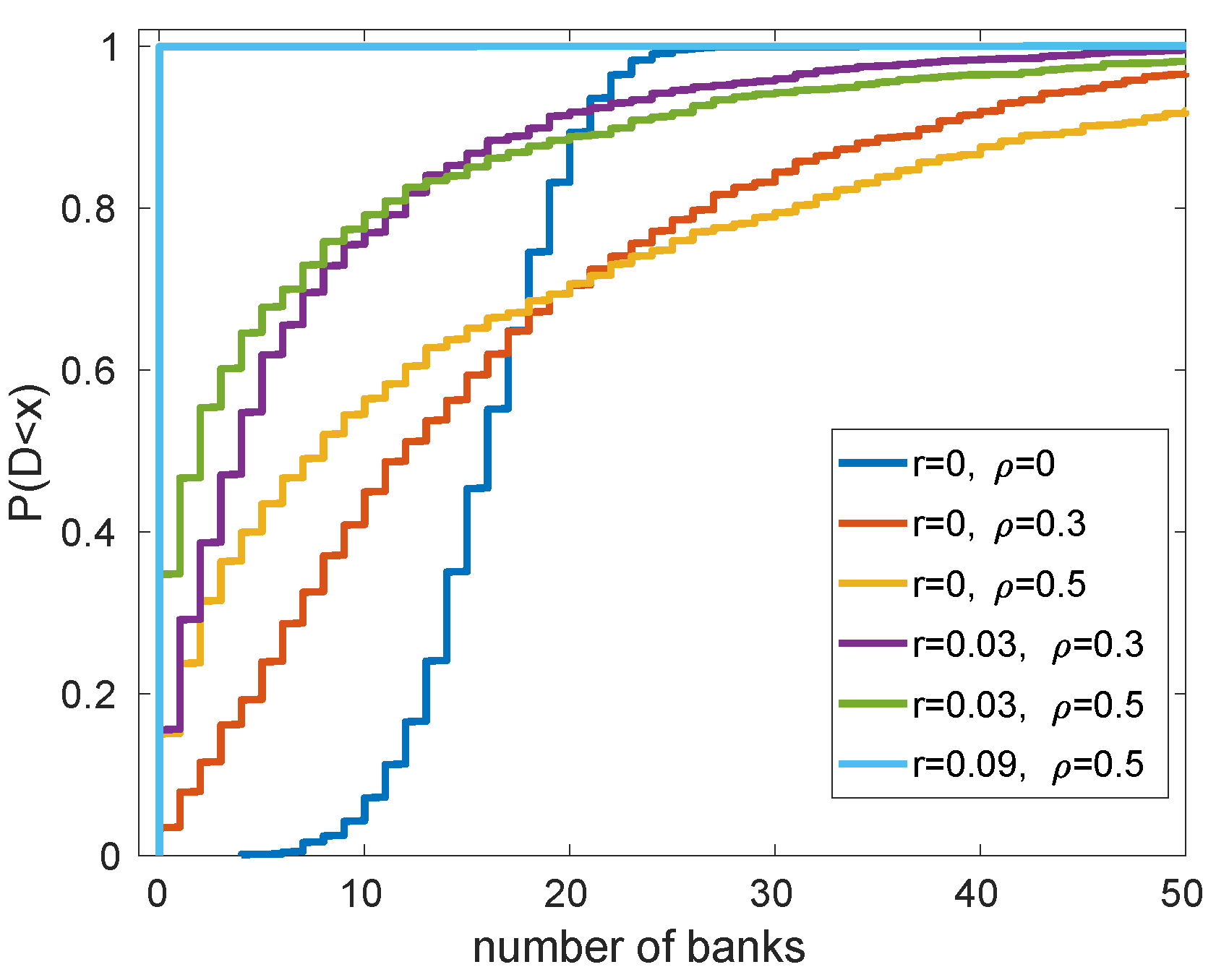
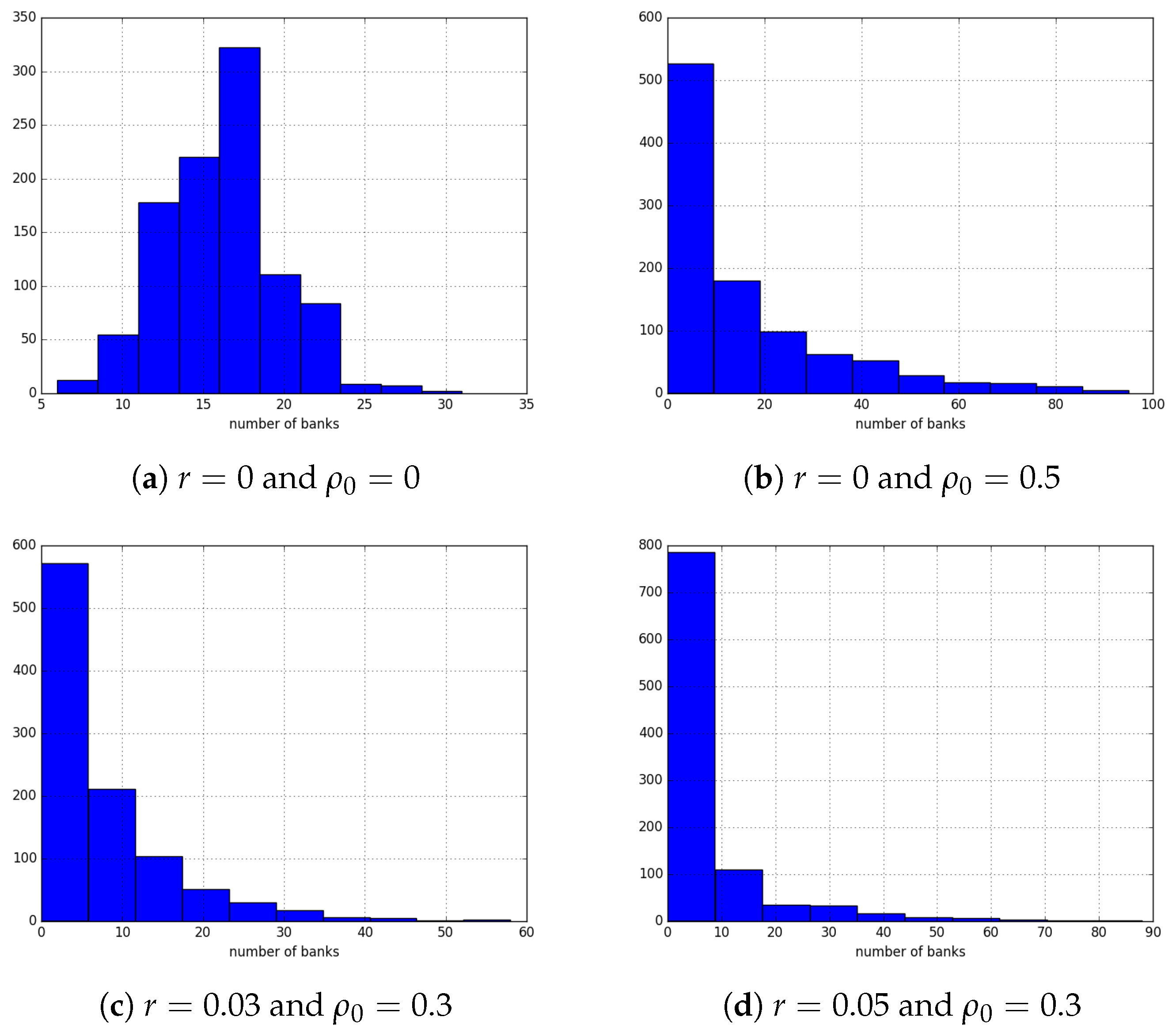
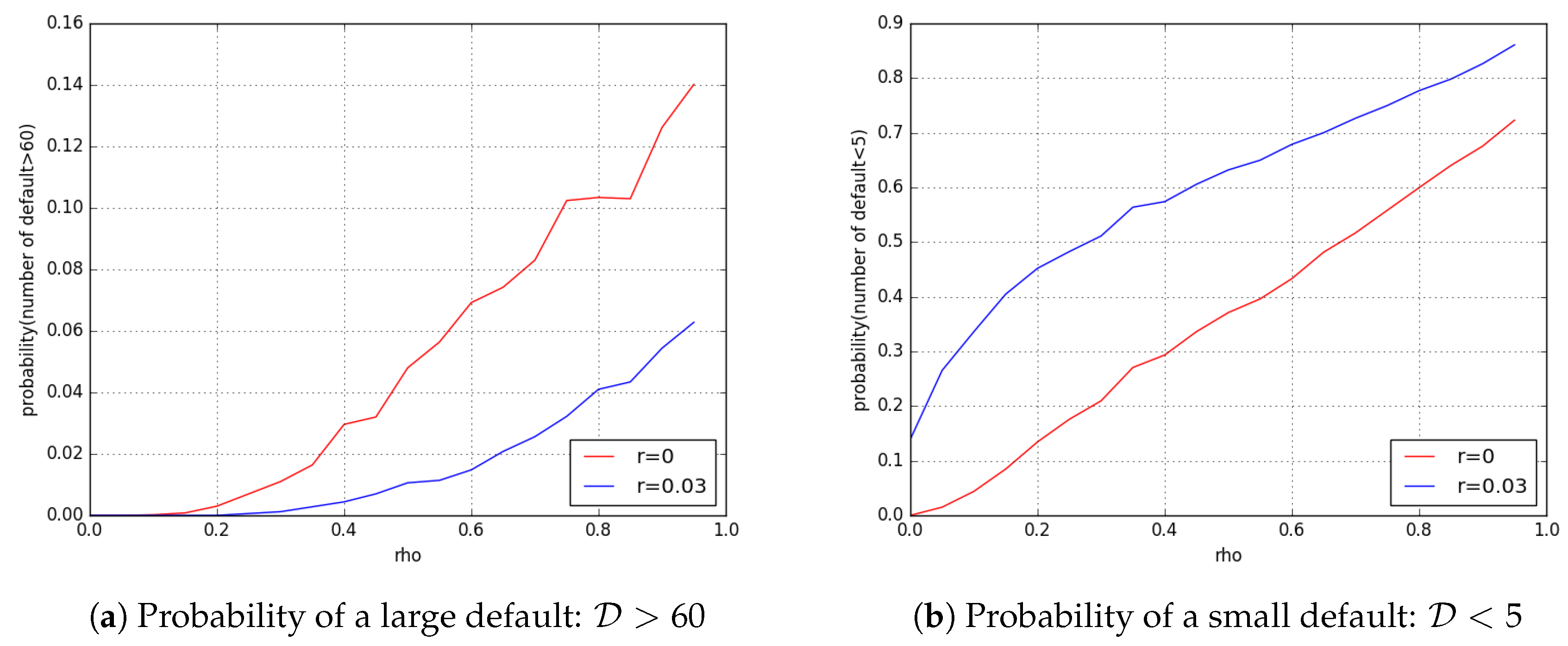
Under such optimal choices of the actors, we study the dynamics of logarithmic net worth of banks, and the distribution of defaults. A default of the
ith bank is understood in the same way as above: when
, the net worth of this bank, falls below some fixed positive threshold. This leads us to understanding systemic risk in this model: how defaults of a few banks can lead to defaults of many other banks (see
Section 3.4).
Besides incorporating the optimal strategy of the central bank, we also generalize the model in Equation (
1) by allowing interbank flow rates from bank
i to bank
j to depend on the banks
, and on time
t, denoting this rate by
. This heterogeneity, together with Ornstein–Uhlenbeck dynamics, resembles to some extent the model by (
Kley et al. 2015). As we show in
Section 4, the matrix
of interbank flow rates corresponds to the stability of the system. We also allow for Brownian motions
to have drifts and to be correlated: that is, we assume
is an
N-dimensional Brownian motion with drift vector
and covariance matrix
A.
1.1. Existing Models and Contributions
The literature on systemic risk is divided into two main categories: graph theoretic models and dynamic models using stochastic differential equations. Graph theoretic formulation of systemic risk came to prominence through
Eisenberg and Noe (
2001). Many works have extended their model and one of the latest works is
Banerjee et al. (
2018). Our work here is in the second group and inspired by
Carmona et al. (
2013). Some of the recent works in this direction are (
Carmona et al. 2018;
Sun 2018). Our work uniquely adds to the existing literature by viewing systemic risk as principal–agent problem with central bank as the principal and private banks as the agents. To our knowledge, we are the first to view the systemic risk through this lens. More specifically, our work adds to existing literature in the following ways:
First, we extend the model in (
Carmona et al. 2013) to include the central bank. This affects the response of the private banks who now make decisions considering the monetary policy of the central bank. Our model allows for the central bank to play a more active role in stabilizing the banking system. This important feature was missing in the work of (
Carmona et al. 2013) where the central bank was considered merely as a clearing house.
Second, we reformulate the problem discussed in (
Carmona et al. 2013) as a principal–agent problem where both, the principal (central bank) and the agent (private banks) maximize their respective utility. We assume that the private banks are risk neutral and central bank as risk averse. This allows us to get closed form solutions for the optimal policy of both the players.
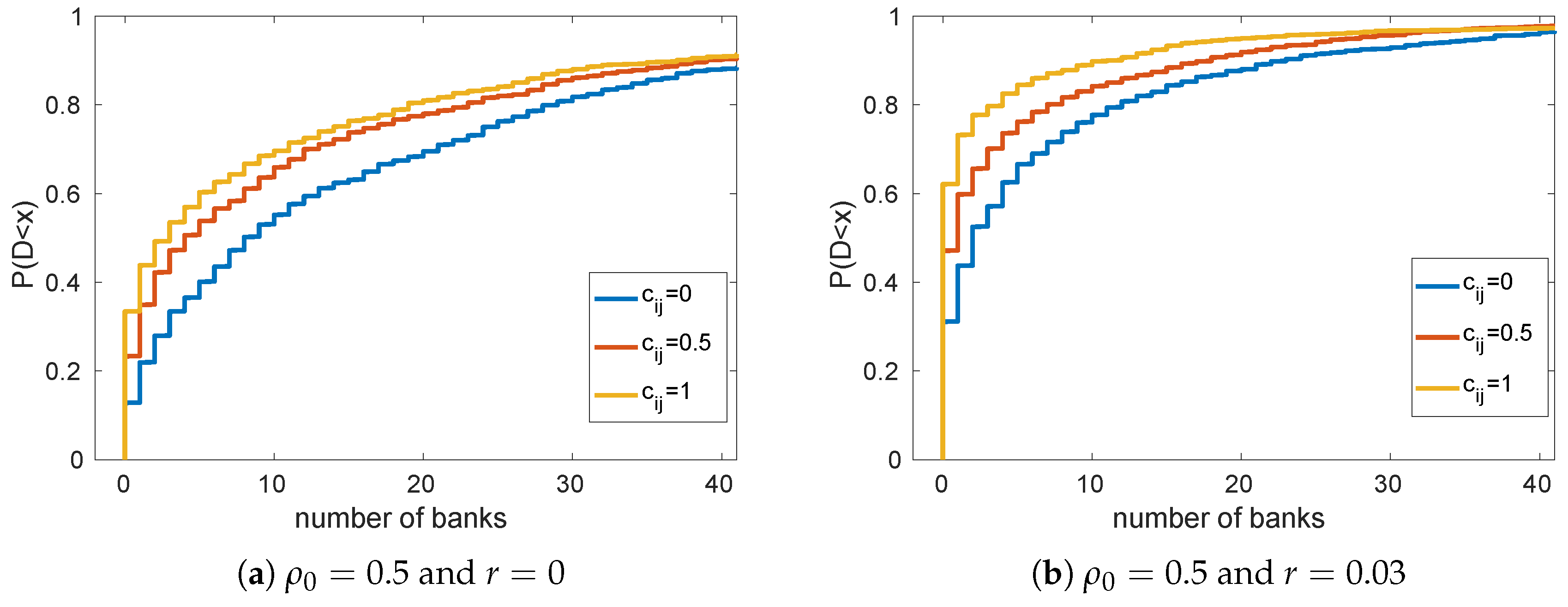
Third, we generalize the flow rates in our model to be different for each pair of private banks. This generalization converts the representative agent model discussed in (
Carmona et al. 2013) into a heterogeneous agent model. This heterogeneity demonstrates a unique feature of the banking system where banks with higher interbank flows are less likely to default than their counterparts with lower interbank flows.
Finally, as we show in
Section 2, the volatility of the wealth process of the private banks is controlled, in contrast to (
Carmona et al. 2013) where the volatility is constant for each bank.
1.2. Organization of the Paper
In
Section 2, we describe the model in terms of stochastic control problem for a system of stochastic differential equations. In
Section 3, we solve the stochastic control problem for each private bank, and in
Section 4, for the central bank (given optimal control for each private bank). In particular, in
Section 3, we study distribution of the number of defaults. This is where we touch the concept of systemic risk: We are interested in its dependence on the parameters of the system, for example correlations between returns on various risky investments.
Section 5 contains results on long-term stability of the system: the fact that the capitals of banks tend to stay close, as opposed to splitting into two or more groups.
Section 6 is devoted to concluding remarks and suggestions for future research. The
Appendix contains some technical proofs.
1.3. Notation
For a vector or a matrix
a, its transpose is denoted by
. We usually think of vectors as column-vectors. The dot product of two vectors
a and
b is denoted by
. The term
standard Brownian motion stands for a one-dimensional Brownian motion with drift coefficient 0 and diffusion coefficient 1. For
, this is called the
total variation norm. Fix a dimension
. Then,
is a vector
with unit components, and we define the following hyperplane in
:
Define the (closed) ball of radius
r on
centered at the origin:
The -dimensional Lebesgue measure on is denoted by . As mentioned above, the symbol or stands for the indicator function of an event A.
2. Description of the Model
2.1. Formal Description
Consider a system of N agents (we call them private banks) which continuously lend money to each other, borrow from the non-banking financial sector, pay back the interest, and invest in some risky portfolios.
We operate on filtered probability space with the filtration satisfying the usual conditions. All the processes which we consider are adapted to the . Let be the net worth (assets minus liabilities) of the ith bank at time t, for . Let be the amount borrowed at the moment t by the ith private bank from the non-banking financial sector. Assume the interest rate for such borrowing is , controlled by the central bank. Then, during the time interval , the ith bank pays back interest . At time t, the ith bank has at its disposal the amount : its own capital plus borrowed amount. This amount is controlled by the ith bank. Herein, we assume perfect competition in the interbank lending market. We also assume that there is no limit on the maximum borrowing of the private banks.
Alternatively, the ith bank might decide to not borrow anything, and instead to even put aside some of its own money in cash (which does not earn any interest). This happens if the investment is not very profitable, or, more precisely, if the return does not outweigh the risk. In this case, we let , and define to be the quantity of cash put aside. The amount invested is still , but the bank does not pay or receive any interest.
We combine these two cases: the ith bank invests the amount at time t into a risky portfolio, and pays interest during the time interval .
At time
t, the
ith bank invests in a portfolio of risky assets with value
. The
ith bank buys
units of this portfolio. Net profit for the time interval
is
Combining all of the above, we get the following system of equations:
Next, we make some assumptions on
, the dynamics of the portfolio processes. A separate question is how banks construct these portfolios out of stocks and other risky assets. This question is separate from the topic of this paper, and we do not study it here. Instead, we assume that these are geometric Brownian motions. This assumption is very simplifying, but we believe it captures to some extent the features of portfolios. The processes
form an
N-dimensional Brownian motion with drift vector
and covariance matrix
. In particular, each
, is a Brownian motion with drift coefficient
and diffusion coefficient
, so it can be represented as
where
is a one-dimensional standard Brownian motion. Although the portfolio process in Equation (
7) is driven by only one Brownian motion, a more general representation:
where
are Brownian motions, can also be considered in our framework. Since
, but
is also a Brownian motion, we fall back to the original portfolio process in Equation (
7).
The covariance between Brownian motions
can be modeled in various ways. (
1.a) All
are independent. Then, the matrix
A is diagonal:
This means that the portfolios of banks are independent.
(1.b) All are the same: . This means that all banks, in fact, use the same portfolio, and they are perfectly correlated. Then, it makes sense to let and .
(
1.c) An intermediate case: for some i.i.d. Brownian motions
, and some coefficients
with
we have:
One can also split N banks into subsets and construct dependence as in Case (1.c) for each subset; portfolio processes corresponding to different subsets are assumed to be independent.
2.2. Main System of Driving Stochastic Equations
Apply Itô’s formula to find the dynamics of
:
Combining Equation (
6) with Equation (
11), we get our main stochastic equation, driving banks’ wealth. For now, it does not contain interbank flows, which are Ornstein–Uhlenbeck-type drifts as in Equation (
1):
Here, we define the
relative investment ratio:
and the following quantity:
Finally, the
ith bank also interacts with other banks, having cash flow in and out. In (
Carmona et al. 2013) and subsequent papers, this interaction is modeled by Ornstein-Uhlenbeck-type drifts
from Equation (
1), with
. Here, we take drifts
which are more general than Equation (
14), and add them to Equation (
12). Here, we assume that the flow rates satisfy
Remark 3. While we generalize the model of (Carmona et al. 2013), the symmetric interbank flows is clearly a simplification of real banking network where the interbank flows tend to be asymmetric. However, this assumption simplifies the problem mathematically as the aggregate wealthis not dependent on the interbank flows and its dynamics can be expressed through the stochastic differential Equation (35). Furthermore, this allows us to solve for the optimal control of the central bank in closed form. Note that in our model, as in (
Carmona et al. 2013), the cash flows (in the original scale, not logarithmic one) do not necessarily add up to zero. Consider possible particular cases:
(2.a) All . Then, there are no cash flows between banks.
(
2.b) All
. For a constant
c, this is the model from (
Carmona et al. 2013).
(
2.c) Let
G be a graph on vertices
. Fix a
for all
. Let
After superimposing these Ornstein–Uhlenbeck-type drifts from Equation (
15) on top of Equation (
12), our main driving equation takes the form
Equation (
17) resembles the model from (
Carmona et al. 2013). However, it also has significant differences: the volatility in Equation (
17) can be controlled (bank
i controls its investment decisions via
which drives the volatility of the process
), unlike in (
Carmona et al. 2013); and the drift coefficient in Equation (
17) is a bit more complicated. For
homogeneous rates: , Equation (
17) takes the form
for
, where
is defined in Equation (
2). Moreover, this modification makes the representative agent model as studied by (
Carmona et al. 2013) into a heterogeneous agent model.
2.3. Interpretation
As in (
Carmona et al. 2013), we consider bank
i to be in bankruptcy at time
t if
, where
D is a given threshold, stipulated by the central bank. The central bank would like to stimulate the activity of banks by persuading them to take risks, but not too much, lest they may become bankrupt. Equation (
12) means that the central bank can use interest rate
as a monetary policy tool to alter the behavior of the private-banks.
Assume that banks start borrowing too much money and investing them in risky assets (leveraging). By doing this, they increase their probability of default. Then, the central bank can raise this interest rate to discourage private banks from excessive borrowing. Conversely, if banks are too cautious in borrowing against future profits and risk-taking, then the central bank can stimulate them by lowering the interest rate. As we show below, this interest rate affects the overall state of the system.
The parameter is determined by the central bank and given to all private banks. These private banks then determine the investment rates , independently of each other. In light of decision-making of the banks, the central bank needs to determine optimal values of these parameters. This setup is similar to the principal–agent problem, but with many agents.
4. Optimal Central Bank Policy
In this section, we assume that the central bank has to choose the interest rate r in an optimal way, so that, after banks make their choice as in the previous section, optimal policy choice is achieved. We assume that banks make optimal (for them) choices and we omit all asterisks from notation of processes. This can be thought of as a principal’s problem within the principal–agent problem framework. Let us now revisit the description of policy making by the central bank.
Its tool is the
interest rate r, which the central bank uses to control the overall amount of capital in the system, measured by the
from Equation (
35). If the interest rate is low, the growth rate
from Equation (
36) and the volatility
from Equation (
37) are large. A more risk-averse central bank can choose therefore a larger
r. One can apply a concave utility function to
, and solve the stochastic control problem for this
r. We apply the exponential (CARA: constant relative risk aversion) utility function to
.
The private banks wish to maximize their expected logarithmic net worth
. However,
in terms of logarithmic capital, their utility function is linear, thus the private banks are risk neutral. Now, if the central bank was risk neutral, similar to the private banks, she would also try to maximize
for a time horizon
. Below, we show that the central bank would then choose zero interest rate
, because this would produce the same result as the private banks were aiming for.
Now, suppose the central bank is risk-averse. This should manifest itself in the utility function being concave (rather than linear). Consider, for example, a commonly used exponential (CARA) utility function:
Assume the central bank maximizes expected terminal utility:
where the supremum in Equation (
41) is chosen over all bounded adapted controls
r. We can alternatively choose instead of Equation (
40) the utility function as
There is no difference between Equation (
40) and Equation (
42) when we try to maximize Equation (
41), but writing Equation (
42) highlights the risk-aversion of the central bank. As
, the function
from Equation (
42) satisfies:
The commonly used
absolute risk aversion is calculated for Equation (
42) as follows:
In other words, is the coefficient of risk aversion (of the central bank relative to private banks). For , the central bank is risk neutral.
Theorem 2. An optimal interest ratefor the problem in Equation (41) is given by a constantwhich maximizes the following expression: Remark 6. It is interesting to note that the optimal interest rate r does not depend on the flow rates. This is because we measure the size of the system by the stochastic process. This process satisfies a stochastic differential equation with coefficients independent of. These coefficients do depend on the optimal controls. However, as we mentioned in Remark 5, these optimal controls , in turn, do not depend on the flow rates, because of our special choice of logarithmic utility function. We want to emphasize that in practice we expect to observe the interbank flow rate to affect the optimal interest rate. Particularly, asymmetric interbank flow rates are more likely to be one of the control variables for the corresponding bank, driving its wealth and consequently affecting the optimal interest rate. The result here is driven by the assumption of symmetric flows i.e., .
Proof. The HJB equation for the function
where the supremum is taken over all bounded adapted controls
, takes the form
with terminal condition
. Try the following form:
From Equation (
45), we can calculate derivatives with respect to
t and
y:
Plug Equation (
46) into Equation (
44). Because
, we can rewrite Equation (
44) as
This, in turn, is equivalent to
Since we have
and
, for compatibility we need to show that
for all
t. From the terminal condition
combined with Equation (
45), we have:
. Equation (
47) can be written as
, which gives us
. Therefore,
is positive.
Finally, let us do the verification argument to complete the proof. The idea is similar to the verification argument in Theorem 1. Assume
is our constant control from Equation (
43), found from Equation (
44), and
is some other admissible (adapted bounded) control. Apply the function
to the process
. By Itô’s formula,
Comparing Equation (
44) with Equation (
48), we get that
is a supermartingale for the control
r, but a martingale for the control
. Indeed, by boundedness of
, the expectation of the stochastic integral in Equation (
48) is zero. Since
, we get:
, with equality for the control
. The result immediately follows from here. □
Let us find the
r which corresponds to the maximum in the right-hand side of (
47). This depends on the structure of the vector
g and the matrix
A.
If
for all
, then all investments are too unprofitable to borrow money for them. Then, the interest rate policy cannot influence the behavior of private banks. This corresponds to the case of the
liquidity trap, when conventional monetary policy no longer works. From now on until the end of this section, let us assume that all investments are attractive:
(
3.a) Assume
: all investments are the same. Then, we have:
The maximum is attained at
for
and at any
for
. This has the following meaning: the case
corresponds to less risk-averse central bank, and, to increase the total quantity of capital in the system, it wishes to slash the interest rate to zero. For the case
, however, the central bank is very risk-averse, and it increases the interest rate to prevent excessive borrowing and overheating of the financial system.
(
3.b) Independent portfolio process:
, where
is as defined in Equation (
24). Then,
This function attains maximum:
In the general case, we do not have an explicit form for the optimal r in case . If and , we have . Note that here the central bank chooses expansionary monetary policy (zero interest rate ) for larger values of compared to Case (3.a). This has the following interpretation: If the portfolios of banks are independent, then this creates diversification in the system and reduces risk. Therefore, even a relatively risk-averse central bank (large ) can pursue aggressive expansionary monetary policy.
(
3.c) Correlated portfolio process with same growth rates
and volatilities
. Assume the driving Brownian motions of these portfolio process are correlated as in Equation (
10). After calculation, we get:
Then, we can find optimal
r: this is
Note that for we get Case (3.a), and for we get Case (3.b). Case (3.c) is intermediate: there is diversification between portfolios of private banks, but this diversification is not complete. Therefore, a risk-averse central bank can pursue more expansionary monetary policy than in Case (3.a), but less so than in Case (3.b).
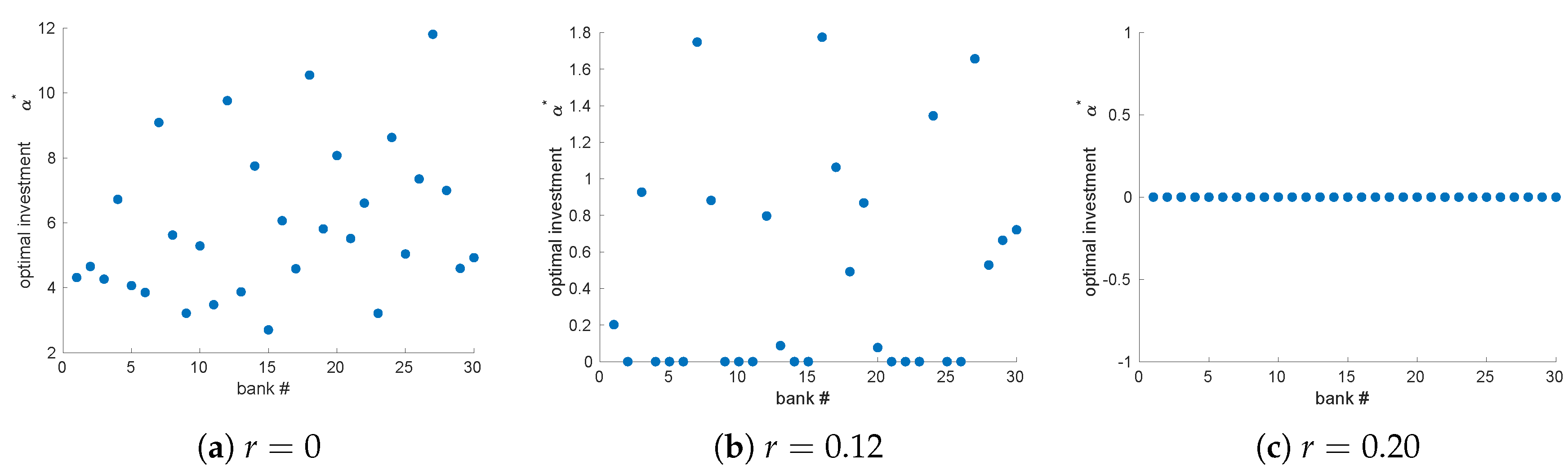
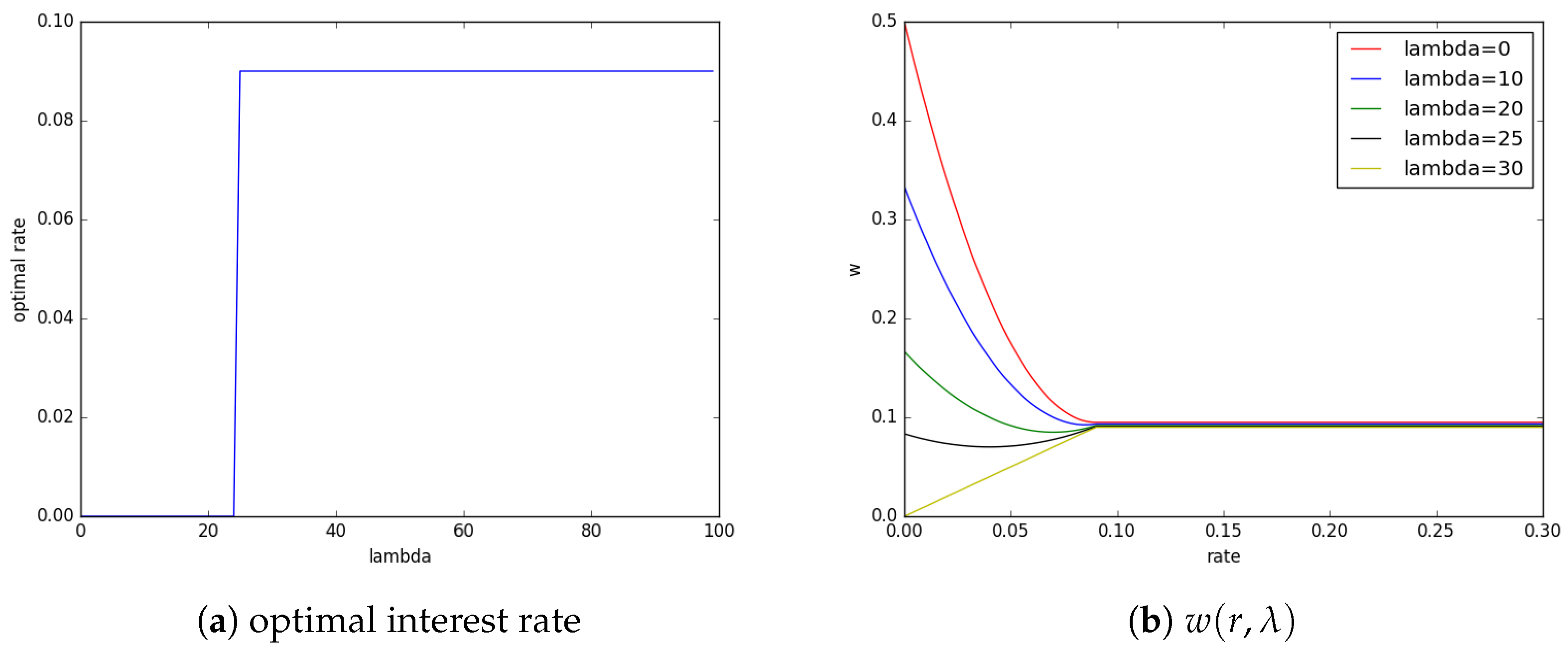
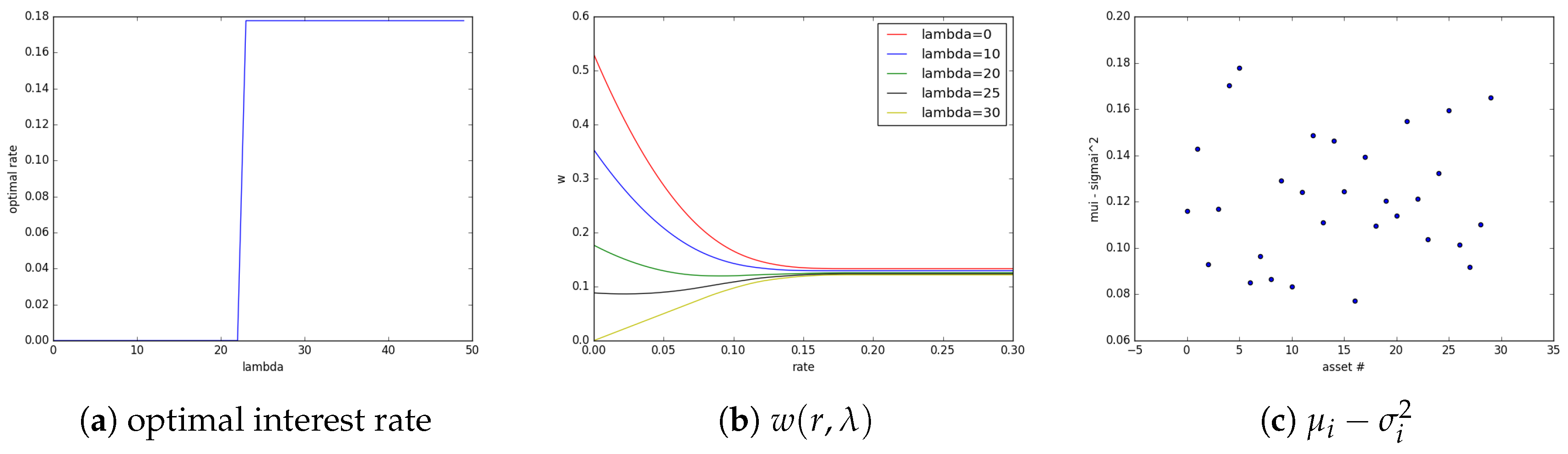
To illustrate the impact of risk aversion
on the optimal interest rate, we simulate three scenarios. First, in
Figure 9, we assume uncorrelated portfolio process, each with same mean and volatility
for
. This is Case (3.a), which is discussed above in this section.
Next, in
Figure 10, we assume independent portfolio process but with mean and standard deviation
i.i.d uniform on
. This is Case (3.b), which is discussed above in this section. However, to our surprise, we observe the optimal interest rate to have only one jump as we increase the risk aversion parameter
.
Finally, in
Figure 11, we assume correlated portfolio process with
and mean and standard deviation
drawn from i.i.d uniform
. This is a generalized version of Case (3.c) discussed above. We observe that, due to correlation in the portfolio process, even a relatively less risk averse central bank is forced to raise the interest rate.
Remark 7. The optimization problems discussed in this section maximized the expected utility of the central bank. This is in contrast to a more common measure of discounted expected utility:However, if the discounting term γ is not dependent on controlled interest rate r, the optimal policy remains the same as proposed in Theorem 2.
Remark 8. In the current formulation, the private banks solve their problems given r, and the central bank in anticipation of them solves for r incorporating the future decisions of the private banks. In practice, this is similar to central banks announcing the policy rate to which the private players react. Reversing the order of the solution makes the problem mathematically uninteresting and its economics impractical. Within this scenario, Equations (12) and (13) imply that the optimal interest rate for the central bank, thus the central bank is just an observer with no ability to direct the economy. This is in sharp contrast to the real economy where central banks play an active role through the monetary policy. 5. Long-Term Stability
In this section, we analyze the long-term behavior of the centered process:
It takes values in the hyperplane
. In other words, we are trying to find whether log capitals of banks stay together as time
t goes to infinity, or they split into two or more “clouds”. The key parameters are rates
of interbank cash flows. Under certain fairly general conditions on these rates, the process (
49) is ergodic: It has a unique stationary distribution; and for any initial conditions, it converges to this distribution as
. This section has two results. Theorem 3 deals with the case of flow rates
being time-independent:
. Lemma 1 covers the general case.
Assume the central bank has already chosen the interest rate
, as above. Then,
is a Brownian motion with drift coefficient
and diffusion coefficient
. We have:
Here, the process:
is an
N-dimensional Brownian motion with drift vector and covariance matrix
and
from Equations (
32) and (
33). The centered process in Equation (
49) satisfies the SDE
Here,
for
. Note that
is a
-valued Brownian motion. It has drift vector
and covariance matrix
Therefore,
is a Markov process. Denote by
its transition function. Define the following measure norm on
for a function
:
We denote the Euclidean norm of a vector
by
Theorem 3. Assume the flow ratesare constant. Define the graph G on the set of vertices:iff. If G is connected, then:
(a)has a unique stationary distribution π on Π, which is multivariate normal.
(b) The transition function satisfies for some constants: (c) For any bounded measurable functionwe have, almost surely: Proof. From the properties of solutions of SDE and nondegeneracy of the covariance matrix
of
M, we have the following positivity property:
The generator of
for all twice continuously differentiable functions
is given by:
Here,
is the following matrix:
Now, plug this function
V from Equation (
54) for a suitable
into the generator in Equation (
56). Then,
Combining Equation (
58) with Equation (
56), we get:
Using Lemma A4 below, we get:
There exists a constant
such that for all
, we have:
. Combining this observation with Equations (
59) and (
60), we get:
Choose
, then Equation (
61) takes the form
Note that, as
, we have:
. Therefore, for some constants
,
Recall the definition of the ball
in Equation (
5). Since
and
V are continuous, we have:
Combining Equation (
62) with Equations (
63) and (
64), we get:
Finally, combine Equation (
65) with the Feller property of
(i.e., for a bounded continuous function f, the map
is also bounded and continuous for the transition function
P of
), and with the positivity property in Equation (
55). Apply Lemma A1 from
Appendix A to Lebesgue reference measure
and the function
V from Equation (
54). This completes the proof of (a) (the uniqueness of a stationary distribution), as well as of (b). The fact that this stationary distribution
is multivariate normal follows from the observation that
is a multidimensional Ornstein–Uhlenbeck process on the hyperplane
.
To finish the proof of Theorem 3, let us show (c): This is similar to the proof of (
Ichiba et al. 2011, Theorem 1). Take any
. Adjusting the proof of Equation (
65) above, we find that there exists a positive constant
such that
Let
be the hitting moment of the ball
, for a fixed
. Apply (
Meyn and Tweedie 1993b, Theorem 4.3(a)), with the function
V from Equation (
54), with
,
. Then,
Use the fact that
V is bounded on compact subsets to verify assumption (b) in Lemma A2. Assumption (a) of this lemma follows from the observation that the covariance matrix of
is constant. Now, apply Lemma A2 from (
Khasminskii 2012, Theorem 4.1, Theorem 4.2), cited as (
Ichiba et al. 2011, Proposition 1). This completes the proof of part (c) of Theorem 3. □
Lemma 1. Assume the flow rates are given bywhereis a function such thatandare real numbers as in Theorem 3.
Then, the conclusion of Theorem 3
is the same, minus the conclusion that π is multivariate normal. Proof. Similar to Theorem 3, but with the following changes: Instead of Equation (
59), we have:
There exist
such that
for
,
. Therefore, for such
x, the estimate (
62) is preserved with
changed to
. The rest of the proof is similar to that of Theorem 3. □
Note, however, that, if the graph
G is disconnected, then this stability breaks down. Indeed, assume
G has connected components
and
(only two for sake of notational simplicity; analysis is the same for more than two connected components), and the flow rates
are positive constants if
i and
j are adjacent,
if not. By Theorem 3, we get:
are ergodic, that is, they satisfy an inequality similar to Equation (
54). Here,
However, these averages from Equation (
66) are, in fact, Brownian motions with certain drift and diffusion coefficients, which are easy to calculate from Equation (
50). They are correlated, but not perfectly. Therefore,
is not ergodic, and the process
defined in Equation (
49) is also not ergodic. Private banks are separated into two groups, which “drift” from each other.
6. Concluding Remarks
We studied a model of
N private banks exchanging money through interbank flows, borrowing from the non-banking financial sector under an interest rate set by the central bank, and investing in portfolios consisting of risky assets; these portfolios are modeled by correlated geometric Brownian motions. This represents an enhancement of the model in Equation (
1), which is obtained in (
Carmona et al. 2013) as a result of banks borrowing from each other. We generalize the interbank flows from (
Carmona et al. 2013), making them heterogeneous.
Each private bank maximizes its expected terminal logarithmic utility. The central bank maximizes exponential utility function of the total size of the system. We are able to solve the control problems for each private banks and the central bank because of this special choice of utility functions. The resulting dynamics looks a bit like Equation (
1), except that each private bank has its own growth rate and volatility in the driving Brownian motion, and the flow rates
depend on
i and
j.
Our setup allowed us to study systemic risk and distribution of defaults under different market and investment scenarios. We also observe common economic phenomena of liquidity trap (where the monetary policy fails to boost the investment in risky assets) naturally arising from the model.
For future research, one can consider the case when some but not all portfolios satisfy (and are therefore unprofitable). In addition, it might be interesting to consider different utility functions for private banks, for example power utility. Since the corresponding Hamilton–Jacobi–Bellman equations are likely to be intractable, the problem might be analyzed using mean-field formulation, each bank is competing against the “mass of banks”.