Credibility Methods for Individual Life Insurance

Abstract

Credibility theory is used widely in group health and casualty insurance. However, it is generally not used in individual life and annuity business. With the introduction of principle-based reserving (PBR), which relies more heavily on company-specific experience, credibility theory is becoming increasingly important for life actuaries. In this paper, we review the two most commonly used credibility methods: limited fluctuation and greatest accuracy (Bühlmann) credibility. We apply the limited fluctuation method to M Financial Group’s experience data and describe some general qualitative observations. In addition, we use simulation to generate a universe of data and compute Limited Fluctuation and greatest accuracy credibility factors for actual-to-expected (A/E) mortality ratios. We also compare the two credibility factors to an intuitive benchmark credibility measure. We see that for our simulated data set, the limited fluctuation factors are significantly lower than the greatest accuracy factors, particularly for low numbers of claims. Thus, the limited fluctuation method may understate the credibility for companies with favorable mortality experience. The greatest accuracy method has a stronger mathematical foundation, but it generally cannot be applied in practice because of data constraints. The National Association of Insurance Commissioners (NAIC) recognizes and is addressing the need for life insurance experience data in support of PBR—this is an area of current work.

1. Introduction

1.1. Background

Insurance is priced based on assumptions regarding the insured population. For example, in life and health insurance, actuaries use assumptions about a group’s mortality or morbidity, respectively. In auto insurance, actuaries make assumptions about a group of drivers’ propensity toward accidents, damage, theft, etc.

The credibility ratemaking problem is the following: suppose that an individual risk has better (or worse) experience than the other members of the risk class. Note that the individual risk might actually be a group—for example, a group of auto insurance policyholders or an employer with group health coverage for its employees.

To what extent is the experience credible? How much of the experience difference can be attributed to random variation and how much is due to the fact that the individual is actually a better or worse risk than the rest of the population? To what extent should that experience be used in setting future premiums?

We can formulate the problem as follows.

• Denote losses by $X_j$ and assume that we have observed independent losses $\mathbf{X}=(X_1,X_2,\dots ,X_n)$. Note that $X_j$ might be the annual loss amount from policyholder j, or the loss in the $j^{th}$ period, depending on the context.
• Let $\xi =E[X_j]$ and ${\sigma }^2=\mathrm{Var}(X_j)$.
• Let $S={\sum }_{j=1}^n{X}_j$ and let $\overline{X}=\frac{S}{n}$ be the sample mean.

  -

  Observe that $E[S]=n\xi ,E[\overline{X}]=\xi ,\mathrm{Var}(S)=n{\sigma }^2$, and $\mathrm{Var}(\overline{X})=\frac{{\sigma }^2}{n}$.

• Let M be some other estimate of the mean for this group. M might be based on industry data or large experience studies on groups similar to the risk class in question.

Credibility theory provides actuaries with a method for combining $\overline{X}$ and M for pricing. The resulting credibility estimate is:

$$P=Z\overline{X}+(1-Z)M,$$

(1)

and Z is called the credibility factor.

1.2. Significance

Credibility theory is important for actuaries because it provides a means for using company- or group-specific experience in pricing and risk assessment. Norberg (1989) addressed the application of credibility theory to group life insurance. In the United States, however, while credibility theory is used widely in health and casualty insurance, it is generally not used in life and annuity business. The 2008 Practice Note of the American Academy of Actuaries’ (AAA’s) Life Valuation Subcommittee observes, “For some time, credibility theory has been applied within the property and casualty industry in order to solve business problems. This has not been the case within the life, annuity and health industries. Therefore, examples of the use of credibility theory and related practices are somewhat difficult to find and somewhat simplistic in their content” (AAA 2008). Similarly, the 2009 report (Klugman et al. 2009) notes, “The major conclusion from this survey of 190 US insurers is that credibility theory is not widely adopted among surveyed actuaries at United States life and annuity carriers to date in managing mortality-, lapse- and expense-related risks.”

Actuarial Standard of Practice 25 (ASOP 25) recommends that credibility theory be used, and provides guidance on credibility procedures for health, casualty, and other coverages. In 2013, the Actuarial Standards Board revised ASOP 25 to include the individual life practice area. Thus, it will be important for life actuaries to start to use credibility methodology (ASB 2013).

Moreover, credibility theory is increasingly important for life actuaries, as the Standard Valuation Law (SVL) is changing to require that principle-based reserving (PBR) be used in conjunction with the traditional formulaic approaches prescribed by state insurance regulations. PBR relies more heavily on company-specific experience. Thus, it will be important for actuaries to have sound credibility methodology (NAIC and CIPR 2013). There is a proposed ASOP for PBR that places significant emphasis on credibility procedures (ASB 2014).

1.3. Overview of Paper

Our paper is structured as follows. In Section 2, we provide a brief overview of the two most common credibility methods: limited fluctuation (LF) and greatest accuracy (GA) or Bühlmann credibility. We will see that the LF method is easy to apply, but has several significant shortcomings. On the other hand, GA has a stronger mathematical foundation, but it generally cannot be applied in practice because of data constraints. In Section 3, we summarize some of the results of (Klugman et al. 2009), in which the authors illustrate an application of both the LF and GA methods to mortality experience from the Society of Actuaries (SOA) 2004–2005 Experience Study. In Section 4, we apply the LF method to M Financial’s experience data and share some qualitative observations about our results. In Section 5, we use simulation to generate a “universe” of data. We apply the LF and GA credibility methods to the data and compare the results to an intuitive (though not mathematically grounded) benchmark “credibility factor”. Based on the results of the qualitative comparison of the methods in Section 5, we document our conclusions and recommendations in Section 6.

2. Brief Overview of Credibility Methods

The two most common methods for computing the credibility factor Z are limited fluctuation (LF) credibility and greatest accuracy (GA) or Bühlmann credibility.

2.1. Limited Fluctuation Credibility

2.1.1. Full Credibility

The limited fluctuation method is most commonly used in practice. To apply LF, one computes the minimum sample size so that $\overline{X}$ will be within distance r of the true mean $\xi$ with probability p. In other words, we seek n such that:

$$\mathrm{pr}\left(-r\le \frac{\overline{X}-\xi }{\xi }\le r\right)\ge p.$$

(2)

Here, the sample size can be expressed in terms of number of claims, number of exposures (e.g., person-years), or aggregate claims. If the sample size meets or exceeds the minimum, then full credibility ($Z=1$) can be assigned to the experience data. Otherwise, partial credibility may be assigned based on the ratio of the actual sample size to the size required for full credibility.

Observe that Equation (2) yields the following equivalent conditions:

$$\begin{array}{ccc}\hfill \mathrm{pr}(-r\xi \le \overline{X}-\xi \le r\xi )& \ge & p⟺\hfill \\ \hfill \mathrm{pr}\left(\frac{-r\xi }{\sigma /\sqrt{n}}\le \frac{\overline{X}-\xi }{\sigma /\sqrt{n}}\le \frac{r\xi }{\sigma /\sqrt{n}}\right)& \ge & p.\hfill \end{array}$$

Denote the random variable $\frac{\overline{X}-\xi }{\sigma /\sqrt{n}}$ by Y. Then we seek n so that:

$$\mathrm{pr}\left(\frac{-r\xi }{\sigma /\sqrt{n}}\le Y\le \frac{r\xi }{\sigma /\sqrt{n}}\right)\ge p.$$

This condition holds if and only if:

$$2\Phi \left(\frac{r\xi }{\sigma /\sqrt{n}}\right)-1\ge p,$$

where $\Phi (u)$ is the standard normal cumulative distribution function (CDF) evaluated at u, assuming that Y has (approximately) a standard normal distribution.

Finally, we see that condition Equation (2) holds if and only if:

$$\frac{r\xi }{\sigma /\sqrt{n}}\ge y_p,$$

or, equivalently,

$$n\ge {\left(\frac{y_p}{r}\right)}^2{\left(\frac{\sigma }{\xi }\right)}^2=n_f,$$

(3)

where $y_p$ is the $\frac{1+p}{2}$-percentile of the standard normal distribution. We denote this critical value of n for which full credibility is awarded by $n_f$.

From Equation (3), we have the following:

$$Z=1⟺n\ge n_f⟺\mathrm{Var}(\overline{X})=\frac{{\sigma }^2}{n}\le {\xi }^2{\left(\frac{r}{y_p}\right)}^2.$$

(4)

This condition has intuitive appeal—full credibility is awarded if the observations are not too variable.

For example, suppose $r=0.05$ and $p=0.90$. Then, we seek n so that the probability is at least 90% that the relative error in $\overline{X}$ is smaller than 5%. We have that:

• $\frac{1+p}{2}=0.95,$
• $y_p=1.645,$
• ${\left(\frac{y_p}{r}\right)}^2\approx 1082$,

and for full credibility, we require that:

$$n\ge 1082{\left(\frac{\sigma }{\xi }\right)}^2.$$

Similarly, if we choose $r=0.03$ and $p=0.90$, ${\left(\frac{y_p}{r}\right)}^2\approx 3007$, and the standard for full credibility is:

$$n\ge 3007{\left(\frac{\sigma }{\xi }\right)}^2.$$

We computed the standard for full credibility to control the deviation of $\overline{X}$ from its mean $\xi$. We remark that, alternatively, we could compute n to control the error in S relative to its mean $n\xi$. Following the derivation above, the same criterion as in Equation (3) results. This is not surprising, as S is a scalar multiple of $\overline{X}$.

2.1.2. Application to Life Insurance

Suppose now that the $X_j$ are Bernoulli random variables that assume the values 1 or 0 with probabilities q and $1-q$, respectively. In the life insurance context, the random variable S counts the number of deaths. $S={\sum }_{j=1}^n{X}_j$ has a binomial distribution, and under appropriate conditions, we can approximate the distribution of S with the Poisson distribution with mean and variance $\lambda =nq$. Note that $\lambda$ is the expected number of deaths in a group of n lives. Applying Equation (3) with $\lambda =n\xi =nq$, the standard for full credibility is:

$$\lambda =nq=\mathrm{expected} \mathrm{number} \mathrm{of} \mathrm{claims}\ge {\left(\frac{y_p}{r}\right)}^2.$$

(5)

In practice, we replace the expected number of claims by the observed number of claims, applying full credibility if at least 1082 (or 3007), for example, are observed.

Remark 1.

In some derivations, λ is used to represent the expected number of claims per policy; thus, the credibility standard is written as $n\lambda \ge {\left(\frac{y_p}{r}\right)}^2$ (e.g., see (Klugman et al. 2012)). In our derivation above, we used λ to represent the expected number of claims for the group of n lives. Thus, the standard is expressed as in Equation (5).

2.1.3. Partial Credibility

Suppose now that full credibility is not justified (i.e., that $n<n_f$). What value of $Z<1$ should we assign in computing the credibility estimate Equation (1)? In (Klugman et al. 2012), the authors note, “A variety of arguments have been used for developing the value of Z, many of which lead to the same answer. All of them are flawed in one way or another.” They present the following derivation. We choose the value of Z in order to control the variance of the credibility estimate P in Equation (1). Observe first that:

$$\mathrm{Var}(P)=Z^2\mathrm{Var}(\overline{X})=Z^2\frac{{\sigma }^2}{n}.$$

From Equation (4), we see that when $Z<1$, we cannot ensure that $\mathrm{Var}(\overline{X})$ is small. Thus, we choose the value of $Z<1$ so that $\mathrm{Var}(P)$ is fixed at its upper bound when $Z=1$. In other words, we choose Z so that:

$$\mathrm{Var}(P)=Z^2\mathrm{Var}(\overline{X})=Z^2\frac{{\sigma }^2}{n}={\xi }^2{\left(\frac{r}{y_p}\right)}^2;$$

thus, we set:

$$Z=\sqrt{n}\left(\frac{\xi }{\sigma }\right)\left(\frac{r}{y_p}\right)=\sqrt{\frac{n}{n_f}}.$$

(6)

Remark 2.

1.

If full credibility is not justified (i.e., if $n<n_f$), the partial credibility factor Z is the square root of the ratio of the number of observations n to the number of observations $n_f$ required for full credibility.

2.

Observe that as σ increases, Z decreases. Thus, lower credibility is awarded when the observations are more variable. Again, this is consistent with our intuition.

3.

In Equation (6), the term:

$$\sqrt{n}\left(\frac{\xi }{\sigma }\right)=\frac{\xi }{(\sigma /\sqrt{n})}=\frac{E[\overline{X}]}{\sqrt{Var(\overline{X})}}$$

is the mean of the estimator divided by the standard deviation of the estimator $\overline{X}$ of the unknown mean ξ.

4.

We can write the formula Equation (6) succinctly to include both the full and partial credibility cases by writing:

$$\begin{array}{ccc}Z\hfill & =\hfill & min\left\{1,\sqrt{n}\left(\frac{\xi }{\sigma }\right)\left(\frac{r}{y_p}\right)\right\}=min\left\{1,\frac{E[estimator]}{\sqrt{Var(estimator)}}\left(\frac{r}{y_p}\right)\right\}\hfill \\ & =\hfill & min\left\{1,\sqrt{\frac{n}{n_f}}\right\}\hfill \end{array}.$$

(7)

2.1.4. Strengths and Weaknesses of the Limited Fluctuation Approach

The LF method is simple to apply and, unlike GA credibility, it relies only on company-specific data. Thus, LF is used widely in practice. However, it has numerous shortcomings. For example:

• There is no justification for choosing an estimate of the form Equation (1).
• There is no guarantee of the reliability of the estimate M, and the method does not account for the relative soundness of M versus $\overline{X}$.
• The choices of p and r are completely arbitrary. Note that as $r\to 0$ or $p\to 1$, $n_f\to \infty$. Thus, given any credibility standard $n_f$, one can select a value of r and p to justify it!

2.2. Greatest Accuracy (Bühlmann) Credibility

Another common approach is greatest accuracy (GA) or Bühlmann credibility. In this approach, we assume that the risk level of the members of the risk class are described by a parameter $\Theta$, which varies by policyholder. Note that we assume here that the risk class has been determined by the usual underwriting process, that is, that all of the “standard” underwriting criteria (e.g., smoker status, health history, driving record, etc.) have already been considered. Thus, $\Theta$ represents the residual risk heterogeneity within the risk class. We assume that $\Theta$ and its distribution are unobservable. An obvious choice for the premium would be ${\mu }_{n+1}(\theta ):=E[X_{n+1}|\Theta =\theta ]$.

Suppose we restrict ourselves to estimators that are linear combinations of the past observations. That is, estimators of the form:

$${\alpha }_0+\sum _{j=1}^n{\alpha }_j{X}_j.$$

Define the expected value of the hypothetical means $\mu$ by:

$$\mu =E[E[X_j|\theta ]].$$

One can show that, under certain conditions, the credibility premium $P=Z\overline{X}+(1-Z)\mu$ minimizes the squared error loss:

$$Q=E\{{[{\mu }_{n+1}(\Theta )-{\alpha }_0-\sum _{j=1}^n{\alpha }_j{X}_j]}^2\},$$

where the credibility factor is:

$$Z=\frac{n}{n+k}.$$

Here n is the sample size and:

$$k=\frac{\nu }{a}=\frac{E[\mathrm{Var}(X_j|\theta )]}{\mathrm{Var}(E[X_j|\theta ])}=\frac{\mathrm{expected} \mathrm{process} \mathrm{variance}}{\mathrm{variance} \mathrm{of} \mathrm{the} \mathrm{hypothetical} \mathrm{means}}.$$

It turns out that P is also the best linear approximation to the Bayesian premium $E[X_{n+1}|\mathbf{X}]$.

We observe that under the GA method, the following intuitive results hold:

• $Z\to 1$ as $n\to \infty$.
• For more homogeneous risk classes (i.e., those whose value of a is small relative to $\nu$), Z will be closer to 0. In other words, the value of $\mu$ is a more valuable predictor for a more homogenous population. However, for a more heterogeneous group (i.e., those whose value of a is large relative to $\nu$), Z will be closer to 1. This result is appealing. If risk classes are very similar to each other (a is small relative to $\nu$), the population mean $\mu$ should be weighted more heavily. If the risk classes are very different from each other (a is large relative to $\nu$), the experience data should get more weight.

Strengths and Weaknesses of the Greatest Accuracy Method

The GA method has a more sound mathematical foundation in the sense that we do not arbitrarily choose an estimator of the form in Equation (1). Rather, we choose the best estimator (in the sense of mean-squared error) among the class of estimators that are linear in the past observations. Moreover, unlike LF, GA credibility takes into account how distinctive a group or risk class is from the rest of the population. However, in practice, companies do not have access to the data required to compute the expected process variance a or the variance in the hypothetical means $\nu$. These quantities rely on (proprietary) data from other companies. As a result, GA credibility is rarely used in practice.

2.3. Other Credibility Methods

The credibility ratemaking problem can be framed in the context of generalized linear mixed models (GLMMs). We refer the reader to (Frees et al. 1999), (Nelder and Verrall 1997), and (Christiansen and Schinzinger 2016) for more information. In fact, the GA method presented in Section 2.2 is a special case of the GLMM—see (Frees et al. 1999) and (Klinker 2011) for details. Expressing credibility models in the framework of GLMMs is advantageous as they allow for more generality and flexibility. Moreover, one can use standard statistical software packages for data analysis. However, for our purposes, and for our simulated data set, the additional generality of GLMMs was not required. Other methods include mixed effects models, hierarchical models, and evolutionary models. We refer the reader to (Buhlmann and Gisler 2005), (Dannenbburg et al. 1996), and (Goovaerts and Hoogstad 1987).

3. Previous Literature: Application of Credibility to Company Mortality Experience Data

In (Klugman et al. 2009), the authors apply both the LF and GA methods to determine credibility factors for companies’ actual-to-expected (A/E) mortality ratio in terms of claim counts and amounts paid. Expected mortality is based on the 2001 VBT and actual mortality is from 10 companies that participated in the Society of Actuaries (SOA) 2004–2005 Experience Study. The authors develop the formulae for the A/E ratios and the credibility factors and include an Excel spreadsheet for concreteness.

We apply the methods and formulae of (Klugman et al. 2009) in the work that follows in Section 4 and Section 5. For completeness and readability, we briefly summarize the notation and formulae.

3.1. Notation

Assume that there are n lives.

• $f_i$ is the fraction of the year for which the ith life was observed.
• $d_i=1$ if life i died during the year; otherwise, $d_i=0$.
• $q_i$ is the observed mortality rate.
• $q_i^s$ is the standard table mortality rate.
• We assume that $q_i=m_c{q}_i^s$ (i.e., that the actual mortality is a constant multiple of the table).
• $A_c={\sum }_{i=1}^n{d}_i=$ the actual number of deaths.
• $E_c={\sum }_{i=1}^n{f}_i{q_i}^s=$ the expected number of deaths.
• ${\widehat{m}}_c=\frac{A_c}{E_c}=$ the estimated actual-to-expected (A/E) mortality ratio based on claim counts.

Observe that $A_c$ and $E_c$ give the actual and expected number of deaths. We define similar quantities for the actual and expected dollar amounts paid as follows. Let $b_i$ be the benefit amount for policy i. Then we define

• $A_d={\sum }_{i=1}^n{b}_i{d}_i=$ the actual amount paid.
• $E_d={\sum }_{i=1}^n{b}_i{f}_i{q_i}^s=$ the expected amount paid.
• ${\widehat{m}}_d=\frac{A_d}{E_d}=$ the estimated actual-to-expected (A/E) mortality ratio based on claim amounts.

3.2. Limited Fluctuation Formulae

In order to compute the credibility factor, we need the mean and variance of the estimators ${\widehat{m}}_c$ and ${\widehat{m}}_d$. We present the results for ${\widehat{m}}_c$; the results for ${\widehat{m}}_d$ are similar. One can show that:

$$E[{\widehat{m}}_c]=\frac{{\sum }_{i=1}^{n}E[d_i]}{E_c}=\frac{{\sum }_{i=1}^n{f}_i{q}_i}{E_c}=\frac{{\sum }_{i=1}^n{f}_i{m}_c{q}_i^s}{E_c}=m_c$$

and

$$\mathrm{Var}({\widehat{m}}_c)=\frac{{\sum }_{i=1}^n{f}_i{q}_i(1-f_i{q}_i)}{E_c^2}=\frac{{\sum }_{i=1}^n{f}_i{m}_c{q}_i^s(1-f_i{m}_c{q}_i^s)}{E_c^2}.$$

(8)

If $q_i^s$ is sufficiently small, we can assume that $(1-f_i{m}_c{q}_i^s)$ is approximately 1, and the expression above for the variance simplifies:

$$\mathrm{Var}({\widehat{m}}_c)\approx \frac{{\sum }_{i=1}^n{f}_i{m}_c{q}_i^s}{E_c^2}=\frac{m_c}{E_c}.$$

(9)

Now, combining the expressions for the mean and variance of the estimator ${\widehat{m}}_c$ with the expression for the credibility factor given in Equation (7), we have that:

$$Z=min\left\{1,\left(\frac{r}{y_p}\right)\left(\frac{{\sum }_{i=1}^n{f}_i{m}_c{q}_i^s}{\sqrt{{\sum }_{i=1}^n{f}_i{m}_c{q}_i^s(1-f_i{m}_c{q}_i^s)}}\right)\right\}.$$

If we use the approximation for the variance given in Equation (9), we have:

$$Z=min\left\{1,\left(\frac{r}{y_p}\right)\sqrt{\sum _{i=1}^n{f}_i{m}_c{q}_i^s}\right\}.$$

Finally, replacing the unknown quantity $m_c$ with its estimate from the observed data $\widehat{m_c}=\frac{A_c}{E_c}$, the expressions simplify as:

$$\begin{array}{ccc}Z\hfill & =\hfill & min\left\{1,\left(\frac{r}{y_p}\right)\left(\frac{{\sum }_{i=1}^n{f}_i{q}_i^s}{\sqrt{{\sum }_{i=1}^n{f}_i{q}_i^s(1-f_i{\widehat{m}}_c{q}_i^s)}}\right)\sqrt{\frac{A_c}{E_c}}\right\}\hfill \\ & \approx \hfill & min\left\{1,\left(\frac{r}{y_p}\right)\sqrt{A_c}\right\}.\hfill \end{array}$$

(10)

Observe that the final expression in Equation (10) is equivalent to the expression in Equation (6). Recall that if $r=0.05$ and $p=0.90$, the approximate expression in Equation (10) becomes:

$$Z=min\left\{1,\sqrt{\frac{A_c}{1082}}\right\}.$$

Similarly, if $r=0.03$ and $p=0.90$, the approximate expression in Equation (10) becomes:

$$Z=min\left\{1,\sqrt{\frac{A_c}{3007}}\right\}.$$

We remark that these parameters and the resulting requirement of 3007 claims for full credibility are prescribed by the Canadian Committee on Life Insurance Financial Reporting (Canadian Institute of Actuaries 2002).

3.3. Greatest Accuracy Formulae

We define the notation as in Section 3.1. Following (Klugman et al. 2009), we suppress the subscripts c and d for count and dollar, respectively. We add the subscript h to emphasize that we are computing the credibility factor for company h, $h=1,\dots ,r$. Thus, for example, $A_h$ is the actual dollar amount (or claim count) for company h, $E_h$ is the expected dollar amount (or claim count), and $f_{hi}$ the fraction of the year for which the ith life from company h was observed. We denote the number of lives in company h by $n_h$.

We let $m_h$ denote the true mortality ratio for company h and we assume that mean and variance of $m_h$ are given by $\mu$ and ${\sigma }^2$, respectively.

We present the formulas for the credibility factors based on dollar amounts and remark that one can compute the credibility factors based on claim counts by setting the benefit amounts $b_{hi}$ equal to 1.

In (Klugman et al. 2009), the authors posit an estimator of the form $Z{\widehat{m}}_h+W$ and use calculus to show that

$$\begin{array}{cc}Z=\frac{E_h}{E_h+\frac{\mu }{{\sigma }^2{E}_h}{B}_h-\frac{{\mu }^2+{\sigma }^2}{{\sigma }^2{E}_h}{C}_h},\hfill & W=(1-Z)\mu \hfill \end{array}$$

minimize the mean squared error

$$E[{(m_h-(Z{\widehat{m}}_h+W))}^2],$$

where

$$\begin{array}{ccc}{B}_h=\sum _{i=1}^{n_h}{b}_{hi}^2{f}_{hi}{q}_{hi}^s\hfill & \mathrm{and}\hfill & C_h=\sum _{i=1}^{n_h}{b}_{hi}^2{f}_{hi}^2{(q_{hi}^s)}^2.\hfill \end{array}$$

Note that the credibility factor for company h depends on the experience data of all companies.

Moreover, we need an estimate for $\mu$ and ${\sigma }^2$. In Klugman et al. (2009), the authors present an intuitive and unbiased estimator for the mean mortality ratio $\mu$,

$$\widehat{\mu }=\frac{{\sum }_{h=1}^r{A}_h}{{\sum }_{h=1}^r{E}_h}=\frac{A}{T}=\frac{\mathrm{total} \mathrm{actual} \mathrm{deaths} \mathrm{over} \mathrm{all} \mathrm{companies}}{\mathrm{total} \mathrm{expected} \mathrm{deaths} \mathrm{over} \mathrm{all} \mathrm{companies}}.$$

To derive an estimator for the variance ${\sigma }^2$, the authors derive formulas for the expected weighted squared error

$$E\left[\sum _{h=1}^r{E}_h{({\widehat{m}}_h-\widehat{\mu })}^2\right]$$

in terms of $\mu$ and ${\sigma }^2$. This results in the estimator

$${\widehat{\sigma }}^2=\frac{{\sum }_{h=1}^r{E}_h{({\widehat{m}}_h-\widehat{\mu })}^2-\widehat{\mu }\left({\sum }_{h=1}^r\frac{B_h}{E_h}-\frac{1}{T}{\sum }_{h=1}^r{B}_h\right)+{\widehat{\mu }}^2\left({\sum }_{h=1}^r\frac{C_h}{E_h}-\frac{1}{T}{\sum }_{h=1}^r{C}_h\right)}{T-\frac{1}{T}{\sum }_{h=1}^r{E}_h^2-{\sum }_{h=1}^r\frac{C_h}{E_h}+\frac{1}{T}{\sum }_{h=1}^r{C}_h}.$$

4. LF Analysis Applied to M Financial’s Data: Qualitative Results

We applied the LF method to M Financial’s data to compute credibility factors for the A/E ratios based on M’s experience data. In this section, we describe our calculations and share some qualitative observations about our results.

We computed the credibility factors using four different methods. For each method, we computed an aggregate credibility factor as well as specific factors for sex and smoker status. Thus, for each of the four methods, we computed five credibility factors: aggregate, male nonsmoker, female nonsmoker, male smoker, and female smoker. In each case, the actual mortality is based on M Financial’s 2012 Preliminary Experience Study and the expected mortality is based on the 2008 VBT.

First, we used the methods described in (Klugman et al. 2009) and Section 3.2 to compute the LF credibility factors for M Financial’s observed A/E ratios based on claim counts. We computed the credibility factors using both the “exact” and approximate expressions given in Equation (10). We denoted the resulting credibility factors by $Z_c^e$ and $Z_c^a,$ respectively. We also computed the credibility factors for the overall mortality rate

$$\widehat{q}=\frac{\mathrm{number} \mathrm{of} \mathrm{claims}}{\mathrm{total} \mathrm{exposures}}.$$

We denoted the resulting credibility factor by $Z_q$. Finally, we used the methods described in Section 3.1 and Section 3.2 above and Section 2a of (Klugman et al. 2009) to compute the LF credibility factors for M Financial’s observed A/E ratios based on amounts—retained net amount at risk (NAR)—instead of claim counts. We denoted the resulting credibility factor by $Z_{NAR}.$

The values of $Z_c^a,Z_c^e$, and $Z_q$ were remarkably close for the aggregate credibility factor and for each sex/smoker status combination. More specifically, the maximum relative difference among the factors was 3%. Thus, while computing a credibility factor for the overall mortality rate $\widehat{q}$ is too simplistic, in this case, the resulting credibility factors were remarkably close to the credibility factors based on claim counts.

The credibility factors $Z_{NAR}$ for the A/E ratio based on retained NAR were significantly lower than the credibility factors based on claim counts. The relative difference ranged from 47% to 64%, depending on the sex/smoker status. This is not surprising. As we observed in Remark 2 of Section 2.1.3, the credibility factor should decrease as the variance increases. When we compute the A/E ratio for NAR, there is an additional source of randomness—namely, whether claims occurred for high-value or low-value policies.

This raises the question of whether to use claim counts or NAR as the basis for the credibility factors. According to (Klugman 2011), “If there is no difference in mortality by amount, there really is no good statistical reason to use amounts. They add noise, not accuracy. If there is a difference, then the mix of sales has an impact. As long as the future mix will be similar, this will provide a more accurate estimate of future mortality.”

5. Qualitative Comparison of Credibility Methods Using a Simulated Data Set

As we described in Section 2, the LF method is easy to apply, as it relies only on company-specific data. However, it has several significant shortcomings. The GA method addresses these shortcomings, but requires data from other companies. Because experience data is proprietary, GA is rarely used in practice.

In this section, we examine the performance of the LF and GA credibility methods on a simulated data set, and we compare the resulting credibility factors with an intuitive, though not mathematically grounded, “credibility factor.”

5.1. Overview

In the simulation, we created a dataset consisting of 1 million individuals. More specifically, we created 20 risk classes or populations of 50,000 individuals each and computed the A/E ratio for each of the risk classes. Expected mortality was based on the 2008 VBT, and actual mortality was based on simulation from the table, or a multiple of it. Thus, the hypothetical means—the A/E ratio for each risk class—were known. To generate the experience data, we sampled from the risk classes and computed the observed A/E ratios.

Then, given the observed A/E ratios, the “industry average” (expected value of the hypothetical means or overall A/E ratio for the universe), and the known hypothetical means, we computed credibility factors three different ways: GA, LF, and an intuitively pleasing (though not mathematically grounded) benchmark credibility factor. We applied the GA and LF methods as in (Klugman et al. 2009).

We contrast the credibility results in a series of figures. The most notable result is that LF with the “standard” range and probability parameters yielded a significantly lower credibility factor than the other methods when the number of claims was small. Thus, the LF method might understate the credibility for companies with good mortality experience.

5.2. Generating the “Universe”

We generated 20 risk classes, or populations, of 50,000 people each. Thus, the universe consisted of 1 million individuals. Each of the 20 populations had a different age distribution and had an A/E ratio prescribed a priori. More specifically, the A/E ratio for each risk class was prescribed by scaling the 1-year 2008 VBT probabilities $q_x$ by a multiplier ${\alpha }_h\in \{0.73,0.76,\dots ,1.30\},h=1,\dots ,20$.

Using the scaled 2008 VBT table, we computed ${}_t{q}_x$ for $t\le 20$ and for various values of x. These values gave the cumulative distribution function (CDF) of the random variable $T(x)$, the remaining future lifetime of $(x)$. Then, we generated the outcomes of $T(x)$ in the usual way. Namely, we generated outcomes from the uniform distribution on $(0,1)$ and inverted the CDF to determine the outcome of the random variable $T(x)$. If $T(x)<20$, then a claim occurred during the 20-year period; otherwise, no claim occurred.

We then calculated the following:

• The ratio $m_h$ of actual deaths to expected deaths over the 20-year time period, $h=1,\dots ,20$. In other words, we computed the hypothetical mean for each of the 20 risk classes. These values ranged from 0.71 to 1.28.
• The overall A/E ratio $\mu =0.95$ for the universe of 1 million individuals.

5.3. Generating the Experience Data and Computing the LF and GA Credibility Factors

We then generated experience data for each of the 20 risk classes. We viewed the experience data as the experience of a particular company, as in (Klugman et al. 2009). We fixed the number n of policyholders (e.g., $n=500,n=1500,\dots$) and randomly selected n “lives” from each of the risk classes. We computed the observed A/E ratio ${\widehat{m}}_h$ and we computed the credibility factors ${\tilde{Z}}_h^{LF}$ and ${\tilde{Z}}_h^{GA}$ using the LF and GA methods, respectively, as described in (Klugman et al. 2009) and in Section 3.

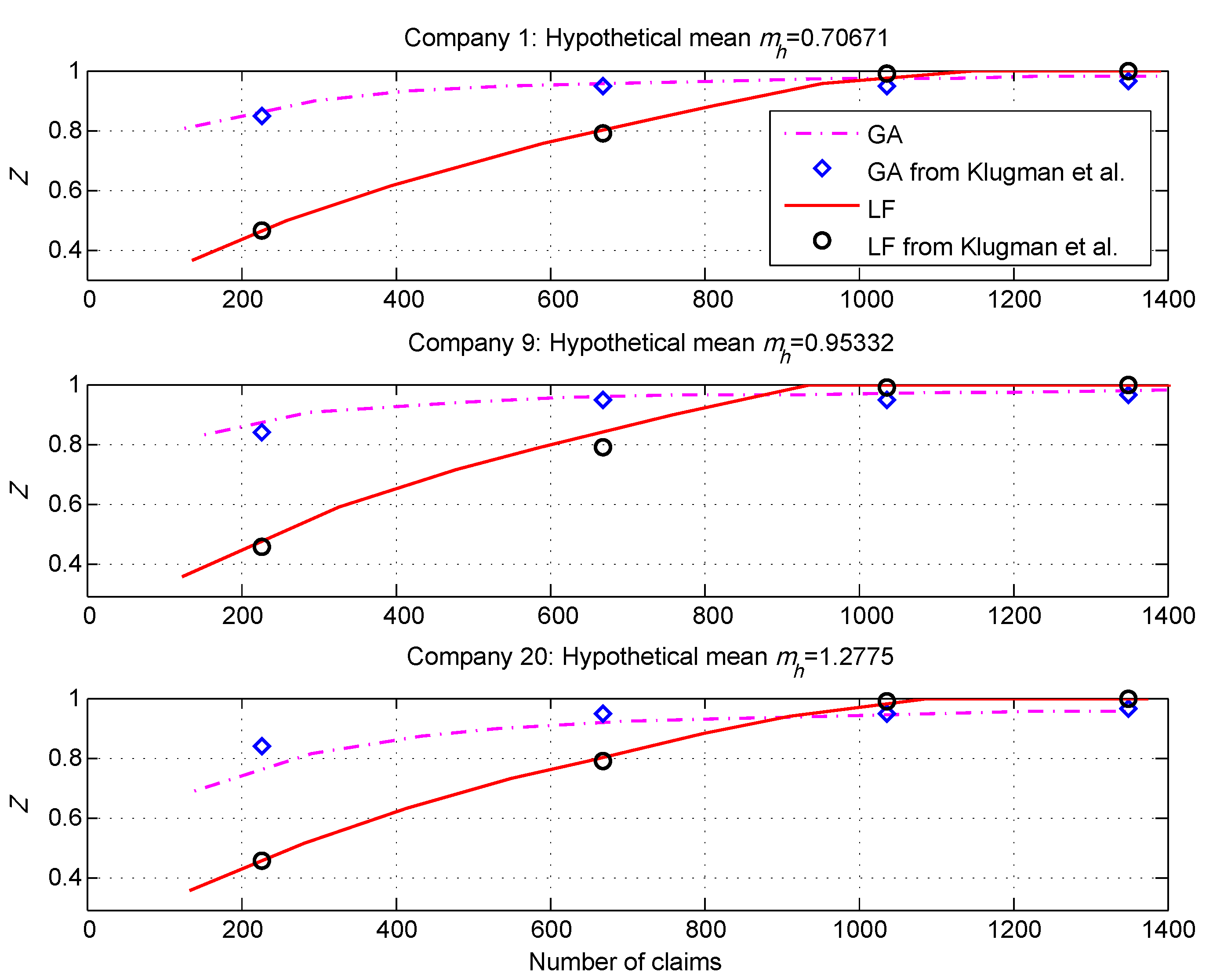
In Figure 1, we show the LF and GA credibility factors for three “companies” (risk classes) from our simulated data set and contrast our results with the results from (Klugman et al. 2009), which are based on real data. The results are remarkably consistent.

We observe that, without exception, the LF factors were considerably lower than the GA factors for small numbers of claims. We observed further as the number of claims approached the LF threshold for full credibility, the LF factors exceeded the GA factors. It is not surprising that the factors differed significantly or that the curves would cross, as the underlying methods are so different. A similar phenomenon was observed in (Klugman et al. 2009).

5.4. An Intuitively Appealing Benchmark “Credibility Factor”

We wanted to compare the LF and GA credibility factors with an intuitively appealing benchmark. To achieve this, we posed the question, “In repeated draws of experience data from the risk classes, how frequently is the observed A/E ratio ${\widehat{m}}_h$ closer than the ‘industry average’ $\mu$ to the true value (hypothetical mean) $m_h$?” Thus, we generated 2000 trials of experience data for n policyholders from each risk class.

We introduce the following notation.

• Let h refer to the risk class or population; $h=1,\dots ,20$.
• Let $n=$ number of policyholders in the company’s experience data; $n=500,1500,\dots$
• Let $i=$ trial; $i=1,\dots ,2000$.
• Let $\mu =$ the A/E ratio for the universe of 1 million individuals. In the simulation, we had $\mu \approx 0.95$.
• Let ${\widehat{m}}_{hni}=$ the observed A/E ratio for company h, trial i, when there are n policyholders in the group.
• Let $m_h$ be the true A/E ratio for population h. Recall that this was prescribed a priori when we generated the 20 populations.
• Let $Z_{hn}$ be the credibility factor for company h when there are n policyholders in the group.

We computed an intuitively appealing benchmark credibility factor $Z_{hn}$ as follows. For each of the 2000 trials, define

$$I_{hni}=\left\{\begin{array}{cc}1\hfill & |{\widehat{m}}_{hni}-m_h|<|\mu -m_h|,\\ 0\hfill & \mathrm{otherwise}.\end{array}\right.$$

Thus, $I_{hni}$ indicates whether the observed A/E ratio ${\widehat{m}}_{hni}$ or the “industry average” $\mu =0.95$ is more representative of the true mean $m_h$.

Then, we define $Z_{hn}=\frac{1}{2000}{\sum }_{i=1}^{2000}{I}_{hni}$. Thus, $Z_{hn}$ computed this way is the proportion of the 2000 trials for which the experience data was more representative of the risk class’s A/E ratio than the universe’s A/E ratio $\mu$.

This definition of Z has intuitive appeal. The weight given to ${\widehat{m}}_h$ should be the proportion of the time that it is a better representation of the true mean $m_h$ than $\mu$. However, we emphasize that there is no mathematical underpinning for this choice. It seems that we could just as easily use the square root of the proportion, or the proportion squared, for example. Moreover, in practice, one could not compute the benchmark factor. The benchmark factor simply allows us to compare, in our simulated universe, the LF and GA results with an intuitively appealing measure.

We wish to compare the benchmark factor to the LF and GA factors computed in Section 5.3. To make the comparison meaningful, we must express $Z_{hn}^B$ as a function of the number of claims. Thus, we introduce the following notation:

• Let $d_{hni}=$ actual number of deaths for company h, trial i, when there are n policyholders.
• Let $d_{hn}=\frac{1}{2000}{\sum }_{i=1}^{2000}{d}_{hni}$. That is, $d_{hn}$ is the average actual number of deaths over the 2000 trials for company h when there are n policyholders.
• Denote $d_{hn}$ by $d_h$. We will suppress the index n. Observe that $d_h$ is analogous to $A_h$, the actual number of claims for company h, from (Klugman et al. 2009).
• Let ${\tilde{Z}}_{hd}^B$ be the benchmark credibility factor for company h when there are d claims. Thus we express the credibility factor $\tilde{Z}$ as a function of $d_h=d_{hn}$. This will make the comparison with the LF and GA results meaningful.
• Let ${\tilde{Z}}_{hd}^{LF}$ and ${\tilde{Z}}_{hd}^{GA}$ be the credibility factors for company h when there are d claims computed via the LF and GA methods, respectively. We computed these factors in Section 5.3.

5.5. Qualitative Comparison of the Credibility Methods

We computed the benchmark factor in Section 5.4. We also computed credibility factors for the simulated data set using the GA and LF methods as in (Klugman et al. 2009). For LF, we used the common parameter choices $r=0.05$ and $p=0.9$ and the Canadian standard $r=0.03$ and $p=0.9$ (Canadian Institute of Actuaries 2002). In other words, under the LF method, we assigned full credibility if the probability that the relative error in the A/E ratio is less than 0.05 (or 0.03) was at least 90%. Recall that from the approximate expression in Equation (10), these parameter choices yielded 1082 and 3007 claims, respectively, as the standards for full credibility.

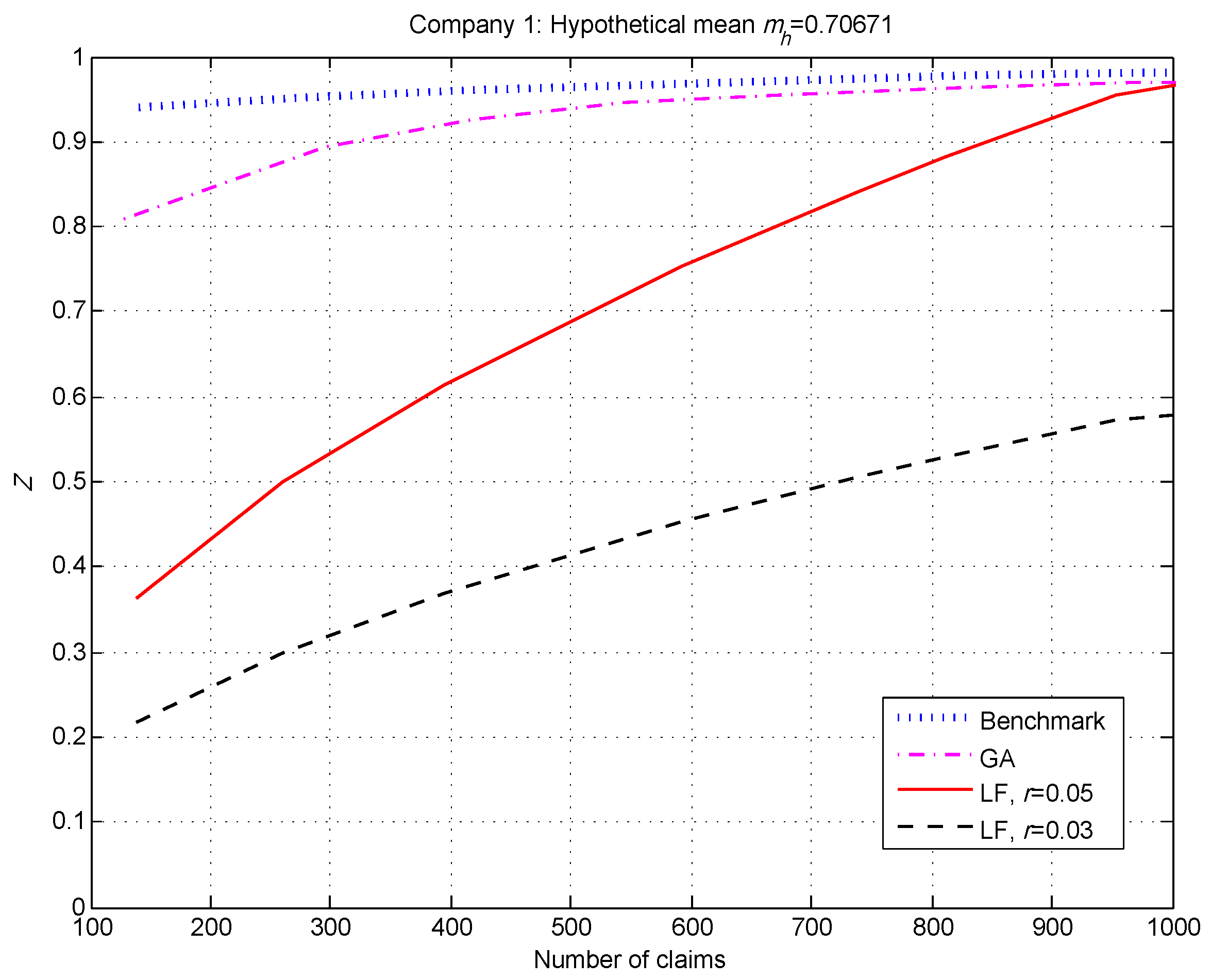
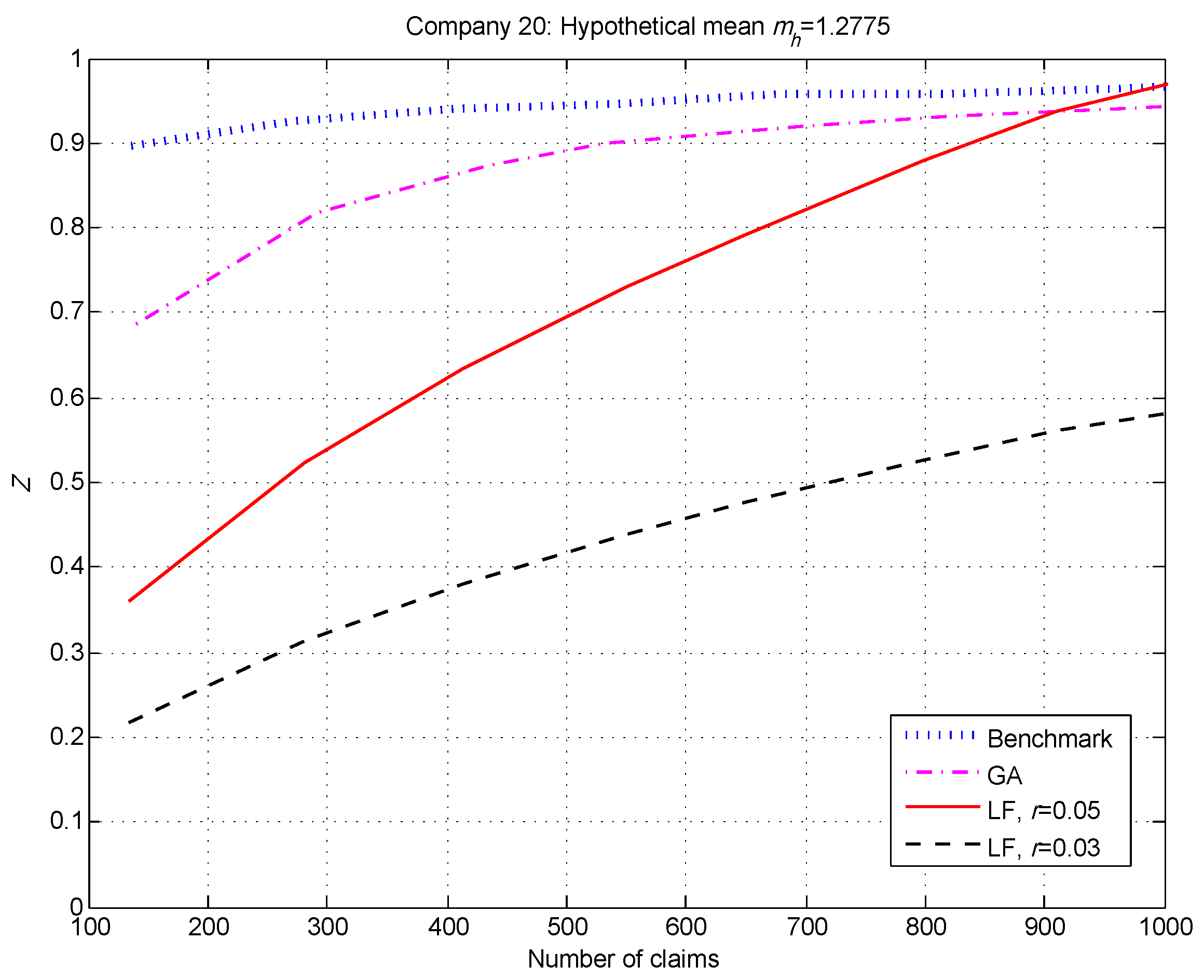
We summarize our observations for the 20 companies (risk classes) below, and show the credibility factors for 3 of the 20.

• Generally speaking, the benchmark and GA factors were similar and considerably higher than the LF factors when the number of claims was small—see Figure 2 and Figure 3.
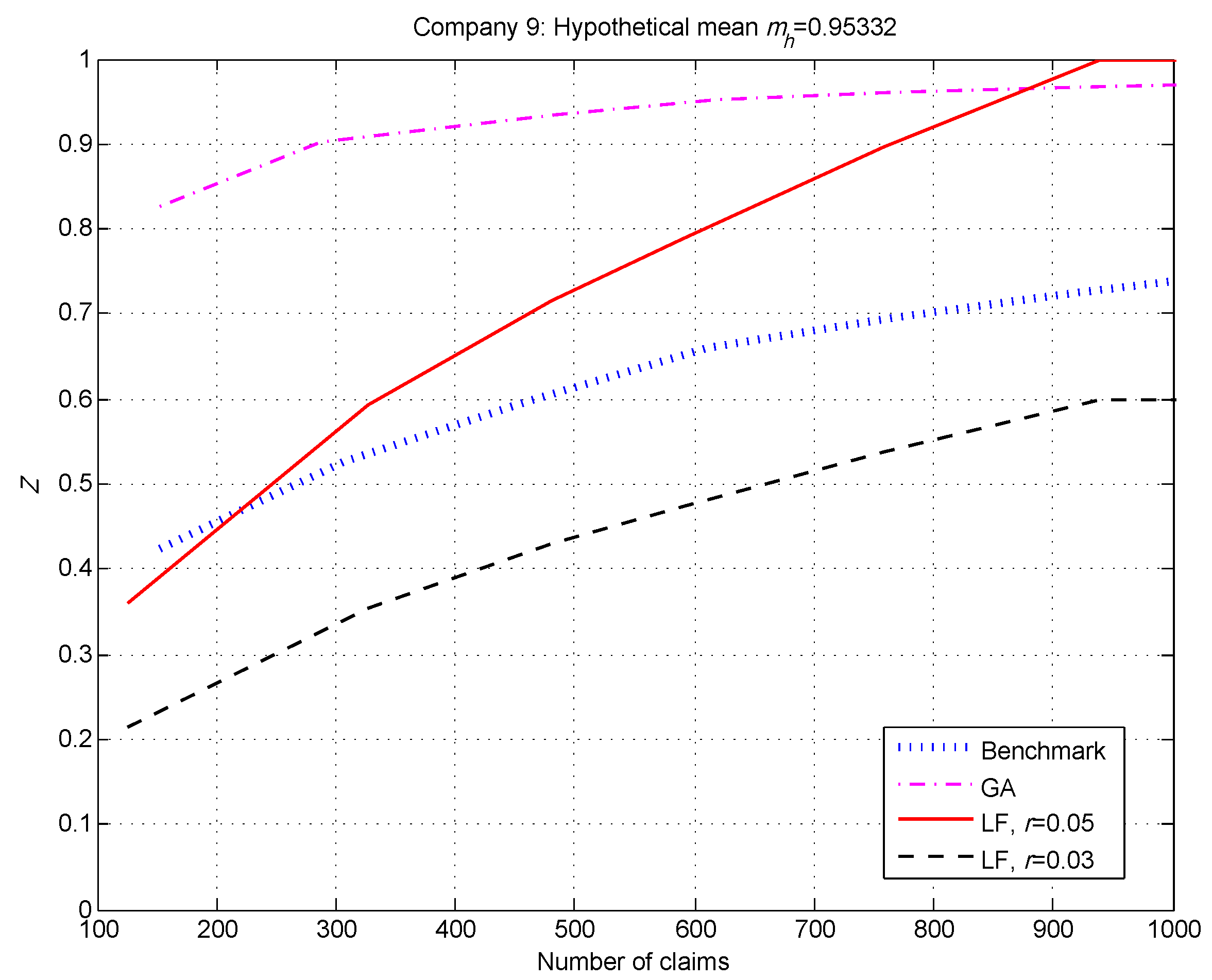
• The exception to Observation 1 occurred when the hypothetical mean $m_h$ was close to the overall population mean $\mu \approx 0.95$—see Figure 4. This is not surprising, as the benchmark factor is the relative frequency in 2000 trials that the observed A/E ratio ${\widehat{m}}_h$ is closer to the true hypothetical mean $m_h$ than the overall population mean $\mu$. When $m_h$ is very close to $\mu$, it is unlikely that ${\widehat{m}}_h$ will land closer—that is, the event $|{\widehat{m}}_h-m_h|<|\mu -m_h|$ is unlikely, resulting in a smaller benchmark Z.
• For our simulated data set, and for the real data in (Klugman et al. 2009), the GA method produced significantly higher credibility factors at low numbers of claims than the LF method with $r=0.05$. Of course, the difference was even more pronounced when we chose the Canadian standard $r=0.03$.

6. Conclusions and Recommendations

Without exception, the LF factors based on the full credibility requirement of 1082 claims were significantly lower than the GA factors when the number of claims was small. Of course, the disparity was greater when we used 3007 as the standard for full credibility.

Our analysis suggests that the LF method may significantly understate the appropriate credibility factor for populations with exceptionally good mortality experience, such as M Financial’s clientele. Thus, our analysis provides support for awarding higher credibility factors than the LF method yields when the number of claims is low.

The NAIC recognizes that there is a need for life insurance experience data in support of PBR. The PBR Implementation Task Force are developing an Experience Reporting Framework for collecting, warehousing, and analyzing experience data. This is ongoing work; see (AAA 2016) and (NAIC 2016), for example.