On the Failure to Reach the Optimal Government Debt Ceiling
Abstract
:1. Introduction
1.1. Economic Motivations
1.2. Contributions
2. The Bounded Government Intervention Model
3. The Value Function and the Verification Theorem
4. The Solution
4.1. Construction of the Solution
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- .
4.2. Verification of the Solution
4.3. The Debt Policy Generated by the Optimal Debt Ceiling
4.4. Numerical Solutions
5. Time to Reach the Debt Ceiling
5.1. The Theoretical Result
- (i)
- If or, equivalently, , then
- (ii)
- If or, equivalently, , thenwhere and is the Gamma function, and is the incomplete Gamma function defined byFurthermore,
5.2. Application 1: Countries with Big Economic Growth
5.3. Application 2: Countries with Moderate Economic Growth
5.4. Application 3: Time to Reach the Optimal Debt Ceiling
6. Comparative Statics Analysis
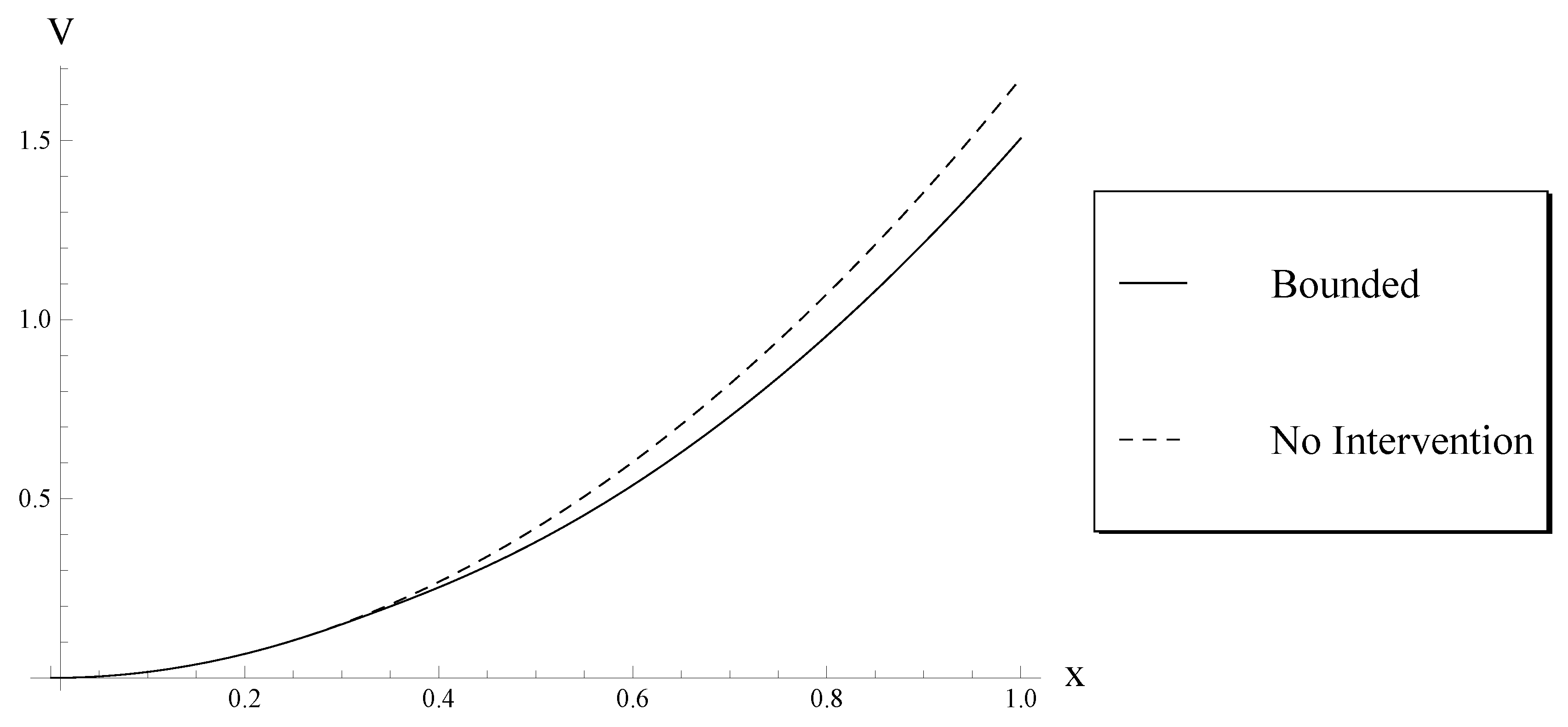
- Compare the results of the debt policy associated with the optimal debt ceiling with the policy of non-government intervention.
- Compare the results of the debt policy associated with the optimal debt ceiling presented in this paper with the policy derived in the unbounded model of Cadenillas and Huamán-Aguilar (2016).
- Analyze the effects of some parameters on the optimal debt ceiling.
6.1. The Debt Policy Associated with the Optimal Debt Ceiling versus the Non-Intervention Policy
6.2. The Bounded Model versus the Unbounded Model
6.3. The Effects of , g, and on the Optimal Debt Ceiling
7. Summary of Analysis
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Proof of Proposition 2
Appendix C. Proof of Lemma 2
Appendix D. Proof of Proposition 3
Appendix E. Mathematica Code
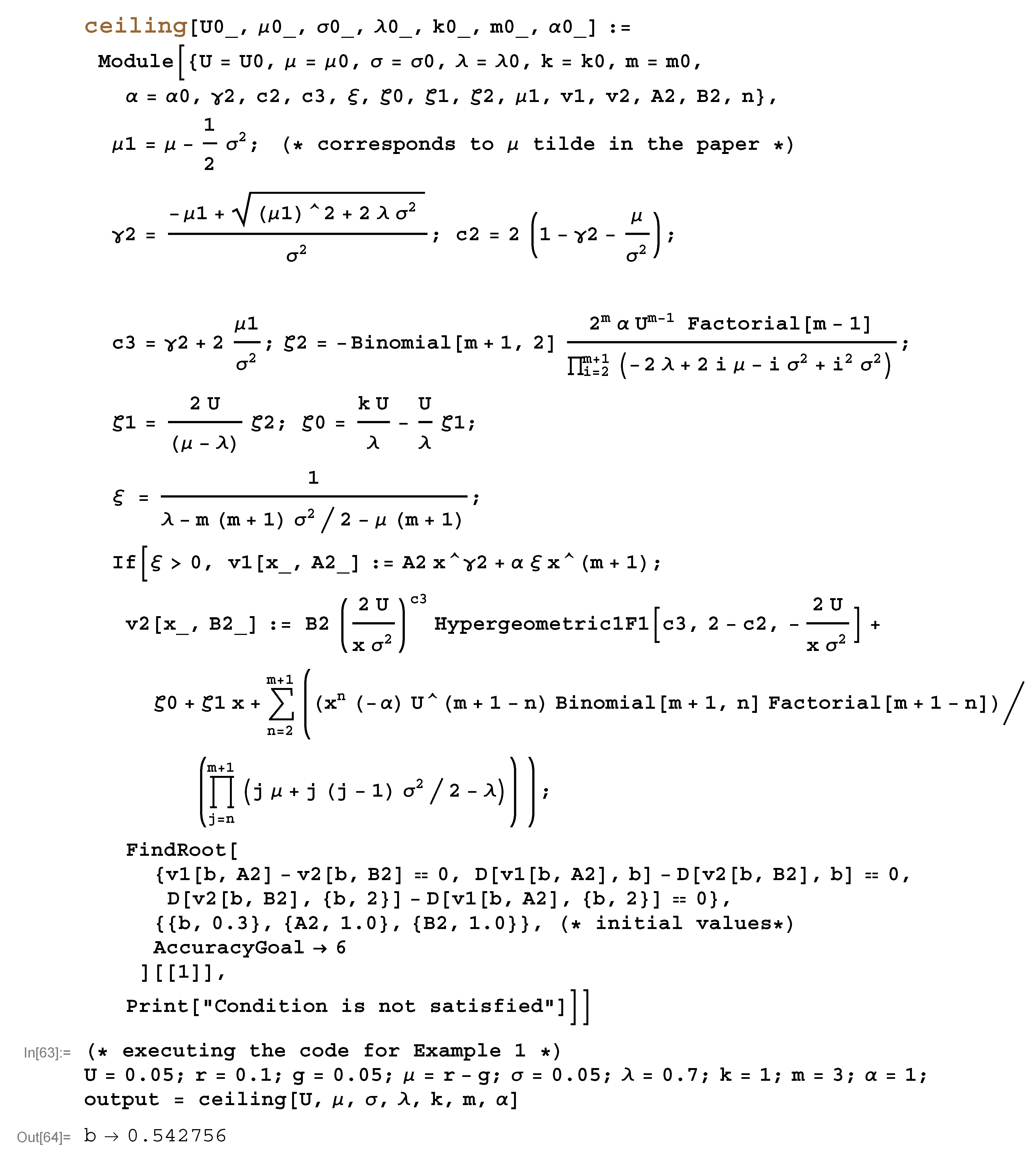
References
- Aiyagari, S. Rao, and Ellen R. McGrattan. 1998. The optimum quantity of debt. Journal of Monetary Economics 42: 447–69. [Google Scholar] [CrossRef]
- Balassone, Fabrizio, and Daniele Franco. 2000. Assessing fiscal sustainability: A review of methods with a view to EMU. In Fiscal Sustainability. Edited by Banca d’Italia. Rome: Bank of Italy, pp. 21–60. [Google Scholar]
- Barro, Robert J. 1989. The Ricardian approach to budget deficits. Journal of Economic Perspectives 3: 37–54. [Google Scholar] [CrossRef]
- Barro, Robert J. 1999. Notes on optimal debt management. Journal of Applied Economics 2: 281–89. [Google Scholar]
- Bell, William Wallace. 2004. Special Functions for Scientists and Engineers. Mineola: Dover Publications Inc. [Google Scholar]
- Blanchard, Olivier J., Jean-Claude Chouraqui, Robert Hagemann, and Nicola Sartor. 1990. The sustainability of fiscal policy: New answers to an old question. OECD Economic Studies 15: 7–36. [Google Scholar]
- Blanchard, Olivier. 2017. Macroeconomics, 7th ed. Boston, USA: Pearson Ed. Inc. [Google Scholar]
- Bohn, Henning. 1995. The sustainability of budget deficits in a stochastic economy. Journal of Money, Credit, and Banking 27: 257–71. [Google Scholar] [CrossRef]
- Brandimarte, Paolo. 2002. Numerical Methods in Finance: A MATLAB-Based Introduction. Hoboken: John Wiley & Sons. [Google Scholar]
- Cadenillas, Abel, and Ricardo Huamán-Aguilar. 2016. Explicit formula for the optimal government debt ceiling. Annals of Operations Research 247: 415–49. [Google Scholar] [CrossRef]
- Cadenillas, Abel, and Fernando Zapatero. 1999. Optimal Central Bank intervention in the foreign exchange market. Journal of Economic Theory 87: 218–42. [Google Scholar] [CrossRef]
- Council of the European Communities. 1992. Treaty on European Union. Brussels and Luxembourg: ECSC-EEC-EAEC. [Google Scholar]
- Das, Udaibir S., Michael Papapioannou, Guilherme Pedras, Faisal Ahmed, and Jay Surti. 2010. Managing Public Debt and Its Financial Stability Implications. Working Paper 10/280. Washington, DC, USA: IMF. [Google Scholar]
- Domar, Evsey D. 1944. The “Burden of the Debt” and the National Income. The American Economic Review 34: 798–827. [Google Scholar]
- Dornbusch, Rudiger, and Mario Draghi, eds. 1990. Public Debt Management: Theory and History. Cambridge: Cambridge University Press. [Google Scholar]
- Eaton, Jonathan, and Mark Gersovitz. 1981. Debt with potential repudiation: Theoretical and empirical analysis. Review of Economic Studies 48: 289–309. [Google Scholar] [CrossRef]
- Ferrari, Giorgio. 2018. On the Optimal Management of Public Debt: A Singular Stochastic Control Problem. SIAM Journal on Control and Optimization 56: 2036–73. [Google Scholar] [CrossRef]
- Fleming, Wendell H., and Halil Mete Soner. 2006. Control Markov Processes and Viscosity Solutions, 2nd ed. New York: Springer. [Google Scholar]
- Gersbach, Hans. 2014. Government Debt-Threshold Contracts. Economic Enquiry 52: 444–58. [Google Scholar] [CrossRef]
- Ghosh, Atish, Jun I. Kim, Enrique Mendoza, Jonathan Ostry, and Mahvash Qureshi. 2013. Fiscal Fatigue, Fiscal Space and Debt Sustainability in Advanced Economies. The Economic Journal 123: 4–30. [Google Scholar] [CrossRef]
- Holmstrong, Bengt, and Jean Tirole. 1998. Private and public supply of liquidity. The Journal of Political Economy 106: 1–40. [Google Scholar] [CrossRef]
- Huamán-Aguilar, Ricardo, and Abel Cadenillas. 2015. Government Debt Control: Optimal Currency Portfolio and Payments. Operations Research 63: 1044–57. [Google Scholar] [CrossRef]
- IMF and World Bank. 2001. Guidelines for Public Debt Management. Discussion Paper. Washington: IMF and World Bank. [Google Scholar]
- IMF and World Bank. 2003. Guidelines for Public Debt Management. Amended Version. Discussion Paper. Washington: IMF and World Bank. [Google Scholar]
- IMF. 2002. Assessing Sustainability. Washington: IMF. [Google Scholar]
- Karlin, Samuel, and Howard Taylor. 1975. A First Course in Stochastic Processes, 2nd ed. New York: Academic Press. [Google Scholar]
- Karlin, Samuel, and Howard Taylor. 1981. A Second Course in Stochastic Processes. New York: Academic Press. [Google Scholar]
- Kristensson, Gerhard. 2010. Second Order Differential Equations, Special Functions and Their Classification. New York: Springer. [Google Scholar]
- Kydland, Finn E., and Edward C. Prescott. 1977. Rules rather than discretion: The inconsistency of optimal plans. Journal of Political Economy 85: 473–91. [Google Scholar] [CrossRef]
- Mas-Colell, Andreu, Michael Dennis Whinston, and Jerry R. Green. 1995. Microeconomic Theory. New York: Oxford University Press. [Google Scholar]
- Neck, Reinhard, and Jan-Egbert Sturm, eds. 2008. Sustainability of Public Debt. Cambridge: MIT Press. [Google Scholar]
- Ostry, Jonathan David, Atish R. Ghosh, Jun I. Kim, and Mahvash S. Qureshi. 2010. Fiscal Space. Staff Position Paper no SPN/10/11. Washington DC, USA: IMF. [Google Scholar]
- Pratt, John W. 1964. Risk aversion in the small and in the large. Econometrica 32: 122–36. [Google Scholar] [CrossRef]
- Romer, David. 2002. Advanced Macroeconomics, 2nd ed. New York: McGraw-Hill/Irwin. [Google Scholar]
- Ross, Sheldon M. 1996. Stochastic Processes, 2nd ed. New York: John Wiley & Sons, Inc. [Google Scholar]
- Shah, Anwar, ed. 2005. Fiscal Management. Washington: The World Bank. [Google Scholar]
- Taylor, John B. 1979. Estimation and control of a macroeconomic model with rational expectations. Econometrica 47: 1267–86. [Google Scholar] [CrossRef]
- Uctum, Merih, and Michael R. Wickens. 2000. Debt and Deficit Ceilings, and Sustainability of Fiscal Policies: An Intertemporal Analysis. Oxford Bulletin of Economics and Statistics 62: 197–222. [Google Scholar] [CrossRef]
- Wheeler, Graeme. 2004. Sound Practice in Government Debt Management. Washington, DC: The World Bank. [Google Scholar]
- Woo, Jaejoon, and Manmohan S. Kumar. 2015. Public Debt and Growth. Economica 82: 705–739. [Google Scholar] [CrossRef]
| 1 | That was simply the median of the debt ratios of those European countries. Although it was not binding, it was considered as a reference value. For more details, please see Footnote 3 of this paper. |
| 2 | Optimal debt is the debt ratio that arises as a result of welfare analysis considering that debt, on the one hand, smooths consumption and, on the other hand, has negative effects in wealth distribution; see, for example, Aiyagari and McGrattan (1998) or Barro (1999). Credit ceiling is the level of debt above which the country is not allowed to borrow in the financial markets; see, for example, Eaton and Gersovitz (1981). Debt limit is the debt level at which a debt crises takes place; see, for instance, Ostry et al. (2010). |
| 3 | Article 104c of the Maastricht Treaty Council of the European Communities (1992) says the following: “2. The Commission shall monitor the development of the budgetary situation and of the stock of government debt in the Member States with a view to identifying gross errors. In particular, it shall examine compliance with budgetary discipline on the basis of the following two criteria: (a) whether the ratio of the planned or actual government deficit to gross domestic product exceeds a reference value, unless either the ratio has declined substantially and continuously and reached a level that comes close to the reference value;—or, alternatively, the excess over the reference value is only exceptional and temporary and the ratio remains close to the reference value; (b) whether the ratio of government debt to gross domestic product exceeds a reference value, unless the ratio is sufficiently diminishing and approaching the reference value at a satisfactory pace. The reference values are specified in the protocol on the excessive deficit procedure annexed to this Treaty”. In the Maastricht Treaty, the “ratio of the planned or actual government deficit to gross domestic product” is the debt ratio, and the “reference value” is the debt ceiling (which was selected as 60%). Thus, the Maastricht Treaty does not mention explicitly any bound for the government interventions. Similarly, the debate in the USA Senate about the selection of the debt ceiling does not mention any bound for the government interventions. |
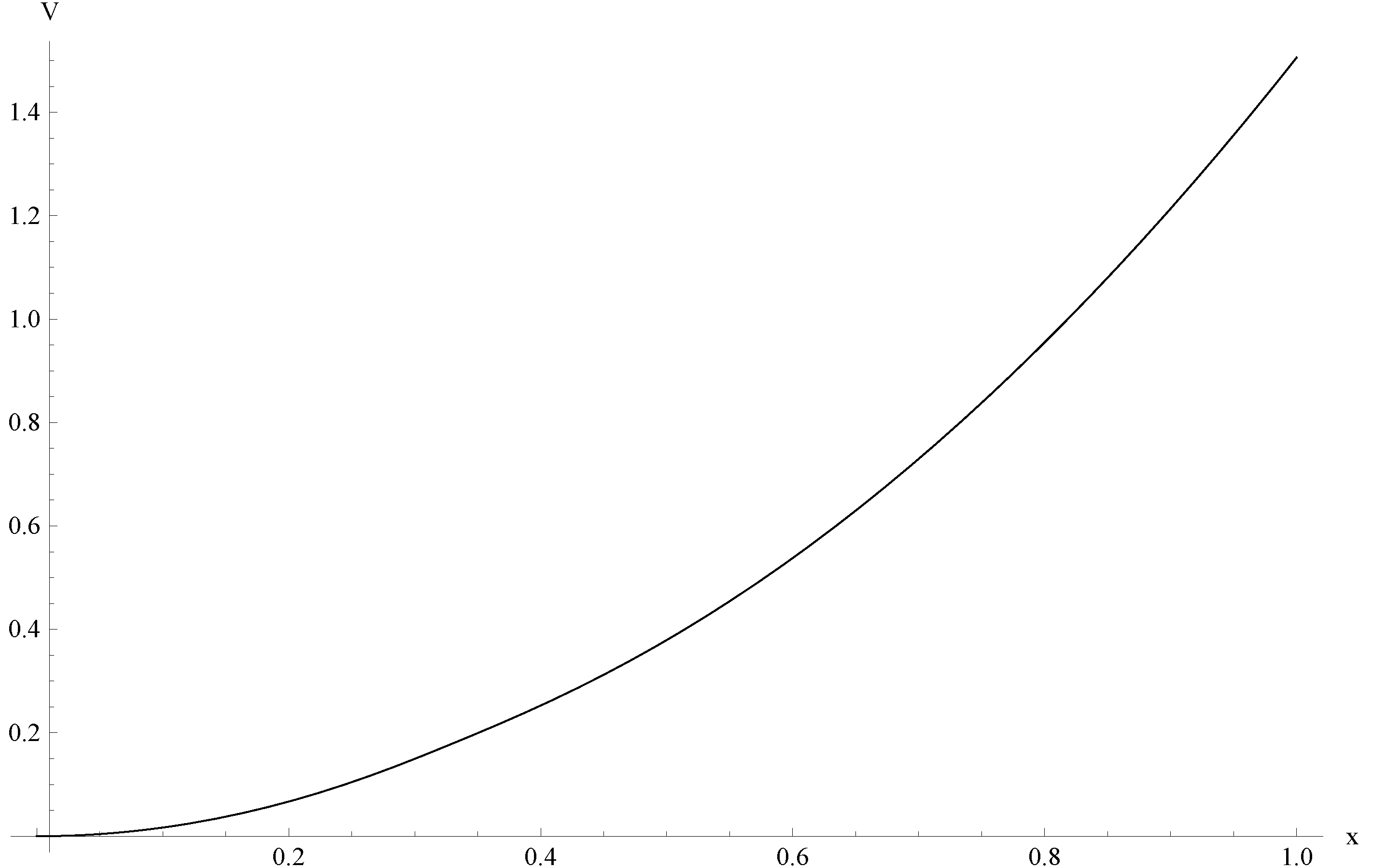
| c | |||
|---|---|---|---|
| 0.60 | 0.01538 | 0.00000 | |
| 0.60 | 0.19876 | 0.00000 | |
| 0.60 | 0.99542 | 0.00215 | |
| 0.60 | 1.00000 | 0.89679 | |
| 0.60 | 1.00000 | 0.99998 |
| b | |||
|---|---|---|---|
| 0.60982 | 0.02356 | 0.00000 | |
| 0.62576 | 0.29127 | 0.00000 | |
| 0.64324 | 0.99598 | 0.00215 | |
| 0.65495 | 1.00000 | 0.89679 | |
| 0.65808 | 1.00000 | 0.99998 |
| b | 0.300024 | 0.310426 | 0.331213 | 0.331325 | 0.331352 |
| 0.609820 | 0.310426 | 0.241035 | |
| 0.662425 | 0.331283 | 0.254845 | |
| 0.662704 | 0.331352 | 0.254886 | |
| 0.310426 | 0.263990 | 0.253090 | |
| 0.331283 | 0.303408 | 0.282346 | |
| 0.331352 | 0.303466 | 0.282397 | |
| 0.310426 | 0.301363 | 0.295110 | |
| 0.331283 | 0.349697 | 0.359007 | |
| 0.331352 | 0.350220 | 0.359954 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadenillas, A.; Huamán-Aguilar, R. On the Failure to Reach the Optimal Government Debt Ceiling. Risks 2018, 6, 138. https://doi.org/10.3390/risks6040138
Cadenillas A, Huamán-Aguilar R. On the Failure to Reach the Optimal Government Debt Ceiling. Risks. 2018; 6(4):138. https://doi.org/10.3390/risks6040138
Chicago/Turabian StyleCadenillas, Abel, and Ricardo Huamán-Aguilar. 2018. "On the Failure to Reach the Optimal Government Debt Ceiling" Risks 6, no. 4: 138. https://doi.org/10.3390/risks6040138
APA StyleCadenillas, A., & Huamán-Aguilar, R. (2018). On the Failure to Reach the Optimal Government Debt Ceiling. Risks, 6(4), 138. https://doi.org/10.3390/risks6040138






