Abstract
Scientific discussions have emphasized that the main problem with the current deposit insurance system is that the current system does not evaluate the risks that banks assume to calculate the deposit insurance premiums in many countries of the European Union (E.U.). Thus, the prevailing system does not safeguard a sufficient level of stability in the banking system. Scientific studies show that the deposit insurance system should consider not only the risk indicators for individual banks, but it must also consider the systemic risk of banks that affects the stability of the banking system. Hence, the question arises as to whether measurements of systemic risk in a common E.U. risk-based deposit insurance system are a formal necessity or if they are a value-adding process. Expanding the discussion of scientists, this article analyzes how contributions to insurance funds would change the banks of Lithuania following the introduction of the E.U.’s overall risk-based deposit insurance system and after taking into consideration the additional systemic risk. The research results that were obtained provide evidence that the introduction of a risk-based deposit insurance system would redistribute payments to the deposit insurance fund between banks operating in Lithuania, and, thereby, would contribute to a reduction in the negative effects of the deposit insurance system and would improve the stability in the financial system.
1. Introduction
One of the major ways in which banks raise funds is through deposit-taking. The importance of this activity for banks is undeniable, and the major effective principles of a deposit insurance system have been defined by the Bank for International Settlements (Bank for International Settlements 2014). In June 2009, the Bank for International Settlements and the Basel Committee presented the main principles for an effective deposit insurance system for the first time, which have been subsequently updated every few years. The basic functions and objectives of deposit insurance are to protect consumers and to improve the stability of the financial markets that are provided for in European Directive 94/19/EC due to guarantee schemes (Gerhardt and Lannoo 2011). The efficiency of a deposit insurance system depends on three factors, which are: The macro-economic environment of the financial system’s structure, the regulation of risk restriction and supervision, and the legal and judicial systems as well as the accounting and disclosure systems. So, identically designed deposit insurance systems may not have the same effects on the financial system’s stability and the protection of depositors due to differences in the environment under which they operate. A deposit insurance system not only contributes to the protection of depositors, it also affects the decisions that their own bank makes and the whole banking system (Andries and Nistor 2016; Allen et al. 2011; Ellis 2013; Enkhbold and Otgonshar 2013; Gómez-Fernández-Aguado et al. 2014; Ioannidou and Penas 2010; Prean and Stix 2011). The global financial crisis, which has disclosed the instability of the banking system, has shown that the main problems that are associated with the banking business are the extent of the risks that banks assume and the small volume of insurance that is available to their customers and depositors. An important aspect of a deposit insurance system is to have the deposit insurance fund be of an optimal size, since the financing of a deposit insurance system is different in European Union (E.U.) countries.
Scientific discussions (Bernet and Walter 2009; Gerhardt and Lannoo 2011; Gómez-Fernández-Aguado and Partal-Ureña 2013) that have been conducted previously cover the main types of financing for deposit insurance systems that are prevalent, such as ex-ante, ex-post, and mixed, because all of the deposit insurance contributions that are made up until the occurrence of the insured event are valid in 13 E.U. countries, which is based on the regular collection of contributions to the fund. The main advantage of this type of financing is that all of the contributions that are collected from the members, including the poorly managed banks, can be used immediately in the event of financial instability (Gerhardt and Lannoo 2011).
Upon analyzing the peculiarities of the deposit insurance system, and focusing on certain forms of the importance of deposit insurance, it has been found that this is valid for modern banking systems around the world. Demirguc-Kunt et al. (2014) and Gerhardt and Lannoo (2011), conducting research on implicit and explicit deposit insurance systems, have found that that an implicit deposit insurance system has a positive impact on the entire financial system. On the other hand, Altunb and Thornton (2013) have opined that the usage of an explicit deposit insurance system increases the level of private capital inflows, which, in turn, determines that countries with an explicit deposit insurance system are more attractive to depositors and investors due to the anticipated additional security measures that banks will take because of the deposit insurance that will enable them to provide higher returns. The importance of the implicit system has also been highlighted by Boyle et al. (2015), who stated that the respondents from countries that were faced with a hypothetical bank collapse, where there was no explicit deposit insurance system in place, would withdraw a higher proportion of their funds from the insured accounts and would be required to pay higher interest rates for these accounts than those respondents whose countries had in place an explicit deposit insurance system. The influence of an explicit deposit insurance system on the banking crises largely depends on the overall economic development of the country, since the deposit insurance system in less-developed countries would interact with the country’s economic development, and, thereby, would create higher probabilities of banking crises (Khan and Dewan 2011). However, almost all of the countries in Europe have an explicit deposit insurance system in place, which typically insures deposits up to the statutory limit of compensation. Therefore, it is necessary to look for opportunities that would ensure financial stability in countries that are less developed in terms of the economy.
In most member states of the E.U., and in the countries of the European Economic Area, the same deposit insurance rates are valid. However, it is often observed that countries issue guarantees that exceed the pre-determined limits during banking crises (Cannas et al. 2014). The deposit insurance systems that are valid in the E.U. provide insufficient protection for depositors, since contributions are not based on a risk assessment of the banks, which means that one of the basic functions of deposit insurance is not considered. Therefore, the E.U. has attempted to create a common deposit insurance system, based on an assessment of the risk that banks assume, for several years now. Since 2008, the European Commission has presented three different deposit insurance systems, the latest of which was introduced only in the middle of 2015. Scientific discussions (Acharya et al. 2011; Andries and Nistor 2016; Brownlees and Engle 2011; De Jonghe et al. 2015; Laeven et al. 2014, 2016; Londono and Tian 2014; Mensah and Premaratne 2017; Oordt and Zhou 2015) have focused their attention on the fact that the system that prevails in many E.U. countries does not evaluate the risks that banks assume to calculate the deposit insurance premiums. Therefore, the present system does not provide sufficient stability to the banking system, while contributing to the systemic growth of risk among banks through the increasing number of links among banks and the banking integration interface.
Systemic risk is especially important in today’s financial system, where there is significant banking interdependence, and regulatory authorities can no longer afford to deal with, and focus only on, the risk that an individual bank faces. Therefore, researchers emphasize analyzing the deposit insurance system and evaluating systemic risk to create an effective deposit insurance system (Acharya et al. 2010; Allen and Tang 2016; Laeven et al. 2016; Lee et al. 2015). According to Acharya et al. (2010), an effective assessment of deposit insurance premiums would include an evaluation of systemic risk, which would essentially justify the need for deposit insurance. Leur et al. (2017) observed that the global financial crisis of 2008, and the later debt crisis in the European countries, determined the continuing interest in spreading systemic risk across the institutions that constitute the financial system. Thus, the ambition of the E.U. to develop and implement a unified risk-based deposit insurance system through the scientific research that demonstrates the importance of systemic risk shows the gravity of the problem and highlights this research’s practical significance. However, it is necessary to consider whether measurements of systemic risk in a common European Union risk-based deposit insurance system are a formal necessity or if they are a value-adding process. In answering this question, and contributing to the ongoing scientific debate on what impact the collection of contributions would have on the introduction of a common E.U. risk-assessment-based deposit insurance system and the systemic risk assessment, this study aims to determine how contributions to the insurance fund of banks that operate in Lithuania would change after the introduction of a general E.U. risk-based deposit insurance system, in addition to performing a systemic risk assessment of the system.
The remainder of this article is structured as follows. Section 1 presents a literature review. Section 2 goes on to present the methodology that is employed to conduct the research. Section 3 reflects on the impact that banks that operate in Lithuania would face due to the introduction of a common E.U. risk-assessment-based deposit insurance system that is in accordance with the methodology that is presented in the European Banking Authority’s guidelines (Model 1). It will additionally assess the systemic risk with the main indicators of risk that are presented in (Model 2). The final section presents the conclusions that have been drawn through the research.
2. Literature Review
To equalize differences in the deposit insurance system and to improve its effectiveness, the European Commission has, since 2008, been aiming to create a common European Union risk-based deposit insurance system. The year 2008 saw the launch of three deposit insurance system models, starting with the extremely flexible and easily adaptable single indicator system (Single Indicator Model) (European Commission 2009), then assigning minimum weights for certain risk categories and key risk indicators (Multiple Indicators Model) (European Commission 2009), and finally establishing an aggregate risk weight (ARW) (EBA Guidelines 2015). The first two risk-based deposit insurance methods differ from one another in terms of the determination of the risk profiles of banks, the selection of risk indicators that define the risk profile the best, and the summation method, which is used to connect all of the risk indicators into a single index that shows the overall risk profile of the bank (Galliani et al. 2012). In the most recent deposit insurance premium calculation guidelines (EBA Guidelines 2015), minimal weight requirements for risk categories are provided for banks, and five risk categories have been evaluated to identify the key risk indicators, where, in each of the five categories, one or two risk indicators are evaluated (EBA Guidelines 2015). According to Gómez-Fernández-Aguado and Partal-Ureña (2013), the creation of a risk-based deposit insurance system would contribute to the more credible management of banks and would reduce the number of contributions that go towards less risky banks. Following up on their research, Gómez-Fernández-Aguado et al. (2014) think that it is necessary to include additional risk measures to evaluate the deposit insurance premiums, which would enable banks to be managed better. It would also lead to the regulation of the E.U.’s market discipline, leading to an improvement in the stability of the banks.
However, studies that various authors have conducted have shown that it is necessary to evaluate not only the main categories of risk, but also the level of systemic risk (Allen and Tang 2016; Acharya et al. 2010; Laeven et al. 2016; Frey and Hledik 2018; Lee et al. 2015). Allen and Tang (2016) state that systemic risk is externally generated in the global macroeconomics of financial institutions with the help of extreme tail risks that work individually. According to the authors, systemic risk needs to be managed in financial institutions of all types and sizes; i.e., it is necessary to measure each individual contribution of a bank to manage the global systemic risk (Allen and Tang 2016). Although the model that the European Commission presented in 2015 is more complex and involves assessing risks to a greater extent, it still does not consider one of the most important assessments: That of the existence of systemic risk. Thus, the model should be extended to include the assessment of this risk in the calculation of deposit insurance premiums (Acharya et al. 2011; Brownlees and Engle 2011; Gómez-Fernández-Aguado et al. 2014; Lakstutiene et al. 2017; Lee et al. 2015; Londono and Tian 2014; Oordt and Zhou 2015; Varotto and Zhao 2014). These scientific discussions intensified in 2009 as Bernet and Walter noted that the deposit insurance system should be evaluated using four different categories of bank risk by extending one of the indicator models, wherein each category would have a certain contribution rate, and the calculated contribution should be multiplied by a systemic risk coefficient (Bernet and Walter 2009). Since systemic risk stems from external coefficients, when one financial institution’s failure to discharge its obligations causes negative effects on other institutions and the economy, the determination of deposit insurance premiums, including a systemic risk assessment, would justify the importance of the deposit insurance system (Acharya et al. 2010). This view has also been shared by Lee et al. (2015), who found that deposit insurance based on contribution rates with systemic risk can mitigate any distortions that are present in the financial system. However, according to the European directives, there is no requirement to evaluate and analyze potential sources of systemic risk, which could lead credit institutions to produce greater systemic risk and raise the number of negative changes that occur in the overall system. Therefore, according to Gómez-Fernández-Aguado et al. (2014), E.U. authorities should consider possible changes, including the evaluation of systemic risk in the deposit insurance funding schemes, because it has been observed that a variety of issues that are related to deposit insurance systems have been addressed during the financial crises. Kuzubas et al. (2016) also stress that the global financial crisis in 2008 drew attention to the importance of the non-compliance of the systemic effects of banks and to systemic risk reduction, because in an inter-bank network, idiosyncratic shocks affect the stability of the entire system.
The global financial crisis of 2008 has revealed the huge impact that global financial stability faces due to excessive risk-taking by banks, especially considering the underestimated and unregulated systemic consequences of risk-taking (Battaglia and Gallo 2017). Anginer et al. (2014) determined that, although financial safety nets increase the risk that banks face and the fragility of systemic banking, both individual bank risk as well as systemic risk have been lower in countries during the global financial crisis that have had a deposit insurance system in place. Brownlees and Engle (2011, 2017), assessing the systemic risk, recommend that the capital of the bank be calculated, something that the bank will require when the financial crisis begins, and Acharya et al. (2011) offers to assess systemic risk as the insufficient capital of a separate bank if the whole system is facing a capital failure.
It should be noted that the systemic risk level often is related to the size of the bank. De Jonghe et al. (2015) observe that banks have become larger and more diversified over the past two decades. However, the global financial crisis showed the negative side of this increase in size and diversification: Larger banks have a higher tail risk, and diversification determines higher systemic risk (De Jonghe et al. 2015). The size of a bank has also been highlighted by Black et al. (2016), who evaluate systemic risk as the distress insurance premium (DIP), which combines features such as the size of the bank and the probability of default. Therefore, the lack of a systemic risk assessment is especially important for large banks that often pay lower deposit insurance premiums than small banks (Lee et al. 2015). Laeven et al. (2014) agree with such an opinion, and say that the big banks are riskier and create more systemic risk since they have less capital and less stable funding than small banks. However, scientists claim that the current amount of banking regulation, when the risk of each bank is assessed, may be insufficient for large banks, because the risk that big banks face is not greater than that of the smaller banks even if we evaluate the big banks separately. Therefore, they should be subject to further regulation, and systemic risk should be assessed using the expected capital shortfall of a financial subject conditional on a prolonged market decline—SRISK indicator (Laeven et al. 2014). The impact of government and the importance of regulation are emphasized by Andries and Nistor (2016), who evaluate systemic risk through the risk that each individual bank faces and the systemic contribution using the Value at Risk (VaR) methodology, and then go on to analyze the impact of government and that of the regulatory system on each bank and their contribution towards systemic risk and individual risk. In later studies, Laeven et al. (2016) used the CoVar and SRISK systemic risk assessment methods to confirm the findings of previous studies, which state that systemic risk increases with the size of a bank, i.e., the bigger the bank, the more systemic risk it has.
Scientists contributing to the debate on the methods that are to be used to assess systemic risk complement each other’s research, modifying research methods and adjusting assumptions. Brownlees and Engle (2011, 2017) developed a simulation environment that allows us to determine a collision with capital shortfalls in the overall system. Varotto and Zhao (2014), applying a very similar approach to that of Brownlees and Engle (2011), measured the limit of discharge of the obligations of a bank with a systemic risk indicator, which identifies the moment when the assets of the bank would be less than the bank’s debt in a future period. De Souza et al. (2016) measure systemic risk through the DebtRank method, and they seek to determine an additional stress in the financial system due to external shocks in one or more financial institutions. Oordt and Zhou’s (2015) assessment of systemic risk is based on a market analysis, and systemic risk has been assessed as the sensitivity of the bank’s returns on the share price to very large adverse shocks in the financial system. This method is based on the returns from the stock prices and market capitalization, and it can be applied to the shares of all banks that are publicly traded on the stock exchange. Note that the reliability and the results of most models that have been applied depend on the ability of the participants of the financial market to assess the financial risk, which is based on financial market data, and the required information in certain models, which is provided only in the internal environment of the banks. Thus, some models are applied with restrictions. The scientific research and discussion that assesses the general E.U. risk-assessment-based deposit insurance system’s design and the implementation of systemic risk assessment raise many questions that can be answered only by expanding the range of research in the following ways: Analyzing scientific research, combining and adapting different methods, and performing research according to a country-specific model.
3. Study Data and Methodology
On 25 May 2015, the European Banking Authority presented guidelines for new premium calculation methodologies of deposit guarantee schemes (European Parliament and Council Directive 2014), and the European Parliament’s directive was adopted for the creation of a new deposit guarantee system. According to the new default resolutions, contributions to the deposit insurance system should be based on the amount of insured deposits and the corresponding degree of risk that each participant in the system incurs. It is stated that such a system for calculating the contributions of deposit guarantees reduces the occurrence of moral hazards in banks. Under this deposit insurance scheme, participating institutions may foresee lower contributions to lower-risk sectors, which are managed by national law (European Parliament and Council Directive 2014).
According to the guidelines of the European Banking Institution, the annual contributions to the Deposit Guarantee Scheme (DGS), with respect to each authority of the state, are calculated using the equation given below:
where Ci is the annual contribution of the participating institution; CR is the contribution rate (which is the same across all state institutions in a given year); ARWi is the aggregate risk weight of the participating institution; CDi is the volume of insured deposits of the participating institution; and µ is the adjustment coefficient (which is the same across all state institutions in a given year) (EBA Guidelines 2015).
Ci = CR × ARWi × CDi × µ
Calculation of the deposit insurance fund’s annual target amount and the contribution rate (CR) each year should be based on a number of assumptions: (1) DGS that started to collect deposit insurance premiums before the occurrence of the insured event (ex-ante) have to reach the target size of the deposit guarantee system of their institutions’ members in 10 years; (2) contributions to the DGS must be spread across the 10 years as evenly as possible; and (3) the annually collected contributions must be equal to the annual target level of the premiums fixed for the given year (EBA Guidelines 2015). The adjustment coefficient should be used to ensure that all annual contributions (the total amount of all contributions) is 1/10th of the targeted level.
Calculation of the aggregate risk weight (ARW) of each participating institution should be calculated individually and based on the evaluation of various risk indicators, including capital, asset quality, liquidity and funding, business management and model, as well as the potential loss on the deposit guarantee due to system risk categories. The minimum ARW rate should fluctuate between 50% and 75%, while the maximum ARW rate should be fixed between 150% and 200%. A wider range can be determined only for important reasons. Without the main risk indicators, the deposit guarantee system may include additional risk indicators that are important to a determination on the risk profile of each of the members of the participating institutions. The amount of weight that is assigned to all risk indicators in the premium calculation deposit guarantee system model must be equal to 100%. While allocating individual risk weights, the minimum weight requirements for risk categories and key risk indicators are given. The DGS should allocate the remaining 25% between the identified risk categories, assigning them to additional risk indicators and/or increasing the minimum weights for the main risk indicators. However, the distribution of the remaining 25% is also subject to several requirements. If only key risk indicators are used, then the remaining 25% is to be allocated strictly between risk categories (24% for capital, 24% for liquidity and funding, 18% for asset quality, 17% for business model and management, and 17% for potential losses due to the DGS).
It should be noted that a determination of the minimum amount of contribution should take proper care of the inevitable moral hazard assessment when determining the flat-rate payments and assess the potential risks of barriers to service access in the banking sector. Contributions to the DGS may be reduced if a member state participates in the institutional guarantee system, which is separate from the DGS. This choice was intended to acknowledge patterns that would protect a credit institution by ensuring its liquidity and solvency. If a member state, which is also a member of a separate institutional safeguards system, makes use of such an option, the value of the common risk coefficient (ARW) may be reduced, considering the additional protection that the institutional guarantee system provides. In this case, a reduction in the contribution can be carried out by adding additional risk indicators that are associated with membership in the institutional guarantee system or including it into the risk category of Business model and management. The membership rate of the Institutional Guarantee System should reflect the additional solvency and liquidity, which is additionally provided to each member (EBA Guidelines 2015). The weight of each additional risk indicator, or the weight increase of the main indicator of risk, should not be greater than 15%, with the exception of additional qualitative indicators that are related to the results of a comprehensive assessment of the risk profile and management of the member institution. Additionally, minimal weights, which are specified for risk category, should be maintained by moving weights on to other indicators that are in the same risk group if at least one of the main indicators is not used.
The aggregate risk weight (ARW) in each participating institution must be assessed individually and be based on the evaluation of various risk indicators from each of the risk categories. It is emphasized that the calculation of the contributions to deposit guarantee systems is only one of the possible models, because each member state can develop its own premium calculation model and submit that for approval. A common deposit insurance system should help to unify the deposit insurance systems in all E.U. countries, and contribute to a reduction in the moral hazard risk and an enhancement in the stability of the overall financial system. This proves, once again, that the development of a common E.U. deposit insurance system, which had started from the creation of a simple single index model and then moved on to the inclusion of several risk indicators, laid the foundation for the calculation of a risk-based deposit insurance premium. In 2015, the risk evaluation included one additional group of risk indicators, and some of the replacement risk indicators produced conditions suitable for the creation of an aggregate risk weight assessment model, which is free to deal with the possibilities of systemic risk and to provide critical assessments. Although the latest model for the calculation of E.U. deposit insurance premiums should be able to assess the risks that banks take more accurately, it still cannot estimate one of the most important risks, i.e., the size of the systemic risk in banks.
The question of whether it is necessary for the E.U. to have a common risk-based deposit insurance system is beyond the scope of this discussion. However, there has not yet been a decision on what kind of bank risks must be evaluated to calculate risk-based deposit insurance premiums. Therefore, we perform a risk assessment on banks operating in Lithuania to determine how premiums would change these banks after the introduction of the common E.U. risk-based deposit insurance system.
Two models have been presented in the research. In the first model (Model 1), only those key risk indicators presented in the European Banking Authority’s guidelines are evaluated (EBA Guidelines 2015). In the second model (Model 2), systemic risk is further assessed with the main risk indicators presented in References (Acharya et al. 2011; Andries and Nistor 2016; Brownlees and Engle 2011, 2017; De Jonghe et al. 2015; Laeven et al. 2014, 2016; Londono and Tian 2014; Oordt and Zhou 2015; Varotto and Zhao 2014). The study has determined the risk groups that the banks operating in Lithuania fall into in terms of systemic risk. We consider the influence that a systemic risk assessment would have on the contributions of the banks that operate in Lithuania, and whether the inclusion of systemic risk is a value-adding process in a common European Union deposit insurance system. Systemic risk and risk-based deposit insurance premiums are important topics in the Lithuanian banking system, as in 2012–2013 two of its banks became bankrupt. The collected deposit insurance premiums were not enough to cover the deposit insurance for the depositors, and the Lithuanian state had to contribute to the deposit insurance coverage.
At present, Lithuania operates 13 different banks and branch offices. Most branches are engaged in investment banking, but only six banks are registered in Lithuania. The calculation of deposit insurance premiums requires specific internal data, which can only be found in a bank’s financial reports and explanatory notes. So, the research shows results using data from Lithuanian banks, but the research methodology could be used in other European Union member states. The study assessed all of the banks that are registered in Lithuania, which are: JSC SEB Bank, JSC Swedbank, JSC DNB Bank, JSC Siauliu Bank, JSC Citadele Bank, and PLLC Medicinos Bank. To perform calculations of the individual risk parameters for each bank, data has been collected from all banks operating in Lithuania from collections of financial reports for the years between 2012 and 2016. A detailed risk assessment of the banks operating in Lithuania, using the European Banking Authority’s method (EBA Guidelines 2015), has been done by Lakstutiene and Barkauskaite (2018) by calculating and analyzing all of the indicators in the risk groups that are presented in the EBA’s guidelines. However, the assessment of systemic risk has been carried out in this study along with the main risk indicators. To obtain a more accurate evaluation of each bank’s systemic risk level, the data from the crisis period has been included, which comprises the data collected between 2008 and 2016. The annual deposit insurance premiums for the deposit insurance fund are calculated separately for each individual bank (See Formula (1)). While calculating the annual contributions of the banks, the correction coefficient has not been included, because the introduction of this coefficient is significant when it is clear that the fund size of the deposit insurance should be adjusted. However, in the first year after the introduction of a deposit insurance system, an adjustment coefficient should not be used. This coefficient should be used when it is intended to ensure that the total annual contributions to the deposit guarantee system are equal to 1/10th of the target level. Additionally, this adjustment coefficient must be the same across all participating institutions in a given year. So, its introduction should not affect the assessment of a risk-based deposit insurance system. This coefficient will raise or reduce the total amount of money that the fund has collected, but will not contribute to the assessment of a bank’s risk.
The contribution rate, which should be the same across all state institutions in a given year, is determined for the launch of a common E.U. deposit guarantee system. A specific amount in the deposit insurance fund should be achieved in 10 years. Therefore, the allocation of the collection of contributions to this fund should be done in as uniform a manner as possible, using amounts of the premium rate. So, the amount in the deposit insurance fund has been specified each year, and has been collected through the annual contributions of the members of the deposit insurance system. The deposit guarantee system has not yet been launched, and a desirable amount of the deposit insurance fund has not been provided. The study has been performed by calculating and evaluating the results of the previous year, and the chosen contribution rate has been taken to be the same for all state institutions in the period between 2012 and 2013.
In determining the aggregate risk weight of a bank (ARW), the risk indicator is determined through the individual risk score of each bank, in accordance with the five categories of risk in the European Banking Authority (EBA)’s guidelines (see Table 1). Individual risk scores for the indicators have been determined by the grouping (bucketing) method. According to this method, the groups are determined for each risk indicator by assigning the upper and lower limits for each group. For the determination of the group rate’s limits, the absolute base is used when the limit of the group reflects the riskiness of an index. In this case, institutions can fall into the same risk group when they have a similar amount of riskiness. When determining the boundaries for the risk groups with the absolute method, it is important to ensure that there is an appropriate and meaningful differentiation between the members of the institution. The IRS points must be between 0 and 100, depending on the rate of risk, where 0 represents the lowest risk value and 100 indicates the highest risk value. There are three groups of indicators for each indicator in the study, in accordance with which the individual risk score has been determined for each indicator (see Table 1). All risk indicators are divided into three risk groups by quintiles (minimum risk, medium risk, and high risk), because a division into smaller risk groups would not be reasonable. We implement the division of risk indicators by quintiles while abiding by the EBA’s Guidelines (2015) as well the previous research that has been conducted by the European Commission (European Commission 2009). The first quintile has been determined to be from 0 to 33, the second from 34 to 66, and the third from 67 to 100.

Table 1.
The European Banking Authority’s risk indicators and groups of individual risk scores.
While determining the individual risk scores of each of the risk indicators, each IRS value of an indicator should be multiplied by the individual risk weight of each indicator:
where Aj is the risk indicator, IWj is the indicator weight, aj is the upper boundary, bj is the lower boundary, and IRSj are the individual risk scores (EBA Guidelines 2015).
The received values have been summed using the arithmetic mean. Then, the aggregate risk score (ARS) value is calculated by the following formula:
where .
The weights of the same set of risk indicators should be used by all participating institutions. Each of them accordingly receives an overall risk score, which should be used for the calculation of the individual contributions of each bank. Aggregate risk weights groups could also be measured by using the bucketing method, where the intervals of the ARS indicators show a respective risk class and a relevant aggregate risk weights value. The number of ARW risk groups must be proportionate to the number of member institutions and their diversity. However, the minimal possible number of risk groups is 4 (see Table 2).

Table 2.
The aggregate risk weight groups and their values.
Each individual member institution should have a corresponding aggregate risk weight (ARWi) value, which is used to calculate its contribution. The ARSi is translated into an aggregate risk weight (ARWi) using the linear formula given below:
where α and β show the upper and lower boundaries, respectively.
ARWi = β + (α − β) × ARSi/100
There must be at least one risk group that shows the average risk that the banks face, at least one risk group that shows low-risk institutions, and at least two risk groups that show high-risk institutions. Based on that, the net stable funding ratio had not been calculated until 2015 (the Basel Committee on Banking Supervision adopted decisions on the final calculation of this indicator on 31 October 2014), and it is not included in the assessment of the riskiness of banks. According to the European Banking Authority’s guidelines on the calculation of payments of contributions to the deposit guarantee systems for the calculation methods (EBA Guidelines 2015), the net stable funding ratio may be excluded from the calculation of risk-based premiums. However, its weight should be reallocated to other indicators. The liquidity coverage ratio is not considered for the years 2012–2014, but for the years 2015 and 2016 the liquidity coverage ratio is used instead of the liquidity ratio. According to the EBA’s instructions (EBA Guidelines 2015), if additional risk indicators are not used, the remaining 25% should be distributed among the categories (Model 1). Model 2, which determines the individual weights of the main risk categories and indicators, is based on the abovementioned minimum risk weights that have been indicated by the EBA, and the remaining 25% is attributed to the systemic degree of risk, as the research that has been conducted by many scientists (Acharya et al. 2011; Andries and Nistor 2016; Brownlees and Engle 2011, 2017; De Jonghe et al. 2015; Kanno 2015; Laeven et al. 2014, 2016; Lee et al. 2015; Londono and Tian 2014; Oordt and Zhou 2015; Varotto and Zhao 2014) has proven that this particular risk assessment and size have a great impact on the stability of the overall financial system. According to the guidelines of the EBA, each additional index weight must not exceed 15%, except for any additional indicators that are related to the comprehensive assessment of the results of the risk profile and the management of the member institution. Therefore, in the case of a systemic risk assessment, an additional risk category is introduced, to which a higher risk weight can be attributed (see Table 3). It is noted that the assessment of systemic risk is the introduction of an additional risk point, and the allocation of 25% to the systemic risk indicator is compatible with the instructions of the EBA.

Table 3.
Risk weights: Minimal, Model 1 and Model 2.
The systemic risk in Lithuania has been assessed using one of the newest systemic risk assessment methods (Oordt and Zhou 2015), which assumes that banks’ shares are publicly traded on the stock exchange. This method is based on the returns of the stock price and market capitalization, and the systemic risk is assessed by the returns on the bank’s share price sensitivity to very large adverse shocks in the financial system. Even though the method of Brownlees and Engle (2011) is one of the most widely used systemic risk evaluation methods, and most authors adjust it to calculate an institution’s systemic risk, the Oordt and Zhou (2015) method is very suitable for the case of Lithuania, since a small number of banks are being assessed. Therefore, the model has been selected to make possible a more accurate assessment of a small number of banks (there are only four banks whose shares are publicly traded in Lithuania). However, this method is also suitable for a large number of banks, because it can be used to construct banking system index, and the number of banks is not limited. Besides, another advantage of applying Oordt and Zhou’s (2015) model in the case of Lithuania is that it can avoid relatively large evaluation errors due to the low number of analyzed banks. This method uses stock returns and market capitalizations data. In Oordt and Zhou’s (2015) systemic risk evaluation method, a bank’s systemic risk level is calculated as the beta coefficient value according to Formula (2):
where is the tail index, which is calculated by the estimator proposed in Hill (1975); and are estimated by the (k + 1)th worst return on the bank’s stock and the Lithuanian banking index; is the non-parametric estimator of tail dependence between and established in multivariate Extreme Value Theory (EVT); and and should follow heavy-tailed distributions with the tail indices and .
The beta coefficient value must be higher than or equal to zero. When calculating the market capitalization of banks and using a bank’s shares data, the actual number of shares for each calculation day is used. To obtain the most accurate results for the systemic risk evaluation, the data from 2008 to 2016 were used in the calculations, because in this method share prices must have large fluctuations in returns to obtain the most accurate results. The results confirmed the research results of Gómez-Fernández-Aguado et al. (2014), Kuzubas et al. (2016), and Anginer et al. (2014), as the largest fluctuations were recorded particularly during the crisis of 2008. Therefore, the analyzed period has been extended with the data from 2008 to 2009. Of the six banks operating in Lithuania, the shares of four are publicly traded on the stock market. However, the data on the shares of two of the banks are not available. The shares of JSC Citadele Bank are not publicly traded on any stock exchange, and one JSC Citadele Bank share belongs to an international group of investors, which is represented by “Ripplewood Advisors LLC”, and 12 other investors with a solid reputation, and the remaining 25% without one share are managed by the European Bank for Reconstruction and Development (Citadele Bank 2015). The shares of PLLC Medicinos Bank are not publicly traded on any stock exchange because it is a type of PLLC Bank. Therefore, it is not possible to estimate the systemic risk of JSC Citadele Bank and PLLC Medicinos Bank. PLLC Medicinos Bank and JSC Citadele Bank have been assigned in the study to the low systemic risk group (the attributed IRS value is 0). During the investigated period of 2012–2013, PLLC Medicinos Bank and JSC Citadele Bank had a 2.7–6.7 times lower guaranteed volume of deposits as compared to JSC Siauliu Bank, and a 17–21.8 times lower volume of deposits as compared to JSC Swedbank. The assets of PLLC Medicinos Bank and JSC Citadele Bank were also significantly lower during the period of the research. Thus, these banks have been classified as small banks in Lithuania.
Avoiding any relatively high evaluation errors, due to the small number of analyzed banks, an index is composed for each bank from the Lithuanian banking system with the S−i based on the four banks. The return of S−i is calculated according to the Formula (3):
where Rj,t is the return of bank j’s shares on t day; and ej,t−1 is bank j’s market capitalization at the end of the previous trading day.
Systemic risk is measured considering the sensitivity of the bank to large shocks in the banking system of Lithuania. While performing VaR calculations (Andries and Nistor 2016; Brownlees and Engle 2011; Londono and Tian 2014), the 10% percentile is used, which shows the threshold at which each bank’s return is considered to be risky. During the period between 2008 and 2016, there were no major shocks in any of the analyzed banks, and the largest negative returns value reached up to 20%. It can be noted that the banking data are mostly distributed between the values of −5% and +5% and have big “tails”, and there were only a few days where the stock price had a fall that was bigger than −5%. The market capitalization data shows that JSC Swedbank had the largest market capitalization over the entire research period. So, the influence and significance of this bank has been the greatest for the whole Lithuanian banking system. In second place, in terms of market capitalization, was JSC SEB Bank, while JSC Siauliu Bank had the lowest market capitalization among the four banks in question over the entire research period of 2008–2016.
After the determination of the ARW coefficients of each bank and the identification of the volume of their insured deposits, a further step is to determine the size of the contribution rate. As has already been mentioned in the section on the evaluation methodology, the contribution rate has no effect on the identification of a bank’s risk, and it is used to ensure a certain level of deposit insurance fund amount. However, the size of the contribution does not have a significant impact on the data analysis of the previous year. The size of each bank’s contribution to the overall E.U. deposit insurance fund is counted based on the basic calculation Formula (1).
To make a more accurate comparison of the contributions in the research for Model 1 and Model 2, a contribution rate of 0.45% size is applied. Such a size of the contribution rate is chosen to better compare the differences between the annual contributions without a risk assessment and the previous deposit insurance system of Lithuania and a common E.U. deposit insurance system. According to the previous deposit insurance system of Lithuania, all commercial banks operating in Lithuania had to pay 0.45% of the total amount of insured deposits (Deposit and Investment Insurance 2016). This percentage was the same for all banks, regardless of the amount of risk they assume. To make a comparison of the contributions, we calculated the relative change between the risk-based deposit insurance contributions and the contributions made under the previous deposit insurance scheme of Lithuania. Since litas was the Lithuanian currency until 2014, and since Lithuania became a member of the E.U. in 2015, the contributions from 2012 to 2014 were translated from litas to euro in the ratio of 1 EUR being equal to 3.4528 litas.
4. Analysis of Results and Comments
To determine the overall risk score of each bank (ARS) and the comprehensive risk score, the systemic risk of each bank is assessed, because the risk weights of individual indicators that are applicable are different in Model 1 and Model 2, and the systemic risk is additionally included into Model 2 (Lakstutiene et al. 2018). When performing the systemic risk assessment, the RS index of Lithuanian banks was calculated, and the meaning of the k parameter was determined by the amended random selection method (bootstrap). When determining 1000 random k values, the calculations shown in Table 4 were used to obtain the meaning of the k values. The relatively low values of the calculated k coefficients showed that Lithuanian banks do not have high stock return volatility and high risk. The stock return histograms of Lithuanian banks for the years 2008–2016 are presented in Figure 1.

Table 4.
The systemic risk assessment results.
Figure 1.
Stock return histograms of Lithuanian banks for the years 2008–2016.
The banks’ k coefficient values ranged from 0.1167 to 0.1446. After setting the values for VaR and VaRS, the values of each bank’s parameters were calculated as and the systemic risk coefficient, β, of each bank was determined (see Table 4).
The evaluation showed the same results as the previous study (Lakstutiene et al. 2018); none of the four banks that operate in Lithuania have a large systemic risk level. The low beta coefficient values were mostly determined by low k coefficients. K coefficient changes have a great effect on the beta coefficient values, and a small amount of negative equity returns affected the low k coefficient values. Even in 2008, during the financial crisis, when the stock prices fell the most, there were only a few significant negative equity return values. JSC Swedbank and JSC SEB Bank can be distinguished from the other banks on the basis of the obtained beta coefficient values.
Figure 2 shows the beta coefficient sensitivity analysis to the VaR parameter. The sensitivity analysis with different VaR percentiles (5%, 10% and 15%) showed the same results for JSC Swedbank and JSC SEB Bank; in all cases, they had higher systemic risk than the other banks.
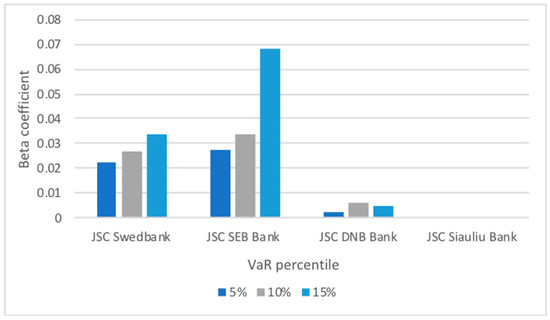
Figure 2.
Beta coefficient sensitivity analysis to the VaR parameter.
Although neither of the banks had a high systemic risk level, as assessed by the average systemic risk value, JSC Swedbank and JSC SEB Bank had a significantly higher systemic risk level than JSC DNB Bank and JSC Siauliu Bank. The results were partly determined by the larger market capitalizations of JSC Swedbank and JSC SEB Bank when compared to the other banks in the Lithuanian market. However, the stock returns of JSC SEB Bank had greater volatility, which implied that the systemic risk of JSC SEB Bank was slightly higher than that of JSC Swedbank. Therefore, JSC Swedbank and JSC SEB Bank were classified as medium systemic risk banks (respectively assigned an IRS value of 50), and JSC DNB Bank and JSC Siauliu Bank were classified as the lowest systemic risk banks (an IRS value of 0). The same systemic risk results were obtained when evaluating the period 2008–2014 (Lakstutiene et al. 2018). Based on the established risk indicators of the individual risk point values and the weights of the individual risk indicators provided (see Table 3), the overall risk score value was calculated for each bank as per Model 1 and Model 2 (see Table 5).

Table 5.
The average risk score (ARS) excluding systemic risk (Model 1) and including systemic risk (Model 2).
The ARS values in the Model 1 and Model 2 cases show the different risk volumes that banks assume, which, during the period of 2012–2016, varied significantly across all banks of Lithuania. Each of the banks was assigned an aggregate risk weight (see Table 6), and received common determined risk scores meanings according to the methodology.

Table 6.
The aggregate risk weight (ARW) excluding systemic risk (Model 1) and including systemic risk (Model 2).
The obtained ARW results show the different bank risk values without evaluating systemic risk (Model 1) and evaluating systemic risk (Model 2). According to Model 1, over the entire research period, the riskiest banks can be considered to be PLLC Medicinos Bank and JSC Siauliu Bank, whose aggregate risk weights over the entire period were the highest. The riskiness of JSC Siauliu Bank, compared with 2012, increased during 2013 to 2014, which was mainly due to an increase in the capital risk indicators and a reduction in the rate of unencumbered assets and guaranteed deposits. It was determined that only in the case of JSC SEB Bank did the comprehensive risk score values of both Model 1 and Model 2 completely coincide. After assessing the systemic risk (Model 2), JSC Swedbank and JSC SEB Bank were assigned to the medium-risk group. All of the other banks that operate in Lithuania were attributed to the lowest risk groups. According to Model 2, the least risky bank during the years 2012–2014 was JSC Citadele Bank, whose aggregate risk weight during 2012 to 2014 fell into the lowest risk category. This has also been confirmed by the research results of Laeven et al. (2014, 2016) and De Jonghe et al. (2015). However, in 2015, JSC Citadele Bank had quite a low liquidity coverage ratio and a higher NPL ratio, which influenced it to have a higher risk-taking level. According to Model 2, the least risky banks in the period 2015–2016 were JSC SEB Bank and JSC DNB Bank. The riskiest of all banks, according to Model 2, can be considered to be JSC Swedbank and JSC SEB Bank, whose average values of aggregate risk weights for the years 2012–2016 were the highest. The obtained systemic risk results confirm the research results of Laeven et al. (2014, 2016), De Jonghe et al. (2015), Lee et al. (2015), and Black et al. (2016), suggesting that systemic risk depends on the size of the bank, and that the major banks are riskier. In determining the aggregate risk weights, according to Formula (1), each bank’s annual contribution to the E.U. deposit insurance fund was calculated. The calculated annual contributions to the overall size of the E.U. deposit insurance fund during the period of 2012–2016 in the banks of Lithuania are presented in Table 7.

Table 7.
The setting of sizes of annual contributions in Lithuanian banks excluding systemic risk (Model 1) and including systemic risk (Model 2) in thousands of EUR.
Analyzing the annual contribution rates, according to Model 1 and Model 2, JSC SEB Bank would have had to make the biggest contributions for the years 2012–2013, and JSC Swedbank would have had to make the biggest contributions for the years 2014–2016. This is due to the high volume of guaranteed deposits and the sufficiently large aggregate risk weights taken by these banks, which accepted a higher than average risk. The minimum contributions to the overall E.U. deposit insurance system would have been paid to JSC Citadele Bank and PLLC Medicinos Bank in 2012 to 2016 in both Model 1 and Model 2. During the period of 2012–2016, JSC Citadele Bank had a higher volume of deposits guaranteed than did PLLC Medicinos Bank. However, due to the smaller aggregate risk weight, the contributions of JSC Citadele Bank in 2012 to 2013 to the common E.U. deposit insurance system would be lower. The increase in the size of JSC Siauliu Bank’s contributions in 2013 when compared to 2012 was mainly due to the guaranteed deposits being doubled.
The results on minimum payments are very similar between Model 2 and Model 1. JSC Citadele Bank would have had to make the smallest contribution for the years 2012–2013, and PLLC Medicinos Bank would have had to make the smallest contribution for the years 2014–2016. After calculating the deposit insurance premiums in Model 2, the aggregate risk weights of JSC DNB Bank, JSC Siauliu Bank, JSC Citadele Bank, and PLLC Medicinos Bank during the period under review were found to be lower than the values from Model 1, because the systemic risk of these banks resulted in these banks being assigned to the lowest-risk groups. Examining the total annual contribution size of all banks operating in Lithuania, it was determined in both Model 1 and Model 2 that the largest amount of contributions made during the period under consideration would have been in 2016. The comparison of the deposit insurance premiums of the banks operating in Lithuania, according to the previous deposit insurance system of Lithuania (without risk assessment) and according to Model 1 and Model 2, is presented in Table 8.

Table 8.
A comparison of the Deposit Insurance Fund contributions of Lithuanian banks from Model 1 and Model 2.
Evaluating the overall contributions of all banks in Model 1 and Model 2, the total amount of contributions made during 2012 to 2014 would have been higher when compared to the previous contributions (without risk assessment). In 2015, on the contrary, banks had to make lower contributions in comparison without risk assessment contributions. Under Model 1, banks generally would have made larger contributions over the entire period than under Model 2. The obtained differences between the results under Model 1 and Model 2, when assessing the general amount of contributions of all banks, were not large and differed by up to 10%. It is important to note that the total amount of contributions made can be adjusted by introducing into the calculation an adjustment coefficient to collect the target deposit insurance fund for a longer period. The differences between the contributions under Model 1 and Model 2 were lower in the major banks of Lithuania: JSC Swedbank and JSC SEB Bank. In most cases, the contributions by the largest Lithuanian banks coincided in both models. The differences between the results under Model 1 and Model 2 of the remaining Lithuanian banks were larger. In all cases of Model 1, the other banks (JSC DNB Bank, PLLC Medicinos Bank, JSC Citadele Bank, and JSC Siauliu Bank) would have had to make larger or the same contributions to the deposit insurance fund than in the case of Model 2. Most of these differences were caused by the fact that the systemic risk in all of the minor banks and JSC DNB Bank resulted in these banks being assigned to the lowest-risk group, and the systemic risk individual risk weight being 25%. Therefore, influence of the systemic risk on the aggregate risk score was significant.
In summary, it can be stated that the assessment of systemic risk, in the case of Lithuania, would redistribute the deposit insurance premiums among the banks. However, the analysis showed that only the two largest Lithuanian banks, Swedbank and SEB Bank, have a slightly higher systemic risk in comparison to the other banks operating in Lithuania. This leads to the insight that in the case of Lithuanian banks, systemic risk should be given less individual risk weight to not reduce the influence of the other risk indicators. The research showed that the total difference in contributions between the two models of evaluation was not very large. However, the inclusion of systemic risk helps to form a more accurate assessment of a bank’s risk, allows us to go beyond the assessment of basic risk indicators, and suggests that the measurement of systemic risk is a value-adding process.
5. Conclusions
When evaluating the risks of all six banks that operate in Lithuania, each indicator had been attributed to low-, medium-, or high-risk groups. The obtained results showed that, when performing the assessment with the two risk-based models (Model 1 excluding systemic risk, and Model 2 including systemic risk) during the period 2012–2014, the total amount of the deposit insurance fund would have been higher than without a risk assessment (i.e., under the previous deposit insurance system of Lithuania). The largest increase in total contributions, under Model 1, was found to reach 39.37% in 2013. The situation would have been the opposite in 2015 and 2016, where the total amount of contributions would have been lower under Model 2 as compared with the previous system in Lithuania, when in Model 1 contributions would have been lower in 2015 but higher in 2016. It is noted that, in the major Lithuanian banks JSC Swedbank and JSC SEB Bank, the risk assessment carried out under both evaluation models was very similar. However, the differences between Model 1 and Model 2 for the smaller banks were larger. The research results of Laeven et al. (2014, 2016), De Jonghe et al. (2015), Lee et al. (2015), and Black et al. (2016) also confirmed that smaller banks have less systemic risk and no significant impact on other market participants, and vice versa: Major banks are riskier. The results show that, after the introduction of a risk-based deposit insurance system, according to Model 1 and Model 2, and as compared to the previous system in Lithuania (without a risk assessment), the largest contribution increase of an individual bank would be +50% percent, and the largest decrease would be −25%.
The results showed that, during the period under consideration, only JSC Swedbank and JSC SEB Bank fell into the medium groups of systemic risk, while all the other banks operating in Lithuania were attributed to the low systemic risk group. The introduction of a risk-assessment-based deposit insurance system and the redistribution of deposit insurance premiums among the banks operating in Lithuania would, thus, contribute to the mitigation of negative deposit insurance system impacts and an improvement in the stability of the financial system. Without the assessment of systemic risk, a deposit insurance fund ignores the interconnections among banks and does not ensure that the banking system will have adequate stability. Since the study found that systemic risk inclusion has a positive influence on a common E.U. deposit insurance system, further studies should examine what results would be obtained in other E.U. countries, and what should be the optimum weight of the systemic risk indicator in a common E.U. deposit insurance system. The introduction of a risk-assessment-based common E.U. deposit insurance system would contribute to the enhancement of financial stability in the overall E.U. banking sector. So, the benefits to the introduction of this system are undeniable. In summary, the study provides an insight that the introduction of a systemic risk indicator will help to provide a more accurate assessment of a bank’s risk, that systemic risk assessment is a value-adding process to the identification of a bank’s risk, and that it is not limited only to the risk assessment of the indicators of individual banks. So, we recommend that systemic risk evaluation be included in the common E.U. risk-based deposit insurance system.
Author Contributions
Writing (original draft preparation), A.B.; Validation and Funding acquisition, A.L.; Writing (review and editing), J.W. and A.L.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Acharya, Viral V., Joao A. C. Santos, and Tanju Yorulmazer. 2010. Systemic Risk and Deposit Insurance Premiums. FRBNY Economic Policy Review 16: 89–99. [Google Scholar] [CrossRef]
- Acharya, Viral, Robert Engle, and Matthew Richardson. 2011. Capital Shortfall: A new approach to ranking and regulating sistemic risks. Paper presented at AEA Meetings, Denver, CO, USA, January 6–9; pp. 1–12. [Google Scholar]
- Allen, Linda, and Yi Tang. 2016. What ‘s the contingency? A proposal for bank contingent capital triggered by systemic risk. Journal of Financial Stability 26: 1–14. [Google Scholar] [CrossRef]
- Allen, Franklin, Elena Carletti, and Agnese Leonello. 2011. Deposit insurance and risk taking. Oxford Review of Economic Policy 27: 464–78. [Google Scholar] [CrossRef]
- Altunb, Yener, and John Thornton. 2013. Deposit insurance and private capital inflows: Further evidence. Journal of International Financial Markets, Institutions & Money 27: 243–47. [Google Scholar]
- Andries, Alin Marius, and Simona Nistor. 2016. Systemic risk, corporate governance and regulation of banks across emerging countries. Economic Letters 144: 59–63. [Google Scholar] [CrossRef]
- Anginer, Deniz, Asli Demirguc-Kunt, and Min Zhu. 2014. How does deposit insurance affect bank risk? Evidence from the recent crisis. Journal of Banking & Finance 48: 312–21. [Google Scholar]
- Bank for International Settlements. 2014. IADI Core Principles for Effective Deposit Insurance Systems. Basel: International Association of Deposit Insurers (IADI), pp. 1–56. [Google Scholar]
- Battaglia, Francesca, and Angela Gallo. 2017. Strong boards, ownership concentration and EU banks’ systemic risk-taking: Evidence from the financial crisis. Journal of International Financial Markets, Institutions and Money 46: 128–46. [Google Scholar] [CrossRef]
- Bernet, Beat, and Susanna Walter. 2009. Design, Structure and Implementation of a Modern Deposit Insurance Scheme. Vienna: The European Money and Finance Forum, pp. 1–86. [Google Scholar]
- Black, Lamont, Ricardo Correa, Xin Huang, and Hao Zhou. 2016. The systemic risk of European banks during the financial and sovereign debt crisis. Journal of Banking & Finance 63: 107–25. [Google Scholar]
- Boyle, Glenn, Roger Stover, Amrit Tiwana, and Oleksandr Zhylyevskyy. 2015. The impact of deposit insurance on depositor behavior during a crisis: A conjoint analysis approach. Journal of Financial Intermediation 24: 590–601. [Google Scholar] [CrossRef]
- Brownlees, Christian T., and Robert F. Engle. 2011. Volatility, Correlation and Tails for Systemic Risk Measurement. Working paper. New York, NY, USA: New York University, pp. 1–37. [Google Scholar]
- Brownlees, Christian T., and Robert F. Engle. 2017. SRISK: A conditional shortfall measure of systemic risk. Review of Financial Studies 30: 48–79. [Google Scholar] [CrossRef]
- Cannas, Giuseppina, Jessica Cariboni, Laleh Kasemi Veisari, and Andrea Pagano. 2014. Updated Estimates of EU Eligible and Covered Deposits. JRC Technical Report. Tokyo: JRC, pp. 1–32. [Google Scholar]
- De Jonghe, Olivier, Maaike Diepstraten, and Glenn Schepens. 2015. Banks’ size, scope and systemic risk: What role for conflicts of interest? Journal of Banking & Finance 61: S3–S13. [Google Scholar]
- De Souza, Rubens Stancato, Thiago Christiano Silva, Benjamin Miranda Tabak, and Solange Maria Guerra. 2016. Evaluating systemic risk using bank default probabilities in financial networks. Journal of Economic Dynamics & Control 66: 54–75. [Google Scholar]
- Demirguc-Kunt, Asli, Edward Kane, and Luc Laeven. 2014. Deposit Insurance Database. International Monetary Fund Working Paper, WP/14/118. Washington, DC, USA: International Monetary Fund, pp. 1–43. [Google Scholar]
- Deposit and Investment Insurance. 2016. Available online: http://www.iidraudimas.lt/lt/indeliu-draudimas/draudimo-objektas (accessed on 11 February 2018).
- EBA Guidelines. 2015. Guidelines on Methods for Calculating Contributions to Deposit Guarantee Schemes. Available online: https://www.eba.europa.eu/documents/10180/1089322/EBA-GL-2015-10+GL+on+methods+for+calculating+contributions+to+DGS.pdf (accessed on 11 February 2018).
- Ellis, Diane. 2013. Deposit Insurance Funding: Assuring Confidence; Washington, DC: Federal Deposit Insurance Corporation, pp. 1–8.
- Enkhbold, Enerelt, and Batnairamdal Otgonshar. 2013. The Effect of Deposit Insurance on Risk Taking in Asian Banks. Asian Journal of Finance & Accounting 5: 104–26. [Google Scholar]
- European Commission. 2009. Possible Models for Risk–Based Contributions to EU Deposit Guarantee Schemes. Geel: European Commission, Joint Research Centre, pp. 1–38. [Google Scholar]
- European Parliament and Council Directive. 2014. European Parliament and Council Directive 2014/49/ES 2014 Years April 16 on Deposit Guarantee Schemes. Available online: http://eur-lex.europa.eu/legal-content/lt/TXT/PDF/?uri=CELEX:32014L0049&from=EN (accessed on 2 July 2018).
- Frey, Rüdiger, and Juraj Hledik. 2018. Diversification and Systemic Risk: A Financial Network Perspective. Risks 6: 54. [Google Scholar] [CrossRef]
- Galliani, Clara, Riccardo De Lisa, and Stefano Zedda. 2012. European Deposit Guarantee Schemes: Revision of Risk Based Contributions Using CDS Spreads. European Commission, JRC Technical Reports. Geel: European Commission, pp. 1–24. [Google Scholar]
- Gerhardt, Maria, and Karel Lannoo. 2011. Options for Reforming Deposit Protection Schemes in the EU. ECRI Policy Brief No. 4. Plymouth Meeting: ECRI, pp. 1–14. [Google Scholar]
- Gómez-Fernández-Aguado, Pilar, and Antonio Partal-Ureña. 2013. Evaluating the effects of the EU directive proposal for riskbased deposit insurance premiums in Spain. Working Paper Series; WP FIECAC 13.01. Sevilla, Spain: Pablo de Olavide University, pp. 1–29. [Google Scholar]
- Gómez-Fernández-Aguado, Pilar, Antonio Partal-Ureña, and Antonio Trujillo-Ponce. 2014. Moving toward risk-based deposit insurance premiums in the European Union: The case of Spain. Applied Economics 46: 1547–64. [Google Scholar] [CrossRef]
- Hill, Bruce M. 1975. A simple general approach to inference about the tail of a distribution. Annals of Statistics 3: 1163–74. [Google Scholar] [CrossRef]
- Ioannidou, Vasso P., and Maria Fabiana Penas. 2010. Deposit insurance and bank risk–taking: Evidence from internal loan ratings. Journal of Financial Intermediation 19: 95–115. [Google Scholar] [CrossRef]
- Kanno, Masayasu. 2015. Assessing systemic risk using interbank exposures in the global banking system. Journal of Financial Stability 20: 105–30. [Google Scholar] [CrossRef]
- Khan, Anichul Hoque, and Hasnat Dewan. 2011. Deposit insurance scheme and banking crises: A special focus on less–developed countries. Empirical Economics 41: 155–82. [Google Scholar] [CrossRef]
- Kuzubas, Tolga Umut, Burak Saltoglu, and Can Seven. 2016. Systemic risk and heterogeneous leverage in banking networks. Physica A 462: 358–75. [Google Scholar] [CrossRef]
- Laeven, Luc, Lev Ratnovski, and Hui Tong. 2014. Bank Size and Systemic Risk. IMF SDN 14/04. Available online: https://www.imf.org/external/pubs/ft/sdn/2014/sdn1404.pdf (accessed on 10 August 2018).
- Laeven, Luc, Lev Ratnovski, and Hui Tong. 2016. Bank size, capital, and systemic risk: Some international evidence. Journal of Banking & Finance 69 S1: S25–S34. [Google Scholar]
- Lakstutiene, Ausrine, and Aida Barkauskaite. 2018. Research on risk-based common European Union deposit insurance system in Lithuanian banks. In Eurasian Business Perspectives, Proceedings of the 20th Eurasia Business and Economics Society Conference. Berlin: Springer, vol. 1, pp. 105–18. [Google Scholar]
- Lakstutiene, Ausrine, Justyna Witkowska, and Edita Leskauskiene. 2017. Transformation of the EU deposit insurance system: evaluation of risk-based insurance premiums on the basis of the example of Lithuanian banks. In Transformations in Business & Economics = Verslo ir ekonomikos transformacijos. Vilnius: Vilnius University, vol. 16, iss. 2, pp. 147–69. [Google Scholar]
- Lakstutiene, Ausrine, Aida Barkauskaite, and Justyna Witkowska. 2018. The importance of systemic risk assessment in a risk-based common European Union deposit insurance system: case of Lithuania. Economic Research-Ekonomska Istraživanja 31: 73–86. [Google Scholar] [CrossRef]
- Lee, Shih-Cheng, Chien-Ting Lin, and Ming-Shann Tsai. 2015. The pricing of deposit insurance in the presence of systematic risk. Journal of Banking & Finance 51: 1–11. [Google Scholar]
- Leur, Michiel C. W., Andre Lucas, and Norman J. Seeger. 2017. Network, market, and book-based systemic risk rankings. Journal of Banking and Finance 78: 84–90. [Google Scholar] [CrossRef]
- Londono, Juan M., and Mary Tian. 2014. Bank Interventions and Options-Based Systemic Risk: Evidence from the Global and Euro-area Crisis; Board of Governors of the Federal Reserve System International Finance Discussion Papers, Number 1117. Washington, DC: Board of Governors of the Federal Reserve System, pp. 1–30.
- Mensah, Jones Odei, and Gamini Premaratne. 2017. Systemic interconnectedness among Asian Banks. Japan and the World Economy 41: 17–33. [Google Scholar] [CrossRef]
- Oordt, Maarten R. C., and Chen Zhou. 2015. Systemic risk of European banks: Regulators and markets. DNB Working Paper, No. 478. Oslo, Norway: DNB, pp. 1–22. [Google Scholar]
- Prean, Nora, and Helmut Stix. 2011. The effect of raising deposit insurance coverage in times of financial crisis—Evidence from Croatian microdata. Economic Systems 35: 496–511. [Google Scholar] [CrossRef]
- Varotto, Simone, and Lei Zhao. 2014. Systemic Risk and Bank Size. Discussion Paper, Number 17. Reading: ICMA Centre, pp. 1–38. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).