Robust Estimations for the Tail Index of Weibull-Type Distribution
Abstract
:1. Introduction
2. Asymptotic Results
3. Robustness
4. Simulations
- (i)
- The bias of the proposed M-estimations is smaller than that of Hill-type estimation and MLE estimation (see columns 2–5 for details).
- (ii)
- The sample variance of our estimations is very close to zero. Note by passing that even with the optimal choice of , the of Hill-type estimations is still relatively larger than the other (see columns 6–9 for details).
- (iii)
- Since the ratios of MSE satisfy , we see that the best rank estimation is , which coincides with the analysis of the relative efficiency (see columns 10–12 and Figure 2).
- (iv)
- For , the is almost zero indicating that for very small samples outperforms Hill-type estimators for almost all ’s. For , does not exceed in most cases which means that there is a set K with at most s = 8 of such that the Hill-type estimators would outperform . Similar argument holds for . Hence, the M-estimations perform better even for small samples.
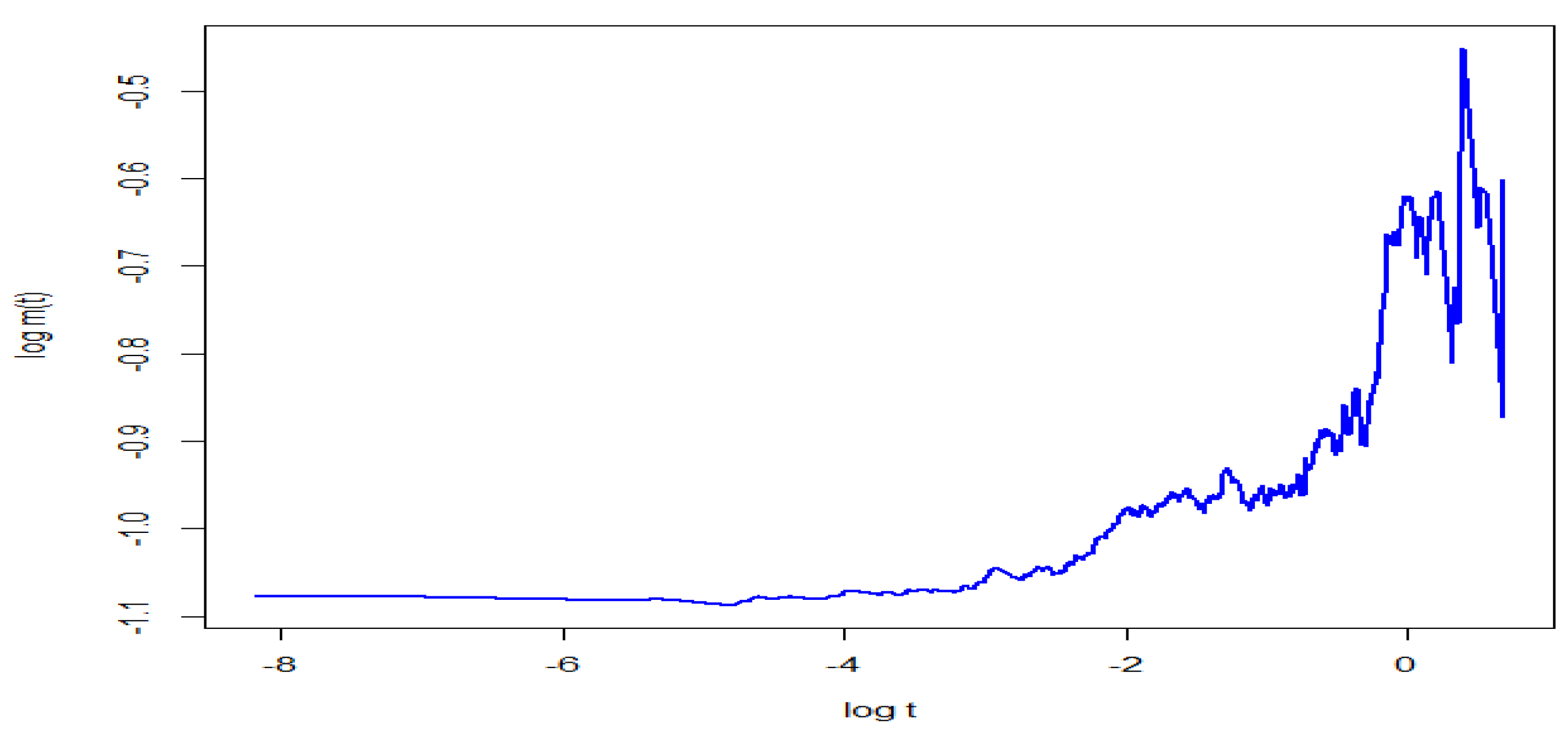
5. Empirical Study
6. Proofs
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arendarczyk, Marek, and Krzysztof Dȩbicki. 2011. Asymptotics of supremum distribution of a Gaussian process over a Weibullian time. Bernoulli 17: 194–210. [Google Scholar] [CrossRef]
- Asimit, Alexandru V., Deyuan Li, and Liang Peng. 2010. Pitfalls in using Weibull tailed distributions. Journal of Statistical Planning and Inference 140: 2018–24. [Google Scholar] [CrossRef]
- Basu, Ayanendranath, Ian R. Harris, Nils L. Hjort, and M. C. Jones. 1998. Robust and efficient estimation by minimising a density power divergence. Biometrika 85: 549–59. [Google Scholar] [CrossRef]
- Beirlant, Jan, and Jozef L. Teugels. 1992. Modeling large claims in non-life insurance. Insurance: Mathematics and Economics 11: 17–29. [Google Scholar] [CrossRef]
- Beran, Jan, and Dieter Schell. 2012. On robust tail index estimation. Computational Statistics & Data Analysis 56: 3430–43. [Google Scholar]
- Bingham, Nicholas H., Charles M. Goldie, and Jozef L. Teugels. 1987. Regular variation. In Encyclopedia of Mathematics and Its Applications. Cambridge: Cambridge University Press, vol. 27, ISBN 9780511721434. [Google Scholar]
- Dȩbicki, Krzysztof, Julia Farkas, and Enkelejd Hashorva. 2018. Extremes of randomly scaled Gumbel risks. Journal of Mathematical Analysis and Applications 458: 30–42. [Google Scholar] [CrossRef]
- Dierckx, Goedele, Jan Beirlant, D. De Waal, and Armelle Guillou. 2009. A new estimation method for Weibull-type tails based on the mean excess function. Journal of Statistical Planning and Inference 139: 1905–20. [Google Scholar] [CrossRef]
- Gardes, Laurent, and Stephane Girard. 2008. Estimation of the Weibull tail-coefficient with linear combination of upper order statistics. Journal of Statistical Planning and Inference 138: 1416–27. [Google Scholar] [CrossRef]
- Girard, Stephane. 2004. A Hill type estimator of the Weibull tail-coefficient. Communications in Statistics-Theory and Methods 33: 205–34. [Google Scholar] [CrossRef]
- Goegebeur, Yuri, Jan Beirlant, and Tertius De Wet. 2010. Generalized kernel estimators for the Weibull-tail coefficient. Communications in Statistics-Theory and Methods 39: 3695–716. [Google Scholar] [CrossRef]
- Goegebeur, Yuri, Armelle Guillou, and Theo Rietsch. 2015. Robust conditional Weibull-type estimation. Annals of the Institute of Statistical Mathematics 67: 479–514. [Google Scholar] [CrossRef]
- Hashorva, Enkelejd, and Zhichao Weng. 2014. Tail asymptotic of Weibull-type risks. Statistics 48: 1155–65. [Google Scholar] [CrossRef]
- Huber, Peter J. 1964. Robust estimation of a location parameter. The Annals of Mathematical Statistics 35: 73–101. [Google Scholar] [CrossRef]
- Kundu, Debasis, Debanjsn Mitra, and Ayon Ganguly. 2017. Analysis of left-truncated and right-censored competing risks data. Computational Statistics & Data Analysis 108: 12–26. [Google Scholar]
- Liu, Yan, and Qihe Tang. 2010. The subexponential product convolution of two Weibull-type distributions. Journal of the Australian Mathematical Society 89: 277–88. [Google Scholar] [CrossRef]
- Serfling, Robert J. 1980. Approximation Theorems of Mathematical Statistics. New York: John Wiley & Sons, ISBN 9780471024033. [Google Scholar]
- Trimborn, Simon, and Wolfgang K. Härdle. 2016. CRIX an Index for Blockchain Based Currencies. SFB 649 Discussion Paper 2016-021. Berlin: Economic Risk. [Google Scholar]
- Vandewalle, Bjorn, Jan Beirlant, and Mia Hubert. 2004. A robust estimator of the tail index based on an exponential regression model. In Theory and Applications of Recent Robust Methods. Berlin and Heidelberg: Springer, pp. 367–76. [Google Scholar]
- Vandewalle, Bjorn, Jan Beirlant, Andreas Christmann, and Mia Hubert. 2007. A robust estimator for the tail index of Pareto-type distributions. Computational Statistics & Data Analysis 51: 6252–68. [Google Scholar]
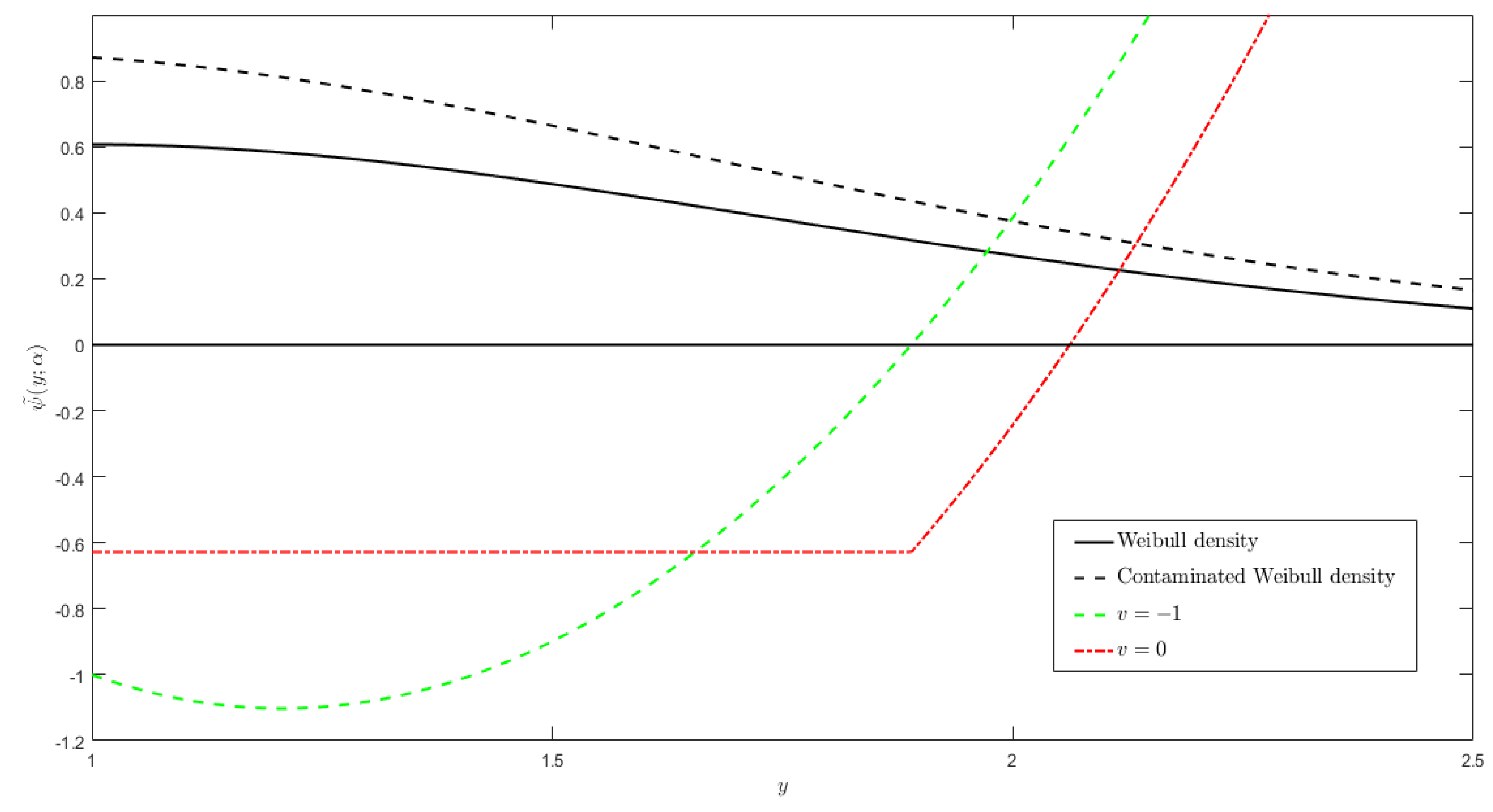
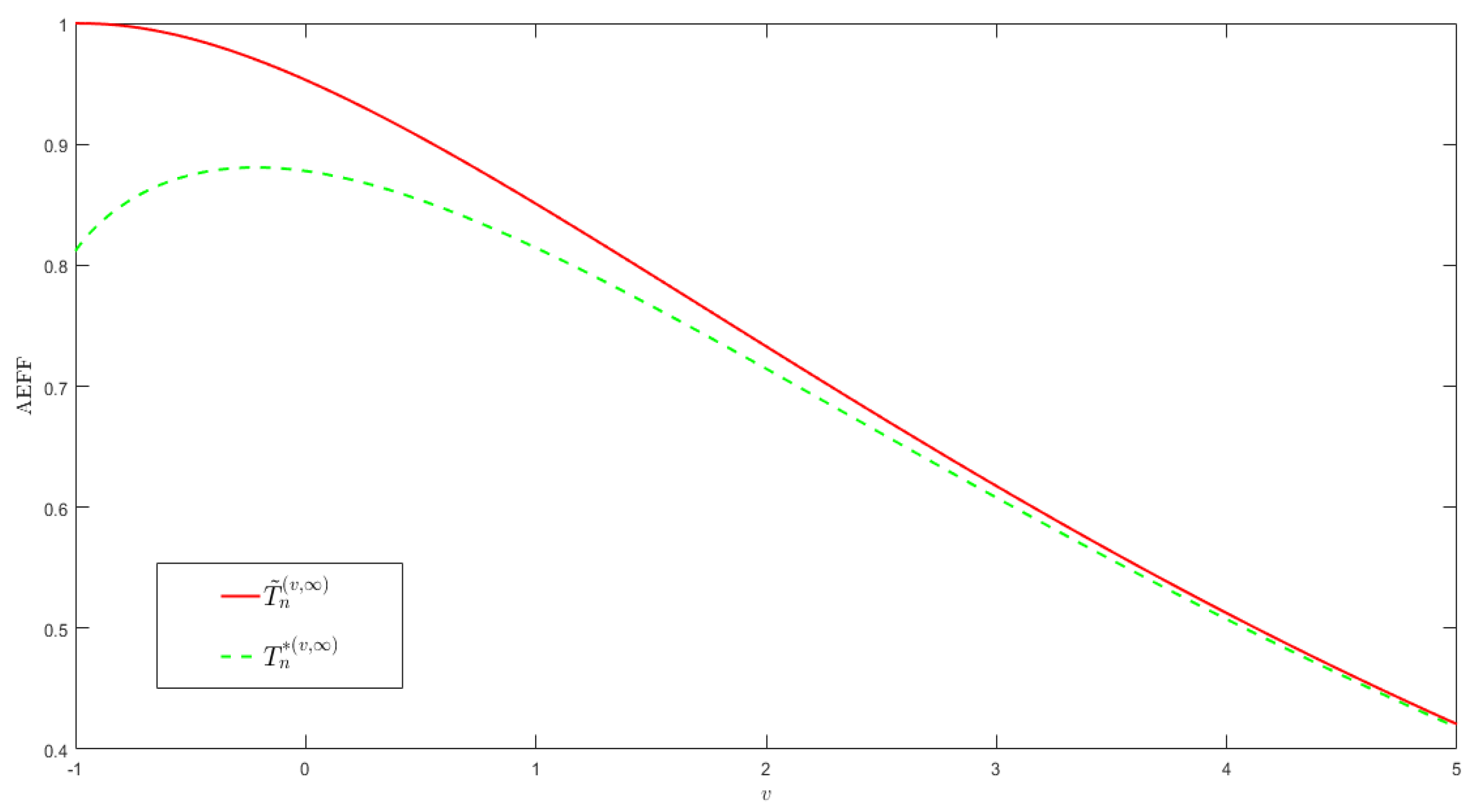
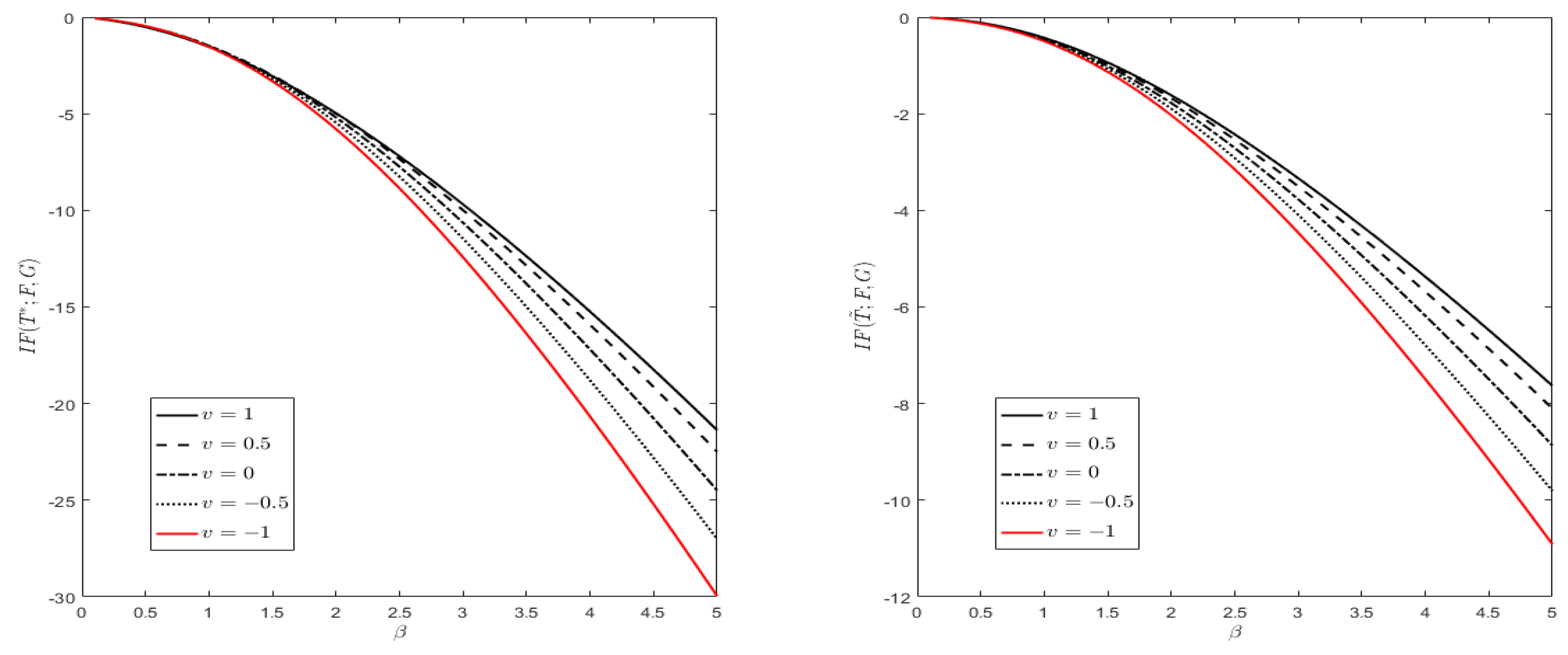
| n | r* | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0.3, 1, 1) | 30 | 0.9217 | 0.8255 | 1.0006 | 1.0005 | 0.0072 | 0.0451 | 0.0018 | 0.0015 | 68.6811 | 8.7774 | 8.3678 | 0.00 |
| 50 | 0.8609 | 0.8435 | 1.0022 | 1.0061 | 0.0068 | 0.0289 | 0.0014 | 0.0015 | 23.1288 | 14.3407 | 13.4344 | 0.00 | |
| 80 | 0.8274 | 0.8326 | 1.0083 | 1.0075 | 0.0041 | 0.0176 | 0.0013 | 0.0016 | 9.7485 | 19.5972 | 19.2393 | 0.00 | |
| 100 | 0.8161 | 0.8368 | 1.0147 | 1.0119 | 0.0030 | 0.0148 | 0.0018 | 0.0015 | 6.2607 | 20.8143 | 20.0842 | 0.00 | |
| (0.1, 1, 1) | 30 | 0.9885 | 0.9343 | 0.9942 | 0.9940 | 0.0007 | 0.0469 | 0.0007 | 0.0006 | 5.7287 | 1.2283 | 1.0561 | 0.00 |
| 50 | 0.9834 | 0.9252 | 0.9949 | 0.9952 | 0.0009 | 0.0269 | 0.0007 | 0.0006 | 3.6407 | 1.8194 | 1.8000 | 0.00 | |
| 80 | 0.9776 | 0.9407 | 0.9962 | 0.9953 | 0.0009 | 0.0189 | 0.0005 | 0.0006 | 1.0006 | 2.5849 | 2.3829 | 0.00 | |
| 100 | 0.9735 | 0.9302 | 0.9964 | 0.9961 | 0.0010 | 0.0130 | 0.0005 | 0.0005 | 0.7138 | 3.2549 | 2.9623 | 0.15 | |
| (0.3, 1, 2) | 30 | 1.2382 | 1.6039 | 1.9960 | 1.9919 | 0.0687 | 0.2408 | 0.0056 | 0.0050 | 74.7362 | 147.2932 | 126.8653 | 0.00 |
| 50 | 1.1347 | 1.6443 | 2.0015 | 1.9963 | 0.0268 | 0.1576 | 0.0045 | 0.0042 | 22.7834 | 158.1670 | 165.1127 | 0.00 | |
| 80 | 1.0851 | 1.6853 | 2.0050 | 2.0039 | 0.0127 | 0.1219 | 0.0039 | 0.0038 | 7.8035 | 197.7217 | 180.3746 | 0.00 | |
| 100 | 1.0731 | 1.6709 | 2.0081 | 2.0073 | 0.0085 | 0.0883 | 0.0042 | 0.0038 | 5.1102 | 223.2889 | 186.3996 | 0.00 | |
| (0.1, 1, 2) | 30 | 1.9245 | 1.8399 | 1.9903 | 1.9859 | 0.0169 | 0.2025 | 0.0026 | 0.0024 | 4.8833 | 9.3566 | 8.4148 | 0.00 |
| 50 | 1.8459 | 1.8506 | 1.9900 | 1.9888 | 0.0239 | 0.1223 | 0.0022 | 0.0021 | 3.1233 | 21.4576 | 18.4649 | 0.00 | |
| 80 | 1.7654 | 1.8392 | 1.9873 | 1.9895 | 0.0228 | 0.0754 | 0.0017 | 0.0017 | 3.0758 | 39.6547 | 35.4584 | 0.00 | |
| 100 | 1.7249 | 1.8681 | 1.9898 | 1.9906 | 0.0190 | 0.0660 | 0.0018 | 0.0018 | 1.9142 | 43.1656 | 45.1557 | 0.00 | |
| (0.3, 2, 1) | 30 | 0.9466 | 0.8640 | 0.9974 | 0.9987 | 0.0047 | 0.0429 | 0.0016 | 0.0021 | 82.5558 | 4.6014 | 3.5335 | 0.00 |
| 50 | 0.9061 | 0.8881 | 0.9955 | 0.9965 | 0.0051 | 0.0298 | 0.0015 | 0.0013 | 22.7834 | 12.7013 | 10.1286 | 0.00 | |
| 80 | 0.8729 | 0.8848 | 0.9944 | 0.9955 | 0.0036 | 0.0172 | 0.0012 | 0.0010 | 3.2990 | 16.1109 | 16.0286 | 0.00 | |
| 100 | 0.8562 | 0.8938 | 0.9970 | 0.9978 | 0.0029 | 0.0152 | 0.0011 | 0.0011 | 1.7146 | 19.8407 | 18.1323 | 0.00 | |
| (0.1, 2, 1) | 30 | 0.9880 | 0.9223 | 0.9953 | 0.9956 | 0.0005 | 0.2773 | 0.0483 | 0.0011 | 5.1904 | 0.8848 | 0.7232 | 0.00 |
| 50 | 0.9852 | 0.9557 | 0.9941 | 0.9952 | 0.0007 | 0.1438 | 0.0261 | 0.0006 | 3.4681 | 1.2380 | 1.1071 | 0.00 | |
| 80 | 0.9808 | 0.9452 | 0.9940 | 0.9942 | 0.0008 | 0.1775 | 0.0165 | 0.0005 | 0.9524 | 2.0353 | 1.6522 | 0.10 | |
| 100 | 0.9762 | 0.9560 | 0.9927 | 0.9939 | 0.0009 | 0.0444 | 0.0148 | 0.0006 | 0.8589 | 2.3773 | 2.2494 | 0.12 | |
| (0.3, 2, 2) | 30 | 1.3019 | 1.6018 | 1.9855 | 1.9853 | 0.0583 | 0.2434 | 0.0030 | 0.0026 | 85.6893 | 153.3920 | 159.4866 | 0.00 |
| 50 | 1.2012 | 1.6589 | 1.9850 | 1.9850 | 0.0228 | 0.1209 | 0.0024 | 0.0021 | 14.7957 | 260.7202 | 270.0256 | 0.00 | |
| 80 | 1.1570 | 1.6701 | 1.9844 | 1.9838 | 0.0099 | 1.1006 | 0.0018 | 0.0017 | 2.5650 | 348.1278 | 345.6587 | 0.00 | |
| 100 | 1.1484 | 1.6771 | 1.9832 | 1.9830 | 0.0069 | 0.0712 | 0.0017 | 0.0017 | 1.4158 | 386.5744 | 370.8852 | 0.00 | |
| (0.1, 2, 2) | 30 | 1.9238 | 1.8054 | 1.9885 | 1.9870 | 0.0161 | 0.1763 | 0.0027 | 0.0032 | 4.3161 | 5.8439 | 6.3442 | 0.00 |
| 50 | 1.8519 | 1.8637 | 1.9886 | 1.9850 | 0.0212 | 0.1201 | 0.0031 | 0.0023 | 3.9388 | 17.6548 | 16.9291 | 0.00 | |
| 80 | 1.7646 | 1.8565 | 1.9869 | 1.9849 | 0.0200 | 0.0696 | 0.0017 | 0.0019 | 1.2588 | 37.7912 | 36.6744 | 0.00 | |
| 100 | 1.7402 | 1.8839 | 1.9849 | 1.9843 | 0.0181 | 0.0756 | 0.0017 | 0.0017 | 0.9791 | 47.8601 | 44.6477 | 0.05 | |
| (0.3, 0.5, 1) | 30 | 0.9320 | 0.7989 | 1.0056 | 1.0065 | 0.0048 | 0.0565 | 0.0012 | 0.0014 | 7.2497 | 7.7231 | 6.7977 | 0.00 |
| 50 | 0.8912 | 0.8250 | 1.0116 | 1.0096 | 0.0051 | 0.0468 | 0.0012 | 0.0013 | 8.8465 | 12.2309 | 10.2765 | 0.00 | |
| 80 | 0.8565 | 0.8130 | 1.0185 | 1.0188 | 0.0034 | 0.0261 | 0.0013 | 0.0012 | 2.8355 | 15.4294 | 14.8902 | 0.00 | |
| 100 | 0.8463 | 0.8368 | 1.0218 | 1.0232 | 0.0024 | 0.0252 | 0.0011 | 0.0012 | 1.3175 | 17.0045 | 16.5285 | 0.00 | |
| (0.1, 0.5, 1) | 30 | 0.9874 | 0.8848 | 0.9968 | 0.9943 | 0.0005 | 0.0428 | 0.0006 | 0.0006 | 5.3788 | 1.2157 | 1.0236 | 0.00 |
| 50 | 0.9853 | 0.9136 | 0.9972 | 0.9952 | 0.0005 | 0.0295 | 0.0005 | 0.0005 | 3.8457 | 1.5111 | 1.4974 | 0.00 | |
| 80 | 0.9799 | 0.9193 | 0.9977 | 0.9975 | 0.0006 | 0.0181 | 0.0004 | 0.0005 | 1.9436 | 2.3528 | 1.9708 | 0.00 | |
| 100 | 0.9783 | 0.9165 | 0.9991 | 0.9989 | 0.0006 | 0.0143 | 0.0005 | 0.0004 | 0.9241 | 2.2865 | 2.1840 | 0.10 | |
| (0.3, 0.5, 2) | 30 | 1.3277 | 1.5964 | 2.0065 | 1.8144 | 0.0713 | 0.2504 | 0.0052 | 0.0004 | 61.5168 | 111.5918 | 15.1011 | 0.00 |
| 50 | 1.2141 | 1.6243 | 2.0185 | 1.8083 | 0.0373 | 0.1607 | 0.0049 | 0.0003 | 31.3754 | 129.6489 | 17.7850 | 0.00 | |
| 80 | 1.1618 | 1.6596 | 2.0357 | 1.8042 | 0.0147 | 0.1047 | 0.0046 | 0.0002 | 13.2211 | 128.0530 | 18.8915 | 0.00 | |
| 100 | 1.1486 | 1.6707 | 2.0386 | 1.8035 | 0.0125 | 0.0974 | 0.0047 | 0.0002 | 4.5564 | 118.1708 | 19.1617 | 0.00 | |
| (0.1, 0.5, 2) | 30 | 1.9443 | 1.8589 | 1.9900 | 1.8040 | 0.0093 | 0.2091 | 0.0020 | 0.0005 | 8.5329 | 6.7537 | 0.3454 | 0.00 |
| 50 | 1.8936 | 1.8745 | 1.9935 | 1.7963 | 0.1316 | 0.6520 | 0.0020 | 0.0003 | 4.9060 | 12.6372 | 0.5832 | 0.00 | |
| 80 | 1.8329 | 1.8271 | 1.9958 | 1.7937 | 0.0720 | 0.6408 | 0.0018 | 0.0002 | 1.3524 | 22.1326 | 0.9232 | 0.00 | |
| 100 | 1.8125 | 1.8538 | 2.0024 | 1.7930 | 0.0670 | 2.8163 | 0.0017 | 0.0002 | 0.9561 | 26.7188 | 1.0363 | 0.08 |
| 0.00 | 0.7711 | 0.7932 | 0.9202 | 0.9359 | 0.0072 | 0.0055 | 0.1277 | 0.2601 |
| 0.05 | 0.7783 | 0.7987 | 0.7925 | 0.6758 | 0.0056 | 0.0060 | 0.0084 | 0.0246 |
| 0.10 | 0.7839 | 0.8047 | 0.8009 | 0.6512 | 0.0002 | 0.0005 | 0.0038 | 0.0028 |
| 0.15 | 0.7841 | 0.8052 | 0.8047 | 0.6484 | 0.0026 | 0.0144 | 0.0258 | 0.0172 |
| 0.20 | 0.7867 | 0.8196 | 0.8305 | 0.6312 | 0.0093 | 0.0117 | 0.0560 | 0.0094 |
| 0.25 | 0.7960 | 0.8313 | 0.7745 | 0.6406 | 0.0046 | 0.0186 | 0.0168 | 0.0075 |
| 0.30 | 0.8006 | 0.8499 | 0.7577 | 0.6331 | 0.0046 | 0.0092 | 0.0038 | 0.0089 |
| 0.35 | 0.7960 | 0.8407 | 0.7539 | 0.6420 | 0.0120 | 0.0084 | 0.0168 | 0.0049 |
| 0.40 | 0.8080 | 0.8491 | 0.7707 | 0.6371 | 0.0008 | 0.0096 | 0.0370 | 0.0029 |
| 0.45 | 0.8072 | 0.8587 | 0.7337 | 0.6400 | 0.0069 | 0.0052 | 0.0208 | 0.0096 |
| 0.50 | 0.8003 | 0.8639 | 0.7545 | 0.6304 | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, C.; Ling, C. Robust Estimations for the Tail Index of Weibull-Type Distribution. Risks 2018, 6, 119. https://doi.org/10.3390/risks6040119
Gong C, Ling C. Robust Estimations for the Tail Index of Weibull-Type Distribution. Risks. 2018; 6(4):119. https://doi.org/10.3390/risks6040119
Chicago/Turabian StyleGong, Chengping, and Chengxiu Ling. 2018. "Robust Estimations for the Tail Index of Weibull-Type Distribution" Risks 6, no. 4: 119. https://doi.org/10.3390/risks6040119
APA StyleGong, C., & Ling, C. (2018). Robust Estimations for the Tail Index of Weibull-Type Distribution. Risks, 6(4), 119. https://doi.org/10.3390/risks6040119




