RMB Exchange Rates and Volatility Spillover across Financial Markets in China and Japan

Abstract

This study examines empirically the volatility spillover effects between the RMB foreign exchange markets and the stock markets by employing daily returns of the Chinese RMB exchange rates and the stock markets in China and Japan during the period in 1998–2018. We find evidence that there exist co-volatility effects among the financial markets in China and Japan, and the volatility of RMB exchange rates contribute to the co-volatility spillovers across the financial markets. Reversely, the return shock from the stock markets can also generate co-volatility spillover to the foreign exchange markets. The bidirectional relationship reveals that both the fundamental hypothesis and the investor-induced hypothesis are valid. Our estimates also show that the spillover effects led by the stock market in Japan are stronger than that from the foreign exchange markets and the Chinese stock markets, implying that market with higher accessibility has greater spillover effects onto other markets. We also found that the average co-volatility spillover effects among the RMB exchange markets and the stock markets in Japan and China are generally negative. These findings have important policy implications for risk management and hedging strategies.

1. Introduction

With China’s economic rise and rapid financial integration with the rest of the world, the increased trade and investment have caused demand in hedging against the foreign exchange risk associated with Renminbi (RMB) to rise substantially (Lien et al. 2013). The recent measures undertaken by the Chinese government to liberalize its financial sector and to internationalize the RMB, especially since the global financial crisis (GFC), have led to high volatility of the RMB exchange rates and increased the volatility spillover effect across the financial markets both in China and across countries. It has been theoretically found that the spillover from the foreign exchange market triggers the long-run volatility to stock market, which reversely introduces both short-run and long-run volatility back to the foreign exchange market (Morales-Zumaquero and Sosvilla-Rivero 2018). Given the rising foreign exchange risk associated with RMB internationalization, it is hence important to investigate the pattern and characteristics of the volatility spillover effect across the financial markets, especially for hedging strategy and for international portfolio decision.

There are two main hypotheses prevailing in the existing literature to explain the spillover effects between the foreign currency market and the stock market, one is the fundamental hypothesis and the other is the investor-induced hypothesis. The fundamental hypothesis highlights the fundamentals of the stock market that is affected due to the change in exchange rates. Since the trade balance is affected due to the change in exchange rates, it subsequently increases the cost of capital and lowers output and real income. Therefore, spillover effects between markets are driven by the fluctuation in the fundamentals of stock market (Dornbusch and Fischer 1980). An alternative approach is the investor-induced hypothesis, which posits that spillover is caused by international investors’ behaviour, where financial market volatility affects investors to modify the composition in investment portfolio because the innovations in the stock market create impact on the wealth and the liquidity of investors (Black 2015). Such hypothesis has been developed to explain stock prices changes in one market causing fluctuation in another market through portfolio holdings from international investors. Empirical evidence is shown by Kodres and Pritsker (2002) and Hong and Stein (2003) that crisis causes international investors to adjust portfolio in different stock markets. More recently, Nishimura et al. (2018) find evidence in support of the investor-induced hypothesis and suggest that the openness of a stock market also increases volatility spillover in stock market. Similar findings are reported by Morales-Zumaquero and Sosvilla-Rivero (2018) who find evidence showing that the presence of intra-spillover and inter-spillover are both valid within foreign exchange markets. However, the existing literature tends to focus on the explanation of spillover within only stock markets or foreign exchange markets. Limited evidence has been shown on co-volatility spillover effects between the foreign exchange market and stock market across countries based on investors’ behaviour.

Due to the financial integration, China’s recent market-oriented reforms of the RMB exchange rate formation mechanism will bring more volatility and risks to its financial system (Ho et al. 2017, 2018; Zhang et al. 2017). Therefore, it is essential to examine and to understand the risk and the volatility spillover effects from the RMB exchange market to financial markets, thereby underpinning possible strategies to hedge against such risk. The purpose of this paper is to employ the diagonal Baba-Engle-Kraft-Kroner Generalized Autoregressive Conditional Heteroskedasticity (BEKK GARCH-M) model to investigate the co-volatility spillover between the RMB foreign exchange market and stock market in China and its key neighbour, Japan, by using bilateral RMB exchange rates against the Japanese yen (JPY) and the US dollar (USD), and stock returns from both countries. We also consider that spillover effects across markets are due to the re-allocation of the resources through rebalancing portfolio by investors to hedge against the risk associated with spillover in line with the investor-induced hypothesis (Baker and Wurgler 2007; Boyer et al. 2006). Our findings suggest that, first, there exists a bidirectional relationship between the volatility spillover effects among the foreign exchange market and the stock markets, and shocks originated from RMB exchange rates and stock markets both affect the co-volatility. In particular, we found that shocks from the on-shore RMB-USD rate have significant spillover effects into the Chinese stock markets, i.e., Shanghai Stock Exchange (SSE) and Shenzhen Stock Exchange (SZSE), which in turn affect the co-volatility between the foreign exchange market and the stock markets. Similar results were obtained when the RMB-USD exchange rates were replaced by the RMB-JPY rates. In addition, the co-volatility spillover effects among the RMB foreign exchange market and the stock markets in Japan and China are found to be negative, which is consistent with the existing studies (Baker and Wurgler 2007; Rojec and Knell 2018; Yarovaya et al. 2017; Yuan 2005), and also has important policy implications for risk management and hedging strategies.

This paper implies the following contributions. First, it extends the validity of the fundamental hypothesis and the investor-induced hypothesis in the context of China by providing further empirical evidence from co-volatility spillover between foreign exchange market and stock market. Second, it advances the knowledge of the effectiveness of China’s market accessibility and internationalisation after its decades long of development and promotion by providing new evidence on the return volatility spillovers. Last, it offers important policy implications to market participants and policy makers on the pattern of co-volatility spillover effects across the financial markets in the two largest Asian countries.

The reminder of the paper is organised as the follows. Section 2 describes the literature review and hypotheses on spillover effects associated with the investor-induced approach. Section 3 discusses the economic models used in this study. In Section 4, we explain the methods and the descriptive analysis of our data. Section 5 reports the empirical results and their implications. Section 6 discusses the results and limitations. Section 7 concludes the paper.

2. Literature Review

2.1. RMB Internationalisation

In recent years, China has undertaken a series of measures to step up RMB internationalisation, including creating bilateral currency swaps, expanding trade settlement in RMB, and establishing and expanding the offshore RMB bond and foreign exchange markets (Ho et al. 2017, 2018). According to Yao and Whalley (2016), RMB as a settlement currency for cross-border trade can be traced back to the 1980s. Since then, the RMB has been frequently used to settle transactions between China and its neighbouring countries, accounting for about 17% of China’s cross-border trade by 2013. China has also signed several bilateral Currency Trade Settlement Agreements with several major trading partners, such as Russia and Australia, and banks in Hong Kong have started to offer RMB retail banking services since 2004 (Ho et al. 2017, 2018). The recent initiative of the Silk Road Economic Belt and the 21st-century Maritime Silk Road (The Belt and Road (B&R) initiative) is another push from China for its currency internationalisation, in which countries along the belt-road are expected to gradually increase the use of RMB in trade and investment settlements and as foreign exchange reserves (Zhang et al. 2017). Since 2009, China has signed a series of ‘loan-for-oil’ cooperation agreements with Russia, Kazakhstan and other countries. The same approach is used in the B&R initiative to promote more bulk commodity transactions and to make more loans in Asian currencies. It was further extended later in August 2015 when China started the RMB denominated settlement of domestic crude oil futures. Moreover, the off-shore RMB market, started initially in Hong Kong in 2004, has been expanded rapidly. Additional evidence for RMB internationalisation can also be seen from the enhancement and the promotion of off-shore RMB international bond market. For instance, the British government launched the first RMB sovereign bond in London in 2014. Later in March 2015, the first public offering of ‘panda bonds’ was completed with a total value of RMB 1 billion. An even larger issue size of RMB 3 billion green financial bonds was issued by Brazil, Russia, India and China (BRICS) New Development Bank in 2016. The RMB has become one of the world’s top 10 most traded currencies. According to the Society for Worldwide Interbank Financial Telecommunication (SWIFT), the RMB has overtaken the Canadian and Australian dollars since 2014 to enter the top five world payments currencies, accounting for a record high share of 2.17 per cent in global payments by value in December 2014. So far 12 cities, including Hong Kong, London, Paris and Sydney, have officially announced the establishment of offshore RMB centres (Ho et al. 2017, 2018).

2.2. Dynamic Correlation and Volatility Spillover Effects

The international economic integration and financial deregulation worldwide have underwired the relationships between financial markets. During this process, volatility spillover originated by shock from one market transmits to another. As such, systematic risk is subsequently increased, lowering the possibility to diversify investment portfolio on a global scale, which leads to growing importance to investigate volatility spillover effects among the markets. Existing literature has found significant presence of spillover effects among stock markets and other markets in the recent years, and confirmed that volatility spillovers affect the joint behaviour of market volatility and market interdependence. For example, Reboredo (2018) examined co-volatility between green bond and financial markets and found that the green bond markets composited with corporate and treasury bond weakly co-moved with stock and energy commodity markets. Liow et al. (2018) found that spillovers are significant to the dynamics of financial market stress and economic policy uncertainty, where the link among the international spillover in multi-country systematic risks are significantly affected by changes in international economic policy. Apostolakis (2016) indicated that financial stress spillovers affected by market risk are significant among Asian economies, in which China is the dominant stress transmitter to other neighbouring countries. Umar and Suleman (2017) examined the interdependence between the Islamic and the conventional equities with the asymmetric effect on the return and volatility transmission. Using the sample from 1996 to 2015, they found that the decoupling hypothesis approach was significantly weak for the Islamic equity post-crisis due to market internalisation, suggesting that the market integration among the Islamic, the US, the UK and Japan equity is strengthened after the GFC. Even though many existing studies attempted to examine the spillover effects, but the findings are yet conclusive, particularly when spillovers are involved in different markets, such as the volatility spillovers between foreign currency market and stock market.

However, the results from the existing studies are mixed on the volatility spillover effects and the direction of the effects between foreign exchange rate and stock return. Jorion (1990) reports that exchange rate fluctuation is not related to stock price, while others find that the links are strong and significant but can be either unidirectional or bidirectional. Unidirectional causality between foreign exchange rate and stock price is suggested in early years of research. For instance, using the error correction mode, Ajayi and Mougouė (1996) find evidence supporting unidirectional causality from stock price to foreign exchange rate and also the existence of both short-run and long-run dynamics between foreign exchange rate and stock price. Abdalla and Murinde (1997) report similar findings using data from India, Korea and Pakistan with a bivariate vector autoregressive model. Yau and Nieh (2006) find that both Taiwan and Japan have a short duration of shock effect on the stock prices from foreign exchange rate market, while the Taiwanese financial market is more sensitive to volatility spillovers than the Japanese market. A more recent study by Zhao (2010) reports that the return spillover effect is not found with the VAR and GARCH models using data from China in 1991–2009, suggesting that a long-term equilibrium relationship is not observed, whereas a bi-directional volatility spillover effect exists between the stock market and the foreign exchange market due to the significant past innovations created in stock market. Yet, this is not the first study report possible bi-direction causality. Granger et al. (2000) find bidirectional causality using the data from Hongkong, Malaysia, Singapore, Thailand and Taiwan, and confirm the existence of a strong feedback relationship between stock price and foreign exchange rate. Adopting Johansen’s cointegration analysis, Kim (2003) finds a positive association between S&P 500 and industrial production, while a negative relationship with the real exchange rate and interest rate. Caporin and McAleer (2012) employ the bivariate UEDCC-GARCH model and report a unidirectional Granger causality relation from stock returns to exchange rates in the US and the UK. They find that the spillovers become bi-directional when using the data among the euro area and Switzerland, as well as between Japan and the US. Kesik et al. (2016) also report a bidirectional causality between BIST100 index and foreign exchange rates due to foreign portfolio investment and international capital flow. Similar results can also be found in Ahmed and Naguib (2017), Hussain and Liew (2005), Rafiq and Yun (2017), Rashid (2007) and Wang et al. (2004), yet they are inconsistent and inconclusive. This study intends to empirically test the validity of the market fundamentals and the investor-induced approach in the context of China, and investigate the effectiveness of the Chinese government’s policy measures and initiatives towards market accessibility and internationalisation, particularly among the financial markets in the two largest Asian countries. In particular, we examine empirically if there is any return volatility spillover from the RMB foreign exchange market to the stock markets, and if there exists a co-volatility spillover effect across the financial markets between China and Japan, as well as how shocks originated from the exchange rate market affect the co-volatility spillovers.

2.3. Research Hypotheses

There are two different theories in explaining volatility spillover effects. The traditional fundamentals hypothesis is developed based on the assumption that the economy is frictionless, and the investors are rational. In this context, stock prices are only affected by news associated with corporate fundamentals. As the market is assumed to be frictionless, return shocks impacted by news will alter stock prices in other countries because of the difference in the market opening and closing times, which causes subsequent spillover effects on the co-volatility. Under the fundamentals hypothesis, the co-volatility spillover effects can be magnified in the context of financial integration and the RMB internationalization, and it is often adopted to justify the positive association and the co-movements between markets (Spantig 2015; Wong and Eng 2017). On the other hand, the investor-induced hypothesis has been widely adopted to explain the negative associations in the co-movement. It postulates that contagion in stock price fluctuation is investor-induced through portfolio adjustment or wealth constraint (Boyer et al. 2006). The same approach can be applied when involving volatility spillover from foreign exchange market. According to Boyer et al. (2006), the investor-induced hypothesis highlights two important indications. First, the co-movement of accessible stock returns with crisis (or volatility) country stocks should increase more than the co-movement of inaccessible stock returns during the crisis, because investors can be better facilitated. Such behaviour leads to negative dynamic correlation between financial markets because international investors (e.g., institutional investors) rebalance portfolio by selling asset in the other market; however, given the background of financial integration and internationalisation, market is more likely to be efficient where information can be quickly spread. Thus, the investors in different countries can be aware of the short-time fluctuations by adopting hedging strategies to minimise the risk caused by spillovers. Under this circumstance, both the fundamentals hypothesis and the investor behaviour offer explanations to the bidirectional relationship in spillover effects between foreign exchange rates and stock markets. We posit that spillover effects from the stock markets are dependent on the return shock from foreign exchange rates, which influence the co-volatility among the foreign exchange markets and the stock markets. Additionally, we posit that a possible bidirectional relationship holds, where the spillover effects from foreign exchange market are dependent on stock market, which causes spillover onto the co-volatility among the markets. Hence, we developed our hypotheses as the follows:

Hypothesis 1a (H1a).

The return shock from the foreign exchange market is associated with the subsequent spillover from the stock markets, which leads spillover to the co-volatility across the financial markets.

Hypothesis 1b (H1b).

The return shock from stock market is associated with the subsequent spillover from the foreign currency markets, which leads spillover to the co-volatility across the financial markets.

Numerous studies have shown that hedging is required when investing across markets due to incomplete financial integration (Chkili 2016; Khalfaoui et al. 2015; Maghyereh et al. 2017). Both H1a and H1b imply that the market is efficient, and investors can obtain easy access to information for hedging strategies. In addition, Boyer et al. (2006) suggest that spillover is more likely to take place during crisis period, which is supported by Nishimura et al. (2018). Furthermore, the investor-induced hypothesis proposes market accessibility as another important factor. A market with higher accessibility is expected to lead the movement of other markets which are less accessible through the wealth constraints of local investors. Hence, if spillover is caused by investor behaviour, the magnitude of co-volatility spillover effects from a market with greater accessibility is higher than that in other markets. By contrast, if changes in fundamentals cause fluctuations, the co-volatility spillover effects are expected to be indifferent from the two markets. Consequently, we develop the following hypothesis:

Hypothesis 2 (H2).

The co-volatility spillover originated from a market (country) with high accessibility is more likely to generate higher spillover to other markets.

To address our research questions and test hypotheses, we choose the stock markets from China and Japan with the assumption that market accessibility is relatively lower in China than in Japan. The rationale is that even though China has progressed substantially in developing its financial market, it is constrained by the relatively short history and segmentation from other global financial markets, retaining lower accessibility than the Japan stock market (Carpenter and Whitelaw 2017). In addition, due to the successive progress in RMB internationalisation, we adopt respectively the RMB-USD and RMB-JPY exchange rates to examine the spillover effects across the financial markets, including Shanghai Stock Exchange Market, Shenzhen Stock Exchange Market, and Tokyo Stock Exchange Market. China and Japan have a long history of international trade, and also experienced a high level of economic interdependence, yet USD is still the most important currency for invoicing and settlement in the bilateral trade between the two countries (Ito et al. 2016; Sato and Shimizu 2018). We then employ the diagonal BEKK GARCH-M model and the VAR model to examine the existence and pattern of the volatility spillovers across the financial markets under these hypotheses in the two largest Asian countries.

3. Econometric Methodology

There are a variety of conditional volatility models used to examine spillover effects, which include the CCC models of Bollerslev (1990), the VARMA-GARCH model of Ling and McAleer (2003), the DCC model of Engle (2002), the BEKK model of Engle and Kroner (1995) and the diagonal BEKK model. However, as McAleer et al. (2009) and Chang et al. (2018) suggested, these models virtually involve theoretical constraints to accommodate volatility spillover effects (see also Chang et al. 2010; Chang and Su 2010; Wu et al. 2011). In this paper, we follow Diebold and Yilmaz (2009) to define volatility spillovers based on forecast error variance decompositions from vector autoregressions (VAR), and employ the BEKK model, in particular, the diagonal BEKK model and the VAR model to empirically investigate the volatility spillover effects between the RMB foreign exchange market and stock markets in China and Japan. We follow Chang et al. (2018) to define co-volatility spillover effect based on the diagonal BEKK model. To show the co-volatility spillover, it is essential to obtain the standardised residuals from the conditional mean of return shocks in the estimated multivariate GARCH models. In Section 3.1 we discuss the features of the full BEKK model, and the diagonal BEKK model. In Section 3.2 we follow Diebold and Yilmaz (2009, 2012) to define the volatility spillover effects used in this study.

3.1. The Diagonal BEKK Model

The GARCH model was proposed by Bollerslev (1986) based on Engle (1982), and it has picked up popularity among academics because of their ability to capture some of these typical stylized facts of financial time series such as such as time varying heteroskedasticity and volatility clustering. There are several studies to employ multivariate conditional volatility models to estimate conditional covariances to capture volatility spillover effects (for details, see McAleer (2005) and Chang et al. (2018)). Despite the popularity, McAleer and Medeiros (2008) report that there are theoretical problems associated with these multivariate conditional volatility models. In particular, they find that the CCC, VARMA-GARCH and VARMA-AGARCH models have static conditional covariances and correlations, implying that accommodating volatility spillovers is not possible. Moreover, the Full BEKK and DCC models have been shown to have no regularity conditions, and hence no asymptotic properties of consistency and asymptotic normality (for further details, see (Chang and McAleer 2018; Chang et al. 2018; McAleer and Hafner 2014)). Due to the limitations in the existing multivariate GARCH models and the concern related to such classical statistical property, this study adopts the Diagonal BEKK (DBEKK) GARCH-M models to estimate the volatility spillover effects.

The full BEKK model adopted in Engle and Kroner (1995) is shown in Equation (1):

$$H_t=C{C}^{\prime }+B{H}_{t-1}B\prime +A{\epsilon }_{t-1}\epsilon {\prime }_{t-1}{A}^{\prime },$$

(1)

The conditional variance consists of full matrix for A and B rather than diagonal matrices using the stochastic process derived in Equation (1). However, the full BEKK model is concerned with too many parameters and is less parsimonious that high computation is demanded in estimation Jayasinghe et al. (2014), as it cannot be derived from stochastic processes. Chang and McAleer (2018) further suggested that unless assumption was in place, no regularity conditions exists for checking the internal consistency of the alternative models, hence no valid asymptotic properties of the quasi-maximum likelihood estimate (QMLE) of the associated parameters. The model convergence can be problematic and less reliable when parameters are as low as five financial assets. The full BEKK mode also suffer from the curse of dimensionality related to the proliferation of parameter, which are hardly interpretable due to the inherent structure used to ensure positive semi-definiteness of the resulting estimated covariance matrices and cannot be estimated dimensions larger than 3. Hence, in empirical analysis, this study employs the diagonal BEKK model to examine the volatility spillover effects. To examine the co-volatility spillover effects among the three markets, our model specification is developed as follows:

$$\begin{gathered} r_t={\lambda }_0+{\lambda }_1{r}_{i,t-1}+{\lambda }_2{r}_{j,t-1}+{\lambda }_3{r}_{k,t-1}+{\epsilon }_t, \\ {r}_t=\left(r_{i,t},r_{j,t},r_{k,t}\right)\prime , \end{gathered}$$

(2)

$${\epsilon }_t=\left({\epsilon }_{i,t},{\epsilon }_{j,t},{\epsilon }_{k,t}\right)~iid N\left(0,H_t\right),$$

(3)

where r_t and ${\epsilon }_t$ are 3 $\times$ 1 vector consisting of returns at time t on the return in spot RMB exchange rate ($r_{i,t}$), index from the financial market in Japan ($r_{j,t}$), and the market index from China ($r_{k,t}$). Parameters ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ denote the coefficient of the past movement of the returns on foreign exchange rate and the market indices. $r_{i,t-1}$, $r_{j,t-1}$ and $r_{k,t-1}$ are 3 $\times$ 1 vector consisting of the previous day movement on the return in spot RMB exchange rate, market indices in Japan and China respectively. ${\epsilon }_t$ denotes 3 $\times$ 1 vector of random errors at time t given all available information at time t − 1, and is assumed to follow normal distribution with mean of 0 and variance of H_t. H_t is the corresponding 3 $\times$ 3 conditional variance and covariance matrix.

$$H_t=C{C}^{\prime }+B{H}_{t-1}B\prime +A{\epsilon }_{t-1}\epsilon {\prime }_{t-1}{A}^{\prime },$$

(4)

In Equation (4), C is an upper triangular 3 $\times$ 3 matrix consisting of constant parameters in the conditional variance and covariance matrices. A and B are both diagonal parameter matrices, which do not need to come from an underlying stochastic process. A captures the relationship between conditional variances and past residual terms $\epsilon$, and B captures the correlation between current conditional variances and past variances. The diagonal positive definite matrix A allows Equation (4) to be derived from the vector random coefficient autoregressive process from Equation (2) due to ${\epsilon }_{t-1}\times \epsilon {\prime }_{t-1}$ is a 3$\times$3 matrix. Since QMLE of the parameters of diagonal BEKK model were consistent and asymptotically normal (McAleer and Medeiros 2008), standard statistical inference on hypothesis testing is valid. Hence, the variance and covariance matrix of the proposed diagonal BEKK model is shown as follows:

$$\begin{gathered} H_T=\left[H_{i,t},H_{j,t},H_{k,t}\right]=\left[\begin{array}{ccc}{h}_{i,t}& h_{ij,t}& h_{ik,t}\\ h_{ji,t}& h_{i,t}& h_{jk,t}\\ h_{ki,t}& h_{kj,t}& h_{k,t}\end{array}\right] \\ =\left[\begin{array}{ccc}{C}_i& 0& 0\\ C_{ij}& C_j& 0\\ C_{ik}& C_{jk}& C_k\end{array}\right]\left[\begin{array}{ccc}{C}_i& C_{ij}& C_{ik}\\ 0& C_j& C_{jk}\\ 0& 0& C_k\end{array}\right]+\left[\begin{array}{ccc}{B}_i& 0& 0\\ 0& B_j& 0\\ 0& 0& B_k\end{array}\right]\left[\begin{array}{ccc}{h}_{i,t-1}& h_{ij,t-1}& h_{ik,t-1}\\ h_{ji,t-1}& h_{j,t-1}& h_{jk,t-1}\\ h_{ki,t-1}& h_{kj,t-1}& h_{k,t-1}\end{array}\right]\left[\begin{array}{ccc}{B}_i& 0& 0\\ 0& B_j& 0\\ 0& 0& B_k\end{array}\right]+ \\ \left[\begin{array}{ccc}{A}_i& 0& 0\\ 0& A_j& 0\\ 0& 0& A_k\end{array}\right]\left[\begin{array}{c}{\epsilon }_{\mathrm{i},t-1}\\ {\epsilon }_{j,t-1}\\ {\epsilon }_{k,t-1}\end{array}\right]\left[\begin{array}{ccc}{\epsilon }_{\mathrm{i},t-1}& {\epsilon }_{j,t-1}& {\epsilon }_{k,t-1}\end{array}\right]\left[\begin{array}{ccc}{A}_i& 0& 0\\ 0& A_j& 0\\ 0& 0& A_k\end{array}\right] \end{gathered}$$

(5)

The definition on co-volatility spillover via the diagonal BEKK model was developed by Chang et al. (2018), which considers the effect of a shock in asset i at time t − 1 on the subsequent co-volatility between i and another asset at t. Following Chang et al. (2018), we define the co-volatility spillover effects as follows:

$$\frac{H_{ijk,t}}{{\epsilon }_{i,t-1}}=A_{ii}{A}_{jj}{A}_{kk}{\epsilon }_{i,t-1},i\ne j,i\ne k,k\ne j,$$

(6)

where $A_{ii},A_{jj}$ and $A_{kk}$ are derived from the diagonal matrix A. $H_{ijk,t}$ is the conditional covariance among asset i, j and k, ${\epsilon }_{j,t-1}$ is the return shock at time t − 1 from asset j. ${\epsilon }_{i,t-1}$ denotes the conditionally heteroskedastic error term, which is the average return shock of market index i at time t − 1. The stochastic processes for return shocks are derived from the standard GARCH (1,1) model for the specification of the conditional volatility. Following the definition from Chang et al. (2018), the test of null hypothesis on co-spillover effects is: H₀: $A_{ii}{A}_{jj}{A}_{kk}=0$.

If the null hypothesis is rejected, i.e., $A_{ii}{A}_{jj}{A}_{kk}>0$, we adopt the definition in Equation (14), which indicates that there is spillover on asset j and k from the return shock of asset i at time t − 1; however, return shocks from asset j and k do not have spillover on asset i concurrently. The magnitude of co-volatility spillover changes and vary over time. In this study, therefore, we use the average return shocks over the sample period to calculate the co-volatility spillover effects.

3.2. Alternative Volatility Spillover Model

To test the volatility spillovers effects, Engle III et al. (1988) developed vector autoregressive (VAR) models, where the volatility spillover from market one is to be observed via the impulse response of shocks to volatility of another market to the volatility of market one. Based on VAR, Diebold and Yilmaz (2009) decompose the error variance of joint asset return forecasts, in which connections among assets are shown by the decomposed error variance as nodes and the weights of links. They are further determined by shares of forecast error variance spillovers. According to Diebold and Yilmaz (2009), the degree of market connectedness can be measured through the one-step-further approach through the spillover index. In particular, the total spillover is considered relative to the total forecast error variation as $a_{0,11}^2+a_{0,12}^2+a_{0,21}^2+a_{0,22}^2=trace\left(A_0{A}_0^{\prime }\right)$, where the components are the 1-setp-ahead errors in forecasting and the total spillover is defined as $a_{0,12}^2+a_{0,21}^2$, and $A_0{A}_0^{\prime }$ is the covariance matrix within the 1-step-ahead error vector. Hence, based on the definition discussed, the spillover index is defined as:

$$S=\frac{a_{0,12}^2+a_{0,21}^2}{trace\left(A_0{A}_0^{\prime }\right)}\times 100$$

(7)

Diebold and Yilmaz (2012) extend the above model to make it invariant on ordering by using generalized impulse response functions to capture spillovers. They define the variance shares as the fraction of the H-step-ahead error variance in forecasting return in market i due to the shock from i. The cross spillover as the fractions of the H-step-ahead error variance in forecasting return in market i affected by shock from market j is also considered. As the generalized impulse response function is used, the sum of the factors of each row of the variance decomposition table is not equal to 1. Hence, Diebold and Yilmaz (2012) have the following generalized H-step-ahead error variance decomposition p-order and N-variable VAR forecasts:

$${\theta }_{ij}^g\left(H\right)=\frac{{\sigma }_{ii}^{-1}{{\displaystyle \sum }}_{h=0}^{H-1}\left(e_i^{\prime }{A}_h{\displaystyle \sum }{e}_j\right){}^2}{{{\displaystyle \sum }}_{h=0}^{H-1}\left(e_i^{\prime }{A}_h{\displaystyle \sum }{e}_j\right)}$$

(8)

where ∑ is the variance matrix for the error vector, ${\sigma }_{ii}$ is the standard deviation of the error term for the ith equation and e_i is the selection vector with one as the ith element and otherwise zero. To use the information available in the variance decomposition matrix to calculate the spillover index, the normalized entry of the variance decomposition matrix is:

$${\tilde{\theta }}_{ij}^g\left(H\right)=\frac{{\theta }_{ij}^g\left(H\right)}{{{\displaystyle \sum }}_{j=1}^N{\theta }_{ij}^g\left(H\right)},\mathrm{where}{{\displaystyle \sum }}_{j=1}^N{\tilde{\theta }}_{ij}^g\left(H\right)=1\mathrm{and}{{\displaystyle \sum }}_{i,j=1}^N{\tilde{\theta }}_{ij}^g\left(H\right)=N$$

(9)

Consequently, Diebold and Yilmaz (2012) construct the total volatility index as:

$$S^g\left(H\right)=\frac{{{\displaystyle \sum }}_{\begin{array}{c}i,j=1\\ i\ne j\end{array}}^N{\tilde{\theta }}_{ij}^g\left(H\right)}{{{\displaystyle \sum }}_{i,j=1}^N{\tilde{\theta }}_{ij}^g\left(H\right)}\times 100=\frac{{{\displaystyle \sum }}_{\begin{array}{c}i,j=1\\ i\ne j\end{array}}^N{\tilde{\theta }}_{ij}^g\left(H\right)}{N}\times 100$$

(10)

To determine the directional spillover due to volatility from different markets, the normalized elements of the generalized variance decomposition matrix is used. The directional market spillover from market i to market j is:

$$S^g\left(H\right)=\frac{{{\displaystyle \sum }}_{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{\tilde{\theta }}_{ij}^g\left(H\right)}{{{\displaystyle \sum }}_{j=1}^N{\tilde{\theta }}_{ij}^g\left(H\right)}\times 100$$

(11)

Similarly, the directional market spillover from market j to market i is:

$$S^g\left(H\right)=\frac{{{\displaystyle \sum }}_{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{\tilde{\theta }}_{ji}^g\left(H\right)}{{{\displaystyle \sum }}_{j=1}^N{\tilde{\theta }}_{ji}^g\left(H\right)}\times 100$$

(12)

Hence, based on Diebold and Yilmaz (2012), the net spillover from market i to all other markets j is calculated as:

$$S_i^g\left(H\right)=S_{ji}^g\left(H\right)-S_{ij}^g\left(H\right)$$

(13)

In this study, to serve as a robustness test for the spillover effects with the DBEKK model, we follow Diebold and Yilmaz (2012) to use 200-day rolling samples and 10-step-ahead forecasts, which permits the assessment of the extent and the nature of spillover variation over time via the corresponding time series of spillover indices.

4. Data and Descriptive Statistics

In the empirical analysis, we use daily time series data to examine the co-volatility spillovers among the returns of RMB foreign exchange rates and the stock markets in China and Japan. To proxy for RMB foreign exchange rates, we employ the on-shore RMB-USD exchange spot rates (RU) and the on-shore RMB-JPY exchange spot rates (RY). For robustness check purpose, we also select the off-shore exchange spot rates between RMB and USD (OFFRU) and between RMB and JPY (OFFRY), because the existing literature shows evidence that the off-shore RMB exchange rates are much dependent on the on-shore rates (Funke et al. 2015; Ren et al. 2018; Xie et al. 2017; Xu et al. 2017). For stock market indices, we use the Tokyo Stock Exchange Price Index (TPX) and the Nihon Keizai Shimbun 225 (NIK) in Japan, and the Shanghai Composite Stock Market Index (SHCI) and the Shenzhen Composite Stock Market Index (SZCI) in China. We collected data from January 5, 1998 to June 1, 2018 for the on-shore RMB to foreign currency exchange rates, totaling 5325 observations, and the same for the market indices. However, as the off-shore RMB foreign exchange market was established only recently, we could only collect the daily off-shore RMB exchange rates from August 24, 2010 to June 1, 2018, with 2029 observations in total.

All the daily data series are collected from Bloomberg Terminal. The daily returns of the foreign exchange rates and the market stock prices are computed based on the corresponding equation:

$$r_{i,t}=100\times \log \left(\raisebox{1ex}{$P_{i,t}$}\!\left/ \!\raisebox{-1ex}{$P_{i,t-1}$}\right.\right),$$

(14)

where $P_{i,t}$ and $P_{i,t-1}$ are the closing prices of the exchange rates or the market indices for trading days t − 1 and t respectively.

Table 1. Descriptive statistics of stock returns and exchange rate changes.

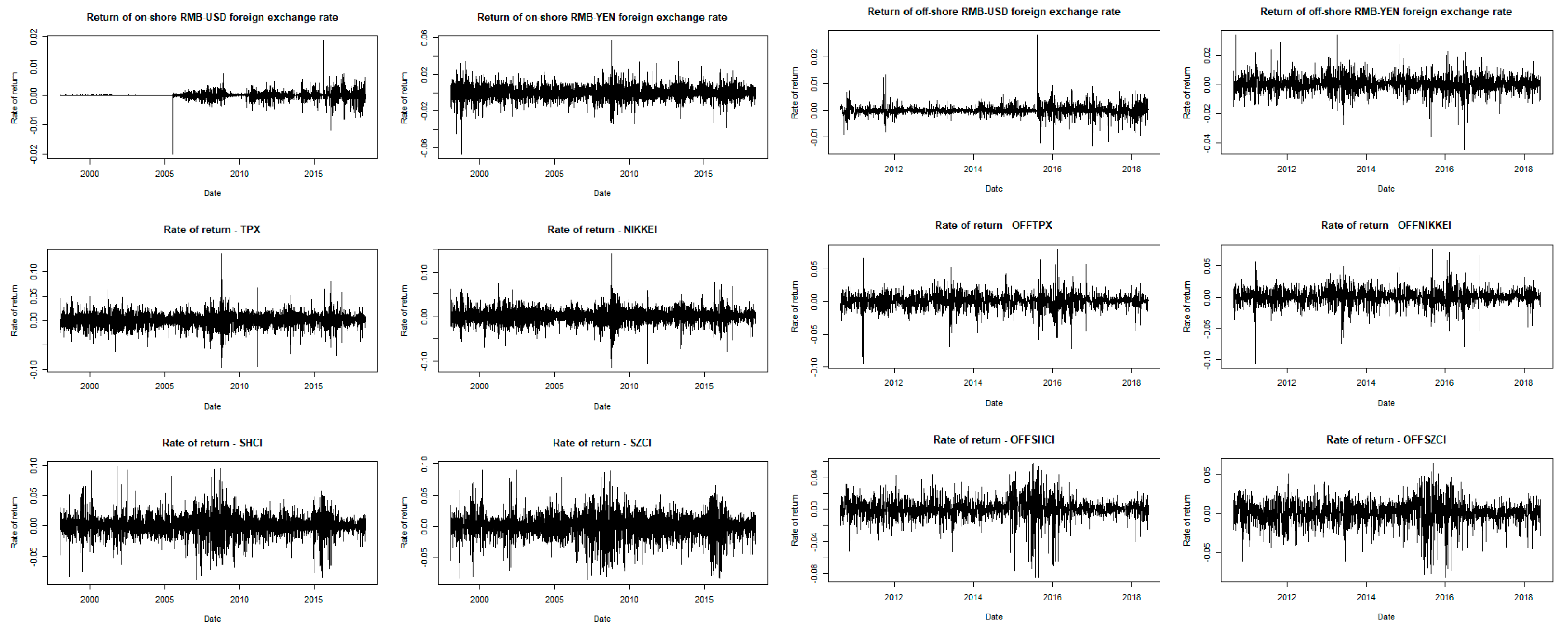
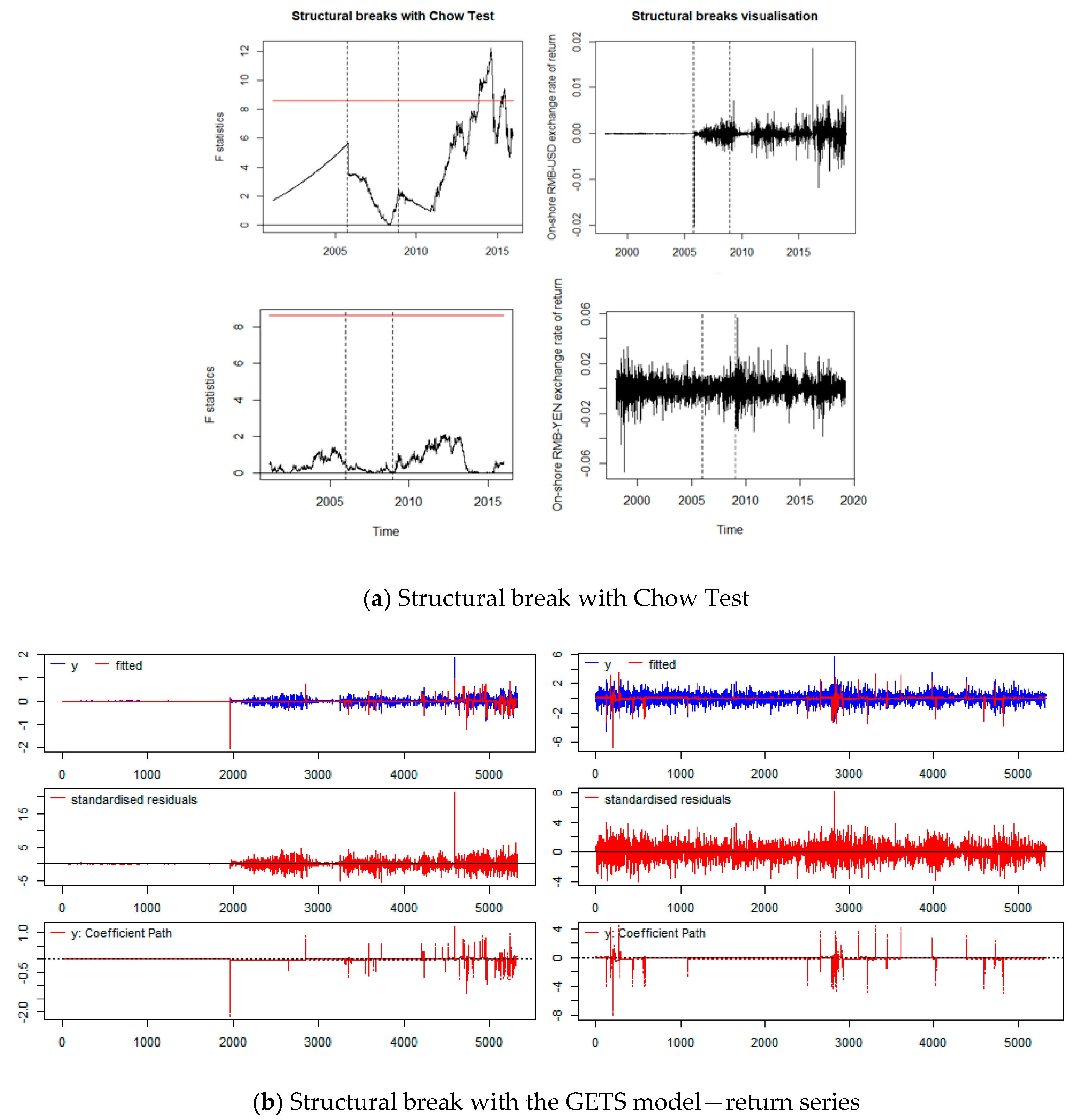
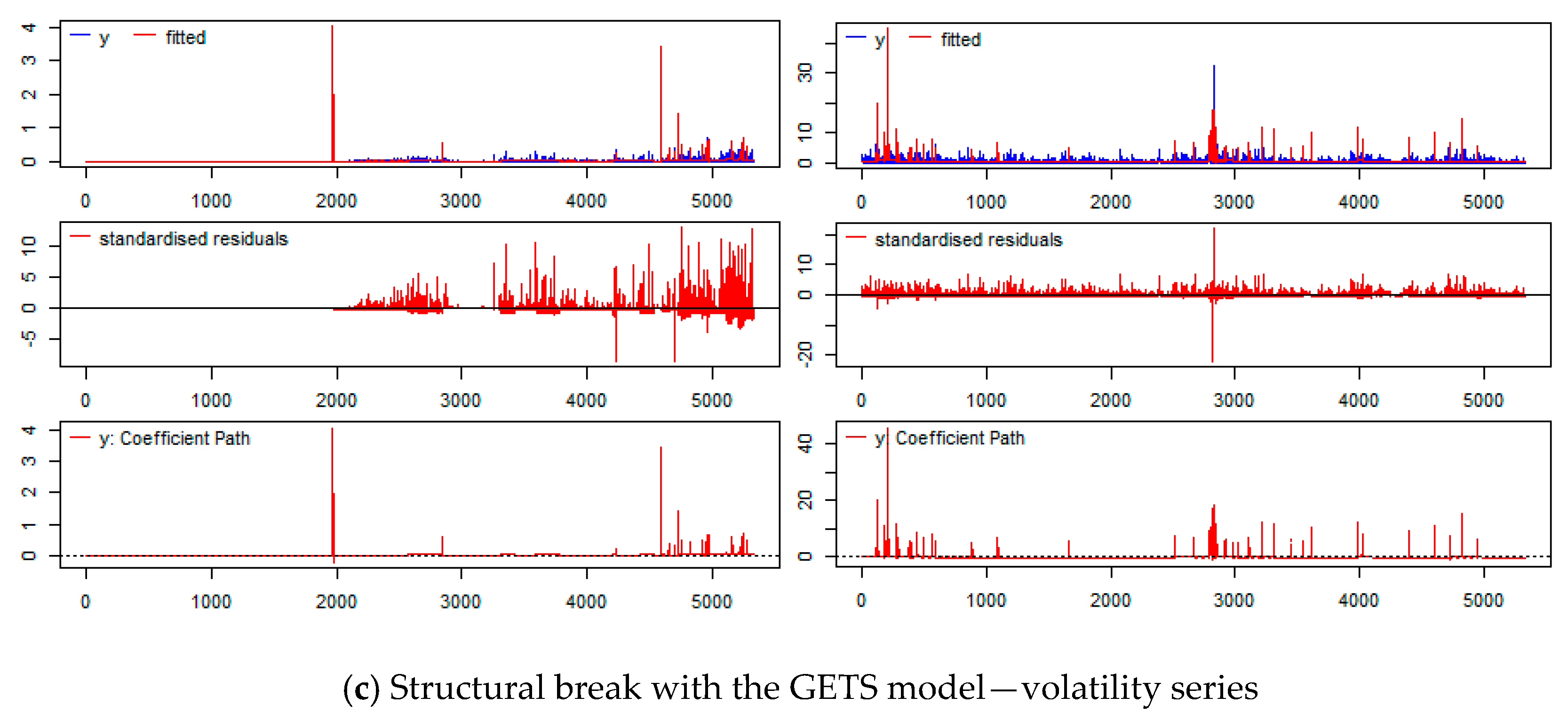
Var.	Mean	Median	Max.	Min.	Std. Dev.	Skew.	Kurt.	Obs.
RUt	−0.0047	0.0000	1.8334	−2.0322	0.1108	−0.5978	46.8882	5325
RYt	0.0037	0.0000	5.6708	−6.7010	0.6737	−0.2760	5.4318	5325
TPXt	0.0077	0.0000	12.8646	−10.0071	1.3351	−0.3204	9.2529	5325
NIKt	0.0073	0.0000	13.2346	−12.1110	1.4694	−0.3511	9.4246	5325
SHCIt	0.0176	0.0000	9.4009	−9.2561	1.5253	−0.3349	8.4486	5325
SZCIt	0.0290	0.0000	9.2435	−8.9303	1.6903	−0.5179	7.0147	5325
OFFRUt	−0.0021	−0.0076	2.7853	−1.4604	0.2117	0.8324	20.4311	2029
OFFRYt	0.0164	0.0145	3.3399	−4.4238	0.5934	−0.1043	4.4867	2029
OFFTPXt	0.0445	0.0090	8.0207	−9.4727	1.2212	−0.4316	6.6657	2029
OFFNIKt	0.0524	0.0000	7.7089	−10.5539	1.3045	−0.4580	6.0365	2029
OFFSHCIt	0.0164	0.0000	5.7636	−8.4909	1.3247	−0.8993	6.8442	2029
OFFSZCIt	0.0344	0.0066	6.5244	−8.2414	1.5797	−0.7938	3.6677	2029

Note: Var. stands for variables, Max. stands for maximum, Min. stands for minimum, Std. Dev. stands for standard deviation, Skew. Stands for skewness, Kurt. Stands for Kurtosis and Obs. stands for observations. RU_t is the daily return of the RMB-USD spot rate, RY_t the daily return of the RMB-JPY spot rate, TPX_t is the daily return of the Tokyo Stock Exchange Tokyo Price Index, NIK_t is the daily return of the Nihon Keizai Shimbun 225 Index, SHCI_t is the daily return of Shanghai Composite Stock Market Index, and SZCI_t is the daily return of Shenzhen Composite Stock Market Index. The prefix OFF corresponds to the off-shore RMB foreign currency exchange period, which starts from August 24, 2008 to July 1, 2018. As such, OFFRU_t is the daily return of the off-shore RMB-USD spot rate, OFFRY_t is the daily return of the off-shore RMB-JPY spot rate, OFFTPX_t is the daily return of the Tokyo Stock Exchange Tokyo Price Index in the off-shore series, OFFNIK_t the daily return of the Nihon Keizai Shimbun 225 Index in the off-shore series, OFFSHCI_t is the daily return of Shanghai Composite Stock Market Index in the off-shore series, OFFSZCI_t is the daily return of Shenzhen Composite Stock Market Index in the off-shore series. All the returns are reported in percentage. The sample period for the full date set starts from January 5, 1998 to July 1, 2018, and the data sets for the off-shore series are collected between August 24, 2008 and July 1, 2018.

shows the descriptive statistics for the daily return of exchange rates and the stock returns in China and Japan. As seen from the table, apart from off-shore RMB-USD exchange rate, all the other returns are negatively skewed with excess kurtosis with a range from the lowest 3.6677 to 46.8882. It is noted that the kurtosis is particularly high for RMB-USD exchange rates in the series, which is largely due to the RMB exchange rate system reform from the dollar-peg to a managed floating exchange rate regime based on market supply and demand with reference to a basket of currencies on 21 July 2005. In comparison, RMB-JPY exchange rates show relatively much milder kurtosis. With regards the market indices, all the means of the ordinary returns are positive. The standard deviations for the two Japanese market indices, TPX and NIK, are very similar, and equal to 1.3351 and 1.4694, respectively. The variation of standard deviations is not much different with the off-shore series of TPX and NIK, where both drop slightly to 1.2212 and 1.3045, respectively. Similar changes can also be found for SHCI and SZCI, where the standard deviations drop slightly in comparison with OFFSHCI and OFFSZCI. We also observe that the means of the returns for all data series have increased while the kurtosis decreased.

Figure 1 presents the returns of the exchange rates and the stock markets. It can be seen that the return series exhibit similar patterns for the pairs of TPX-NIK and SHCI-SZCH indexes, while the returns across both on-shore and off-shore markets are different. It is also noted that the recent reforms to China’s foreign exchange regime have led the RMB exchange rates to higher fluctuations. From late 2008 to 2010, the RMB-USD exchange rates were relatively stable, which is to some extent due to the de facto pegged exchange rate policy and also possibly the artifact of the currencies basket, in which the mixed changes of other major currencies against the U.S. dollar has resulted in a relatively stable exchange value for RMB during this time period. Since 2010, the RMB has once again gradually strengthened against the U.S. dollar up to 2015 and then become weakened against the dollar. In the offshore market, the returns of the RU and RY series are less volatile during this period.

As our sample period covers the major RMB reforms and the GFC, we used the Chow Test and the Automated General-to-Specific (GETS) regression modelling based on indication saturation to test for the structural breaks. We consider the structural breaks both for the returns and the volatility series, in which the volatility level is measured in terms of the realised variance. Figure 2 presents the visualization for the structural breaks test outcome with the Chow Test and the GETS modeling in the return series and the volatility series. As seen from Figure 2, multiple breaks are revealed under the GETS models, where the most significance shifts are in 2005 and 2008. Under the Chow Test, we detect two structural breakpoints in on-shore RMB-USD and on-shore RMB-JPY return series which occurred in 2005:186 and 2008:228. The dates with the return series are consistent under both tests. Additionally, both structural breaks are also conducted in the volatility series, which we found consistent results with the return series. The F statistics is used to test the nonlinear trend of the variables and the GETS model is used to detect the extent of shift of the break within the series context. Both tests on RU and RY reject the null hypothesis, suggesting stationary investigation in the full return series. However, the presence of structural breaks indicates potential nonlinearity within the full data set. Because consistent results are shown in both the return and the volatility series; hence, in Equation (18), we included two dummy variables to control crisis—the 2005 breakpoint and the 2008 breakpoint in the mean equation in the diagonal BEKK model. We allow a time delay of a week to recover from the announcement of the action on RMB foreign currency reformation from the 21 July 2005 to 28 July 2005. For the GFC, we allow a time delay of one year for the recovery, and the dummy variable for 2008 is taken between 22 September 2008 and 22 September 2009. The mean equation after modification is shown in Equation (15):

$$\begin{gathered} r_t={\lambda }_0+{\lambda }_1{r}_{i,t-1}+{\lambda }_2{r}_{j,t-1}+{\lambda }_3{r}_{k,t-1}+{\lambda }_4{D}_{2005}+{\lambda }_5{D}_{2008}+{\epsilon }_t, \\ {r}_t={\left(r_{i,t},r_{j,t},r_{k,t}\right)}^{\prime }, \end{gathered}$$

(15)

where $D_{2005}$ is a dummy variable on the date between the 21 July 2005 to 28 July 2005, and $D_{2008}$ is a dummy variable for date between 22 September 2008 and 22 September 2009.

The unit root tests for the variables are summarised in

Table 2. Unit root test.

	ADF Test		PP Test		Perron (1989) Breakpoint Test
Var.	D.F	p-Value	alpha	p-Value	BP-2005	AIC	BP-2008	AIC
RU	−15.377 ***	0.01	−5515.5 ***	0.01	0.2457 ***	−1.5759	0.2396 ***	−1.5770
RY	−17.522 ***	0.01	−5308.3 ***	0.01	−0.0509 *	2.0497	−0.0513 *	−1.8416
TPX	−17.392 ***	0.01	−4857.1 ***	0.01	−0.1320 ***	3.4117	−0.1371 ***	3.4111
NIK	−17.509 ***	0.01	−5212.9 ***	0.01	−0.1285 ***	3.6033	−0.1283 ***	3.6031
SHCI	−15.535 ***	0.01	−5394.8 ***	0.01	0.1587 ***	3.6729	0.1742 ***	3.6736
SZCI	−15.791 ***	0.01	−5233.0 ***	0.01	0.1074 ***	3.8743	0.1179 ***	3.8754
OFFRU	−11.795 ***	0.01	−1822.2 ***	0.01	–	–	–	–
OFFRY	−12.214 ***	0.01	−1979.2 ***	0.01	–	–	–	–
OFFTPX	−13.480 ***	0.01	−1990.4 ***	0.01	–	–	–	–
OFFNIK	−13.460 ***	0.01	−2219.2 ***	0.01	–	–	–	–
OFFSHCI	−11.800 ***	0.01	−1943.0 ***	0.01	–	–	–	–
OFFSZCI	−11.583 ***	0.01	−1910.0 ***	0.01	–	–	–	–

Note, Var. stands for the variables. D.F is the Dickey-Fuller value of ADF test. BP-2005 is the coefficient of the break point date at 21 July 2005 under the Perron (1989) method. BP-2008 is the coefficient of the break point date at 22 September 2008. AIC is Akaike Info Criterion. This table presents the unit root test under the ADF test, the PP test and the Perron (1989) breakpoint test. Please note that *, *** denote the null hypothesis of unit root, which are rejected at 0. 1 and 0.01 levels of significance, respectively.

. The Augmented Dicker-Fuller (ADF) and Philips-Perron (PP) test were performed to test the existence of unit roots in each return series. We have also conducted the unit root test with the presence of structural breaks according to Perron (1989). In particular, two breakpoint dates, i.e., 21 July 2005 and 22 September 2008, are included in the Perron (1989) test. In the ADF test, the structure of serial correlation in the errors are specified, and the PP test do not assume serial correlation and heteroskedasticity in disturbance. Based on the results in Table 2, all the three tests confirm that the data series are stationary.

5. Empirical Findings

5.1. The Diagonal Baba-Engle-Kraft-Kroner GARCH-M Models

To examine the co-volatility spillover effects across the financial markets, we have arranged the data sets into 16 groups, which is presented in

Table 3. Regression Groups Composition.

Group No.	Variables
1	RU, TPX, SHCI
2	RU, TPX, SZCI
3	RU, NIK, SHCI
4	RU, NIK, SZCI
5	RY, TPX, SHCI
6	RY, TPX, SZCI
7	RY, NIK, SHCI
8	RY, NIK, SZCI
9	OFFRU, OFFTPX, OFFSHCI
10	OFFRU, OFFTPX, OFFSZCI
11	OFFRU, OFFNIK, OFFSHCI
12	OFFRU, OFFNIK, OFFSZCI
13	OFFRY, OFFTPX, OFFSHCI
14	OFFRY, OFFTPX, OFFSZCI
15	OFFRY, OFFNIK, OFFSHCI
16	OFFRY, OFFNIK, OFFSZCI

. For each group, co-volatility spillover effects are tested among the RMB foreign exchange market, the Chinese stock market, and the Japanese stock market. Table 3 shows the composition of the groups.

The co-volatility spillover effects are tested directly from the significance in the matrix A from the diagonal BEKK model. Rejecting the null hypothesis means that the return shock from market j and k at time t − 1 are dependent on the return shock from market i at time t − 1. The return shock originated from market i further causes subsequent spillovers to the co-volatility among the three markets at time t. Consequently, higher return shock from market i at time t − 1 potentially introduces a greater extent of spillover effects, transmitting into the co-volatility among the three markets.

Table 4. Estimation Results of the Mean Equations in the Diagonal BEKK GARCH-M Model.

Group	Var.	RU(−1)	RY(−1)	TPX(−1)	NIK(−1)	SHCI(−1)	SZCI(−1)	D2005	D2008
1	RU	−0.1140 *** (0.0000)		0.0001 (0.3141)		−0.0000 (0.6489)		−0.0022 *** (0.0000)	−0.0000 (0.3595)
	TPX	0.0439 (0.6946)		0.0335 ** (0.0229)		−0.0258 ** (0.0237)		0.0014 (0.4295)	0.0002 (0.8640)
	SHCI	0.2359 ** (0.0193)		0.0022 (0.8588)		0.0119 (0.3947)		0.0082 (0.2692)	0.0039 *** (0.0031)
2	RU	−0.1150 *** (0.0000)		0.0001 (0.3531)			−0.0000 (0.5729)	−0.0022 *** (0.0000)	−0.0000 (0.3908)
	TPX	0.0718 (0.5040)		0.0039 ** (0.0212)			−0.0209 ** (0.0400)	0.0012 (0.4630)	0.0002 (0.8375)
	SZCI	0.3863 ** (0.0115)		0.0012 (0.9296)			0.0398 ** (0.0072)	0.0080 (0.3444)	0.0045 *** (0.0003)
3	RU	−0.1121 *** (0.0000)			0.0000 (0.3265)	−0.0000 (0.6134)		−0.0022 *** (0.0000)	0.0000 (0.7066)
	NIK	0.1212 (0.3371)			−0.0245 * (0.0768)	−0.0244 ** (0.0442)		0.0021 * (0.0778)	−0.0047 (0.1606)
	SHCI	0.2322 *** (0.0222)			0.0034 (0.7584)	0.0110 (0.4307)		0.0047 (0.2679)	0.0026 *** (0.0041)
4	RU	−0.1146 *** (0.0000)			0.0004 (0.3707)		−0.0000 (0.5229)	−0.0022 *** (0.0000)	0.0000 (0.6918)
	NIK	0.1476 (0.2254)			−0.0250 * (0.0708)		−0.0196 * (0.0715)	0.0017 (0.3588)	−0.0041 (0.2300)
	SZCI	0.3725 ** (0.0144)			0.0046 (0.7033)		0.0387 *** (0.0092)	0.0081 (0.3397)	0.0035 *** (0.0008)
5	RY		−0.0675 *** (0.0000)	0.0028 (0.6943)	−0.0076 (0.1646)			0.0020 (0.3113)	−0.0080 (0.1619)
	TPX		0.3126 *** (0.0000)	0.0051 (0.7131)	−0.0192 * (0.0765)			0.0000 (0.7955)	0.0005 (0.6164)
	SHCI		−0.0061 (0.7968)	0.0087 (0.5138)	0.0138 (0.3187)			0.0063 (0.2144)	0.0033 ** (0.0141)
6	RY		−0.0677 *** (0.0000)	0.0028 (0.6934)			−0.0086 * (0.0643)	0.0022 (0.2996)	−0.0007 (0.2100)
	TPX		0.3116 *** (0.0000)	0.0033 (0.8149)			−0.0133 (0.1642)	0.0002 (0.8878)	0.0006 (0.5996)
	SZCI		−0.0264 (0.3325)	0.0059 (0.6908)			0.0381 *** (0.0080)	0.0057 (0.3327)	0.0039 *** (0.0029)
7	RY		−0.0651 *** (0.0000)		0.0001 (0.9911)	−0.0068 (0.2079)		0.0019 (0.3331)	−0.0008 (0.1476)
	NIK		0.3701 *** (0.0000)		−0.0532 *** (0.0001)	−0.0187 (0.1002)		0.0009 (0.5810)	0.0009 (0.4367)
	SHCI		−0.0050 (0.8353)		0.0098 (0.4066)	0.0118 (0.3907)		0.0063 (0.2202)	0.0033 ** (0.0142)
8	RY		−0.0651 *** (0.0000)		0.0001 (0.9861)		−0.0079 * (0.0912)	0.0021 (0.3231)	−0.0007 (0.1974)
	NIK		0.3705 *** (0.0000)		−0.0562 *** (0.0000)		−0.0130 (0.1969)	0.0007 (0.6910)	0.0009 (0.4269)
	SZCI		−0.0250 (0.3564)		0.0069 (0.5839)		0.0361 ** (0.0117)	0.0057 (0.3407)	0.0039 *** (0.0032)

Note, * denotes significance level at 0.1, ** denotes significance level at 0.5, *** denotes significance level at 0.01. The regression results consist the RMB-USD exchange rate (RU), the RMB-JPY exchange rate (RY), TPX, NIK, Shanghai and Shenzhen Stock Exchange Composite Indices. The Table 4 delivers the results from the mean equation of the following diagonal BEKK GARCH-M model in this study: $r_t={\lambda }_0+{\lambda }_1{r}_{i,t-1}+{\lambda }_2{r}_{j,t-1}+{\lambda }_3{r}_{k,t-1}+{\lambda }_4{D}_{2005}+{\lambda }_5{D}_{2008}+{\epsilon }_t$; $r_t=\left(r_{i,t},r_{j,t},r_{k,t}\right)\prime$; ${\epsilon }_t=\left({\epsilon }_{i,t},{\epsilon }_{j,t},{\epsilon }_{k,t}\right) ~iid N\left(0,H_t\right)$; $H_t=C{C}^{\prime }+B{H}_{t-1}B\prime +A{\epsilon }_{t-1}\epsilon {\prime }_{t-1}{A}^{\prime }$. where $r_t$ is a 3$\times$1 vector which changes in different groups. $r_i$, $r_j$ and $r_k$ are the three vectors representing the return of the three assigned market indices in each group. The definition of the groups is presented in Table 3. $r_{i,t-1}$, $r_{j,t-1}$ and $r_{j,t-1}$ are the return of time t − 1. As such, RU(−1) is the return on the RMB-USD spot at time t − 1, RY(−1) is the return on the RMB-JPY spot at time t − 1, TPX(−1) is the return on the TPX at time t − 1, NIK(−1) is the return on the NIK at time t − 1, SHCI(−1) and SZCI(−1) are the returns on Shanghai and Shenzhen Composite Indices at time t − 1. D₂₀₀₅ and D₂₀₀₈ are the dummy variables for the year 2005 and 2008.

presents the estimation results from the conditional mean equation, which is the first moment of the DBEKK model, whereas

Table 5. Estimation Results of the Variance Equations in the Diagonal BEKK GARCH-M Model.

Group	C			A			B
1	RU	TPX	SHCI	RU	TPX	SHCI	RU	TPX	SHCI
RU	0.0000 (0.9970)			0.3426 * (0.0001)			0.9395 * (0.0000)
TPX	−0.0007 (0.8594)	0.0015 (0.4593)			0.2209 * (0.0001)			0.9695 * (0.000)
SHCI	−0.0009 (0.4481)	0.0001 (0.6487)	0.0009 * (0.0000)			0.1730 * (0.0000)			0.9829 * (0.0000)
Log. lik.	68,401.708
2	RU	TPX	SZCI	RU	TPX	SZCI	RU	TPX	SZCI
RU	0.0000 (0.9926)			0.3368 * (0.0001)			0.9416 * (0.0000)
TPX	−0.0008 (0.4795)	0.0014 (0.0826)			0.2196 * (0.0000)			0.9694 * (0.0000)
SZCI	−0.0012 (0.0203)	−0.0006 (0.6341)	0.0007 (0.5659)			0.1975 * (0.0000)			0.9762 * (0.0000)
Log. lik.	67,908.906
3	RU	NIK	SHCI	RU	NIK	SHCI	RU	NIK	SHCI
RU	0.0000 (0.9936)			0.3498 * (0.0001)			0.9368 * (0.0000)
NIK	0.0003 (0.9744)	0.0014 (0.4156)			0.1984 * (0.0000)			0.9769 * (0.0000)
SHCI	0.0001 (0.8852)	0.0001 (0.8597)	0.0009 * (0.0000)			0.1714 * (0.0000)			0.9833 * (0.0000)
Log. lik.	67,908.906
4	RU	NIK	SZCI	RU	NIK	SZCI	RU	NIK	SZCI
RU	0.0000 (0.9970)			0.3426 * (0.0001)			0.9395 * (0.0000)
NIK	−0.0007 (0.8594)	0.0015 (0.4593)			0.2209 * (0.0000)			0.9695 * (0.0000)
SZCI	−0.0001 (0.4481)	0.0001 (0.6487)	0.0009 (0.0000)*			0.1730 * (0.0000)			0.9829 * (0.0000)
Log. lik.	68,401.708
5	RY	TPX	SHCI	RY	TPX	SHCI	RU	TPX	SHCI
RY	0.0005 * (0.0000)			0.1543 * (0.0000)			0.9852 * (0.0000)
TPX	0.0003 (0.0126)	0.0015 * (0.0000)			0.2476 * (0.0000)			0.9628 * (0.0000)
SHCI	−0.0000 (0.9768)	0.0001 (0.0932)	0.0013* (0.0000)			0.2211* (0.0000)			0.9715 * (0.0000)
Log. lik.	51,658.425
6	RY	TPX	SZCI	RY	TPX	SZCI	RU	TPX	SZCI
RY	0.0005 * (0.0000)			0.1503 * (0.0000)			0.9859 * (0.0000)
TPX	0.0003 (0.0139)	0.0014 * (0.0000)			0.2352 * (0.0000)			0.9661 * (0.0000)
SZCI	−0.0000 (0.9739)	0.0002 (0.1851)	0.0022 * (0.0000)			0.2601 * (0.0000)			0.9570 * (0.0000)
Log. lik.	50,920.307
7	RY	NIK	SHCI	RY	NIK	SHCI	RU	NIK	SHCI
RY	0.0005 * (0.0000)			0.1538 * (0.0000)			0.9854 * (0.0000)
NIK	0.0003 (0.0149)	0.0014 * (0.0000)			0.2265 * (0.0000)			0.9699 * (0.0000)
SHCI	0.0000 (0.9555)	0.0001 (0.1655)	0.0013* (0.0000)			0.2219 * (0.0000)			0.9714 * (0.0000)
Log. lik.	51,192.707
8	RY	NIK	SZCI	RY	NIK	SZCI	RU	NIK	SHCI
RY	0.0005 * (0.0000)			0.1498 * (0.0000)			0.9861 * (0.0000)
NIK	0.0003 (0.0169)	0.0013 * (0.0000)			0.2166 * (0.0000)			0.9723 * (0.0000)
SZCI	−0.0000 (0.9415)	0.0002 (0.2125)	0.0022 * (0.0000)			0.2631 * (0.0000)			0.9562 * (0.0000)
Log. lik.	50,451.703

Note, * denotes significance level at 0.01. The table presents the results from the variance equation from the following diagonal BEKK GARCH-M model shown below: $r_t={\lambda }_0+{\lambda }_1{r}_{i,t-1}+{\lambda }_2{r}_{j,t-1}+{\lambda }_3{r}_{k,t-1}+{\lambda }_4{D}_{2005}+{\lambda }_5{D}_{2008}+{\epsilon }_t$; $r_t=\left(r_{i,t},r_{j,t},r_{k,t}\right)\prime$; ${\epsilon }_t=\left({\epsilon }_{i,t},{\epsilon }_{j,t},{\epsilon }_{k,t}\right) ~iid N\left(0,H_t\right)$; $H_t=C{C}^{\prime }+B{H}_{t-1}B\prime +A{\epsilon }_{t-1}\epsilon {\prime }_{t-1}{A}^{\prime }$. where C is an upper triangular matrix consists constant parameters in the conditional variance and covariance matrices, calculated by $C=\left[\begin{array}{cc}\begin{array}{cc}{C}_{ii}& C_{ij}\end{array}& C_{ik}\\ \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}{C}_{jj}\\ 0\end{array}\end{array}& \begin{array}{c}{C}_{jk}\\ C_{kk}\end{array}\end{array}\right]$. A and B are diagonal matrices, calculated by $A=\left[\begin{array}{cc}\begin{array}{cc}{A}_{ii}& 0\end{array}& 0\\ \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}{A}_{jj}\\ 0\end{array}\end{array}& \begin{array}{c}0\\ A_{kk}\end{array}\end{array}\right],B=\left[\begin{array}{cc}\begin{array}{cc}{B}_{ii}& 0\end{array}& 0\\ \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}{B}_{jj}\\ 0\end{array}\end{array}& \begin{array}{c}0\\ B_{kk}\end{array}\end{array}\right]$.

reports the results for the co-volatility effects. Overall, the results from the matrix A confirm the presence of spillover effects on the co-volatility among the foreign exchange markets and the stock markets.

As it can be seen from Table 4, the results show evidence supporting the presence of co-volatility spillover effects for the on-shore RMB-USD foreign exchange rates. In Group 1, RU is particularly influential to the subsequent SHCI co-volatility with RU, and SHCI strongly influences the subsequent TPX co-volatility with SHCI. In regard to the conditional variance equation, the results in Table 5 show that the matrix A are significant for all variables, which indicate that the spillovers originated from RU are transmitted to the subsequent co-volatility among RU, TPX and SHCI. A bidirectional relationship in the spillover is also evident in the results, where the spillover effects from RU and TPX that are dependent on SHIC affect significantly the co-volatility among the three markets. Similar findings are for Groups 2, 3 and 4. This is consistent with the fundamentals hypothesis that information about the capital flow in the foreign exchange market can be transmitted into the stock market, leading to the changes in liquidity. In particular, the return shocks from on-shore RMB-USD exchange rates at time t − 1 are found to cause significant spillovers to the stock market in China (SHCI or SZCI), which are in turn transmitted into the stock markets in Japan and China. The bidirectional relationship shows that the return shocks from SHCI or SZCI maintain similar influence through spillover effects onto TPX or NIK, which in turn generates spillovers onto the subsequent co-volatility among the stock markets and the foreign exchange market. The results from Table 5 further show evidence that the spillover effects are significant for Groups 1 through 4. In the mean equation, it is notable that the coefficients of the return shocks from RU at time t − 1 on SHCI/SZCI are considerably high. In particular, RU is more influential to SZCI (0.3863 and 0.3725) than to SHCI (0.2359 and 0.2322), suggesting that SZCI is more sensitive to RU than SHCI. One possible explanation is that the types of firms listed in both exchanges are different, so are the investors’ assessments of the value and risk of the listed firms and market participants’ different risk preference. Overall, the results from Groups 1 to 4 show evidence supporting our H1a, in which the return shocks from the foreign exchange rate influence the subsequent co-volatility with the stock markets. H1b is partially supported when we look at the effects from SHCI/SZCI to RU, indicating the existence of a strong bidirectional relationship for the spillover effects on co-volatility between the foreign exchange and stock markets.

The RMB-YEN series are presented in Groups 5 to 8 in Table 4 and Table 5. The results are similar to the ones for the RMB-USD exchange rates. It is noted in Group 5 that the spillover effects from RY are significant onto the co-volatility among RY, TPX and SHCI, and similar results are also found for Groups 6, 7 and 8. It is also interesting to note that spillover effects from SHCI or SZCI onto the stock market in Japan are significant, suggesting that shocks from the RMB-JPY exchange rates become an important factor affecting the return volatility in the Japanese stock market. This contrasts with the spillover effects of the RMB-USD exchange rates on the stock markets in China. In addition, the results from Groups 6 and 8 indicate that the return shocks from SZCI at time t−1 are moderately significant to the subsequently RY co-volatility, which suggests the bidirectional relationship for the spillover effects between the RMB-JPY exchange rates and the market returns. As the results from matrix A in Table 5 show the existence of highly significant spillover effects on the co-volatility among SZCI, RY and TPX/NIK, we find evidence supporting our H1a and H1b1.

In the mean equation, we have included two control variables for the break points in 2005 and 2008, and both are found significant. The results confirm the effects of China’s foreign exchange system reforms and the 2008 GFC on the stock markets in China, which in turn will generate spillover effects on the Japanese stock markets. The empirical results in general are consistent with Nishimura et al. (2018) and Morales-Zumaquero and Sosvilla-Rivero (2018), and support the investor-induced hypothesis that international investors are more likely to re-balance portfolios during the crisis.

Table 6. Average Market Shock.

Market	Average Return Shocks
RU	−0.0005
RY	−0.0117
TPX	−0.0441
NIK	−0.0450
SHCI	−0.0080
SZCI	−0.0328
OFFRU	0.0499
OFFRY	−0.0282
OFFTPX	−0.0470
OFFNIK	−0.0395
OFFSHCI	−0.0209
OFFSZCI	−0.0605

presents the average return shocks derived from the standard GARCH models. In comparison, the largest return shocks are from TPX and SZCI. We then calculate the co-volatility spillover effects.

Table 7. Co-Volatility Spillover Effects.

Group	Market	Average Co-Volatility Spillover
1	i = RU, j = TPX, k = SHCI	−0.000006 (0.3246*0.2209*0.1730*(−0.0005))
	i = TPX, j = RU, k = SHCI	−0.000547 (0.3246*0.2209*0.1730*(−0.0441))
	i = SHCI, j = TPX, j = RU	−0.000099 (0.3246*0.2209*0.1730*(−0.0080))
2	i = RU, j = TPX, k = SZCI	−0.000007 (0.3368*0.2196*0.1975*(−0.0005))
	i = TPX, j = RU, k = SZCI	−0.000644 (0.3368*0.2196*0.1975*(−0.0441))
	i = SZCI, j = TPX, k = RU	−0.000479 (0.3368*0.2196*0.1975*(−0.0328))
3	i = RU, j = NIK, k = SHCI	−0.000006 (0.3498*0.1984*0.1714*(−0.0005))
	i = NIK, j = RU, k = SHCI	−0.000535 (0.3498*0.1984*0.1714*(−0.0450))
	i = SHCI, j = NIK, k = RU	−0.000095 (0.3498*0.1984*0.1714*(−0.0080))
4	i = RU, j = NIK, k = SZCI	−0.000007 (0.3426*0.2209*0.1730*(−0.0005))
	i = NIK, j = RU, k = SZCI	−0.000589 (0.3426*0.2209*0.1730*(−0.0450))
	i = SZCI, j = NIK, k = RU	−0.000429 (0.3426*0.2209*0.1730*(−0.0328))
5	i = RY, j = TPX, k = SHCI	−0.000098 (0.1543*0.2476*0.2211*(−0.0117))
	i = TPX, j = RY, k = SHCI	−0.000373 (0.1543*0.2476*0.2211*(−0.0441))
	i = SHCI, j = TPX, j = RY	−0.000068 (0.1543*0.2476*0.2211*(−0.0080))
6	i = RY, j = TPX, k = SZCI	−0.000108 (0.1503*0.2352*0.2601*(−0.0117))
	i = TPX, j = RY, k = SZCI	−0.000405 (0.1503*0.2352*0.2601*(−0.0441))
	i = SZCI, j = TPX, k = RY	−0.000302 (0.1503*0.2352*0.2601*(−0.0328))
7	i = RY, j = NIK, k = SHCI	−0.000090 (0.1538*0.2265*0.2219*(−0.0117))
	i = NIK, j = RY, k = SHCI	−0.000348 (0.1538*0.2265*0.2219*(−0.0450))
	i = SHCI, j = NIK, k = RY	−0.000062 (0.1538*0.2265*0.2219*(−0.0080))
8	i = RY, j = NIK, k = SZCI	−0.000100 (0.1498*0.2166*0.2631*(−0.0117))
	i = NIK, j = RY, k = SZCI	−0.000384 (0.1498*0.2166*0.2631*(−0.0450))
	i = SZCI, j = NIK, k = RY	−0.000280 (0.1498*0.2166*0.2631*(−0.0328))

presents the co-volatility spillover effects for Groups 1 to 8. It is noted that the return shocks from the Japanese stock market (e.g., TPX and NIK) have a much higher average co-volatility spillover than that from the Chinese stock markets. This finding is consistent with the investor-induced hypothesis that return shocks from the market with higher accessibility internationally are more likely to lead to great spillovers. This is further supported by our findings that SHCI has less co-volatility spillover than SZCI. This is consistent with the results discussed earlier. The listed firms in Shenzhen Stock Exchange are usually more diversified and innovative but the firm sizes are relatively smaller compared to the firms listed in Shanghai Stock Exchange. The listed firms in Shenzhen Stock Exchange are generally inclined to disruptive technology, business innovation and corporate sustainability, in which the proportion for foreign owned firms are also higher than that in Shanghai Stock Exchange (Cao et al. 2018; Xiang 2018). Based on the findings that international preference and accessibility have relatively higher average co-volatility spillover effects, we accept H2 that the co-volatility spillovers originated from Japan are more likely to have higher spillover effects onto the other financial markets.

In addition, the results in Table 7 show that there are significant negative associations of the average co-volatility spillover2 for all the financial markets. This has important implications for risk management and hedging strategies. The results also indicate that the financial integration is not completed and underlines the possible hedging strategies against the risk associated in the local market in line with the investor-induced hypothesis, in which domestic investors can obtain the access to other market effectively. Although the influence from international investors is still substantial, domestic investors can minimise the risk through hedging.

5.2. Robustness Test with Vector Autoregression

To further address our research concern and to serve as a robustness check for the spillover effects among the RMB foreign exchange markets and the stock markets, we also adopted the spillover definition from Diebold and Yilmaz (2009, 2012) that is based on VAR model. To compare with the average spillover effects detected through the DBEKK model, we report spillover index for returns in

Table 8. Spillover Table on return by VAR.

To Group 1	From				To Group 2	From
	RU	TPX	SHCI	Contribution from Others		RU	TPX	SZCI	Contribution from Others
RU	99.7	0.1	0.2	0.3	RU	99.6	0.1	0.3	0.4
TPX	0.1	99.6	0.2	0.4	TPX	0.1	99.6	0.2	0.4
SHCI	0.4	3.8	95.8	4.2	SZCI	0.4	2.7	96.9	3.1
Contribution to others	0.6	3.9	0.4	4.9		0.6	2.8	0.5	3.9
Contribution including own	100.3	103.6	96.2	1.6% *		100.1	102.5	97.4	1.3% *
Group 3	RU	NIK	SHCI	Contribution from Others	Group 4	RU	NIK	SZCI	Contribution from Others
RU	99.7	0.1	0.2	0.3	RU	99.6	0.1	0.3	0.4
NIK	0.2	99.6	0.3	0.4	NIK	0.2	99.6	0.2	0.4
SHCI	0.4	3.9	95.6	4.4	SZCI	0.4	2.8	96.8	3.2
Contribution to others	0.6	4.0	0.4	5.1		0.6	2.9	0.5	4.0
Contribution including own	100.3	103.6	96.1	1.7% *		100.2	102.5	97.3	1.3% *
Group 5	RY	TPX	SHCI	Contribution from Others	Group 6	RY	TPX	SZCI	Contribution from Others
RY	99.3	0.4	0.3	0.7	RY	99.3	0.4	0.3	0.7
TPX	6.1	93.7	0.2	6.3	TPX	6.1	93.7	0.2	6.3
SHCI	0.4	3.7	95.9	4.1	SZCI	0.2	2.7	97.1	2.9
Contribution to others	6.5	4.1	0.5	11.1		6.2	3.2	0.5	9.9
Contribution including own	105.8	97.8	96.4	3.7% *		105.5	96.9	97.6	3.2% *
Group 7	RY	NIK	SHCI	Contribution from Others	Group 8	RY	NIK	SZCI	Contribution from Others
RY	99.3	0.4	0.3	0.7	RY	99.3	0.4	0.3	0.7
NIK	5.8	93.9	0.3	6.1	NIK	5.8	94.0	0.2	6.0
SHCI	0.4	3.8	95.8	4.2	SZCI	0.2	2.8	97.0	3.0
Contribution to others	6.2	4.2	0.6	11.0		6.0	3.2	0.6	9.7
Contribution including own	105.6	98.1	96.3	3.7% *		105.3	97.2	97.6	3.2% *

Note: the i,j th entries in the Tables are the estimated contribution to the forecast error variance of country i influenced by innovation from country j. The variance decomposition on return in Table 8 is based on the daily VAR of order 2 identified with a Cholesky factorisation with the ordering from group 1 to group 8. The (i,j)-th value is the estimated contribution of innovation to the variance of the 10-day-ahead return forecast error from market i to the return of market j. * is the spillover index for each group under the definition of Diebold and Yilmaz (2009, 2012).

and for volatility in

Table 9. Spillover Table on volatility by VAR.

To Group 1	From				To Group 2	From
	RU	TPX	SHCI	Contribution from Others		RU	TPX	SZCI	Contribution from Others
RU	99.8	0.1	0.1	0.2	RU	99.8	0.1	0.2	0.2
TPX	0.4	99.4	0.2	0.6	TPX	0.4	99.4	0.2	0.6
SHCI	1.0	1.1	97.9	2.1	SZCI	0.9	0.8	98.3	1.7
Contribution to others	1.5	1.1	0.3	2.9		1.3	0.8	0.4	2.5
Contribution including own	101.3	100.5	98.2	1.0% *		101.1	100.2	98.7	0.8% *
Group 3	RU	NIK	SHCI	Contribution from Others	Group 4	RU	NIK	SZCI	Contribution from Others
RU	99.8	0.1	0.1	0.2	RU	99.8	0.1	0.2	0.2
NIK	0.2	99.6	0.3	0.4	NIK	0.2	99.6	0.2	0.4
SHCI	1.0	0.8	98.1	1.9	SZCI	0.9	0.7	98.4	1.6
Contribution to others	1.2	0.9	0.4	2.4		1.1	0.7	0.4	2.1
Contribution including own	101.0	100.4	98.5	0.8% *		100.8	100.3	98.8	0.7% *
Group 5	RY	TPX	SHCI	Contribution from Others	Group 6	RY	TPX	SZCI	Contribution from Others
RY	98.6	1.3	0.1	1.4	RY	98.6	1.3	0.1	1.4
TPX	4.2	95.6	0.2	4.4	TPX	4.2	95.6	0.2	4.4
SHCI	0.5	1.0	98.4	1.6	SZCI	0.3	0.8	98.9	1.1
Contribution to others	4.8	2.3	0.3	7.4		4.6	2.1	0.3	6.9
Contribution including own	103.4	97.9	98.8	2.5% *		103.1	97.7	99.2	2.3% *
Group 7	RY	NIK	SHCI	Contribution from Others	Group 8	RY	NIK	SZCI	Contribution from Others
RY	98.3	1.6	0.1	1.7	RY	98.2	1.6	0.1	1.8
NIK	5.1	94.7	0.2	5.3	NIK	5.1	94.7	0.2	5.3
SHCI	0.6	0.7	98.7	1.3	SZCI	0.3	0.6	99.1	0.9
Contribution to others	5.7	2.3	0.4	8.3		5.4	2.2	0.3	7.9
Contribution including own	103.9	97.0	99.1	2.8% *		103.6	96.9	99.4	2.6% *

Note, the variance decomposition on volatility in Table 9 is based on the daily VAR of order 2 identified with a Cholesky factorisation with the ordering from group 1 to group 8. The (i,j)-th value is the estimated contribution of innovation to the variance of the 10-day-ahead return forecast error from market i to the volatility of market j. * is the spillover index for each group under the definition of Diebold and Yilmaz (2009, 2012).

. We measure the volatility with the squared returns. As seen from Table 8, innovations to TPX and NIK are responsible for a relatively greater extent of the error variance in forecasting 10-day-ahead returns of the Chinese stock market returns, particularly for the RMB-USD series for Groups 1 to 4. On the other hand, the Chinese market indexes, SHCI and SZCI, receive the most contribution from others indicated through the error variance. This finding supports our results using the DBEKK model and the average spillover effects, where we posit that the market with higher level of accessibility is more likely to cause spillover effects to others due to the investor-induced behaviour. The results from Groups 5 to 8 provide further supportive evidence between stock markets in China and Japan, in which innovation originated from TPX and NIK show relatively higher influence than that from SHCI and SZCI. In addition, TPX and NIK receive relatively greater extent of contribution, suggesting that the Japanese stock market is more likely to be affected by return shocks from RY compared to the Chinese stock market. It is also interesting to note that RY is the most responsible variable for the error variance in forecasting the 10-day-ahead returns among the financial markets. The results also lend support to our Hypotheses 1a and 1b regarding the bidirectional relationship. Additionally, it is apparent the spillover indices in the return series are much higher for RY relative to RU. Based on the results from Table 8, the findings are consistent with our early conclusion and support our Hypotheses 1 and 2.

Further to our results from the DBEKK model, we extend our robustness test in the volatility series by using the squared daily return. The results are reported in Table 9. Overall, the results are consistent with those reported in Table 8, as well as with the average spillover effects determined through the DBKK models. Notably, the volatility series show that even though the total volatility spillovers from foreign exchange market (i.e., RU and RY) to other markets are greater than the reverse effects, the extent is amply small. While the bidirectional relationship holds, the volatility spillover effects from the Chinese markets are found quite small. This is consistent with our Hypothesis 1. Moreover, Table 9 also suggests that the volatility spillovers from the Japanese stock market are greater than that from the Chinese stock market, which is consistent with our results discussed earlier and support our Hypothesis 2.

6. Discussion and Limitation

In this study, we intend to analyse the return volatility spillover effects between the RMB foreign exchange market and the stock markets in Japan and China using the daily return data from 1998 to 2018. Using the DBEKK-GARCH-M model, we found the spillover effects between the foreign exchange market and the stock markets are bidirectional. We further found that return shocks originated from TPX and NIK are greater, which cause spillover effects onto co-volatility among other markets. Such relationship is further supported by the VAR model based on spillover definition of Diebold and Yilmaz (2009, 2012), where we found that innovation from the Japanese stock market (i.e., TPX and NIK) is likely to cause large spillovers onto the other financial markets. However, the results on volatility indicate that RMB-USD and RMB-YEN exchange rates account for a large proportion of the spillovers.

In addition, we found the return volatility spillover effects are most significant in 2005 and 2008 from the DBEKK model. For the exchange rates between RMB and USD, the reform to China’s foreign exchange rate system in 2005 has a substantial impact on the returns volatility, whereas the volatility of the RMB-JPY exchange rates seem to be more influential during the GFC. Due to the relative high volatility in returns, investors are more likely to rebalance their portfolios during these periods. This is consistent with the investor induced hypothesis.

The results from the mean equation in the diagonal BEKK model and the VAR returns series suggest that the returns of the RMB-USD exchange rates are more sensitive to the structural changes than that for the RMB-JPY rates. The co-volatilities between RU and TPX, RU and NIK, RU and SHCI, and RU and SZCI generally show negative associations, which underline the reversed response of the market participants to the volatility spillovers between the markets. This finding shows that RU, TPX/NIK and SHCI/SZCI are useful for hedging and risk management. The significant spillovers among the financial markets are largely due to investors’ rebalancing their portfolio decisions, which supports our Hypothesis 2. We also find evidence supporting the bidirectional relationship of the spillovers among the financial markets, which is consistent with our Hypotheses 1a and 1b. The results for the spillovers from the RMB-JPY rates onto TPX/NIK and SHCI/SZCI and on the co-volatility among the three markets lend further support.

The findings on the average co-volatility spillovers indicate that, even though there are significant spillover effects, impact of the RMB exchange rates on the other financial markets is still limited. This finding has important implications for the impacts of China’s recent reforms to its foreign exchange rate system and RMB internationalisation on the co-volatility between the financial markets in China and Japan. One explanation is that, even though RMB internationalisation has made rapid progress in recent years, the accessibility and openness of Chinese financial markets are still an important issue. It is also associated with China’s capital account control, as well as the underdevelopment of the financial markets and the stock market in China (Dobson and Masson 2009). Our findings show that the return shocks from the Japanese stock market have a much higher average co-volatility spillover than that from the Chinese stock markets and SHCI has lower co-volatility spillovers than SZCI, which lends further support to the investor-induced hypothesis. The results are consistent with the existing studies (Chen and Liu 2008; Nishimura et al. 2018).

This study suffers from a few limitations. One is how to address the impacts of monetary authorities’ announcements from both countries on the return volatility spillovers and co-volatility across these financial markets. Another is how to better proxy market accessibility and across-market capital flows between the Chinese and Japanese financial markets given China’s capital control policy, which would allow us to conduct more appropriate test for the investor-induced hypothesis. These will need to be addressed in our future study.

7. Conclusions

In this study, we have examined the volatility spillover effects between the RMB foreign exchange markets and the stock markets by employing daily returns of the Chinese RMB exchange rates and the stock markets in China and Japan during the period in 1998–2018. Using the DBEKK-GARCH-M model, we find evidence that there exist co-volatility effects among the financial markets in China and Japan, and the volatility of RMB exchange rates contribute to the co-volatility spillovers across the financial markets. Reversely, the return shock from the stock markets can also generate co-volatility spillovers to the foreign exchange markets. The bidirectional relationship reveals that both the fundamental hypothesis and the investor-induced hypothesis are valid. Our estimates also show that the spillover effects led by the stock market in Japan are stronger than that from the foreign exchange markets and the Chinese stock markets, implying that market with higher accessibility has greater spillover effects onto other markets. We also found that the average co-volatility spillover effects among the RMB exchange markets and the stock markets in Japan and China are generally negative. We also found that the average co-volatility spillover among the RMB exchange markets and the stock markets in Japan and China are generally negative. Such relationship is further supported by the VAR model based on spillover definition of Diebold and Yilmaz (2009, 2012). The results from the off-shore exchange rates support the fundamentals hypothesis as the off-shore markets are less regulated than the on-shore market. These findings have important policy implications for risk management and hedging strategies.