On the Volatility Spillover between Agricultural Commodities and Latin American Stock Markets
Abstract
1. Introduction
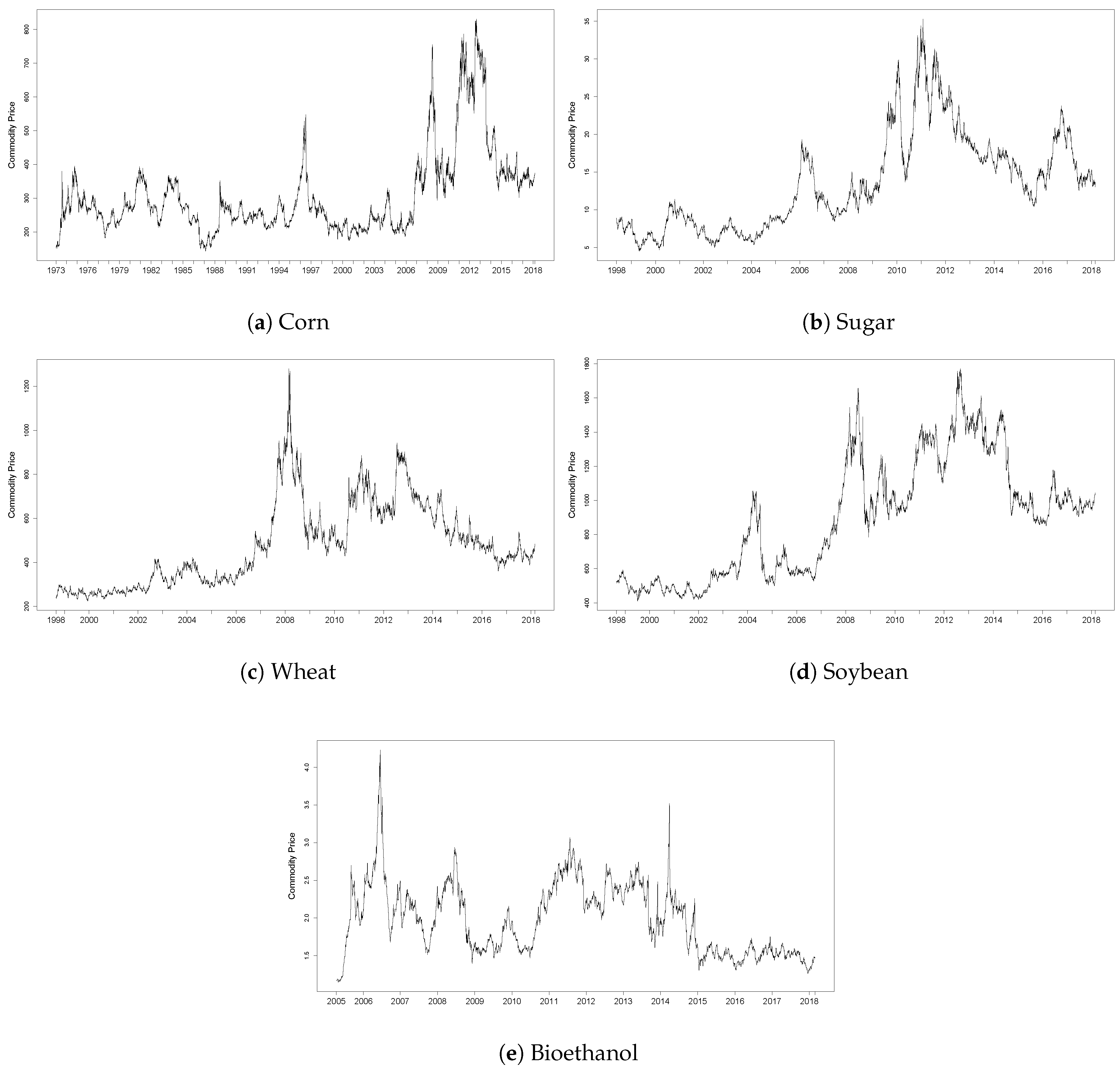
2. Change in Volatility of Agricutural Commodities
3. Econometric Methodology
4. Data and Results
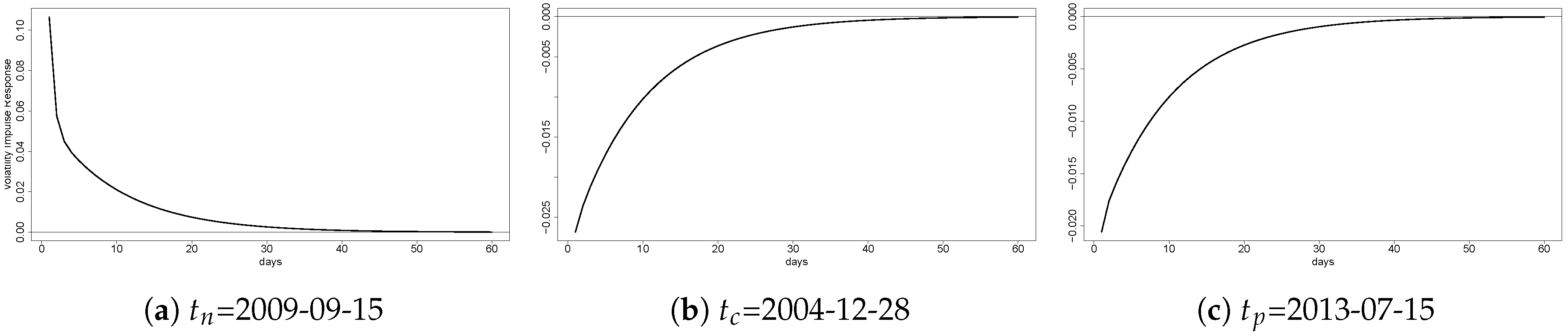
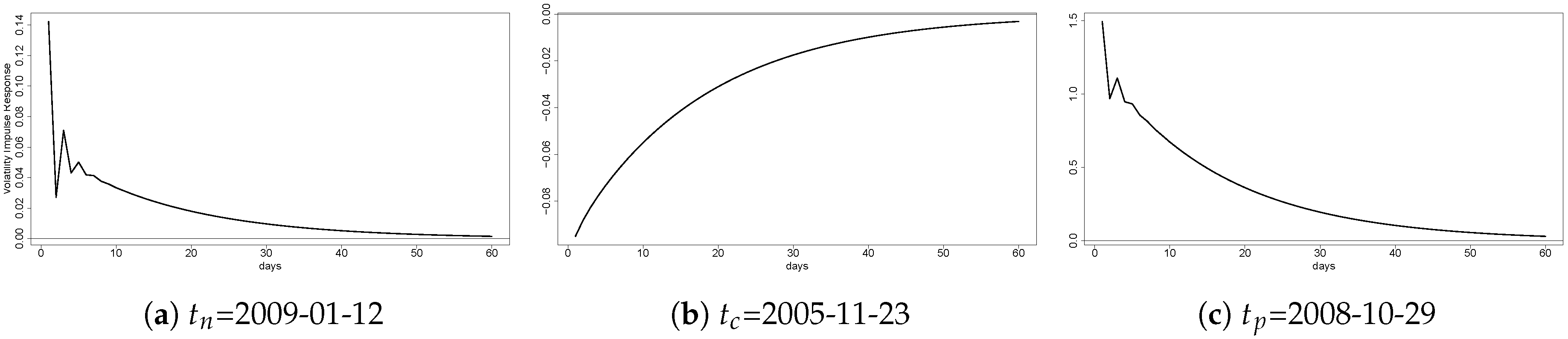
4.1. Volatility Impulse Response from Corn to Chile
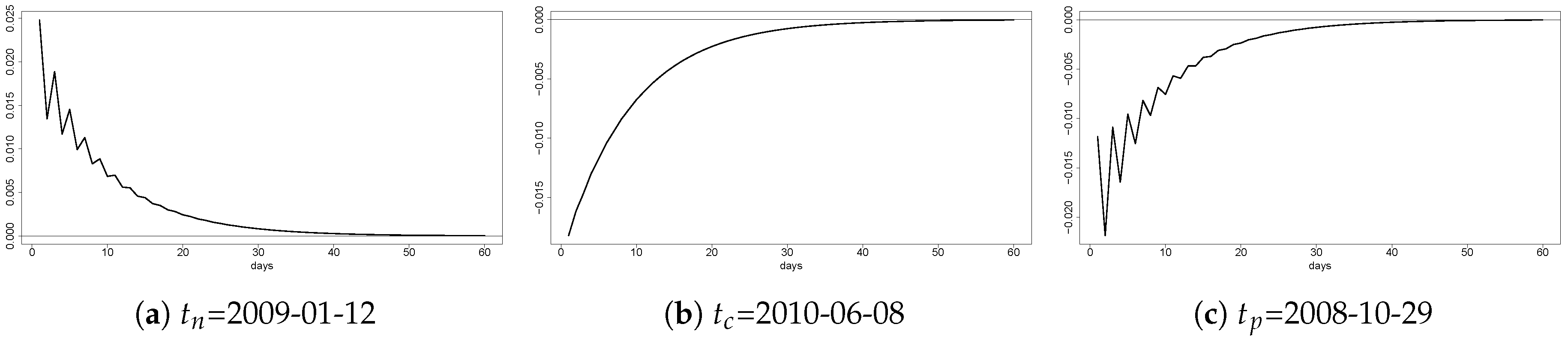
4.2. Volatility Impulse Response from Corn to Colombia
4.3. Volatility Impulse Response from Corn to Peru
4.4. Volatility Impulse Response from Sugar to Peru
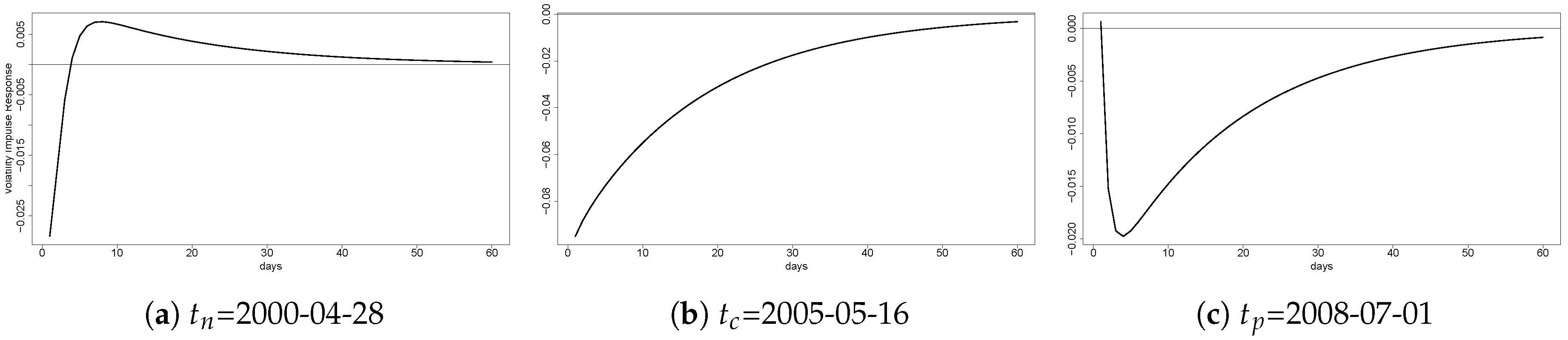
4.5. Volatility Impulse Response from Wheat to Peru
4.6. Volatility Impulse Response from Wheat to Chile
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MGARCH | Multivariate GARCH |
| VIRF | Volatility impulse response function |
| DM | Developing market |
| NFIDM | Net-food importing developing market |
| LR | Likelihood ratio |
References
- Allen, David E., Michael McAleer, Robert Powell, and Abhay K. Singh. 2017. Volatility spillover and multivariate volatility impulse response analysis of GFC news events. Applied Economics 49: 3246–62. [Google Scholar] [CrossRef]
- Amendola, Alessandra, Vincenzo Candila, and Antonio Scognamillo. 2017. On the influence of US monetary policy on crude oil price volatility. Empirical Economics 52: 155–78. [Google Scholar] [CrossRef]
- Amendola, Alessandra, Vincenzo Candila, and Giampiero M. Gallo. 2018. On the asymmetric impact of macro–variables on volatility. Economic Modelling. [Google Scholar] [CrossRef]
- Arouri, Mohamed El Hedi, Jamel Jouini, and Duc Khuong Nguyen. 2012. On the impacts of oil price fluctuations on European equity markets: Volatility spillover and hedging effectiveness. Energy Economics 34: 611–17. [Google Scholar] [CrossRef]
- Bauwens, Luc, Sébastien Laurent, and Jeroen V. K. Rombouts. 2006. Multivariate GARCH models: A survey. Journal of Applied Econometrics 21: 79–109. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bouri, Elie, Maria E. de Boyrie, and Ivelina Pavlova. 2017. Volatility transmission from commodity markets to sovereign CDS spreads in emerging and frontier countries. International Review of Financial Analysis 49: 155–65. [Google Scholar] [CrossRef]
- Casanova, Carlos, Le Xia, and Romina Ferreira. 2016. Measuring Latin America’s export dependency on China. Journal of Chinese Economic and Foreign Trade Studies 9: 213–33. [Google Scholar] [CrossRef]
- Cashin, Paul, and C. John McDermott. 2002. The Long-Run Behavior of Commodity Prices: Small Trends and Big Variability. IMF Staff Papers 49: 175–99. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, and Michael McAleer. 2017. A Simple Test for Causality in Volatility. Econometrics 5: 15. [Google Scholar] [CrossRef]
- Chevallier, Julien, and Florian Ielpo. 2013. Cross-market linkages between commodities, stocks and bonds. Applied Economics Letters 20: 1008–18. [Google Scholar] [CrossRef]
- Clay, Edward. 2002. Food security: Concepts and measurement. In Trade Reforms and Food Security: Conceptualising the Linkages. Rome: FAO, pp. 25–34. [Google Scholar]
- Conover, William J., Mark E. Johnson, and Myrle M. Johnson. 1981. A comparative study of tests for homogeneity of variances, with applications to the outer continental shelf bidding data. Technometrics 23: 351–61. [Google Scholar] [CrossRef]
- Delbianco, Fernando, and Andrés Fioriti. 2018. External cycles and commodities in Latin America and the Caribbean: A cointegration analysis with breaks. Lecturas de Economía 88: 51–76. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate simultaneous generalized ARCH. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Engle, Robert F., Eric Ghysels, and Bumjean Sohn. 2013. Stock Market Volatility and Macroeconomic Fundamentals. Review of Economics and Statistics 95: 776–97. [Google Scholar] [CrossRef]
- Engle, Robert F., Takatoshi Ito, and Wen-Ling Lin. 1990. Meteor showers or heat waves? Heteroskedastic intra-day volatility in the foreign exchange market. Econometrica 58: 525–42. [Google Scholar] [CrossRef]
- FAO. 2015. The State of Agricultural Commodity Markets 2015-16. Technical Report. Rome: FAO. [Google Scholar]
- Gilbert, Christopher L., and Wyn Morgan. 2010. Food price volatility. Philosophical Transactions of the Royal Society of London B: Biological Sciences 365: 3023–34. [Google Scholar] [CrossRef] [PubMed]
- Granger, Clive W.J. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37: 424–38. [Google Scholar] [CrossRef]
- Gruss, Bertrand. 2014. After the boom–commodity prices and economic growth in Latin America and the Caribbean. International Monetary Fund 154: 1–31. [Google Scholar]
- Hafner, Christian M., and Helmut Herwartz. 2006. Volatility impulse responses for multivariate GARCH models: An exchange rate illustration. Journal of International Money and Finance 25: 719–40. [Google Scholar] [CrossRef]
- Hamadi, Hassan, Charbel Bassil, and Tamara Nehme. 2017. News surprises and volatility spillover among agricultural commodities: The case of corn, wheat, soybean and soybean oil. Research in International Business and Finance 41: 148–57. [Google Scholar] [CrossRef]
- Hamao, Yasushi, Ronald W. Masulis, and Victor Ng. 1990. Correlations in price changes and volatility across international stock markets. The Review of Financial Studies 3: 281–307. [Google Scholar] [CrossRef]
- Jin, Xiaoye, Sharon Xiaowen Lin, and Michael Tamvakis. 2012. Volatility transmission and volatility impulse response functions in crude oil markets. Energy Economics 34: 2125–34. [Google Scholar] [CrossRef]
- Kang, Sang Hoon, Hee-un Ko, and Seong-Min Yoon. 2017. Contagion Effects and Volatility Impulse Responses between US and Asian Stock Markets. Korea and the World Economy 18: 111–30. [Google Scholar]
- Kang, Wensheng, Ronald A. Ratti, and Kyung Hwan Yoon. 2015. The impact of oil price shocks on the stock market return and volatility relationship. Journal of International Financial Markets, Institutions and Money 34: 41–54. [Google Scholar] [CrossRef]
- Karali, Berna, and Octavio A. Ramirez. 2014. Macro determinants of volatility and volatility spillover in energy markets. Energy Economics 46: 413–21. [Google Scholar] [CrossRef]
- Lin, Wen-Ling, Robert F. Engle, and Takatoshi Ito. 1994. Do bulls and bears move across borders? International transmission of stock returns and volatility. Review of Financial Studies 7: 507–38. [Google Scholar] [CrossRef]
- Malik, Farooq, and Bradley T. Ewing. 2009. Volatility transmission between oil prices and equity sector returns. International Review of Financial Analysis 18: 95–100. [Google Scholar] [CrossRef]
- Mohammadi, Hassan, and Yuting Tan. 2015. Return and Volatility Spillovers across Equity Markets in Mainland China, Hong Kong and the United States. Econometrics 3: 215–32. [Google Scholar] [CrossRef]
- Nazlioglu, Saban, Cumhur Erdem, and Ugur Soytas. 2013. Volatility spillover between oil and agricultural commodity markets. Energy Economics 36: 658–65. [Google Scholar] [CrossRef]
- Nazlioglu, Saban, Shawkat Hammoudeh, and Rangan Gupta. 2015. Volatility transmission between Islamic and conventional equity markets: Evidence from causality-in-variance test. Applied Economics 47: 4996–5011. [Google Scholar] [CrossRef]
- OECD, and FAO. 2015. Agricultural Outlook 2015–2024. Technical Report. Paris: Organisation for Economic Co-operation and Development (OECD) Publishing. [Google Scholar] [CrossRef]
- Śmiech, Sławomir, Monika Papież, Marek A. Dąbrowski, and Kamil Fijorek. 2018. What drives food price volatility? Evidence based on a generalized VAR approach applied to the food, financial and energy markets. In Economics Discussion Papers. No 2018-55. Kiel: Kiel Institute for the World Economy, vol. 55. [Google Scholar] [CrossRef]
- Tyner, Wallace E. 2008. The US Ethanol and Biofuels Boom: Its Origins, Current Status, and Future Prospects. BioScience 58: 646–53. [Google Scholar] [CrossRef]
- UNDP. 2011. Towards Human Resilience: Sustaining MDG Progress in an Age of Economic Uncertainty. New York: United Nations Development Programme (UNDP). [Google Scholar]
- Vardar, Gülin, Yener Coşkun, and Tezer Yelkenci. 2018. Shock transmission and volatility spillover in stock and commodity markets: Evidence from advanced and emerging markets. Eurasian Economic Review 8: 231–88. [Google Scholar] [CrossRef]
- Von Braun, Joachim. 2008. Food and Financial Crises: Implications for Agriculture and the Poor. Food Policy Report No. 20. Washington: International Food Policy Research Institute (IFPRI). [Google Scholar] [CrossRef]
| 1 | |
| 2 | The food security definition elaborated in the 1996 World Food Summit (Clay 2002) is: “Food security, at the individual, household, national, regional and global levels (is achieved) when all people, at all times, have physical and economic access to sufficient, safe and nutritious food to meet their dietary needs and food preferences for an active and healthy life”. |
| 3 |

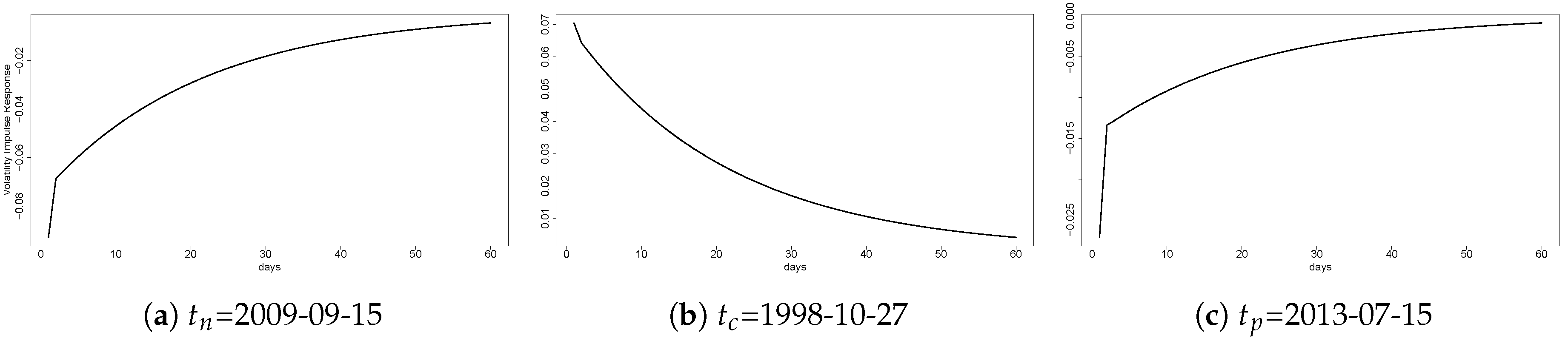
| Commodity | BP | EP | Obs. | Jarque–Bera | Std. Dev. (FS) | Std. Dev. (S1) | Std. Dev. (S2) | Std. Dev. (S3) | Std. Dev. (S4) | Std. Dev. (S5) | Std. Dev. (S6) | Fligner |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corn | 2 Jan 1973 | 28 Feb 2018 | 11,398 | 0.000 | 0.017 | 0.020 | 0.015 | 0.015 | 0.019 | 0.018 | 0.026 | 0.000 |
| (2 Jan 1973/31 Dec 1980) | (2 Jan 1981/31 Dec 1990) | (2 Jan 1991/29 Dec 2000) | (1 Jan 2001/12 Dec 2010) | (3 Jan 2011/28 Feb 2018) | (3 Dec 2007/30 Jun 2009) | |||||||
| Sugar | 22 May 1998 | 28 Feb 2018 | 4,954 | 0.000 | 0.023 | 0.028 | 0.023 | 0.019 | - | - | 0.028 | 0.000 |
| (22 May 1998 /29 Dec 2000) | (2 Jan 2001/12 Dec 2010) | (4 Jan 2011/28 Feb 2018) | (3 Dec 2007/30 Jun 2009) | |||||||||
| Wheat | 27 Aug 1998 | 28 Feb 2018 | 4,912 | 0.000 | 0.020 | 0.016 | 0.021 | 0.018 | - | - | 0.030 | 0.000 |
| (27 Aug 1998/29 Dec 2000) | (2 Jan 2001/31 Dec 2010) | (3 Han 2011/28 Feb 2018) | (3 Dec 2007/30 Jun 2009) | |||||||||
| Soybean | 27 Aug 1998 | 28 Feb 2018 | 4,912 | 0.000 | 0.017 | 0.013 | 0.019 | 0.014 | - | - | 0.028 | 0.000 |
| (27 Aug 1998/29 Dec 2000) | (2 Jan 2001/12 Dec 2010) | (3 Jan 2011/ 28 Feb 2018) | (3 Dec 2007/30 Jun 2009) | |||||||||
| Bioethanol | 27 Apr 2005 | 28 Feb 2018 | 3,230 | 0.000 | 0.022 | 0.021 | 0.022 | - | - | - | 0.022 | 0.002 |
| (27 Apr 2005/31 Dec 2010) | (3 Jan 2011 /28 Feb 2018) | (3 Dec 2007/30 Jun 2009) |
| Statistics | Argentina | Brazil | Chile | Colombia | Peru |
|---|---|---|---|---|---|
| Symbol | MERV | BVSP | IPSA | GXG | SPBLPGPT |
| Begin Period | 8 Oct 1996 | 27 Apr 1993 | 2 Jan 2002 | 22 May 1998 | 31 Mar 1997 |
| End Period | 28 Feb 2018 | 28 Feb 2018 | 28 Feb 2018 | 28 Feb 2018 | 28 Feb 2018 |
| Obs | 5245 | 6149 | 4028 | 4954 | 5072 |
| Min * | −14.765 | −17.208 | −7.236 | −18.038 | −13.291 |
| Max * | 16.117 | 28.832 | 11.803 | 23.547 | 12.816 |
| Mean * | 0.077 | 0.133 | 0.039 | 0.008 | 0.05 |
| Std. Dev. | 0.022 | 0.023 | 0.01 | 0.023 | 0.014 |
| Skew. | −0.307 | 0.489 | 0.013 | −0.077 | −0.416 |
| Kurt. | 4.813 | 10.46 | 10.206 | 6.044 | 10.782 |
| Commodity | Time | Argentina | Brazil | Chile | Colombia | Peru |
|---|---|---|---|---|---|---|
| 0.071 | 0.115 | 0.022 | 0.050 | 0.000 | ||
| Corn | 0.324 | 0.194 | 0.008 | 0.084 | 0.000 | |
| 0.895 | 0.353 | 0.003 | 0.125 | 0.000 | ||
| 0.351 | 0.887 | 0.658 | 0.000 | 0.016 | ||
| Sugar | 0.380 | 0.729 | 0.876 | 0.000 | 0.041 | |
| 0.517 | 0.911 | 0.570 | 0.000 | 0.481 | ||
| 0.279 | 0.994 | 0.081 | 0.185 | 0.062 | ||
| Wheat | 0.404 | 0.997 | 0.080 | 0.687 | 0.048 | |
| 0.577 | 0.949 | 0.046 | 0.619 | 0.018 | ||
| 0.047 | 0.607 | 0.121 | 0.779 | 0.736 | ||
| Soybean | 0.266 | 0.998 | 0.684 | 0.142 | 0.992 | |
| 0.392 | 0.847 | 0.833 | 0.003 | 1.000 | ||
| 0.020 | 0.381 | 0.278 | 0.971 | 0.606 | ||
| Bioethanol | 0.846 | 0.728 | 0.860 | 0.465 | 0.465 | |
| 0.959 | 0.811 | 0.981 | 0.391 | 0.131 |
| j (Origin) | Corn | Corn | Corn | Sugar | Sugar | Wheat | Wheat |
|---|---|---|---|---|---|---|---|
| i (Recipient) | Chile | Colombia | Peru | Colombia | Peru | Chile | Peru |
| −0.003 *** | 0.007 * | −0.002 *** | 0.009 *** | −0.003 *** | 0.003 *** | 0.003 *** | |
| (0.000) | (0.004) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| 0.004 *** | −0.002 | 0.007 * | 0.008 *** | 0.003 *** | −0.004 *** | −0.001 | |
| (0.001) | (0.004) | (0.004) | (0.000) | (0.001) | (0.001) | (0.001) | |
| 0.017 *** | 0.016 *** | −0.016 *** | 0.000 | −0.018 *** | −0.009 *** | 0.013 *** | |
| (0.001) | (0.001) | (0.002) | (0.000) | (0.001) | (0.001) | (0.000) | |
| −0.498 *** | −0.343 *** | 0.548 *** | 1.426 | 0.498 *** | 0.496 *** | 0.475 *** | |
| (0.019) | (0.026) | (0.020) | (16.330) | (0.018) | (0.020) | (0.019) | |
| 0.001 | −0.011 | −0.006 | 1.426 | −0.003 | 0.002 | 0.028 *** | |
| (0.011) | (0.032) | (0.008) | (16.330) | (0.007) | (0.010) | (0.010) | |
| 0.148 ** | −0.011 | 0.063 ** | 1.913 | −0.024 | 0.041 | 0.026 | |
| (0.058) | (0.017) | (0.032) | (15.307) | (0.037) | (0.049) | (0.036) | |
| −0.327 *** | −0.404 *** | −0.036 | 1.013 | 0.343 *** | −0.275 *** | 0.278 *** | |
| (0.040) | (0.041) | (0.033) | (15.307) | (0.024) | (0.021) | (0.024) | |
| 0.801 *** | 0.607 *** | −0.758 *** | 0.339 | −0.823 *** | 0.799 *** | −0.828 *** | |
| (0.018) | (0.052) | (0.011) | (0.756) | (0.012) | (0.020) | (0.015) | |
| 0.022 | −0.963 *** | −0.210 *** | −0.035 | −0.051 *** | 0.019 | 0.183 *** | |
| (0.024) | (0.134) | (0.009) | (0.742) | (0.010) | (0.021) | (0.014) | |
| 0.419 *** | 0.205 *** | −0.236 *** | 0.021 | −0.144 *** | 0.709 *** | 0.189 *** | |
| (0.068) | (0.057) | (0.036) | (0.757) | (0.039) | (0.090) | (0.017) | |
| 0.006 | −0.091 *** | −0.051 | 0.282 | −0.397 *** | −0.781 *** | 0.684 *** | |
| (0.025) | (0.035) | (0.043) | (0.743) | (0.121) | (0.040) | (0.013) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Candila, V.; Farace, S. On the Volatility Spillover between Agricultural Commodities and Latin American Stock Markets. Risks 2018, 6, 116. https://doi.org/10.3390/risks6040116
Candila V, Farace S. On the Volatility Spillover between Agricultural Commodities and Latin American Stock Markets. Risks. 2018; 6(4):116. https://doi.org/10.3390/risks6040116
Chicago/Turabian StyleCandila, Vincenzo, and Salvatore Farace. 2018. "On the Volatility Spillover between Agricultural Commodities and Latin American Stock Markets" Risks 6, no. 4: 116. https://doi.org/10.3390/risks6040116
APA StyleCandila, V., & Farace, S. (2018). On the Volatility Spillover between Agricultural Commodities and Latin American Stock Markets. Risks, 6(4), 116. https://doi.org/10.3390/risks6040116





