Bond Yields, Sovereign Risk and Maturity Structure
Abstract
:1. Introduction
2. Literature Review
3. Sovereign Risk Proxies
4. Hypotheses Formulation
4.1. Relation between Sovereign Risk and Debt Maturity Structure
4.2. Diamond’s Model (1991) and Its Application in the Analysis of the Maturity Structure
4.3. Stock of Debt Influence on the Relationship between Sovereign Bond Yields, Sovereign Risk and Debt Maturity
5. Data and Methodology
5.1. Data
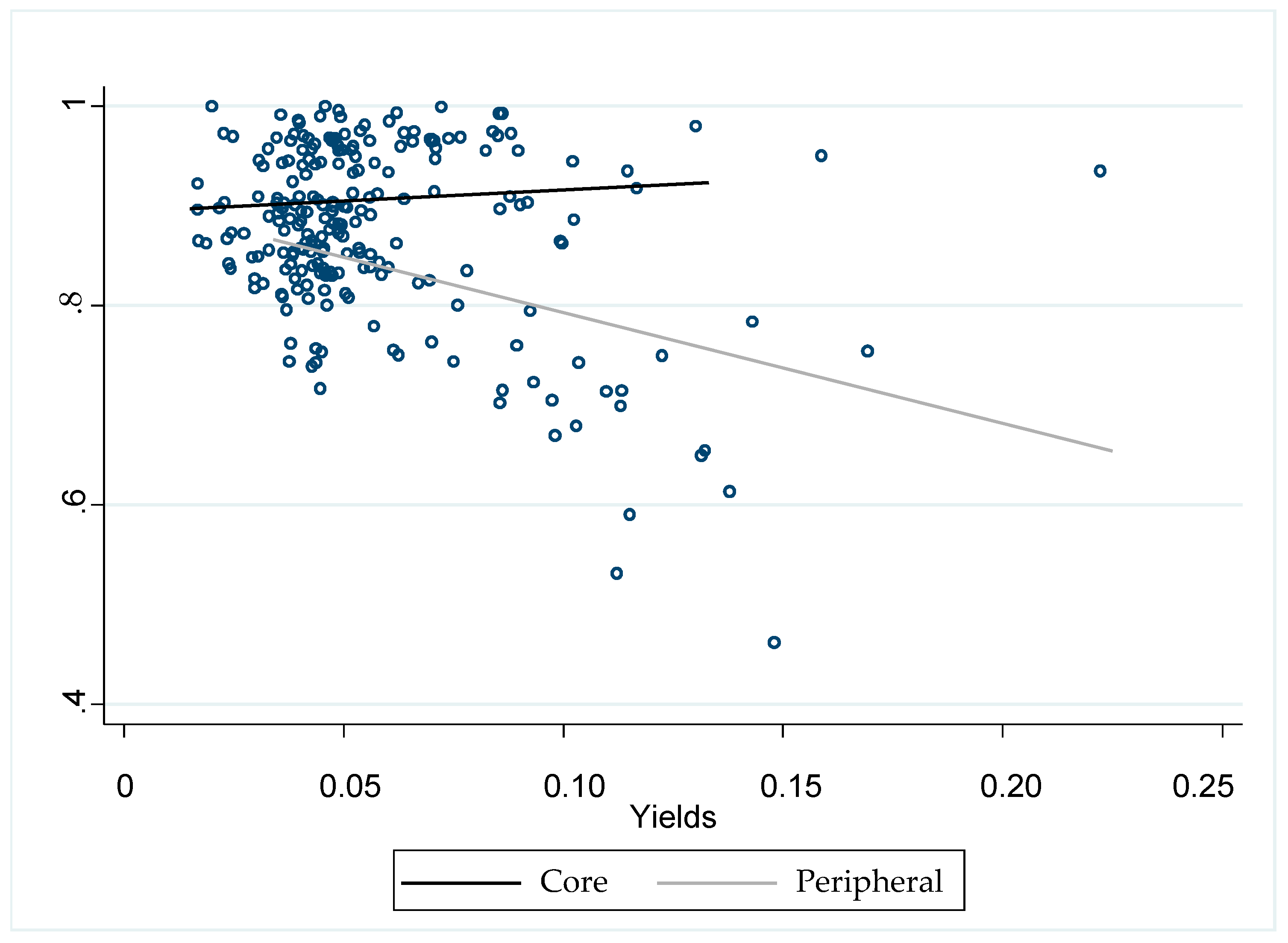
- The dependent variable is the ratio of long-term debt to total debt9. The ratio of long-term debt to total debt allows us to analyze the impact of sovereign risk on the maturity structure of sovereign debt. The data for this variable were obtained from the European Central Bank Statistical Data Warehouse, which collects data from the European System of Central Banks (ESCB), Eurostat and national central banks. This ratio represents the volume of long-term debt from all sectors of the economy to the total debt10.
- We included the average maturity of sovereign debt as the main determinant of the sovereign debt maturity structure. This variable represents residual maturity of sovereign debt expressed in years. The data were obtained from the European Central Bank Statistical Data Warehouse. We considered the following control variables as determinants of sovereign debt maturity structure:
- ▪
- Inflation (Missale and Blanchard 1994; Goudswaard 1990; De Haan et al. 1995): This variable was expressed as the increase compared to the previous period. It is expected that the coefficient for this variable has a negative sign because higher inflation increases uncertainty about the long-term bonds. This uncertainty generates a trend toward investing in short-term maturities. The data were obtained from the European Central Bank Statistical Data Warehouse.
- ▪
- Gross Domestic Product (GDP): This variable was used as a proxy for the business cycle (Goudswaard 1990) and to control the size of the economy. It is expected that an increase in GDP leads to an increase in the debt maturity and therefore a lengthening of the maturity structure. The data were obtained from the Eurostat Statistics Database.
- ▪
- Debt/GDP ratio (Missale and Blanchard 1994; De Haan et al. 1995; Bodnaruk 1999): Data for this variable were obtained from European Central Bank Statistical Data Warehouse11.
- ▪
- Borrowing requirements of the public administration: the borrowing requirement covers all financial transactions in government debt instruments. The data were obtained from European Central Bank Statistical Data Warehouse.
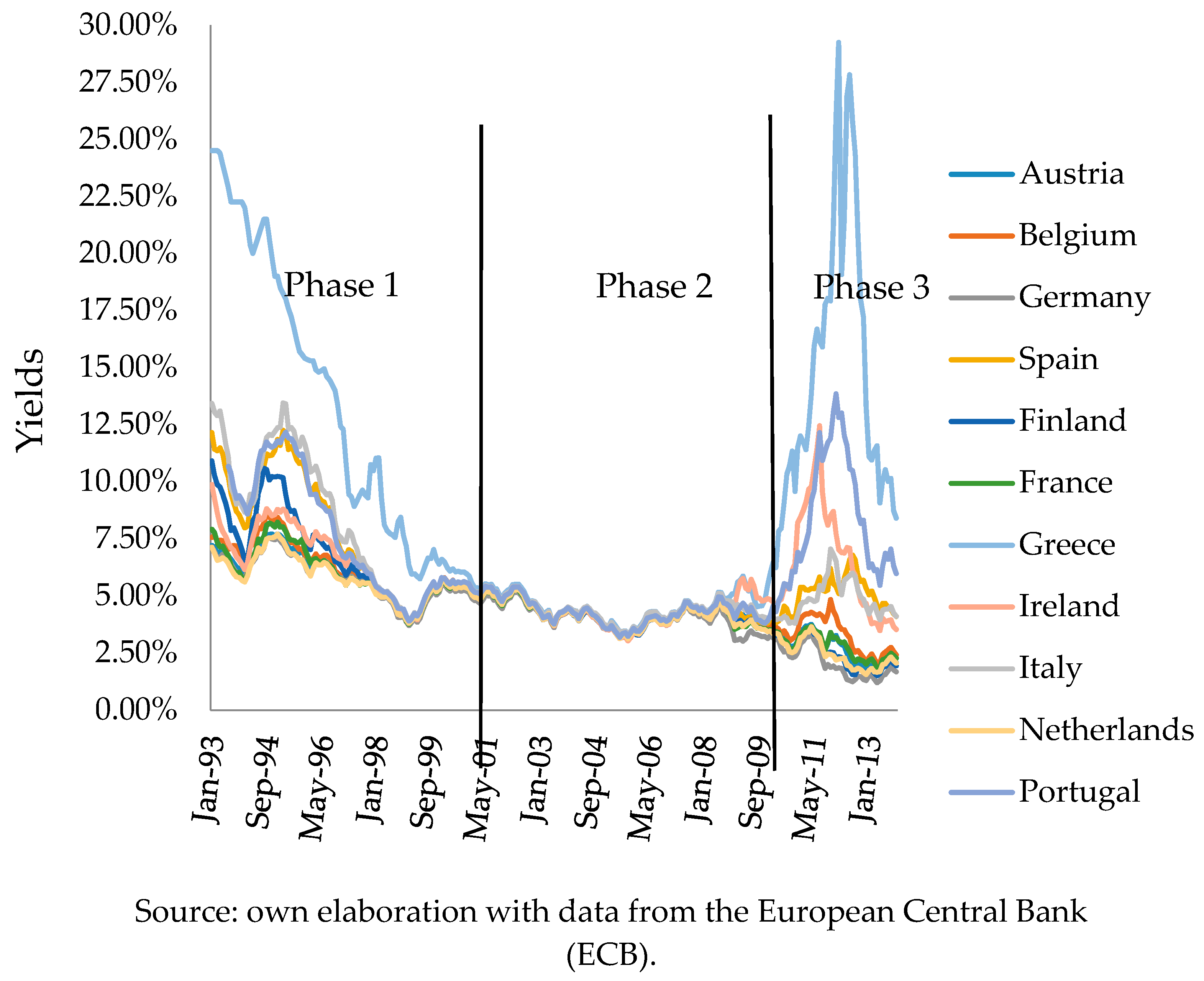
- Annual 10-year sovereign bond yields: This proxy was calculated as the average of the monthly bond yields published in the European Central Bank Statistical Data Warehouse. A high value of returns is generally indicative of greater sovereign risk; therefore, we expect to find a negative relationship with the ratio of long-term debt to total debt.
- Spreads (Broner et al. 2013; Perez 2017): This proxy allowed us to measure the default risk of a country. Spreads were calculated as the difference between the 10-year sovereign bond yields and German bond yields of the same maturity, which were both obtained from European Central Bank Statistical Data Warehouse. We also used risk premiums relative to 10-year U.S. bonds (Bernoth et al. 2012) to include Germany in the study and as a robustness test. Data for U.S. bond yields were obtained from the database of the Federal Reserve Bank of St. Louis. A high spread indicates greater risk, and therefore, the expected sign for this variable is negative.
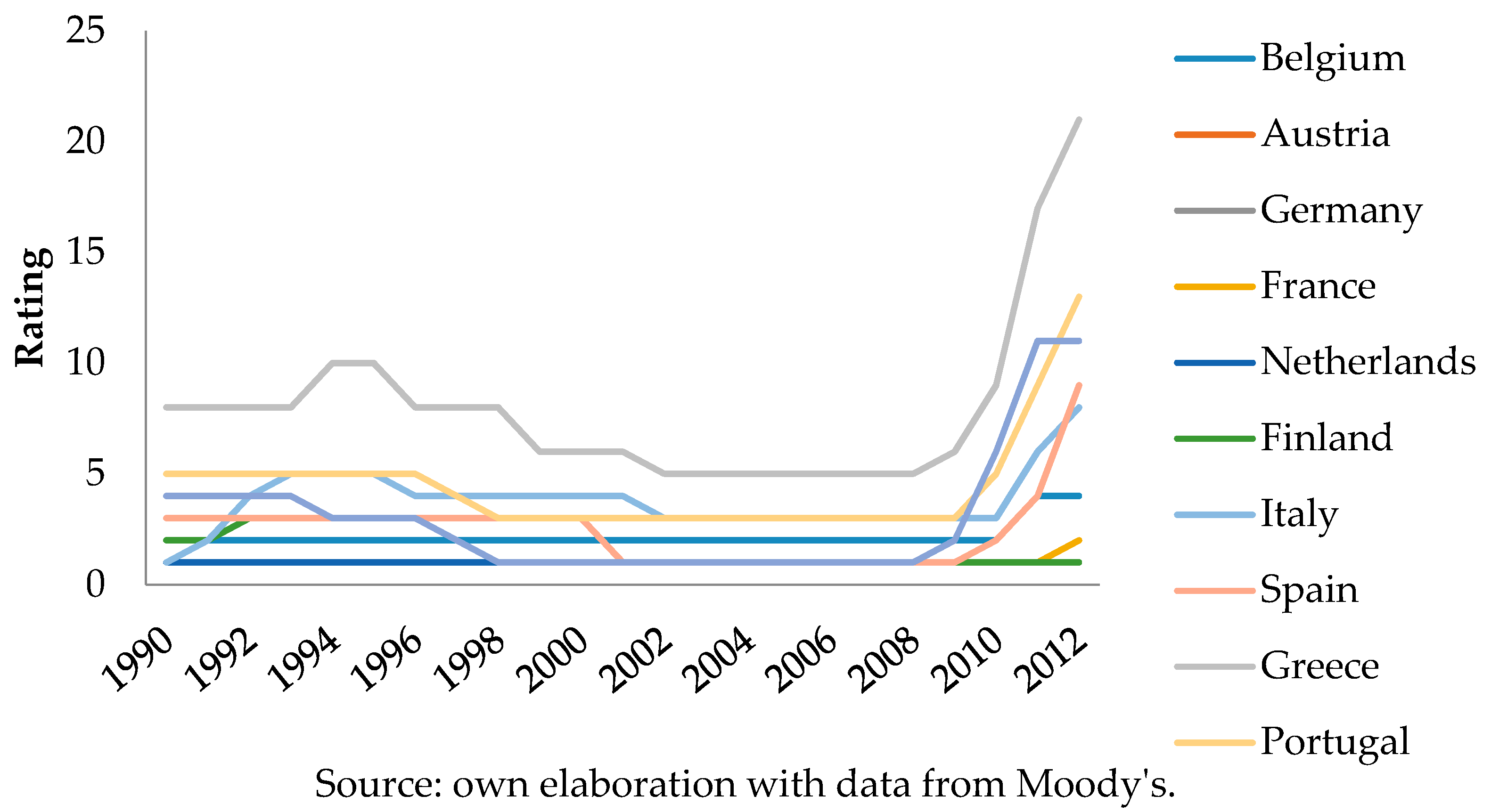
- Sovereign Ratings: We constructed a numerical variable to approximate the Moody’s agency ratings (Remolona et al. 2007). The scale assigned a greater score to ratings with higher risk; therefore, the sign of this variable is expected to coincide with the sign of the rest of sovereign risk proxies. We assigned a value of 1 to the rating Aaa, a value of 2 to Aa1 and so on12. The results are depicted in Figure 1. However, ratings have the disadvantage that their variability is not very high, as they are not frequently reviewed by rating agencies. We expect to find an inverse relation between this proxy and the maturity structure of sovereign debt, as with the other proxies for sovereign risk.
5.2. Methodology
6. Results and Discussion
6.1. Sovereign Bond Yields, Sovereign Risk and Maturity Structure
6.2. Robustness Tests
6.3. Analysis of the Non-Monotonic Relation between Sovereign Bond Yields, Sovereign Risk and Maturity Structure
6.4. Relation between Sovereign Bond Yields, Sovereign Risk and Maturity Structure Depending on the Indebtedness Level
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ağca, Şenay, and Oya Celasun. 2012. Sovereign debt and corporate borrowing costs in emerging markets. Journal of International Economics 88: 198–208. [Google Scholar] [CrossRef]
- Alesina, Alberto, Mark De Broeck, Alessandro Prati, and Guido Tabellini. 1992. Default risk on goverment debt in OECD countries. Economic Policy 7: 427–63. [Google Scholar] [CrossRef]
- Alesina, Alberto, and Guido Tabellini. 1989. External debt, capital flight and political risk. Journal of Development Economics 27: 199–220. [Google Scholar] [Green Version]
- Alfaro, Laura, and Fabio Kanczuk. 2009. Debt Maturity: Is Long-Term Debt Optimal? Review of International Economics 17: 890–905. [Google Scholar] [CrossRef]
- Altman, Edward I., and Herbert A. Rijken. 2004. How rating agencies achieve rating stability. Journal of Banking and Finance 28: 2679–714. [Google Scholar] [CrossRef]
- Altman, Edward I. 1968. Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Arce, Oscar, Sergio Mayordomo, and Juan Ignacio Peña. 2013. Credit-risk valuation in the sovereign CDS and bonds markets: Evidence from the euro area crisis. Journal of International Money and Finance 35: 124–145. [Google Scholar] [CrossRef] [Green Version]
- Arellano, Cristina, and Ananth Ramanarayanan. 2012. Default and the Maturity Structure in Sovereign Bonds. Journal of Political Economy 120: 187–232. [Google Scholar] [CrossRef] [Green Version]
- Baker, Malcolm, Robin Greenwood, and Jeffrey Wurgler. 2003. The maturity of debt issues and predictable variation in bond returns. Journal of Financial Economics 70: 261–91. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring Economic Policy Uncertainty. The Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Barclay, Michael J., and Clifford W. Smith Jr. 1995. The Maturity Structure of Corporate Debt. The Journal of Finance 50: 609–31. [Google Scholar] [CrossRef]
- Bayoumi, Tamim, Morris Goldstein, and Geoffrey Woglom. 1995. Do Credit Markets Discipline Sovereign Borrowers? Evidence from U.S. States. Journal of Money, Credit and Banking 27: 1046–59. [Google Scholar] [CrossRef]
- Berger, Allen N., Marco A. Espinosa-Vega, W. Scott Frame, and Nathan H. Miller. 2005. Debt Maturity, Risk, and Asymmetric Information. The Journal of Finance 60: 2895–923. [Google Scholar] [CrossRef]
- Bernoth, Kerstin, Jürgen Von Hagen, and Ludger Schuknecht. 2012. Sovereign risk premiums in the European government bond market. Journal of International Money and Finance 31: 975–95. [Google Scholar] [CrossRef] [Green Version]
- Bodnaruk, Andriy. 1999. Determinants of Sovereign Debt Term for Transition Countries, EERC MA Program in Economics: Working Paper.
- Boumparis, Periklis, Costas Milas, and Theodore Panagiotidis. 2017. Economic policy uncertainty and sovereign credit rating decisions: Panel quantile evidence for the Eurozone. Journal of International Money and Finance 79: 39–71. [Google Scholar] [CrossRef]
- Büchel, Konstantin. 2013. Do words matter? The impact of communication on the PIIGS’ CDS and bond yield spreads during Europe’s sovereign debt crisis. European Journal of Political Economy 32: 412–431. [Google Scholar] [CrossRef]
- Broner, Fernando A., Guido Lorenzoni, and Sergio L. Schmukler. 2013. Why do emerging economies borrow short term? Journal of the European Economic Association 11: 67–100. [Google Scholar] [CrossRef]
- Broner, Fernando, Aitor Erce, Alberto Martin, and Jaume Ventura. 2014. Sovereign debt markets in turbulent times: Creditor discrimination and crowding-out effects. Journal of Monetary Economics 61: 114–42. [Google Scholar] [CrossRef]
- Brunnermeier, Markus K., and Martin Oehmke. 2013. The Maturity Rat Race. The Journal of Finance 68: 483–521. [Google Scholar] [CrossRef]
- Cole, Harold L., and Timothy J. Kehoe. 2000. Self-fulfilling debt crises. The Review of Economic Studies 67: 91–116. [Google Scholar] [CrossRef]
- Datta, Sudip, Mai Iskandar-Datta, and Ajay Patel. 1999. Bank monitoring and the pricing of corporate public debt. Journal of Financial Economics 51: 435–49. [Google Scholar] [CrossRef]
- Davis, Steven J. 2016. An Index of Global Economic Policy Uncertainty. No. w22740. Cambridge: National Bureau of Economic Research (NBER). [Google Scholar]
- De Haan, Jakob, Bernd Jan Sikken, and Andrew Hilder. 1995. On the relationship between the debt ratio and debt maturity. Applied Economics Letters 2: 484–86. [Google Scholar] [CrossRef]
- Delatte, Anne-Laure, Mathieu Gex, and Antonia López-Villavicencio. 2012. Has the CDS market influenced the borrowing cost of European countries during the sovereign crisis? Journal of International Money and Finance 31: 481–497. [Google Scholar] [CrossRef]
- Diamond, Douglas W. 1991. Debt Maturity Structure and Liquidity Risk. The Quarterly Journal of Economics 106: 709–37. [Google Scholar] [CrossRef]
- Drudi, Francesco, and Raffaela Giordano. 2000. Default risk and optimal debt management. Journal of Banking & Finance 24: 861–91. [Google Scholar]
- Ejsing, Jacob, and Wolfgang Lemke. 2011. The Janus-headed salvation: Sovereign and bank credit risk premia during 2008–2009. Economics Letters 110: 28–31. [Google Scholar] [CrossRef] [Green Version]
- Flannery, Mark J. 1986. Asymmetric Information and Risky Debt Maturity Choice. The Journal of Finance 41: 19–37. [Google Scholar] [CrossRef]
- Kalbaska, Alesia, and Mateusz Gątkowski. 2012. Eurozone sovereign contagion: Evidence from the CDS market (2005–2010). Journal of Economic Behavior & Organization 83: 657–73. [Google Scholar]
- González, Víctor M. 2009. Estructura de vencimiento de la deuda y riesgo de crédito en las empresas españolas. Universia Business Review 22: 88–101. [Google Scholar]
- Goudswaard, Kees P. 1990. Determinants of public debt maturities. De Economist 138: 33–46. [Google Scholar] [CrossRef]
- Guedes, Jose, and Tim Opler. 1996. The Determinants of the Maturity of Corporate Debt Issues. The Journal of Finance 51: 1809–33. [Google Scholar] [CrossRef]
- Hardouvelis, Gikas A., Georgios Karalas, Dimitrios Karanastasis, and Panagiotis Samartzis. 2018. Economic Policy Uncertainty, Political Uncertainty and the Greek Economic Crisis, SSRN Working Paper. Social Science Research Network.
- Hatchondo, Juan Carlos, and Leonardo Martinez. 2013. Sudden Stops, Time Inconsistency, and the Duration of Sovereign Debt. International Economic Journal 27: 217–28. [Google Scholar] [CrossRef]
- Hatchondo, Juan Carlos, Leonardo Martinez, and César Sosa-Padilla. 2011. Debt Dilution and Sovereign Default Risk. IMF Working Paper WP/11/70. Washington, DC: International Monetary Fund. [Google Scholar]
- Hausman, Jerry A. 1978. Specification test in econometrics. Econometrica 46: 1251–71. [Google Scholar] [CrossRef]
- Lee, Hei Wai, Yan Alice Xie, and Jot Yau. 2011. The impact of sovereign risk on bond duration: Evidence from Asian sovereign bond markets. International Review of Economics & Finance 20: 441–51. [Google Scholar]
- Mann, Henry B., and Donald R. Whitney. 1947. On a test of whether one of two random variables is stochastically than the other. Annals of Mathematical Statistics 18: 50–60. [Google Scholar] [CrossRef]
- Missale, Alessandro, and Olivier Jean Blanchard. 1994. The Debt Burden and Debt Maturity. The American Economic Review 84: 309–19. [Google Scholar]
- Mitchell, Karlyn. 1993. The debt maturity choice: an empirical investigation. The Journal of Financial Research 16: 309–20. [Google Scholar] [CrossRef]
- Myers, Stewart C. 1977. Determinants of corporate borrowing. Journal of Financial Economics 5: 147–75. [Google Scholar] [CrossRef]
- Park, Chul Woo. 1999. Maturity structure of public debt and expected bond returns. Journal of Banking & Finance 23: 1407–35. [Google Scholar]
- Perez, Diego J. 2017. Sovereign debt maturity structure under asymmetric information. Journal of International Economics 108: 243–59. [Google Scholar] [CrossRef]
- Remolona, Eli M., Michela Scatigna, and Eliza Wu. 2007. Interpreting sovereign spreads. BIS Quarterly Review, March 14, 27–39. [Google Scholar]
- Scherr, Frederick C., and Heather M. Hulburt. 2001. The debt maturity structure of small firms. Financial Management 30: 85–111. [Google Scholar] [CrossRef]
- Stohs, Mark Hoven, and David C. Mauer. 1996. The Determinants of Corporate Debt Maturity Structure. The Journal of Business 69: 279–312. [Google Scholar] [CrossRef]
- Wilcoxon, Frank. 1945. Individual comparisons by ranking methods. Biometrics Bulletin 1: 80–83. [Google Scholar] [CrossRef]
- Xie, Yan Alice, Sheen Liu, Chunchi Wu, and Bing Anderson. 2009. The effects of default and call risk on bond duration. Journal of Banking & Finance 33: 1700–8. [Google Scholar]
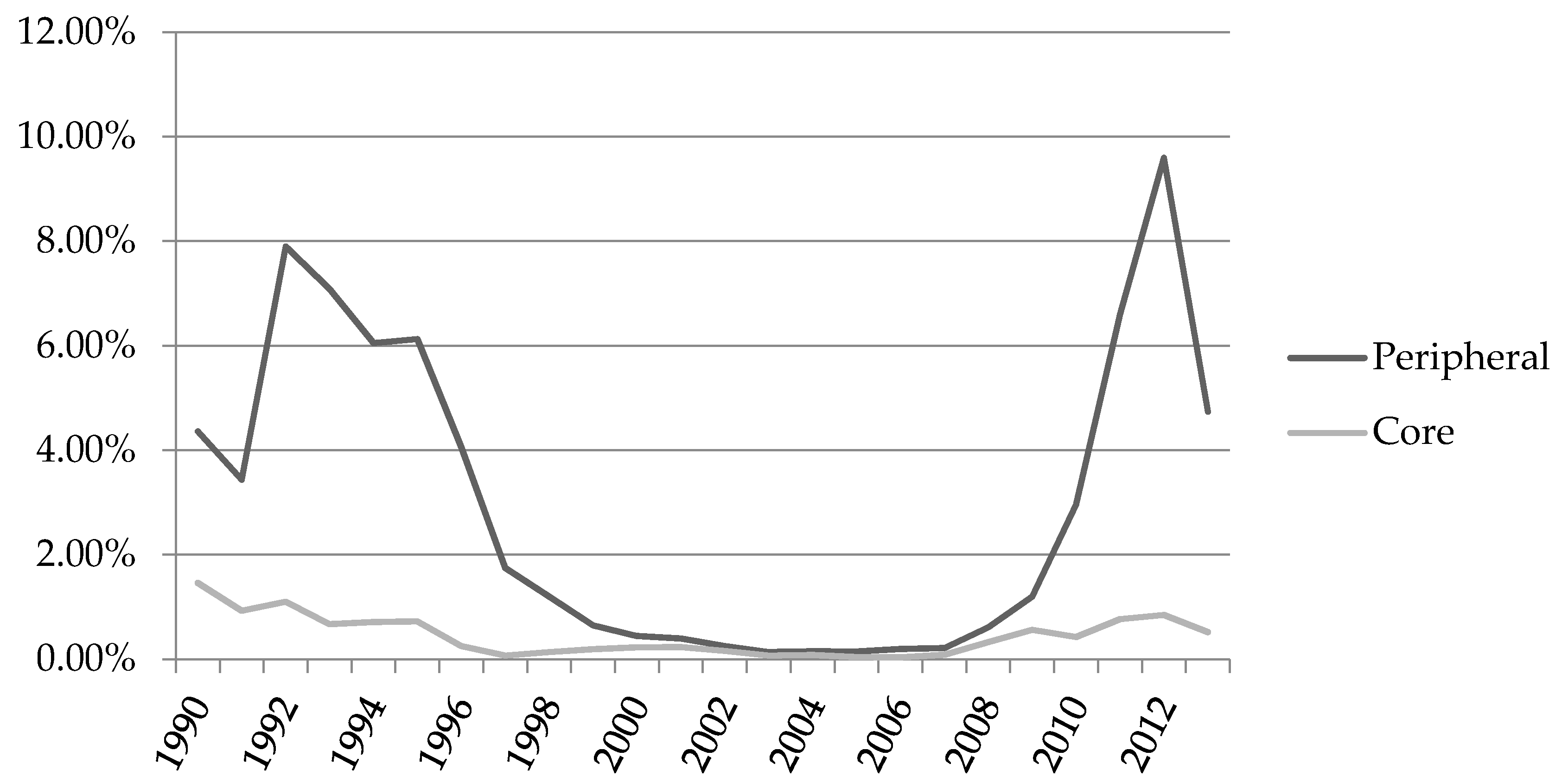
| 1 | Several papers refer to the countries of the Euro area that are not included within peripheral countries as core countries. See Kalbaska and Gątkowski (2012) in this regard. We consider the following core countries: Germany, Austria, Belgium, Finland, France and the Netherlands. |
| 2 | See also Hardouvelis et al. (2018) who analyze the effects of uncertainty in Greece and obtain similar results in the context of Greek debt crisis. Namely, they find that uncertainty lead to an increase in sovereign bond yields in Greek bonds. |
| 3 | See also Hatchondo et al. (2011) for further analysis of the relationship between duration and sovereign default risk. |
| 4 | The countries more affected by the European debt crisis: Greece, Ireland, Italy, Portugal and Spain. |
| 5 | We have used a scale to transform Moody’s ratings into numerical values. We assign the value 1 to the higher rating quality (Aaa), 2 for the following ranking (Aa1) and so on. |
| 6 | In the case of Europe, the difference between the sovereign 10-year bond yields from a European country and that from the same instrument in Germany is used. |
| 7 | Another measure to quantify the sovereign risk is used by Alesina et al. (1992), who use the ratio of sovereign bond yields to corporate bond yields, as well as the difference between them. |
| 8 | The proxies used to approximate sovereign risk are selected according to data availability. |
| 9 | The ECB provides the average maturity of sovereign debt for the period between 1990 and 2013 but does not include Germany and Spain. These data were obtained from the OECD database and the Spanish Treasury. |
| 10 | The ECB provides the ratio of short and long-term debt over GDP and the volumes of short and long-term debt. To construct the ratio of long-term debt to total debt, we consider total debt to be the sum of short and long-term debt, and we subsequently calculate the ratio. The ECB defines government debt as consolidated gross debt, including all sectors of the economy and excluding financial derivatives and loans. |
| 11 | The debt/GDP provided by the ECB includes all sectors of the economy, including regional and local debt and social security funds. |
| 12 | When there is more than one rating during the year, we calculate the average numerical value of the ratings. If there are favorable prospects, we round the value representing the lowest risk and vice versa. |
| 13 | The values of the Hausman (1978) provide a p-value that leads to the rejection of the null hypothesis in our models. Therefore, we choose to use the fixed effects instead of the random effects estimation. However, the results for the random effects estimation provide similar results to those obtained with the OLS or fixed effects estimation. These results are available upon request to the authors. |
| 14 | These tests are considered to be the most appropriate when the series does not follow a normal distribution and when the population variances are not equal. |
| 15 | We also use the Moody’s sovereign rating to measure sovereign risk, but it does not provide significant results, as this variable does not vary much with time. The results for this variable are available upon request to the authors. |
| 16 | A phenomenon can vary between years for reasons that are not adequately captured by the explanatory variables in the model. Therefore, not controlling for temporal variation may lead to a bias in the results. |
| 17 | We also use the VSTOXX index to approximate international risk aversion. The results do not vary regarding the presented in Table 5. |
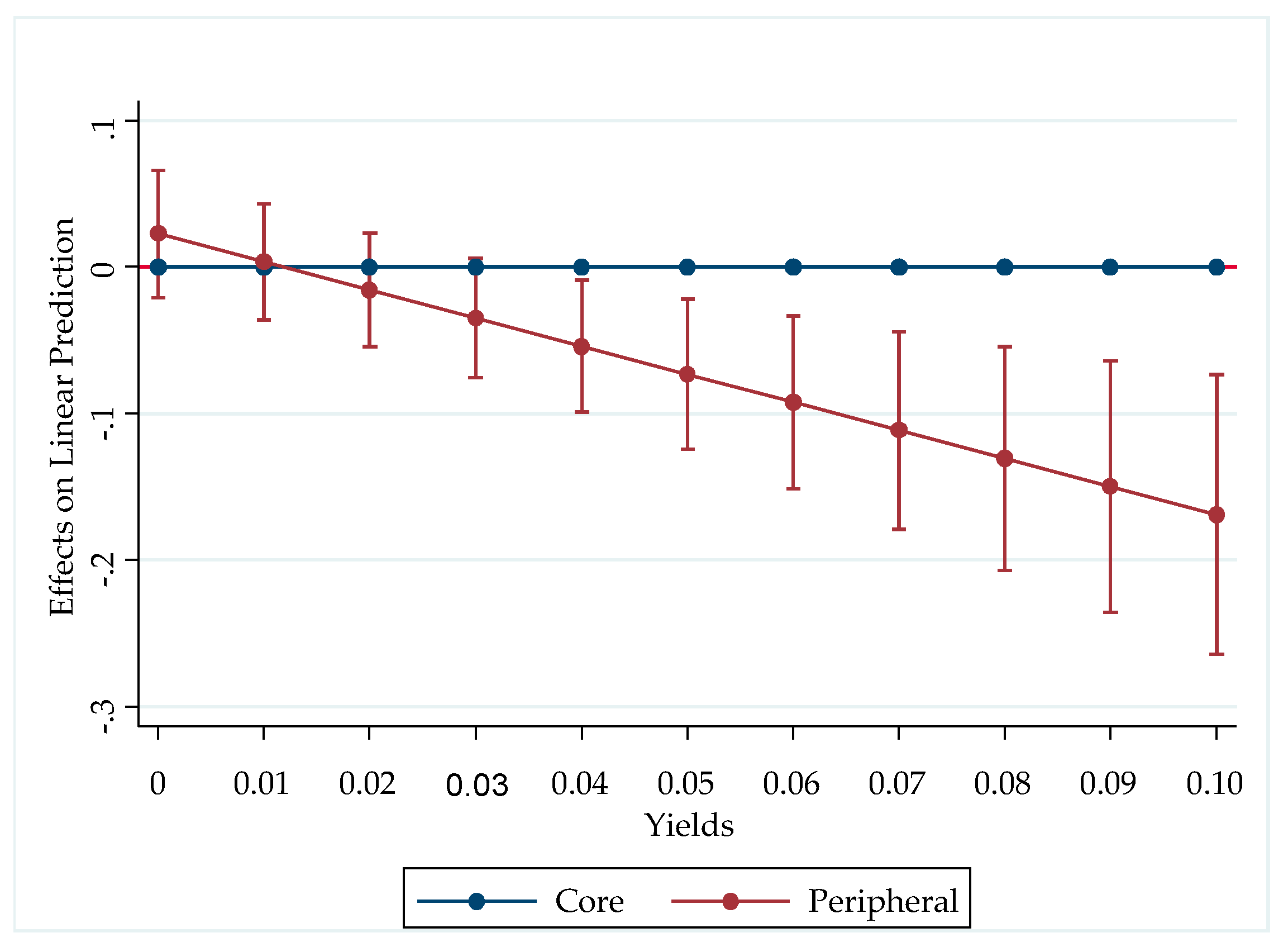
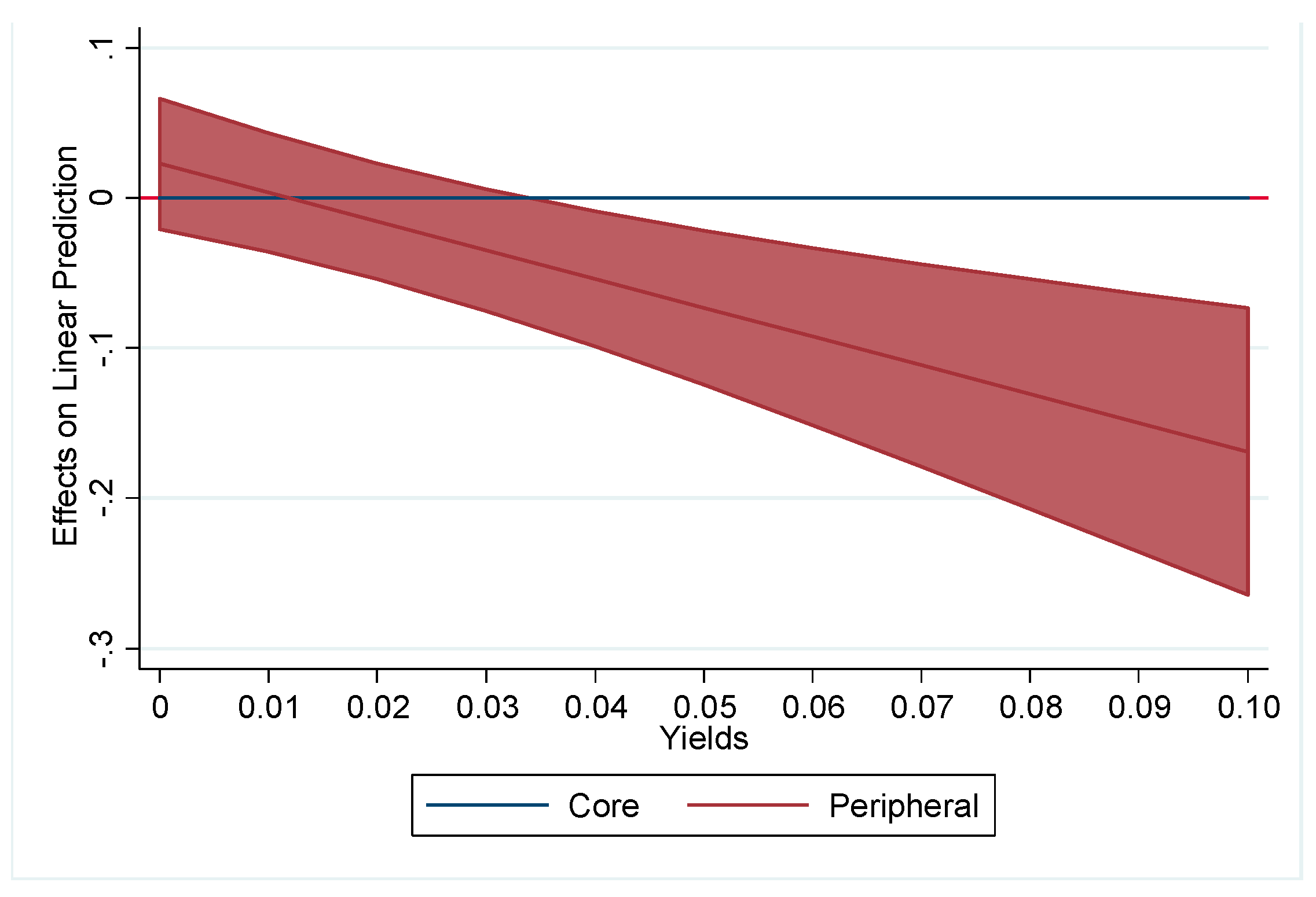
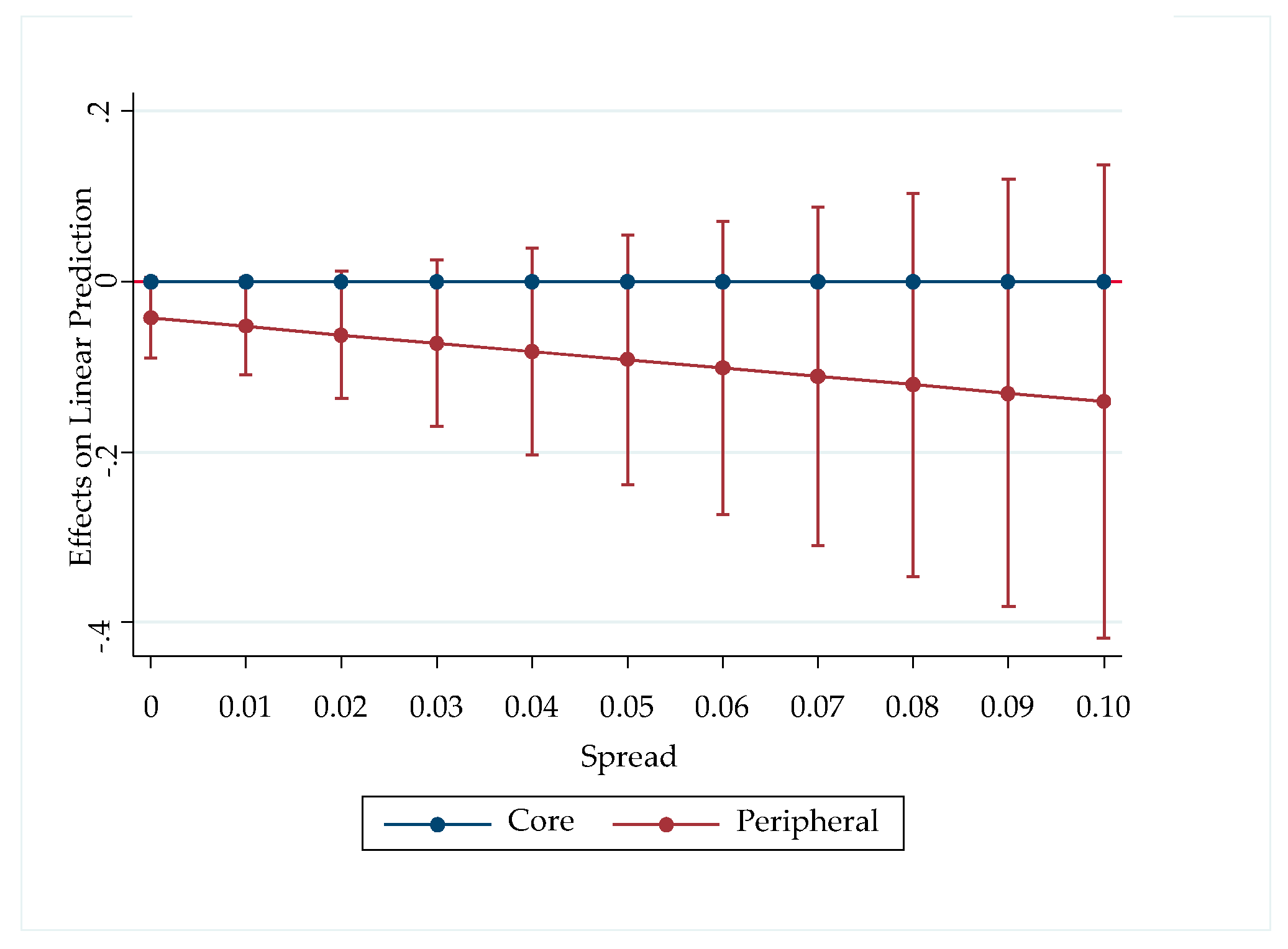
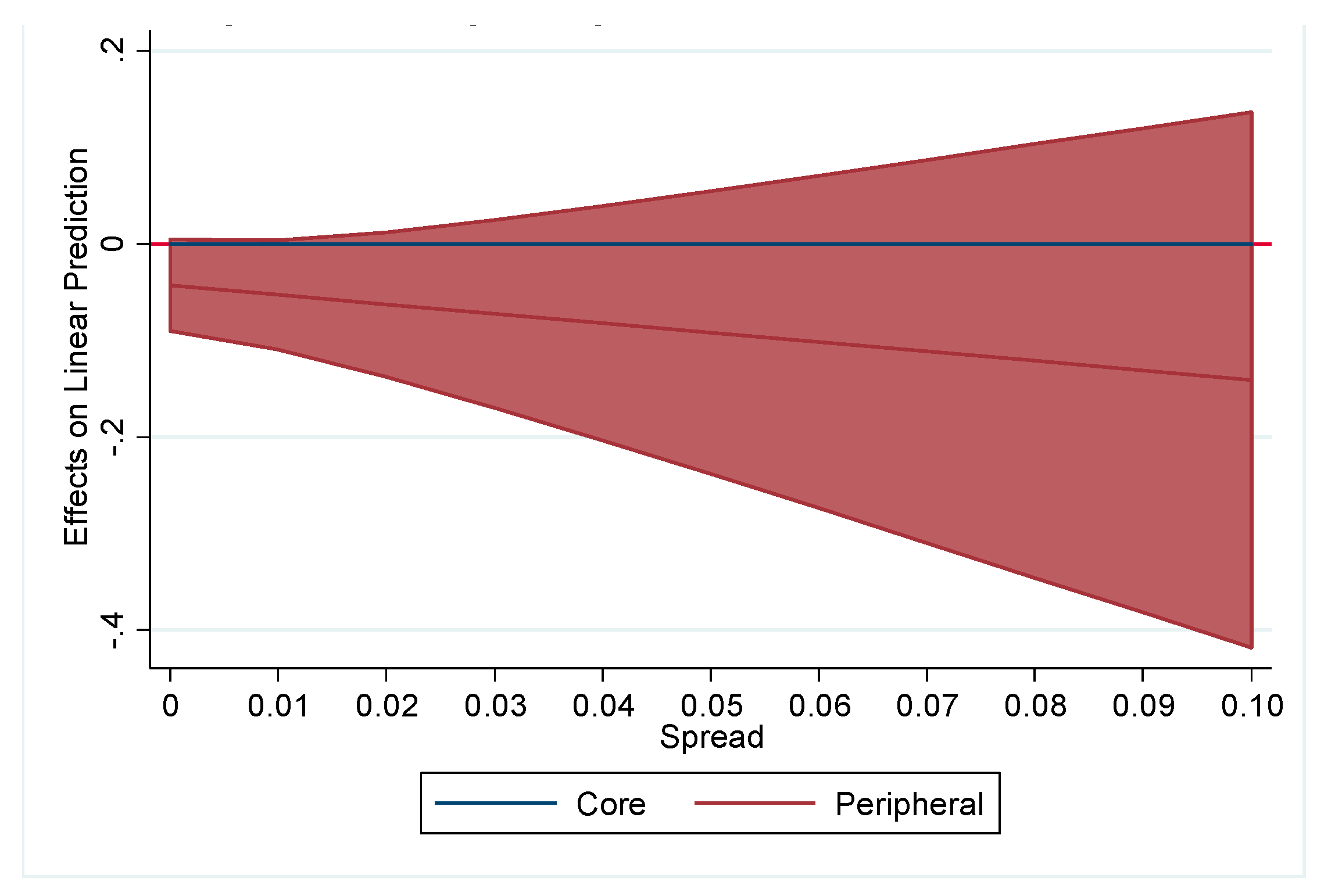
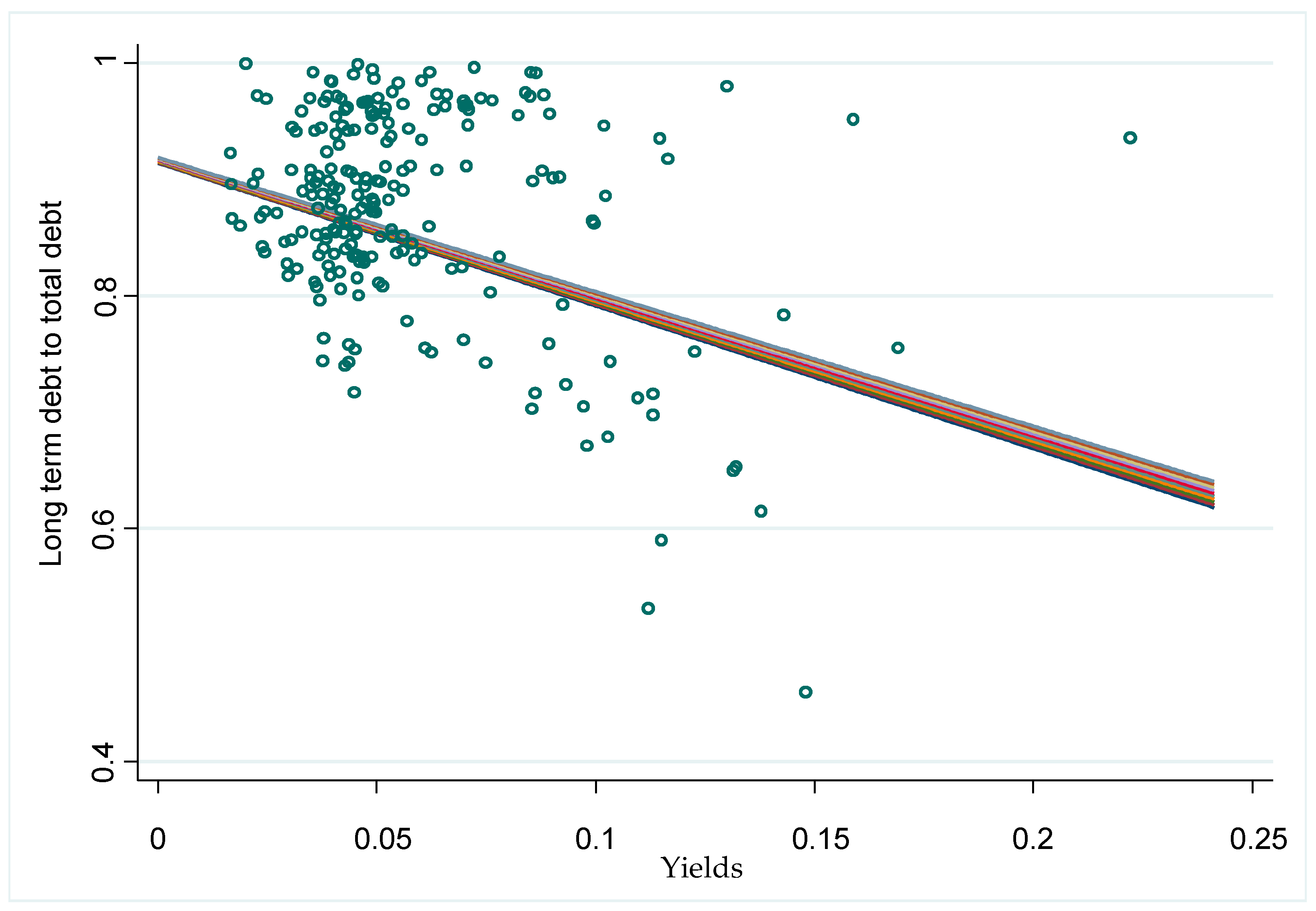
| Hypotheses | Effect of Sovereign Risk on the Maturity Structure of Sovereign Debt | |
|---|---|---|
| If Risk Increases | If Risk Decreases | |
| H1: A variation in sovereign bond yields or in sovereign risk modifies the maturity structure of sovereign debt. | The maturity structure of sovereign debt is shortened | The maturity structure of sovereign debt is lengthened |
| H2: The relationship between, sovereign bond yields, sovereign risk and the maturity structure differs depending on the country risk level. | The maturity structure is shortened (peripheral countries) | The maturity structure is lengthened (peripheral countries) |
| The maturity structure is lengthened (core countries) | The maturity structure is shortened (core countries) | |
| H3: The indebtedness level of the countries influences the relationship between debt maturity and sovereign bond yields and sovereign risk. | The maturity structure is shortened (highly indebted countries) | The maturity structure is lengthened (highly indebted countries) |
| No relationship (less indebted countries) | No relationship (less indebted countries) | |
| Variables | Long-Term Debt to Total Debt Ratio | |
|---|---|---|
| Maturity | Average maturity | + |
| Control Variables | Inflation | + |
| GDP | – | |
| Debt/GDP | – | |
| Borrowing requirements | – | |
| Long-term sovereign bond returns | Yields | – |
| Sovereign risk proxies | Spread | – |
| Spread USA | – | |
| Ratings | – |
| Dependent Variable: Long-Term Debt to Total Debt Ratio | OLS Estimation | Fixed Effects Estimation | ||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | |
| Average maturity | 0.0207 *** | 0.0248 *** | 0.0231 *** | 0.0224 * | 0.0222 * | 0.0229 ** |
| (0.00297) | (0.00309) | (0.00300) | (0.0100) | (0.0101) | (0.00995) | |
| GDP (in logs) | −0.0301 *** | −0.0357 *** | −0.0245 *** | −0.0736 | −0.0342 | −0.0421 |
| (0.0109) | (0.00971) | (0.00901) | (0.0496) | (0.0457) | (0.0452) | |
| Debt/GDP | 0.00673 | 0.0210 | 0.0129 | 0.0157 | 0.0386 | 0.0312 |
| (0.0247) | (0.0243) | (0.0243) | (0.0654) | (0.0726) | (0.0717) | |
| Inflation | 0.00156 | 0.00317 | 0.00286 | 0.00418 | 0.00343 | 0.00432 |
| (0.00334) | (0.00338) | (0.00337) | (0.00486) | (0.00538) | (0.00518) | |
| Borrowing requirements | −0.00364 *** | −0.00295 ** | −0.00249 ** | −0.00305 * | −0.00319 * | −0.00262 * |
| (0.00115) | (0.00124) | (0.00126) | (0.00146) | (0.00146) | (0.00136) | |
| Yields | −0.296 * | −0.599 * | ||||
| (0.171) | (0.266) | |||||
| Spread | −0.574 ** | −0.552 * | ||||
| (0.232) | (0.292) | |||||
| Spread USA | −0.603 *** | −0.660 ** | ||||
| (0.220) | (0.249) | |||||
| Constant | 1.173 *** | 1.181 *** | 1.062 *** | 1.725 ** | 1.162 * | 1.271 ** |
| (0.143) | (0.122) | (0.116) | (0.613) | (0.555) | (0.555) | |
| Country fixed effect | No | No | No | Yes | Yes | Yes |
| Observations | 196 | 181 | 196 | 196 | 181 | 196 |
| R-squared | 0.263 | 0.274 | 0.276 | 0.283 | 0.277 | 0.286 |
| Dependent Variable: Long-Term Debt to Total Debt Ratio | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
|---|---|---|---|---|---|---|
| Average maturity | 0.0239 ** | 0.0250 ** | 0.0237 * | 0.0228 * | 0.0239 ** | 0.0242 ** |
| (0.0106) | (0.00994) | (0.0108) | (0.0104) | (0.0106) | (0.0100) | |
| GDP (in logs) | 0.0620 | 0.0438 | 0.0381 | 0.000112 | 0.0620 | 0.0358 |
| (0.146) | (0.133) | (0.167) | (0.143) | (0.146) | (0.134) | |
| Debt/GDP | 0.0658 | 0.0599 | 0.0679 | 0.0496 | 0.0658 | 0.0583 |
| (0.0955) | (0.102) | (0.0936) | (0.0990) | (0.0955) | (0.101) | |
| Inflation | 0.00712 | 0.00475 | 0.00762 | 0.00326 | 0.00712 | 0.00418 |
| (0.00472) | (0.00482) | (0.00508) | (0.00511) | (0.00472) | (0.00506) | |
| Borrowing requirements | −0.000913 | −0.00252 | −0.000871 | −0.00314 * | −0.000913 | −0.00250 |
| (0.00205) | (0.00146) | (0.00207) | (0.00152) | (0.00205) | (0.00139) | |
| Yields | −0.696 ** | −0.735 ** | ||||
| (0.306) | (0.255) | |||||
| Spread | −0.713 ** | −0.550 * | ||||
| (0.305) | (0.292) | |||||
| Spread USA | −0.696 ** | −0.666 ** | ||||
| (0.306) | (0.253) | |||||
| Constant | −0.0262 | 0.230 | 0.210 | 0.730 | −0.0858 | 0.276 |
| (1.850) | (1.710) | (2.090) | (1.820) | (1.853) | (1.722) | |
| Time fixed effects | Yes | No | Yes | No | Yes | No |
| Trend | No | Yes | No | Yes | No | Yes |
| Observations | 196 | 196 | 181 | 181 | 196 | 196 |
| R-squared | 0.429 | 0.305 | 0.278 | 0.283 | 0.429 | 0.295 |
| Dependent Variable: Long-term Debt to Total Debt Ratio | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Average maturity | 0.00313 | 0.00274 | 0.00313 |
| (0.00299) | (0.00281) | (0.00299) | |
| GDP (in logs) | 0.121 | 0.105 | 0.121 |
| (0.0844) | (0.111) | (0.0844) | |
| Debt/GDP | 0.0363 | 0.0391 | 0.0363 |
| (0.0564) | (0.0541) | (0.0564) | |
| Inflation | 0.0118 ** | 0.0121 ** | 0.0118 ** |
| (0.00407) | (0.00443) | (0.00407) | |
| Borrowing requirements | −0.000651 | −0.000574 | −0.000651 |
| (0.00171) | (0.00174) | (0.00171) | |
| Yields | 0.172 | ||
| (0.330) | |||
| Spread | 0.142 | ||
| (0.340) | |||
| Spread USA | 0.172 | ||
| (0.330) | |||
| VIX | −0.00196 | −0.00203 | −0.00195 |
| (0.00118) | (0.00129) | (0.00117) | |
| LTROs (in logs) | −0.0275 ** | −0.0264 ** | −0.0275 ** |
| (0.00938) | (0.0105) | (0.00943) | |
| Constant | −0.208 | 0.00442 | −0.194 |
| (1.065) | (1.327) | (1.071) | |
| Time fixed effects | Yes | Yes | Yes |
| Observations | 144 | 132 | 144 |
| R-squared | 0.439 | 0.423 | 0.440 |
| Group of Countries | Mean | Median |
|---|---|---|
| Peripheral countries | 0.029 | 0.010 |
| Core countries | 0.004 | 0.002 |
| Wilcoxon rank-sum test | 0.000 *** | |
| K-sample equality-of-medians test | 0.000 *** |
| Dependent Variable: Long-term Debt to Total Debt Ratio | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Average maturity | 0.0296 *** | 0.0358 *** | 0.0330 *** |
| (0.00548) | (0.00592) | (0.00501) | |
| GDP (in logs) | −0.0111 | −0.0297 *** | −0.0160 |
| (0.0131) | (0.00920) | (0.0132) | |
| Debt/GDP | −0.0176 | −0.0105 | −0.0208 |
| (0.0503) | (0.0461) | (0.0489) | |
| Inflation | 0.0154 | 0.0126 | 0.00887 |
| (0.0132) | (0.0121) | (0.0127) | |
| Borrowing requirements | 0.00109 | 0.000554 | 0.00125 |
| (0.00216) | (0.00204) | (0.00228) | |
| Yields | 1.456 *** | ||
| (0.492) | |||
| Spread | 0.320 | ||
| (1.556) | |||
| Spread USA | 0.133 | ||
| (1.384) | |||
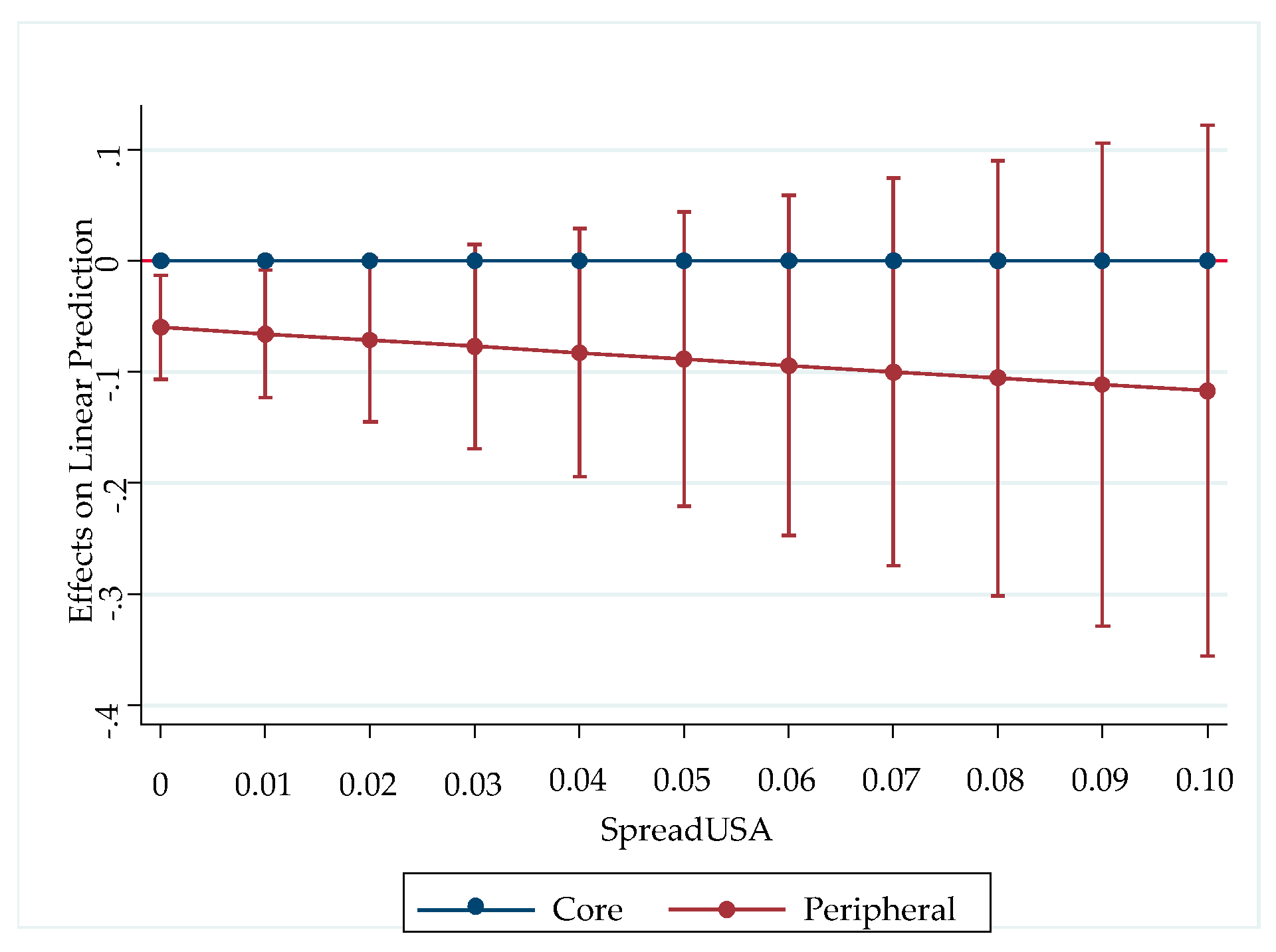
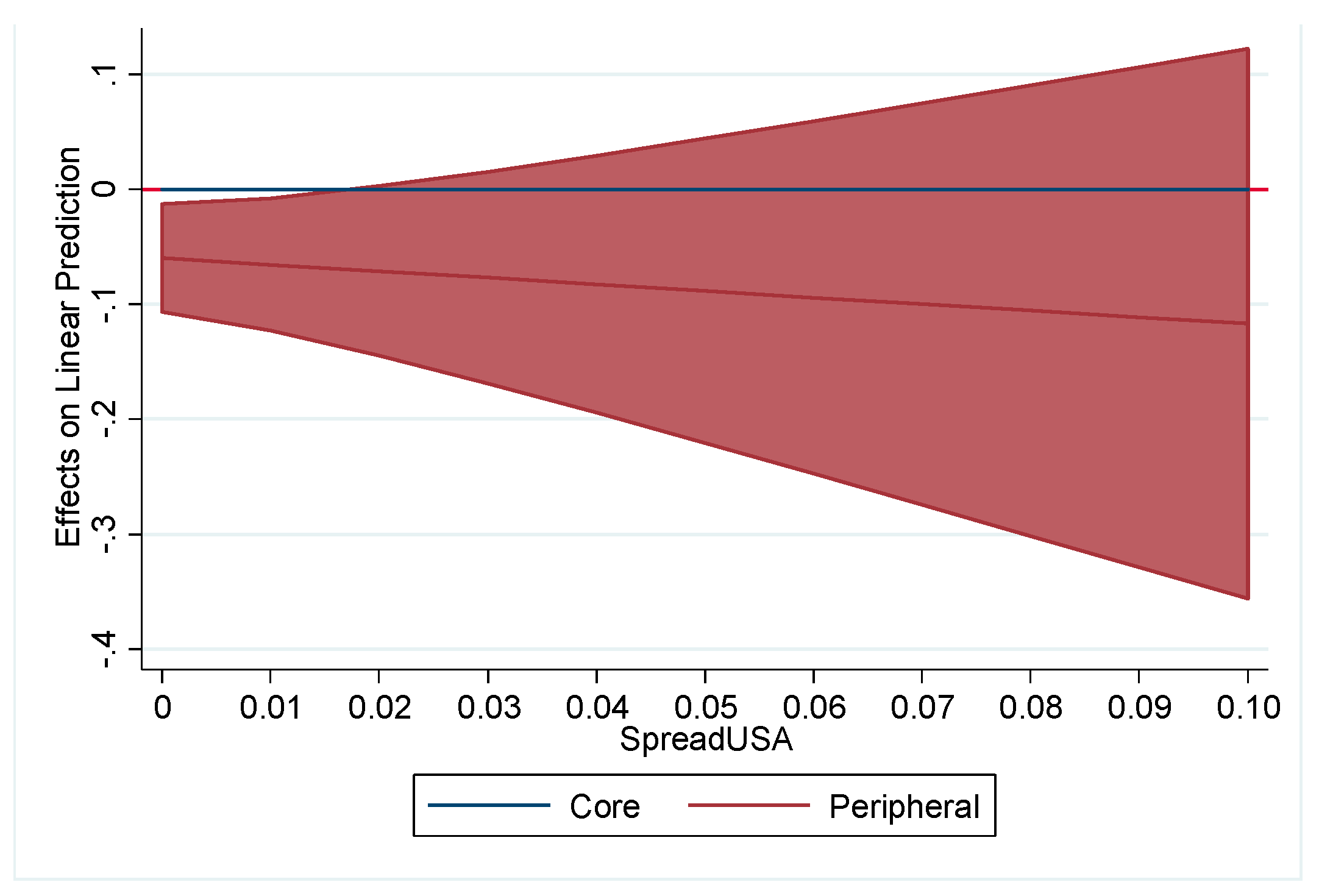
| Peripheral | 0.0229 | −0.0429 * | −0.0597 ** |
| (0.0221) | (0.0243) | (0.0240) | |
| PeripheralxYields | −1.918 *** | ||
| (0.546) | |||
| PeripheralxSpread | −0.976 | ||
| (1.374) | |||
| PeripheralxSpreadUSA | −0.571 | ||
| (1.126) | |||
| Constant | 0.683 *** | 1.010 *** | 0.879 *** |
| (0.197) | (0.138) | (0.156) | |
| Time fixed effects | Yes | Yes | Yes |
| Observations | 196 | 181 | 196 |
| R-squared | 0.484 | 0.389 | 0.377 |
| Dependent Variable: Long-term Debt to Total Debt Ratio | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Average maturity | 0.0237 * | 0.0258 * | 0.0252 ** |
| (0.0105) | (0.0114) | (0.0109) | |
| GDP (in logs) | 0.0851 | 0.0400 | 0.0672 |
| (0.151) | (0.174) | (0.150) | |
| Inflation | 0.00583 | 0.00518 | 0.00499 |
| (0.00427) | (0.00503) | (0.00477) | |
| Borrowing requirements | −0.00123 | −0.00180 | −0.00173 |
| (0.00183) | (0.00180) | (0.00175) | |
| Yields | 1.191 | ||
| (0.878) | |||
| Spread | 1.425 | ||
| (1.412) | |||
| Spread USA | −1.206 | ||
| (0.793) | |||
| Debt/GDP | 0.180 ** | 0.0995 | 0.0900 |
| (0.0773) | (0.0895) | (0.0908) | |
| Debt/GDPxYields | −1.436 ** | ||
| (0.547) | |||
| Debt/GDPxSpread | −1.464 | ||
| (0.891) | |||
| Debt/GDPxSpreadUSA | −1.206 | ||
| (0.793) | |||
| Constant | −0.506 | 0.128 | −0.197 |
| (1.916) | (2.175) | (1.907) | |
| Time fixed effects | Yes | Yes | Yes |
| Observations | 196 | 181 | 196 |
| R-squared | 0.482 | 0.456 | 0.451 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Fernández, M.; González-Velasco, C. Bond Yields, Sovereign Risk and Maturity Structure. Risks 2018, 6, 109. https://doi.org/10.3390/risks6040109
González-Fernández M, González-Velasco C. Bond Yields, Sovereign Risk and Maturity Structure. Risks. 2018; 6(4):109. https://doi.org/10.3390/risks6040109
Chicago/Turabian StyleGonzález-Fernández, Marcos, and Carmen González-Velasco. 2018. "Bond Yields, Sovereign Risk and Maturity Structure" Risks 6, no. 4: 109. https://doi.org/10.3390/risks6040109
APA StyleGonzález-Fernández, M., & González-Velasco, C. (2018). Bond Yields, Sovereign Risk and Maturity Structure. Risks, 6(4), 109. https://doi.org/10.3390/risks6040109





