1. Introduction
In risk analysis and actuarial science, measuring risks and their contribution is of both theoretical and practical interest. In the literature, there exists a large amount of research on risk measures for the univariate risk. For a random risk
X, at level
the popular
value-at-risk (VaR)
and
expected shortfall (ES)
See (
Denuit et al. 2005;
Jorion 2007) for comprehensive overviews on risk measures of univariate risks. However, in actuarial risk analysis, the interaction among risks within a portfolio has been found to play an important role in determining the measure of risk and thus should not be ignored. After the recent financial crisis, the regulatory and scientific discussion on interaction among risks have been significantly intensified. The interaction among risks of institutions in a market or components in a portfolio is closely related to the systemic risk, which usually occurs when a component in a portfolio or even the whole portfolio suffers from the loss of some other component in the same portfolio. Typically, there are two types of measures for the degree of interaction among risks–co-risk measures and risk contribution measures. For example, the
conditional value-at-risk (CoVaR) due to (
Adrian and Brunnermeier 2016) and the
conditional expected shortfall (CoES) due to (
Mainik and Schaanning 2014) are two typical co-risk measures. Specifically, both CoVaR and CoES of a random risk of a component employ its conditional distribution given that another component (or even the whole portfolio) is under stress. For more on different co-risk measures, one may refer to (
Kylman 2011;
Huang et al. 2012) and references therein. On the other hand, the risk contribution measure intends to quantify the effect of a stressful situation for one component on the risk of another component through comparing a co-risk measure and its univariate version. For example, the difference between CoVaR of a component and the VaR of the same component. For more examples of risk contribution measures, we refer readers to (
Girardi and Ergün 2013;
Mainik and Schaanning 2014;
Adrian and Brunnermeier 2016) and reference therein. Also, see (
Bisias et al. 2012) for a recent extensive overview on different systemic risk measures.
Paired risks are not uncommon in actuarial science and insurance practice. For example, in life insurance, when modelling probability behaviour of the insured’s mortality, it is important to divide the insureds according to their marriage status. It has been confirmed that there exists dependence between lifetimes of a couple. For more discussions on the dependence of couple’s mortalities, one may refer to (
Denuit et al. 2001;
Jagger and Sutton 1991;
Jevtić and Hurd 2017). When measuring the contribution of a component to systemic risk, usually the risk of this institution and the risk of another institution or even the whole system will be jointly considered as paired risks. See for example, (
Acharya et al. 2017;
Karimalis and Nomikos 2018) and references therein.
The existing studies on co-risk measure and risk contribution measure mainly investigate how the change of marginal distributions and dependence structure affects the paired risks. For instance, (
Mainik and Schaanning 2014) studied the dependence consistency of CoVaR and some other systemic risks measures, and they found that given the marginal distribution unchanged, a more concordant dependence structure results in a larger CoVaR. Recently, (
Sordo et al. 2018) extended this finding to CoES,
CoVaR and
CoES under positive dependence structure through showing that a more concordant dependence structure tends to incur a larger CoES,
CoVaR and
CoES, respectively, whenever the marginal distribution possesses some specific stochastic orderings. Most research along this line investigates how the degree of dependence impacts on the risk level of a given component in a risk pair. However, risk interaction is two-way. The stressful event of one risk in a pair has its own effect on the other risk, and vice versa. To obtain a whole picture on the risk level of paired risks, it is reasonable to consider the co-risk measures or risk contribution measures of either components simultaneously. Furthermore, it has been shown that different components in the same financial system usually possess different degrees of systemic importance and hence different risk levels. In (
Zhou 2010) several measures of risk interaction were estimated from market data to check whether a bank of larger size has a smaller risk, and it was found that a big bank did not necessarily take a smaller risk of bankruptcy and different banks did have different risk levels. This reveals that paired risks with different marginal may have different level of risk interaction, and thus several interesting questions concerned with risk interaction levels of paired risks arise naturally: for financial institutions in a portfolio or financial system, whether does the stressful situation of one component affect the risk of another component more heavily than the stressful situation of the latter affects the risk of the former one? Also, how do the risk distribution and dependence structure play a role in the interaction between two risks?
This paper aims to investigate how the marginal distributions and the symmetry of dependence structure of two paired risks impact on their co-risk measures and risk contribution measures. For example, the popular CoVaR, CoES, and CoVaR, CoES. In this study we employ the copula functional to formulate the dependence structure between the paired risks. For the symmetric copula, the stochastically higher marginal risk is found to have a larger CoVaR, and for asymmetric copula with more probability mass on the region above (beneath) the diagonal line, a stochastically larger marginal risk is proved to attain a higher CoVaR at the stress level above (below) a threshold. Concerning the CoES, and , the larger marginal risk in the sense of increasing convex order, dispersive order and excess wealth order is shown to have a larger CoES, and respectively in the context of a positively dependent and symmetric copula. As for the asymmetric copula, similar comparing results are developed at the stress level above a threshold, which is determined by the stress level of the conditioned risk and the copula.
The rest of the present paper is organised as follows:
Section 2 recalls several related notions and technical results concerned with detailed discussions in the sequel.
Section 3 presents the comparison results on CoVaR and CoES, and the comparison results on
and
are developed in
Section 4. Finally, in
Section 5 several numerical examples based on Monte Carlo simulation are employed to illustrate the main findings.
2. Some Preliminaries
For ease of reference, let us present several related concepts and technical results to be used during the discussion in the coming sections.
Stochastic orders
Denote , and , probability distribution functions and quantile functions of random variables X and Y, respectively.
Definition 1. A random variable X is said to be smaller than another one Y in the
usual stochastic order, denoted as , if for all ;
increasing convex order, denoted as , if for any increasing convex function φ, provided the expectations exit;
dispersive order, denoted as , if for all such that ;
excess wealth order, denoted as , if for all .
Lemma 1. For two random variables X and Y, if and only iffor any increasing convex function . Co-risk measures
The systemic risk measure is usually utilized to quantify a financial institution’s contribution to the risk of other financial institutions or even the entire financial system. Typically, the co-risk measures can be viewed as the traditional risk measures conditioning on a certain risky scenario affecting another institution.
Definition 2. For two random variables X and Y, and ,
the CoVaR of Y at stress level β given that X is under stress at level α is the CoES of Y at stress level β given that X is under stress at level α is
Risk contribution measures
Apart from the co-risk measures, risk contribution measures are also introduced to quantify the systemic risk in risk management. Unlike co-risk measures, this class of measures captures the marginal effect of an institution to the risk of another institution or the overall financial system.
Definition 3. For two random variables X and Y, and ,
the ΔCoVaR of Y at stress level β given that X is under stress at level α is the ΔCoES of Y at stress level β given that X is under stress at level α is
Statistical dependence
It is well-known that statistical dependence is crucial in studying joint probability behavior of multiple risks and hence of the portfolio aggregation. Ever since the novel work of (
Sklar 1959), the copula function has become the most popular tool in modelling the statistical dependence among concerned random variables due to mathematical and statistical tractability.
Definition 4. For a random vector with joint distribution function F, and univariate marginal distribution functions , if there exists some such thatthen is called the copula
of . Definition 5. A random variable X is said to be stochastically increasing in Y, denoted as , ifand a random vector is said to be positive dependent through the stochastic order (PDS) if both and . According to (
Cai and Wei 2012), a random vector
is PDS if and only if its copula is PDS. This characterization will be utilized to derive some results in the sequel. Note that for any absolutely continuous copula
C, the PDS property is equivalent to
For more on copula theory one may refer to the monograph (
Nelsen 1999). Also we recall one more technical lemma due to Theorem 3.1(b) in (
Mainik and Schaanning 2014), serving as an implicit expression of the conditional value-at-risk in terms of copula.
Lemma 2. For a vector having distribution function , the copula of , if is continuous, thenfor any . In order to compare the degree of risk interaction of paired risks, we consider measures CoVaR, CoES,
CoVaR and
CoES. Given
, for any
, denote
and
the solutions of equations
respectively. If
, then
U,
V are both uniformly distributed, and then,
and
are the
th quantiles of the conditional random variables
and
, respectively.
Arrangement monotonicity
A real function
is said to be
arrangement increasing (AI) if
The function
g is said to be
arrangement decreasing (AD) when the inequality (
1) is reversed.
Arrangement monotone functions are useful in risk management and operations research. For more on AI functions and various stochastic versions of AI, one may refer to (
Boland and Proschan 1988;
Li and Li 2018). In this study we will employ AI and AD copulas as two typical alternatives for the symmetric copula. Note that an AI (AD) copula is of more (less) dependence above the diagonal line on the plane.
3. Co-Risk Measures
Let us first investigate how the magnitude of marginal risks affects the corresponding CoVaR. In specific, we propose several sufficient conditions for
Theorem 1. For a random vector with copula ,
if is symmetric, then is equivalent to (2) for , if is AI, then implies (2) for such that , and if is AD, then implies (2) for such that .
Proof. Case 1: Let
. Note that
is equivalent to
Due to the symmetry of
C,
gets the copula
for
. According to Lemma 2, we have, for
,
and
where
Owing to (
3),
is equivalent to
Case 2: By Lemma 2 again we have
In light of (
3), it suffices for us to verify that
for
.
Note that, for any
,
The AI property of
C implies
for
, and hence it holds that
for
such that
. This, in combination with the nondecreasing property of the distribution function, yields
. Similarly, for
such that
, it holds that
and hence we have
. Since
and
are equivalent to
and
respectively, it holds that
if and only if
. Therefore, we conclude that
for
such that
.
Case 3 can be verified in a similar manner to Case 2. □
According to Theorem 1, when paired risks have exchangeable copula, namely, the interaction between them is symmetric, the only factor determining the level of co-risk measure is the marginal distribution. When the interaction between risks is asymmetric, namely one risk may have more impact on the other one, both the marginal distribution and the dependence structure play a role in determining the level of co-risk measure. Also, under either one of the two scenarios a stochastically larger marginal risk intends to incur a larger co-risk.
As per Theorem 1, if one of the concerned paired risks is stochastically larger and the underlying copula of the two risks is AI, then its CoVaR conditioning on the other one may serve as a consistent upper bound on the systemic risk of this pair, especially in the situation that both risks are under high stress levels.
As a continued discussion on the effect of marginal distribution and dependence structure on the CoVaR, in what follows we have a parallel discussion on the CoES, which is actually the average of CoVaR on stress levels above a threshold. To be specific, we propose some conditions sufficient to
for some typical
.
Theorem 2. For a random vector with a PDS copula ,
if is symmetric, then implies (4) for all , and if is AI, then implies (4) for such that .
Proof. According to the proof of Theorem 12 in (
Sordo et al. 2018),
where
is a convex function and the indicator function
equals 1 if
A is true and 0 if not. Similarly,
Case 1: Due to the symmetric
, it holds that
for any
. For a PDS
, the
is shown to be increasing and convex in the proof of Theorem 12 in (
Sordo et al. 2018). Then, by Lemma 1, it follows from
that
Case 2: In a similar manner to the proof of Theorem 1, for
, one can show that
and hence
For any
, one has
and hence
. Using that
, we have, for any
,
On the other hand, similar to the proof of Case 1, we can verify that the PDS
results in the increasing and convex
. Thus,
implies
and then it holds that,
That is,
for
such that
. □
Since CoES measures the averaged CoVaR at stress levels above some threshold, intuitively, a more divergent loss (in the sense of the increasing convex order) should result in a larger CoES when the concerned risk is under a sufficient high level of stress. This intuition is confirmed by the finding of Theorem 2.
It worths remarking that unlike the equivalence in the first assertion of Theorem 1, the sufficient condition of Theorem 2 under the symmetric copula case is not necessary. When the copula is symmetric, the inequality (
4) is equivalent to that
where
defined in (
5) is some specific increasing and convex function. But the equivalence of
provided in Lemma 1 requires that the above inequality holds for any increasing and convex function. Thus, the first assertion in Theorem 2 is not necessary.
4. Risk Contribution Measures
In this section, we switch our focus to the risk contribution measures
CoVaR and
CoES. In parallel to the previous study on co-risk measure, we bring forth several sufficient conditions for the following ordering result.
Theorem 3. For a random vector with a PDS copula , if is
symmetric, then implies (7) for , AI, then implies (7) for such that , and AD, then implies (7) for such that .
Proof. Note that (
7) is equivalent to
where
and
are distorted versions of
X and
Y induced by the concave distortion transforms
respectively. Moreover, it holds that, for
,
Case 1: Note that the exchangeability of
C implies that
. From Lemma 14 in (
Sordo et al. 2018) the desired result follows immediately.
Case 2: Note that
and
can be rephrased as
respectively. By the definitions of
and
, we have
When are such that , it is shown in the proof of Theorem 1 that .
Therefore, we can conclude that
Case 3: can be verified in a similar manner to Case 2. □
The risk contribution measure
quantifies the effect on
Y brought forth by risk
X under stress. As shown in (
Sordo et al. 2018), under a stronger positive dependence structure, a more dispersive risk will result in a larger
CoVaR. Following the same logic, Theorem 3 reveals that for paired risks with symmetric or asymmetric dependence, a more dispersive marginal risk incurs a larger risk contribution measure at a higher or lower stress level, depending on the specific structure of the copula. It should be pointed out that for symmetric copula, (
7) is equivalent to
a special case of the necessary condition for
presented in Lemma 14 of (
Sordo et al. 2018). Thus, the first assertion of Theorem 3 is sufficient but not necessary.
Next result presents sufficient conditions for the inequality
Theorem 4. For a random vector with PDS copula ,
if is symmetric, then implies (8) for , and if is AI, then implies (8) for such that .
Proof. Similar to the proof of Theorem 23 in (
Sordo et al. 2018), we have, for
,
and
where
is given in (
5),
is given in (
6), and
. Note that copula
is PDS and
implies
Case 1: As is shown in the first assertion of Theorem 2, the exchangeability of
C implies that
, and hence the conclusion follows from (
9).
Case 2: As is shown in the proof of the second assertion of Theorem 2, the AI copula
along with
implies that
, and hence it holds that
Thus, we reach the conclusion by combining (
9) and (
10). □
Roughly speaking, the risk contribution measure based on CoES is an average of the risk contribution measure based on CoVaR. Naturally, similar property of
CoVaR may be inherited by the
CoES. Theorem 4 confirms this intuition and provides two scenarios, where a larger risk in the sense of excess wealth order leads to a larger
CoES. Note that for symmetric copula one can check that the inequality in (
8) is actually equivalent to (
9), is a special case of the general condition equivalent to
presented in Theorem 8 (ii) of (
Sordo 2008). Therefore, the first assertion of Theorem 4 is not necessary.
5. Numerical Examples Based on Simulation
To close this study, we carry out Monte Carlo experiments to illustrate the main findings in the previous sections. In general, the joint distribution function of dependent paired risks is complex and the corresponding co-risk measures and risk contribution measures do not have explicit closed form. Lemma 2 facilitates us to obtain a sample of observations of the concerned risks. Moreover, it is well-known that for most regular parametric distributions, the error rate of using the empirical distribution and quantile to approximate the population distribution and quantile is bounded by the reciprocal squared root of the sample size. See for reference, (
Reiss 1974;
Van der Vaart 1998). Thus, we can illustrate the theoretical findings by using the sample version of co-risk and risk contribution measures based on large number of observations of concerned risks.
Throughout all experiments, we start with the Gumbel copula
which is clearly symmetric. As per (5.43) of (
McNeil et al. 2005), the following modification
is asymmetric for
and
. For ease of reference, we call
the
asymmetric Gumbel copula with dependence parameters
.
In all simulation experiments, we set
for the copula
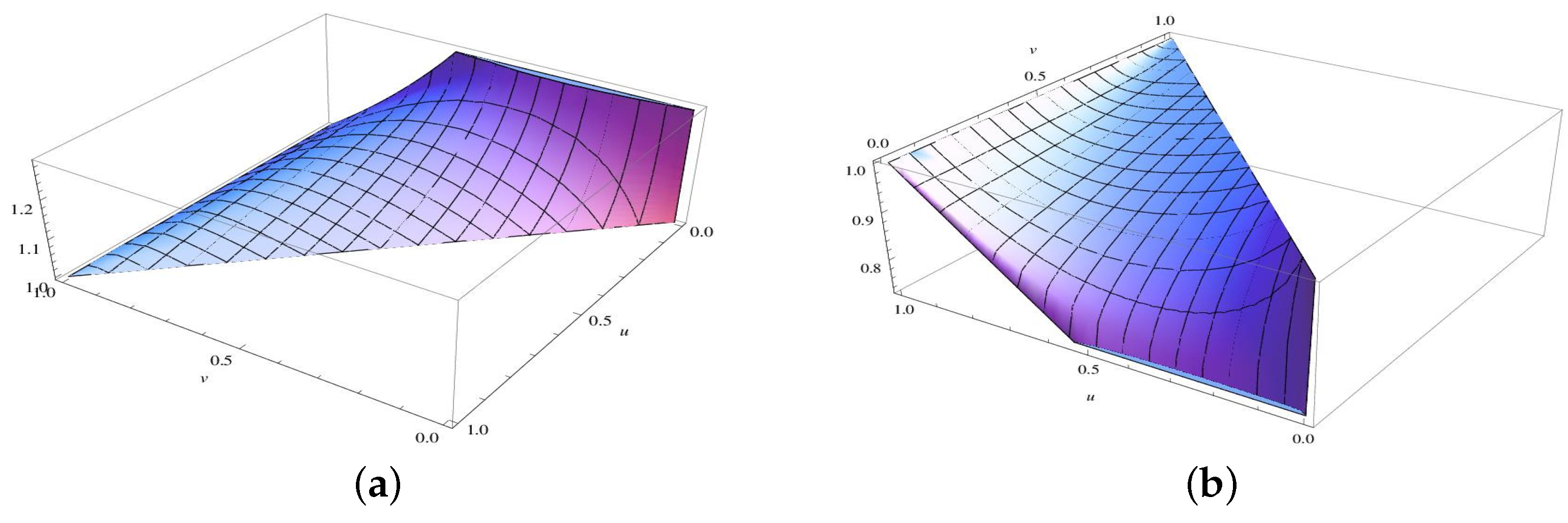
of the concerned paired risks. It is observed that
for
in
Figure 1a and
for
in
Figure 1b. Also, as is seen
Figure 2 both second-order derivatives of
with respect to
u and
v are non-positive, and this verifies that
is PDS.
To produce a sample of the paired risks , we first generate a bivariate sample from the population having the copula of as the joint distribution, and then we calculate the marginal quantiles at this sample to obtain a desired sample of based on Definition 4.
Note that, if we directly simulate samples of paired risks following a given joint distribution and estimate the population CoVaR and other risk measures, there will be few suitable observations when the stress level is close to 1, the extreme level, which is often the concern of risk management. Without enough suitable observations, the estimated values could be very different from their true versions. To circumvent this rareness, we don’t directly draw observations from the joint population distribution of the paired risks. Instead, we first obtain a random sample of one margin U, and then generate a corresponding sample from the population of the conditional random variable , where has joint distribution , the copula of , and is a given stress level of U. The validness of this sample procedure is guaranteed by Lemma 2. Precisely, the simulation is carried out in accordance with the following steps.
For each stress level and , generate a sample of observations of and a sample of observations of , respectively.
For
, based on
’s and
’s calculate respectively the adjusted empirical distribution functions
At each stress level
, for each stress level
, employ the sample
th-quantiles
to estimate the measures
and
, respectively. Also, calculate the sample versions
for
and
, respectively.
As for the risk contribution measures
and
, the following empirical estimators are used.
It should be remarked here that to mitigate the approximation error we simply use the population version for the marginal VaR and ES when deriving these estimators.
In what follows, let us consider four scenarios of having different combinations of marginal distributions.
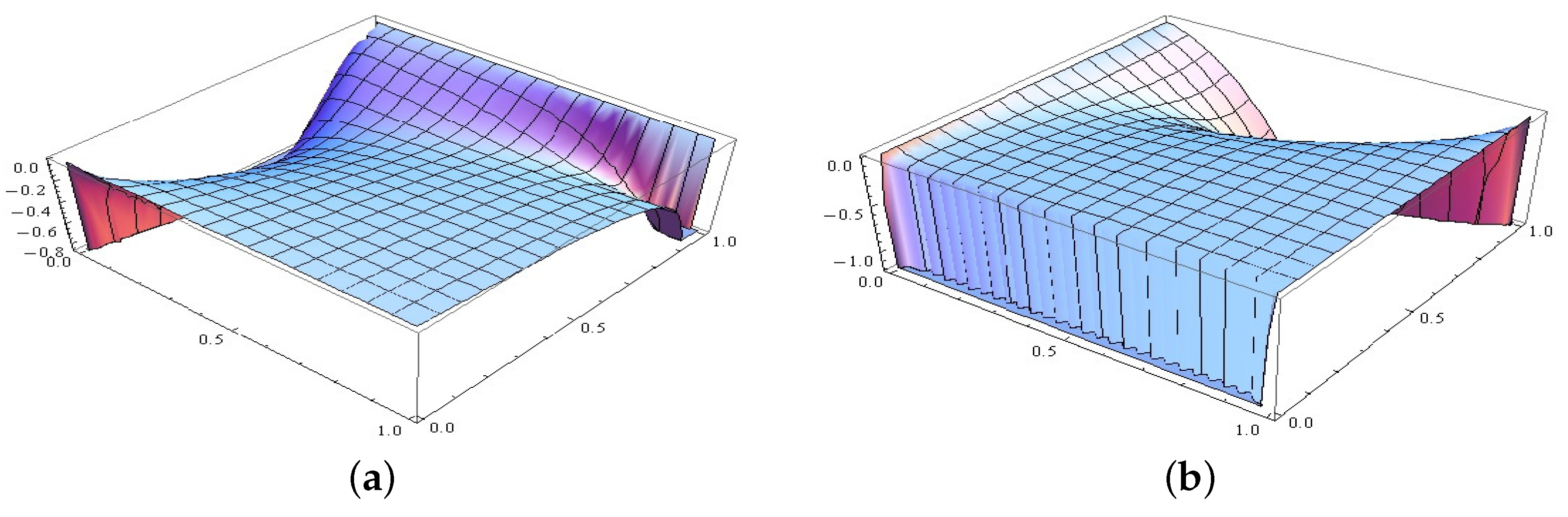
For
and
, exponentially distributions with parameters 2 and 1, respectively, it is plain that
. By the second assertion of Theorem 1, we have
Figure 3a plots
. The difference surface is seen to be always above the horizontal surface on the region
, and this confirms the finding of Theorem 1. On the other hand, although the copula
fails to satisfy condition in the third assertion of Theorem 1, the surface above the horizontal surface on the region
in
Figure 3a hints that the third assertion of Theorem 1 may still be true when the requirement on dependence structure is violated.
For
and
, two normal distributions, according to Table 1.1 of (
Müller and Stoyan 2002),
is valid. By the second assertion of Theorem 2,
for
. This is illustrated by the surface of
Figure 3b. Actually, the corresponding difference is still nonnegative when
.
For
and
, two Weibull distributions, Example 16 of (
Sordo et al. 2018) proves that
.
Figure 3c plots the difference between
and
, and this difference surface confirms the finding of the second assertion of Theorem 3.
For
and
, two Weibull distributions, as per Example 24 of (
Sordo et al. 2018), we have
. Under this setting, the second assertion of Theorem 4 proves that
for
. Also, this fact is justified by the difference surface of
Figure 3d.
The findings in the previous sections assert that the effect of stressful situations of the larger marginal risk (in the sense of some stochastic order) on the other marginal risk is more significant than that of the smaller marginal risk on the larger one when the copula of the risk pair is AI, namely, the dependence structure possesses some asymmetry. However, it is not clear how large such a difference can be. As illustrated in the numerical examples, the difference varies quite differently and may be large at the extreme scenario, where both the stress levels are close to 1. Note that larger value of the risk measures usually indicates higher risk, and a larger difference implies that one of the marginal risk may suffer more from the risky situation of the other one. Hence, in the practice of risk management concerning risk spread inside paired risks, one may treat the paired risks as a whole, and pay attention to one’s failure spreading to the other and vice versa, instead of just concerning one specific risk’s effect.
6. Concluding Remarks
Co-risk measures and risk contribution measures have been introduced to measure the degree of systemic risk ever since the financial crisis. Capturing the dependence of paired risks these measures reflect the interaction between the corresponding marginal risks. The present study contributes to the existing literature on risk interaction by showing that the underlying dependence structure plays a vital role in determining the level of risk interactions of the marginal risks between paired risks. Specifically, the larger marginal risk in the sense of some stochastic orders is found to have a larger CoVaR, CoES, CoVaR and CoES, respectively, at high stress levels (extreme scenarios usually concerned in risk management) in the context of AI copula. Also, the same phenomenon is observed at low stress levels for CoVaR and CoVaR in the setting of AD copula. Therefore, the level of risk interaction of components in a risk pair is usually different as long as the marginal risks are of different distributions or the dependence structure is asymmetric.
This study reiterates the importance of accurately modelling the dependence structure of paired risks in practice. Under certain dependence structure, marginal risks in a pair could posses different levels of risk interaction even when they are homogenous. Furthermore, the effect of the stressful situation of one risk on the other one may be consistently larger than that vice versa at the extreme case. This indicates that in a portfolio the failure of one component may potentially spread faster or impact more heavily on another component than does the failure of other components. Our findings show the existence of a potential difference between interaction levels of marginal risks in a pair; However, several things are to be exploited: What is the exact difference? Are there any bounds on the difference under specific dependence structures or marginal distributions? Answers to these questions can provide more guidance to apply the co-risk measures and risk contribution measures into the practice of risk management. It is of both theoretical and practical interest to pursue these unsolve problems in the future study.