Bayesian Adjustment for Insurance Misrepresentation in Heavy-Tailed Loss Regression
Abstract
:1. Introduction
2. Heavy-Tailed Loss Models under Misrepresentation
2.1. The Misrepresentation Problem
2.2. Weibull Model with Additional Correctly-Measured Risk Factors
2.3. Lognormal Model with Multiple Risk Factors Subject to Misrepresentation
2.4. Pareto Model for Predictive Analytics on Misrepresentation Risk
3. Identifiability
- (i)
- implies ,
- (ii)
- for any , there exists some in the closure of such that for each .
- (i)
- General Weibull,
- (ii)
- Lognormal,
- (iii)
- Two-parameter Pareto.
- (i)
- For our model, the PDF of the general Weibull is given by:with the transform being the MGF of given by:
- (ii)
- The PDF of the lognormal distribution is given by:with the transform being the MGF of given by:
- (iii)
- For the two-parameter Pareto distribution used in our model, the PDF is given by:with the transform being the MGF of given by:
- (i)
- Y follows a distribution from the families of Weibull, lognormal and Pareto,
- (ii)
- corresponding to V (or any element in ) is non-zero,
- (iii)
- or for any .
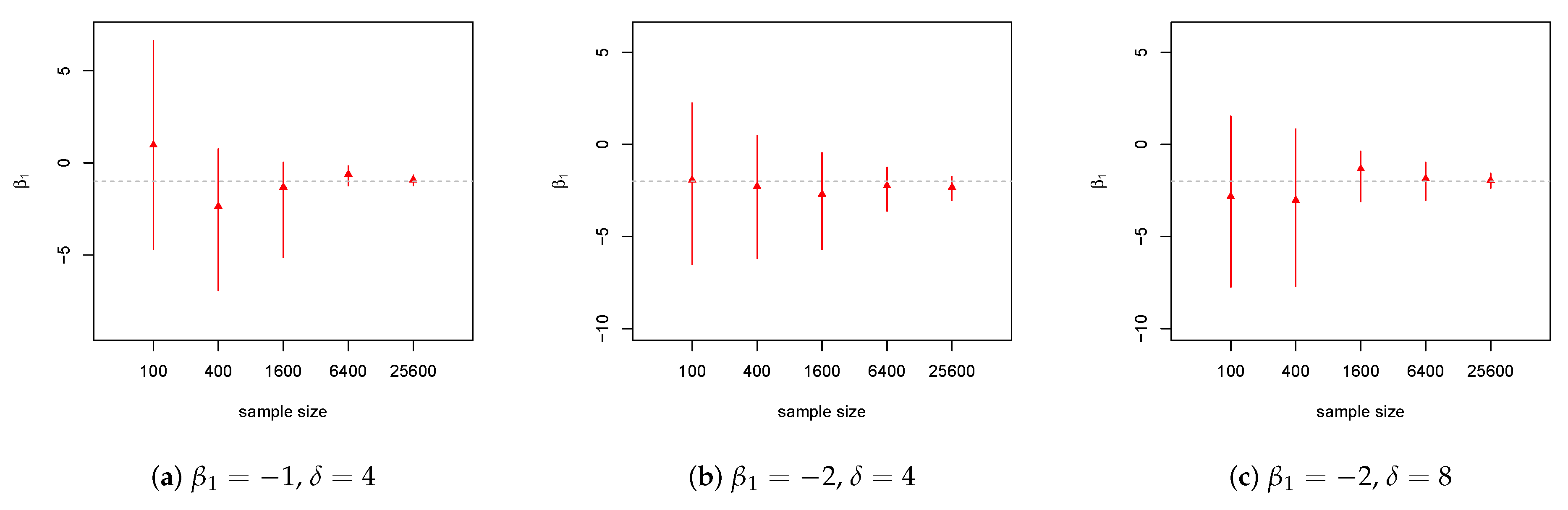
4. Simulation Studies
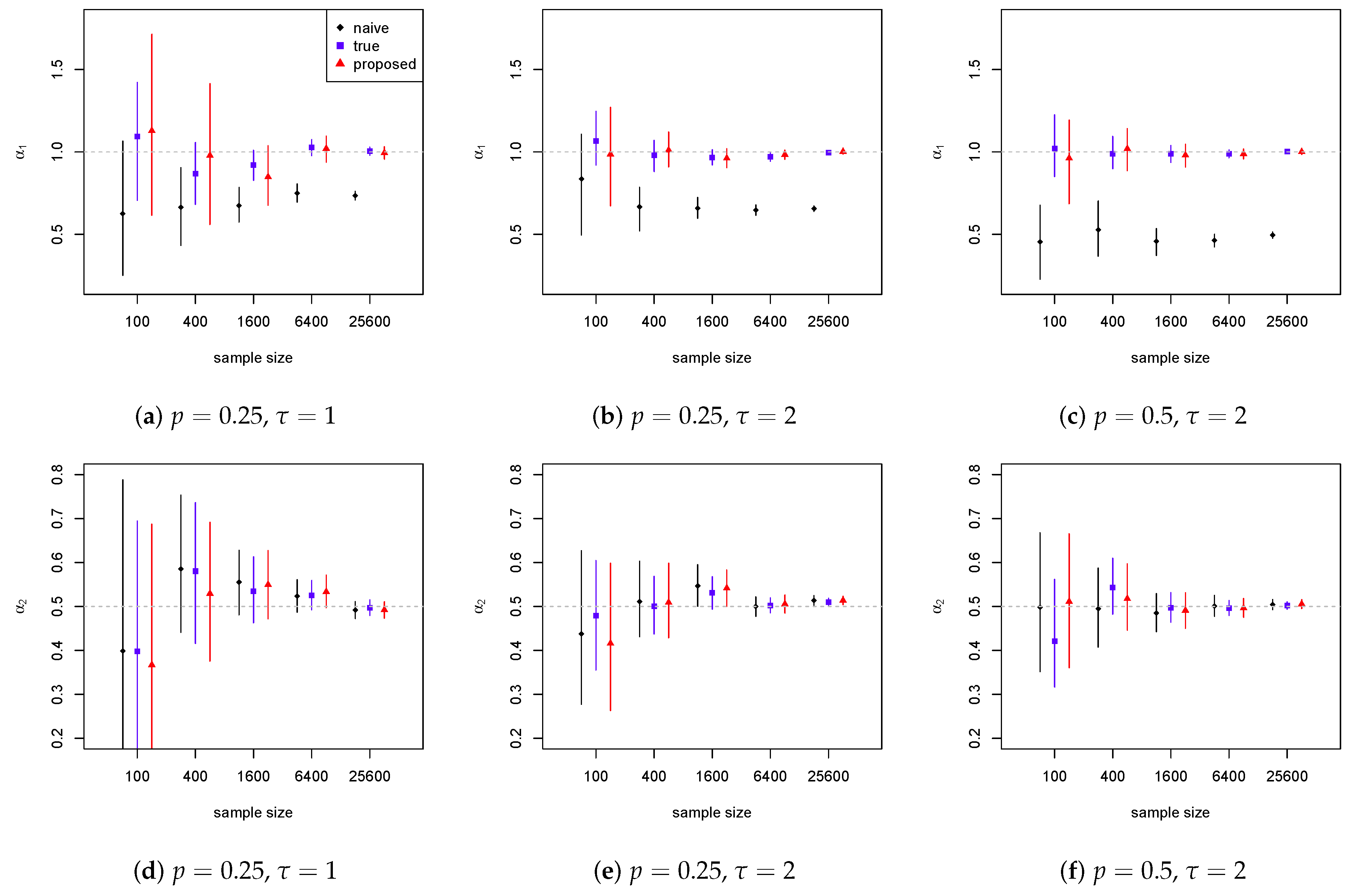
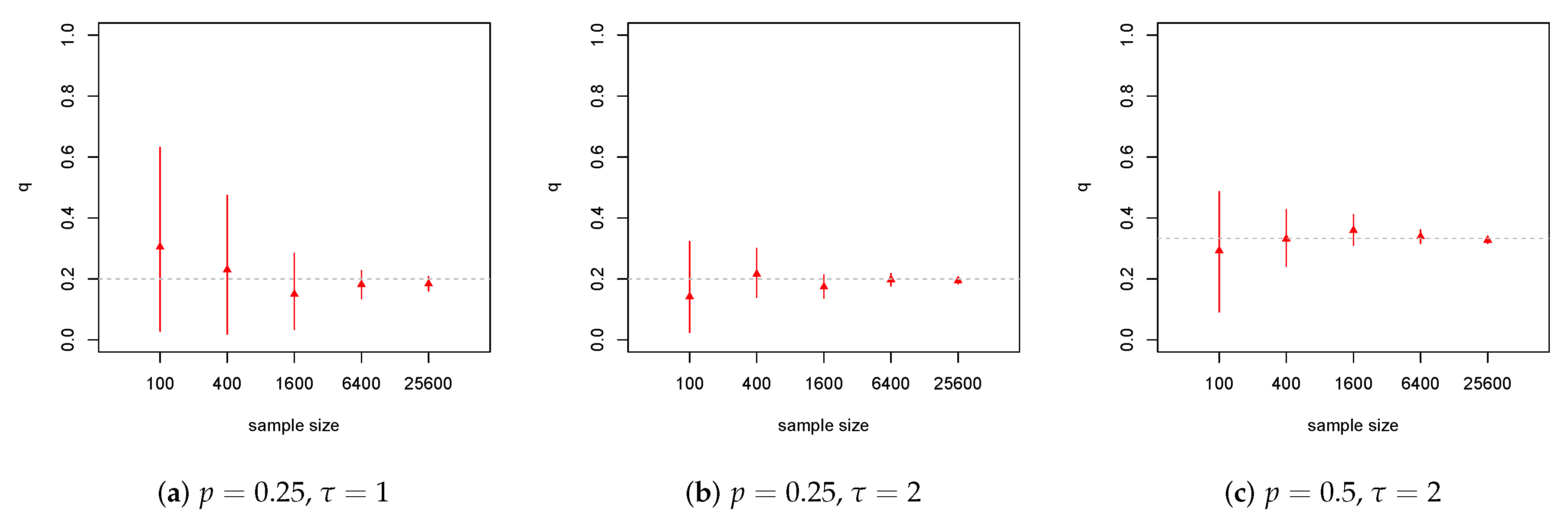
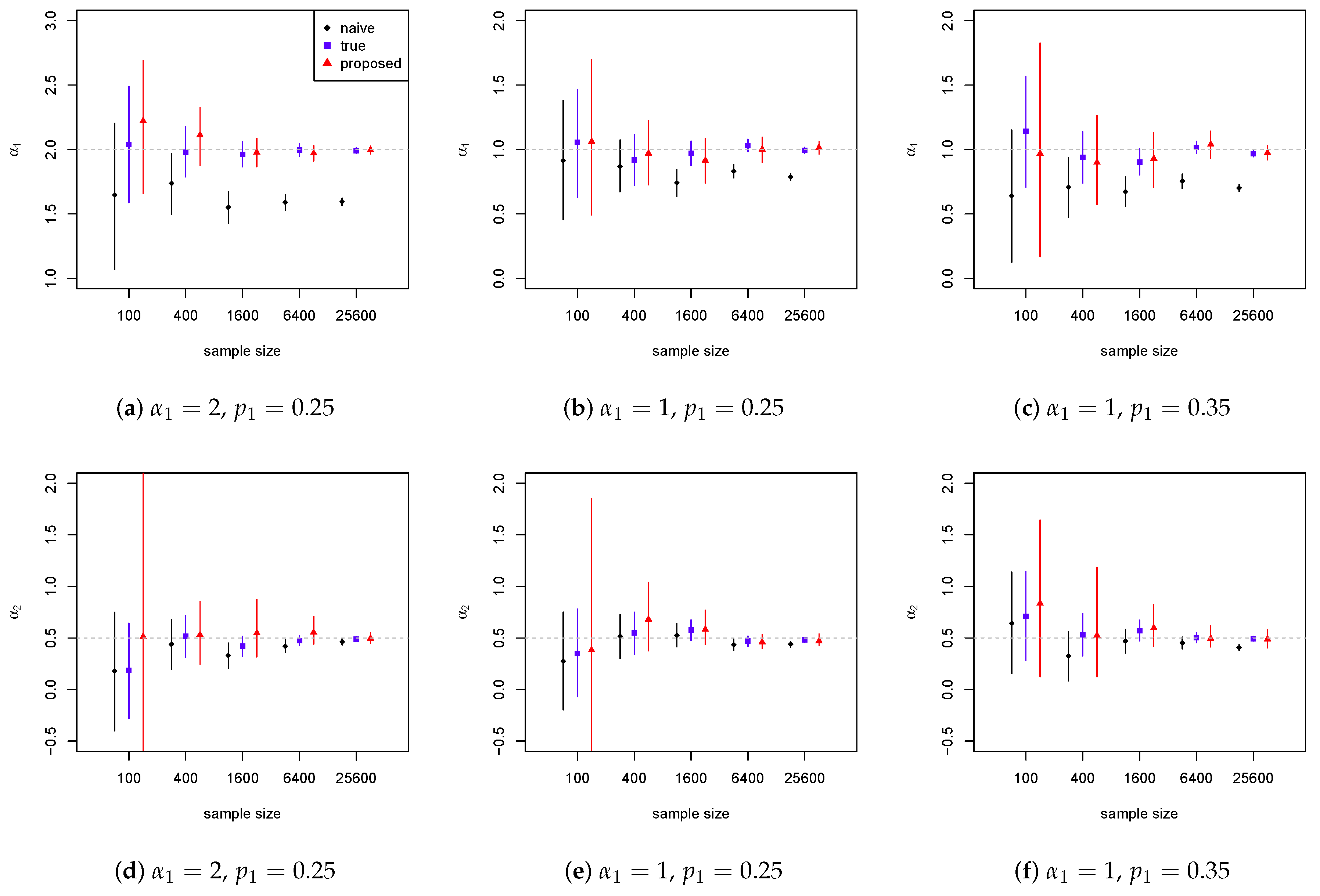
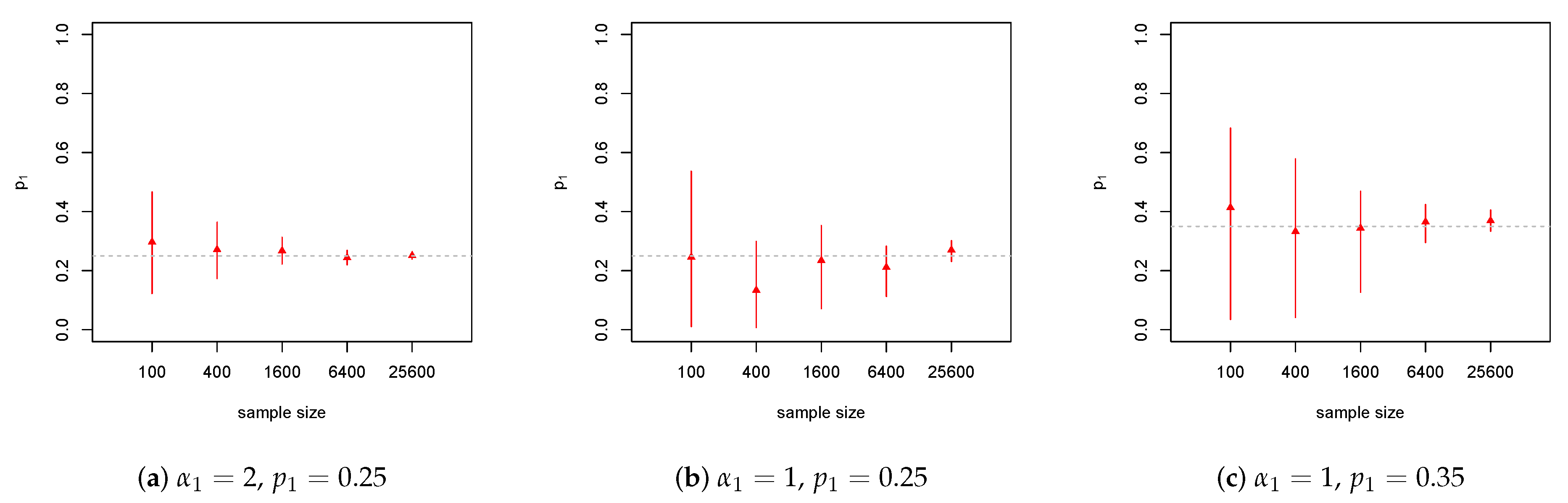
4.1. Weibull Model
4.2. Lognormal Model
4.3. Pareto Model
5. Loss Severity Analysis Using Medical Expenditure Data
6. Conclusions
Acknowledgments
Funding
Conflicts of Interest
Abbreviations
| GLMs | Generalized linear models |
| MLE | Maximum likelihood estimation |
| BUGS | Bayesian inference using Gibbs sampling |
| MCMC | Markov chain Monte Carlo |
| CDFs | Cumulative distribution functions |
| MGF | Moment generating function |
| Probability density function | |
| MEPS | Medical Expenditure Panel Survey |
| DIC | Deviance information criterion |
| PPACA | Patient Protection and Affordable Care Act |
| SD | Standard deviation |
References
- Ahmad, Khalaf E. 1988. Identifiability of finite mixtures using a new transform. Annals of the Institute of Statistical Mathematics 40: 261–5. [Google Scholar] [CrossRef]
- Bermúdez, Lluís, and Dimitris Karlis. 2015. A posteriori ratemaking using bivariate Poisson models. Scandinavian Actuarial Journal 2017: 148–58. [Google Scholar]
- Brockman, M.J., and T.S. Wright. 1992. Statistical motor rating: making effective use of your data. Journal of the Institute of Actuaries 119: 457–543. [Google Scholar] [CrossRef]
- Chandra, Satish. 1977. On the mixtures of probability distributions. Scandinavian Journal of Statistics 4: 105–12. [Google Scholar]
- David, Mihaela. 2015. Auto insurance premium calculation using generalized linear models. Procedia Economics and Finance 20: 147–56. [Google Scholar] [CrossRef]
- Gustafson, Paul. 2014. Bayesian statistical methodology for observational health sciences data. In Statistics in Action: A Canadian Outlook. Edited by Jerald F. Lawless. London: Chapman and Hall/CRC, pp. 163–76. [Google Scholar]
- Haberman, Steven, and Arthur E. Renshaw. 1996. Generalized linear models and actuarial science. The Statistician 45: 407–36. [Google Scholar] [CrossRef]
- Hahn, P. Richard, Jared S. Murray, and Ioanna Manolopoulou. 2016. A Bayesian partial identification approach to inferring the prevalence of accounting misconduct. Journal of the American Statistical Association 111: 14–26. [Google Scholar] [CrossRef]
- Hao, Xuemiao, and Qihe Tang. 2012. Asymptotic ruin probabilities for a bivariate lévy-driven risk model with heavy-tailed claims and risky investments. Journal of Applied Probability 49: 939–53. [Google Scholar] [CrossRef]
- Hua, Lei. 2015. Tail negative dependence and its applications for aggregate loss modeling. Insurance: Mathematics and Economics 61: 135–45. [Google Scholar] [CrossRef]
- Jiang, Wenxin, and Martin A. Tanner. 1999. On the identifiability of mixtures-of-experts. Neural Networks 12: 1253–8. [Google Scholar] [CrossRef]
- Klein, Nadja, Michel Denuit, Stefan Lang, and Thomas Kneib. 2014. Nonlife ratemaking and risk management with bayesian generalized additive models for location, scale, and shape. Insurance: Mathematics and Economics 55: 225–49. [Google Scholar] [CrossRef]
- Peng, Liang, and Yongcheng Qi. 2017. Inference for Heavy-Tailed Data: Applications in Insurance and Finance. Cambridge: Academic Press. [Google Scholar]
- Qi, Yongcheng. 2010. On the tail index of a heavy tailed distribution. Annals of the Institute of Statistical Mathematics 62: 277–98. [Google Scholar] [CrossRef]
- Scollnik, David P.M. 2001. Actuarial modeling with MCMC and BUGS. North American Actuarial Journal 5: 96–124. [Google Scholar] [CrossRef]
- Scollnik, David P.M. 2002. Modeling size-of-loss distributions for exact data in WinBUGS. Journal of Actuarial Practice 10: 202–27. [Google Scholar]
- Scollnik, David P.M. 2015. A Pareto scale-inflated outlier model and its Bayesian analysis. Scandinavian Actuarial Journal 2015: 201–20. [Google Scholar] [CrossRef]
- Sun, Liangrui, Michelle Xia, Yuanyuan Tang, and Philip G. Jones. 2017. Bayesian adjustment for unidirectional misclassification in ordinal covariates. Journal of Statistical Computation and Simulation 87: 3440–68. [Google Scholar] [CrossRef]
- Xia, Michelle, and Paul Gustafson. 2016. Bayesian regression models adjusting for unidirectional covariate misclassification. The Canadian Journal of Statistics 44: 198–218. [Google Scholar] [CrossRef]
- Xia, Michelle, and Paul Gustafson. 2018. Bayesian inference for unidirectional misclassification of a binary response trait. Statistics in Medicine 37: 933–47. [Google Scholar] [CrossRef] [PubMed]
- Xia, Michelle, Lei Hua, and Gary Vadnais. 2018. Embedded predictive analysis of misrepresentation risk in GLM ratemaking models. Variance: Advancing the Science of Risk. in press. [Google Scholar]
- Yang, Yang, Kaiyong Wang, Jiajun Liu, and Zhimin Zhang. 2018. Asymptotics for a bidimensional risk model with two geometric lévy price processes. Journal of Industrial & Management Optimization, 765–72. [Google Scholar] [CrossRef]



| Implies | t | |||
|---|---|---|---|---|
| Weibull | and | ∞ | ||
| Lognormal | and | ∞ | ||
| Pareto | and | ∞ |
| DIC | Gamma | Lognormal | Pareto | Weibull |
|---|---|---|---|---|
| Unadjusted | 16,007 | 15,860 | 15,865 | 15,934 |
| Adjusted | 16,231 | 16,357 | 15,757 | 16,008 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, M. Bayesian Adjustment for Insurance Misrepresentation in Heavy-Tailed Loss Regression. Risks 2018, 6, 83. https://doi.org/10.3390/risks6030083
Xia M. Bayesian Adjustment for Insurance Misrepresentation in Heavy-Tailed Loss Regression. Risks. 2018; 6(3):83. https://doi.org/10.3390/risks6030083
Chicago/Turabian StyleXia, Michelle. 2018. "Bayesian Adjustment for Insurance Misrepresentation in Heavy-Tailed Loss Regression" Risks 6, no. 3: 83. https://doi.org/10.3390/risks6030083
APA StyleXia, M. (2018). Bayesian Adjustment for Insurance Misrepresentation in Heavy-Tailed Loss Regression. Risks, 6(3), 83. https://doi.org/10.3390/risks6030083





