Extreme Portfolio Loss Correlations in Credit Risk
Abstract
1. Introduction
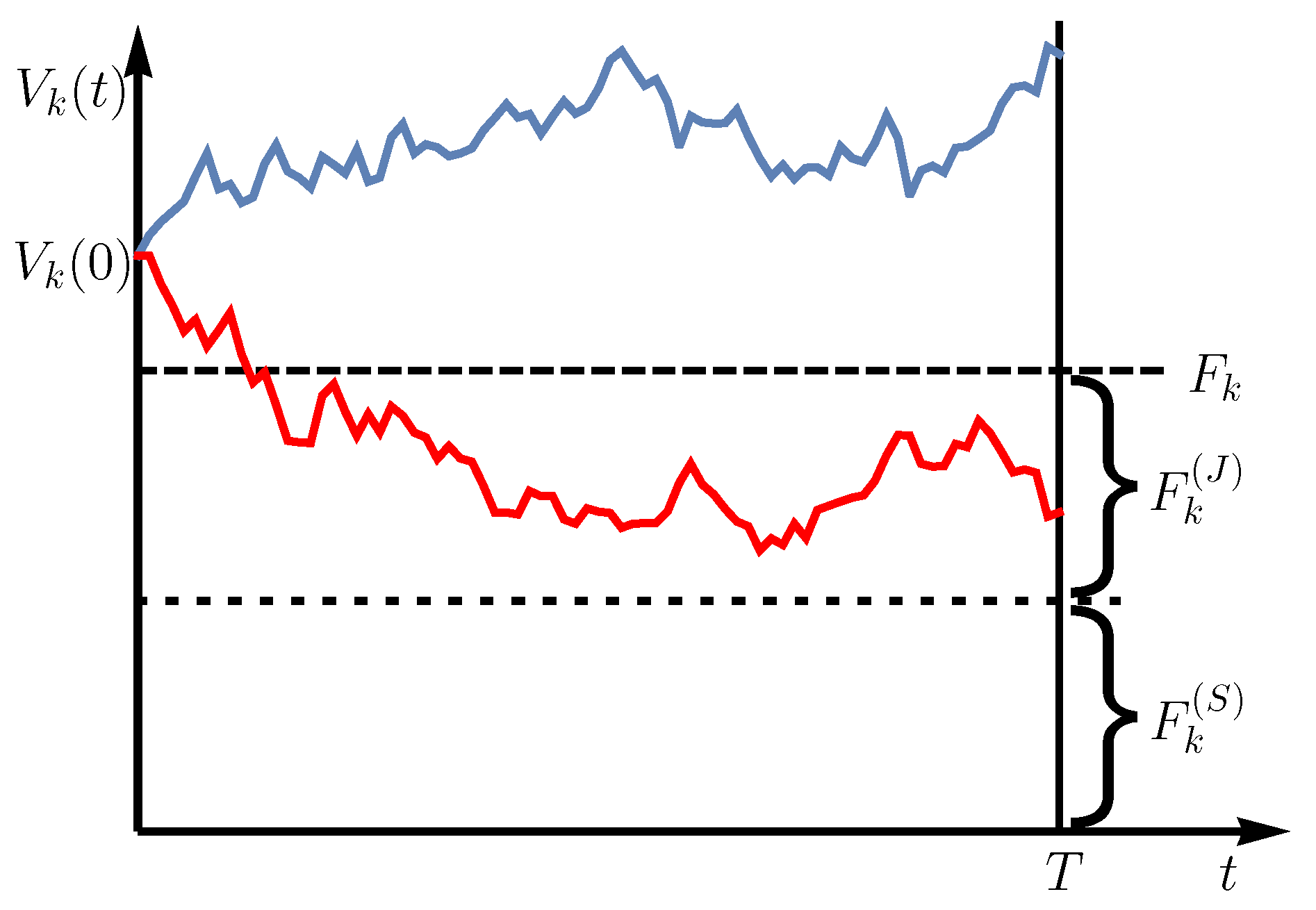
2. Model
2.1. Average Distribution
2.2. Average Loss Distribution
2.3. Homogeneous Portfolio
2.4. Distribution of the Loss Given Default
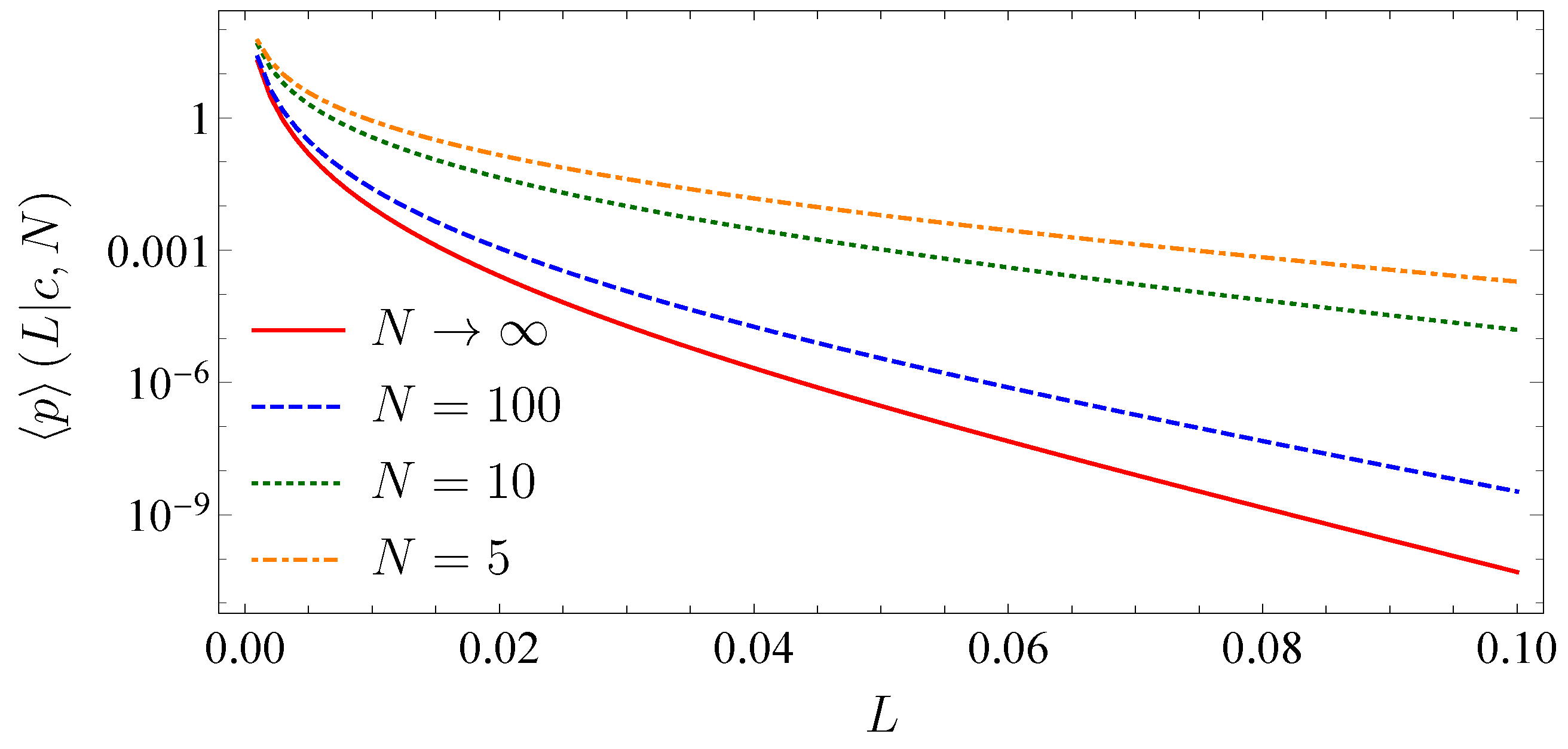
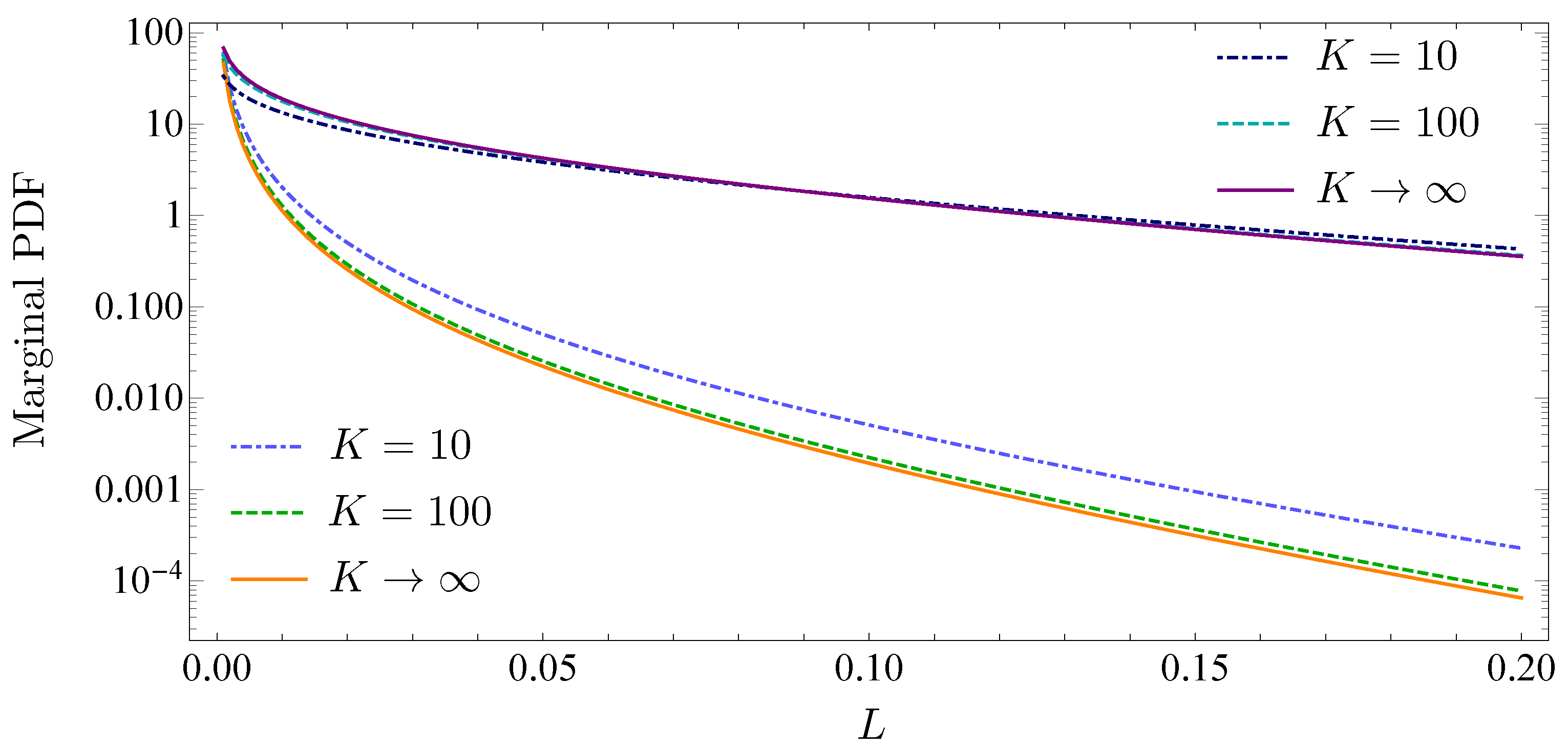
2.5. Infinitely Large Portfolios
2.6. Absence of Subordination
Absence of Subordination on Several Markets
2.7. Absence of Subordination and Infinitely Large Portfolios
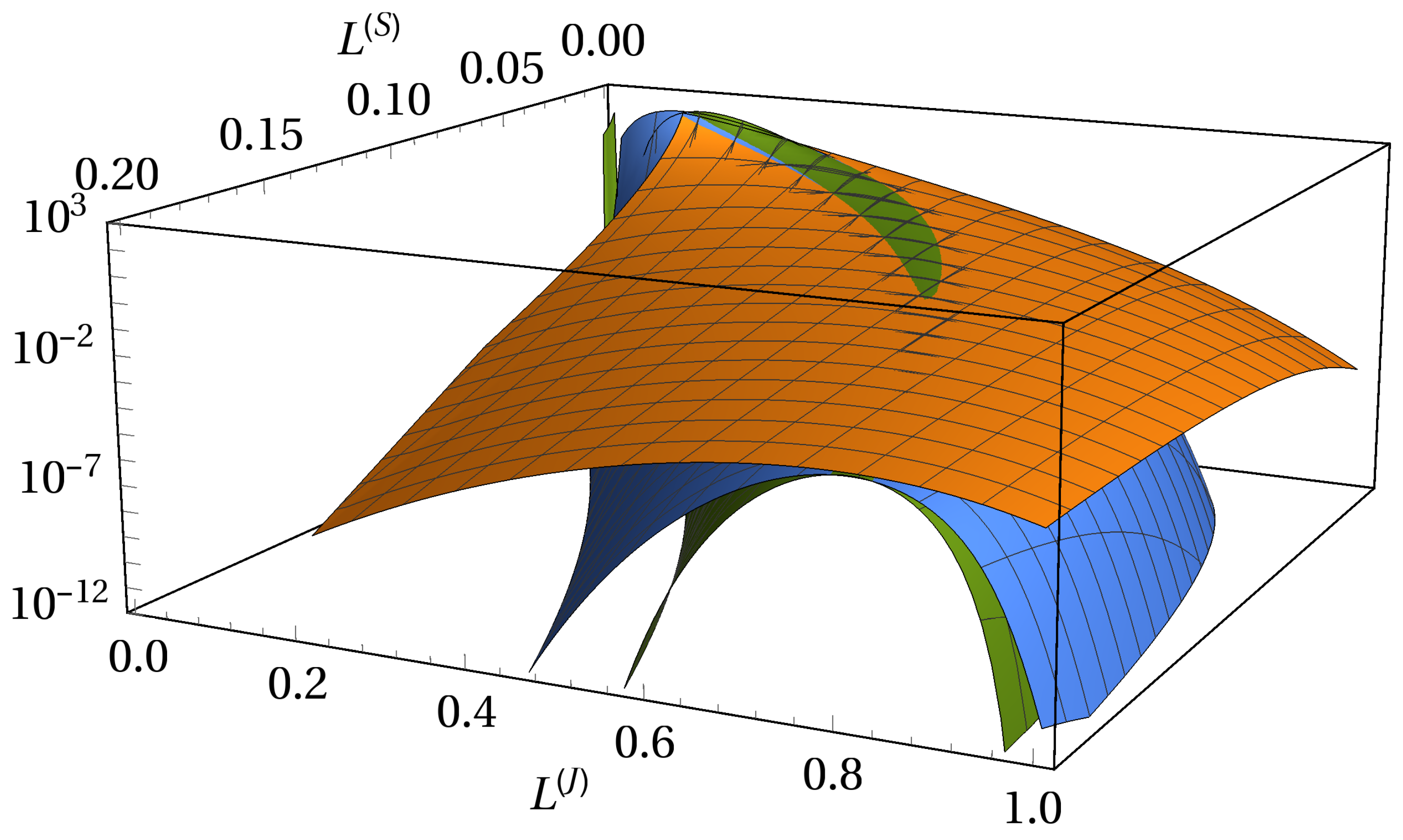
3. Model Calibration and Visualization of the Results
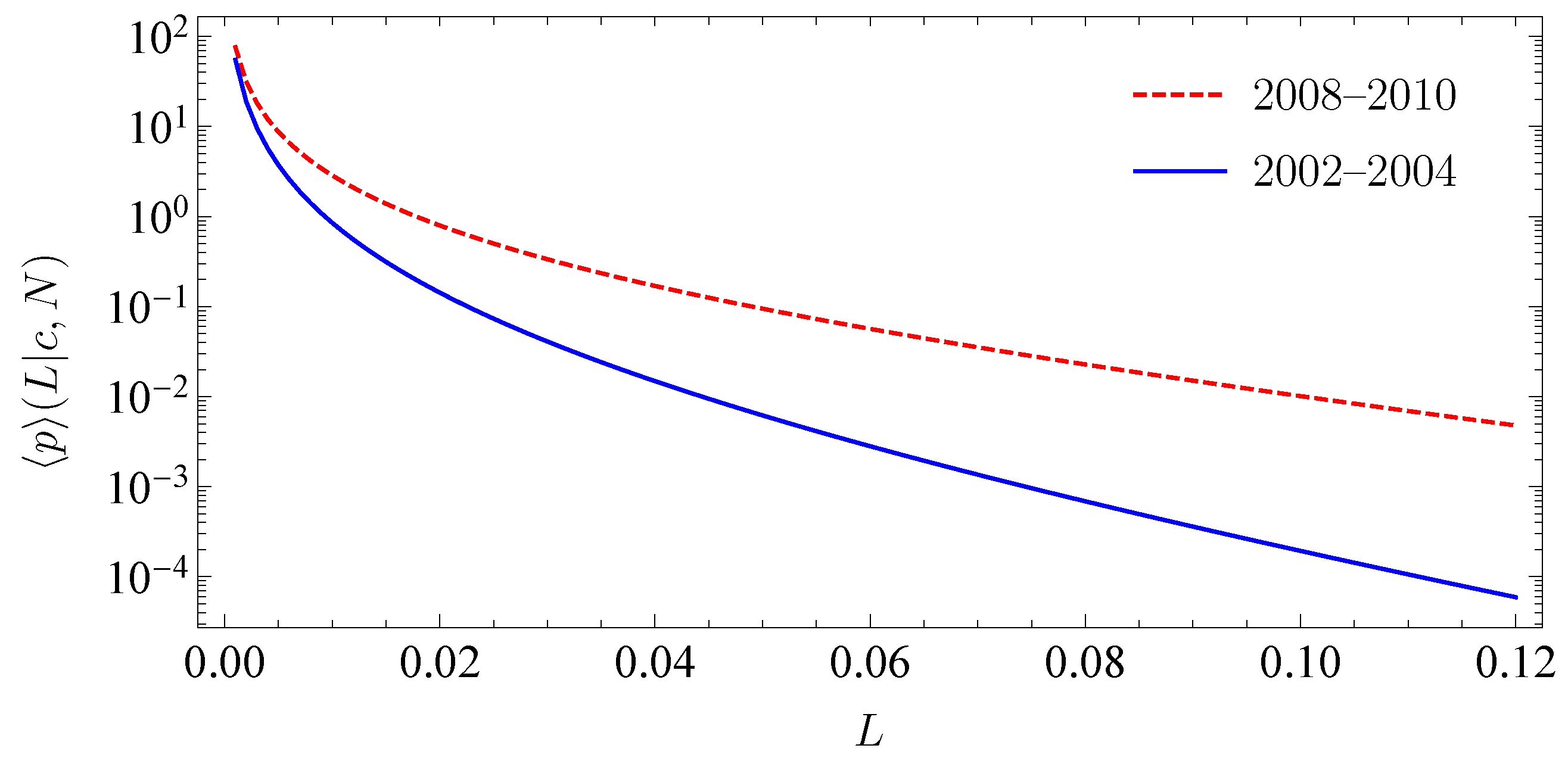
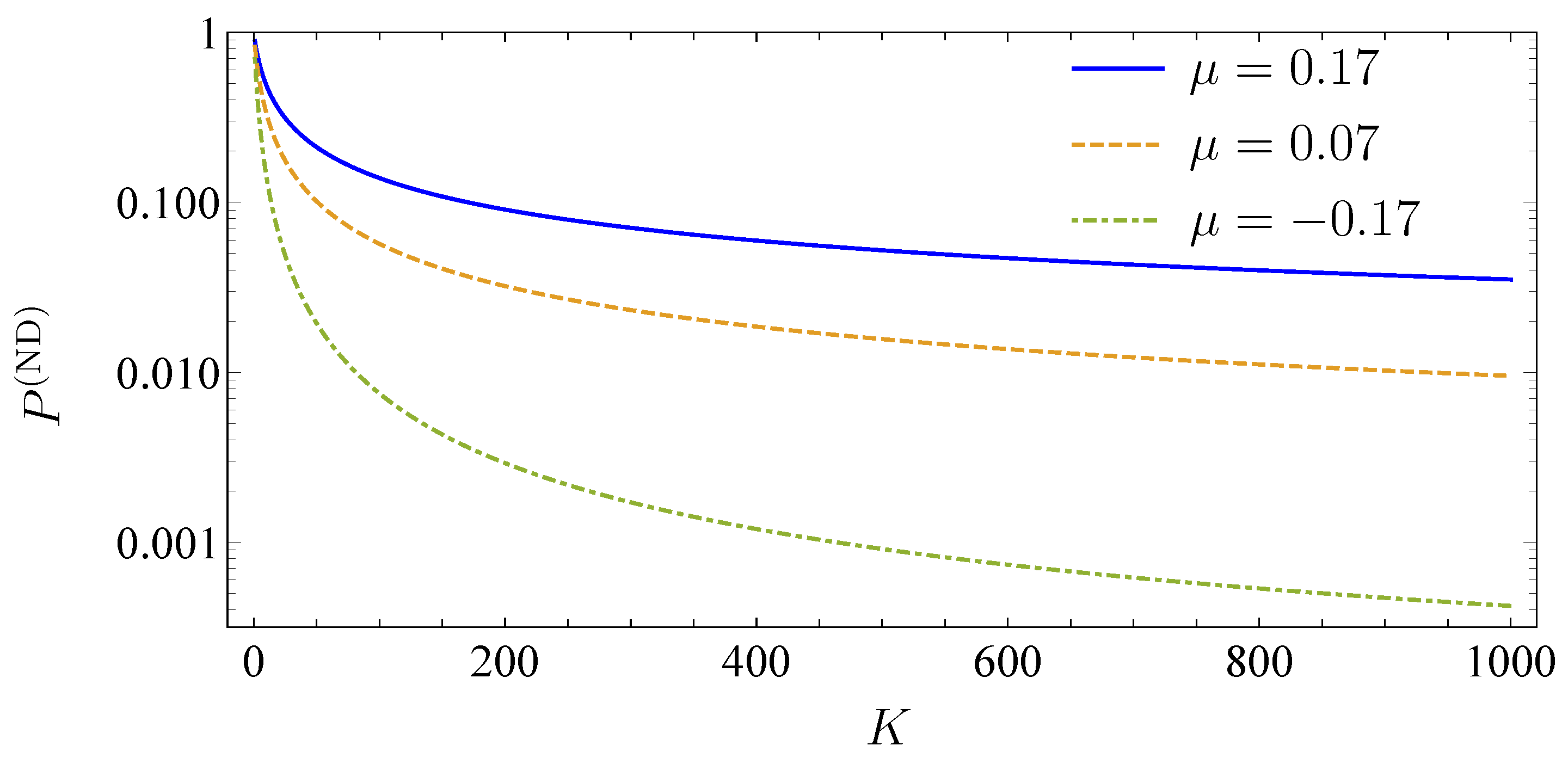
3.1. Adjustability to Different Market Situations
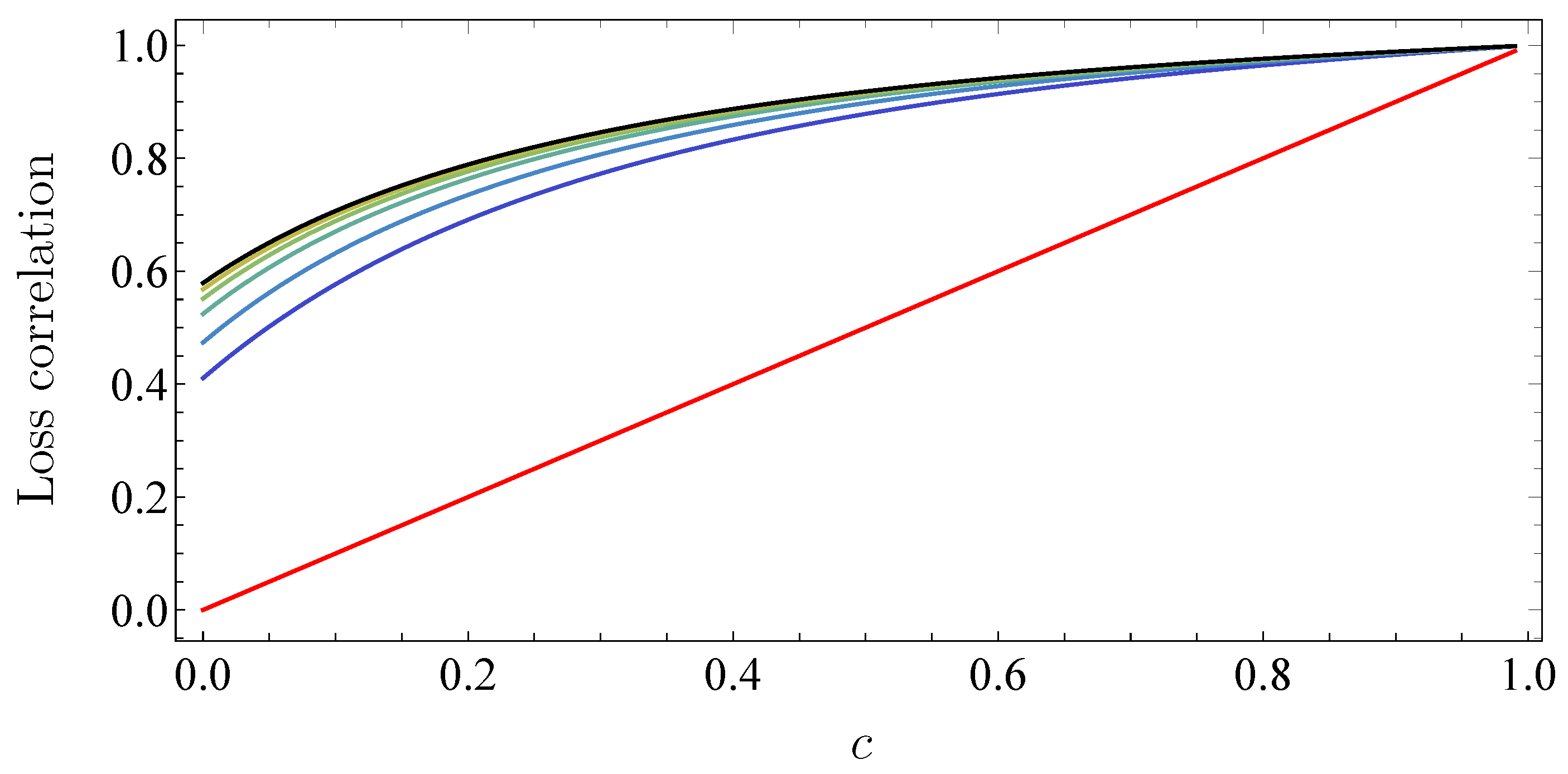
3.2. One Portfolio, Two Markets
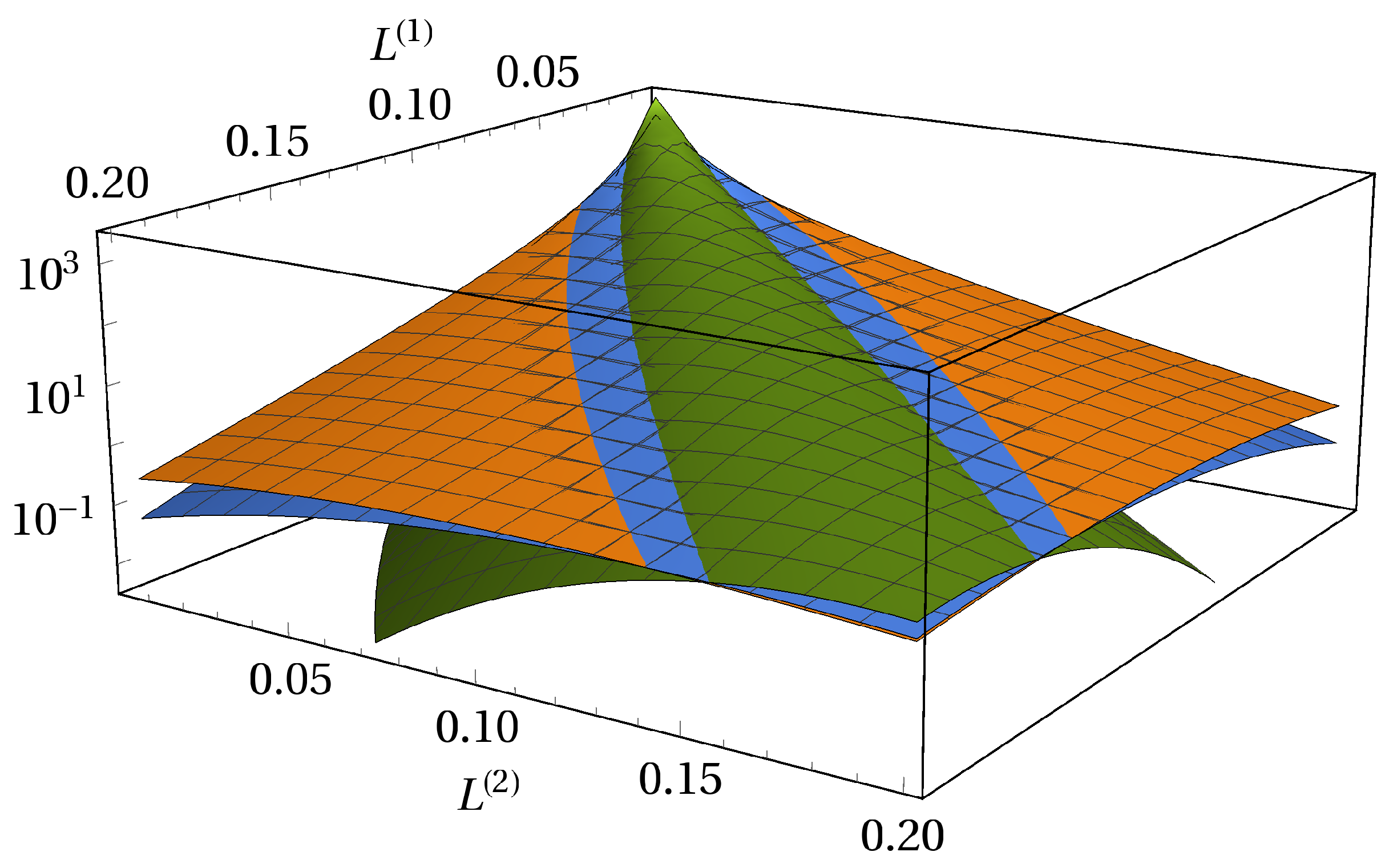
3.3. Absence of Subordination and Disjoint Portfolios of Equal Size
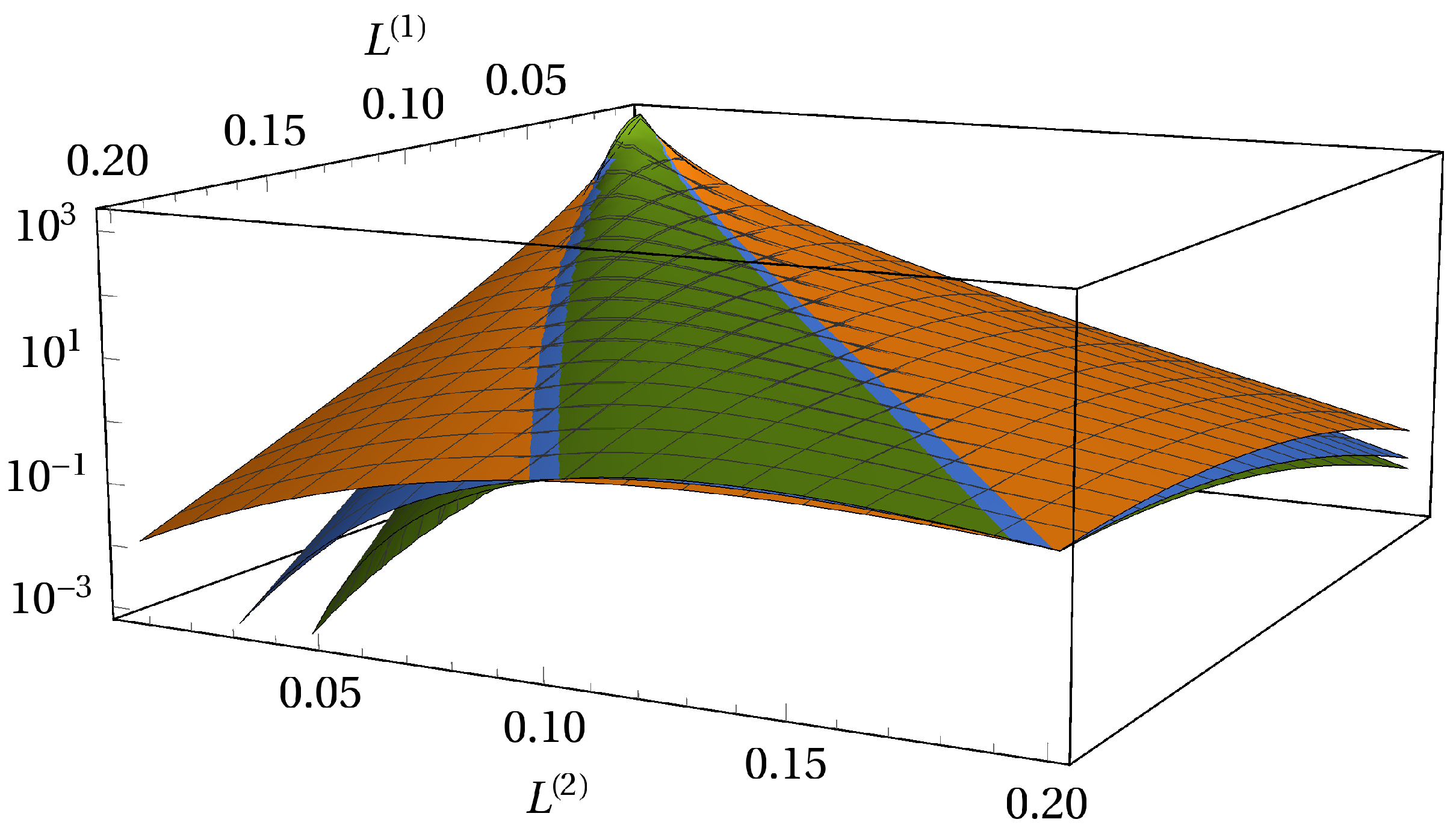
3.4. Absence of Subordination and Disjoint Portfolios of Various Sizes
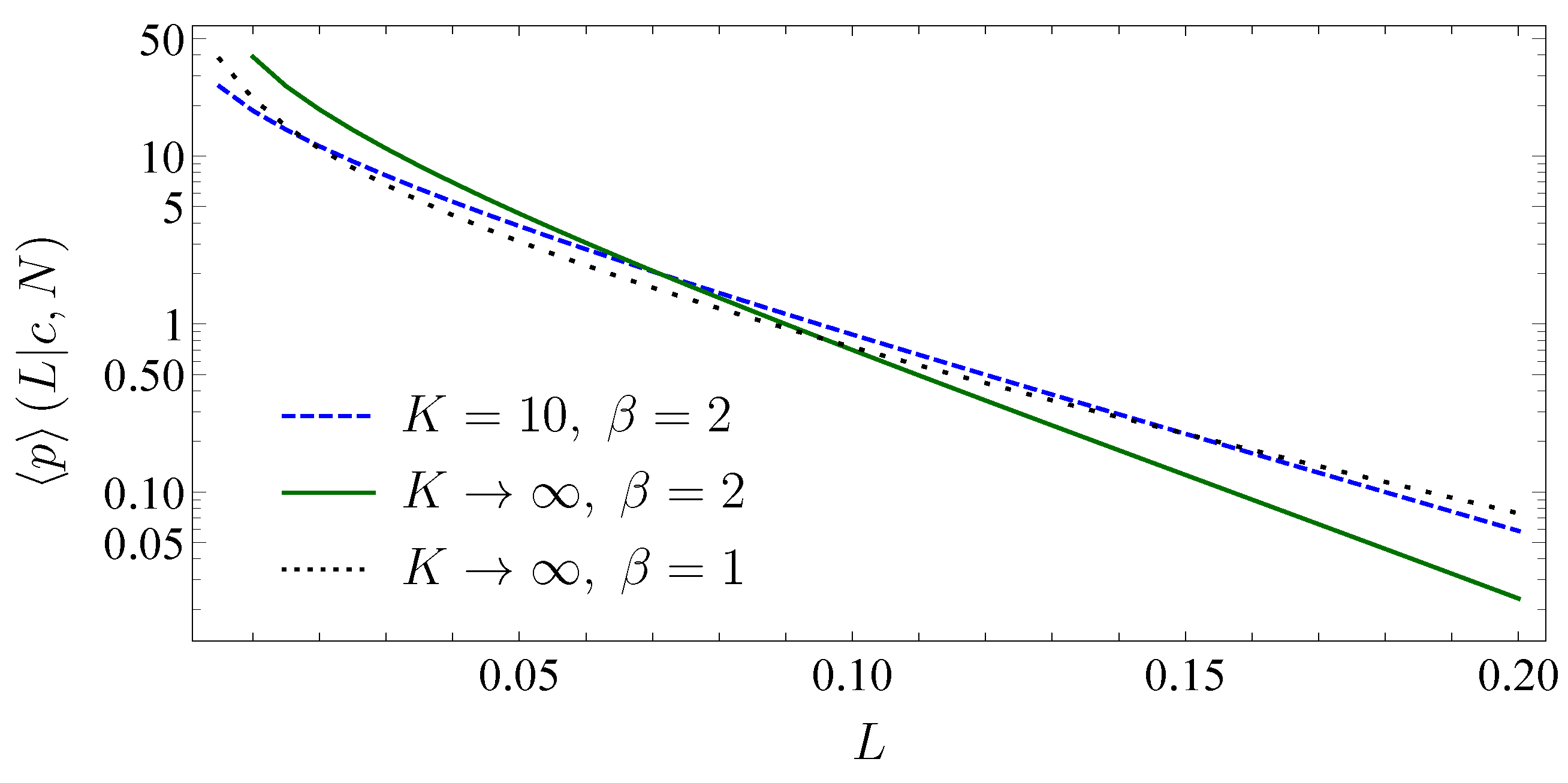
3.5. Subordinated Debt
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Moments
References
- An, Xudong, Yongheng Deng, Joseph B. Nichols, and Anthony B. Sanders. 2015. What is subordination about? Credit risk and subordination levels in commercial mortgage-backed securities (CMBS). The Journal of Real Estate Finance and Economics 51: 231–53. [Google Scholar] [CrossRef]
- Avkiran, Necmi K., Christian M. Ringle, and Rand K. Y. Low. 2018. Monitoring transmission of systemic risk: Application of partial least squares structural equation modeling in financial stress testing. Journal of Risk. [Google Scholar] [CrossRef]
- Bardoscia, Marco, Stefano Battiston, Fabio Caccioli, and Guido Caldarelli. 2017. Pathways towards instability in financial networks. Nature Communications 8: 14416. [Google Scholar] [CrossRef] [PubMed]
- Benmelech, Efraim, and Jennifer Dlugosz. 2009. The alchemy of CDO credit ratings. Journal of Monetary Economics 56: 617–34. [Google Scholar] [CrossRef]
- Bielecki, Tomasz R., and Marek Rutkowski. 2013. Credit Risk: Modeling, Valuation and Hedging. Berlin: Springer Science & Business Media. [Google Scholar]
- Black, Fischer S., and John C. Cox. 1976. Valuing corporate securities: Some effects of bond indenture provisions. The Journal of Finance 31: 351–67. [Google Scholar] [CrossRef]
- Bluhm, Christian, Ludger Overbeck, and Christoph Wagner. 2016. Introduction to Credit Risk Modeling. Boca Raton: CRC Press. [Google Scholar]
- Chava, Sudheer, Catalina Stefanescu, and Stuart Turnbull. 2011. Modeling the loss distribution. Management Science 57: 1267–87. [Google Scholar] [CrossRef]
- Chetalova, Desislava, Thilo A. Schmitt, Rudi Schäfer, and Thomas Guhr. 2015. Portfolio return distributions: Sample statistics with stochastic correlations. International Journal of Theoretical and Applied Finance 18: 1550012. [Google Scholar] [CrossRef]
- Corsi, Fulvio, Stefano Marmi, and Fabrizio Lillo. 2016. When micro prudence increases macro risk: The destabilizing effects of financial innovation, leverage, and diversification. Operations Research 64: 1073–88. [Google Scholar] [CrossRef]
- Crouhy, Michel, Dan Galai, and Robert Mark. 2000. A comparative analysis of current credit risk models. Journal of Banking & Finance 24: 59–117. [Google Scholar]
- Duan, Jin-Chuan. 1994. Maximum likelihood estimation using price data of the derivative contract. Mathematical Finance 4: 155–67. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth J. Singleton. 1999. Modeling term structures of defaultable bonds. The Review of Financial Studies 12: 687–720. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Nicolae Garleanu. 2001. Risk and valuation of collateralized debt obligations. Financial Analysts Journal 57: 41–59. [Google Scholar] [CrossRef]
- Egloff, Daniel, Markus Leippold, and Paolo Vanini. 2007. A simple model of credit contagion. Journal of Banking & Finance 31: 2475–92. [Google Scholar]
- Elizalde, Abel. 2005. Credit Risk Models II: Structural Models. Documentos de Trabajo CEMFI. Madrid: CEMFI. [Google Scholar]
- Giesecke, Kay, and Stefan Weber. 2004. Cyclical correlations, credit contagion, and portfolio losses. Journal of Banking & Finance 28: 3009–36. [Google Scholar]
- Giesecke, Kay, and Stefan Weber. 2006. Credit contagion and aggregate losses. Journal of Economic Dynamics and Control 30: 741–67. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2004. Tail approximations for portfolio credit risk. The Journal of Derivatives 12: 24–42. [Google Scholar] [CrossRef]
- Glasserman, Paul, and Jesus Ruiz-Mata. 2006. Computing the credit loss distribution in the Gaussian copula model: A comparison of methods. Journal of Credit Risk 2: 33–66. [Google Scholar] [CrossRef]
- Goetzmann, William N., Lingfeng Li, and K. Geert Rouwenhorst. 2005. Long-term global market correlations. Journal of Business 78: 1–38. [Google Scholar] [CrossRef]
- Gorton, Gary, and Anthony M. Santomero. 1990. Market discipline and bank subordinated debt: Note. Journal of Money, Credit and Banking 22: 119–28. [Google Scholar] [CrossRef]
- Hatchett, Jon P. L., and Reimer Kühn. 2009. Credit contagion and credit risk. Quantitative Finance 9: 373–82. [Google Scholar] [CrossRef]
- Heitfield, Eric, Steve Burton, and Souphala Chomsisengphet. 2006. Systematic and idiosyncratic risk in syndicated loan portfolios. Journal of Credit Risk 2: 3–31. [Google Scholar] [CrossRef]
- Hull, John C. 2009. The credit crunch of 2007: What went wrong? Why? What lessons can be learned? Journal of Credit Risk 5: 3–18. [Google Scholar] [CrossRef]
- Humphrey, Jacquelyn E., Karen L. Benson, Rand K. Y. Low, and Wei-Lun Lee. 2015. Is diversification always optimal? Pacific-Basin Finance Journal 35: 521–32. [Google Scholar] [CrossRef]
- Ibragimov, Rustam, and Johan Walden. 2007. The limits of diversification when losses may be large. Journal of Banking & Finance 31: 2551–69. [Google Scholar]
- Itô, Kiyosi. 1944. Stochastic integral. Proceedings of the Imperial Academy 20: 519–24. [Google Scholar] [CrossRef]
- Lando, David. 2009. Credit Risk Modeling: Theory and Applications. Princeton: Princeton University Press. [Google Scholar]
- Lighthill, Michael J. 1958. An introduction to Fourier Analysis and Generalised Functions. Cambridge: Cambridge University Press. [Google Scholar]
- Longstaff, Francis A., and Arvind Rajan. 2008. An empirical analysis of the pricing of collateralized debt obligations. The Journal of Finance 63: 529–63. [Google Scholar] [CrossRef]
- Low, Rand Kwong Yew, Jamie Alcock, Robert Faff, and Timothy Brailsford. 2013. Canonical vine copulas in the context of modern portfolio management: Are they worth it? Journal of Banking & Finance 37: 3085–99. [Google Scholar]
- Low, Rand Kwong Yew. 2017. Vine copulas: Modeling systemic risk and enhancing higher-moment portfolio optimisation. Accounting and Finance. [Google Scholar] [CrossRef]
- Lucas, André, Pieter Klaassen, Peter Spreij, and Stefan Straetmans. 2001. An analytic approach to credit risk of large corporate bond and loan portfolios. Journal of Banking & Finance 25: 1635–64. [Google Scholar]
- Mainik, Georg, and Paul Embrechts. 2013. Diversification in heavy-tailed portfolios: Properties and pitfalls. Annals of Actuarial Science 7: 26–45. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press. [Google Scholar]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Mühlbacher, Andreas, and Thomas Guhr. 2018. Credit risk meets random matrices: Coping with non-stationary asset correlations. Risks 6: 42. [Google Scholar] [CrossRef]
- Münnix, Michael C., Takashi Shimada, Rudi Schäfer, Francois Leyvraz, Thomas H. Seligman, Thomas Guhr, and H. Eugene Stanley. 2012. Identifying states of a financial market. Scientific Reports 2: 644. [Google Scholar] [CrossRef] [PubMed]
- Münnix, Michael C., Rudi Schäfer, and Thomas Guhr. 2014. A random matrix approach to credit risk. PLoS ONE 9: e98030. [Google Scholar] [CrossRef] [PubMed]
- Nitschke, Tobias. 2014. Ensemble-Ansatz zur Modellierung des Kreditrisikos im Falle im Mittel unkorrelierter Märkte. Bachelor’s thesis, University of Duisburg-Essen, Duisburg, Germany. [Google Scholar]
- Sandoval, Leonidas, and Italo De Paula Franca. 2012. Correlation of financial markets in times of crisis. Physica A 391: 187–208. [Google Scholar] [CrossRef]
- Schäfer, Rudi, Markus Sjölin, Andreas Sundin, Michal Wolanski, and Thomas Guhr. 2007. Credit risk—A structural model with jumps and correlations. Physica A 383: 533–69. [Google Scholar] [CrossRef]
- Schmitt, Thilo A., Desislava Chetalova, Rudi Schäfer, and Thomas Guhr. 2013. Non-stationarity in financial time series: Generic features and tail behavior. Europhysics Letters 103: 58003. [Google Scholar] [CrossRef]
- Schmitt, Thilo A., Desislava Chetalova, Rudi Schäfer, and Thomas Guhr. 2014. Credit risk and the instability of the financial system: An ensemble approach. Europhysics Letters 105: 38004. [Google Scholar] [CrossRef]
- Schmitt, Thilo A., Desislava Chetalova, Rudi Schäfer, and Thomas Guhr. 2015. Credit risk: Taking fluctuating asset correlations into account. Journal of Credit Risk 11: 73–94. [Google Scholar] [CrossRef]
- Schönbucher, Philipp J. 2001. Factor models: Portfolio credit risks when defaults are correlated. The Journal of Risk Finance 3: 45–56. [Google Scholar] [CrossRef]
- Schönbucher, Philipp J. 2003. Credit Derivatives Pricing Models: Models, Pricing and Implementation. Hoboken: John Wiley & Sons. [Google Scholar]
- Sicking, Joachim, Thomas Guhr, and Rudi Schäfer. 2018. Concurrent credit portfolio losses. PLoS ONE 13: e0190263. [Google Scholar] [CrossRef] [PubMed]
- Song, Dong-Ming, Michele Tumminello, Wei-Xing Zhou, and Rosario N. Mantegna. 2011. Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Physical Review E 84: 026108. [Google Scholar] [CrossRef] [PubMed]
- Wagner, Wolf. 2010. Diversification at financial institutions and systemic crises. Journal of Financial Intermediation 19: 373–86. [Google Scholar] [CrossRef]
- Wishart, John. 1928. The generalised product moment distribution in samples from a normal multivariate population. Biometrika 20A: 32–52. [Google Scholar] [CrossRef]
- Wollschläger, Marcel, and Rudi Schäfer. 2016. Impact of nonstationarity on estimating and modeling empirical copulas of daily stock returns. Journal of Risk 19: 1–23. [Google Scholar] [CrossRef]
- Yahoo! n.d. Finance. Available online: http://finance.yahoo.com (accessed on 15 May 2018).

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mühlbacher, A.; Guhr, T. Extreme Portfolio Loss Correlations in Credit Risk. Risks 2018, 6, 72. https://doi.org/10.3390/risks6030072
Mühlbacher A, Guhr T. Extreme Portfolio Loss Correlations in Credit Risk. Risks. 2018; 6(3):72. https://doi.org/10.3390/risks6030072
Chicago/Turabian StyleMühlbacher, Andreas, and Thomas Guhr. 2018. "Extreme Portfolio Loss Correlations in Credit Risk" Risks 6, no. 3: 72. https://doi.org/10.3390/risks6030072
APA StyleMühlbacher, A., & Guhr, T. (2018). Extreme Portfolio Loss Correlations in Credit Risk. Risks, 6(3), 72. https://doi.org/10.3390/risks6030072



