Credit Risk Meets Random Matrices: Coping with Non-Stationary Asset Correlations
Abstract
1. Introduction
2. Random Matrix Theory for Non-Stationary Asset Correlations
2.1. Wishart Model for Correlation and Covariance Matrices
2.2. New Interpretation and Application of the Wishart Model
3. Modeling Fluctuating Asset Correlations in Credit Risk
3.1. Random Matrix Approach
3.2. Average Loss Distribution
3.3. Adjusting to Different Market Situations
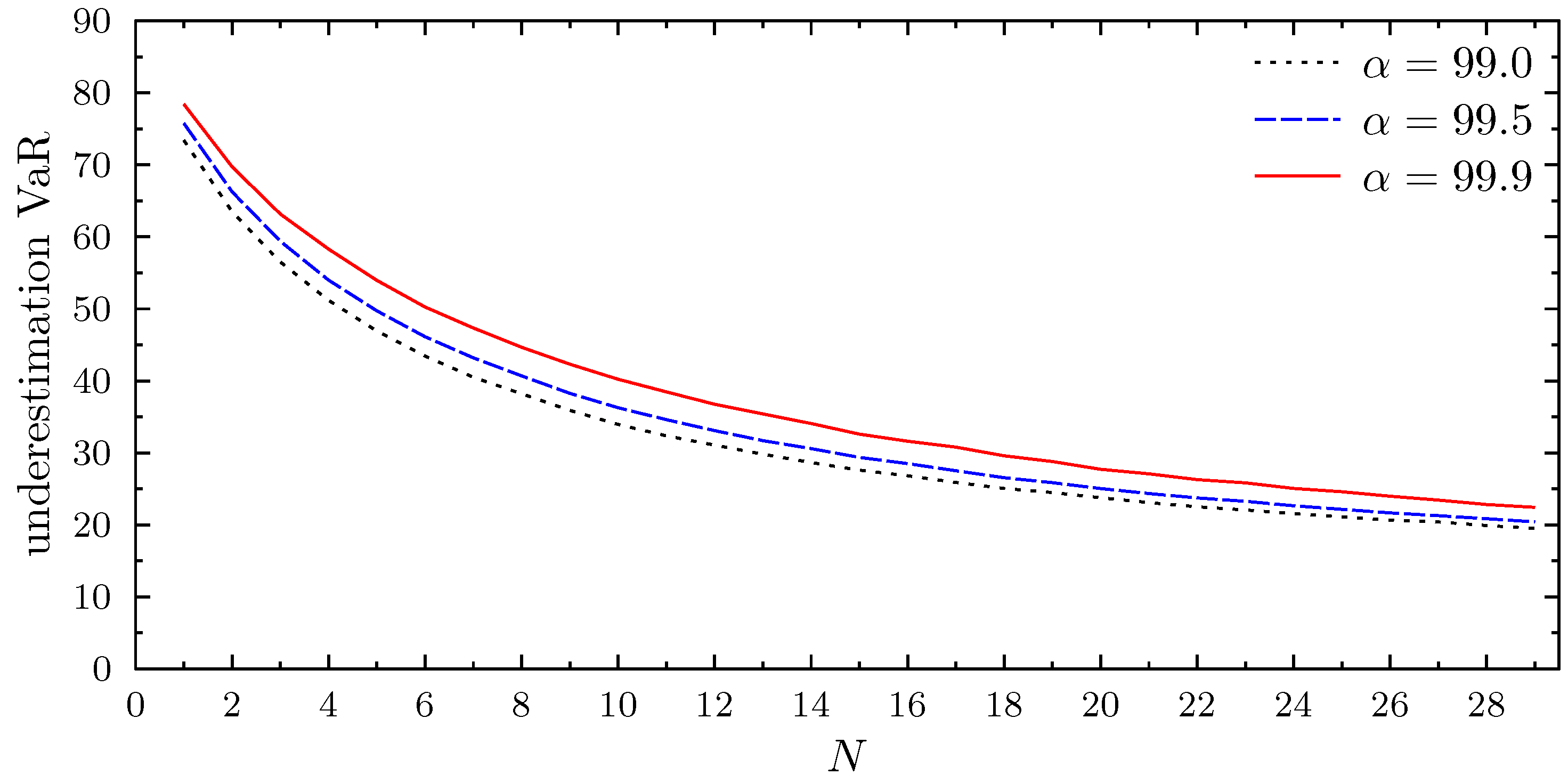
3.4. Value at Risk and Expected Tail Loss
4. Concurrent Credit Portfolio Losses
4.1. Simulation Setup
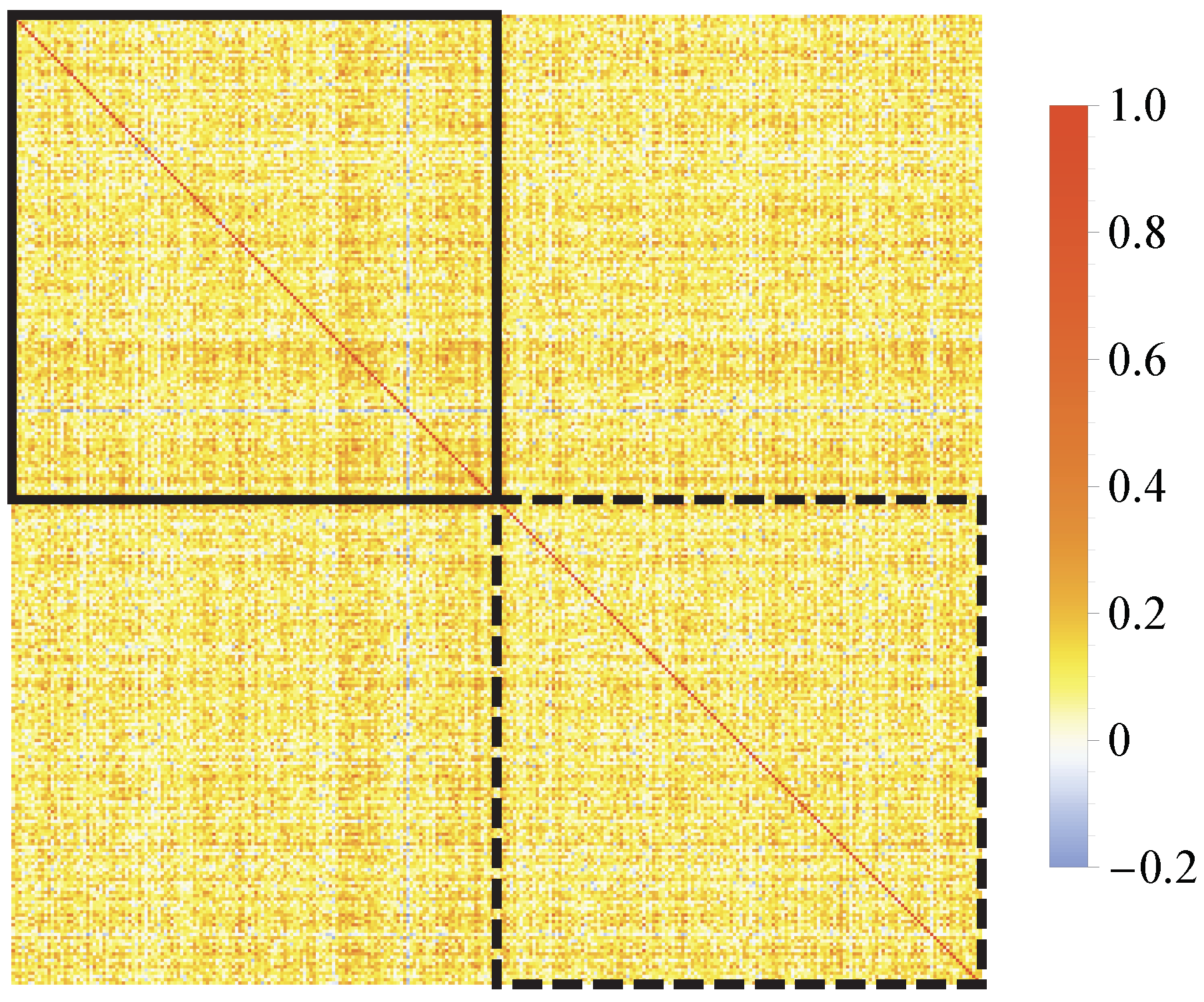
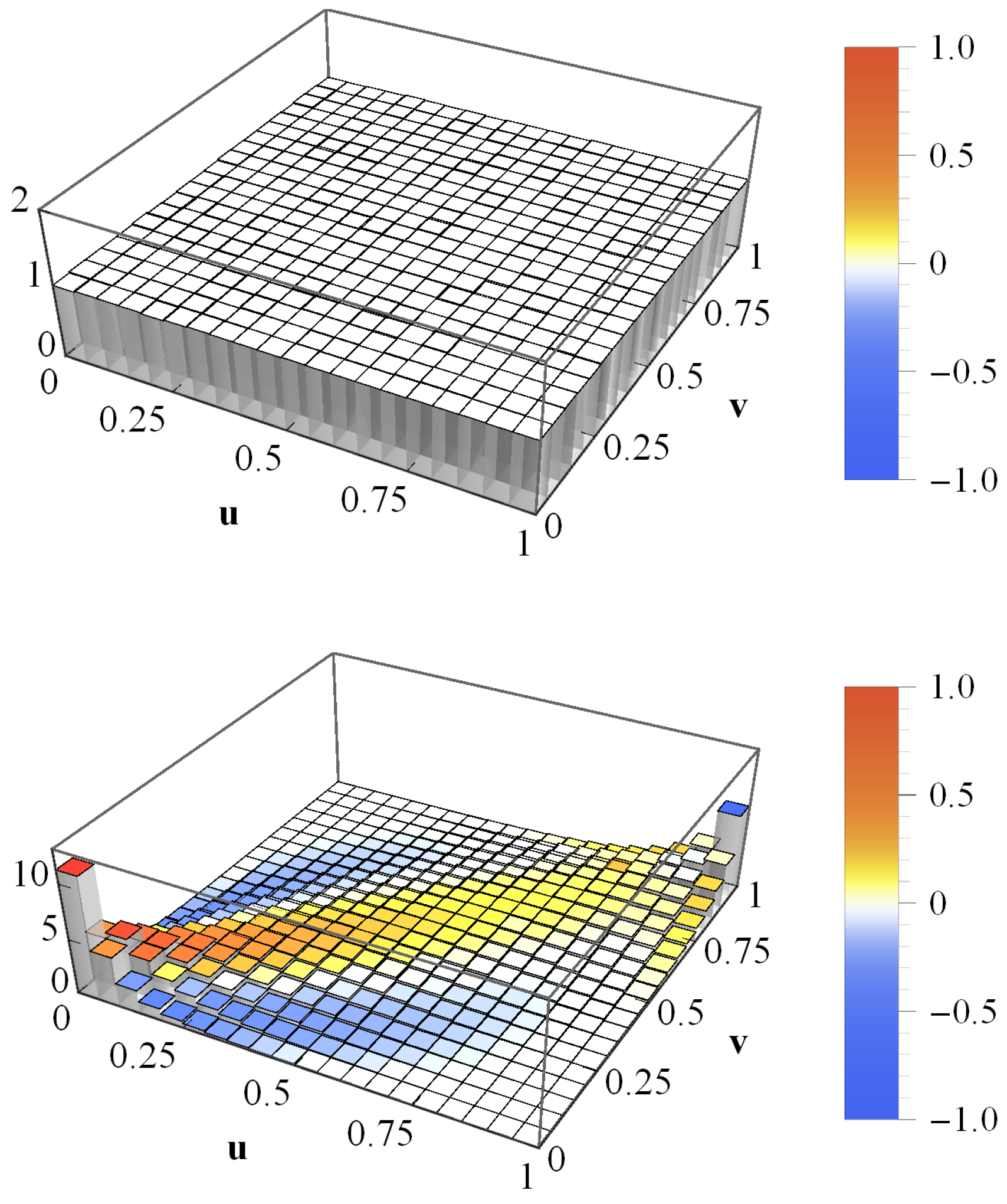
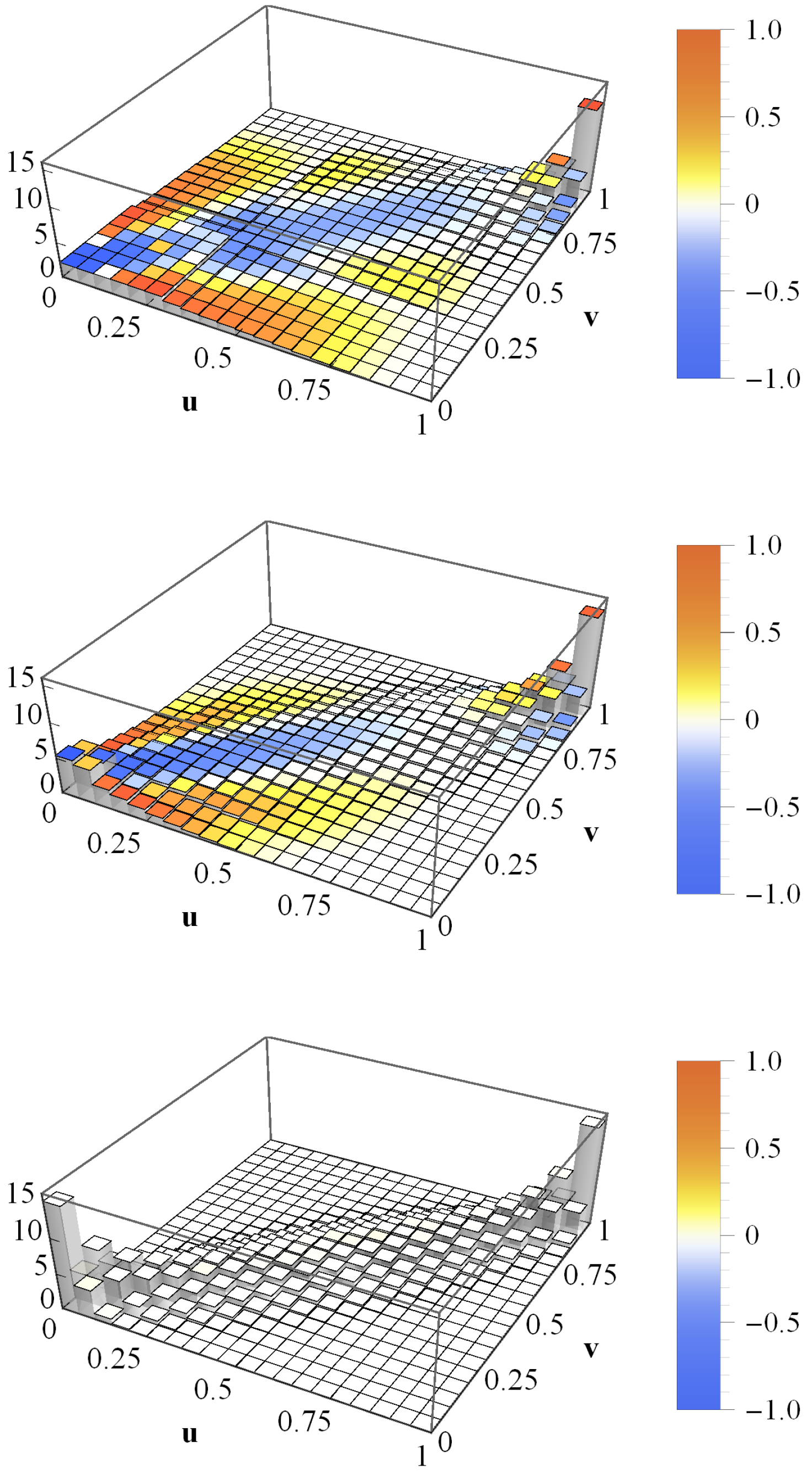
4.2. Empirical Credit Portfolios
5. Discussion
Acknowledgments
Conflicts of Interest
References
- Benmelech, Efraim, and Jennifer Dlugosz. 2009. The alchemy of CDO credit ratings. Journal of Monetary Economics 56: 617–34. [Google Scholar] [CrossRef]
- Bernaola-Galván, Pedro, Plamen Ch. Ivanov, Luís A. Nunes Amaral, and H. Eugene Stanley. 2001. Scale invariance in the nonstationarity of human heart rate. Physical Review Letters 87: 168105. [Google Scholar] [CrossRef] [PubMed]
- Bielecki, Tomasz R., and Marek Rutkowski. 2013. Credit Risk: Modeling, Valuation and Hedging. Berlin: Springer Science & Business Media. [Google Scholar]
- Black, Fisher. 1976. Studies of stock price volatility changes. In Proceedings of the 1976 Meetings of the American Statistical Association, Business and Economics Statistics Section. Alexandria: American Statistical Association, pp. 177–81. [Google Scholar]
- Bluhm, Christian, Ludger Overbeck, and Christoph Wagner. 2016. Introduction to Credit Risk Modeling. Boca Raton: CRC Press. [Google Scholar]
- Bouchaud, Jean-Philippe, and Marc Potters. 2003. Theory of Financial Risk and Derivative Pricing: From Statistical Physics to Risk Management. Cambridge: Cambridge University Press. [Google Scholar]
- Chava, Sudheer, Catalina Stefanescu, and Stuart Turnbull. 2011. Modeling the loss distribution. Management Science 57: 1267–87. [Google Scholar] [CrossRef]
- Chetalova, Desislava, Thilo A. Schmitt, Rudi Schäfer, and Thomas Guhr. 2015. Portfolio return distributions: Sample statistics with stochastic correlations. International Journal of Theoretical and Applied Finance 18: 1550012. [Google Scholar] [CrossRef]
- Crouhy, Michel, Dan Galai, and Robert Mark. 2000. A comparative analysis of current credit risk models. Journal of Bank. & Finance 24: 59–117. [Google Scholar]
- Di Gangi, Domenico, Fabrizio Lillo, and Davide Pirino. 2018. Assessing Systemic Risk due to Fire Sales Spillover through Maximum Entropy Network Reconstruction. Available online: https://ssrn.com/abstract=2639178 (accessed on 27 February 2018).
- Duan, Jin-Chuan. 1994. Maximum likelihood estimation using price data of the derivative contract. Mathematical Finance 4: 155–67. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Nicolae Garleanu. 2001. Risk and valuation of collateralized debt obligations. Financial Analysts Journal 57: 41–59. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth J. Singleton. 1999. Modeling term structures of defaultable bonds. The Review of Financial Studies 12: 687–720. [Google Scholar] [CrossRef]
- Elizalde, Abel. 2005. Credit Risk Models II: Structural Models. Documentos de Trabajo CEMFI. Madrid: CEMFI. [Google Scholar]
- Eom, Young H., Jean Helwege, and Jing-zhi Huang. 2004. Structural models of corporate bond pricing: An empirical analysis. The Review of Financial Studies 17: 499–544. [Google Scholar] [CrossRef]
- Gao, Jinbao. 1999. Recurrence time statistics for chaotic systems and their applications. Physical Review Letters 83: 3178. [Google Scholar] [CrossRef]
- Giada, Lorenzo, and Matteo Marsili. 2002. Algorithms of maximum likelihood data clustering with applications. Physica A 315: 650–64. [Google Scholar] [CrossRef]
- Giesecke, Kay. 2004. Credit risk modeling and valuation: An introduction. In Credit Risk: Models and Management, 2nd ed. Edited by David Shimko. London: RISK Books, pp. 487–526. [Google Scholar]
- Glasserman, Paul. 2004. Tail approximations for portfolio credit risk. The Journal of Derivatives 12: 24–42. [Google Scholar] [CrossRef]
- Glasserman, Paul, and Jesus Ruiz-Mata. 2006. Computing the credit loss distribution in the Gaussian copula model: A comparison of methods. Journal of Credit Risk 2: 33–66. [Google Scholar] [CrossRef]
- Gouriéroux, Christian, and Razvan Sufana. 2004. Derivative Pricing with Multivariate Stochastic Volatility: Application to Credit Risk. Working Papers 2004-31. Palaiseau, France: Center for Research in Economics and Statistics. [Google Scholar]
- Gouriéroux, Christian, Joann Jasiak, and Razvan Sufana. 2009. The Wishart autoregressive process of multivariate stochastic volatility. Journal of Econometrics 150: 167–81. [Google Scholar] [CrossRef]
- Guhr, Thomas, and Bernd Kälber. 2003. A new method to estimate the noise in financial correlation matrices. Journal of Physics A 36: 3009. [Google Scholar] [CrossRef]
- Hatchett, Jon P. L., and Reimer Kühn. 2009. Credit contagion and credit risk. Quantitative Finance 9: 373–82. [Google Scholar] [CrossRef]
- Hegger, Rainer, Holger Kantz, Lorenzo Matassini, and Thomas Schreiber. 2000. Coping with nonstationarity by overembedding. Physical Review Letters 84: 4092. [Google Scholar] [CrossRef] [PubMed]
- Heitfield, Eric, Steve Burton, and Souphala Chomsisengphet. 2006. Systematic and idiosyncratic risk in syndicated loan portfolios. Journal of Credit Risk 2: 3–31. [Google Scholar] [CrossRef]
- Heise, Sebastian, and Reimer Kühn. 2012. Derivatives and credit contagion in interconnected networks. The European Physical Journal B 85: 115. [Google Scholar] [CrossRef]
- Hull, John C. 2009. The credit crunch of 2007: What went wrong? Why? What lessons can be learned? Journal of Credit Risk 5: 3–18. [Google Scholar] [CrossRef]
- Ibragimov, Rustam, and Johan Walden. 2007. The limits of diversification when losses may be large. Journal of Bank. & Finance 31: 2551–69. [Google Scholar]
- Itô, Kiyosi. 1944. Stochastic integral. Proceedings of the Imperial Academy 20: 519–24. [Google Scholar] [CrossRef]
- Koivusalo, Alexander F. R., and Rudi Schäfer. 2012. Calibration of structural and reduced-form recovery models. Journal of Credit Risk 8: 31–51. [Google Scholar] [CrossRef]
- Laloux, Laurent, Pierre Cizeau, Jean-Philippe Bouchaud, and Marc Potters. 1999. Noise dressing of financial correlation matrices. Physical Review Letters 83: 1467. [Google Scholar] [CrossRef]
- Lando, David. 2009. Credit Risk Modeling: Theory and Applications. Princeton: Princeton University Press. [Google Scholar]
- Li, David X. 2000. On default correlation: A copula function approach. The Journal of Fixed Income 9: 43–54. [Google Scholar] [CrossRef]
- Lighthill, Michael J. 1958. An introduction to Fourier Analysis and Generalised Functions. Cambridge: Cambridge University Press. [Google Scholar]
- Longstaff, Francis A., and Arvind Rajan. 2008. An empirical analysis of the pricing of collateralized debt obligations. The Journal of Finance 63: 529–63. [Google Scholar] [CrossRef]
- Mainik, Georg, and Paul Embrechts. 2013. Diversification in heavy-tailed portfolios: Properties and pitfalls. Annals of Actuarial Science 7: 26–45. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press. [Google Scholar]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. The Journal of finance 29: 449–70. [Google Scholar]
- Meudt, Frederik, Martin Theissen, Rudi Schäfer, and Thomas Guhr. 2015. Constructing analytically tractable ensembles of stochastic covariances with an application to financial data. Journal of Statistical Mechanics 2015: P11025. [Google Scholar] [CrossRef]
- Muirhead, Robb J. 2005. Aspects of Multivariate Statistical Theory, 2nd ed. John Wiley & Sons: Hoboken. [Google Scholar]
- Münnix, Michael C., Rudi Schäfer, and Thomas Guhr. 2014. A random matrix approach to credit risk. PLoS ONE 9: e98030. [Google Scholar] [CrossRef] [PubMed]
- Münnix, Michael C., Takashi Shimada, Rudi Schäfer, Francois Leyvraz, Thomas H. Seligman, Thomas Guhr, and H. Eugene Stanley. 2012. Identifying states of a financial market. Scientific Reports 2: 644. [Google Scholar] [CrossRef] [PubMed]
- Nelsen, Roger B. 2007. An Introduction to Copulas. New York: Springer Science & Business Media. [Google Scholar]
- Pafka, Szilard, and Imre Kondor. 2004. Estimated correlation matrices and portfolio optimization. Physica A 343: 623–34. [Google Scholar] [CrossRef][Green Version]
- Plerou, Vasiliki, Parameswaran Gopikrishnan, Bernd Rosenow, Luís A. Nunes Amaral, and H. Eugene Stanley. 1999. Universal and nonuniversal properties of cross correlations in financial time series. Physical Review Letters 83: 1471. [Google Scholar] [CrossRef]
- Plerou, Vasiliki, Parameswaran Gopikrishnan, Bernd Rosenow, Luís A. Nunes Amaral, Thomas Guhr, and H. Eugene Stanley. 2002. Random matrix approach to cross correlations in financial data. Physical Review E 65: 066126. [Google Scholar] [CrossRef] [PubMed]
- Rieke, Christoph, Karsten Sternickel, Ralph G. Andrzejak, Christian E. Elger, Peter David, and Klaus Lehnertz. 2002. Measuring nonstationarity by analyzing the loss of recurrence in dynamical systems. Physical Review Letters 88: 244102. [Google Scholar] [CrossRef] [PubMed]
- Sandoval, Leonidas, and Italo De Paula Franca. 2012. Correlation of financial markets in times of crisis. Physica A 391: 187–208. [Google Scholar] [CrossRef]
- Schäfer, Rudi, Markus Sjölin, Andreas Sundin, Michal Wolanski, and Thomas Guhr. 2007. Credit risk—A structural model with jumps and correlations. Physica A 383: 533–69. [Google Scholar] [CrossRef]
- Schmitt, Thilo A., Desislava Chetalova, Rudi Schäfer, and Thomas Guhr. 2013. Non-stationarity in financial time series: Generic features and tail behavior. Europhysics Letters 103: 58003. [Google Scholar] [CrossRef]
- Schmitt, Thilo A., Desislava Chetalova, Rudi Schäfer, and Thomas Guhr. 2014. Credit risk and the instability of the financial system: An ensemble approach. Europhysics Letters 105: 38004. [Google Scholar] [CrossRef]
- Schmitt, Thilo A., Desislava Chetalova, Rudi Schäfer, and Thomas Guhr. 2015. Credit risk: Taking fluctuating asset correlations into account. Journal of Credit Risk 11: 73–94. [Google Scholar] [CrossRef]
- Schönbucher, Philipp J. 2001. Factor models: Portfolio credit risks when defaults are correlated. The Journal of Risk Finance 3: 45–56. [Google Scholar] [CrossRef]
- Schönbucher, Philipp J. 2003. Credit Derivatives Pricing Models: Models, Pricing and Implementation. Hoboken: John Wiley & Sons. [Google Scholar]
- Schwert, G. William. 1989. Why does stock market volatility change over time? The Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Sicking, Joachim, Thomas Guhr, and Rudi Schäfer. 2018. Concurrent credit portfolio losses. PLoS ONE 13: e0190263. [Google Scholar] [CrossRef] [PubMed]
- Song, Dong-Ming, Michele Tumminello, Wei-Xing Zhou, and Rosario N. Mantegna. 2011. Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Physical Review E 84: 026108. [Google Scholar] [CrossRef] [PubMed]
- Tumminello, Michele, Tomaso Aste, Tiziana Di Matteo, and Rosario N. Mantegna. 2005. A tool for filtering information in complex systems. Proceedings of the National Academy of Sciences USA 102: 10421–26. [Google Scholar] [CrossRef] [PubMed]
- Wishart, John. 1928. The generalised product moment distribution in samples from a normal multivariate population. Biometrika 20A: 32–52. [Google Scholar] [CrossRef]
- Yahoo! n.d. Finance. Available online: http://finance.yahoo.com (accessed on 9 February 2018).
- Zhang, Yiting, Gladys Hui Ting Lee, Jian Cheng Wong, Jun Liang Kok, Manamohan Prusty, and Siew Ann Cheong. 2011. Will the US economy recover in 2010? A minimal spanning tree study. Physica A 390: 2020–50. [Google Scholar] [CrossRef]
- Zia, Royce K. P., and Per Arne Rikvold. 2004. Fluctuations and correlations in an individual-based model of biological coevolution. Journal of Physics A 37: 5135. [Google Scholar] [CrossRef][Green Version]
- Zia, Royce K. P., and Beate Schmittmann. 2006. A possible classification of nonequilibrium steady states. Journal of Physics A 39: L407. [Google Scholar] [CrossRef]
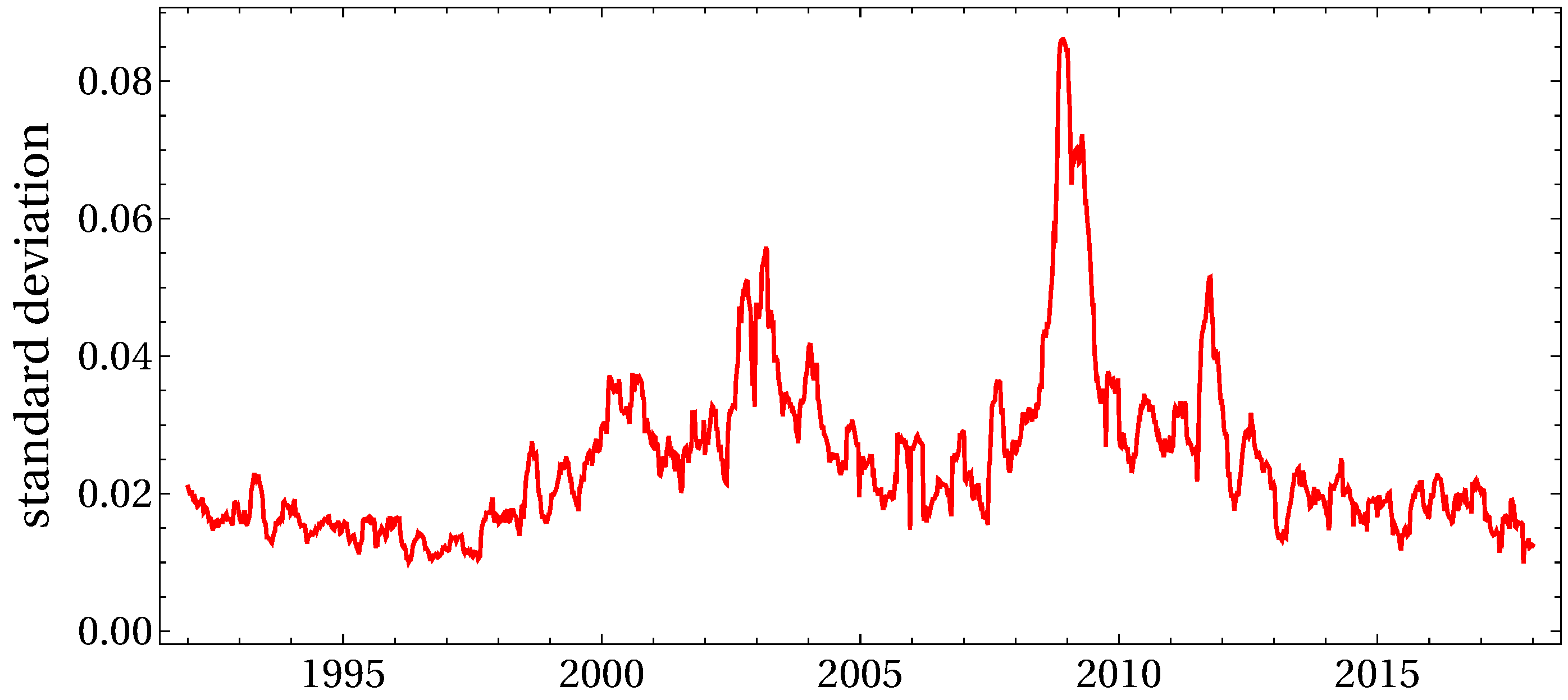
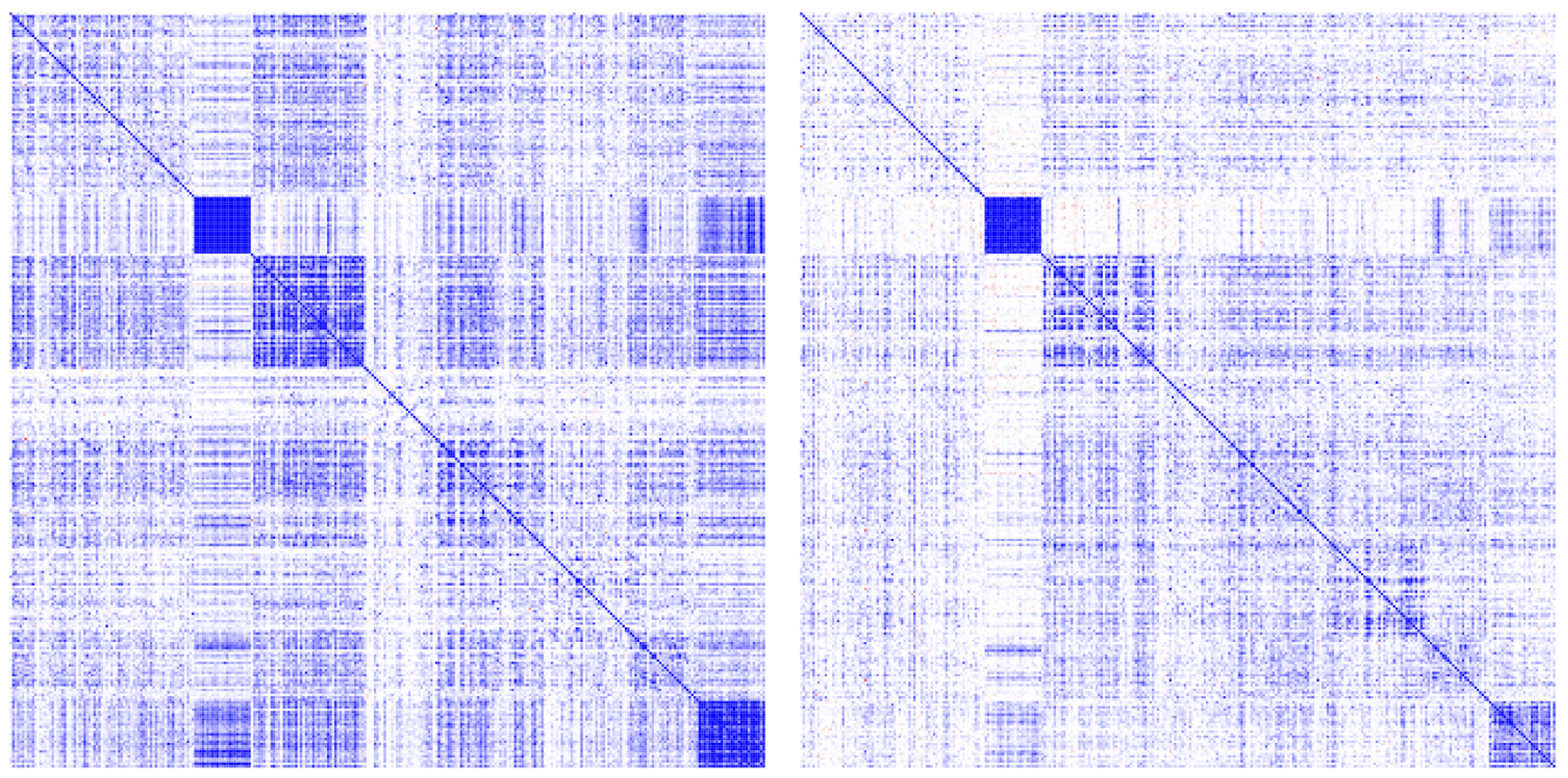
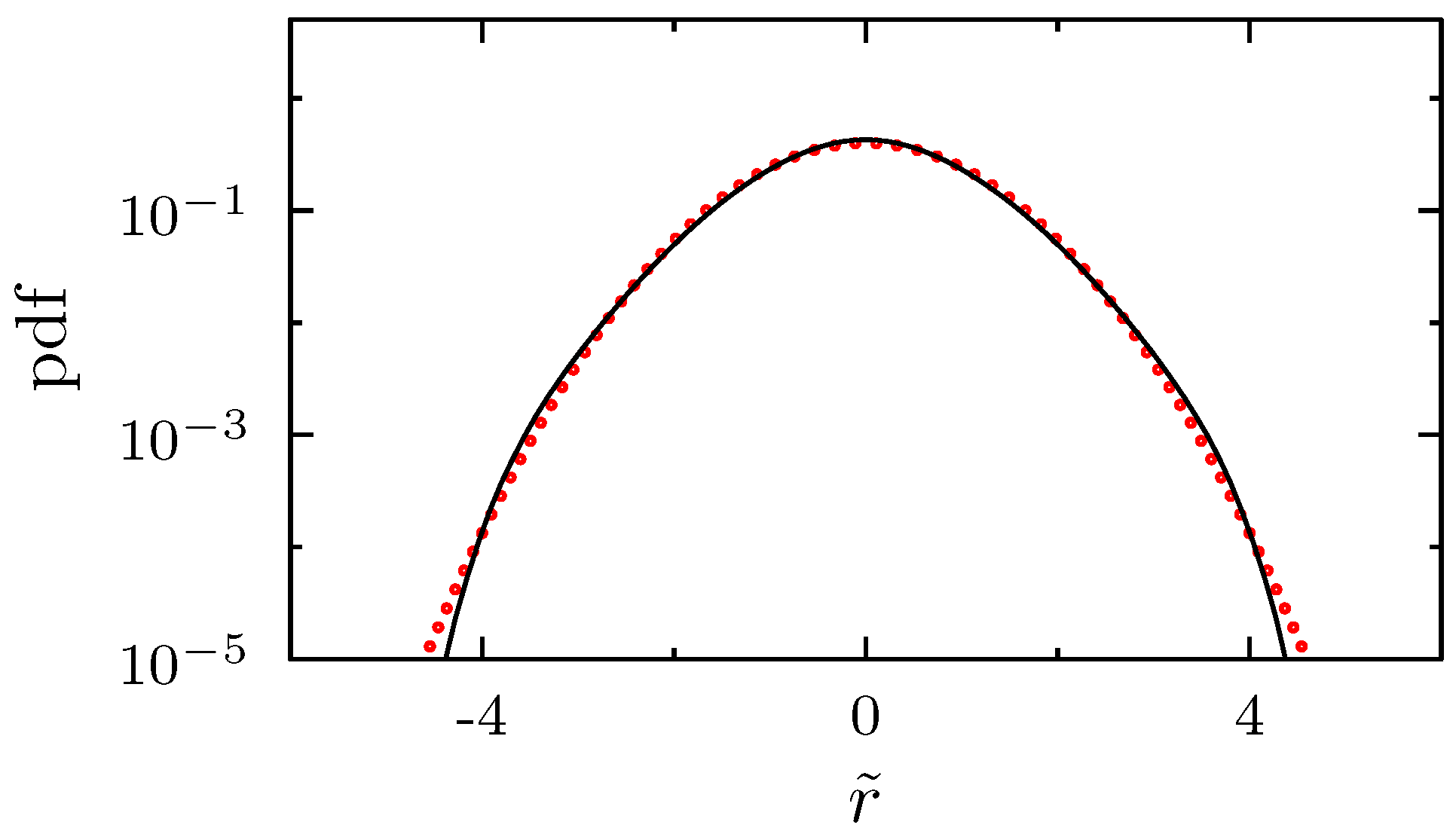
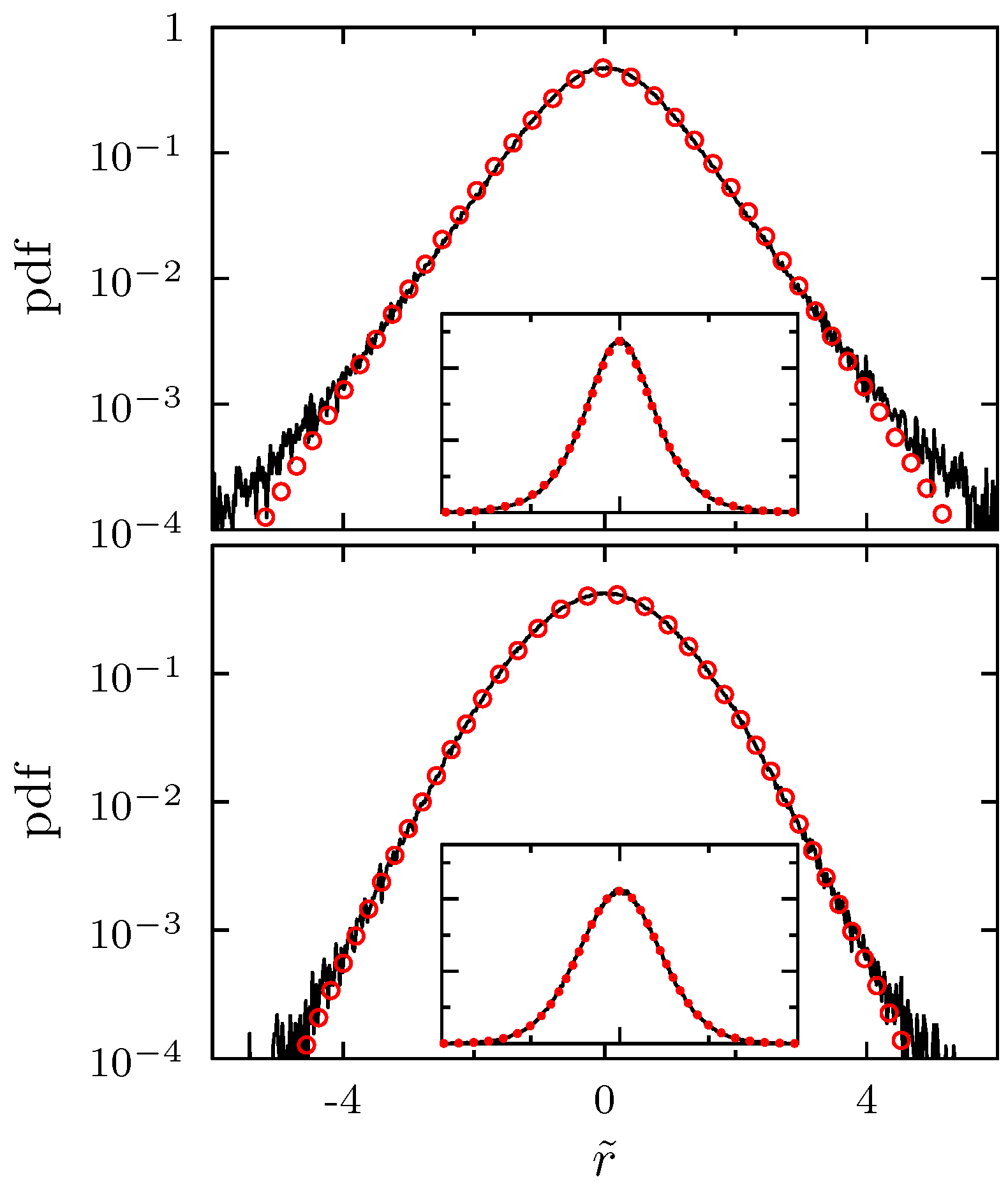
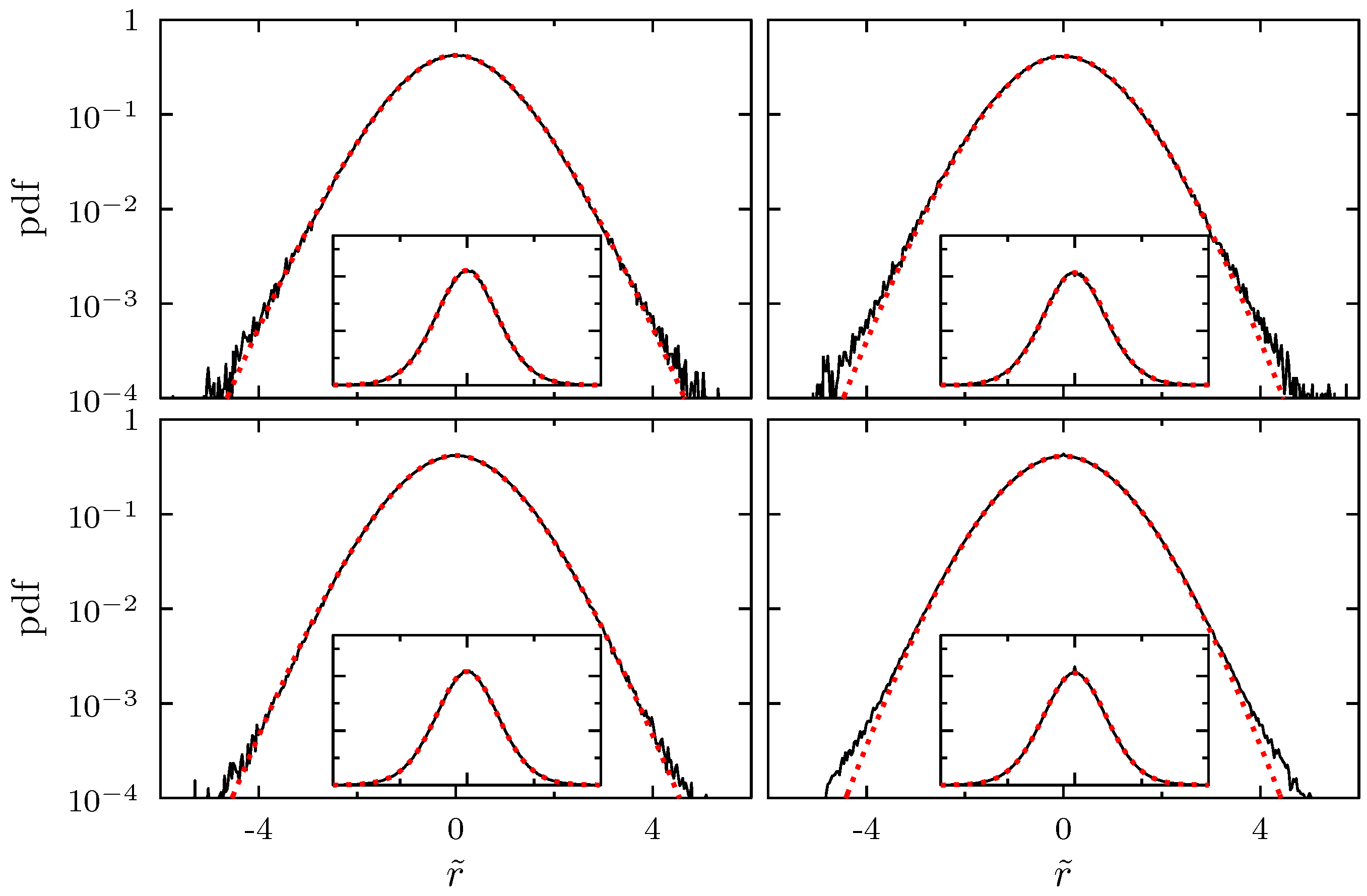
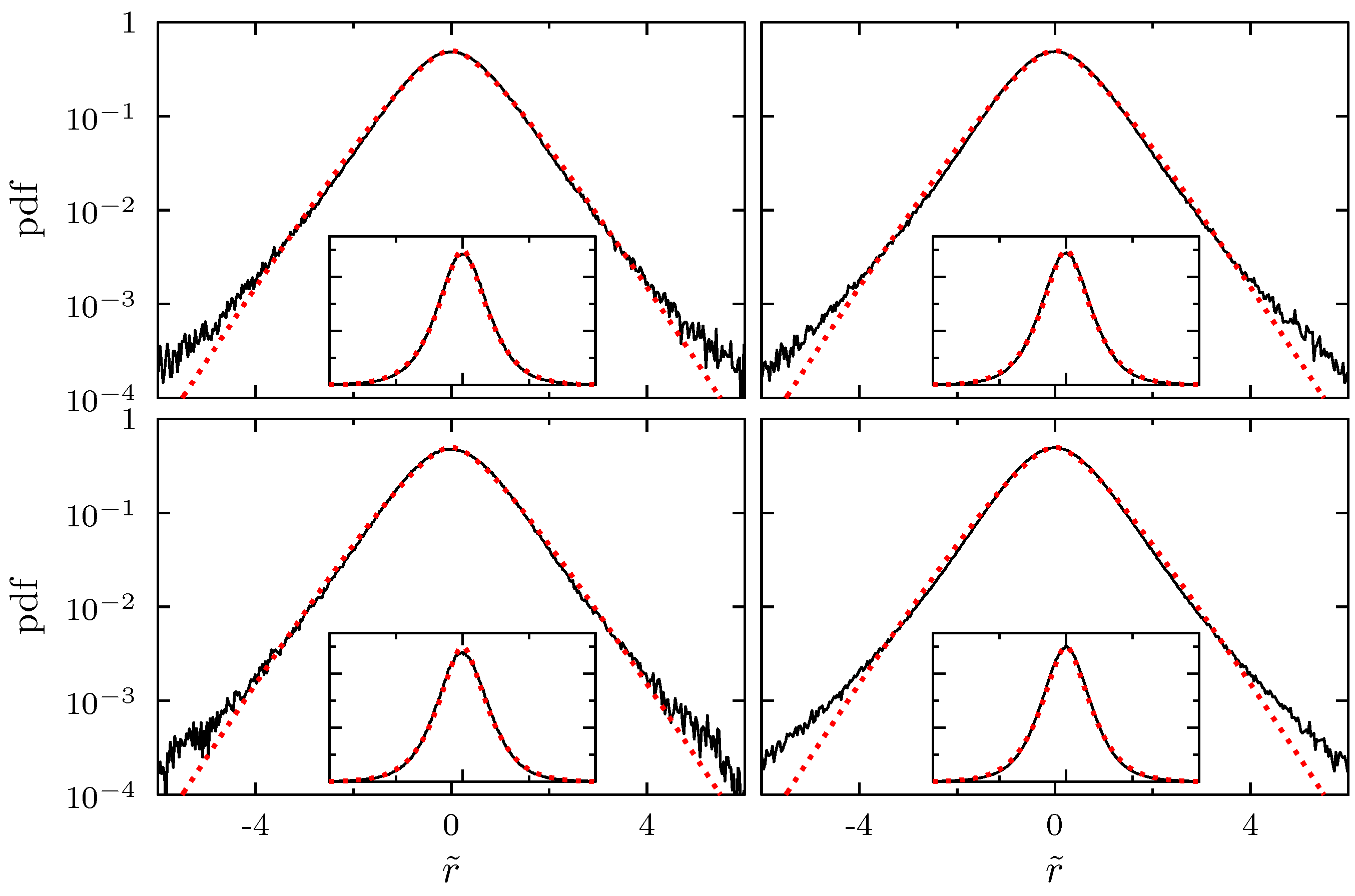
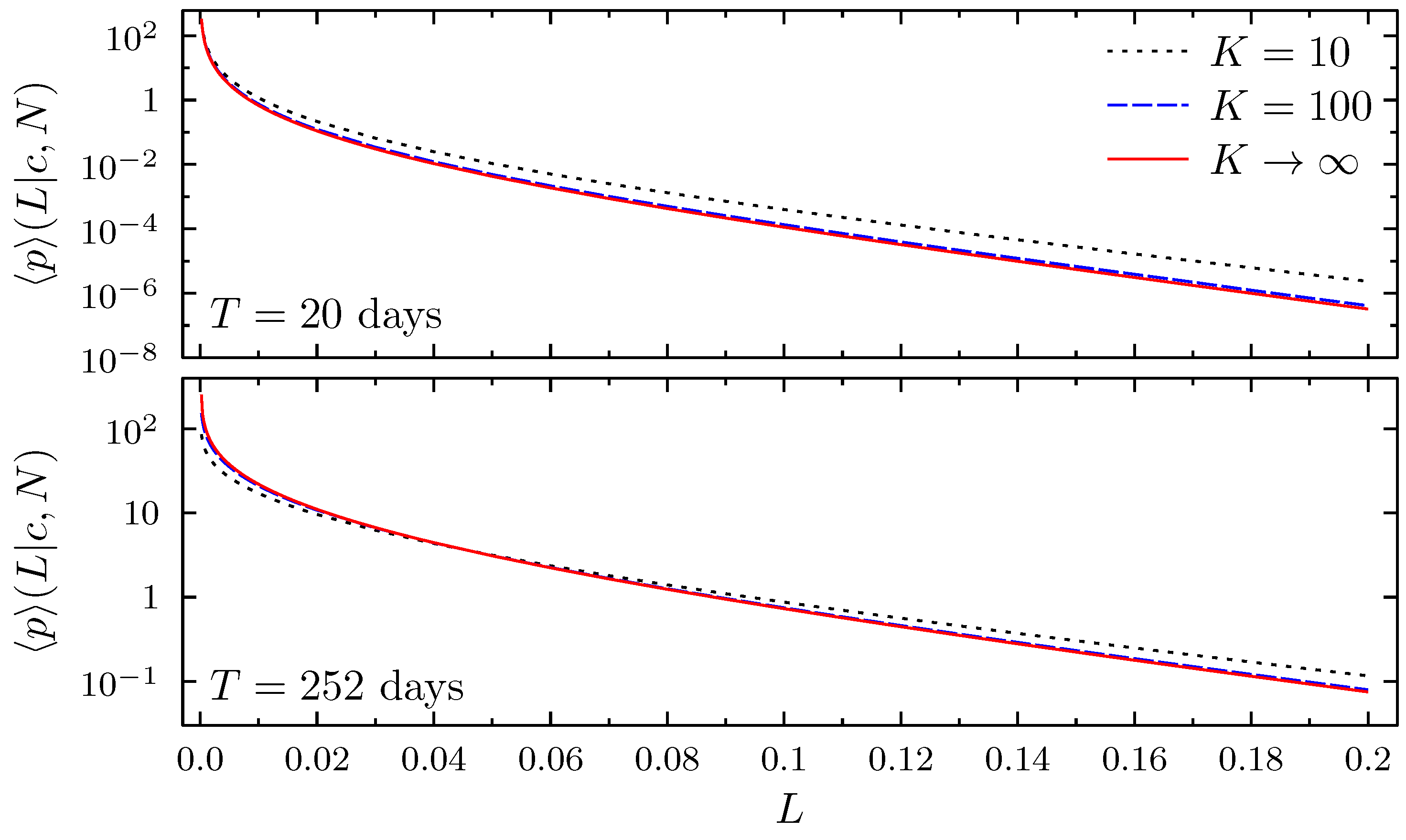
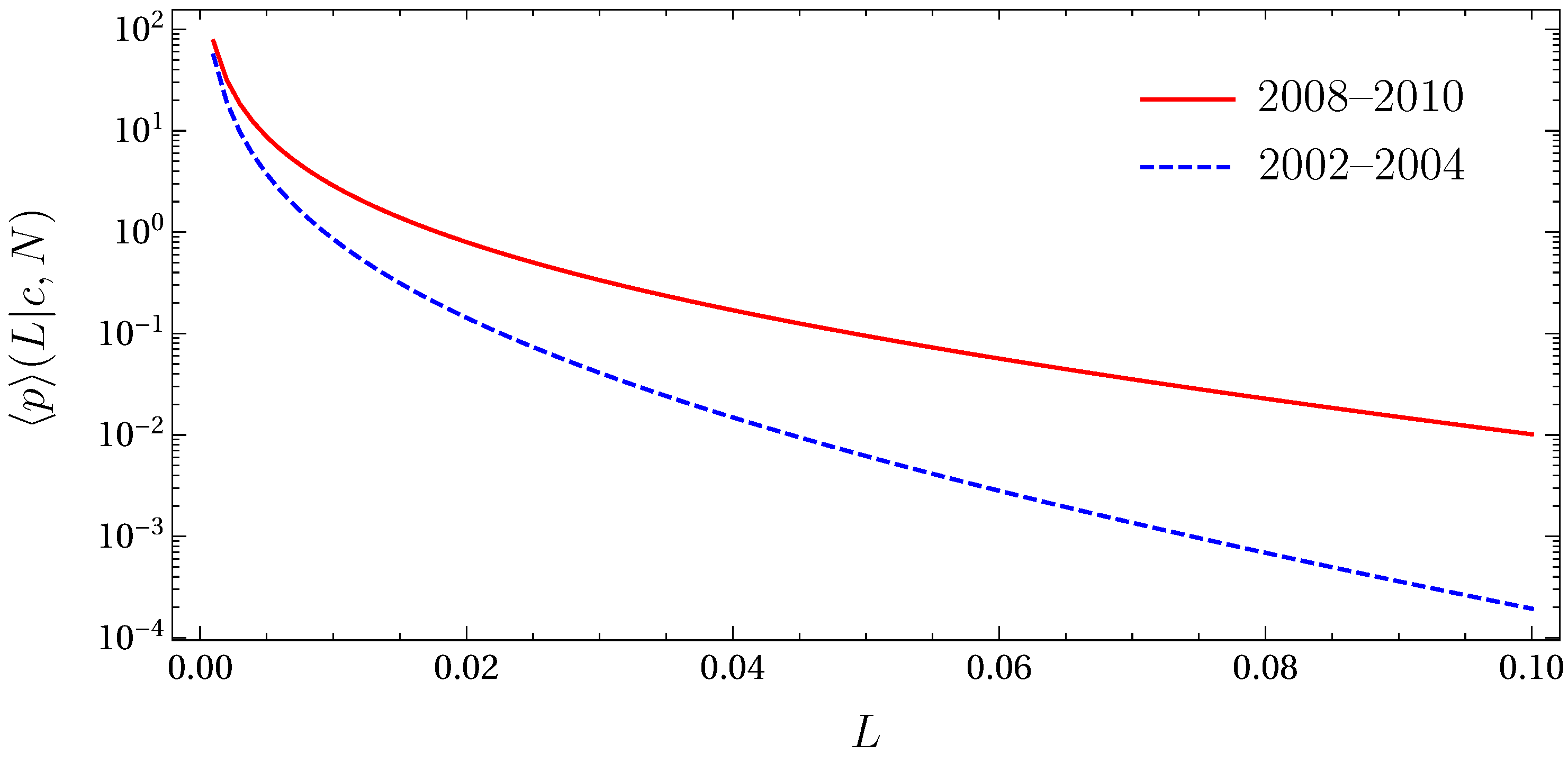
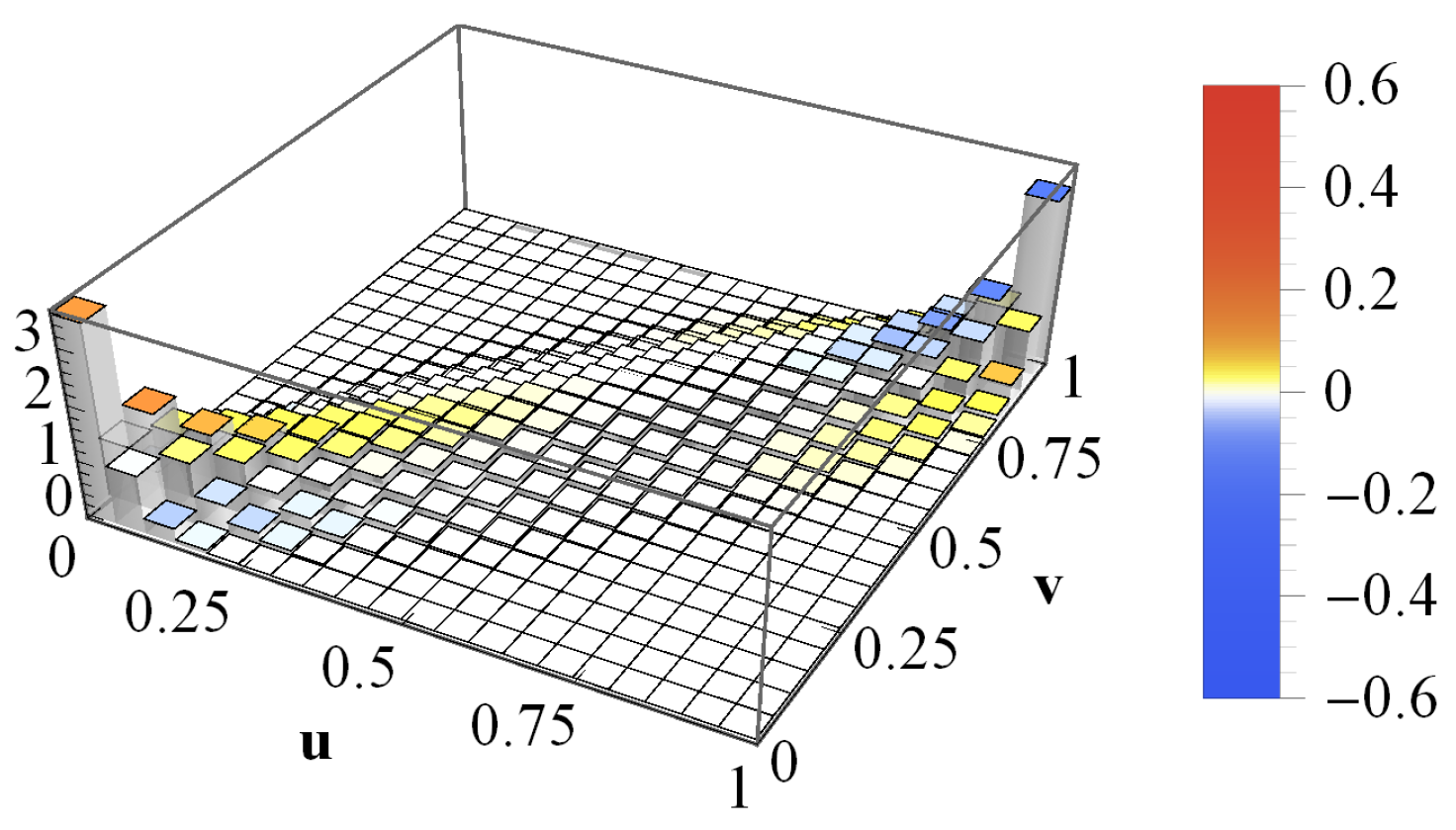
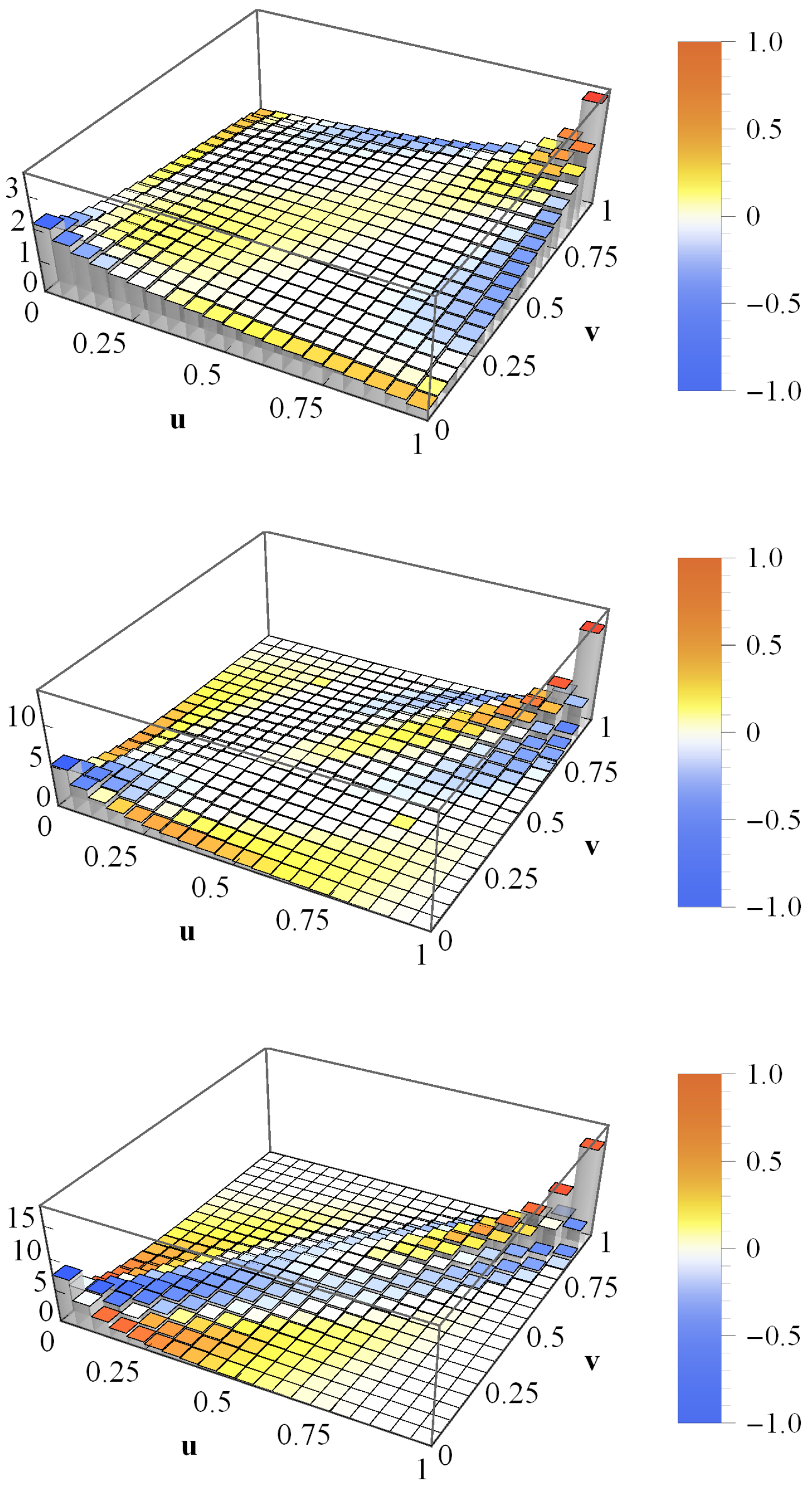
| Time Horizon for Estimation | K | in Month | in Month | c | |
|---|---|---|---|---|---|
| 2002–2004 | 436 | 5 | 0.10 | 0.015 | 0.30 |
| 2008–2010 | 478 | 5 | 0.12 | 0.01 | 0.46 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mühlbacher, A.; Guhr, T. Credit Risk Meets Random Matrices: Coping with Non-Stationary Asset Correlations. Risks 2018, 6, 42. https://doi.org/10.3390/risks6020042
Mühlbacher A, Guhr T. Credit Risk Meets Random Matrices: Coping with Non-Stationary Asset Correlations. Risks. 2018; 6(2):42. https://doi.org/10.3390/risks6020042
Chicago/Turabian StyleMühlbacher, Andreas, and Thomas Guhr. 2018. "Credit Risk Meets Random Matrices: Coping with Non-Stationary Asset Correlations" Risks 6, no. 2: 42. https://doi.org/10.3390/risks6020042
APA StyleMühlbacher, A., & Guhr, T. (2018). Credit Risk Meets Random Matrices: Coping with Non-Stationary Asset Correlations. Risks, 6(2), 42. https://doi.org/10.3390/risks6020042




