Abstract
Advanced machine learning has achieved extraordinary success in recent years. “Active” operational risk beyond ex post analysis of measured-data machine learning could provide help beyond the regime of traditional statistical analysis when it comes to the “known unknown” or even the “unknown unknown.” While machine learning has been tested successfully in the regime of the “known,” heuristics typically provide better results for an active operational risk management (in the sense of forecasting). However, precursors in existing data can open a chance for machine learning to provide early warnings even for the regime of the “unknown unknown.”
1. Introduction
Operational risk (OpRisk) is defined by the Basel Committee on Banking Supervision (BCBS) (2017a) as the risk of loss resulting from inadequate or failed internal processes, people, and systems, or from external events including legal risk. Within the new Based III framework, the standardised approach for measuring minimum operational-risk capital requirements replaces all existing approaches in the previous Basel II framework. This new standardised approach methodology is based on: (i) the Business Indicator (BI) as a financial-statement-based proxy for operational risk; (ii) the Business Indicator Component (BIC) calculated by multiplying the BI by a set of regulatory-determined marginal coefficients; and (iii) the Internal Loss Multiplier (ILM) as a scaling factor based on a bank’s average historical losses.
The Basel Committee on Banking Supervision (BCBS) (2017b) pointed out that, “The financial crisis highlighted two main shortcomings with the existing operational risk framework. First, capital requirements for operational risk proved insufficient to cover operational risk losses incurred by some banks. Second, the nature of these losses—covering events such as misconduct, and inadequate systems and controls—highlighted the difficulty associated with using internal models to estimate capital requirements for operational risk.” With this revised approach comes an implicit paradigm shift, as banks will be incentivised for actively fighting OpRisk (resulting in a lower scaling factor on the long run) instead of being incentivised for optimizing internal models to estimate distribution function for recorded losses. Any active ex ante management of OpRisk is the task of the business line (i.e., the “first line of defence” as defined by the Institute of Internal Auditors (IIA) (2013) with: (i) business line; (ii) central OpRisk management; and (iii) internal audit. Only the first line of defence has the chance to fight against OpRisk if an early warning system can detect “risk” before losses occur. The challenge is the correct separation between the majority of correct and a fraction of suspicious events based on some “learned” patterns especially for high-severity, but low-frequency events. Can the recent advances in “machine learning” help to forecast critical events before losses materialise?
Machine learning has achieved extraordinary success in recent years. Nonlinear learning is now the platinum standard for various challenging machine learning, e.g., in processing of natural language, playing sophisticated games such as Go or Poker, or driving vehicles (nearly) autonomously. Two main developments are accountable for those successes: the vast sets of available data and the massive increase in available computer power. This tipping point of available resources also lead to a shift from the original approaches of artificial intelligence (AI) fifty years ago, i.e., from the idea of computational “understanding” to data-driven computational statistics and pattern recognition.
State-of-the-art machine learning such as Relation Networks (RN, Santoro et al. 2017), Convolutional Neural Networks (CNN, first by Fukushima 1980; standard reference: (LeCun et al. 1999), current e.g.,: (Szegedy et al. 2015; Conneau et al. 2017)), Generative Adversarial Networks (GAN, Goodfellow et al. 2014) or the recently rediscovered Long Short-Term Memory feedback network (LSTM, Hochreiter and Schmidhuber 1997) are not elementary approaches, but combinations of basic methods of machine learning such as kernel methods or decision tree (Mohri et al. 2012) together with advanced artificial neutral networks (ANN). Machine learning can offer new approaches to risk management compared to traditional (statistical) methods, but has assumptions and limitations. Recently Jürgen Schmidhuber (2015) provided an excellent review about “learning” with the current techniques, which would be recommended for further details.
However, one has to be careful as any kind of “machine learning” is either based on large data sets (i.e., statistical approach based on measured data in the past) or on predefined set of rules (i.e., learing to play games). As Domingos (2016) wrote in a blog:
In reality, the main purpose of machine learning is to predict the future. Knowing the movies you watched in the past is only a means to figuring out which ones you’d like to watch next. … If something has never happened before, its predicted probability must be zero — what else could it be?
On the other hand, Domingos (2012) admitted that “data alone is not enough,” any prediction is limited and classifiers—as one example for machine learning—always need some ex ante knowledge.
In a nutshell, machine learning based on vast data sets can recognize patterns, reduce dimensionality, and extract estimations for statistical means of features, even if there is a great amount of “noise” in the data. Active management of operational risk has to deal with a power law1 behaviour of risk events (“fat tails” of the distributions with “rare evnts”), where no “regular” behaviour can be assumed a priori from date measurements from the past, as “rare” implies nonsufficient statistics. Nevertheless, there could be hidden pattern (in the sense of precursors of rare events), for which machine learning could be useful to provide early warnings.
The scope of this paper is to examine the (possible) implementations of machine leaning compared to (human) heuristics for an “active” operational risk management. In contrast to the established ex post statistical analysis of measured OpRisk data, the questions of this paper are:
- Is there an opportunity to apply machine learning to predict the future beyond statistical estimations of average distribution functions to support active operational risk management?
- For what regime of the “unknown”—rare events or even unforeseen event types—could machine learning be applied?
- Has machine learning always benefited compered to human heuristics when it should be implemented for fighting OpRisk events?
Those three questions will be discussed starting from a review of the typical power-law behaviour of operational risk data with three (overlapping) regimes of the “known”, the “unknown”, and the “unknown unknown”. For all three regimes, the advantages and disadvantages of machine learning will be analysed and discussed. It should be remarked that an “active” OpRisk management fighting events before losses occur is a different approach compared to the established perspective on operational risk to monitor/measure occurred losses and estimate capital requirements with ex post data about bank’s average historical losses. For a detailed discussion of ex post operational risk controlling, the reader should refer to the literature, e.g., “Modeling, Measuring and Hedging Operational Risk” by Marcelo G. Cruz (2002).
2. Active Operational Risk Management and the Domains of the “Unknown”
To set the scene for the discussion, the aspect of an “active” in operational risk management has to be defined and separated from statistical methods for operational risk controlling.
First, a principle difference between OpRisk and other types of risks such as market risk or credit risk results from the different perspectives. The starting point for market risk or credit risk is always a portfolio of assets. For such a portfolio, a typical risk indicator such as, e.g., value-at-Risk can be calculated ex post and for every potential new transaction to a portfolio, the incremental risk can be calculated ex ante. Contrary, OpRisk is usually seen from an ex post perspective to calculate and report risk indicators. However, an active OpRisk management require early-warning mechanisms to make decisions about potential events which can be seen at the horizon.
The second difference can be derived from Figure 1, as both the aggregated loss data taken from Basel Committee’s ‘2008 Loss Data Collection Exercise for Operational Risk’ (in the following: Basel Committee on Banking Supervision (BCBS) 2009) and the data set of Nagafuji et al. (2011) for loss data among Japanese banks show a clear power-law behavior for the tail of the frequency-severity distribution. As already pointed out by Moscadelli (2004); De Fontnouvelle et al. (2005); Giacometti et al. (2007), such data for severity S (equaling monetary loss due to OpRisk events) and frequency F(S) can be fitted with a power law distribution F(S) ∝ S −λ. For a more detailed analysis, a Generalized Pareto Distribution (GPD; see, e.g., (Chavez-Demoulin et al. 2006; Ferreira and de Haan 2014; Ferreira and Ferreira 2017)) or other sophisticated statistical distributions can be applied, but for the scope of this paper, a power law provides the simplest fit to data with “fat tails” following Occam’s razor and reveals the fundamental difference in the shape of the distribution to the “peaked” Gaussian-like distribution used for market and credit risk.
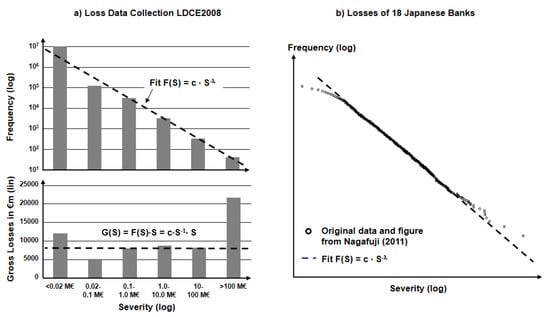
Figure 1.
Distribution of number of losses (frequency) and gross loss amount by severity of loss reported by Basel Committee on Banking Supervision (BCBS) 2009 and data of Nagafuji et al. (2011) for loss severity distributions among Japanese banks (for details, please refer to the respective publications). The frequency-severity distribution Basel Committee on Banking Supervision (BCBS) 2009 is plotted in double logarithmic scales, while the total amount-severity distribution is a lin-log plot (see detailed discussion in (Milkau and Neumann 2012)).
Third, power law distributions are typical for “destructive” phenomena, which range from insurance events such as earthquakes, fires, or avalanches, to distribution of the mass of asteroids (created by destructive collisions) and fragments in heavy ion collisions (see Clauset et al. 2009; Trautmann et al. 1993). Therefore, the severity S and frequency F(S) are plotted in a double logarithmic diagram in Figure 1, and the power-law distribution is a straight line with log10(F) = const − (λ • log10(S)). This representation is the same as the fatality-frequency diagrams2 in quantitative risk assessment for complex technical installations as discussed by Aven (2011). Power-laws distribution need not have an infinite first moment, but always have some divergent moment. However, typically operational risk data in banks can be fitted with a power law with a lambda smaller than 1, which makes this type of distribution problematic for calculations of economic capital due to an infinite mean value.
The fourth difference is associated with the third one, as a power-law distribution implies that unprecedented events (i.e., event not available in any data set) could be very catastrophic in the sense of “one-claim-causes-ruin” as coined by Nešlehová et al. (2006).
Looking at the difference between an estimation of future events within a measured distribution and a prediction about the “unknown” in the sense of Knight (1921), Aven (2016) discussed the different concepts of “risk” in current terminology as especially useful for risk managing in typical high-risk industries [quote]:
“aleatory (representing variation) and epistemic (due to lack of knowledge). For aleatory uncertainty there is broad agreement about using probabilities with a limiting relative frequency interpretation. However, for representing and expressing epistemic uncertainty, the answer is not so straightforward.”
An illustration is given in Figure 2, with a measured distribution of OpRisk events in business line transaction banking. Taking into account work of Motet and Bieder (2017); Aven (2016); Milkau (2012); Kwakkel and Pruyt (2011); Samson et al. (2009), one can build a bridge from the “known” to the “unknown unknown” for Risk R = {Event, Consequence, “measured” Frequency and “estimated” probability including SoK3: (Strength of Knowledge supporting P)}4:
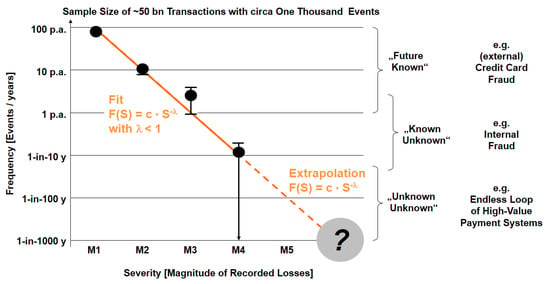
Figure 2.
Comparison of a distribution of operational risk events based on decade years of OpRisk data (including error bars and fit function; data taken from (Milkau 2012)) with the three different domains of the Knightian “unknowns” and typical examples for actual OpRisk events. The three domains are overlapping in reality and the separation depends on the data set to be analysed.
- Historical loss data with actual (equaling measured) events, defined by R0 = {E, L, N; SoK = 1} with type of OpRisk event E, loss L, recorded number of events N. For aggregated events, a statistical measurement error can be added Ri = {Ei, Li, Ni, σi; SoK = 1}.
- Operational risk R = {E, L, Ps; SoK} with a Bayesian interpretation of Ps as a subjective measure of uncertainty about the risk as seen through the eyes of the analyst and based on some assumptions and some knowledge about the “risk-generating process,” i.e., the Bayesian perspective (usually with an assumption that the underlying process is going to be repeated for an infinite number of times).
- Estimation of (future) risk R* = {E, L, Pf*, U(Pf*), SoK} while the probability Pf of the relative frequency is unknown as no empirical data are available (the “extrapolation” area for magnitudes >10 million € in Figure 2), when the risk generating process is time-dependent (i.e., nonstationary), or when assumptions for an extrapolation show large variations (e.g., in risk self-assessment). An estimation for R* includes an estimated Pf*, the uncertainty U of this probability U(Pf*), and the Strength of Knowledge SoK, on which the estimation is based.
- Uncertainty of “unknown” future with replacement of the frequency-interpreted probability Pf by the uncertainty U(SoK) itself, giving a risk perspective RU = {E, L, U(SoK)}. This is more than a simple algebraic replacement, as it shifts the concept of risk from the calculation of probabilities (with a given SoK) to the question of uncertainties of ex ante knowledge (with SoK << 1).
- The “unknown unknown”, i.e., the risk of “one-claim-causes-ruin” with no historical knowledge and low probability Pf e.g., about 1-in-10,000 years. Such events are not repeatable (as one event is, per definition, a final catastrophe), which contradicts the assumption of the probabilistic interpretation and which indicated a break from “measurable” monetary loss to “possible” disaster with no knowledge: RD = (E, Disaster, SoK ≈ 0). As an intermediate conclusion, one can ask the question whether any kind of machine learning based on measured data could handle those aspects of risk far beyond the existing data.
3. Applications of Machine Learning for the “Known”
Credit card fraud could be seen as a reasonable proxy for OpRisk in the high frequency/low severity domain and can be taken as an illustrative example for the development over the last decades. Along with the introduction of electronic card payments (replacing the card imprinter and the paper slip), this combat changed from ex post reporting of fraud (with weekly “hot list” bulletins passed to the merchants) to real-time authorization in the early 1980s. The fraud management in credit card authorization systems includes two main steps:
- feature extraction about customers’ behaviour pattern to pay by card as classification criteria;
- classification of a single transaction at checkout “on the fly” with an authorization requested.
Banks and credit card companies (e.g., VISA) started in the mid-1990s to test and implement the first artificial neural networks (ANN) as an additional component to enhance the fraud detection systems (see e.g., PRNewswire 1993; Ghosh and Reilly 1994; Ehramikar 2000; Pun 2011). Today, e.g., VISA applies a combination of machine learning methods from statistical techniques such as regression analysis via decision trees to ANN to provide classification.5 A similar example—but focussed on corporate fraud payments—was developed recently by Vocalink Analytics (a Mastercard company) and NatWest and launched as Corporate Fraud Insights (Vocalink 2018). However, VISA (CyberSource 2016) pointed out the limitations of machine learning [emphasis by the authors]:
- “Machine learning relies on good input data”.6
- “Machine learning is only as good as the human data scientists behind it”.
- “Machine learning is often a black box, especially when self-learning techniques are employed. The machine can learn the wrong thing”.
- “A way to counteract the downsides of machine learning is to combine an automated machine learning system with a rules-based approach”.
One critical factor in understanding the machine learning “black boxes” results from a holistic perspective. With a wrong tuning, the learner could be rather effective in identifying fraudulent events, but with the collateral damage of many false positive identifications. Classifying consumers as “false positive” is annoying for a buyer not able to pay with the card. As Bhalla (2016) ellaborated:
“major consumer pain point of being falsely declined when trying to make a purchase”.
First, one has to think about the basic definition of “risk.” Since 2009, there is a new ISO 31000 definition of risk (see Purdy 2010), which shifted emphasis from the ex post perspective to the possibility of an achievement of an objective (e.g., a commercial objective to generate a profit from credit card issuing including risk coverage of fraud, but also cost for customer retention). When risk is defined like this, it reveals more that managing risk is a process of optimization that makes the achievement of those objectives more likely. Active risk management has to reduce the overall risk, e.g., in cards business but with a holistic perspective7 about machine learning from increasing true positive hit rate to reducing “public” customer complaints (as a part of reputational risk management).
Second, one can usually observe a misunderstanding of the performance of a binary classifier (with true positive rate/hit rate and true negative rate versus positive predictive “PPV” and negative predictive value “NPV”). A recent example—although not associated with financial services—was described by Spielkamp (2017): the confrontation of ProPublica (a nonprofit news organization) and Northpointe, (the developer company) about COMPAS. COMPAS is a software used in the USA to forecast which criminals are most likely to reoffend.
The question was whether, “blacks are almost twice as likely as whites to be labelled a higher risk but not actually reoffend”. Without going into the details, the main conclusion was according to Krishna Gummadi, head of the Networked Systems Research Group at the Max Planck Institute for Software Systems in Germany, that both positions (the software is biased or not) were “right,” as ProPublica compared [quote] “false positive rates and false negative rates for blacks and whites and found them to be skewed in favor of whites. Northpointe, in contrast, compared the PPVs for different races and found them to be similar”.
Third, Dietvorst et al. (2015, 2016) elaborated about a natural “algorithm aversion,” i.e., that “people erroneously avoid algorithms after seeing them err,” although the performance of machine algorithms was better compared to human forecasts. As a consequence, any discussion about machine learning in OpRisk managing with experts and management has to take into account the psychological dimension of “decisions” made by machines.
As a synopsis for the first domain of the “known,” three issues can be summarized concerning machine learning:
- There are differences of OpRisk types (e.g., credit card fraud versus delayed corporate actions), which all have to be treated differently and with different machine learning approaches.
- A combination of existing data plus ex ante knowledge (typically described by “rules”) is needed to train the learners to extract individual patterns.
- A holistic understanding of the (commercial) objectives t is required to avoid a “right” fine-tuning of the learners to the “wrong” goals. There is a meta-risk to solve a single problem (e.g., fine-tuning of fraud protection systems), but increase the holistic business risk due to inappropriate model assumptions.
4. Machine Learning and Heuristic for the “Known Unknown”
In the domain of the “Known Unknown,” there is a general problem for any kind of generalisation due to the limited available data (or in other works risk of “overfitting”). A well-known example in the case of classifiers is the problem of bias and variance, or underfitting versus overfitting. Hastie et al. (2009) defined:
- Bias as a machine learning’s tendency to learn a wrong thing consistently (due to erroneous assumptions in the underlying learning algorithm, e.g., in linear “leaners”);
- Variance as the tendency to learn random “noise” irrespective of the real signal (e.g., in decision trees or random forests).
This problem applies to all forms of supervised learning, whether classification, regression (function fitting), or a structured output learning. All models of supervised learning assume labelled input of right and wrong example data. For the domain of the “Known Unknown” this issue is illustrated in Figure 3 with a very simple but general example: A game of darts is used to explain the situation of OpRisk events with frequencies of 1 event p.a. to 1 event in a decade (see Figure 2). We can derive a generalized sample (equaling one round of darts with n = 20) from the existing historical records of OpRisk data within the whole data set of 50 billion transactions in one decade. However, the OpRisk events in this domain are rather solitary events without a reasonable generalization:
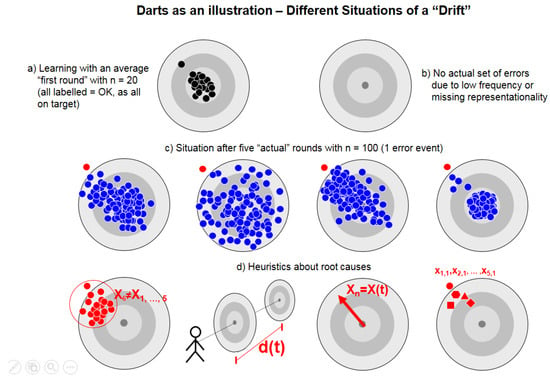
Figure 3.
Throwing darts as illustration for the challenges in the domain of rare OpRisk events (one in a year to one in a decade). See text for more explanations.
- In this domain, it is not possible to provide data with a “negative” label—so what should the learner learn?
- If we add some known rules of the game (only darts on the target are “OK”), we already have a classifier (in the sense of “x2 + y2 < r2”), which does not require any learner.
- The challenge of active risk management in the first line of defence would be to “predict” a trend, which could possibly lead to an OpRisk event—but ex ante.
In Figure 3, the illustrative example shows a situation with (a) a typical data set for events with the label “OK,” which (b) indicated the problem that no generalizable negative event is present. The four graphs (c) describe possible developments in this game after five more rounds of 10 (equaling 50 actual events). In all scenarios, one event is out-of-target with a similar position outside the disc, but the route courses (d) for the scenarios are different:
- shift of the barycentre of the fifth series (by chance);
- literally “moving target” due to a drift of the dart board;
- constant drift of the barycentre of the series;
- singular “lemons” (e.g., the first try in a series or, literally, the first cars produced on Mondays).
Without any ex ante experience, or “heuristics,” about such possible trends, it would not be feasible to extract any reasonable early-warning signal from a trend of few significant events. In such cases—and even more with 50 billion transaction in a decade with few OpRisk events to learn from—heuristics provides high effectiveness (see Gigerenzer and Brighton 2009; Gigerenzer et al. 2011; Gigerenzer and Gaissmaier 2011).
For the domain of the “known unknown,” it is crucial that long-term experience of the experts is included to detect early-warning signals for future OpRisk events. The idea of “data only” falls short in this middle domain of a power law distribution of OpRisk events.8 The use of ex ante knowledge is illustrated in Figure 4 (taken from (Bott and Milkau 2015)) with a time series of reconciliation data in transaction banking. One known source of derivations from a benchmark emerge from the introduction of new products, which were tested but show unexpected effects in real production. Those new products are introduced in a ramp-up procedure, starting with few transactions at the beginning and an increase over some time. The experience (i.e., heuristics) is a typical pattern for problem (if any) with repeated precursors at the beginning, followed by extended sequence of events and a “delayed” situation with significant derivation from the defined benchmark. Based on these heuristics, even patterns with a noncritical behaviour can be potential early-warning indicators. Although it is impossible to monitor all possible trends for OpRisk events, a number of such “ways into risk” are known usually (e.g., derivations in reconciliation, delayed payments, clustering of cancellations, timing correlation of first and second step of tasks with four-eye-principles, increase of allocated system resources, etc.).
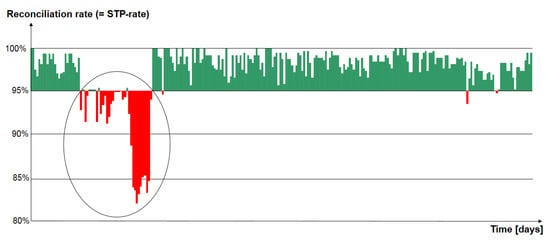
Figure 4.
Example for an ongoing monitoring of a straight-through-processing (“STP”) reconciliation process over one year with a typical development of a risky situation: 1. repeated precursors; 2. extended sequence of precursors, “delayed” situation with significant derivation from the defined benchmark; i.e., 95% STP rate (see detailed discussion in (Bott and Milkau 2015)).
In the domain of the “known unknown,” a combination of heuristics (“what to learn”) and advanced machine learning (“how to learn”) can be a helpful tool for active risk management in the first line of defence with enhanced detection of early warning patterns. In those cases, more simple learners9 have practical advantages and can help to avoid an additional model risk from “black box” tools, which can provide false positive warnings with financial losses due to “emergency shutdown” in a business line. However, each sentry knows that keeping watch for things that happen rarely but with large impact is a very boring task. Technology is better for performing this.
Finally, yet importantly, there are some similarities between such an active OpRisk management and computer games (e.g., with attacks to be fought off, or developments to be predicted and circumvented). As state-of-the-art machine learning, like deep reinforcement learning, achieved tremendous success in playing games, it will be an open issue for future research, whether these sophisticated techniques could provide benefits for the first line of defence.
5. Machine Learning It the “Unknown Unknown”
For a discussion of the domain of “once in a lifetime events,” it is important to recall the scope of the business. The Conduct Costs Project Report 2016 (McCormick and Stears 2016) for the top 20 banks with highest conduct costs reported a grand total for 2011–2015 GBP bn 252.25 and (one year overlapping) for 2008–2012 GBP bn 197.76, which roughly results in global conduct costs of GBP bn 40 p.a. This magnitude has to be compared to publicly reported OpRisk events, in which typically the final financial loss is smaller compared to the nominal value of the transaction. One example is the accidentally transferred payment at German state bank KfW recently [quoted from Reuters (2017)]:
“German state bank Kfw accidentally transferred 7.6 billion euros ($8.2 billion) to four other banks but got the money back, incurring costs of 25,000 euros, executive board member Guenther Braeunig said on Wednesday.”
KfW explained the event in a press release [quote from (KFW 2017)]:
“In the afternoon of 20 February 2017, a mistake in configuration works performed by an experienced IT programmer of KfW caused a temporary system bug in a payment transaction software. This led to multiple payments being made by KfW to four banks.”
This example can illustrate two features, which are rather characteristic for the discussion of the “Unknown Unknown”
- A gap between actual financial losses (reported data for the event including applied measures to contain the loss) and potential “worst case” scenarios (for a situation that never happened before in reality);
- Complexity of the root cause, which is typically a coincidence of many “elementary” causes.
The “Strength of Knowledge” (SoK) for the “Unknown Unknown” is SoK << 1. Therefore, a naïve application of machine learning can be an additional source of risk (i.e., model risk), as the extrapolation can be misunderstood for its prediction power (see Figure 5). Nevertheless, the power-law behaviour of the OpRisk event distribution can provide some qualitative guideline to “get a feeling” for the “Unknown Unknown.” For a detailed theoretical introduction about power laws in theory and nature, the reader is referred to a recent review of Marković and Gros (2014). For the purpose of this paper, the chief economist of the Bank of England, Andrew G. Haldane (2012), summarized basic insight about power laws in a speech focused on risk management in banking. He explained two possible mechanisms: self-organized criticality (“SOC,” proposed in the seminal work of (Bak et al. 1987)) and highly optimised tolerance (“HOT,” compilation by Carlson and Doyle (2002)).
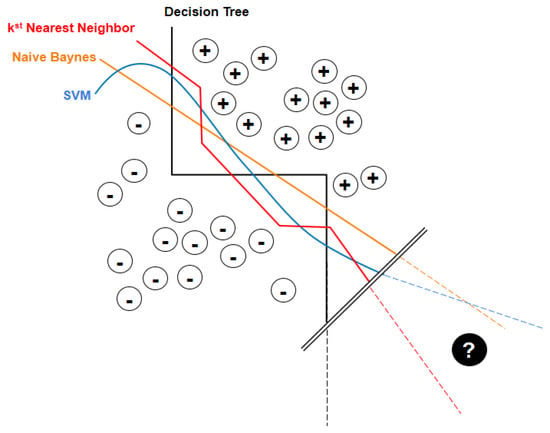
Figure 5.
Problem of a classification based on a training data set with two classes of events “+” and “−”, when extrapolated into a domain far off the existing data (based on discussion of different AI methods in (Domingos 2012)).
Summarized from Haldane (2012), both mechanisms can be illustrated with the development of forest fires as an example:
- In the SOC framework, one would imagine an area, where trees are naturally and randomly growing with occasional lightning strikes that could cause a fire. Over longer time, the forest will “organise” itself (internally) into a meta-stable state: most of the time, fires are small and contained, but on rare occasions, a random lightning strike can cause the forest to be lost.
- In the HOT framework, the forest is not “self-organising,” but a (human) forester takes concern for the expected yield of the forest with a trade-off: a more densely filled forest makes for superior expected yield, but it also exposes the forest to higher fire risk. The human (external) response is to build firebreaks: larger in number where lightning strikes, fewer where they are rare. This arrangement maximises expected yield. However, it will also result in occasional “systemic” forest fires (as, e.g., scrub will be removed, which typically leads to small fires in free nature, which “clean” the forest).
If this assumption is right, catastrophic events would be rooted in smaller events and there could be a “hidden” trace from the “known” to the “unknown.”10 Future research at the crossroad of machine learning and operational risk will be needed to get more insight.
6. Outlook: Fighting Risk with Machine Reasoning
Although the scope of this paper is on machine learning and feature extraction, Artificial Intelligence has the potential to go beyond the task of classification, as machine reasoning is able to make decisions in situations without predefined solutions. For an introduction to machine reasoning, the reader is referred to the work of Bottou (2014) “From machine learning to machine reasoning.”
As machine reasoning does not require vast amounts of data, but is based on formalised experience, machine reasoning can bridge the gap for the use in an active OpRisk management in the first line of defence. Following Boos (2017), the building blocks of a machine reasoning systems are:
- Knowledge Items (KI) as atomic pieces of experts’ knowledge about OpRisk management and possible action in the first line of business to react;
- Knowledge Core (KC) as accessible semantic map of an organization’s data based on KIs plus information about the structure of an organization;
- Machine Reasoning (MR) to solve ambiguous and complex problems.
An approach “KI ⇒ KC ⇒ MR” has been applied for automatic decision making in other contexts, but could likewise be applied to OpRisk management to fight risk by real-time automation, if an early warning for OpRisk is triggered. Such machine reasoning is already used in other situations (such as data center ticket management, etc.), but not in actual production in transaction banking.
The advantage of machine reasoning would be the instant reaction to new situation (as illustrated in Figure 6). If the actual situation is changing (indicated by the move of a barrier in the labyrinth in Figure 6), the system would be able to use the stored KI in the KC to derive a new solution to the challenge (leaving the labyrinth). Applied to real-time response to predicted OpRisk event, an “adaptive automation” could be helpful in transaction banking with a tremendous magnitude of transaction and only few warnings for OpRisk events, which is a rather boring situation for humans but not for machines. Nevertheless, such an approach requires verification in real-world situation in a first line of defence.
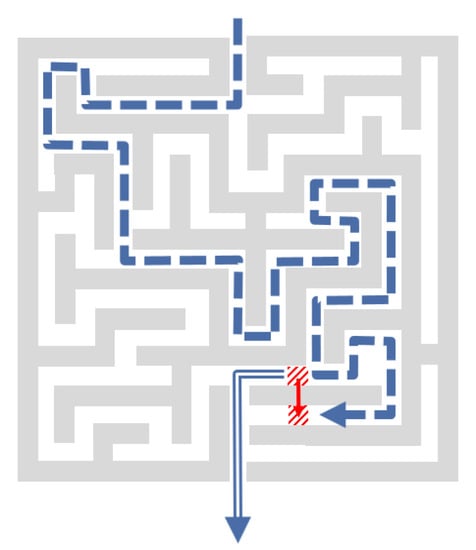
Figure 6.
Machine reasoning illustrated by the example of “way through a labyrinth” (based on discussion in (Boos 2017)).
7. Conclusions
The characteristic power-law behaviour of operational risk with the three regimes of the “known,” the “known unknown,” and the “unknown unknown” is a challenge for any mathematical method trying to include all under one umbrella. Traditionally operational risk controlling was dominated by the ex post calculation of economic capital, which implies, inter alia, the assumption of a repeatable situation. Current approaches of an active ex ante operational risk focuss on “learned” patterns to fight OpRisk before losses will occur. However, this approach faces the problem of (limited) history of measured data compared to the long-term power-law-like behaviour with a “fat tail” with few or no events available to train a machine learning algorithm. An overview is given in Table 1 with a comparison of different statistical and machine learning approaches for the three different regimes in operational risk management.

Table 1.
Comparison of different statistical and machine learning approaches for the three different regimes in operational risk management.
While typical machine learning uses available data sets to extract features and make estimations for future distributions, this approach is only justified for the domain of the “Known” with sufficient existing OpRisk data. In the domain of the “Known Unknown” with rare or even solitaire data, data-dependent machine learning cannot provide a better understanding. Long-term experience of the experts (“heuristics”) is crucial to detect early warning signals. In the future, a combination of heuristics (“what to learn”) and advanced machine learning (“how to learn”) can support active risk management in the first line of defence with enhanced extraction of early warning patterns.
In the (extrapolated) domain of the “Unknown Unknown,” any prediction should be treated with strong awareness to model risk due to naïve application of such methods. However, the underlying power-law systematics can give a guidance how to test machine learning to provide early warning forecasts with searching for “small” precursors for delayed severe OpRisk events.
Future research is required to enable machine learning of “hidden” pattern in the domains with few/solitary OpRisk data but where machine learning can be combined with heuristics and/or with information about the whole “environment,” in which OpRisk events can occur.
Acknowledgments
The authors thank Rudi Schäfer, Frankfurt, and unknown referees for valuable comments and discussion.
Author Contributions
Udo Milkau and Jürgen Bott equally contributed to this paper (for conception, analysis and writing).
Conflicts of Interest
The authors declare no conflict of interest. The opinion expressed in this paper are the individual ones of the authors and do not represent the companies or academic institutions they are engaged with.
References
- Aven, Terje. 2011. Quantitative Risk Assessment. Cambridge: Cambridge University Press. [Google Scholar]
- Aven, Terje. 2016. Risk assessment and risk management: Review of recent advances on their foundation. European Journal of Operational Research 253: 1–13. [Google Scholar] [CrossRef]
- Bak, Peter, Chao Tang, and Kurt Wiesenfeld. 1987. Self-organized criticality: An explanation of the 1/f noise. Physical Review Letters 59: 381–84. [Google Scholar] [CrossRef] [PubMed]
- Basel Committee on Banking Supervision (BCBS). 2009. Results from the 2008 Loss Data Collection Exercise for Operational Risk. LDCE2008. Basel: Bank for International Settlement. [Google Scholar]
- Basel Committee on Banking Supervision (BCBS). 2017a. Basel III: Finalising Post-Crisis Reforms. Basel: BCBS. [Google Scholar]
- Basel Committee on Banking Supervision (BCBS). 2017b. High-Level Summary of Basel III Reforms. Basel: BCBS. [Google Scholar]
- Bhalla, Ajay. 2016. Quote in: Mastercard Rolls Out Artificial Intelligence Across its Global Network. Press Release. Purchase: Mastercard, November 30, Available online: newsroom.mastercard.com/press-releases/mastercard-rolls-out-artificial-intelligence-across-its-global-network/ (accessed on 18 July 2017).
- Bott, Jürgen, and Udo Milkau. 2015. Outsourcing risk: A separate operational risk category? Journal of Operational Risk 10: 1–29. [Google Scholar] [CrossRef]
- Bottou, Léon. 2014. From machine learning to machine reasoning. Machine Learning 94: 133–49. [Google Scholar] [CrossRef]
- Boos, Hans-Christian. 2017. AI is about Machine Reasoning—Or when Machine Learning is just a fancy plugin. Personal communication. [Google Scholar]
- Carlson, Jean M., and John Doyle. 2002. Complexity and robustness. Proceedings of the National Academy of Sciences USA 99: 2538–45. [Google Scholar] [CrossRef] [PubMed]
- Chavez-Demoulin, Valerie, Paul Embrechts, and Johana Neslehova. 2006. Quantitative models for operational risk: extremes, dependence and aggregation. Journal of Banking and Finance 30: 2635–58. [Google Scholar] [CrossRef]
- Clauset, Aaron, Cosma Rohilla Shalizi, and Mark E. J. Newman. 2009. Power-law distributions in empirical data. SIAM Review 51: 661–703. [Google Scholar] [CrossRef]
- Conneau, Alexis, Holger Schwenk, Loïc Barrault, and Yann Lecun. 2017. Very Deep Convolutional Networks for Text Classification. Available online: arxiv.org/abs/1606.01781 (accessed on 14 July 2017).
- Cruz, Marcelo G. 2002. Modeling, Measuring and Hedging Operational Risk. Chichester: John Wiley & Sons. [Google Scholar]
- Cser, Andras. 2017. The Forrester Wave™: Risk-Based Authentication, Q3 2017. Cambridge: Forrester Research. [Google Scholar]
- CyberSource. 2016. The Role of Machine Learning in Fraud Management. Foster City: CyberSource Corporation, Available online: www.cybersource.com/content/dam/cybersource/NA_Machine_Learning_Whitepaper.pdf (accessed on 23 July 2017).
- De Fontnouvelle, Patrick, Eric. S. Rosengren, and John S. Jordan. 2005. Implications of Alternative Operation-al Risk Modeling Techniques. NBER Working Paper No. w11103. Chicago: University of Chicago Press. [Google Scholar]
- Degen, Matthias, Paul Embrechts, and Dominik D. Lambrigger. 2007. The quantitative modeling of operational risk: Between g-and-h and EVT. Astin Bulletin 37: 265–91. [Google Scholar] [CrossRef]
- Dietvorst, Berkeley J., Joseph P. Simmons, and Cade Massey. 2015. Algorithm aversion: People erroneously avoid algorithms after seeing them err. Journal of Experimental Psychology: General 144: 114–26. [Google Scholar] [CrossRef] [PubMed]
- Dietvorst, Berkeley J., Joseph P. Simmons, and Cade Massey. 2016. Overcoming Algorithm Aversion: People Will Use Imperfect Algorithms If They Can (Even Slightly) Modify Them. Management Science 64: 1155–70. [Google Scholar] [CrossRef]
- Domingos, Pedro. 2012. A few useful things to know about machine learning. Communications of the ACM 55: 78–87. [Google Scholar] [CrossRef]
- Domingos, Pedro. 2016. Available online: Ten Myths about Machine Learning. Available online: https://medium.com/@pedromdd/ten-myths-about-machine-learning-d888b48334a3 (accessed on 12 July 2017).
- Ehramikar, Soheila. 2000. The Enhancemeat of Credit Card Fraud Detectioa Systems Using Machine Learning Methodology, University of Toronto. Available online: www.collectionscanada.ca/obj/s4/f2/dsk1/tape3/PQDD_0023/MQ50338.pdf (accessed on 23 July 2017).
- Ferreira, Ana, and Laurens de Haan. 2014. The generalized Pareto process; with a view towards application and simulation. Bernoulli 20: 1717–37. [Google Scholar] [CrossRef]
- Ferreira, Marta, and Helena Ferreira. 2017. Analyzing the Gaver—Lewis Pareto Process under an Extremal Perspective. Risks 5: 33. [Google Scholar] [CrossRef]
- Fukushima, Kunihiko. 1980. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics 36: 93–202. [Google Scholar] [CrossRef]
- Giacometti, Rosaella, Svetlozar Rachev, Anna Chernobai, Marida Bertocchi, and Giorgio Consigli. 2007. Heavy-tailed distributional model for operational losses. Journal of Operational Risk 2: 55–90. [Google Scholar] [CrossRef]
- Gigerenzer, Gerd, and Henry Brighton. 2009. Homo Heuristicus: Why Biased Minds Make Better Infer-ences. Topics in Cognitive Science 1: 107–43. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, Gerd, Ralph Hertwig, and Thorsten Pachur. 2011. Heuristics: The Foundations of Adaptive Behavior. Oxford: Oxford University Press. [Google Scholar]
- Gigerenzer, Gerd, and Wolfgang Gaissmaier. 2011. Heuristic Decision Making. Annual Review of Psychology 62: 451–82. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, Ian J., Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative Adversarial Networks. Available online: arxiv.org/abs/1406.2661 (accessed on 14 July 2017).
- Ghosh, Sushmito, and Douglas L. Reilly. 1994. Credit Card Fraud Detection with a Neural-Network. Paper presented at Twenty-Seventh Annual Hawaii International Conference on System Sciences, Wailea, HI, USA, January 4–7; Washington, DC: IEEE, vol. 2, pp. 621–30. [Google Scholar]
- Haldane, Andrew. 2012. Tails of the unexpected. Paper presented at The Credit Crisis Five Years on: Unpacking the Crisis Conference, Edinburgh, UK, June 8–9. [Google Scholar]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning. New York: Springer Science + Business Media, Second Edition, 2013. [Google Scholar]
- Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. Long Short-term Memory. Neural Computation 9: 1735–80. [Google Scholar] [CrossRef] [PubMed]
- Institute of Internal Auditors (IIA). 2013. The Three Lines of Defense in Effective Risk Management and Control. Position Paper. Lake Mary: IIA. [Google Scholar]
- Jones, Nicola. 2017. How machine learning could help to improve climate forecasts. Nature News, August 23. [Google Scholar]
- KFW. 2017. Payment Transactions of KfW—What Has Happened? KfW Press Release, Undated. Available online: www.kfw.de/KfW-Group/Newsroom/Aktuelles/Zahlungsverkehr-der-KfW.html (accessed on 2 April 2017).
- Knight, Frank H. 1921. Risk, Uncertainty, and Profit. New York: Harper. [Google Scholar]
- Kwakkel, Jan H., and Erik Pruyt. 2011. Exploratory Modelling and Analysis, an approach for model-based foresight under deep uncertainty. Paper presented at 4th International Seville Conference on Future-Oriented Technology Analysis, Sevilla, Spain, May 12–13; Edited by Effie Amanatidou. Sevilla: FTA, pp. 1–20. [Google Scholar]
- Lapuschkin, Sebastian, Alexander Binder, Grégoire Montavona, Klaus-Robert Muller, and Wojciech Samek. 2016. Analyzing Classifiers: Fisher Vectors and Deep Neural Networks. Paper presented at 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, June 26–July 1; Piscataway: IEEE. [Google Scholar]
- LeCun, Yann, Patrick Haffner, Léon Bottou, and Yoshua Bengio. 1999. Object Recognition with Gradient Based Learning. In Shape, Contour and Grouping in Computer Vision. Lecture Notes in Computer Science Book Series (LNCS). Berlin: Springer, vol. 1681, pp. 319–45. [Google Scholar]
- Liu, Yunjie, Evan Racah, Prabhat, Joaquin Correa, Amir Khosrowshahi, David Lavers, Kenneth Kunkel, Michael Wehner, and William Collins. 2016. Application of Deep Convolutional Neural Networks for Detecting Extreme Weather in Climate Datasets. Available online: arXiv:1605.01156v1 (accessed on 24 August 2017).
- Marković, Dimitrije, and Claudius Gros. 2014. Power laws and self-organized criticality in theory and nature. Physics Reports 536: 41–74. [Google Scholar] [CrossRef]
- McCormick, Roger, and Chris Stears. 2016. Conduct Costs Project Report 2016. Surrey: CCP Research Foundation CIC, Available online: http://conductcosts.ccpresearchfoundation.com/conduct-costs-results (accessed on 29 July 2017).
- Milkau, Udo. 2012. Adequate Communication about Operational Risk in the Business Line. Journal of Operational Risk 8: 35–57. [Google Scholar] [CrossRef]
- Milkau, Udo, and Frank Neumann. 2012. The first line of defence in operational risk management—The perspective of the business line. Journal of Financial Transformation 34: 155–64. [Google Scholar]
- Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. 2012. Foundations of Machine Learning. Cambridge: MIT Press. [Google Scholar]
- Moscadelli, Marco. 2004. The Modelling of Operational Risk: Experience with the Analysis of the Data Collected by the Basel Committee. Bank of Italy Working Papers Series Number 517; Rome: Bank of Italy. [Google Scholar]
- Motet, Gilles, and Corinne Bieder. 2017. The Illusion of Risk Control—What Does It Take to Live With Uncertainty? Berlin: Springer. [Google Scholar]
- Nagafuji, Tsuyoshi, Takayuki Nakata, and Yugo Kanzaki. 2011. A Simple Formula for Operational Risk Capital: A Proposal Based on the Similarity of Loss Severity Distributions Observed among 18 Japanese Banks. Available online: https://www.fsa.go.jp/frtc/english/seika/perspectives/2011/20110520.pdf (accessed on 12 November 2012).
- Nešlehová, Johana, Paulk Embrechts, and Valerie Chavez-Demoulin. 2006. Infinite-mean models and the LDA for operational risk. The Journal of Operational Risk 1: 3–25. [Google Scholar] [CrossRef]
- PRNewswire. 1993. Visa and Hnc Inc. Develop Neural Network as a Weapon to Fight Fraud. TM-SF007-1246 08/10/93. Available online: www.thefreelibrary.com (accessed on 14 July 2017).
- Pun, Joseph King-Fung. 2011. Improving Credit Card Fraud Detection using a Meta-Learning Strategy. Ph.D. thesis, University of Toronto, Toronto, ON, Canada. Available online: tspace.library.utoronto.ca/bitstream/1807/31396/3/Pun_Joseph_KF_201111_MASc_thesis.pdf (accessed on 23 July 2017).
- Purdy, Grant. 2010. ISO 31000:2009—Setting a New Standard for Risk Management. Risk Analysis 30: 881–86. [Google Scholar] [CrossRef] [PubMed]
- Reuters. 2017. German State Bank KfW Accidentally Transferred 7.6 billion euros. Reuters. March 29. Available online: http://www.reuters.com/article/us-kfw-mistrade-idUSKBN1700W8 (accessed on 29 July 2017).
- Samson, Sundeep, James A. Reneke, and Margaret M. Wiecek. 2009. A review of different perspectives on uncertainty and risk and an alternative modeling paradigm. Reliability Engineering & System Safety 94: 558–67. [Google Scholar]
- Santoro, Adam, David Raposo, David G. T. Barrett, Mateusz Malinowski, Razvan Pascanu, Peter Battaglia, and Timothy Lillicrap. 2017. A Simple Neural Network Module for Relational Reasoning. Available online: arxiv.org/abs/1706.01427 (accessed on 14 July 2017).
- Schmidhuber, Jürgen. 2015. Deep learning in neural networks: An overview. Neural Networks 61: 85–117. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, Jürgen. 2017. Künstliche Intelligenz wird alles ändern. Talk given at Petersberger Gespräche, September 16, Bonn, Germany. [Google Scholar]
- Shalev-Shwartz, Shai, and Shai Ben-David. 2014. Understanding Machine Learning: From Theory to Algorithms. New York: Cambridge University Press. [Google Scholar]
- Spielkamp, Matthias. 2017. Inspecting Algorithms for Bias. MIT Technology Review. June 12. Available online: https://www.technologyreview.com/s/607955/inspecting-algorithms-for-bias/ (accessed on 23 July 2017).
- Szegedy, Christian, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. 2015. Going deeper with convolutions. Paper presented at IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, June 7–12. [Google Scholar]
- Trautmann, Wolfgang, Udo Milkau, Uli Lynen, and Josef Pochodzalla. 1993. Systematics of the power law parameter and minimum angular momenta for fragment production. Zeitschrift für Physik A Hadrons and Nuclei 344: 447–54. [Google Scholar] [CrossRef]
- Vocalink. 2018. Available online: http://connect.vocalink.com/2018/april/natwest-teams-up-with-vocalink-analytics-to-protect-corporate-customers-from-fraud/ (accessed on 5 April 2018).
| 1 | For the scope of this paper and the discussion about the tail of the distribution, this simplification on “power law” (or Pareto distributions) is sufficient. For further discussion such as generalized Pareto distributions or g-and-h distribution, the reader is referred to the literature (see e.g., Degen et al. 2017). |
| 2 | Sometimes also called “probability-impact diagrams.” |
| 3 | The concept of the “Strength of Knowledge” emerges on the borderline of statistics and didactical communication about statistical results. As Figure 2 will show later in this paper, all information is contained in the data and in the description about the conditions how the data was taken. Usually, one would assume that the Frequency of events and the Time of the measurement follow the inequation 1/F << T to avoid nonsignificant data set. However, in the case of “very fat tails” like in power-law distributions, one also has to deal with situations 1/F > T, i.e., extrapolations to very rare event types. |
| 4 | It has to be noted that in context of machine learning there is also a definition of “risk” for the empirical error, i.e., the error a classifier incurs over the training sample (see Shalev-Shwartz and Ben-David 2014). From an OpRisk perspective, this would be a model risk. |
| 5 | Another example is Risk-Based Authentication for online banking access (see Cser 2017). |
| 6 | This apparently simple requirement could be challenging with real-world training data sets, as recently shown with an intriguing example by Lapuschkin et al. (2016) that learners could “learn” artefacts, which were correlated with the real content by chance and were not detected beforehand. |
| 7 | Recently Jürgen Schmidhuber (2017) discussed ideas how AI-powered robots can be provided with “artificial curiosity,” which is one way to find new solutions in situation with limited resources including social cooperation. If overall profitability is treaded as a limited resource, there can be a way for AI to learn to achieve holistic benefits, even without explicit training. |
| 8 | It should be noted that this situation resamples similar problems in other fields of machine learning such as, e.g., autonomous vehicles. For many extreme situations, especially situations leading to accidents, the initial models are trained with few data points, which often do not generalize well. To learn dangerous situations, recorded video data have to be combined with synthetic, computer generated video, e.g., for a tree falling on a street due to a storm. This combination of actual data with synthetic data based on heuristics and learning in case of very limited data requires more research about machine learning and models for the handling extremes events. |
| 9 | In principle, the simplest “learners” are rule-based “Key Risk Indicators” (KRI). Typical KRIs in banking are, e.g., “continuous days of vacation <10” or “cancelled trades.” In the first case, there is a heuristics based on the well-known “rouge trader” events that traders should take a fortnight of vacation once a year with somebody else taking over the responsibility for their portfolios. In the second one, some pattern of “cancelled trades” (from a simple monitoring of enhanced numbers to derivation over time from a “normal” pattern) can be an indication, but usually there are no or not enough right positive cases to learn from with some significant statistics. |
| 10 | A similar approach was reported recently by Liu et al. (2016); Jones (2017) for a total different field of research, i.e., detecting extreme weather in climate data sets, with Convolutional Neural Network (CNN) classification system and Deep Learning technique for tackling climate pattern detection problems. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).