Stable Value Funds Performance †
Abstract
:1. Introduction
2. Background
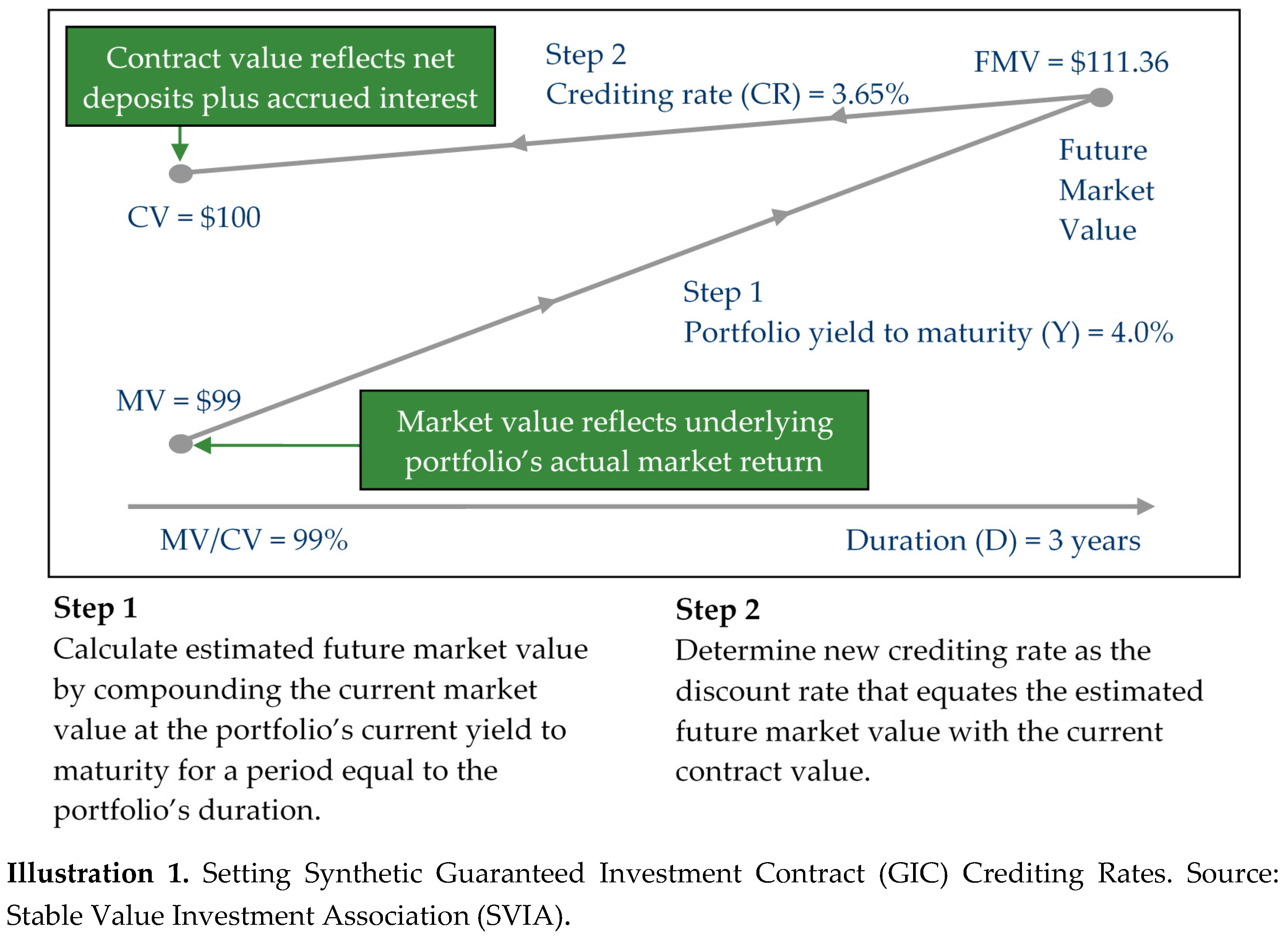
3. Crediting Rate Formula
- CR: crediting rate applied to the accounts of investors in the SV funds
- MV: market value of the underlying portfolio
- CV: contract value of the underlying portfolio
- D: duration of the underlying portfolio or duration of a benchmark portfolio
- Y: yield of the underlying portfolio, as described further below.
4. Performance Measurement
- Stochastic dominance methods do not provide guidance into the construction of a portfolio from various individual securities.
- Stochastic dominance methods do not provide an equilibrium price for securities.
5. Data
6. Results
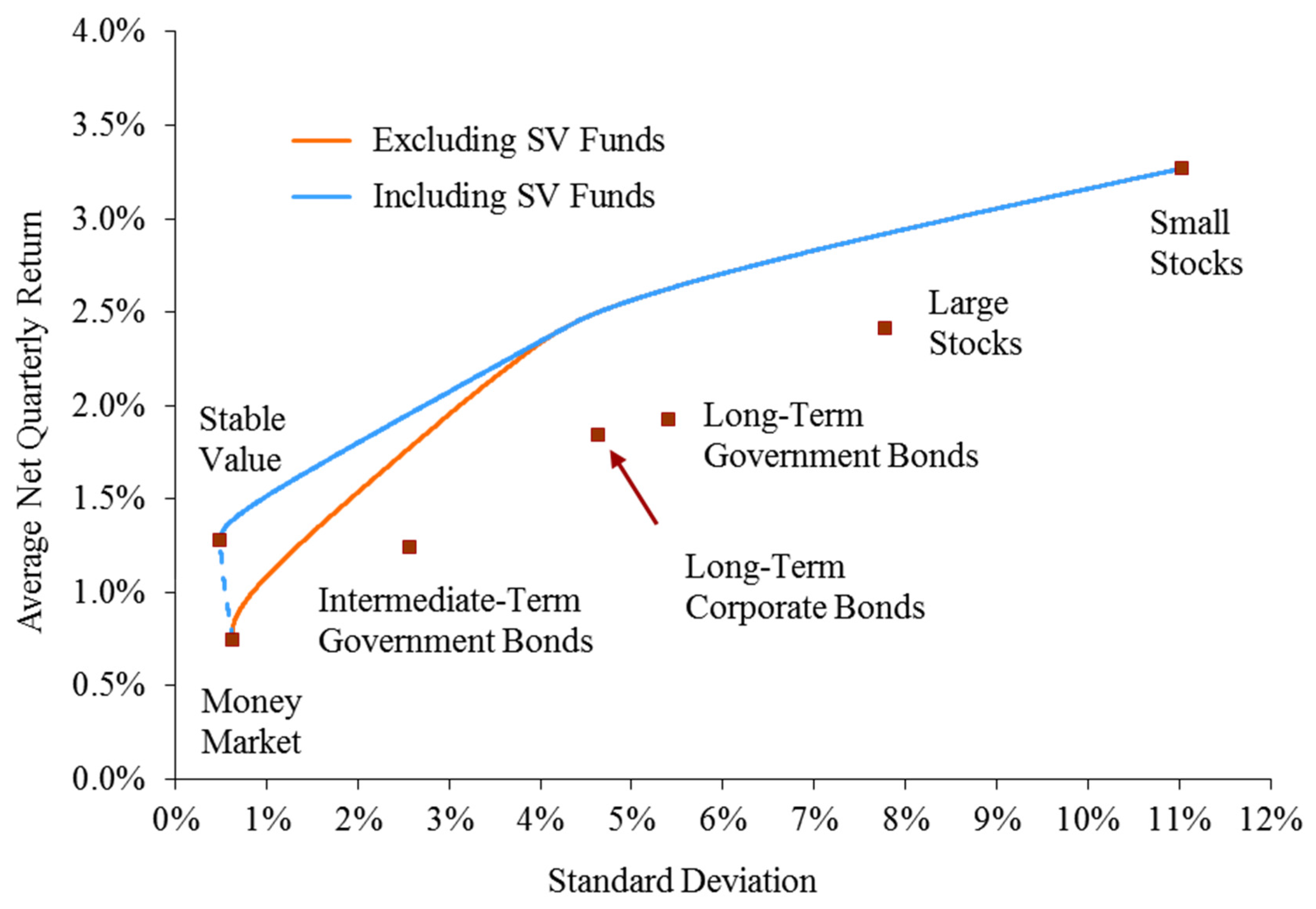
6.1 Mean-Variance Analysis
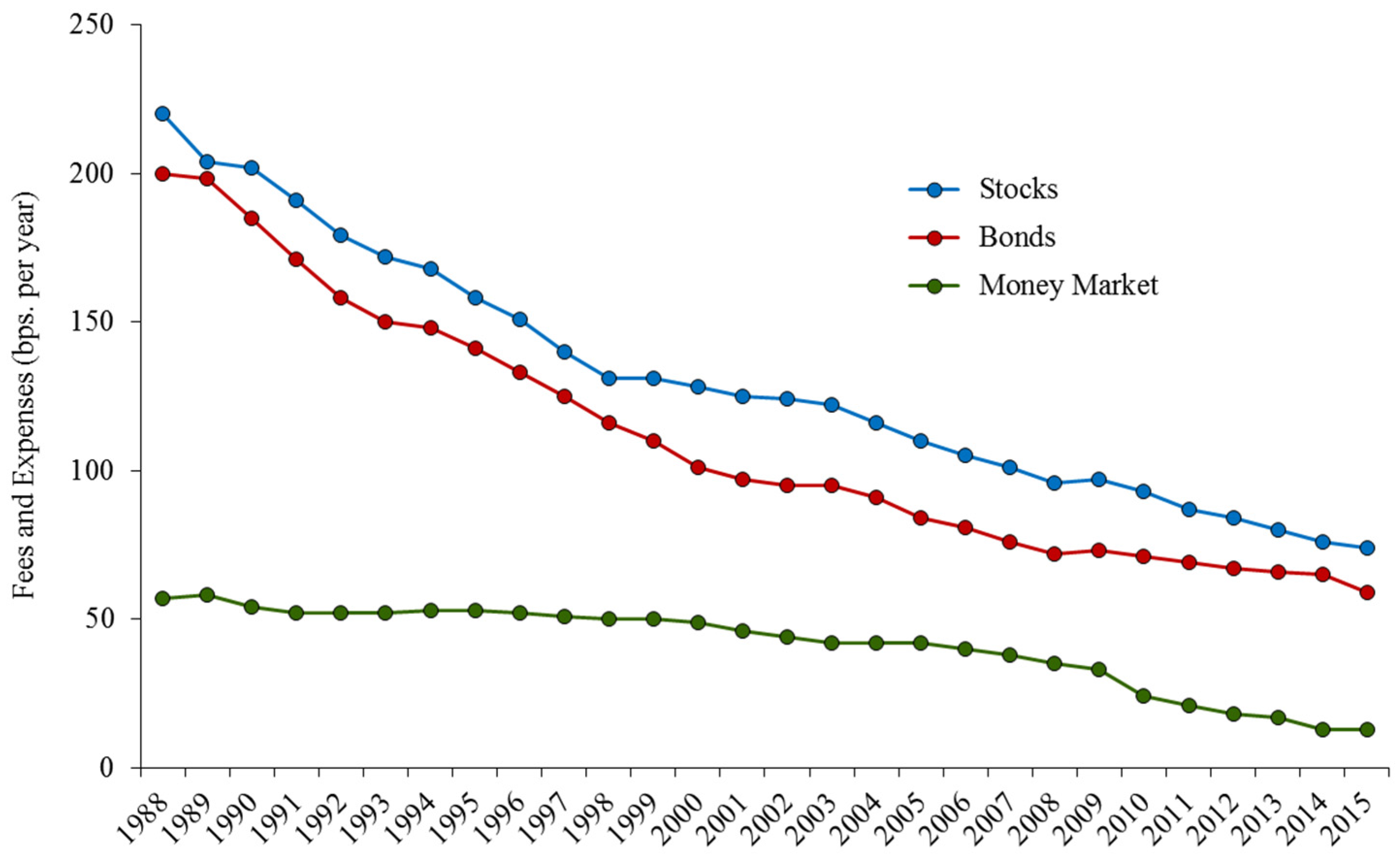
6.2. Stochastic Dominance Analysis
6.3. Intertemporal Optimization Analysis
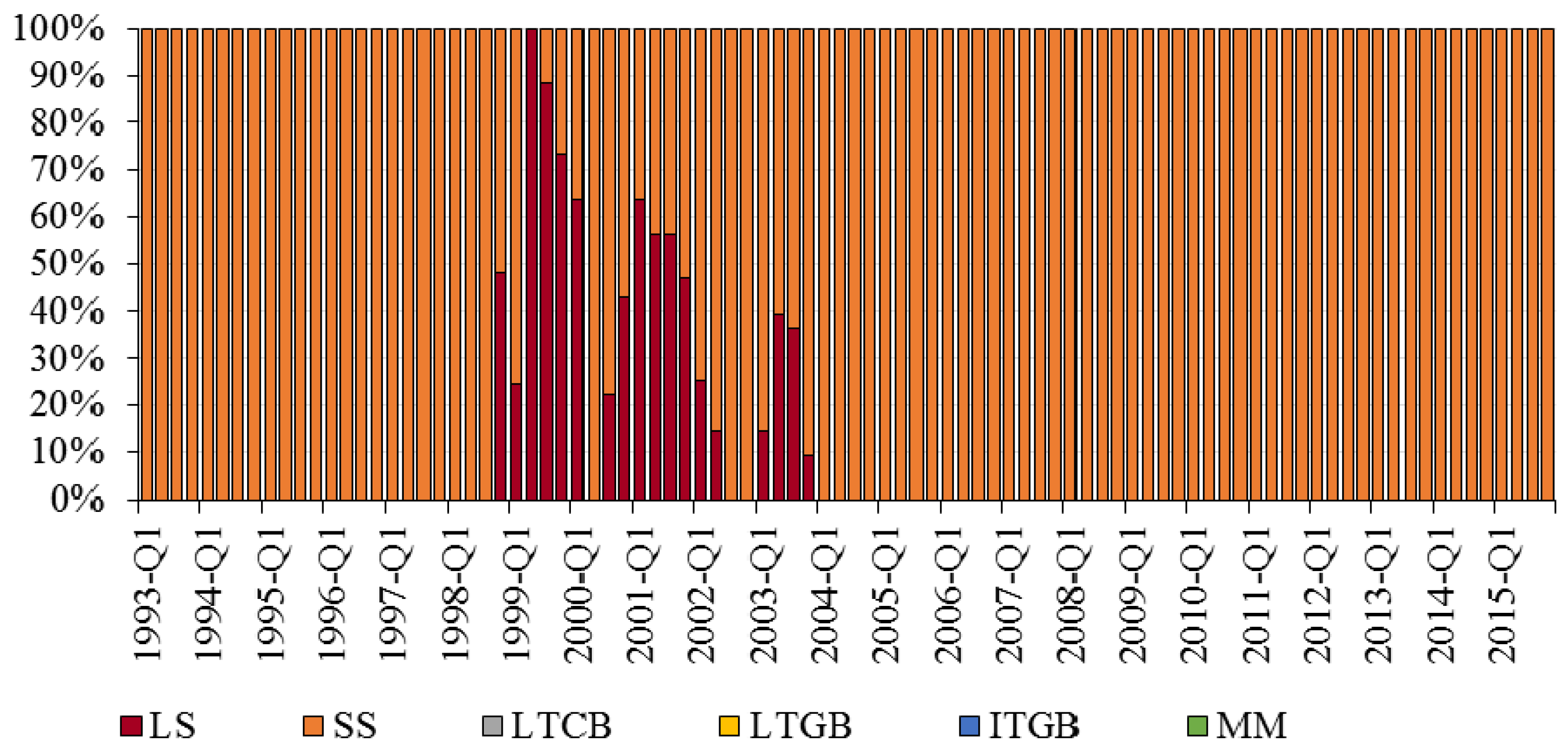
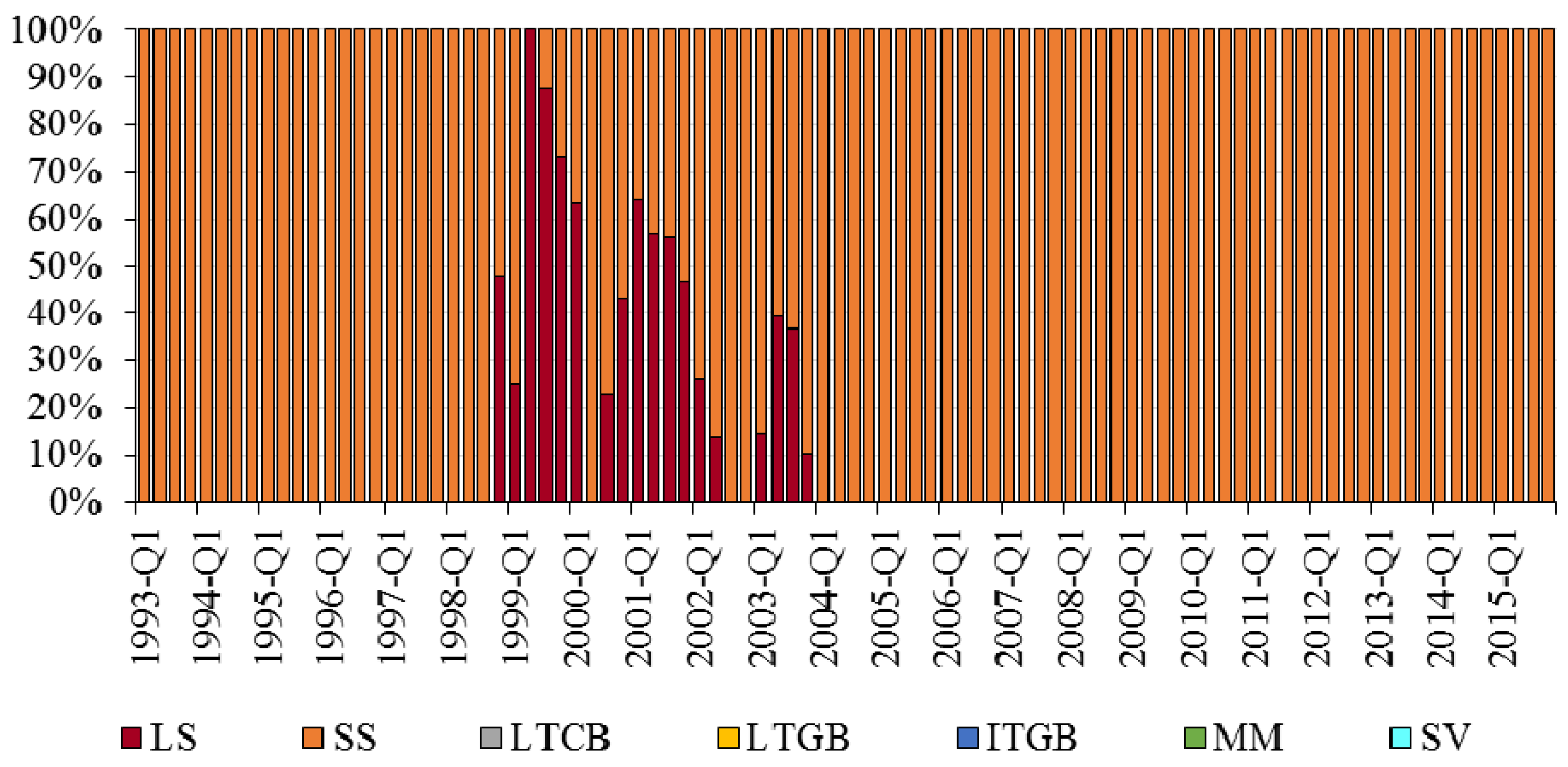
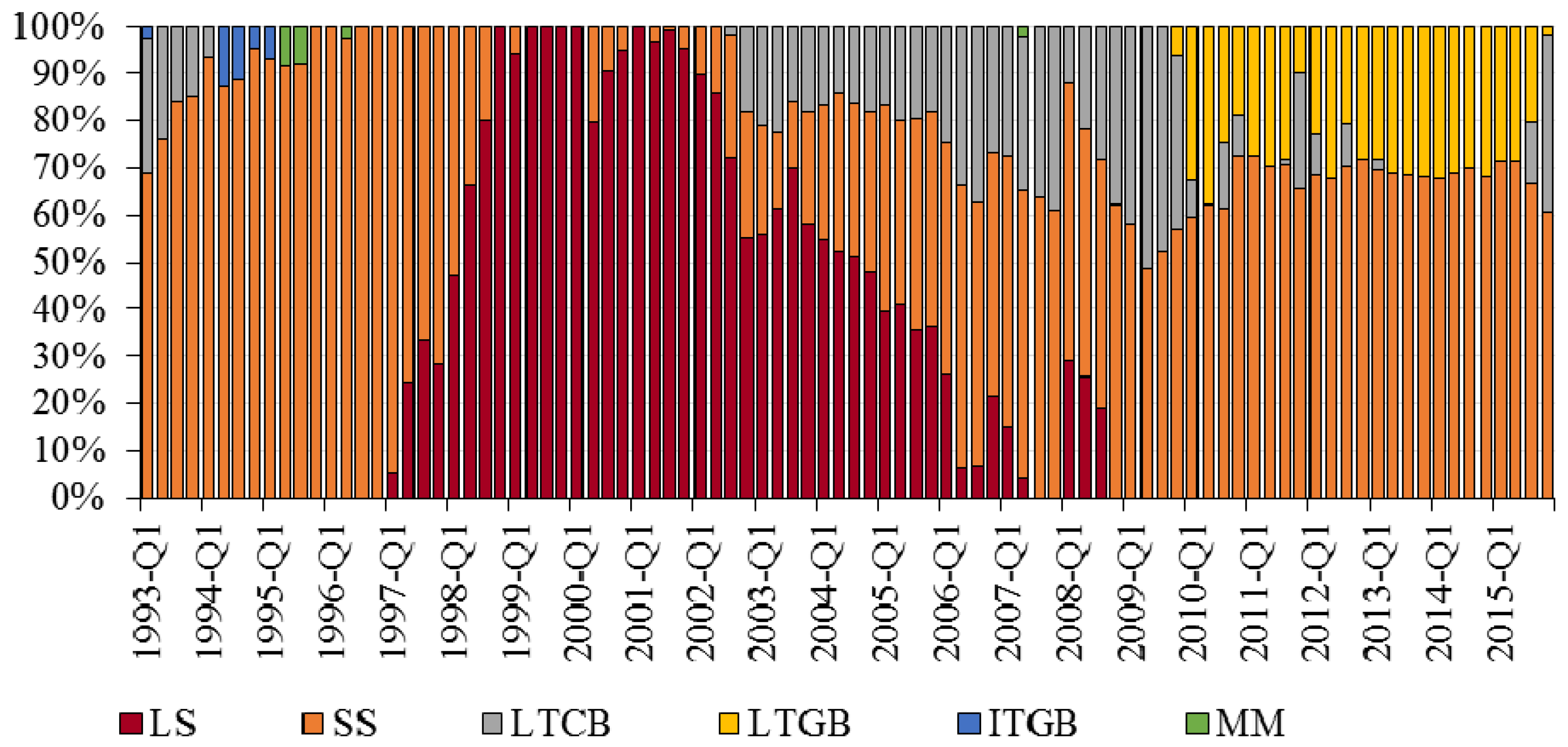
6.4. Optimal Portfolio Returns Q1-1993–Q4-2015
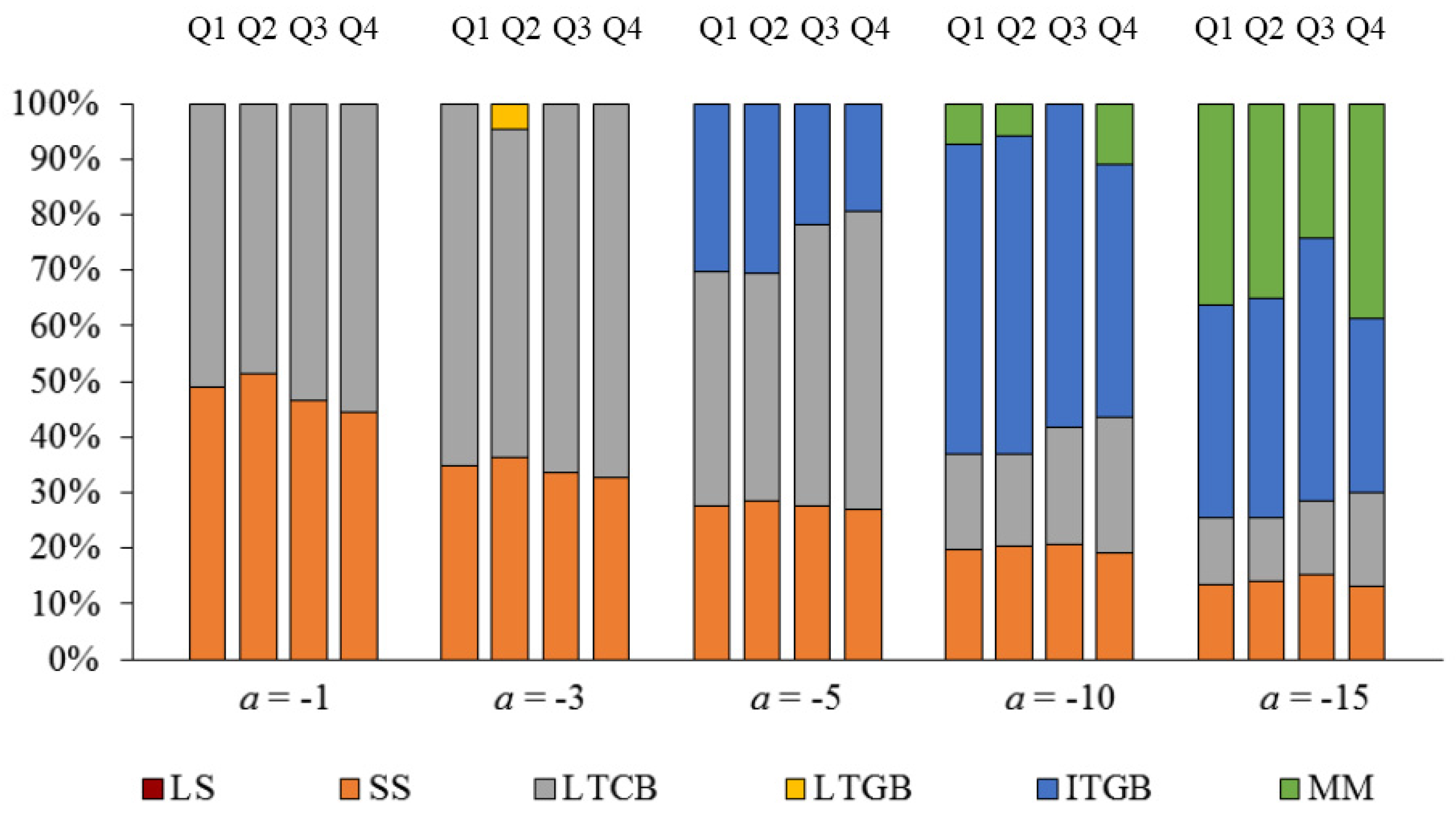
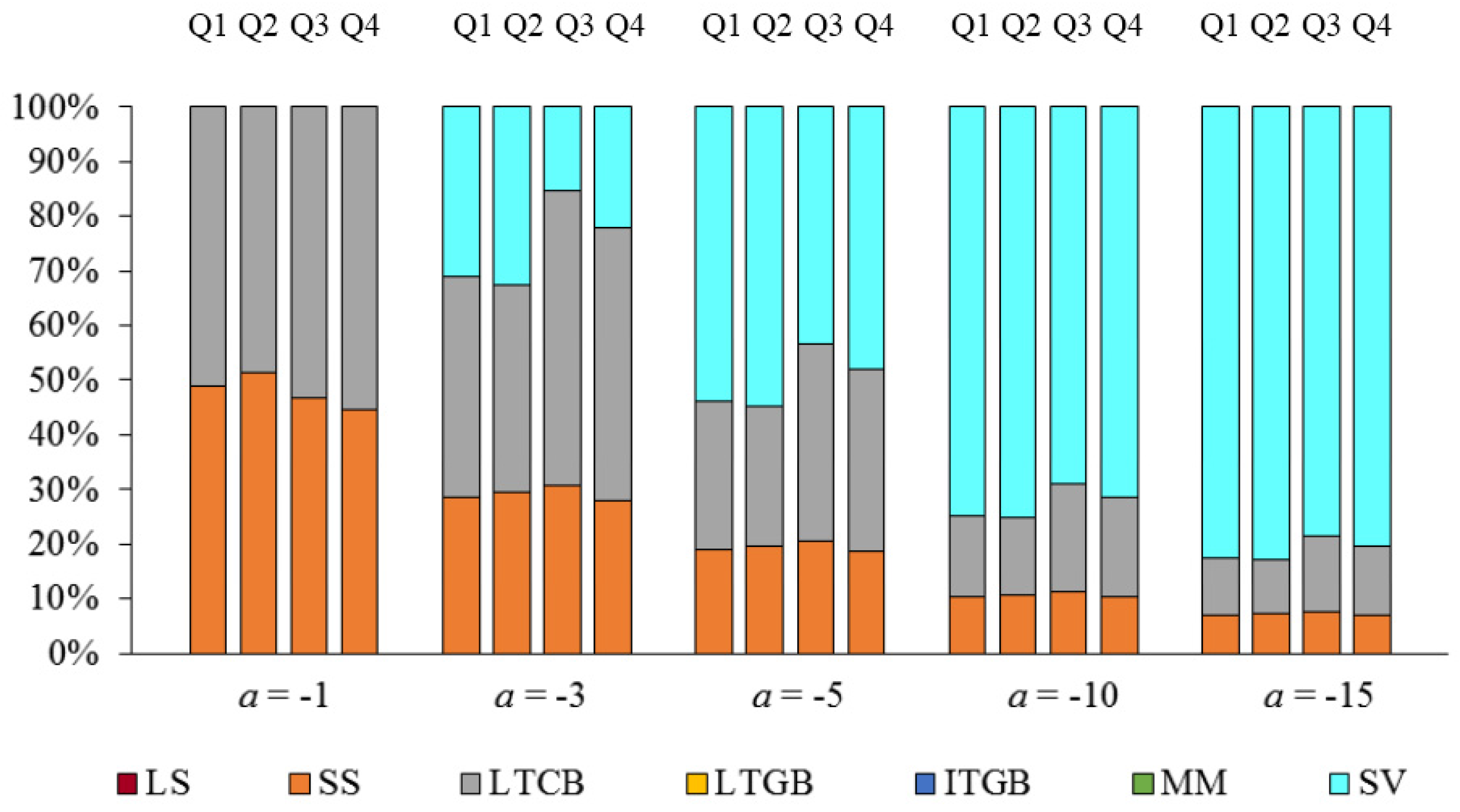
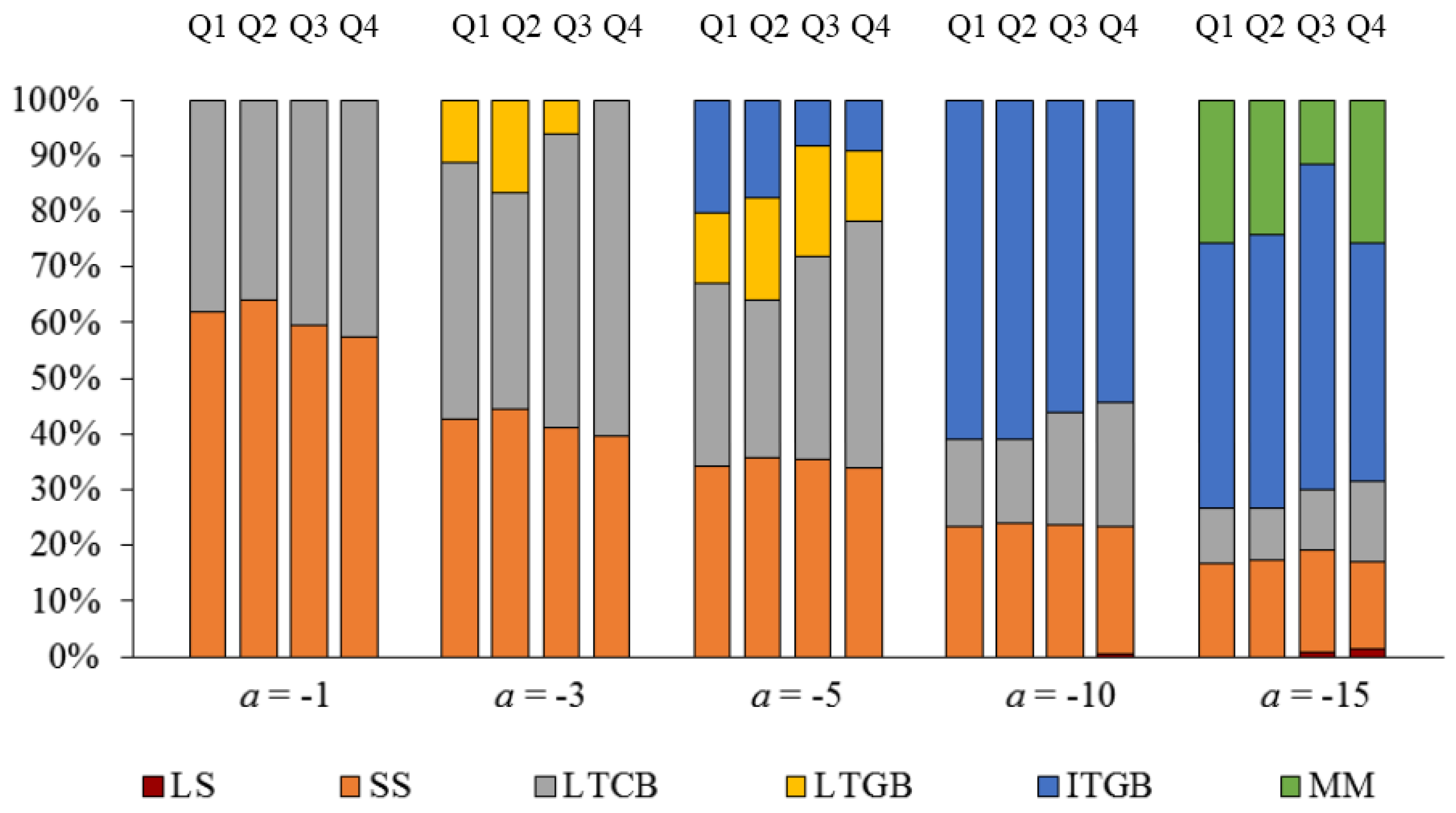
6.5. Sensitivity to Expected Stock Returns
7. Robustness Analysis
7.1. Period Q2-1973–Q3-1988
7.2. Mean-Variance Analysis
7.3. Sharpe and Sortino Ratios
7.4. Stochastic Dominance
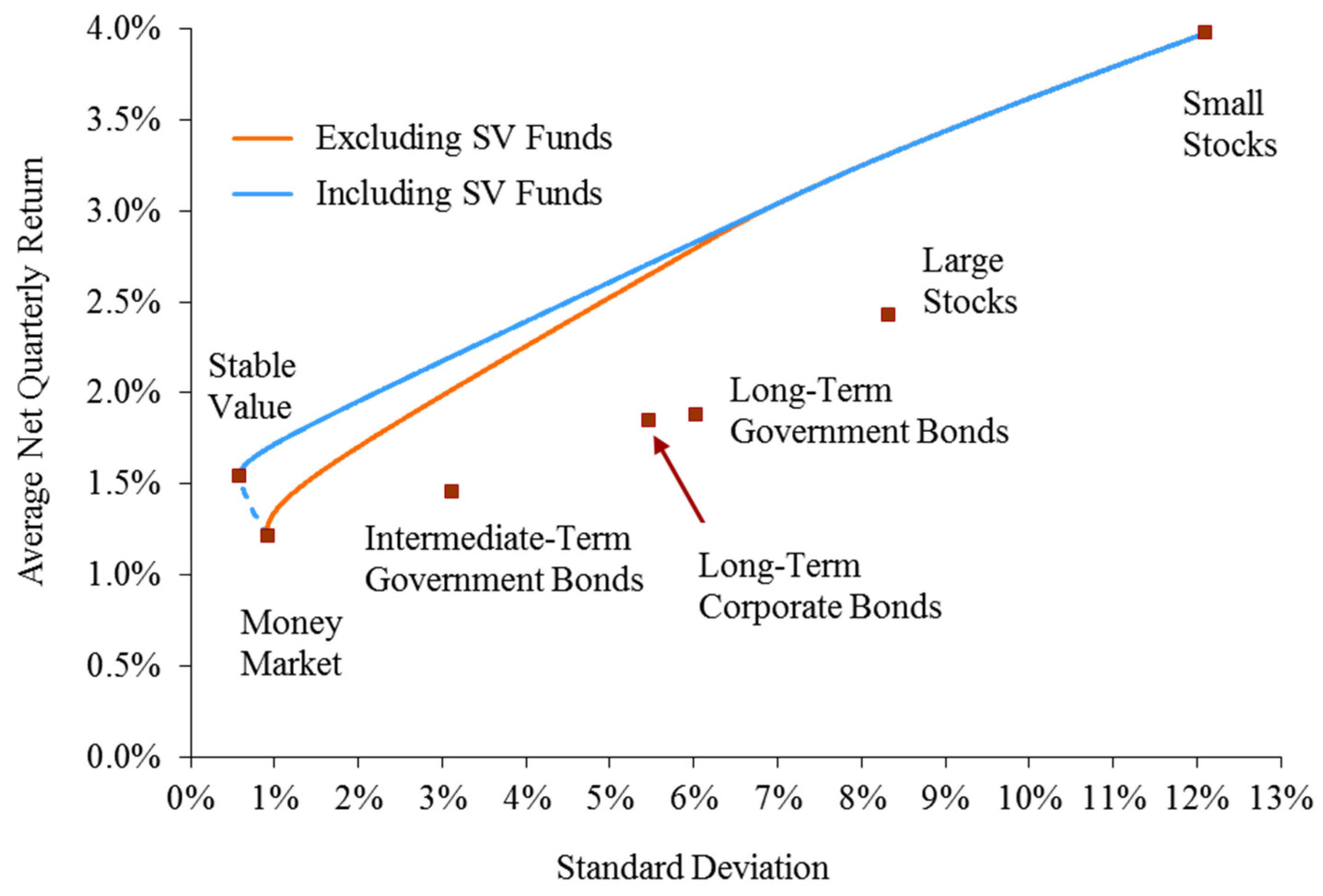
7.5. Full Sample Q2-1973–Q4-2015
7.6. Mean-Variance Analysis
7.7. Sharpe and Sortino Ratios
7.8. Stochastic Dominance
8. The Value Proposition, Challenges and Future Prospects
- (1)
- FASB’s accounting standard (FASB 2005), which grants contract value accounting protocol to SV funds rather than mark-to-market accounting, requires the overall portfolio to be of overall very high credit quality. If it is not, a fund cannot use contract value accounting.
- (2)
- SV fund investment guidelines set the overall direction of the portfolio and usually have stringent quality standards, limits in allocations to specific asset classes, and duration limits. Since SV is a conservative investment, the guidelines reflect this. The key principles of the Stable Value Investment Association reinforce the plan rules.
- (3)
- Wrap providers require and police specific asset credit quality standards in order to obtain their wrap. They also have set a limit that is generally between one and five percent for a credit bucket into which any ‘troubled’ assets are placed. The SV fund manager usually has a set time period to rehabilitate the assets in the credit bucket. If the manager violates the terms of the wrap contract, the wrap is potentially void.
- (4)
- In the event that a wrap provider exits the business, other wrap providers have historically divided up the vacant share. For example, a typical structure had six wrap providers each underwriting 16.5% of the coverage. If one provider exited the business, the other five had contractually agreed to increase their coverage such that each provider would cover 20%. Today this arrangement is disappearing and the step-up provision is typically for only 90 days. If an existing wrap provider exits the business, the exit could transpire over (typically) a 3.5 year time frame, and if another provider were not found, the funds associated with that segment would go into cash, lowering the overall fund yields but maintaining their character as SV assets.
- (5)
- The Stable Value Investment Association’s membership reports from their annual surveys show no use of any leverage. Even if the plan investment guidelines permitted leverage, it is doubtful that a wrap provider would ever allow it and to date none have undertaken it. In light of the recent financial crisis, which was precipitated and exacerbated, in part, by high leverage, SV funds are in a relatively advantageous position.
9. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- AitSahlia, Farid, Thomas Doellman, and Sabuhi Sardarli. 2017. Mean-Variance Spanning Tests: The Fiduciary Case in 401(k) Plans. Working Paper (February 2017). Available online: http://bear.warrington.ufl.edu/aitsahlia/Spanning_paper.pdf (accessed on 12 December 2017).
- Albert, Steven M., and John Duffy. 2012. Differences in Risk Aversion between Young and Older Adults. Neuroscience and Neuroeconomics. [Google Scholar] [CrossRef] [PubMed]
- Arditti, Fred. 1967. Risk and the Required Return on Equity. Journal of Finance 22: 19–36. [Google Scholar] [CrossRef]
- Babbel, David F., and Miguel Herce. 2009. Stable Value Funds: Performance from 1973 through 2008. Working Paper. Philadelphia: Wharton Financial Institutions Center. [Google Scholar]
- Babbel, David F., and Miguel Herce. 2007. A Closer Look at Stable Value Funds Performance. Working Paper. Philadelphia: Wharton Financial Institutions Center. [Google Scholar]
- Babbel, David F., and Miguel Herce. 2011. Stable Value Funds: Performance to Date. Working Paper. Philadelphia: Wharton Financial Institutions Center. [Google Scholar]
- Bogle, John C. 2005. The Relentless Rules of Humble Arithmetic. Financial Analysts Journal 61: 22–35. [Google Scholar] [CrossRef]
- Cvitanić, Jakša, Vassilis Polimenis, and Fernando Zapatero. 2008. Optimal Portfolio Allocation with Higher Moments. Annals of Finance 4: 1–28. [Google Scholar] [CrossRef]
- Dichev, Ilia D. 2007. What Are Stock Investors’ Actual Historical Returns? Evidence from Dollar-Weighted Returns. American Economic Review 97: 386–401. [Google Scholar] [CrossRef]
- Dohmen, Thomas, Armin Falk, David Huffman, and Uwe Sunde. 2007. Are Risk Aversion and Impatience Related to Cognitive Ability? IZA Discussion Paper No. 2735. Bonn: Forschunginstitut zur Zukunft der Arbeit. [Google Scholar]
- Donahue, Paul J. 2016. Fundamental Investment Principles of DC Option Selection Prove Optimality of Stable Value. Society of Actuaries, Pension Section News 88: 15–18. [Google Scholar]
- Donahue, Paul J. 2006. Plan Sponsor Fiduciary Duty for the Selection of Options in Participant-Directed Defined Contribution Plans and the Choice between Stable Value and Money Market. Akron Law Review 39: 9. [Google Scholar]
- Douglas, George W. 1969. Risk in the Equity Markets: An Empirical Appraisal of Market Efficiency. Yale Economic Essays 9: 3–45. [Google Scholar]
- Elton, Edwin J., Martin J. Gruber, and Christopher R. Blake. 2007. Participant Reaction and the Performance of Funds Offered by 401(k) Plans. Journal of Financial Intermediation 16: 2, (April 2007). [Google Scholar] [CrossRef]
- Fabozzi, Frank J., ed. 1998. The Handbook of Stable Value Investments. Pennsylvania: Frank J. Fabozzi Associates, New Hope. [Google Scholar]
- FASB. 2005. Reporting of Fully Benefit-Responsive Investment Contracts Held by Certain Investment Companies Subject to the AICPA Investment Company Guide and Defined Contribution Health and Welfare and Pension Plans. FSP AAG INV-1 and SOP 94-4-1. Norwalk: FASB. [Google Scholar]
- Fernández, Pablo, Alberto Ortiz Pizarro, and Isabel Fernández Acín. 2015. Discount Rate (Risk-Free Rate and Market Risk Premium) Used for 41 Countries in 2015: A Survey. (November 2015). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2598104 (accessed on 12 December 2017).
- Fernández, Pablo, Vitaly Pershin, and Isabel Fernández Acín. 2017. Discount Rate (Risk-Free Rate and Market Risk Premium) Used for 41 Countries in 2017: A Survey. (April 2017). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2954142 (accessed on 13 February 2018).
- Gale, William G., David C. John, and Bryan Kim. 2016. You Get What You Pay For: Guaranteed Returns in Retirement Saving Accounts. In Brookings Economic Studies. Washington: Brookings Institution. [Google Scholar]
- GAO (United States Government Accountability Office). 2011. 401(k) Plans: Certain Investment Options and Practices that May Restrict Withdrawals Not Widely Understood; Report to the Chairman, Special Committee on Aging, U.S. Senate, GA0-11-291. Washington: GAO. Available online: http://www.gao.gov/new.items/d11291.pdf (accessed on 13 February 2018).
- Grauer, Robert R., and Nils H. Hakansson. 1982. Higher Return, Lower Risk: Historical Returns on Long-Run, Actively Managed Portfolios of Stocks, Bonds and Bills, 1936–1978. Financial Analysts Journal 38: 39–53. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1985. Returns on Levered, Actively Managed Long-Run Portfolios of Stocks, Bonds and Bills, 1934–1983. Financial Analysts Journal 41: 24–43. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1986. A Half Century of Returns on Levered and Unlevered Portfolio of Stocks, Bonds, and Bills, with and without Small Stocks. Journal of Business 59: 2, 287–318. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1987. Gains from International Diversification: 1968–85 Returns on Portfolios of Stocks and Bonds. Journal of Finance 42: 721–39. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1993. On the Use of Mean-Variance and Quadratic Approximations in Implementing Dynamic Investment Strategies: a Comparison of Returns and Investment Policies. Management Science 39: 856–71. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1995. Gains from Diversifying Into Real Estate: Three Decades of Portfolio Returns Based on the Dynamic Investment Model. Real Estate Economics 23: 117–59. [Google Scholar] [CrossRef]
- Hadar, Josef, and William R. Russell. 1969. Rules for Ordering Uncertain Prospects. American Economic Review 59: 25–34. [Google Scholar]
- Hanoch, Giora, and Haim Levy. 1969. The Efficiency Analysis of Choices Involving Risk. Review of Economic Studies 36: 335–46. [Google Scholar] [CrossRef]
- Hakansson, Nils. 1971. On Optimal Myopic Portfolio Policies, With and Without Serial Correlation of Yields. Journal of Business 44: 324–34. [Google Scholar] [CrossRef]
- Hakansson, Nils. 1974. Convergence to Isoelastic Utility and Policy in Multiperiod Portfolio Choice. Journal of Financial Economics 1: 201–24. [Google Scholar] [CrossRef]
- Harrati, Amal Cherifa. 2014. Understanding Risk Aversion in Older Americans: New Approaches Using Genetic Data. Ph.D. Dissertation, University of California at Berkeley, Berkeley, CA, USA. [Google Scholar]
- Hewitt, Aon. 2017. AHIC Stable Value Quarterly. Chicago: Aon Hewitt Investment Consulting, Inc. [Google Scholar]
- Huberman, Gur, and Stephen Ross. 1983. Portfolio Turnpike Theorems, Risk Aversion and Regularly Varying Utility Functions. Econometrica 51: 1104–19. [Google Scholar] [CrossRef]
- Kruk, Joshua M., Matthew G. Gleason, Steven A. Wallace, and Jason L. Wyman. 2012. Customized Performance Benchmarks for Stable Value Funds. U.S. Patent No. 8,170,944 B1, May 1. Available online: https://www.google.com/patents/US8170944 (accessed on 13 February 2018).
- LaBarge, Karen Peterson. 2012. Stable Value Funds: Considerations for Plan Sponsors. The Vanguard Group (July 2012). Available online: https://institutional.vanguard.com/iam/pdf/ICRSVF.pdf?cbdForceDomain=false (accessed on 13 February 2018).
- Leland, Hayne. 1972. On Turnpike Portfolios. In Mathematical Methods in Investment and Finance. Edited by Karl Shell and G. P. Szego. Amsterdam: Elsevier Science Publishing Co., Inc. [Google Scholar]
- Levy, Haim. 2006. Stochastic Dominance: Investment Decision Making Under Uncertainty, 2nd ed. New York: Springer. [Google Scholar]
- Malloy, Christopher J., Tobias J. Moskowitz, and Annette Vissing-Jørgensen. 2009. Long-Run Stockholder Consumption Risk and Asset Returns. Journal of Finance 64: 2427–79. [Google Scholar] [CrossRef]
- Markowitz, Harry M. 1987. Mean-Variance Analysis in Portfolio Choice and Capital Markets. Oxfor: Basil Blackwell. [Google Scholar]
- MetLife. 2010. 2010 Stable Value Study: A Survey of Plan Sponsors and Stable Value Fund Providers. Available online: https://www.metlife.com/assets/cao/institutional-retirement/MetLife-2010-Stable-Value-Study-exp6-14.pdf (accessed on 13 February 2018).
- MetLife. 2015. 2015 Stable Value Study: A Survey of Plan Sponsors and Stable Value Fund Providers. Available online: https://www.metlife.com/assets/cao/institutional-retirement/2015StableValueStudy_WEBFINAL.pdf (accessed on 13 February 2018).
- Mossin, Jan. 1968. Optimal Multiperiod Portfolio Policies. Journal of Business 41: 215–29. [Google Scholar] [CrossRef]
- Myers, Randy. 2016. Wild Ducks and Stable Returns: A History of the Synthetic GIC at 25. Baltimore: Transamerica Stable Value Solutions, Inc. [Google Scholar]
- Paradis, Victoria M. 2001. Challenges of Measuring Performance for Stable Value Funds. Journal of Performance Measurement 5: 3. [Google Scholar]
- Pedersen, Christian, and Stephen Satchell. 2002. On the Foundation of Performance Measures under Asymmetric Returns. Quantitative Finance 2: 217–23. [Google Scholar] [CrossRef]
- Redding, Lee S. 2009. The G Fund: Portfolio Effects of a Dominant Asset. Journal of Pension Economics and Finance 8: 225–38. [Google Scholar] [CrossRef]
- Riley, William B., Jr., and K. Victor Chow. 1992. Asset Allocation and Individual Risk Aversion. Financial Analysts Journal 48: 32–37. [Google Scholar] [CrossRef]
- Ross, Stephen. 1974. Portfolio Turnpike Theorems for Constant Policies. Journal of Financial Economics 1: 171–98. [Google Scholar] [CrossRef]
- Sharpe, William F. 1994. The Sharpe Ratio. Journal of Portfolio Management 21: 49–58. [Google Scholar] [CrossRef]
- Siegel, Jeremy J. 2005. Perspectives on the Equity Risk Premium. Financial Analysts Journal 61: 61–73. [Google Scholar] [CrossRef]
- Sortino, Frank, and Robert Van der Meer. 1991. Downside risk. Journal of Portfolio Management 17: 27–31. [Google Scholar] [CrossRef]
- Sortino, Frank A., and Lee N. Price. 1994. Performance Measurement in a Downside Risk Framework. Journal of Investing 3: 59–65. [Google Scholar] [CrossRef]
- Stable Value Investment Association (SVIA). 2017. 3Q 2017 Stable Value Quarterly Characteristics Survey. Washington: SVIA. [Google Scholar]
- Stable Value Investment Association (SVIA). 2005. Response to FASB December 9, 2004 Questions Regarding Commingled Stable Value Funds. Washington: SVIA. [Google Scholar]
- Tang, Ning, Olivia S. Mitchell, Gary R. Mottola, and Steve P. Utkus. 2010. The Efficiency of Sponsor and Participant Portfolio Choices in 401(k) Plans. Journal of Public Economics 94: 1073–85. [Google Scholar] [CrossRef]
- VanDerhei, Jack, Sarah Holden, Luis Alonso, and Steven Bass. 2017. 401(k) Plan Asset Allocation, Account Balances, and Loan Activity in 2015. No. 436. Washington: Employee Benefit Research Institute, Available online: https://www.ebri.org/pdf/briefspdf/EBRI_IB_436_K-update.3Aug17.pdf (accessed on 13 February 2018).
| 1 | Our previous working papers (Babbel and Herce 2007, 2009, 2011) ended at the depths of the Great Recession and did not include the most recent data from the past seven years. |
| 2 | |
| 3 | |
| 4 | There is, however, a recent study in the professional actuarial literature that does broach on performance of SV funds, although that it not its primary focus. Donahue (2016) reports some SV returns, volatilities and correlations over the most recent 5, 10, and 15 years. He also provides useful information about varieties of SV fund structures. Additionally, customized performance benchmarks have been developed for SV funds. These measures incorporate client-specific factors in assessing the funds’ overall crediting rates. See Kruk et al. (2012). |
| 5 | The Stable Value Investment Association (SVIA) reported 164,913 member plans as of December 2015 and members had $742 billion under management as of the third quarter of 2017. The SVIA has no current estimate on additional SV funds managed by nonmembers, but one estimate from 2010 pegged it at around $250 billion. In any case, total assets managed in SV plans exceed $800 billion and perhaps even approach $1 trillion. |
| 6 | As reported in: “Is It Prudent for Investors to Use Target-Date Funds for Retirement Savings?” Wall Street Journal, updated Marcy 17, 2017. https://www.wsj.com/articles/is-it-prudent-for-investors-to-use-target-date-funds-for-retirement-savings-1489975382. Interestingly, in 2006 before the passage of the Pension Protection Act of 2006 (PPA), wherein the Department of Labor granted a safe harbor (from lawsuits) for plan sponsors who chose target date funds as the default investment choice for their employees, stable value funds accounted for about 60% of the assets in 401(k) plans that offered them as an investment option, according to VanDerhei et al. (2017). This dropped to only 49% by 2014. Moreover, the percentage of plans including SV among its investment alternatives dropped from 51% in 2006 to 35% in 2014. Notwithstanding these legislative initiatives, SV’s popularity in terms of assets under management continues to keep pace with target date funds. https://www.stablevalue.org/index.php/news/article/stable-value-assets-continue-to-grow. |
| 7 | According to VanDerhei et al. (2017), older participants in their 60s hold about 20% of their assets in SV, whereas younger participants in their 20s typically allocate less than 5% to SV (see Chart 23). https://www.ebri.org/pdf/briefspdf/EBRI_IB_436_K-update.3Aug17.pdf. Current statistics are available at www.stablevalue.org. |
| 8 | We do not incorporate these 2016 data in our performance analyses because the SBBI data series for two of our alternative asset classes is not being maintained after 2015, and we did not wish to introduce a statistical discontinuity by piecing together alternative sources with divergent survey protocols as proxies for the original data series for a gain of only a single year. |
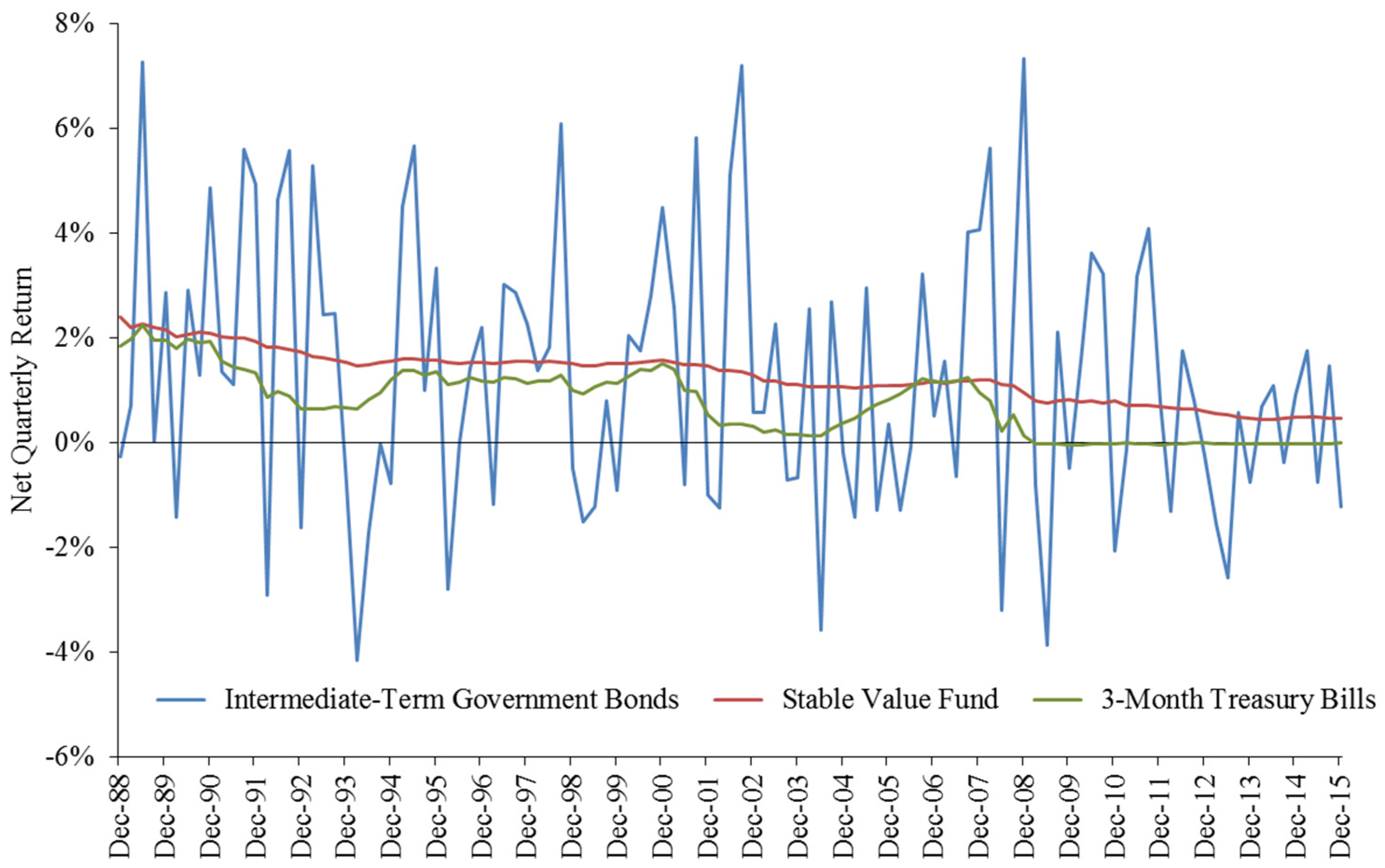
| 9 | They also dominated even more strongly the returns exhibited on the Barclays-Lehman mixed index of intermediate government/credit bonds up through 2015, but in the current study this index was replaced by only intermediate government bonds, which manifested higher historical returns and lower variance than the mixed index. |
| 10 | See MetLife (2010, pp. 38–39). An excellent historical review of stable value funds, with an emphasis on the development of synthetic stable value, is provided by Myers (2016). |
| 11 | |
| 12 | In our earlier studies, we used money market funds, but with the near disappearance of such funds post the Great Recession, we switched to T-bills in this study. The results of those studies were very similar to what we observed in the present study. |
| 13 | |
| 14 | Indeed, as reported by Douglas (1969), John Lintner’s initial cross sectional tests conducted in 1965 found that residual risk, which according to the Capital Asset Pricing Theory’s version of mean-variance analysis is not supposed to be priced by the marketplace, was indeed important to investors. More rigorous studies since then have reconfirmed these early findings. For example, Cvitanić et al. (2008) have found that ignoring higher moments can lead to significant overinvestment in risky securities, especially when volatility is high. |
| 15 | Our stable value index (equal-weighted average of individual returns) is based on assets under management of approximately $540 billion as of the end of 2015. Our composite index, which covered approximately 75,000 plans, included general account funds, externally managed separate account funds, and commingled funds. An alternative index available from Hueler Companies focuses on commingled funds. The Hueler Index is an equal-weighted total return average across all participating funds covered by Hueler and represents approximately 75% of the stable value pooled funds in the industry. Hueler Companies also construct indices on sub-samples of externally managed separate account funds (which in aggregate constituted about one-third of all stable value funds). See http://www.hueler.com/. We found the Hueler index of commingled fund quarterly returns to be 99.8% correlated with quarterly returns on our equal-weighted composite index, and about 0.43 basis points apart per quarter, over the period Q1-1989 through Q4-2015. |
| 16 | Annual fund fees and expenses from 1980 through 1989 are from ICI’s Research Fundamentals, Vol. 14, No. 6, October 2005, pp. 3, 6, and 7. Annual fund fees and expenses from 1999 through 2015 were personally communicated to the authors by ICI. With regard to using the ICI’s fees and expenses numbers, their averages reflect both institutional and retail pricing and both kinds of funds are prevalent in plan sponsored retirement programs. However, using only institutional pricing would understate the full cost of intermediation, as discussed and summarized in an enlightening article citing several scholarly studies. http://www.pattonfunds.com/pdf/The-Hidden-Costs-of-Mutual-Funds-WSJ-(00027720).PDF. We regard the use of ICI’s numbers as a good compromise but in any case, as our study will show, the results are so overwhelming that they are unlikely to change appreciably by using only reported institutional pricing. See also (Bogle 2005; Dichev 2007) for additional support. |
| 17 | Stable Value crediting rates are net of contract and management fees through 2008. Due to changes in crediting rate reporting to the SVIA, from 2009 on returns are net of contract fee only. We have subtracted 15 basis points per year from annualized crediting rates from Q1-2009 through Q4-2015 in order to net out management fees. |
| 18 | Early working papers created both equal-weighted and value-weighted average return indexes and our analyses showed similar results. However, an investor in SV can invest in only one SV fund per plan, so the value-weighted concept does not apply, unlike its intuitive appeal for mutual funds for stocks and bonds. Therefore, this study is based only on an equal-weighted index of SV returns. |
| 19 | |
| 20 | See Sortino and Price (1994) and Sortino and Van der Meer (1991) for a description of the Sortino Ratio. The theoretical foundations for the Sortino Ratio are provided in Pedersen and Satchell (2002). |
| 21 | |
| 22 | For stable value and money market funds, the quarterly return is assumed to be known (declared crediting rate for stable value and promised quarterly yield on 90-day T-bills for money market). For the other asset classes (stock and intermediate/long-term bond funds), the returns are not known at the start of the optimization quarter. (Again, in our earlier studies where money market fund returns were used instead of the quarterly T-bill yield proxy, similar results were obtained.) |
| 23 | This was done to ensure that we captured multiple full business cycles in our estimations, as recently cycles have lengthened markedly. (See, for example, http://www.nber.org/cycles.html). Because correlations across asset classes are sometimes quite different during the expansion portion of a cycle than during the contraction phase, robust estimations are best made across both phases of several full cycles. |
| 24 | An alternative that would take into account the term structure of interest is to employ a strict pure expectations theory by setting the expected returns on all bond portfolios equal to their current quarterly certainty equivalent (i.e., the current quarterly Treasury bill rate) plus either a theory-based or a historical short-term risk spread. However, we felt there was no compelling justification to wed ourselves to one of several theories of the term structure of interest while introducing additional model error, and that the current bond yield adequately incorporated market expectations for the purposes of this study. |
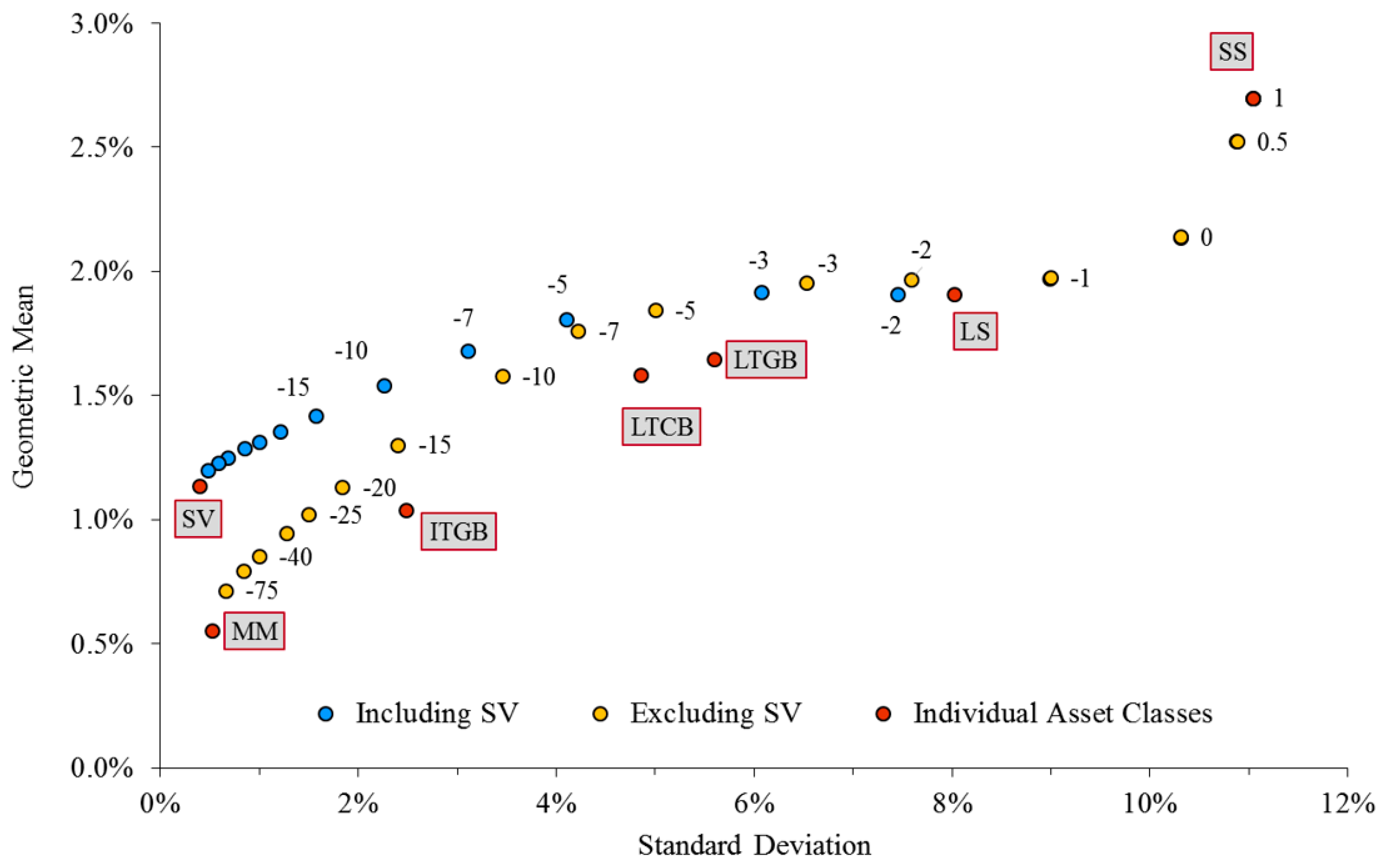
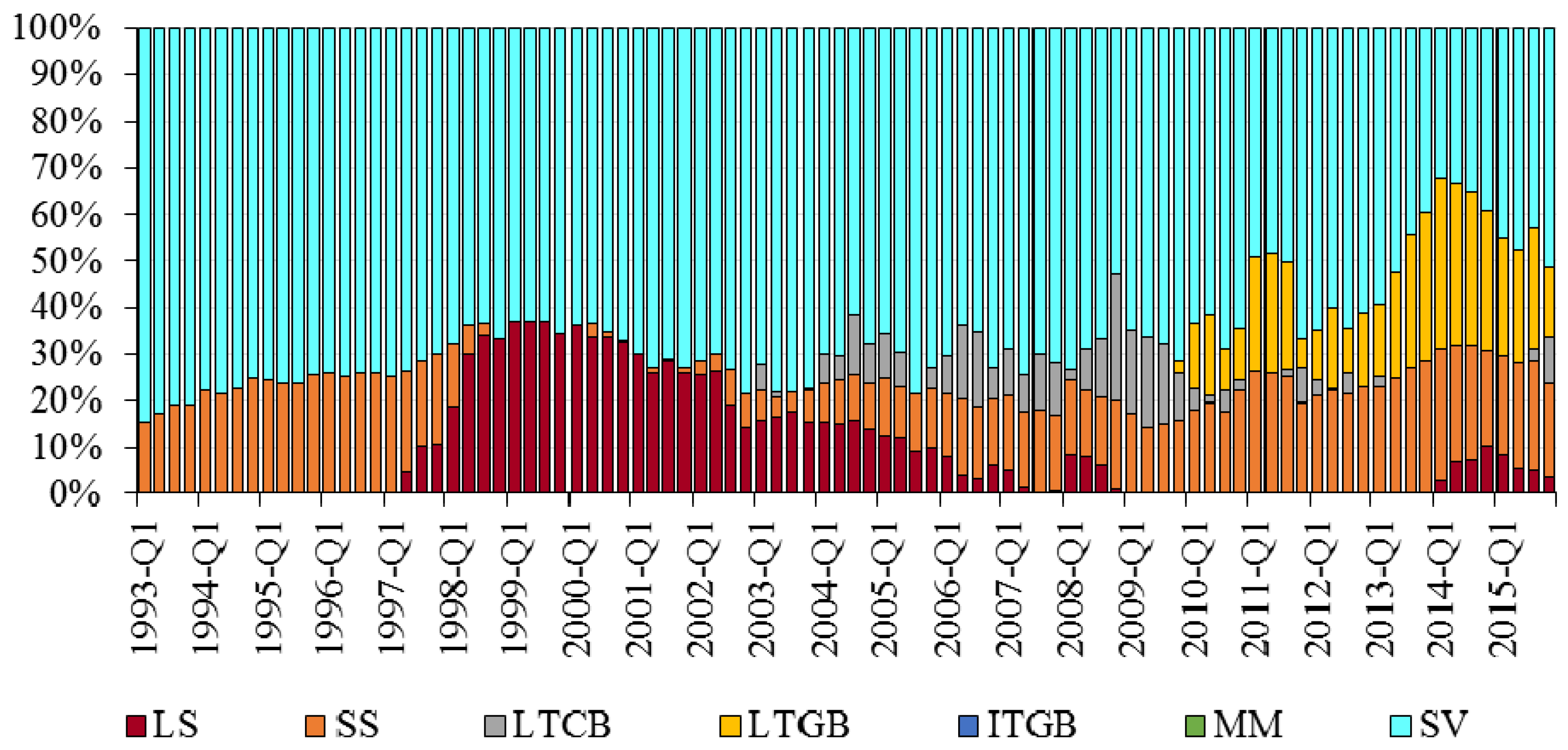
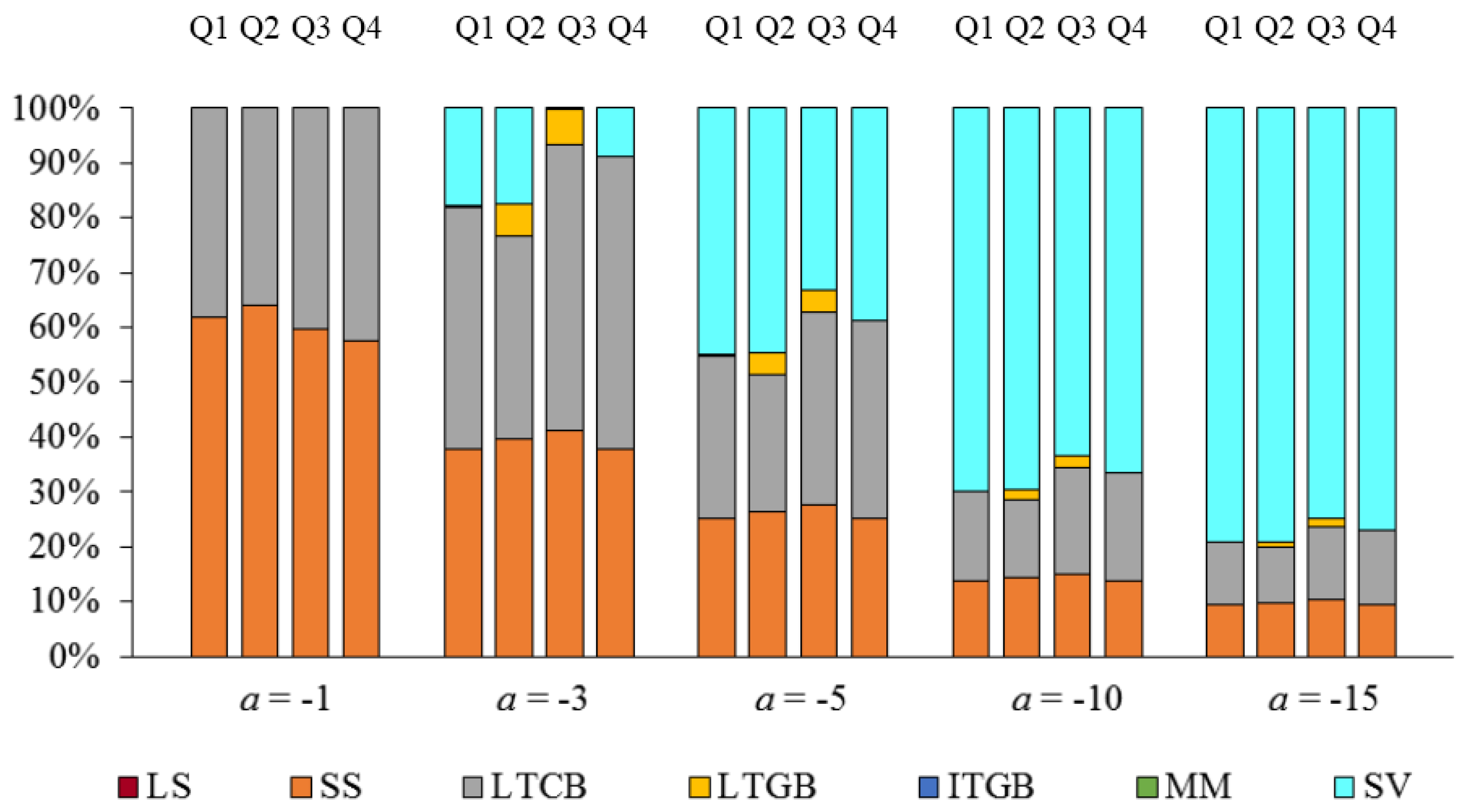
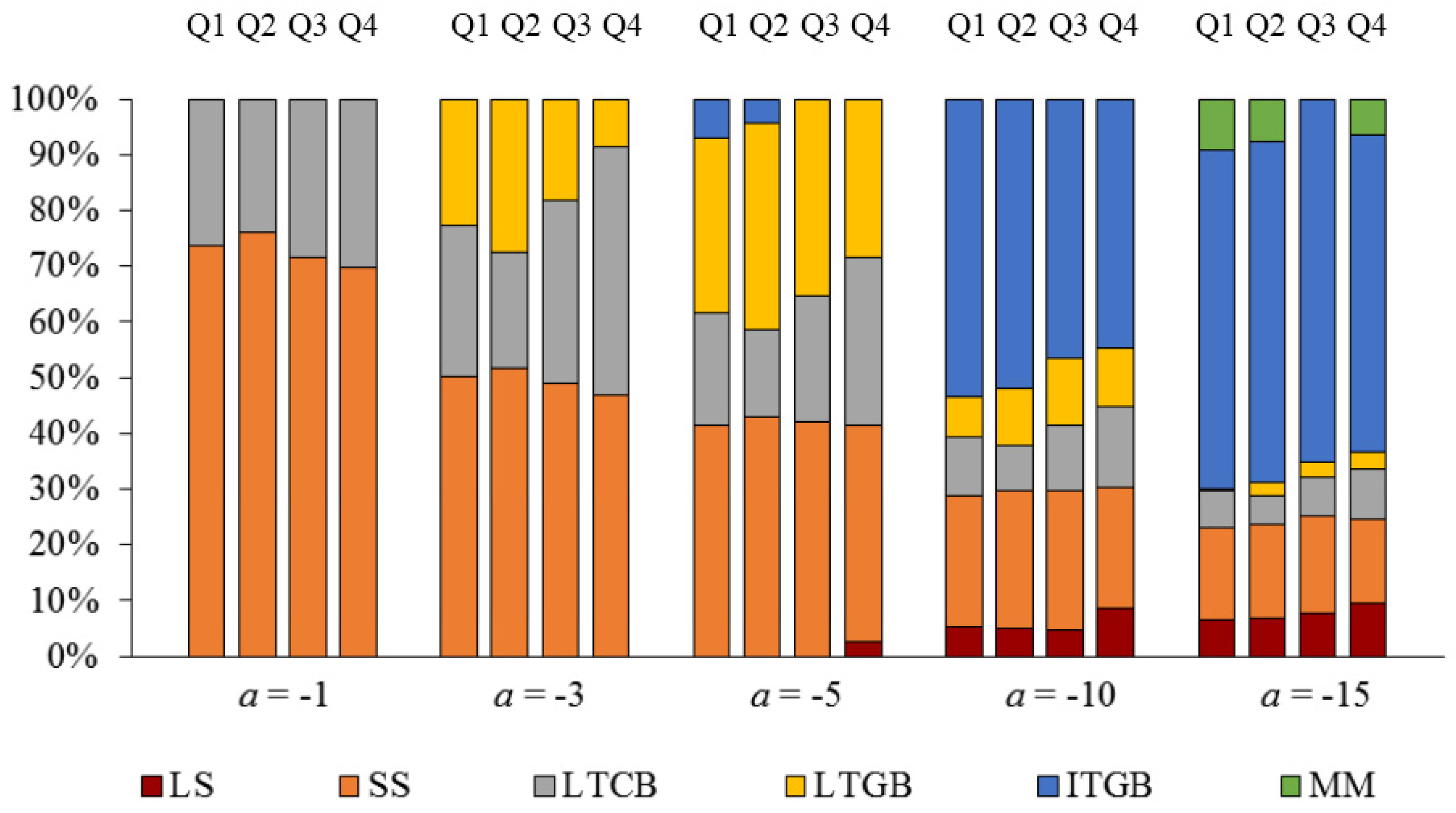
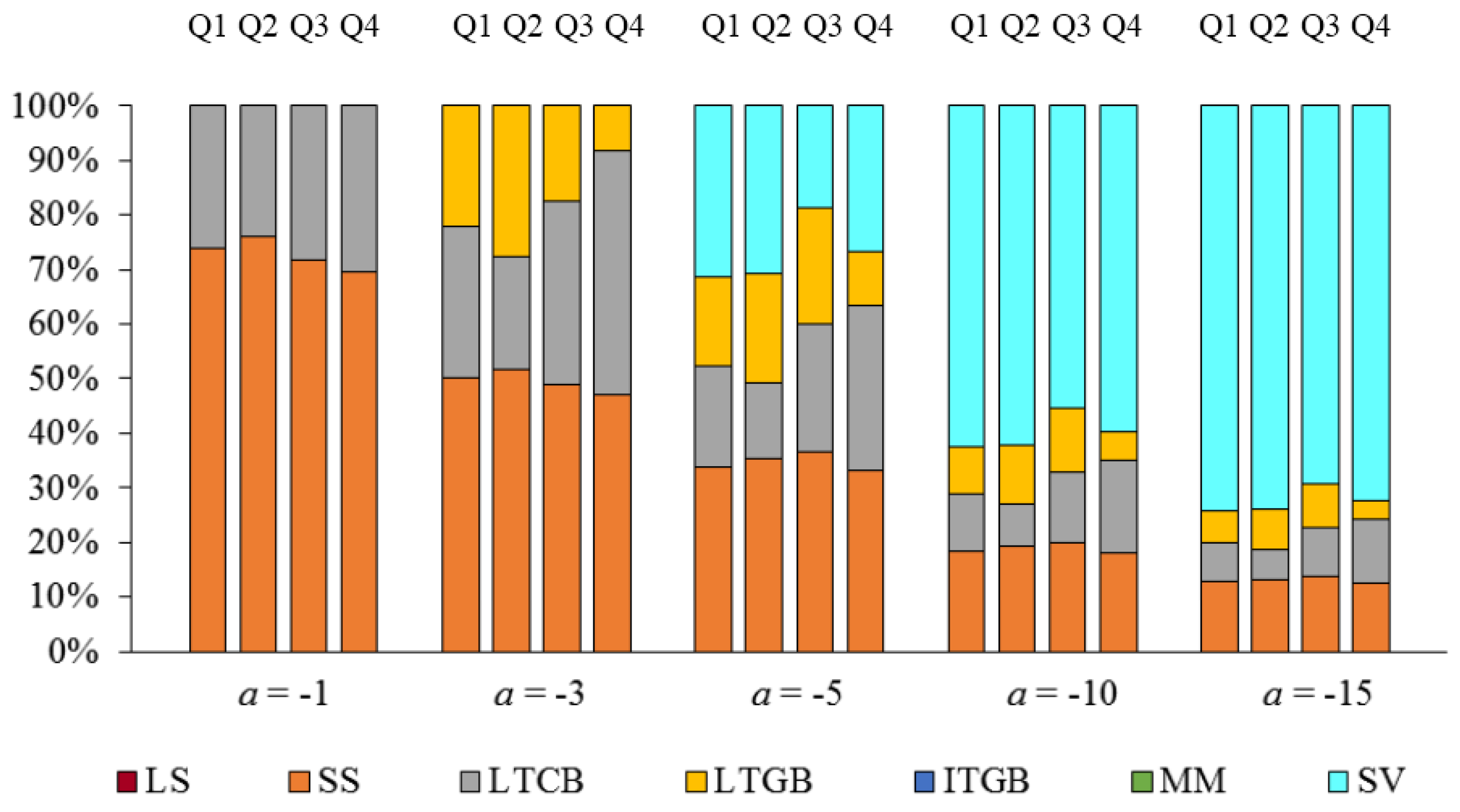
| 25 | For the sake of brevity, only results for 2015 are shown here. Complete results for all years in the period 1993 through 2015 are available from the authors upon request. |
| 26 | Many SV funds use the Lehman Intermediate Government/Credit Bond yield series as a benchmark. We use the wrapped index based on this series (provided to us by the SVIA, for the period of February 1973 through February 2008) as our proxy for SV returns prior to the beginning of our SV average return series in Q4-1988. More specifically, we regress the series of quarterly SV returns on the Lehman intermediate government/credit wrapped series quarterly returns over the period Q4-1988 through Q4-2007 (the period during which the two series’ quarterly returns overlap) and extrapolate the SV return series for the period Q2-1973 through Q3-1988. |
| 27 | In particular, the correlation between small stocks and both long-term and intermediate-term bonds turns out to have been very different in the two sample periods. Thus, the correlation between small stock returns and long-term corporates is −13.5% for the Q4-1988–Q4-2015 period and +26.1% for the period Q2-1973–Q3-1988; the correlation between small stock returns and long-term treasuries is −35.3% for the Q4-1988–Q4-2015 period and +20.4% for the period Q2-1973–Q3-1988; and the correlation between small stock returns and intermediate-term treasuries is −37.5% for the Q4-1988–Q4-2015 period and +15.3% for the period Q2-1973–Q3-1988. During the later sample, these correlation coefficients went from moderately positive to moderately negative, contributing to the more bowed-out efficient frontiers. |
| 28 | The later sample includes the period at the end of 2006 and most of 2007 when money market rates were higher than SV rates. In addition to this, the earlier sample includes long periods during the late 1970s and early 1980s when the same relationship happened. |
| 29 | Specifically, the correlation between small stocks returns and long-term corporates is −13.5% for the Q4-1988–Q4-2015 period and +6.5% for the period Q2-1973–Q4-2015; the correlation between small stocks returns and long-term treasuries is −35.3% for the Q4-1988–Q4-2015 period and −8.7% for the period Q2-1973–Q4-2015; and the correlation between small stocks returns and intermediate-term treasuries is −37.5% for the Q4-1988–Q4-2015 period and −9.5% for the period Q2-1973–Q4-2015. |
| 30 | The most notable exception of which we are aware was linked to the sudden Lehman Brothers bankruptcy in September of 2008. This resulted in a small monthly decline in fund value of 1.7% in December, albeit an overall positive return over the year of 2%. In another instance, a fund manager (State Street) infused an additional $610 million into its SV fund to offset some investment losses that it felt should not accrue to plan participants, but the fund was not in jeopardy. One supplemental savings fund associated with Chrysler was not subject to the Employee Retirement Income Security Act (ERISA) and the protective umbrella from creditors that it affords. Additionally, it may not have been eligible for accounting under FASB. However, in any case, Chrysler liquidated the fund and realized the loss for participants in advance of any potential claim by other creditors. There have been other funds that experienced severe stress, yet they weathered the worst part of the storm and have managed their market-to-book asset ratios back into the traditional ranges. Of course, there is always the peril that just because an investment fund has “stable value” in its name or otherwise masquerades as such, it may not conform to the essential indicia of a stable value fund. For example, http://www.sec.gov/litigation/complaints/2009/comp21010.pdf. |
| 31 | In an earlier version of this study, http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1465755, we found that long-term government bonds stochastically dominated, in the second and higher degrees, large stocks over the period January 1989–December 2008. This very interesting result was largely due to poor stock performance during the crash of 2007–2008. Relatively high large stock returns during the years since have made this dominance disappear for the period 1989–2015. |
| 32 | We remind the reader of these two cautions with a concise synopsis from the blog of Oxford University’s Professor Simon Wren-Lewis: “When that pioneering economist David Hume wrote about the problem of induction, he talked about the possibility that the sun would not rise one morning. There is no way we can know ‘for sure’ that it will rise. (In contrast, we know for sure that 1 + 1 = 2.) Just because the theories we have suggest it will rise each morning, and those theories have been right so far, does nothing to ensure they will continue to be right. “The problem with this example is that it is very difficult to imagine the sun not rising every morning. Bertrand Russell had perhaps a better example. The chicken that is fed by the farmer each morning may well have a theory that it will always be fed each morning—it becomes a ‘law’. And it works every day, until the day the chicken is instead slaughtered.” The remainder of the post is worth reading and referenced below. https://mainlymacro.blogspot.com/2013/11/bertrand-russells-chicken-and-why-it.html. |
| 33 | |
| 34 | See AitSahlia et al. (2017) for an approach that might have some promise in examining the possible improvements attainable. While that study does not consider SV funds directly, the methodology appears capable of answering some preliminary questions. |
| 35 | Nonetheless, during the Great Recession of 2008–2009 the large and rapid decline in equity values motivated many investors to flee toward safer assets, including SV and short-term government bonds. This sent yields plumeting to very low levels at the very time SV fund managers were seeking to place additional cash, resulting in a rapid decline in the crediting rates they could offer to investors. At that time SV assets were not used in target date funds, so we cannot be sure what the overall effect would have been on SV-laden target date funds and on SV funds in general. |
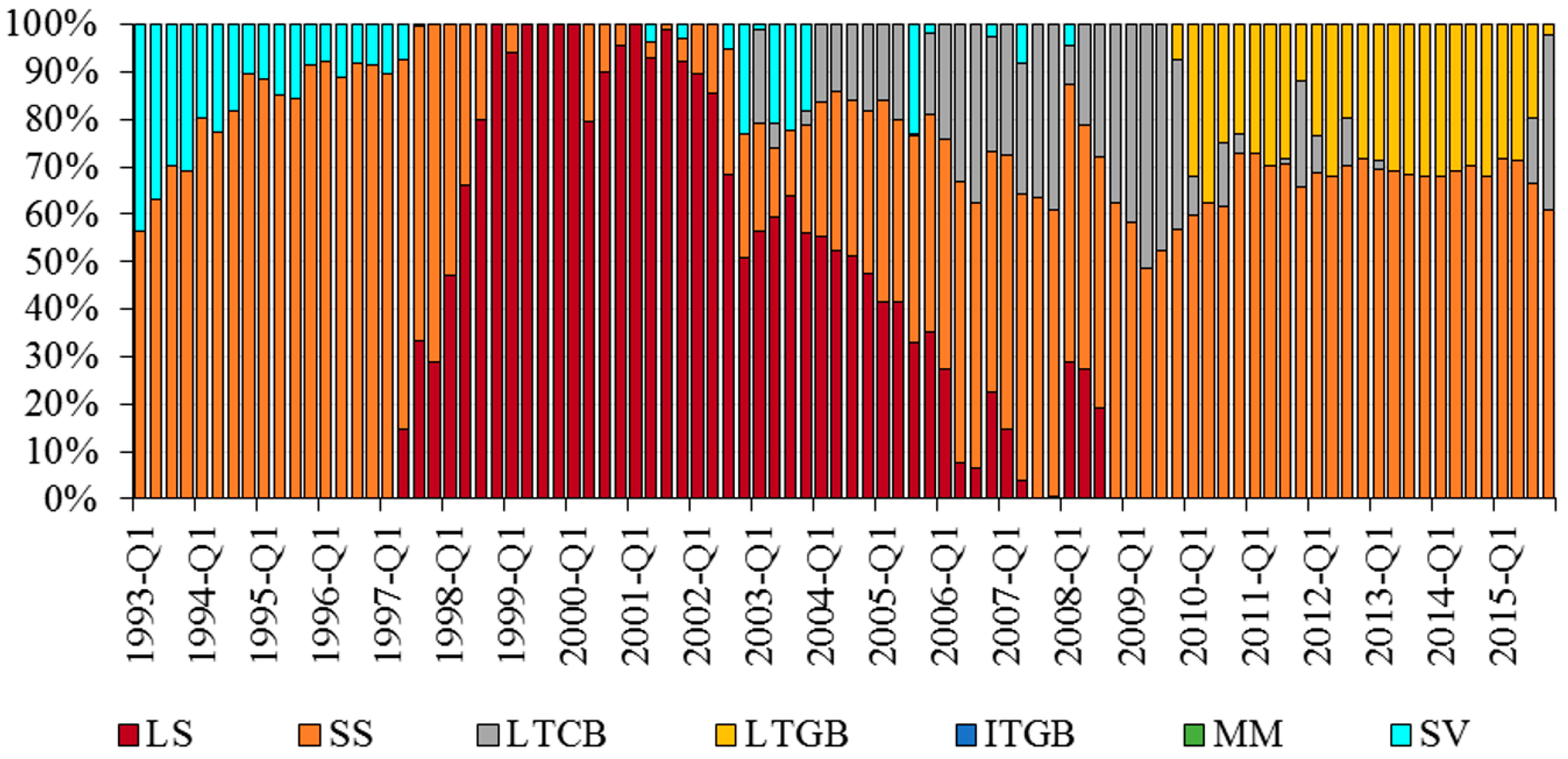
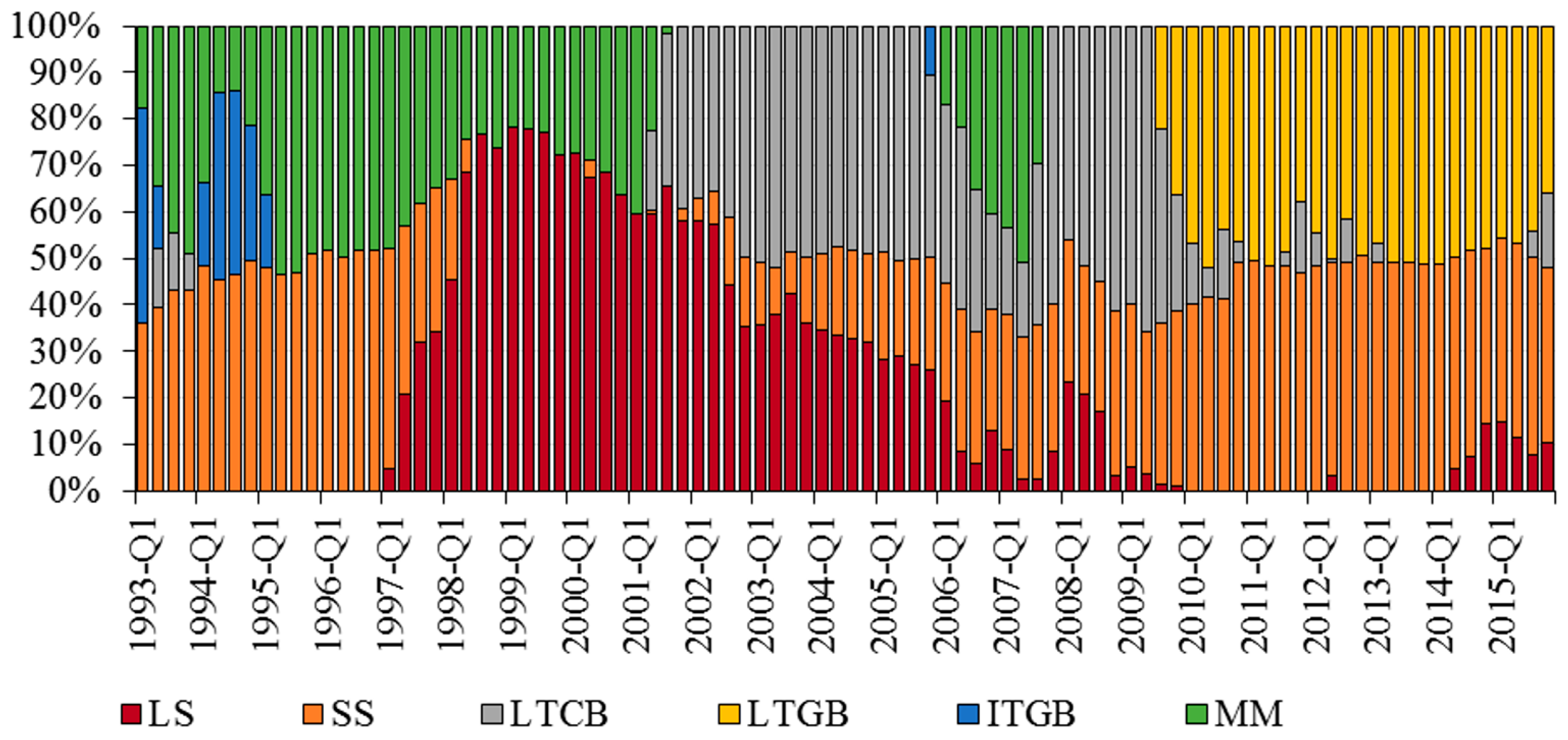
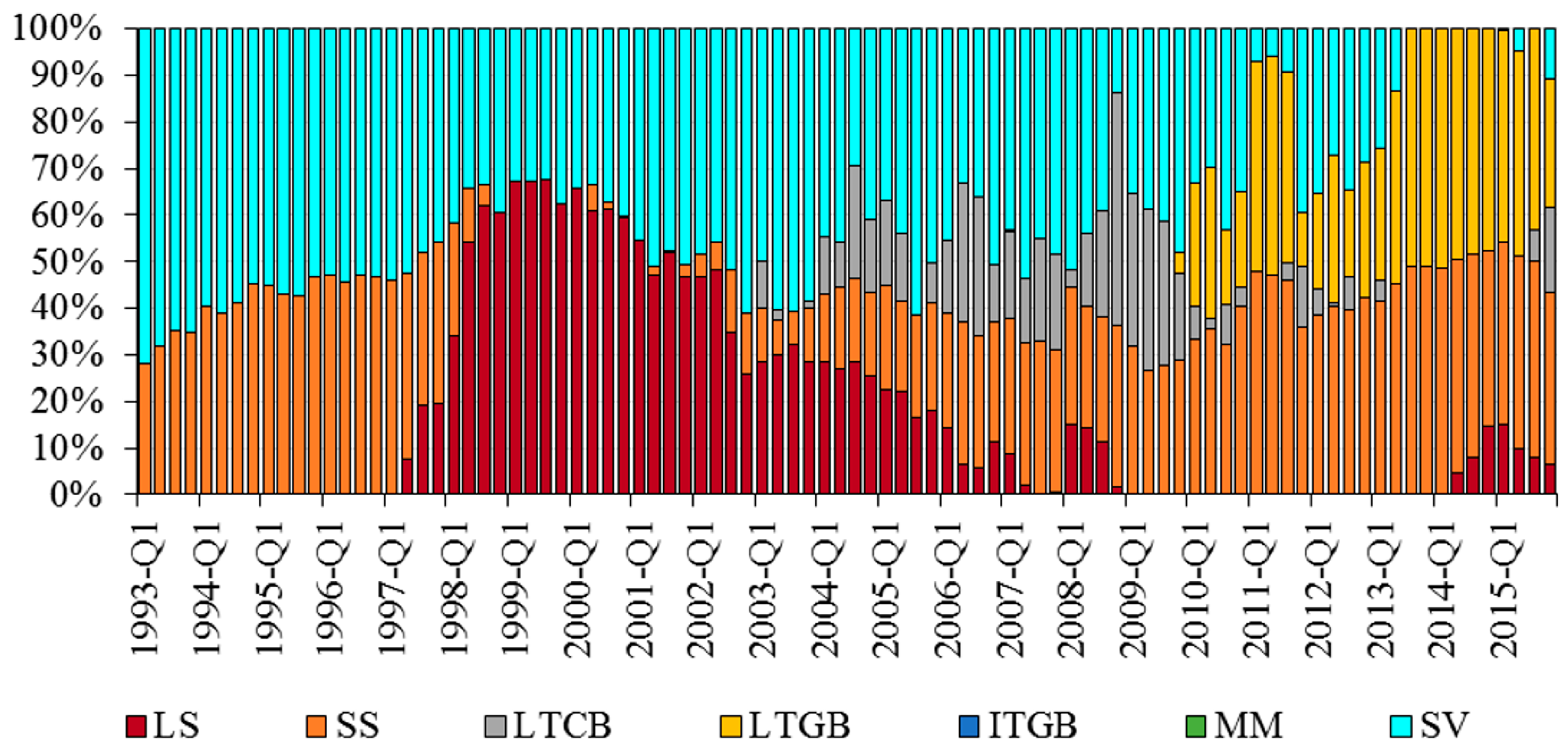
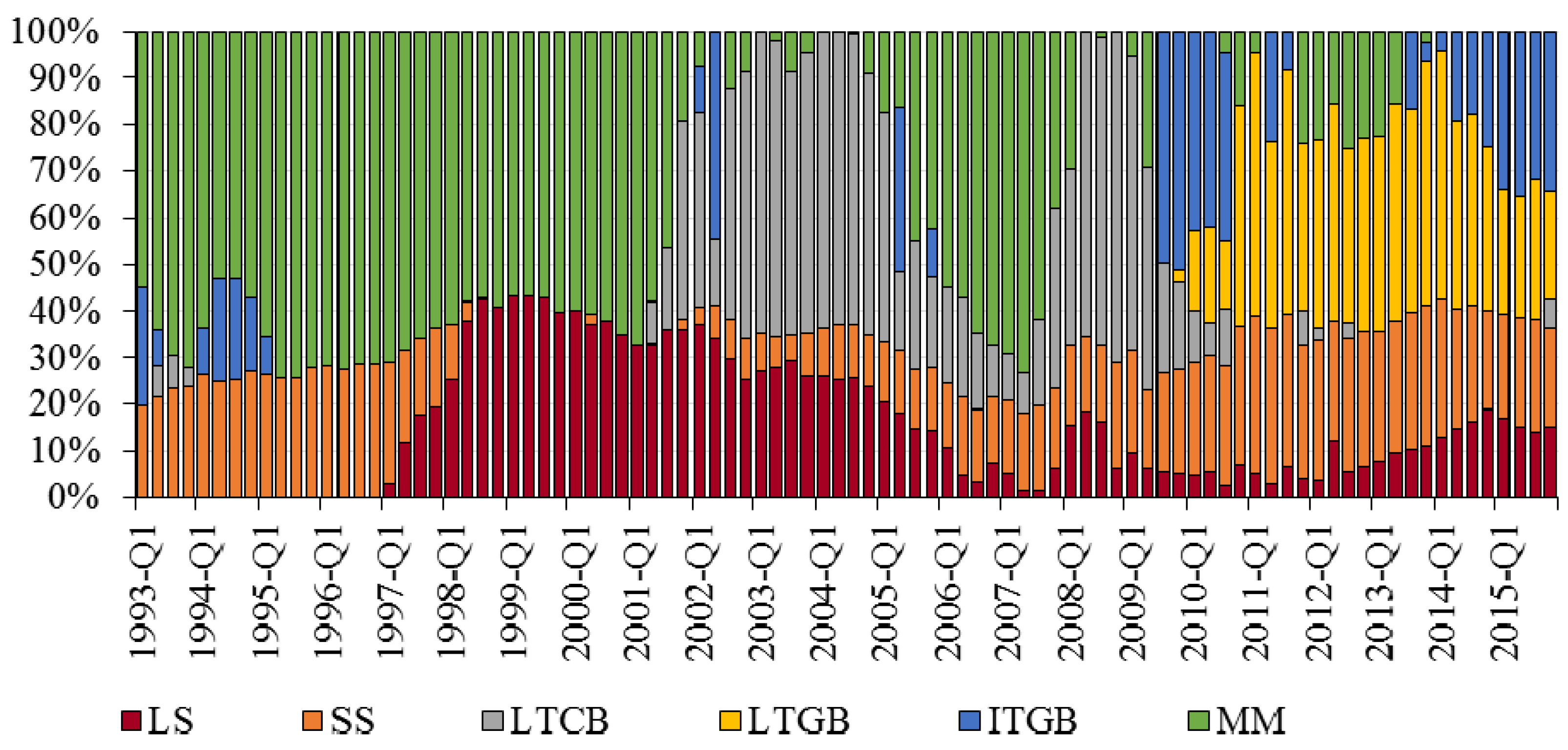
| LS | SS | LTCB | LTGB | ITGB | MM | SV | |
|---|---|---|---|---|---|---|---|
| Mean | 2.41% | 3.27% | 1.84% | 1.93% | 1.24% | 0.75% | 1.28% |
| Median | 2.71% | 3.44% | 1.64% | 1.31% | 0.99% | 0.82% | 1.37% |
| Maximum | 20.97% | 28.67% | 23.18% | 21.00% | 7.33% | 2.24% | 2.40% |
| Minimum | −22.18% | −26.98% | −12.61% | −8.39% | −4.15% | −0.05% | 0.44% |
| Std. Dev. | 7.78% | 11.03% | 4.64% | 5.41% | 2.58% | 0.63% | 0.49% |
| Skewness | −0.604 | −0.250 | 0.638 | 0.671 | 0.326 | N/A | N/A |
| Kurtosis | 0.721 | 0.260 | 3.886 | 1.235 | −0.390 | N/A | N/A |
| Jarque–Bera | 8.992 | 1.440 | 75.970 | 15.103 | 2.616 | N/A | N/A |
| Probability | 0.011 | 0.487 | 0.000 | 0.001 | 0.270 | N/A | N/A |
| Asset Class | ||||||||
|---|---|---|---|---|---|---|---|---|
| Expected Return | Standard Deviation | Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Money Market | Stable Value |
| 1.28% | 0.49% | 0.00% | 0.29% | 0.53% | 0.00% | 0.00% | 0.00% | 99.17% |
| 1.38% | 0.62% | 0.11% | 3.47% | 0.00% | 5.64% | 0.00% | 0.00% | 90.78% |
| 1.48% | 0.89% | 0.42% | 6.51% | 0.00% | 11.10% | 0.00% | 0.00% | 81.97% |
| 1.58% | 1.22% | 0.73% | 9.54% | 0.00% | 16.56% | 0.00% | 0.00% | 73.17% |
| 1.68% | 1.57% | 1.03% | 12.54% | 0.00% | 21.96% | 0.00% | 0.00% | 64.47% |
| 1.78% | 1.92% | 1.33% | 15.58% | 0.00% | 27.42% | 0.00% | 0.00% | 55.67% |
| 1.88% | 2.28% | 1.64% | 18.62% | 0.00% | 32.88% | 0.00% | 0.00% | 46.86% |
| 1.98% | 2.64% | 1.94% | 21.62% | 0.00% | 38.27% | 0.00% | 0.00% | 38.17% |
| 2.08% | 3.01% | 2.25% | 24.65% | 0.00% | 43.73% | 0.00% | 0.00% | 29.36% |
| 2.18% | 3.38% | 2.56% | 27.69% | 0.00% | 49.19% | 0.00% | 0.00% | 20.56% |
| 2.28% | 3.75% | 2.86% | 30.73% | 0.00% | 54.65% | 0.00% | 0.00% | 11.75% |
| 2.37% | 4.11% | 3.16% | 33.73% | 0.00% | 60.05% | 0.00% | 0.00% | 3.06% |
| 2.47% | 4.51% | 0.00% | 40.81% | 0.00% | 59.19% | 0.00% | 0.00% | 0.00% |
| 2.57% | 5.06% | 0.00% | 48.23% | 0.00% | 51.77% | 0.00% | 0.00% | 0.00% |
| 2.67% | 5.74% | 0.00% | 55.56% | 0.00% | 44.44% | 0.00% | 0.00% | 0.00% |
| 2.77% | 6.51% | 0.00% | 62.98% | 0.00% | 37.02% | 0.00% | 0.00% | 0.00% |
| 2.87% | 7.35% | 0.00% | 70.41% | 0.00% | 29.59% | 0.00% | 0.00% | 0.00% |
| 2.97% | 8.22% | 0.00% | 77.73% | 0.00% | 22.27% | 0.00% | 0.00% | 0.00% |
| 3.07% | 9.14% | 0.00% | 85.16% | 0.00% | 14.84% | 0.00% | 0.00% | 0.00% |
| 3.17% | 10.08% | 0.00% | 92.58% | 0.00% | 7.42% | 0.00% | 0.00% | 0.00% |
| 3.27% | 11.03% | 0.00% | 100.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Asset Class | |||||||
|---|---|---|---|---|---|---|---|
| Expected Return | Standard Deviation | Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Money Market |
| 0.78% | 0.63% | 0.00% | 0.80% | 1.50% | 0.00% | 0.00% | 97.70% |
| 0.91% | 0.71% | 0.00% | 3.31% | 2.55% | 2.84% | 3.10% | 88.20% |
| 1.03% | 0.90% | 0.81% | 5.40% | 1.80% | 6.63% | 7.56% | 77.80% |
| 1.16% | 1.14% | 2.10% | 7.18% | 0.89% | 10.51% | 11.88% | 67.44% |
| 1.28% | 1.41% | 3.40% | 8.97% | 0.00% | 14.42% | 16.25% | 56.96% |
| 1.40% | 1.69% | 4.60% | 10.74% | 0.00% | 17.61% | 20.59% | 46.47% |
| 1.53% | 1.98% | 5.81% | 12.52% | 0.00% | 20.83% | 24.96% | 35.88% |
| 1.65% | 2.27% | 7.02% | 14.28% | 0.00% | 24.02% | 29.29% | 25.39% |
| 1.78% | 2.57% | 8.23% | 16.06% | 0.00% | 27.25% | 33.67% | 14.80% |
| 1.90% | 2.87% | 9.43% | 17.82% | 0.00% | 30.44% | 38.00% | 4.31% |
| 2.02% | 3.18% | 10.36% | 19.89% | 0.00% | 37.86% | 31.89% | 0.00% |
| 2.15% | 3.50% | 11.09% | 22.14% | 0.00% | 48.17% | 18.60% | 0.00% |
| 2.27% | 3.83% | 11.81% | 24.38% | 0.00% | 58.37% | 5.45% | 0.00% |
| 2.40% | 4.20% | 4.39% | 33.58% | 0.00% | 62.03% | 0.00% | 0.00% |
| 2.52% | 4.75% | 0.00% | 44.38% | 0.00% | 55.62% | 0.00% | 0.00% |
| 2.65% | 5.55% | 0.00% | 53.68% | 0.00% | 46.32% | 0.00% | 0.00% |
| 2.77% | 6.50% | 0.00% | 62.89% | 0.00% | 37.11% | 0.00% | 0.00% |
| 2.89% | 7.56% | 0.00% | 72.19% | 0.00% | 27.81% | 0.00% | 0.00% |
| 3.02% | 8.67% | 0.00% | 81.40% | 0.00% | 18.60% | 0.00% | 0.00% |
| 3.14% | 9.84% | 0.00% | 90.70% | 0.00% | 9.30% | 0.00% | 0.00% |
| 3.27% | 11.02% | 0.00% | 99.91% | 0.00% | 0.09% | 0.00% | 0.00% |
| Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Stable Value | |
|---|---|---|---|---|---|---|
| Mean of Excess Returns | 1.66% | 2.52% | 1.09% | 1.18% | 0.49% | 0.53% |
| STDEV of Excess Returns | 7.78% | 11.09% | 4.66% | 5.38% | 2.49% | 0.30% |
| Target Semi-Deviation | 5.16% | 6.72% | 2.55% | 2.85% | 1.43% | 0.09% |
| Sharpe Ratio | 0.214 | 0.227 | 0.234 | 0.219 | 0.199 | 1.764 |
| Sortino Ratio | 0.322 | 0.375 | 0.428 | 0.414 | 0.347 | 5.649 |
| Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Stable Value | |
|---|---|---|---|---|---|---|
| Mean of Excess Returns | 7.25% | 10.39% | 4.45% | 5.02% | 2.14% | 2.17% |
| STDEV of Excess Returns | 17.72% | 22.17% | 8.29% | 12.04% | 5.29% | 1.18% |
| Target Semi-Deviation | 10.29% | 10.09% | 3.76% | 6.05% | 2.99% | 0.37% |
| Sharpe Ratio | 0.409 | 0.469 | 0.537 | 0.417 | 0.404 | 1.838 |
| Sortino Ratio | 0.705 | 1.030 | 1.184 | 0.830 | 0.715 | 5.795 |
| Does an Asset in Rows [1]–[7] Stochastically Dominate an Asset in Columns [a]–[g]? | Large Stocks [a] | Small Stocks [b] | Long–Term Corporate Bonds [c] | Long–Term Gov’t Bonds [d] | Interm.–Term Gov’t Bonds [e] | Money Market [f] | Stable Value [g] | |
|---|---|---|---|---|---|---|---|---|
| [1] | Large Stocks | N | N | N | N | N | N | |
| [2] | Small Stocks | N | N | N | N | N | N | |
| [3] | Long-Term Corporate Bonds | N | N | N | N | N | N | |
| [4] | Long-Term Government Bonds | N | N | N | N | N | N | |
| [5] | Intermediate-Term Government Bonds | N | N | N | N | N | N | |
| [6] | Money Market | N | N | N | N | N | N | |
| [7] | Stable Value | N | N | N | N | 2nd Degree and Higher | 1st Degree and Higher | |
| Mean | STDEV | |||
| LS | 1.91% | 8.02% | ||
| SS | 2.70% | 11.04% | ||
| LTCB | 1.59% | 4.85% | ||
| LTGB | 1.65% | 5.59% | ||
| ITGB | 1.04% | 2.49% | ||
| MM | 0.55% | 0.52% | ||
| SV | 1.13% | 0.39% | ||
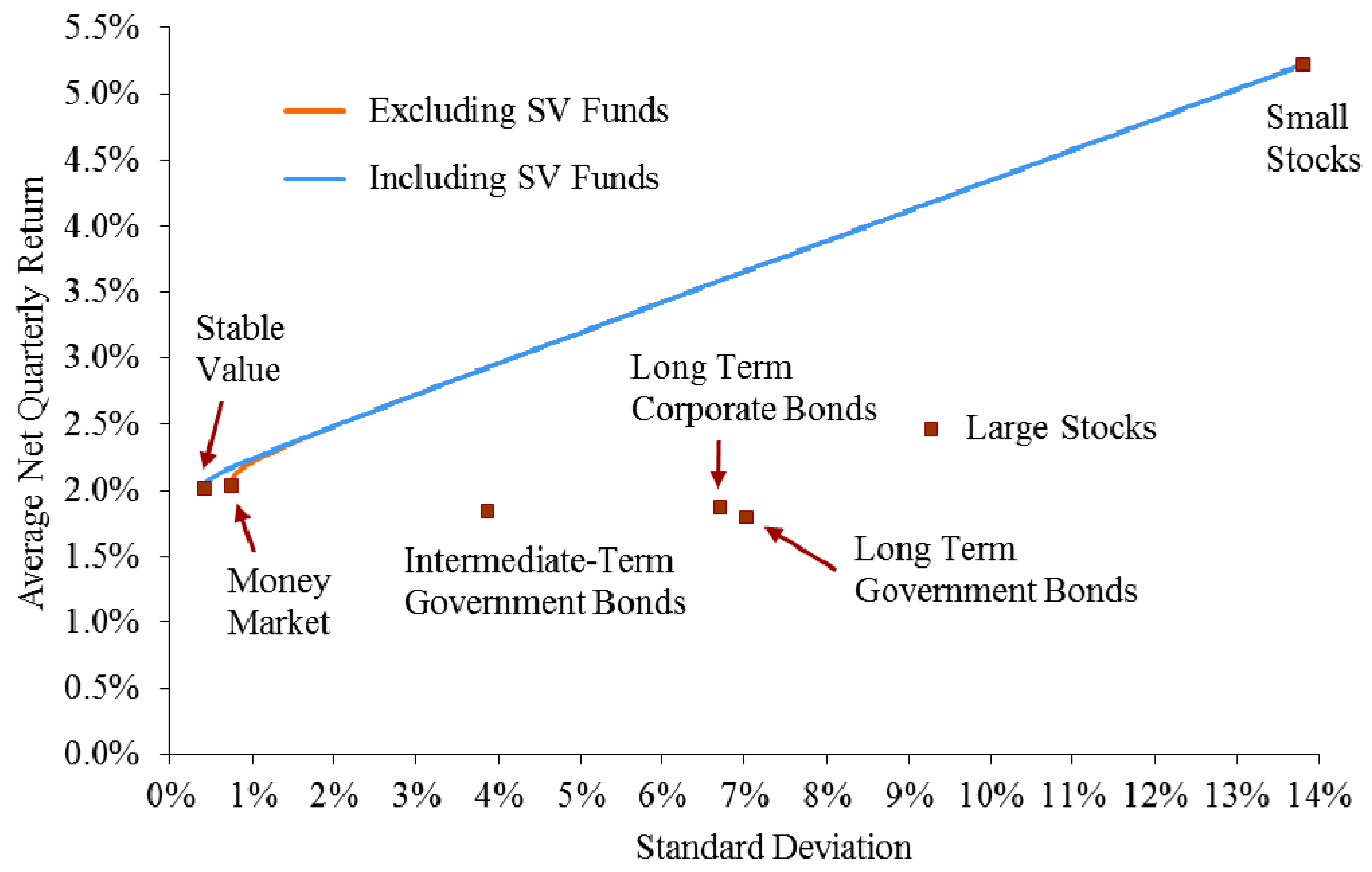
| Exclude SV | Include SV | |||
| Value of a | Mean | STDEV | Mean | STDEV |
| 1.00 | 2.70% | 11.04% | 2.70% | 11.04% |
| 0.75 | 2.63% | 10.94% | 2.63% | 10.94% |
| 0.50 | 2.52% | 10.88% | 2.52% | 10.87% |
| 0.25 | 2.29% | 10.53% | 2.29% | 10.52% |
| 0 | 2.14% | 10.31% | 2.14% | 10.31% |
| −1 | 1.98% | 8.99% | 1.97% | 8.99% |
| −2 | 1.97% | 7.58% | 1.91% | 7.45% |
| −3 | 1.96% | 6.53% | 1.92% | 6.07% |
| −5 | 1.85% | 5.00% | 1.81% | 4.10% |
| −7 | 1.76% | 4.22% | 1.68% | 3.10% |
| −10 | 1.58% | 3.45% | 1.54% | 2.26% |
| −15 | 1.30% | 2.40% | 1.42% | 1.57% |
| −20 | 1.13% | 1.83% | 1.35% | 1.21% |
| −25 | 1.02% | 1.49% | 1.31% | 0.99% |
| −30 | 0.95% | 1.27% | 1.29% | 0.85% |
| −40 | 0.85% | 0.99% | 1.25% | 0.68% |
| −50 | 0.79% | 0.84% | 1.23% | 0.58% |
| −75 | 0.72% | 0.65% | 1.20% | 0.48% |
| LS | SS | LTCB | LTGB | ITGB | MM | SV | |
|---|---|---|---|---|---|---|---|
| Mean | 2.45% | 5.22% | 1.86% | 1.79% | 1.83% | 2.03% | 2.01% |
| Median | 2.69% | 5.64% | 1.11% | 0.39% | 1.03% | 1.85% | 2.01% |
| Maximum | 22.37% | 44.26% | 23.71% | 23.85% | 16.06% | 3.93% | 2.64% |
| Minimum | −25.74% | −28.47% | −13.73% | −15.02% | −6.86% | 1.09% | 1.40% |
| Std. Dev. | 9.28% | 13.81% | 6.72% | 7.04% | 3.88% | 0.76% | 0.42% |
| Skewness | −0.490 | 0.175 | 0.702 | 0.863 | 1.183 | N/A | N/A |
| Kurtosis | 0.948 | 0.496 | 1.705 | 1.715 | 2.983 | N/A | N/A |
| Jarque–Bera | 4.806 | 0.953 | 12.601 | 15.289 | 37.452 | N/A | N/A |
| Probability | 0.090 | 0.621 | 0.002 | 0.000 | 0.000 | N/A | N/A |
| Asset Class | ||||||||
|---|---|---|---|---|---|---|---|---|
| Expected Return | Standard Deviation | Large Stocks | Small Stocks | Long–Term Corp. Bonds | Long–Term Gov’t Bonds | Interm.–Term Gov’t Bonds | Money Market | Stable Value |
| 2.02% | 0.41% | 0.00% | 0.28% | 0.00% | 0.00% | 0.00% | 13.58% | 86.14% |
| 2.18% | 0.79% | 0.00% | 5.14% | 0.00% | 0.00% | 0.00% | 31.92% | 62.94% |
| 2.34% | 1.41% | 0.00% | 10.00% | 0.00% | 0.00% | 0.00% | 50.26% | 39.74% |
| 2.50% | 2.07% | 0.00% | 14.91% | 0.00% | 0.00% | 0.00% | 68.80% | 16.28% |
| 2.66% | 2.73% | 0.00% | 19.81% | 0.00% | 0.00% | 0.00% | 80.19% | 0.00% |
| 2.82% | 3.40% | 0.00% | 24.80% | 0.00% | 0.00% | 0.00% | 75.20% | 0.00% |
| 2.98% | 4.09% | 0.00% | 29.85% | 0.00% | 0.00% | 0.00% | 70.15% | 0.00% |
| 3.14% | 4.78% | 0.00% | 34.84% | 0.00% | 0.00% | 0.00% | 65.16% | 0.00% |
| 3.30% | 5.47% | 0.00% | 39.83% | 0.00% | 0.00% | 0.00% | 60.17% | 0.00% |
| 3.46% | 6.16% | 0.00% | 44.88% | 0.00% | 0.00% | 0.00% | 55.12% | 0.00% |
| 3.62% | 6.85% | 0.00% | 49.87% | 0.00% | 0.00% | 0.00% | 50.13% | 0.00% |
| 3.78% | 7.54% | 0.00% | 54.86% | 0.00% | 0.00% | 0.00% | 45.14% | 0.00% |
| 3.94% | 8.24% | 0.00% | 59.91% | 0.00% | 0.00% | 0.00% | 40.09% | 0.00% |
| 4.10% | 8.93% | 0.00% | 64.90% | 0.00% | 0.00% | 0.00% | 35.10% | 0.00% |
| 4.26% | 9.63% | 0.00% | 69.89% | 0.00% | 0.00% | 0.00% | 30.11% | 0.00% |
| 4.42% | 10.33% | 0.00% | 74.93% | 0.00% | 0.00% | 0.00% | 25.07% | 0.00% |
| 4.58% | 11.02% | 0.00% | 79.93% | 0.00% | 0.00% | 0.00% | 20.07% | 0.00% |
| 4.74% | 11.71% | 0.00% | 84.92% | 0.00% | 0.00% | 0.00% | 15.08% | 0.00% |
| 4.90% | 12.42% | 0.00% | 89.96% | 0.00% | 0.00% | 0.00% | 10.04% | 0.00% |
| 5.06% | 13.11% | 0.00% | 94.95% | 0.00% | 0.00% | 0.00% | 5.05% | 0.00% |
| 5.22% | 13.80% | 0.00% | 99.95% | 0.00% | 0.00% | 0.00% | 0.05% | 0.00% |
| Asset Class | ||||||||
|---|---|---|---|---|---|---|---|---|
| Expected Return | Standard Deviation | Large Stocks | Small Stocks | Long–Term Corp. Bonds | Long–Term Gov’t Bonds | Interm.–Term Gov’t Bonds | Money Market | |
| 2.05% | 0.74% | 0.59% | 0.63% | 0.00% | 0.00% | 0.00% | 98.79% | |
| 2.21% | 0.99% | 0.00% | 5.64% | 0.00% | 0.00% | 0.00% | 94.36% | |
| 2.37% | 1.54% | 0.00% | 10.63% | 0.00% | 0.00% | 0.00% | 89.37% | |
| 2.53% | 2.17% | 0.00% | 15.57% | 0.00% | 0.00% | 0.00% | 84.43% | |
| 2.68% | 2.83% | 0.00% | 20.56% | 0.00% | 0.00% | 0.00% | 79.44% | |
| 2.84% | 3.50% | 0.00% | 25.50% | 0.00% | 0.00% | 0.00% | 74.50% | |
| 3.00% | 4.18% | 0.00% | 30.49% | 0.00% | 0.00% | 0.00% | 69.51% | |
| 3.16% | 4.86% | 0.00% | 35.43% | 0.00% | 0.00% | 0.00% | 64.57% | |
| 3.32% | 5.55% | 0.00% | 40.42% | 0.00% | 0.00% | 0.00% | 59.58% | |
| 3.48% | 6.23% | 0.00% | 45.36% | 0.00% | 0.00% | 0.00% | 54.64% | |
| 3.64% | 6.92% | 0.00% | 50.35% | 0.00% | 0.00% | 0.00% | 49.65% | |
| 3.79% | 7.60% | 0.00% | 55.29% | 0.00% | 0.00% | 0.00% | 44.71% | |
| 3.95% | 8.29% | 0.00% | 60.28% | 0.00% | 0.00% | 0.00% | 39.72% | |
| 4.11% | 8.98% | 0.00% | 65.22% | 0.00% | 0.00% | 0.00% | 34.78% | |
| 4.27% | 9.67% | 0.00% | 70.21% | 0.00% | 0.00% | 0.00% | 29.79% | |
| 4.43% | 10.36% | 0.00% | 75.15% | 0.00% | 0.00% | 0.00% | 24.85% | |
| 4.59% | 11.05% | 0.00% | 80.14% | 0.00% | 0.00% | 0.00% | 19.86% | |
| 4.74% | 11.74% | 0.00% | 85.08% | 0.00% | 0.00% | 0.00% | 14.92% | |
| 4.90% | 12.43% | 0.00% | 90.07% | 0.00% | 0.00% | 0.00% | 9.93% | |
| 5.06% | 13.12% | 0.00% | 95.01% | 0.00% | 0.00% | 0.00% | 4.99% | |
| 5.22% | 13.81% | 0.00% | 100.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| LS | SS | LTCB | LTGB | ITGB | SV | |
|---|---|---|---|---|---|---|
| Mean of Excess Returns | 0.43% | 3.19% | −0.17% | −0.23% | −0.20% | −0.02% |
| STDEV of Excess Returns | 9.38% | 13.92% | 6.65% | 6.93% | 3.73% | 0.73% |
| Target Semi-Deviation | 6.64% | 7.83% | 4.35% | 4.39% | 2.38% | 0.30% |
| Sharpe Ratio | 0.045 | 0.229 | −0.025 | −0.034 | −0.053 | −0.024 |
| Sortino Ratio | 0.064 | 0.408 | −0.038 | −0.053 | −0.082 | −0.060 |
| LS | SS | LTCB | LTGB | ITGB | SV | |
|---|---|---|---|---|---|---|
| Mean of Excess Returns | 2.65% | 14.41% | −0.56% | −0.94% | −0.96% | 0.03% |
| STDEV of Excess Returns | 17.39% | 23.18% | 13.97% | 13.54% | 7.23% | 3.00% |
| Target Semi-Deviation | 11.47% | 9.48% | 8.26% | 8.08% | 4.71% | 1.19% |
| Sharpe Ratio | 0.152 | 0.622 | −0.040 | −0.069 | −0.133 | 0.010 |
| Sortino Ratio | 0.231 | 1.521 | −0.068 | −0.116 | −0.203 | 0.026 |
| Does an Asset in Rows [1]–[7] Stochastically Dominate an Asset in Columns [a]–[g]? | Large Stocks [a] | Small Stocks [b] | Long–Term Corporate Bonds [c] | Long–Term Gov’t Bonds [d] | Interm.–Term Gov’t Bonds [e] | Money Market [f] | Stable Value [g] | |
|---|---|---|---|---|---|---|---|---|
| [1] | Large Stocks | N | N | N | N | N | N | |
| [2] | Small Stocks | N | N | N | N | N | N | |
| [3] | Long-Term Corporate Bonds | N | N | 3rd Degree and Higher | N | N | N | |
| [4] | Long-Term Government Bonds | N | N | N | N | N | N | |
| [5] | Intermediate-Term Government Bonds | N | N | N | 2nd Degree and Higher | N | N | |
| [6] | Money Market | N | N | 2nd Degree and Higher | 2nd Degree and Higher | 2nd Degree and Higher | N | |
| [7] | Stable Value | N | N | 2nd Degree and Higher | 2nd Degree and Higher | 2nd Degree and Higher | N | |
| LS | SS | LTCB | LTGB | ITGB | MM | SV | |
|---|---|---|---|---|---|---|---|
| Mean | 2.43% | 3.98% | 1.85% | 1.88% | 1.46% | 1.21% | 1.54% |
| Median | 2.71% | 4.28% | 1.36% | 0.97% | 1.03% | 1.23% | 1.53% |
| Maximum | 22.37% | 44.26% | 23.71% | 23.85% | 16.06% | 3.93% | 2.64% |
| Minimum | −25.74% | −28.47% | −13.73% | −15.02% | −6.86% | −0.05% | 0.44% |
| Std. Dev. | 8.33% | 12.11% | 5.47% | 6.03% | 3.12% | 0.92% | 0.58% |
| Skewness | −0.548 | 0.025 | 0.707 | 0.779 | 1.032 | N/A | N/A |
| Kurtosis | 0.880 | 0.570 | 2.939 | 1.711 | 3.125 | N/A | N/A |
| Jarque–Bera | 14.077 | 2.333 | 75.763 | 38.143 | 99.912 | N/A | N/A |
| Probability | 0.001 | 0.311 | 0.000 | 0.000 | 0.000 | N/A | N/A |
| Asset Class | ||||||||
|---|---|---|---|---|---|---|---|---|
| Expected Return | Standard Deviation | Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Money Market | Stable Value |
| 1.54% | 0.58% | 0.00% | 0.07% | 0.00% | 0.00% | 0.00% | 0.00% | 99.93% |
| 1.66% | 0.81% | 0.00% | 4.63% | 0.00% | 3.13% | 0.00% | 0.00% | 92.23% |
| 1.79% | 1.28% | 0.00% | 9.17% | 0.00% | 6.45% | 0.00% | 0.00% | 84.38% |
| 1.91% | 1.80% | 0.00% | 13.71% | 0.00% | 9.76% | 0.00% | 0.00% | 76.53% |
| 2.03% | 2.34% | 0.00% | 18.25% | 0.00% | 13.07% | 0.00% | 0.00% | 68.68% |
| 2.15% | 2.89% | 0.00% | 22.79% | 0.00% | 16.38% | 0.00% | 0.00% | 60.83% |
| 2.27% | 3.45% | 0.00% | 27.33% | 0.00% | 19.69% | 0.00% | 0.00% | 52.98% |
| 2.39% | 4.01% | 0.00% | 31.86% | 0.00% | 23.00% | 0.00% | 0.00% | 45.13% |
| 2.52% | 4.57% | 0.00% | 36.40% | 0.00% | 26.32% | 0.00% | 0.00% | 37.28% |
| 2.64% | 5.14% | 0.00% | 40.94% | 0.00% | 29.63% | 0.00% | 0.00% | 29.43% |
| 2.76% | 5.70% | 0.00% | 45.48% | 0.00% | 32.94% | 0.00% | 0.00% | 21.58% |
| 2.88% | 6.26% | 0.00% | 50.02% | 0.00% | 36.25% | 0.00% | 0.00% | 13.73% |
| 3.00% | 6.83% | 0.00% | 54.56% | 0.00% | 39.56% | 0.00% | 0.00% | 5.88% |
| 3.12% | 7.39% | 0.00% | 59.41% | 0.00% | 40.59% | 0.00% | 0.00% | 0.00% |
| 3.25% | 7.99% | 0.00% | 65.21% | 0.00% | 34.79% | 0.00% | 0.00% | 0.00% |
| 3.37% | 8.62% | 0.00% | 71.01% | 0.00% | 28.99% | 0.00% | 0.00% | 0.00% |
| 3.49% | 9.28% | 0.00% | 76.81% | 0.00% | 23.19% | 0.00% | 0.00% | 0.00% |
| 3.61% | 9.97% | 0.00% | 82.61% | 0.00% | 17.39% | 0.00% | 0.00% | 0.00% |
| 3.73% | 10.67% | 0.00% | 88.40% | 0.00% | 11.60% | 0.00% | 0.00% | 0.00% |
| 3.85% | 11.38% | 0.00% | 94.20% | 0.00% | 5.80% | 0.00% | 0.00% | 0.00% |
| 3.98% | 12.11% | 0.00% | 100.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Asset Class | |||||||
|---|---|---|---|---|---|---|---|
| Expected Return | Standard Deviation | Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Money Market |
| 1.23% | 0.91% | 1.09% | 0.02% | 1.30% | 0.00% | 0.00% | 97.59% |
| 1.37% | 1.04% | 0.00% | 4.52% | 0.00% | 5.09% | 0.00% | 90.38% |
| 1.51% | 1.38% | 0.00% | 8.43% | 0.00% | 9.42% | 0.00% | 82.15% |
| 1.64% | 1.80% | 0.00% | 12.34% | 0.00% | 13.74% | 0.00% | 73.92% |
| 1.78% | 2.27% | 0.00% | 16.24% | 0.00% | 18.06% | 0.00% | 65.69% |
| 1.92% | 2.76% | 0.00% | 20.19% | 0.00% | 22.43% | 0.00% | 57.38% |
| 2.06% | 3.26% | 0.00% | 24.10% | 0.00% | 26.75% | 0.00% | 49.15% |
| 2.19% | 3.76% | 0.00% | 28.01% | 0.00% | 31.07% | 0.00% | 40.92% |
| 2.33% | 4.27% | 0.00% | 31.92% | 0.00% | 35.40% | 0.00% | 32.69% |
| 2.47% | 4.78% | 0.00% | 35.82% | 0.00% | 39.72% | 0.00% | 24.46% |
| 2.60% | 5.30% | 0.00% | 39.77% | 0.00% | 44.09% | 0.00% | 16.14% |
| 2.74% | 5.82% | 0.00% | 43.68% | 0.00% | 48.41% | 0.00% | 7.91% |
| 2.88% | 6.34% | 0.00% | 47.69% | 0.00% | 52.31% | 0.00% | 0.00% |
| 3.02% | 6.90% | 0.00% | 54.21% | 0.00% | 45.79% | 0.00% | 0.00% |
| 3.15% | 7.53% | 0.00% | 60.73% | 0.00% | 39.27% | 0.00% | 0.00% |
| 3.29% | 8.22% | 0.00% | 67.32% | 0.00% | 32.68% | 0.00% | 0.00% |
| 3.43% | 8.94% | 0.00% | 73.84% | 0.00% | 26.16% | 0.00% | 0.00% |
| 3.56% | 9.70% | 0.00% | 80.37% | 0.00% | 19.63% | 0.00% | 0.00% |
| 3.70% | 10.48% | 0.00% | 86.89% | 0.00% | 13.11% | 0.00% | 0.00% |
| 3.84% | 11.28% | 0.00% | 93.41% | 0.00% | 6.59% | 0.00% | 0.00% |
| 3.98% | 12.11% | 0.00% | 100.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Stable Value | |
|---|---|---|---|---|---|---|
| Mean of Excess Returns | 1.22% | 2.76% | 0.64% | 0.67% | 0.24% | 0.33% |
| STDEV of Excess Returns | 8.39% | 12.16% | 5.48% | 6.01% | 3.01% | 0.57% |
| Target Semi-Deviation | 5.69% | 7.12% | 3.23% | 3.42% | 1.78% | 0.25% |
| Sharpe Ratio | 0.145 | 0.227 | 0.116 | 0.111 | 0.081 | 0.584 |
| Sortino Ratio | 0.213 | 0.388 | 0.197 | 0.195 | 0.137 | 1.320 |
| Large Stocks | Small Stocks | Long-Term Corp. Bonds | Long-Term Gov’t Bonds | Interm.-Term Gov’t Bonds | Stable Value | |
|---|---|---|---|---|---|---|
| Mean of Excess Returns | 5.61% | 11.83% | 2.66% | 2.89% | 1.03% | 1.40% |
| STDEV of Excess Returns | 17.53% | 22.34% | 10.77% | 12.76% | 6.15% | 2.24% |
| Target Semi-Deviation | 10.67% | 10.00% | 5.10% | 6.53% | 3.55% | 1.03% |
| Sharpe Ratio | 0.320 | 0.529 | 0.247 | 0.227 | 0.168 | 0.626 |
| Sortino Ratio | 0.526 | 1.183 | 0.522 | 0.443 | 0.291 | 1.358 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babbel, D.F.; Herce, M.A. Stable Value Funds Performance. Risks 2018, 6, 12. https://doi.org/10.3390/risks6010012
Babbel DF, Herce MA. Stable Value Funds Performance. Risks. 2018; 6(1):12. https://doi.org/10.3390/risks6010012
Chicago/Turabian StyleBabbel, David F., and Miguel A. Herce. 2018. "Stable Value Funds Performance" Risks 6, no. 1: 12. https://doi.org/10.3390/risks6010012
APA StyleBabbel, D. F., & Herce, M. A. (2018). Stable Value Funds Performance. Risks, 6(1), 12. https://doi.org/10.3390/risks6010012





