Implied Distributions from GBPUSD Risk-Reversals and Implication for Brexit Scenarios

Abstract

Much of the debate around a potential British exit (Brexit) from the European Union has centred on the potential macroeconomic impact. In this paper, we instead focus on understanding market expectations for price action around the Brexit referendum date. Extracting implied distributions from the GBPUSD option volatility surface, we originally estimated, based on our visual observation of implied probability densities available up to 13 June 2016, that the market expected that a vote to leave could result in a move in the GBPUSD exchange rate from 1.4390 (spot reference on 10 June 2016) down to a range in 1.10 to 1.30, i.e., a 10–25% decline—very probably with highly volatile price action. To quantify this more objectively, we construct a mixture model corresponding to two scenarios for the GBPUSD exchange rate after the referendum vote, one scenario for “remain” and one for “leave”. Calibrating this model to four months of market data, from 24 February to 22 June 2016, we find that a “leave” vote was associated with a predicted devaluation of the British pound to approximately 1.37 USD per GBP, a 4.5% devaluation, and quite consistent with the observed post-referendum exchange rate move down from 1.4877 to 1.3622. We contrast the behaviour of the GBPUSD option market in the run-up to the Brexit vote with that during the 2014 Scottish Independence referendum, finding the potential impact of Brexit to be considerably higher.

1. Introduction

This work develops and expands upon a predictive analysis that was carried out in early June 2016, in advance of the Brexit referendum of 23 June 2016. In the United Kingdom [UK] general election of 2015, the Conservative Party campaigned on the basis of holding a public referendum on whether the UK should remain a part of the European Union [EU]. The election was held on 7 May 2015 and the Conservative Party was elected into government. Since then, and up to the date of writing this paper1, much attention has been focused on the possible scenarios attached to the “Brexit” question. Much of the analysis has been on potential macroeconomic impact from the UK exiting the EU. For example, HM Treasury (2016) recently published a report which discussed the potential economic impact on the UK of leaving. They suggested that:

“the effect of this profound shock would be to push the UK into recession and lead to a sharp rise in unemployment.”

In contrast to this macroeconomic analysis, this paper discusses market expectations of how assets were expected to trade following Brexit. We focus on extracting expectations for price action following a Brexit vote using the foreign exchange options market. Many market commentators (Worrachate 2016) predicted that in the event of a “leave” vote, that the British pound [GBP] would depreciate—potentially dramatically (a GBP devaluation of 20% was predicted by at least one currency manager in the event of Brexit), although this view was by no means universally held. A recent poll of currency forecasters by Reuters (2016) suggested that GBPUSD would fall 9% in the event of a leave vote, while it would rise 4% in the event of a “remain” vote. We seek to understand whether these analyst forecasts were also reflected in the GBPUSD volatility market.

On 22 February 2016, the UK Prime Minister David Cameron made a speech to the House of Commons, in which a referendum date of 23 June 2016 was set.

The announcement of the timing of the referendum date makes it possible to apply more quantitative methods than economic forecasting to the analysis of how the British pound was expected to perform after the Brexit referendum date, based on information available in the markets beforehand.

While this study refers to a small time window around a particular referendum date, similar methods have been employed by previous analyses in the literature to make inferences of potential or historical moves in FX spot markets based on the information contained within traded volatility markets. Malz (1996) analyses the case of the British pound/Deutsche Mark exchange rate in the context of the European Exchange Rate Mechanism. Hanke et al. (2015); Hertrich and Zimmermann (2017); Hui et al. (2016) and Jermann (2017) consider the case of EURCHF, which had a floor at 1.20 enforced by the Swiss National Bank [SNB] between 6 September 2011 to 15 January 2015. More recently, Clark and Amen (2017) and Dupire (2017) present event studies modelling FX spot moves around Brexit and the 2016 US election result (specifically the Mexican peso), with recent 2017 French elections being examined in Dupire (2017). Similarly to the modelling of the FX event risk around these elections, in Section 8 of this work we consider the case of the Scottish 2014 independence referendum.

These examples show that the methodology presented in this work has a wider applicability beyond the isolated, albeit important, event of Brexit.

2. Options Markets

Options markets are a forward looking measure of the market’s expectation of how tradeable assets perform. It is described in the general case by Breeden and Litzenberger (1978) and, in the context of foreign exchange, by Malz (1997), that a complete knowledge of the prices of traded options at all strikes is sufficient to infer future risk-neutral probability distributions.

While obviously the outcome of the Brexit referendum vote was unknown beforehand, the referendum date was known in advance. When there is an event risk whose timing is known, such as an election or an economic data event, options markets will incorporate that informational content into the price of tradeable assets, as reflected in the expected volatility of that event and, notably, the skew resulting from event risk on that date.

This paper therefore seeks to analyse information available in the short-dated volatility skew in GBPUSD options to assess the market expectation for GBPUSD as we cross over the expiry threshold, corresponding to FX spot on 24 June 2016, when the result was known. We also analyse EURGBP, though the main focus of this paper is GBPUSD.

3. Data

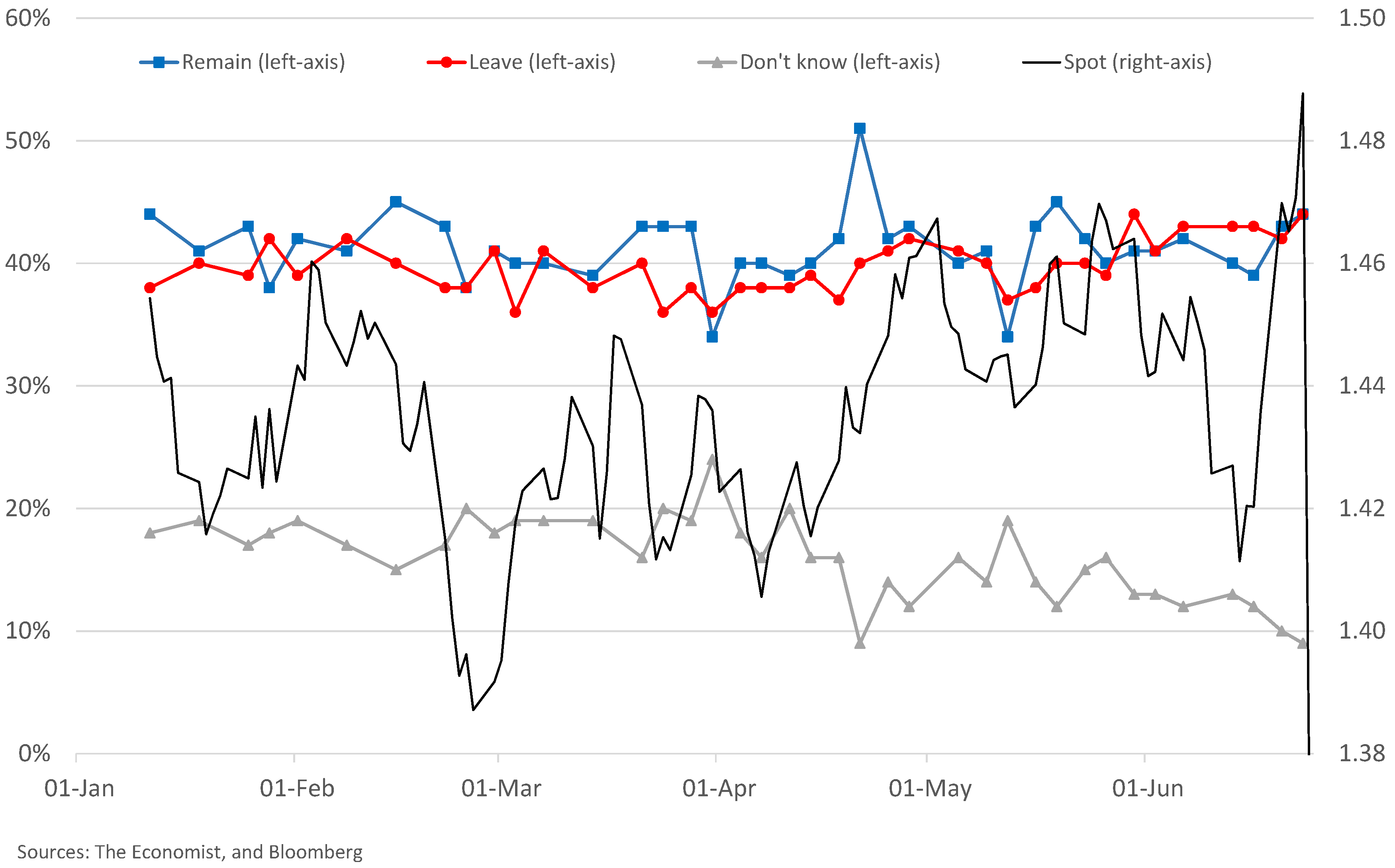
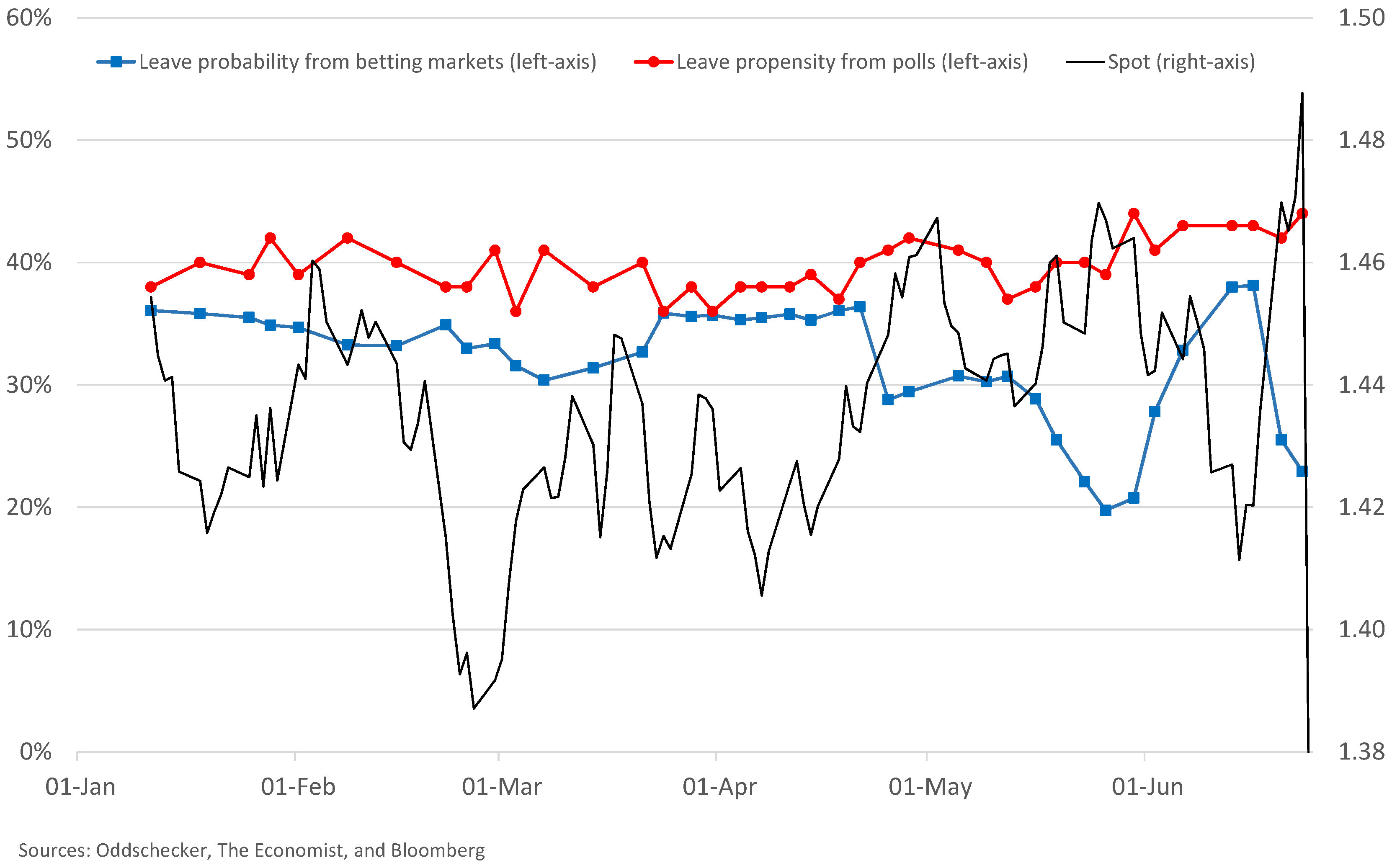
We have obtained historical spot and implied volatility quotes from Bloomberg (www.bloomberg.com), together with poll data from The Economist (www.economist.com). For the poll data, Figure 1 shows how during 2016 the propensity to vote “remain” generally held a very slight lead among respondents over the propensity to vote “leave”; however when the “leave” propensity exceeded “remain” in polls then this was usually followed by a sharp decline in GBPUSD spot. This suggested that a “leave” vote on 23 June 2016 would be significantly negative for GBPUSD.

Figure 2a shows time series for 25-delta and Figure 2b shows 10-delta risk reversals, of various expiries, from 1 May 2015 to 1 June 2016 together with GBPUSD spot. There are several key features to observe. Firstly, we see the risk reversals converging towards zero in late 2015 during the relatively innocuous period up to 5 November 2015, at which date they start to move into increasingly negative territory over a week or two. This period coincides with David Cameron’s Chatham House speech2 of 10 November 2015, in which he outlined four key demands for renegotiation of British membership of the EU, as a prelude to an eventual British referendum on whether to continue as a part of it.

The risk reversals shown in Figure 2 continued to become more negative over the rest of 2015 and into the early part of 2016, up until 20 February 2016, when the Brexit referendum date was announced. At this point, all options with time to expiry in excess of four months were exposed to Brexit risk, and the 6M and 1Y risk reversals moved further away from zero. As seen in Figure 2a, 25-delta risk reversals of 3M tenor and shorter moved in a separate cluster between −0.5 and −1.5 until 23 March 2016, when the 3M 25-delta risk reversal had, at that point, 23 June 2016 as its expiry date, and therefore experienced a large negative spike as the Brexit uncertainty became reflected in the market quote. Similarly, the 2M 25-delta risk reversal moved dramatically between 25 and 26 April 2016, and the 1M 25-delta risk reversal moved from −1.3 to −5.4 from 25 May to 26 May 2016. However, that was just the start of very rapid moves in the volatility skew, as the 1M 25-delta risk reversal continued to move lower, from −5.4 on 26 May to −7.9 on 10 June 2016—a quite extreme risk reversal by any measure. Similar behaviour was mirrored in the 10-delta risk reversals, as seen in Figure 2b, indicating a very high degree of skew.

The risk reversals in Figure 2 embed extensive market specific information about the potential asset price distribution of the GBPUSD exchange rate after the Brexit referendum date. Note that we use the market data as is, rather than engaging in any data cleansing, as these data correspond to actual tradeable quantities as marked by Bloomberg.

Our objective in this paper is to extract quantitative insight into the potential effect upon FX spot rates of a “leave” vote, from these data.

4. Method

Following standard practice (Clark 2011; Malz 2014), we build volatility smiles ${\sigma }_{\mathrm{imp}}\left(K\right)$ for the option expiry tenors $T_j$ in the analysis period, in order to be able to construct implied probability distributions. FX volatility smiles are given by delta and tenor, as described in Malz (1997) and Jermann (2017). We have market data from Bloomberg corresponding to at-the-money straddles and 25-delta and 10-delta strangles and risk reversals with expiries corresponding to the overnight maturity, at 1, 2 and 3 weeks, and at 1, 2, 3, 6 and 12 months, these being the principal tenors. For each expiry $T_j$, let us denote the five market quotes from the volatility surface by ${\sigma }_{ATM}$, ${\sigma }_{25-d-SS}$, ${\sigma }_{10-d-SS}$, ${\sigma }_{25-d-RR}$ and ${\sigma }_{10-d-RR}$. This means we have five implied volatilities ${\sigma }_{10-d-P}$, ${\sigma }_{25-d-P}$, ${\sigma }_{ATM}$, ${\sigma }_{25-d-C}$ and ${\sigma }_{10-d-C}$ which satisfy

$$\begin{array}{cc}\hfill {\sigma }_{x-d-SS}& =\frac{1}{2}[{\sigma }_{x-d-C}+{\sigma }_{x-d-P}]-{\sigma }_{ATM},\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill {\sigma }_{x-d-RR}& ={\sigma }_{x-d-C}-{\sigma }_{x-d-P},\hfill \end{array}$$

(1b)

with $x\in \{25,10\}$ and where the strikes $K_{10-d-P}$, $K_{25-d-P}$, $K_{ATM}$, $K_{25-d-C}$ and $K_{10-d-C}$ are chosen so that

$$\begin{array}{cc}\hfill {\sigma }_{\mathrm{imp}}\left(K_i\right)& ={\sigma }_i,\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill \Delta (-1,K_{x-d-P},T,{\sigma }_{x-d-P})& =-x/100,\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill \Delta (+1,K_{x-d-C},T,{\sigma }_{x-d-C})& =x/100,\hfill \end{array}$$

(2c)

$$\begin{array}{cc}\hfill \Delta (+1,K_{ATM},T,{\sigma }_{ATM})+\Delta (-1,K_{ATM},T,{\sigma }_{ATM})& =0,\hfill \end{array}$$

(2d)

with $\omega =-1$ for a put and $\omega =+1$ for a call in

$$\Delta (\omega ,K,T,\sigma )=\left\{\begin{array}{cc}\omega N\left(\omega d_1\right),\hfill & \mathrm{for}\mathrm{GBPUSD},\hfill \\ \omega \frac{K}{F_{0,T}}N\left(\omega d_2\right),\hfill & \mathrm{for}\mathrm{EURGBP}.\hfill \end{array}\right.$$

(3)

For example, a 25-delta call has a strike ${\sigma }_{25-d-C}$ chosen (relative to today’s spot rate $S_0$) so that it has a delta of 0.25, and a 10-delta put has a delta of −0.10. We use premium adjusted deltas for EURGBP but not for GBPUSD in (3), in line with market conventions, and solve numerically for $K_i$ using Brent’s method.

Once converted into a strike based representation we can now extend3 the set of volatility smiles ${\sigma }_{\mathrm{imp}}\left(K\right)$ over tenors $T_j$ to an entire volatility surface ${\sigma }_{\mathrm{imp}}(K,T)$ by using flat forward volatility interpolation in time for ${\sigma }_{10-d-P}$, ${\sigma }_{25-d-P}$, ${\sigma }_{ATM}$, ${\sigma }_{25-d-C}$ and ${\sigma }_{10-d-C}$ and polynomial in delta smile interpolation, as described in Clark (2011).

Having an entire volatility surface, we can price call and put options of any strike K and maturity T by using $\sigma ={\sigma }_{\mathrm{imp}}(K,T)$ in the Black-Scholes equation. As the price $C(K,T)$ of call options are known, we can follow the standard Breeden-Litzenberger analysis (Breeden and Litzenberger 1978), using (4) to back out the implied asset distribution $f_{S_T}^d\left(K\right)$ in the domestic risk-neutral measure:

$$f_{S_T}^d\left(K\right)=e^{r^{d}T}\frac{{\partial }^{2}C(K,T)}{\partial K^2}.$$

(4)

5. Mixture Model Approach

In order to address the deficiencies of the Breeden-Litzenberger approach, namely, the noisiness of the interpolation introduced by taking the numerical second derivative, we construct a mixture model, following the approaches of Hanke et al. (2015), Brigo and Mercurio (2000; 2002), Brigo et al. (2003), Brigo et al. (2004) and Jermann (2017). Unlike Brigo et al. (2004) and Jermann (2017), who model the possibility of a regime switch potentially occurring at any time, we construct a model with a specific probability $P_L$ of a Brexit “leave” event at the referendum date, where $T^{*}$ denotes the time to the referendum date.

In the event of a vote for Brexit, i.e a “leave” vote, we model this outcome with a post-referendum exchange rate $S_{T^{*}}$ obtained by integrating the stochastic process $d{S}_t={\mu }_L{S}_{t}dt+{\sigma }_L{S}_{t}d{W}_t$ from 0 to $T^{*}$, subject to “leave” drift and volatility terms ${\mu }_L$ and ${\sigma }_L$. If, however, the “remain” vote is successful, we model the post-referendum distribution for $S_{T^{*}}$ using the standard Black-Scholes model $d{S}_t={\mu }_R{S}_{t}dt+{\sigma }_R{S}_{t}d{W}_t$ with a compensated drift ${\mu }_R$ and a “remain” volatility ${\sigma }_R$. Note that both ${\sigma }_L$ and ${\sigma }_R$ are expressed as annualised volatilities.

Risk-neutrality requires that

$$F_{0,T^{*}}={\mathbb{E}}^d\left[S_{T^{*}}\right]=(1-P_L)S_{0}exp\left({\mu }_R{T}^{*}\right)+P_L{S}_{0}exp({\mu }_L{T}^{*}),$$

(5)

so the “remain” scenario has a terminal distribution for $S_{T^{*}}$ consistent with that of a Black-Scholes model with a compensated risk-neutral drift term

$${\mu }_R=\frac{1}{T^{*}}ln\left(\frac{F_{0,T^{*}}-P_L{S}_{0}exp\left({\mu }_L{T}^{*}\right)}{S_0(1-P_L)}\right).$$

(6)

The terminal distribution of FX rates under our mixture model can be written as

$$S_{T^{*}}=\left\{\begin{array}{cc}{S}_{0}exp\left(({\mu }_R-\frac{1}{2}{\sigma }_R^2)T^{*}+{\sigma }_R{W}_{T^{*}}\right),\hfill & \mathrm{with}\mathrm{probability}1-P_L,\hfill \\ S_{0}exp\left(({\mu }_L-\frac{1}{2}{\sigma }_L^2)T^{*}+{\sigma }_L{W}_{T^{*}}\right),\hfill & \mathrm{with}\mathrm{probability}{P}_L.\hfill \end{array}\right.$$

(7)

Valuation of any European option with strike K is simply obtained by taking a weighted sum of the two Black-Scholes prices corresponding to integration of the payout function over the two density kernels.

We integrate the equation in the second case of (7), thereby obtaining the random variable

$$S_{T^{*},L}=S_{L}exp\left(\left({\sigma }_L\xi \sqrt{T^{*}}-\frac{1}{2}{\sigma }_L^2{T}^{*}\right)\right),$$

(8)

where $S_L=S_{0}exp\left({\mu }_L{T}^{*}\right)$ denotes the point estimate for the FX rate under the “leave” scenario and $\xi \sim N(0,1)$, as in Section 2.4 of Clark (2011). Our objective is to use the information embedded in market volatility surfaces to estimate “leave” probabilities $P_L$ and 95% confidence intervals (using the quantile function of $\xi$) for the random variable $S_{T^{*},L}$ which we use to model the GBPUSD FX spot distribution immediately after the event of a “leave” vote.

The standard Black-Scholes model has two terms $\mu$ and $\sigma$. The first term can be obtained by risk-neutrality and the second term can be obtained from a single implied volatility observable in the market (which we denote as ${\sigma }_R$ in the above). In contrast, our mixture model has three extra unknown terms $\{S_L,{\sigma }_L,P_L\}$, and since we have not one but five implied volatilities, we are able to conduct a least-squares calibration using a Levenberg-Marquardt optimisation. We impose the constraints that $0\le P_L\le 1$ as $P_L$ is a probability, that ${\sigma }_L>{\sigma }_R$ (making the not unreasonable model assumption that dispersion would increase after a “leave” vote), and that $S_L<S_0$ – i.e., that a “leave” vote would be associated with a devaluation of the British pound (see Section 7 for justification).

We have calibrated the mixture model to four months of FX market data, from 24 February to 22 June 2016, in order to obtain a sufficiently long time window for the analysis. This also allows us to perform some robustness checks on the parameter stability over this period of analysis, though it should be noted that the period of time just before the Brexit referendum was characterised by particularly volatile price action in the financial markets, and one would not realistically expect a great degree of parameter smoothness given the high degree of uncertainty and potential market disruption around the Brexit referendum date.

6. Results

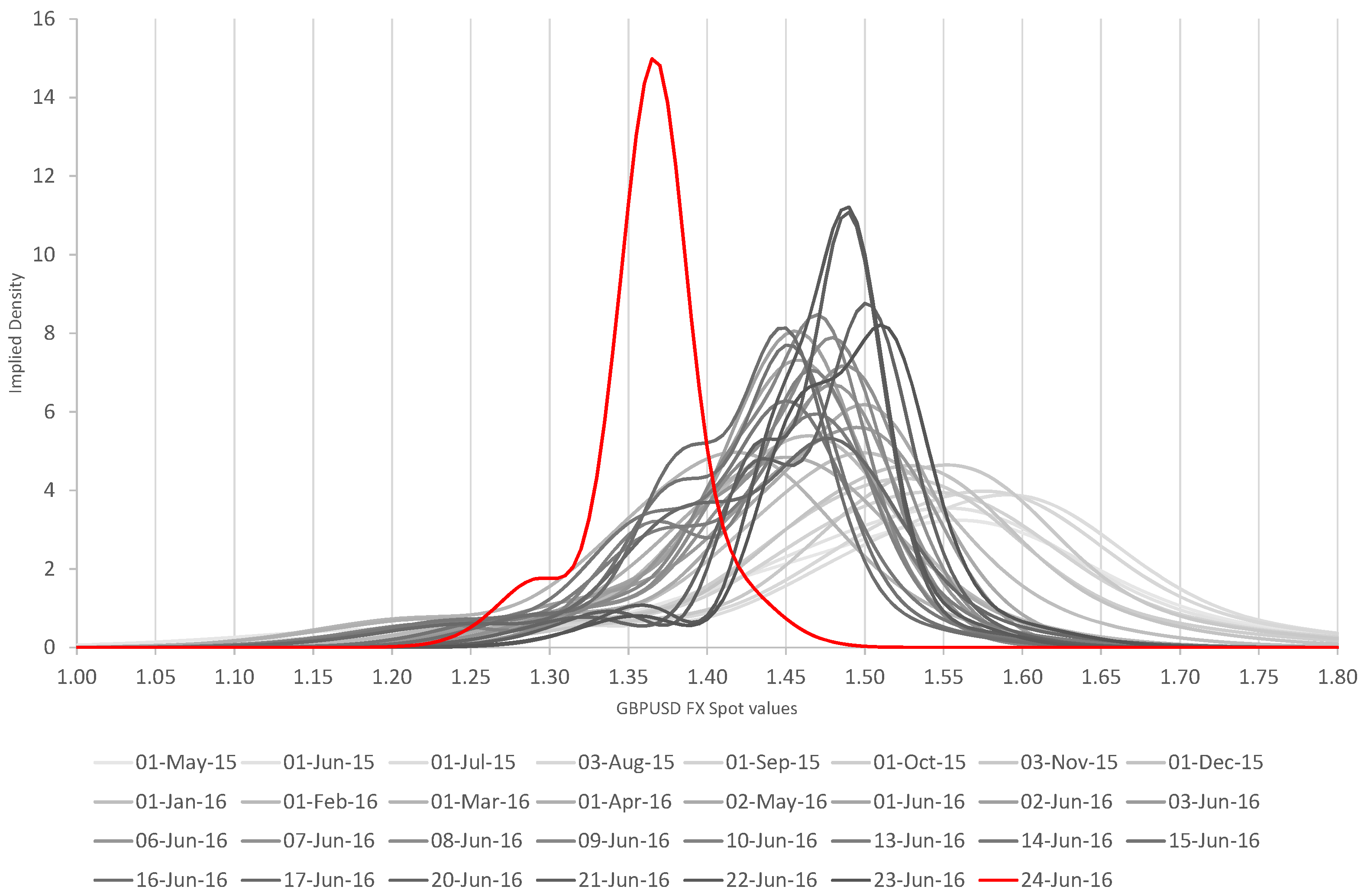
In Figure 3, we tabulate the implied densities for GBPUSD from 1 May 2015 through to 23 June 2016 for options expiring at the very beginning of the day after the referendum date (when the announcement is expected), together with the implied density as seen on Friday 24 June 2016 for the GBPUSD spot distribution early on the morning of Monday 27 June 2016.

In early June 2016 we have relatively moderate levels for the risk reversals, as shown in Figure 2. The probability density function on 1 June 2016 (relative to $S_0=1.4416$) has some downside risk, but is quite sharply peaked around 1.45 due to 1M implied volatilities of 21.1% and 1M 10-delta risk reversals of −10.54. During the first eight trading days of June 2016, the 1M 10-delta risk reversals moved even lower, from −10.54 down to −13.9 on 10 June 2016. This indicates a very high degree of skewness. While the implied distributions are only fitted to volatilities at the benchmark strikes, we can still see evidence of probability mass between 1.10 and 1.35, and certainly below the 10-delta put strike of 1.2960 computed on 10 June 2016. Note that in the absence of any volatility benchmark strikes below the 10-delta put, all we can say is that there is some implied probability mass below that strike, but with limited opportunity to infer directly where the distribution is clustered.

At the date of writing this article4, therefore, we estimated post-referendum levels of [1.10, 1.30] in the event of a “leave” vote, and [1.46, 1.48] in the case of a “remain” vote. In the event of a “leave” vote, we expected a very high degree of volatility as GBPUSD moves well below 1.30, much as happened in January 2015 after the EURCHF defence level of 1.20 was breached (Hanke et al. 2015; Jermann 2017).

Densities shown in Figure 3 are with respect to a post-Brexit GBPUSD spot reference of $S_0=1.3622$ on Friday 24 June 2016, $S_0=1.4877$ on Thursday 23 June 2016 (and the prevailing spot rates on the previous dates).

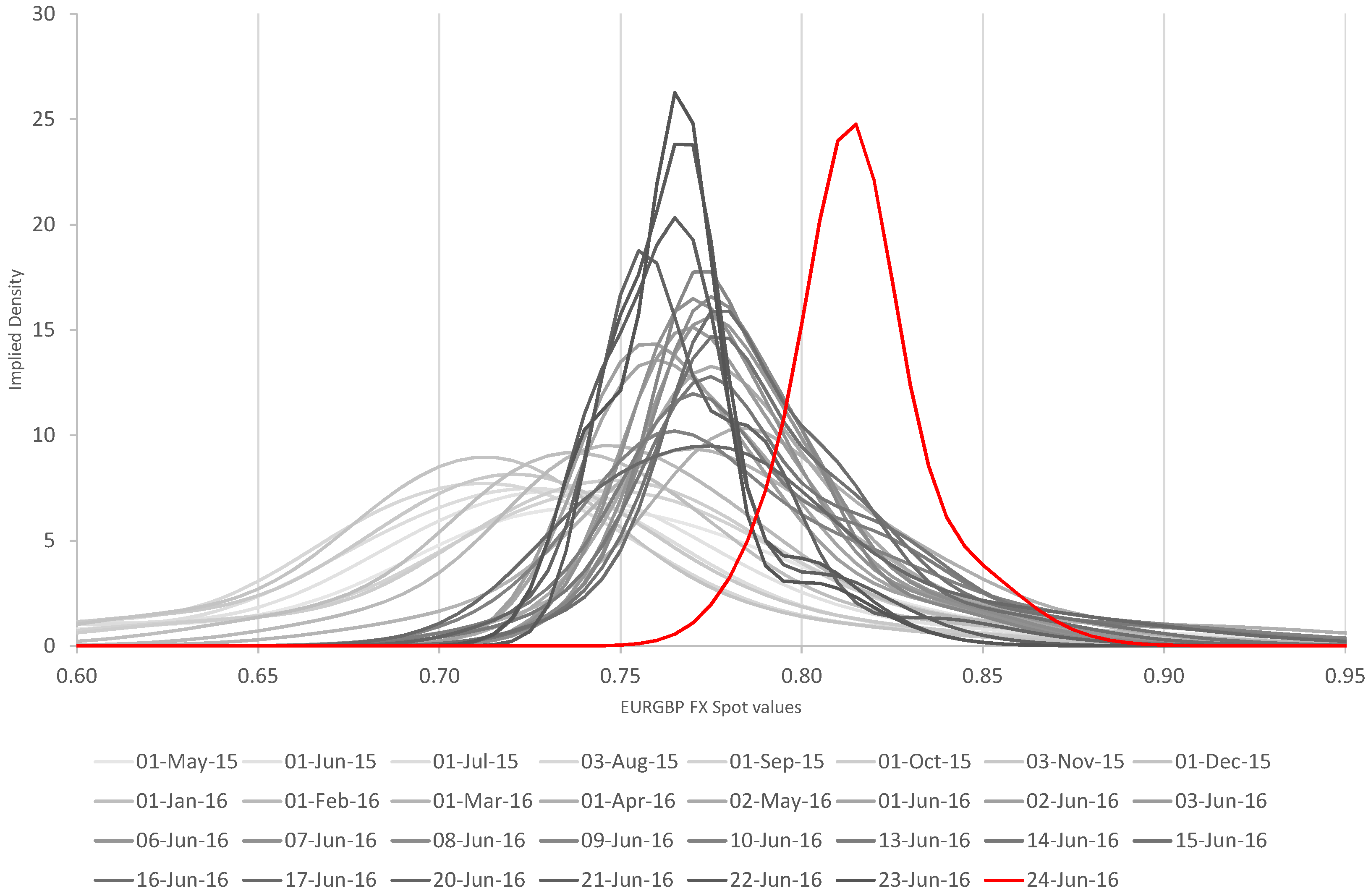
We also apply the same analysis for EURGBP, finding significant probability mass between 0.825 and 0.95 at the referendum date (relative to EURGBP spot reference of $S_0=0.7885$ on 17 June 2016 and, as before, prevailing spot rates on previous dates). Results are shown in Figure 4.

In an attempt to quantify the “leave” scenario and its implications for GBPUSD, we have calibrated the mixture model of Section 5 to the GBPUSD volatility surface on all trading days from 24 February to 22 June 2016. We tabulate the results in

Table 1. Calibrated mixture model parameters from 24 February to 22 April 2016.

Date	${\mathit{S}}_0$	${\mathit{P}}_{\mathit{L}}$	${\mathit{S}}_{\mathit{L}}$	${\mathit{S}}_{\mathit{L}}/{\mathit{S}}_0-1$	95% CI for ${\mathit{S}}_{{\mathit{T}}^{*},\mathit{L}}$		${\mathbf{\sigma }}_{\mathit{R}}$	${\mathbf{\sigma }}_{\mathit{L}}$
24 February 2016	1.3927	30.8%	1.3250	−4.9%	1.0316	1.6184	8.8%	18.6%
25 February 2016	1.3962	31.5%	1.3319	−4.6%	1.0390	1.6247	8.4%	18.6%
26 February 2016	1.3871	32.0%	1.3252	−4.5%	1.0383	1.6120	8.3%	18.4%
29 February 2016	1.3917	32.6%	1.3340	−4.1%	1.0553	1.6128	8.2%	18.1%
01 March 2016	1.3952	32.5%	1.3378	−4.1%	1.0656	1.6100	8.1%	17.7%
02 March 2016	1.4078	32.4%	1.3541	−3.8%	1.0824	1.6258	7.9%	17.6%
03 March 2016	1.4178	33.4%	1.3666	−3.6%	1.0982	1.6349	7.9%	17.3%
04 March 2016	1.4229	33.0%	1.3711	−3.6%	1.1072	1.6351	7.7%	17.0%
07 March 2016	1.4265	33.5%	1.3773	−3.4%	1.1209	1.6337	7.7%	16.7%
08 March 2016	1.4215	33.3%	1.3737	−3.4%	1.1211	1.6262	7.6%	16.6%
09 March 2016	1.4217	33.5%	1.3753	−3.3%	1.1255	1.6252	7.5%	16.5%
10 March 2016	1.4281	33.7%	1.3830	−3.2%	1.1322	1.6339	7.6%	16.6%
11 March 2016	1.4382	32.7%	1.3936	−3.1%	1.1534	1.6337	7.1%	15.8%
14 March 2016	1.4302	33.5%	1.3885	−2.9%	1.1602	1.6167	7.0%	15.4%
15 March 2016	1.4151	33.5%	1.3701	−3.2%	1.1405	1.5998	7.3%	15.7%
16 March 2016	1.4259	34.1%	1.3800	−3.2%	1.1483	1.6117	7.4%	15.8%
17 March 2016	1.4482	33.9%	1.4011	−3.3%	1.1691	1.6331	7.5%	15.7%
18 March 2016	1.4476	34.5%	1.4015	−3.2%	1.1702	1.6328	7.6%	15.7%
21 March 2016	1.4369	34.7%	1.3902	−3.3%	1.1690	1.6113	7.7%	15.4%
22 March 2016	1.4208	35.6%	1.3751	−3.2%	1.1413	1.6089	8.2%	16.5%
23 March 2016	1.4117	27.9%	1.3189	−6.6%	1.0065	1.6314	9.5%	22.3%
24 March 2016	1.4153	27.4%	1.3159	−7.0%	1.0107	1.6210	9.5%	21.9%
25 March 2016	1.4132	27.7%	1.3156	−6.9%	1.0099	1.6212	9.6%	22.0%
28 March 2016	1.4254	30.6%	1.3471	−5.5%	1.0402	1.6540	9.6%	22.3%
29 March 2016	1.4384	27.2%	1.3403	−6.8%	1.0542	1.6264	9.4%	20.7%
30 March 2016	1.4378	26.6%	1.3394	−6.8%	1.0519	1.6269	9.4%	21.0%
31 March 2016	1.4360	27.9%	1.3453	−6.3%	1.0555	1.6350	9.5%	21.3%
01 April 2016	1.4227	27.8%	1.3326	−6.3%	1.0490	1.6161	9.5%	21.1%
04 April 2016	1.4264	27.6%	1.3383	−6.2%	1.0718	1.6048	9.2%	20.2%
05 April 2016	1.4161	28.5%	1.3349	−5.7%	1.0632	1.6067	9.5%	20.8%
06 April 2016	1.4123	27.8%	1.3246	−6.2%	1.0629	1.5864	9.8%	20.3%
07 April 2016	1.4056	28.8%	1.3222	−5.9%	1.0596	1.5849	9.9%	20.6%
08 April 2016	1.4128	30.4%	1.3377	−5.3%	1.0779	1.5975	9.6%	20.4%
11 April 2016	1.4239	30.2%	1.3520	−5.1%	1.1070	1.5970	9.4%	19.4%
12 April 2016	1.4275	31.3%	1.3611	−4.7%	1.1158	1.6064	9.4%	19.5%
13 April 2016	1.4204	31.1%	1.3552	−4.6%	1.1200	1.5904	9.4%	19.0%
14 April 2016	1.4155	32.4%	1.3566	−4.2%	1.1203	1.5929	9.5%	19.2%
15 April 2016	1.4202	30.6%	1.3590	−4.3%	1.1322	1.5858	9.4%	18.5%
18 April 2016	1.4278	33.0%	1.3801	−3.3%	1.1684	1.5918	9.0%	17.6%
19 April 2016	1.4398	37.5%	1.4026	−2.6%	1.2009	1.6043	8.4%	16.7%
20 April 2016	1.4332	37.7%	1.3991	−2.4%	1.2071	1.5911	8.1%	16.1%
21 April 2016	1.4323	37.8%	1.3993	−2.3%	1.2120	1.5866	8.1%	15.9%
22 April 2016	1.4403	39.5%	1.4118	−2.0%	1.2282	1.5955	7.9%	15.6%

and

Table 2. Calibrated mixture model parameters from 25 April to 22 June 2016.

Date	${\mathit{S}}_0$	${\mathit{P}}_{\mathit{L}}$	${\mathit{S}}_{\mathit{L}}$	${\mathit{S}}_{\mathit{L}}/{\mathit{S}}_0-1$	95% CI for ${\mathit{S}}_{{\mathit{T}}^{*},\mathit{L}}$		${\mathbf{\sigma }}_{\mathit{R}}$	${\mathbf{\sigma }}_{\mathit{L}}$
25 April 2016	1.4482	42.8%	1.4305	−1.2%	1.2643	1.5968	7.6%	14.4%
26 April 2016	1.4582	22.6%	1.3546	−7.1%	1.1698	1.5394	9.3%	16.0%
27 April 2016	1.4543	23.2%	1.3549	−6.8%	1.1727	1.5371	9.2%	16.0%
28 April 2016	1.4609	23.3%	1.3620	−6.8%	1.1818	1.5423	9.2%	15.9%
29 April 2016	1.4612	23.7%	1.3684	−6.3%	1.1856	1.5512	9.2%	16.2%
02 May 2016	1.4673	23.2%	1.3737	−6.4%	1.2001	1.5472	9.4%	15.8%
03 May 2016	1.4535	23.7%	1.3639	−6.2%	1.1845	1.5432	9.6%	16.6%
04 May 2016	1.4496	25.0%	1.3650	−5.8%	1.1768	1.5533	9.8%	17.6%
05 May 2016	1.4485	26.9%	1.3732	−5.2%	1.1839	1.5625	9.5%	17.9%
06 May 2016	1.4427	23.1%	1.3495	−6.5%	1.1766	1.5223	9.5%	16.6%
09 May 2016	1.4407	25.0%	1.3604	−5.6%	1.1875	1.5332	9.5%	17.2%
10 May 2016	1.4442	23.7%	1.3580	−6.0%	1.1915	1.5245	9.7%	16.7%
11 May 2016	1.4448	26.0%	1.3682	−5.3%	1.2027	1.5337	9.4%	16.7%
12 May 2016	1.4451	25.0%	1.3677	−5.4%	1.2038	1.5316	9.5%	16.8%
13 May 2016	1.4365	22.8%	1.3439	−6.4%	1.1860	1.5018	10.0%	16.4%
16 May 2016	1.4402	24.9%	1.3649	−5.2%	1.2061	1.5236	9.8%	17.1%
17 May 2016	1.4463	24.7%	1.3737	−5.0%	1.2286	1.5188	9.2%	15.8%
18 May 2016	1.4599	31.8%	1.4141	−3.1%	1.2637	1.5645	8.3%	16.4%
19 May 2016	1.4611	33.2%	1.4203	−2.8%	1.2744	1.5662	8.3%	16.1%
20 May 2016	1.4502	32.0%	1.4089	−2.8%	1.2700	1.5479	8.3%	15.7%
23 May 2016	1.4484	41.5%	1.4266	−1.5%	1.2974	1.5557	8.3%	15.2%
24 May 2016	1.4636	42.7%	1.4464	−1.2%	1.3241	1.5686	8.2%	14.5%
25 May 2016	1.4697	43.0%	1.4536	−1.1%	1.3325	1.5747	8.2%	14.5%
26 May 2016	1.4670	26.2%	1.3841	−5.6%	1.2358	1.5324	9.2%	18.1%
27 May 2016	1.4623	22.6%	1.3784	−5.7%	1.2207	1.5362	10.0%	19.7%
30 May 2016	1.4640	26.7%	1.4060	−4.0%	1.2592	1.5528	9.8%	19.4%
31 May 2016	1.4483	32.3%	1.4006	−3.3%	1.2511	1.5500	10.8%	20.3%
01 June 2016	1.4416	39.2%	1.4067	−2.4%	1.2538	1.5596	11.3%	21.3%
02 June 2016	1.4423	39.7%	1.4130	−2.0%	1.2740	1.5520	10.6%	19.8%
03 June 2016	1.4518	31.9%	1.3676	−5.8%	1.2025	1.5328	13.4%	23.9%
06 June 2016	1.4442	25.8%	1.3600	−5.8%	1.2081	1.5118	14.4%	23.8%
07 June 2016	1.4545	28.1%	1.3825	−4.9%	1.2359	1.5292	13.3%	23.5%
08 June 2016	1.4504	27.5%	1.3865	−4.4%	1.2511	1.5218	13.2%	22.4%
09 June 2016	1.4458	32.1%	1.4002	−3.2%	1.2742	1.5263	12.7%	21.6%
10 June 2016	1.4257	29.2%	1.3461	−5.6%	1.1033	1.5889	18.8%	43.6%
13 June 2016	1.4270	31.2%	1.3497	−5.4%	1.1287	1.5708	22.4%	44.5%
14 June 2016	1.4114	29.9%	1.3369	−5.3%	1.1417	1.5321	22.4%	41.6%
15 June 2016	1.4204	35.7%	1.3769	−3.1%	1.2023	1.5515	18.8%	38.9%
16 June 2016	1.4203	39.1%	1.3914	−2.0%	1.2319	1.5510	18.3%	37.5%
17 June 2016	1.4358	15.3%	1.2900	−10.2%	1.0893	1.4906	35.3%	49.7%
20 June 2016	1.4698	18.0%	1.3779	−6.3%	1.2308	1.5249	26.1%	46.0%
21 June 2016	1.4652	26.1%	1.4198	−3.1%	1.2588	1.5809	22.9%	57.3%
22 June 2016	1.4707	45.3%	1.4378	−2.2%	1.3323	1.5434	26.7%	44.2%

and illustrate in Figure 5. Relative to each analysis date and the FX spot prevailing on that date, we show the implied probability of a “leave” vote and the midpoint $S_L$ of the spot price distribution in the event of a Brexit “leave” vote, together with the expected GBP percentage appreciation $S_L/S_0-1$ (negative numbers, which are ubiquitous for this model since $S_L<S_0$, indicate devaluation). Finally we show a 95% confidence interval for the realised post-referendum FX spot rate for GBPUSD in the event of a “leave vote”, together with “remain” and “leave” volatilities ${\sigma }_R$ and ${\sigma }_L$ respectively.

We see a high degree of parameter stability attached to the expected GBP devaluation in the event of a “leave” vote, which is in a range between 1.1% and 10.2% throughout the period of analysis, with a mean expected devaluation of 4.5%, which is less of an extreme market move than we would have expected by visual observation of the probability distributions. The probabilities of a “leave” vote are less robust, but still relatively stable, within the range 15.3% to 45.3%, with a mean value of 30.6%. It is interesting that even at the beginning of our analysis, back in late February 2016, the mixture model was estimating “leave” probabilities slightly above 30%, which is very close to the mean value over the entire analysis period. The time series for $P_L$ is relatively stationary, and in fact most of the uncertainty in $P_L$ occurs in the final few days before the referendum, which very likely mirrors the real-world uncertainty that was prevailing both in the news and in the markets.

A single point estimate $S_L$ for $S_{T^{*},L}$ is reported in Table 1 and Table 2, which has a mean value of 1.3705 (with a minimum of 1.2900 and a maximum of 1.4536). This is remarkably close to the actual value for GBPUSD after the referendum, as we have $S_0=1.3622$ on Friday 24 June 2016, which suggests that the estimation technique correctly maps distributions to referendum scenarios. However, we also report 95% confidence intervals for the post-referendum FX spot rate $S_{T^{*},L}$ in the event of a“leave” vote, and see a considerable amount of dispersion in this quantity, which is to be expected given the magnitude of ${\sigma }_R$. In all cases, though, the 95% confidence interval contains the observed spot fixing of 1.3622 after the referendum date.

7. Betting Markets and Attribution of Modes

Following the original preprint publication, we were asked—what evidence do you have that the lower mode of the GBPUSD distribution is associated with a “leave” vote, and that the higher mode corresponds to a “remain” vote? In order to answer this, we show in Figure 6 not one but two sets of tabulated quantities pertaining to the final vote being for the UK to leave the EU, using both polls of polls data as detailed in Section 3 above (an average individual propensity to vote for “leave” based on small samples) as well as betting market odds (an implied probability of “leave” across the aggregate population) obtained from bookmaker quotes from the Oddschecker web site (www.oddschecker.com). The use of betting market odds in conjunction with options volatility data is also employed in Hanke et al. (forthcoming).

Note that the “leave” propensity in polls does not directly relate to the probability of “leave” for two reasons: firstly in the limiting case of a poll sampling the entire population, the polls will still be split following reported voting intentions (assuming honesty) but the referendum decision will be known with complete certainty, and secondly most polls have a “don’t know” response option.

Visually, in Figure 6, we see that the decreasing probability across late April 2016 of a “leave” result implied from betting markets is correlated with a strengthening of GBPUSD over the same period, and the increasing probability observed over late May and early June 2016 of the same “leave” result correlates to a weakening of GBPUSD over that period. While neither the probability for “leave” from betting markets nor the propensity for “leave” from polls was an especially good predictor of the final vote for the UK’s independence from the EU, we can see correlation between a “leave” event and GBPUSD weakness. We believe this observation substantiates our attribution that the probability tail for GBPUSD below 1.30 would be associated with a vote for “leave”. 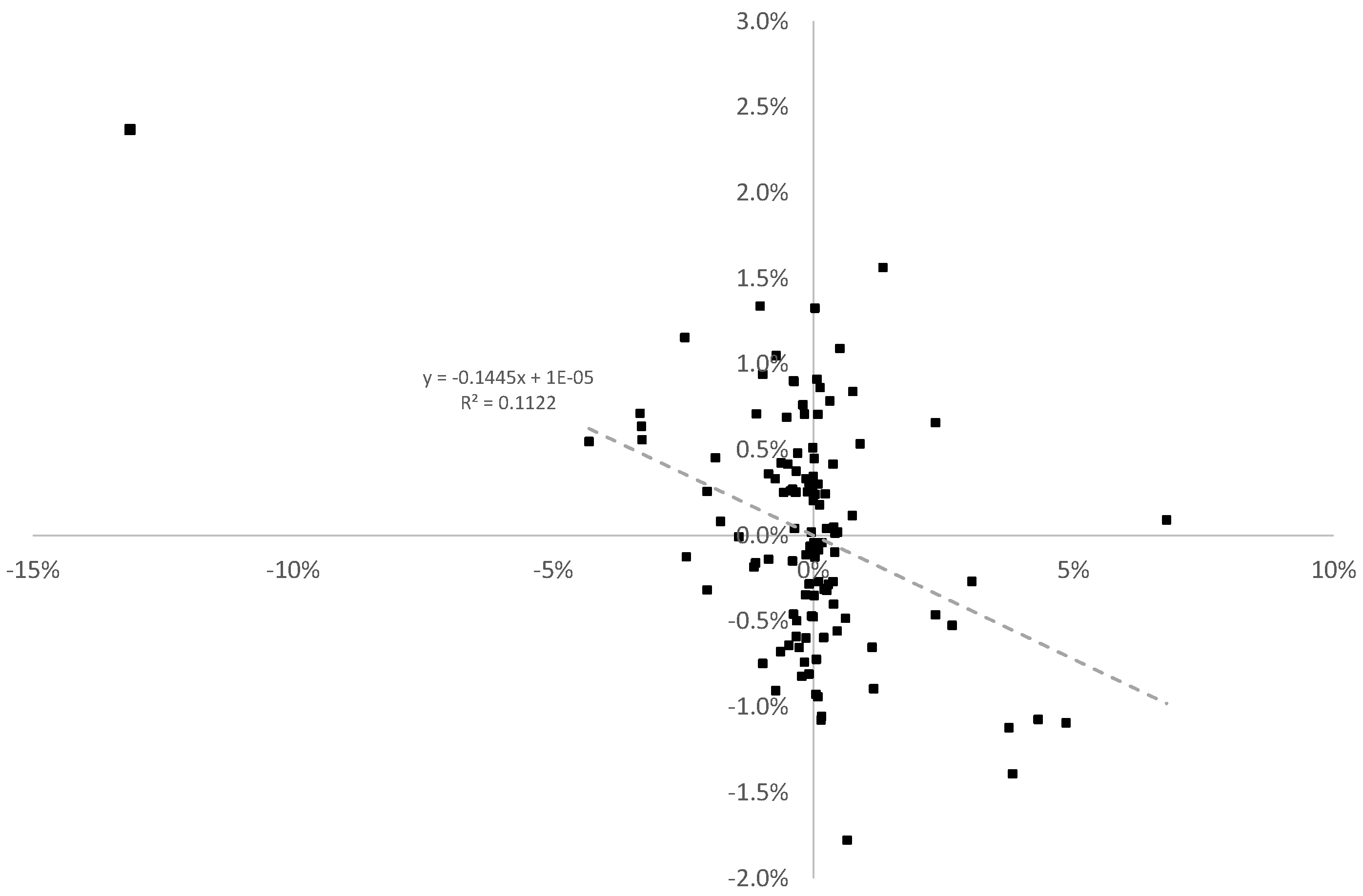In Figure 7, we graph the percentage change in GBPUSD against the absolute change in the betting market implied probability of a “leave” vote, using the same time stencil as the “poll of polls” sampling data. A simple linear regression indicates that a 1% increase in the probability of a “leave” vote is correlated with a 0.16% decrease in GBPUSD (albeit with an $R^2$ coefficient of determination of only 0.205), nevertheless yielding the directionality we argue for. For completeness, we show in Figure 7 the linear regression with the data point on 20 June 2016 excluded, as this corresponds to rebased betting odds at the beginning of the final week, where we see a 0.1445% decrease in GBPUSD for a 1% increase in the probability of a “leave” vote, with a $R^2$ coefficient of determination of 0.1122.

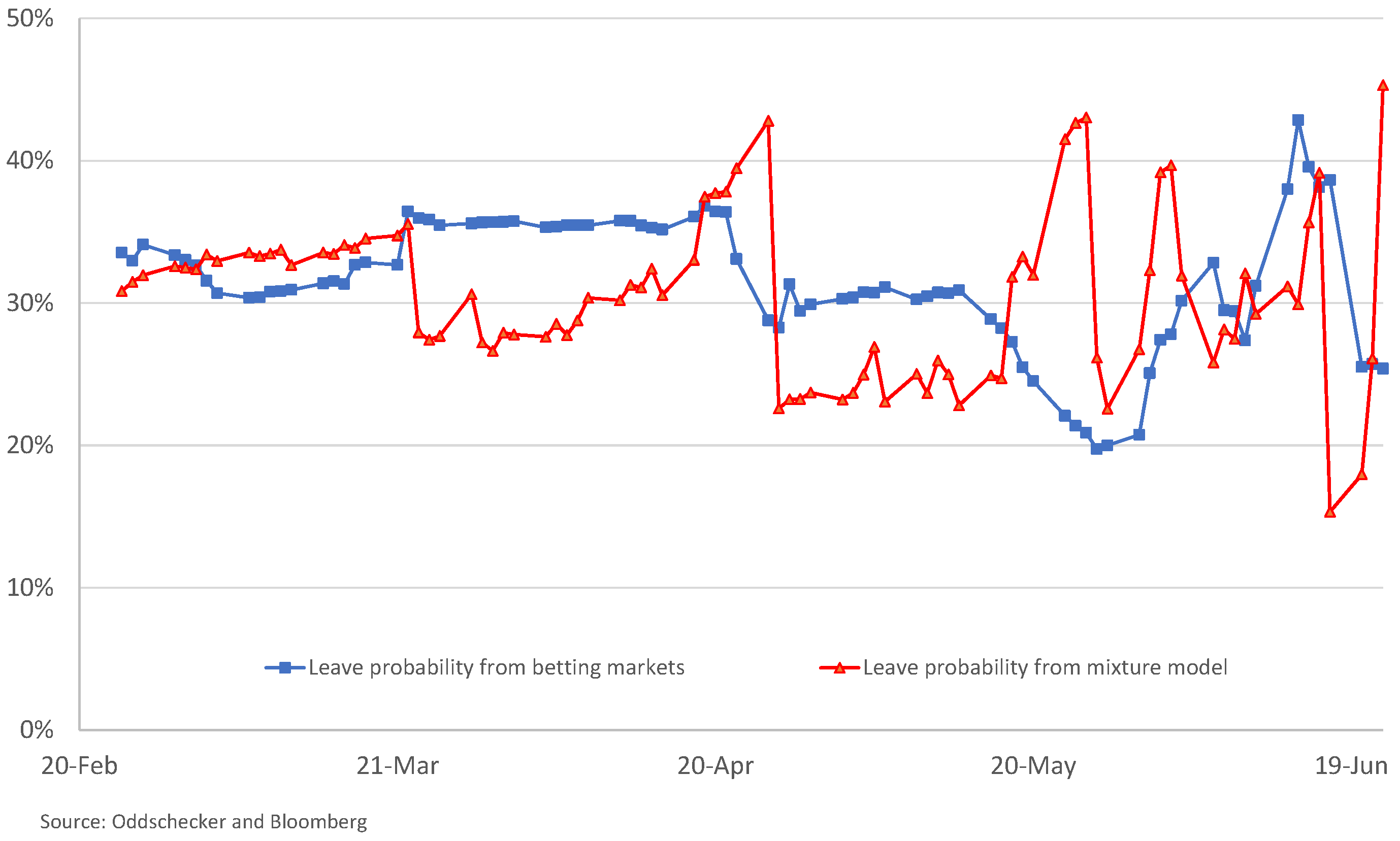
Finally, we show in Figure 8 how the implied “leave” probabilities from our mixture model relate to those from betting markets. We find they are in very good agreement, though the implied “leave” probabilities obtained from the mixture model calibrated to FX volatility surfaces experience quite a lot of variation. It is an open question whether this is a property of the interpolation with respect to time, or the calibration procedure of the mixture model itself, and one that we believe warrants further analysis.

It should be noted that all the implied probabilities in this work refer to risk-neutral distributions rather than real world distributions. The predictive analysis of this work extends to a horizon of a few weeks at most, though, and the effect of any difference in drift between real-world and risk-neutral measures is small compared to the potential moves in GBPUSD and EURGBP in the event of a “leave” vote.

8. Comparison with Scottish Referendum 2014

Many market commentators find it informative to draw parallels between the Brexit referendum and an earlier referendum on whether Scotland should remain in Great Britain. This referendum was held on 18 September 2014. GBPUSD overnight implied volatilities spiked as high as 27.03% during the trading day of 18 September 2014, pending the result. In the end, as predicted by various polls, the Scottish public voted to stay in Great Britain.

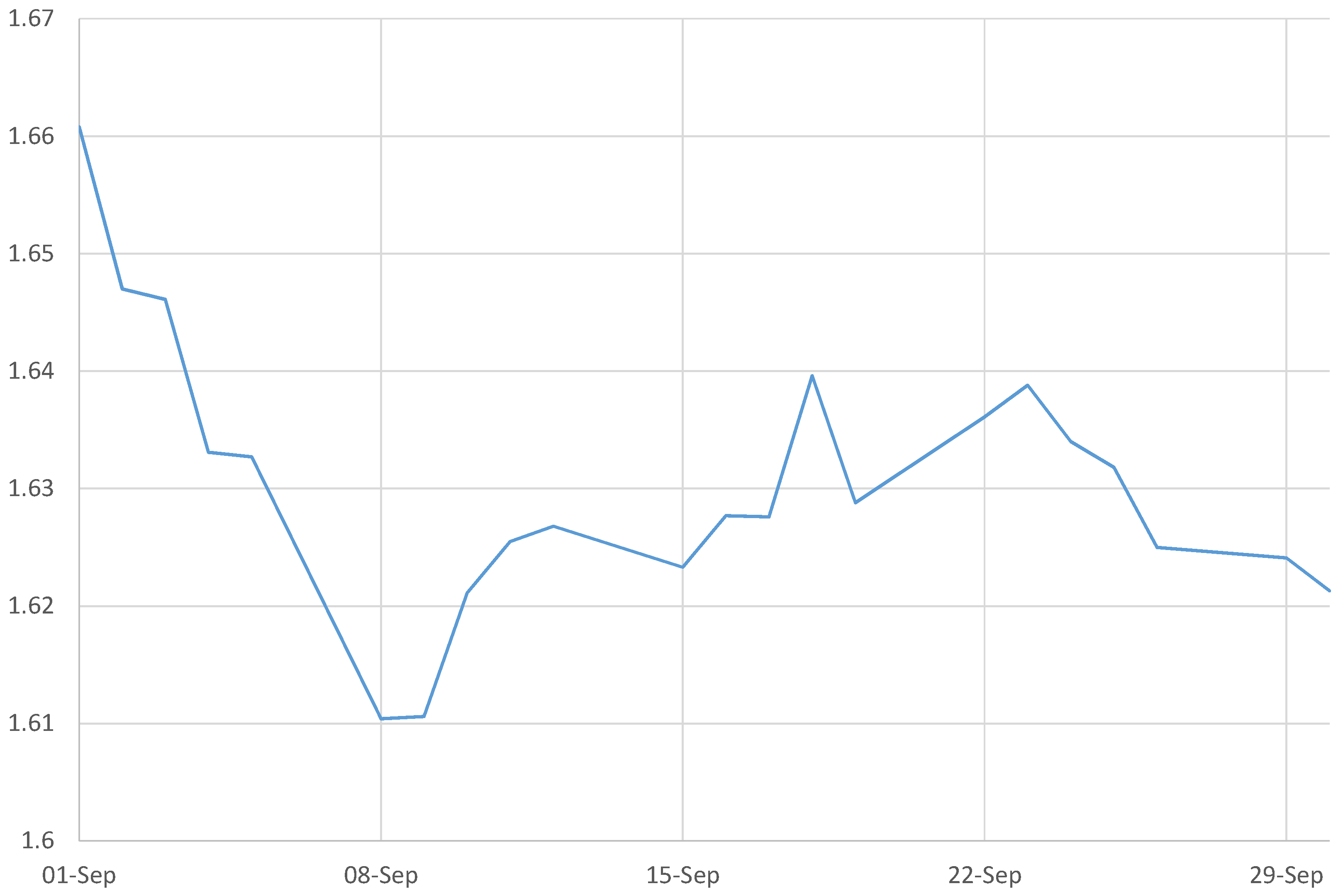
Figure 9 shows GBPUSD spot spiking up to 1.6396 on the day of the referendum, as the eventual result had been already priced in, before retracing back down to 1.6288 the day after, on the back of profit taking and continuing pessimism about the UK economy.

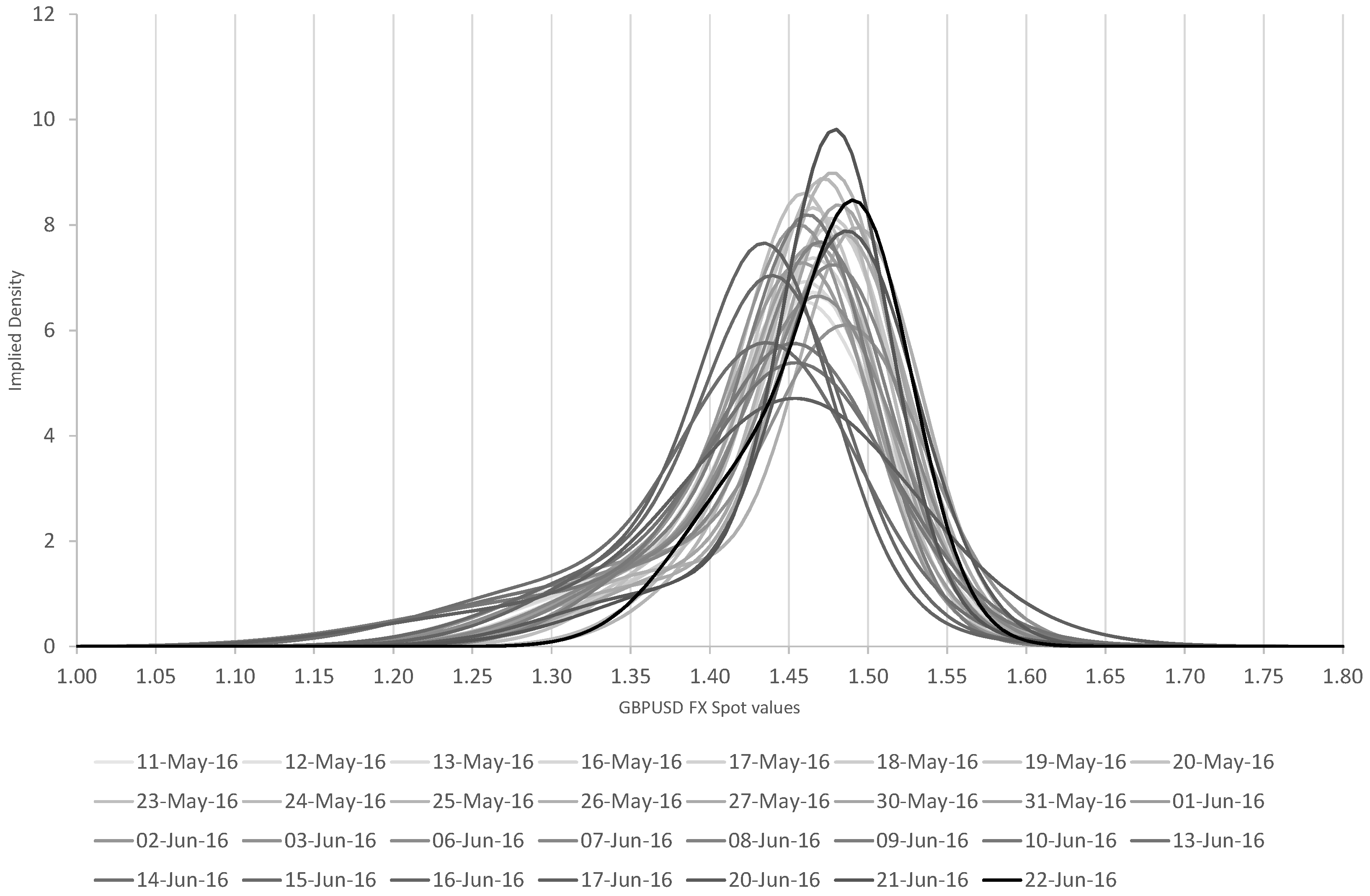
We apply a similar analysis to look at the implied probability distributions before the referendum date of the terminal spot rate for GBPUSD after the referendum vote. Constructing implied densities for the spot price distribution at the end of the referendum day, we see definite skew in the densities in Figure 10.

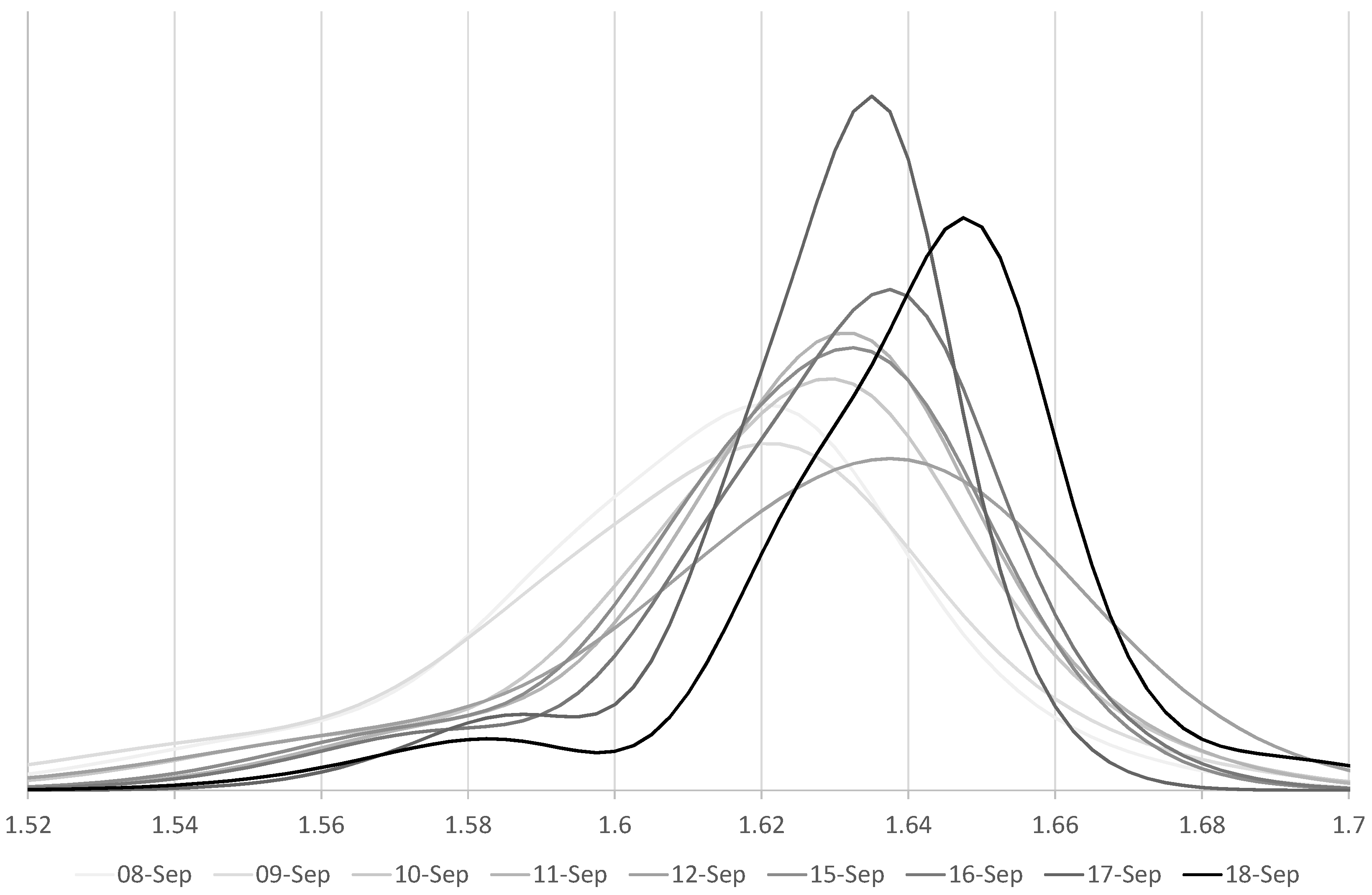
The probability density function on 8 September 2014, with ten days until the referendum date, is quite dispersed, with a mode around 1.62 (relative to $S_0=1.6104$) and a heavy left tail corresponding to probability mass between 1.55 and 1.61. As we move forward towards the referendum date itself, we continue to see an elevated probability mass between 1.50 and 1.60, and particularly so on the last two days (17 and 18 September 2014) when we see bimodality—the market having one smaller peak around [1.58, 1.59]—which we interpret as a scenario where Scotland votes for independence—together with larger modes centred around [1.63, 1.65] corresponding to a “yes” vote for Scotland remaining within the United Kingdom. The probability skew on 18 September 2014 is particularly skewed due to a large spike in overnight implied volatilities to 27.03% and 25-delta risk reversals of −5.75%.

The outcome of the referendum, with Scotland voting 55.3% to remain in the UK and 44.7% to leave, and a move in GBPUSD to 1.6288 and subsequently trading in the [1.62, 1.64] range, is consistent with the implied distributions computed from volatility skew data shown in Figure 10.

We can see a small amount of probability mass in the overnight density between 1.55 and 1.60, presumably corresponding to a scenario in which Scotland decides to leave the Union, but the bulk of the probability density is in the region between 1.60 and 1.70 (which we interpret as the scenario in which Scotland remains in the UK).

All this uncertainty vanished after the referendum outcome was decided (Scotland voting “Yes” to remain in the UK), leading to a much more symmetric and lognormal distribution the day after, relative to a spot rate of 1.6288, which is certainly consistent with the probability densities in Figure 10.

9. Conclusions

We have applied option pricing theory to analyse information embedded in the volatility surfaces for GBPUSD, obtaining implied distributions for the GBPUSD exchange rate at two referendum dates—firstly, the Brexit referendum date on 23 June 2016 and secondly, the Scottish independence referendum date on 18 September 2014. In the second case, we find asset price distributions which are consistent with the observed post-referendum spot price data after the event. In the first case we find significant tail mass probability corresponding to a potential Brexit “leave” vote, in addition to the main mode of the distribution, though we are naturally constrained by the inability of standard delta-based FX quotes to map out the extreme tails of the distribution.

In order to quantify more objectively the two possible scenarios attached to the Brexit referendum, we construct a mixture model and calibrate it to the observed GBPUSD volatility surfaces on all trading days from 24 February to 22 June 2016. In doing so, we estimate that a vote for “leave” would be associated with a devaluation of the British pound, either a relative devaluation of about 4.5% or an absolute decline to a level around 1.3705. This objective approach is more conservative than our earlier heuristic method which estimated possible GBPUSD devaluation to the range 1.10 to 1.30, or a 10–25% decline. In actuality, the point estimate from the mixture model was the best predictor, whereas the 8.44% devaluation in GBP experienced immediately after the “leave” vote is between the two estimates for the percentage decline in the British pound after a vote for “leave”.

10. Afterword

This paper is the final version of a preprint dated 13 June 2016 that originally appeared on SSRN (https://ssrn.com/abstract=2794888) on 14 June 2016, in advance of the referendum date of 23 June 2016.