Backtesting the Lee–Carter and the Cairns–Blake–Dowd Stochastic Mortality Models on Italian Death Rates
Abstract
:1. Introduction
- an important research front on problems related to the parameter estimations (Booth et al. 2006), with many applications also in the actuarial and economics literature (Loisel and Serant 2007); and
- extension of the forecasting analysis with disaggregated projections on demographic subsets to maintain consistency at the aggregate level (Lee and Miller 2001; Li and Lee 2005; Li 2010).
- fixed horizon backtests: lookback and lookforward windows of 20 years;
- jumping fixed-length horizon backtests: lookback window of 20 years and lookforward window of 5 years (short-term projections); and
- rolling fixed-length horizon backtests: lookback window of fixed-length (20 years) and a contracting lookforward window from 20 to 2 years of projections.
2. Model Specifications
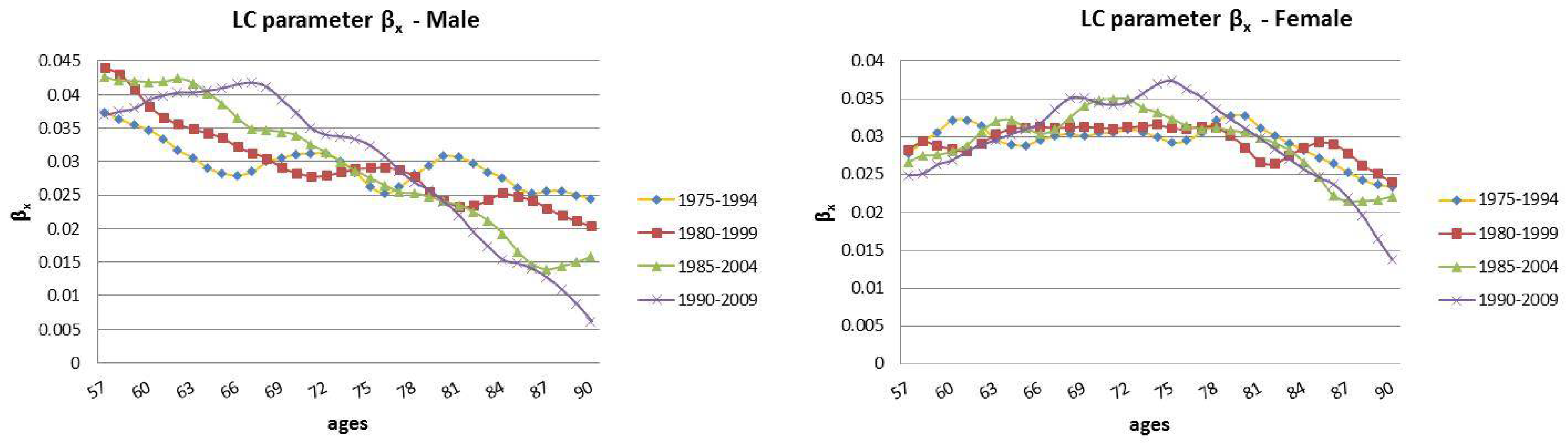
2.1. The Lee–Carter Model
- is the time index representing the level of mortality at time t;
- represents the average trend of mortality on the time horizon at age x;
- represents a measure of the sensitivity in movement from the parameter . In particular, describes the relative speed of mortality changes, at each age, when changes; and
- is the homoskedastic error term, which incorporates historical trends not considered by the model. It is assumed to be .
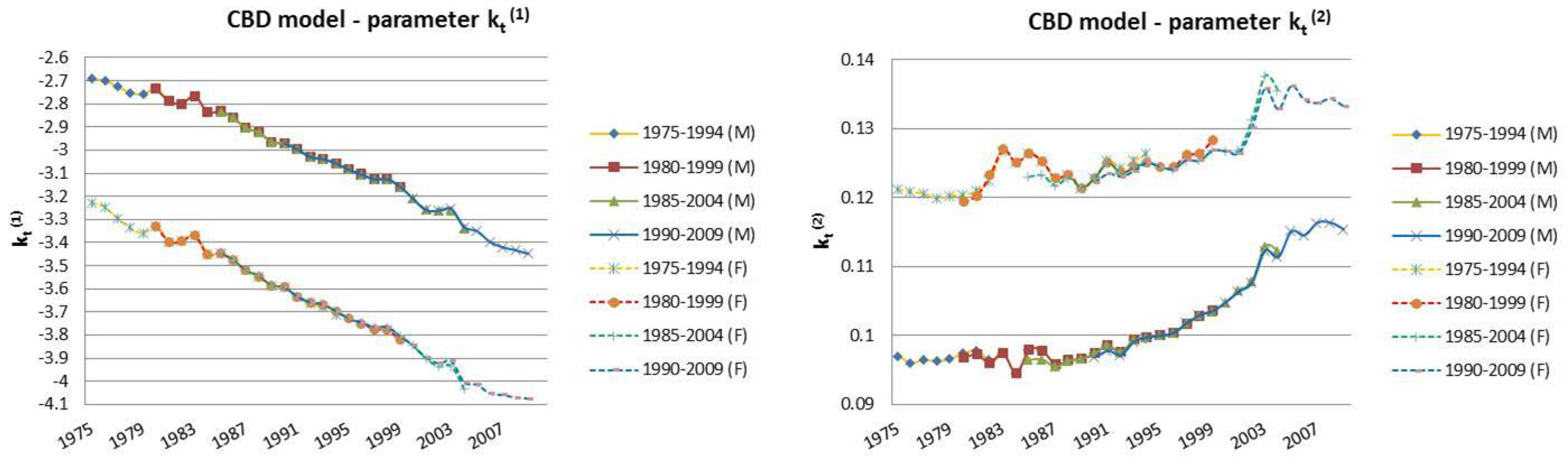
2.2. The Cairns–Blake–Dowd Model
- and are two stochastic processes and represent the two time indexes of the model;
- and represent, respectively, the death and the survival probability, at time t for an individual aged x;
- is the logit transformation of , with representing the mortality odds;
- is the mean age of the considered interval of ages; and
- is the error term that encloses the historical trend that the model does not express. All of the error terms are i.i.d following the Normal distribution with mean 0 and variance .
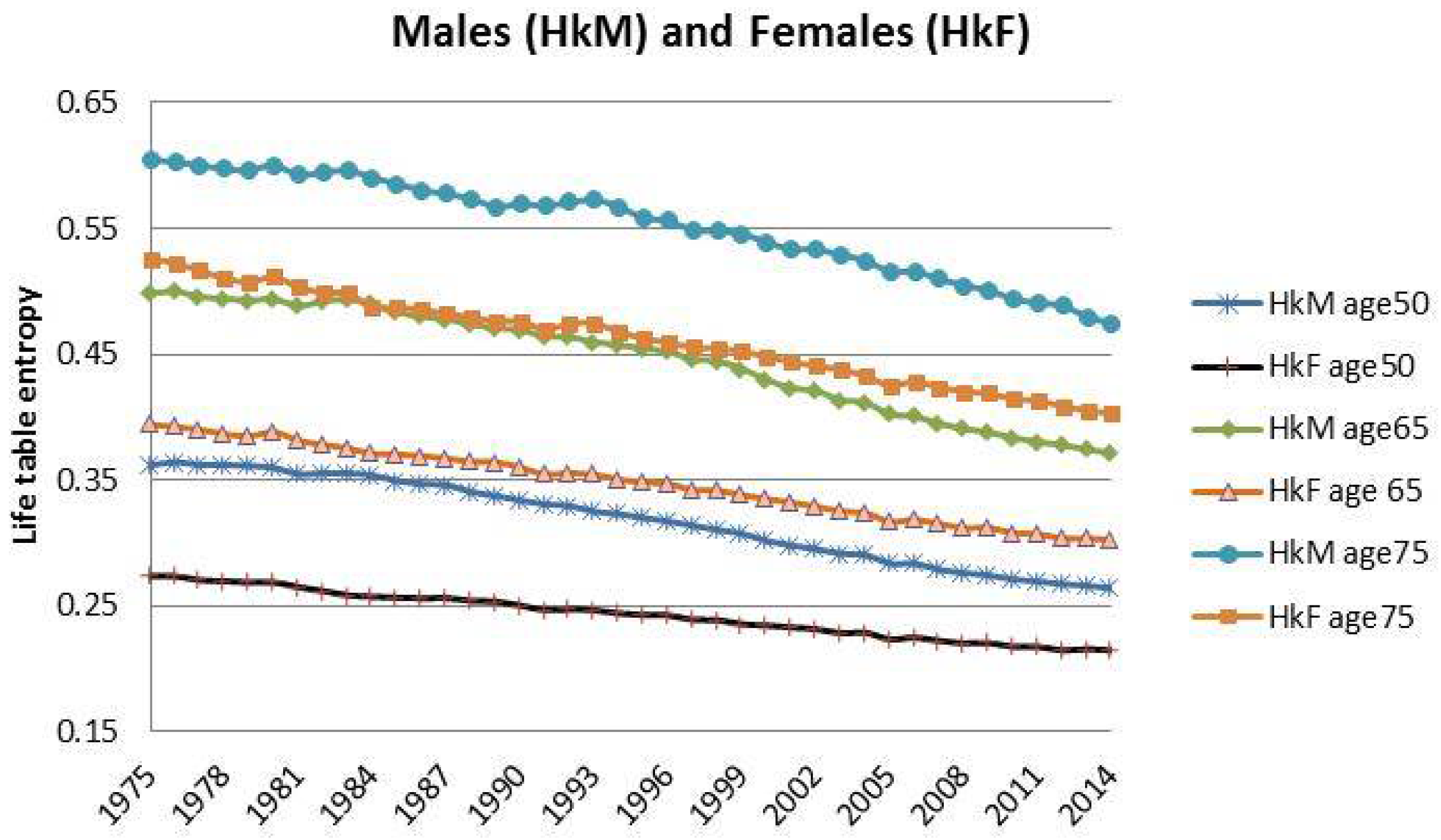
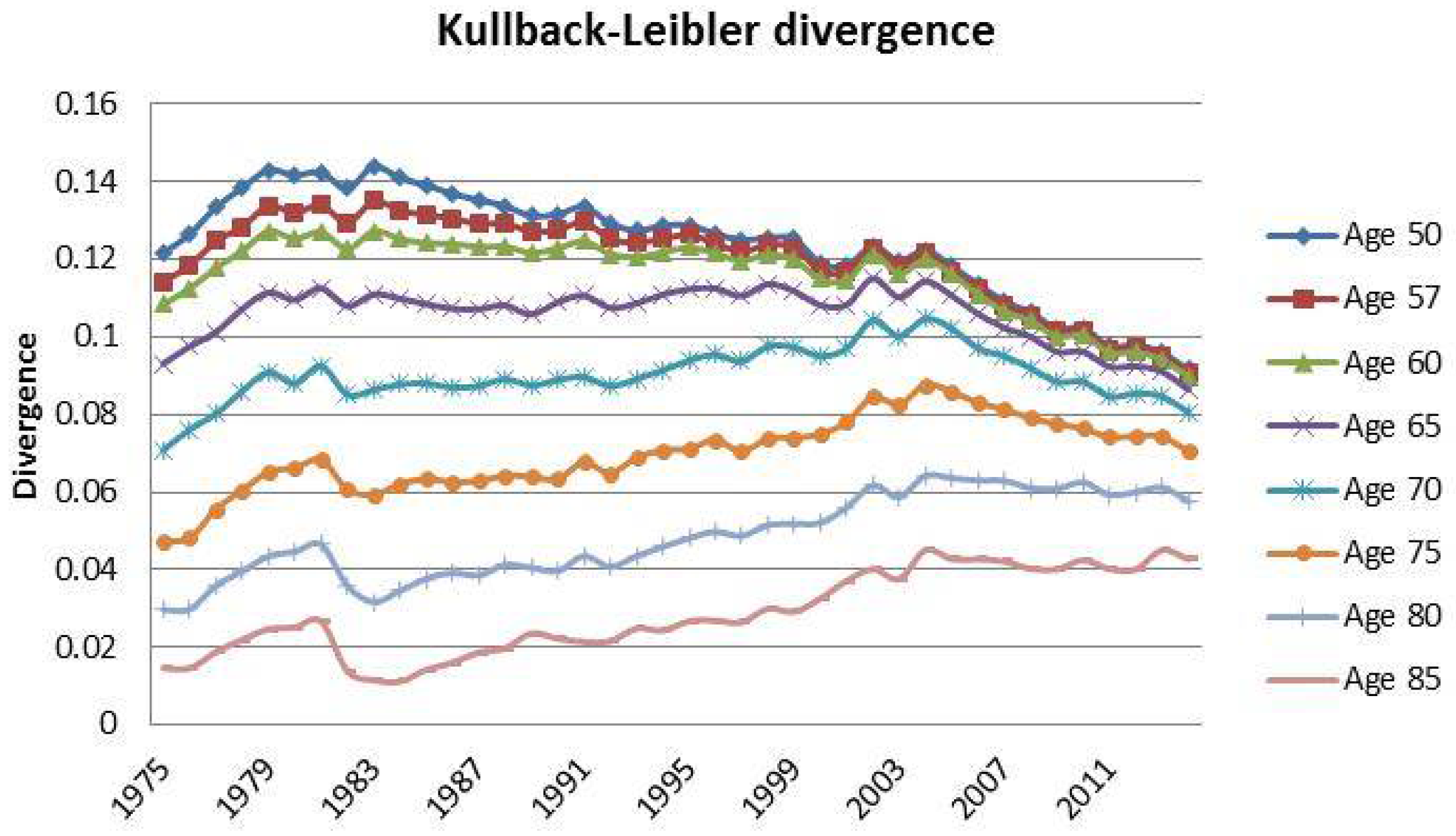
3. Case Study: Italian Mortality Data from 1975 to 2014
4. Backtesting Analysis
- The fixed horizon backtest uses a fixed twenty-year historical “lookback” interval, , and a fixed “lookforward” horizon, (20 years).
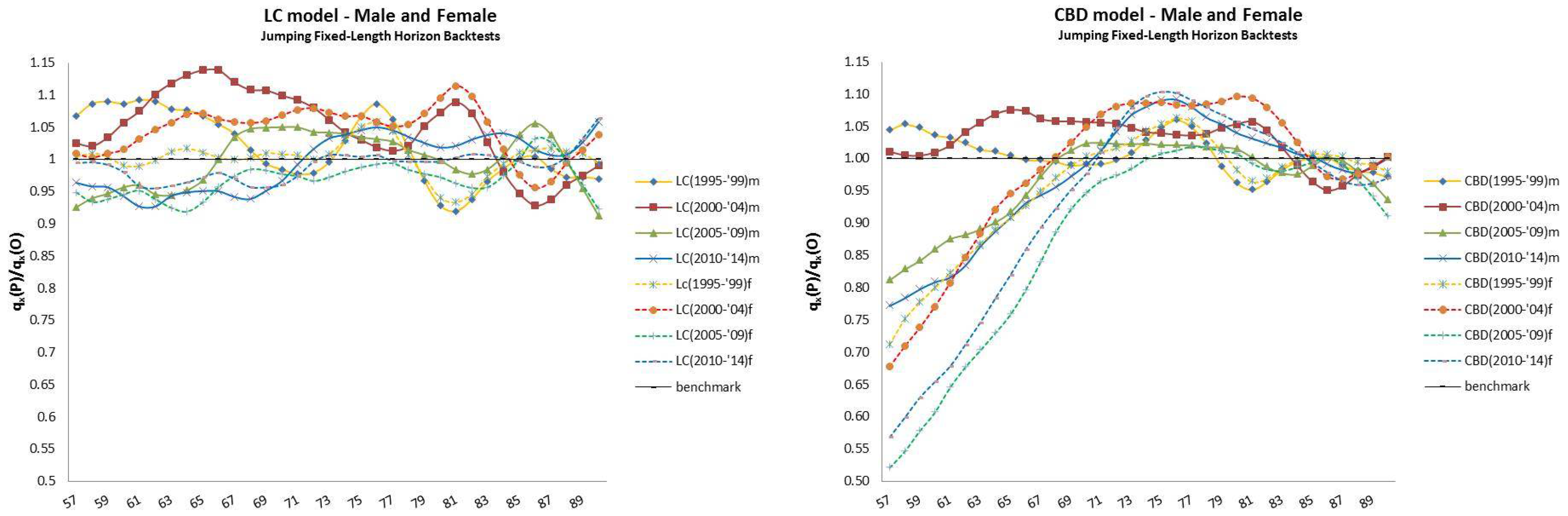
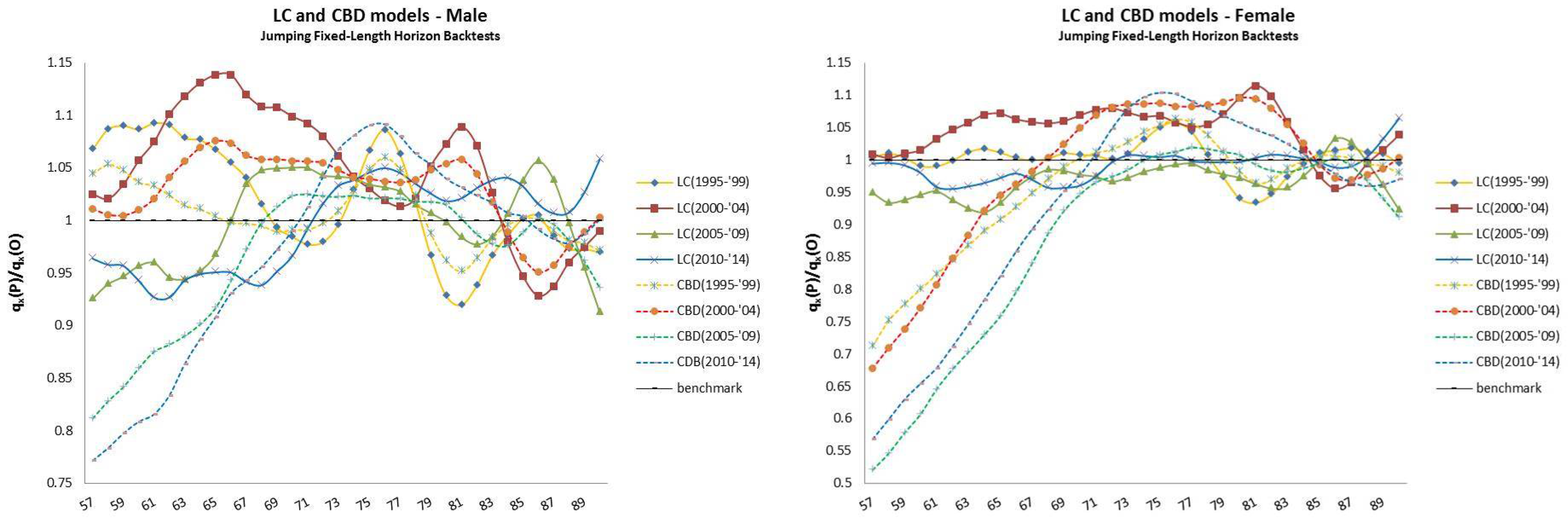
- The jumping fixed-length horizon backtests make short run projections of five years10 and keep fixed the length of the “lookback” horizon (20 years), but make jumps of five years ahead to cover the “lookforward” interval, . This analysis is divided into four groups of estimations and forecast, described in Table 2.
- Finally, the rolling fixed-length horizon backtests keep fixed the length of the “lookback” horizon (i.e., 20 years) and let it roll ahead year by year. The projections are made over the remaining horizon, keeping fixed the last year of the projection at . This analysis is divided into nineteen groups of estimations and forecast, described in Table 3.
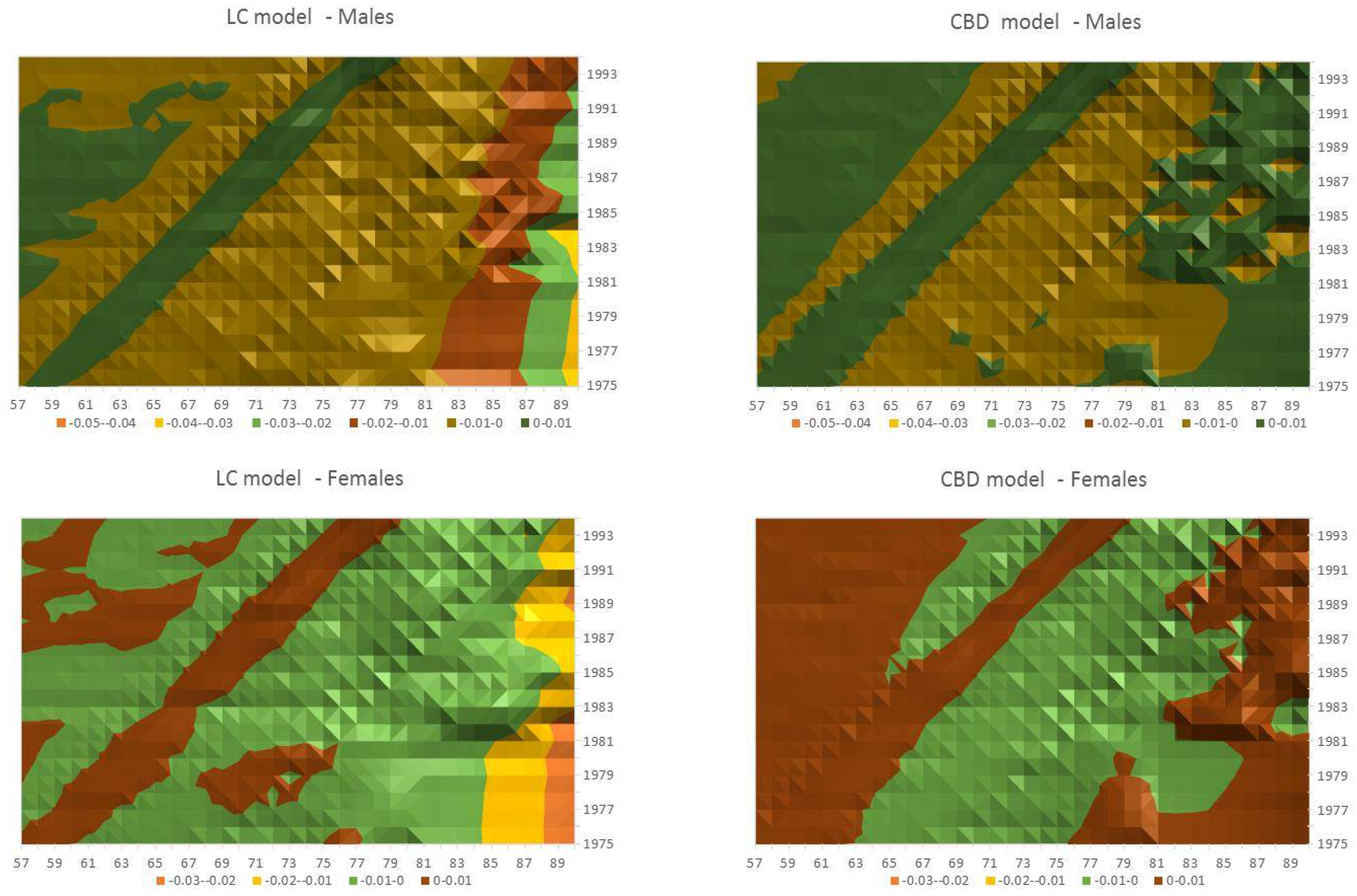
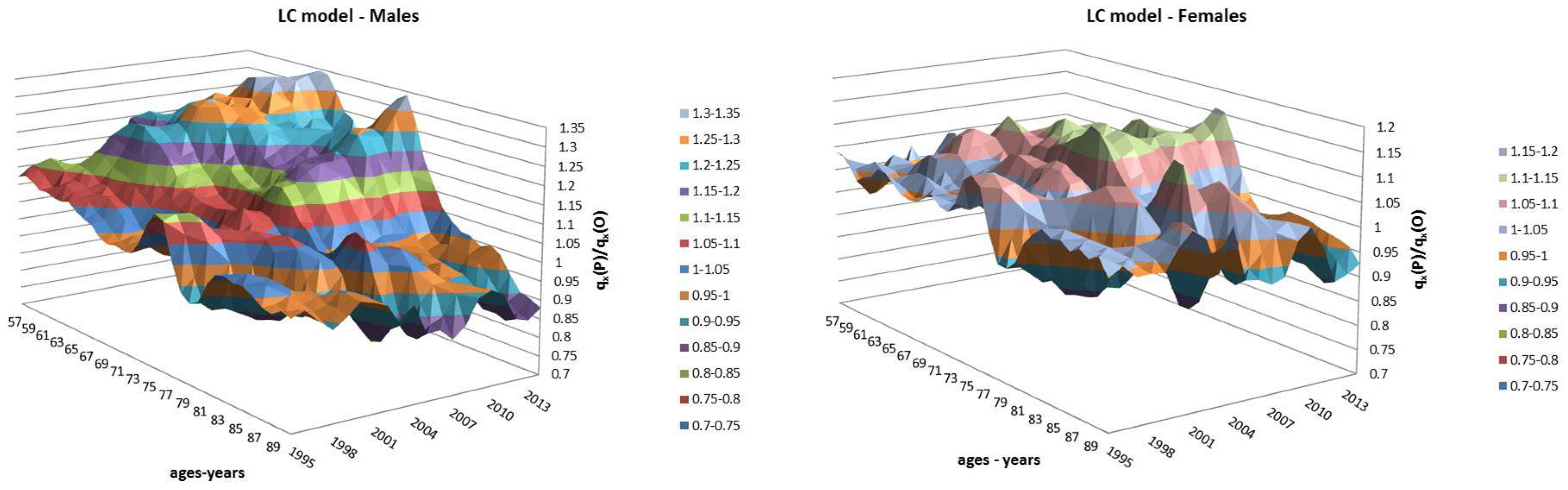
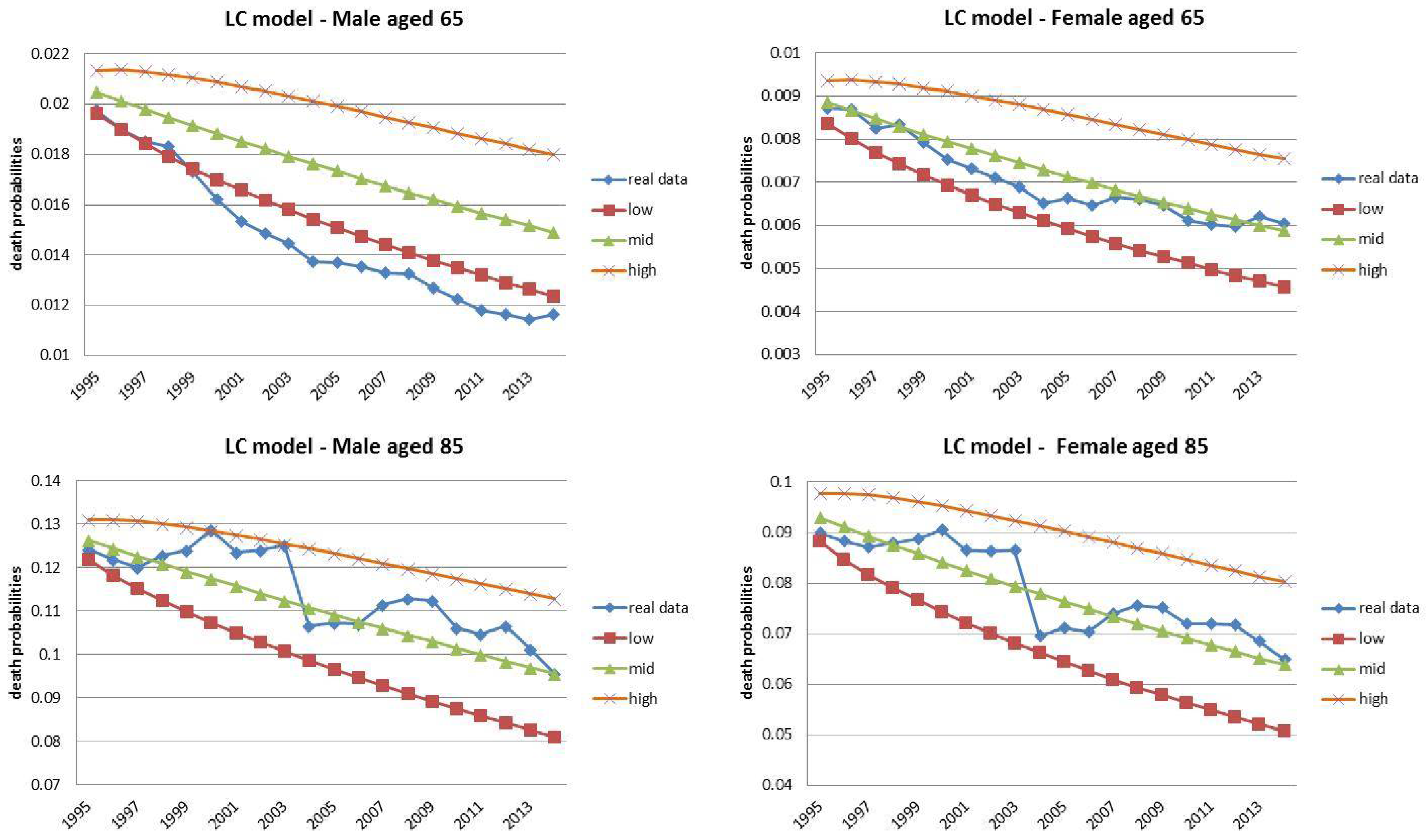
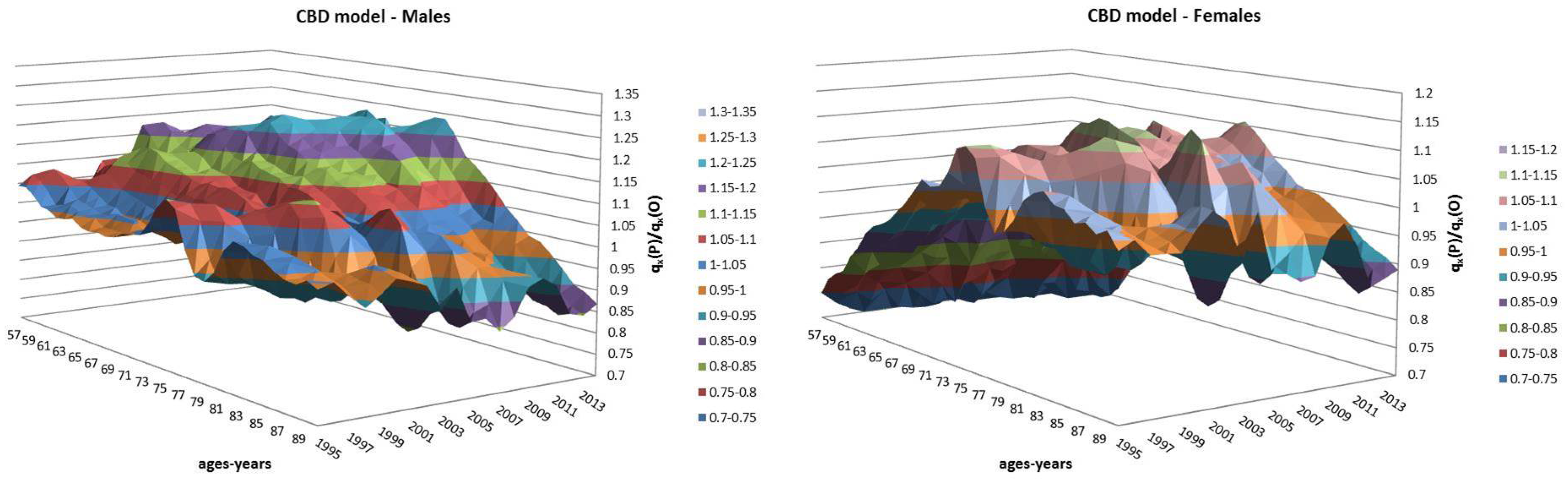
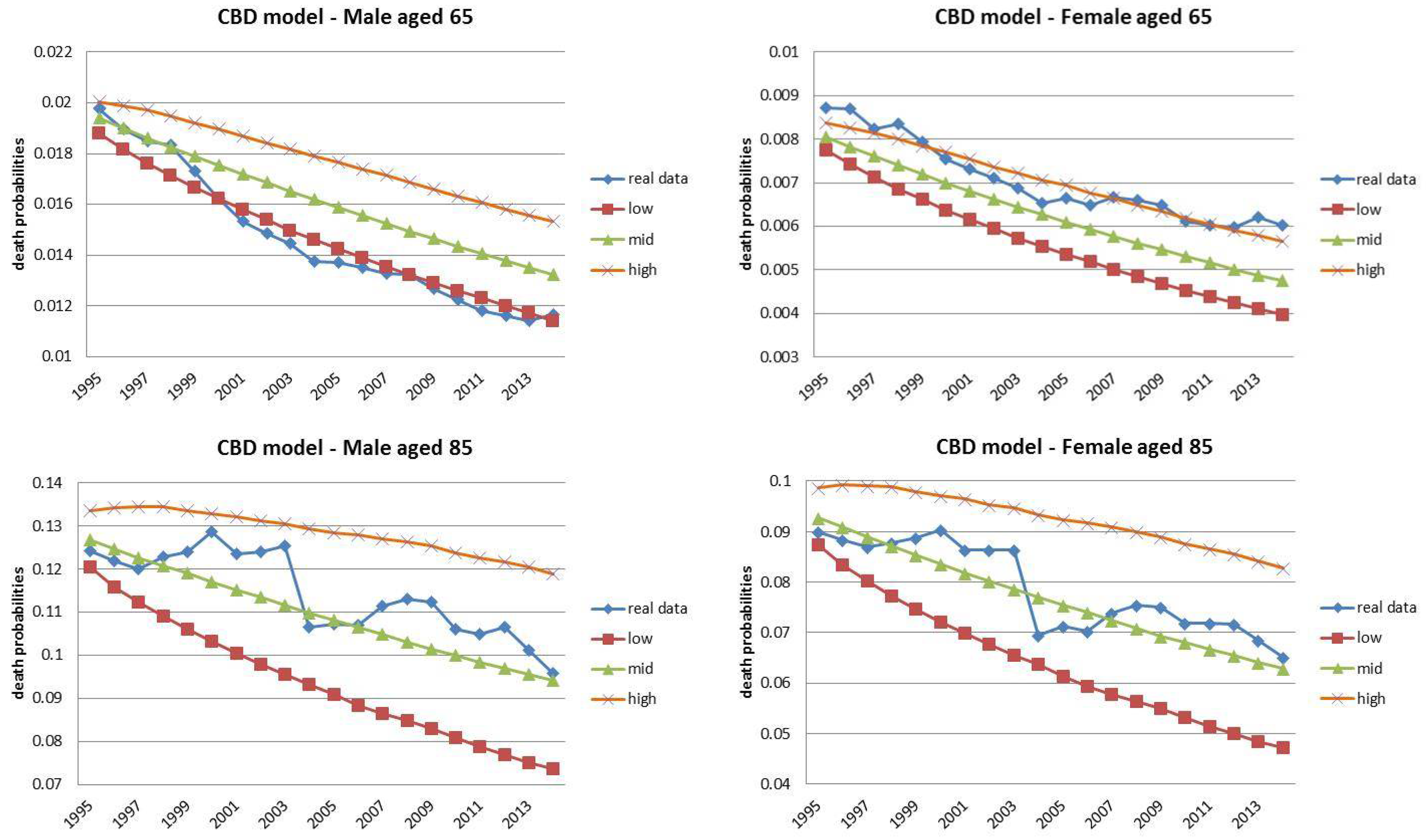
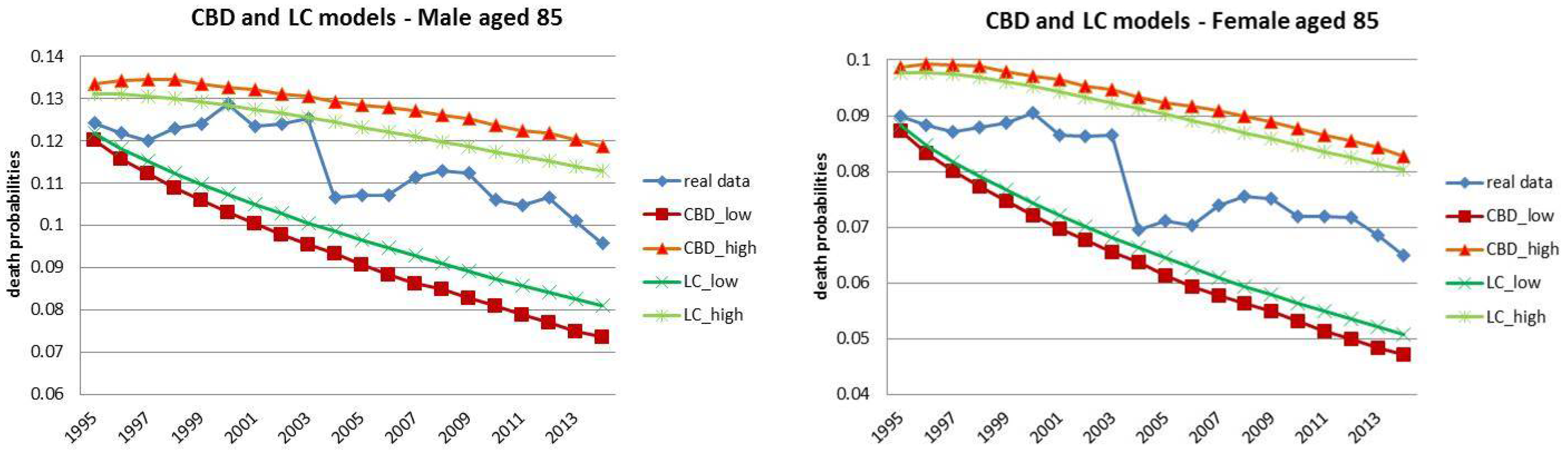
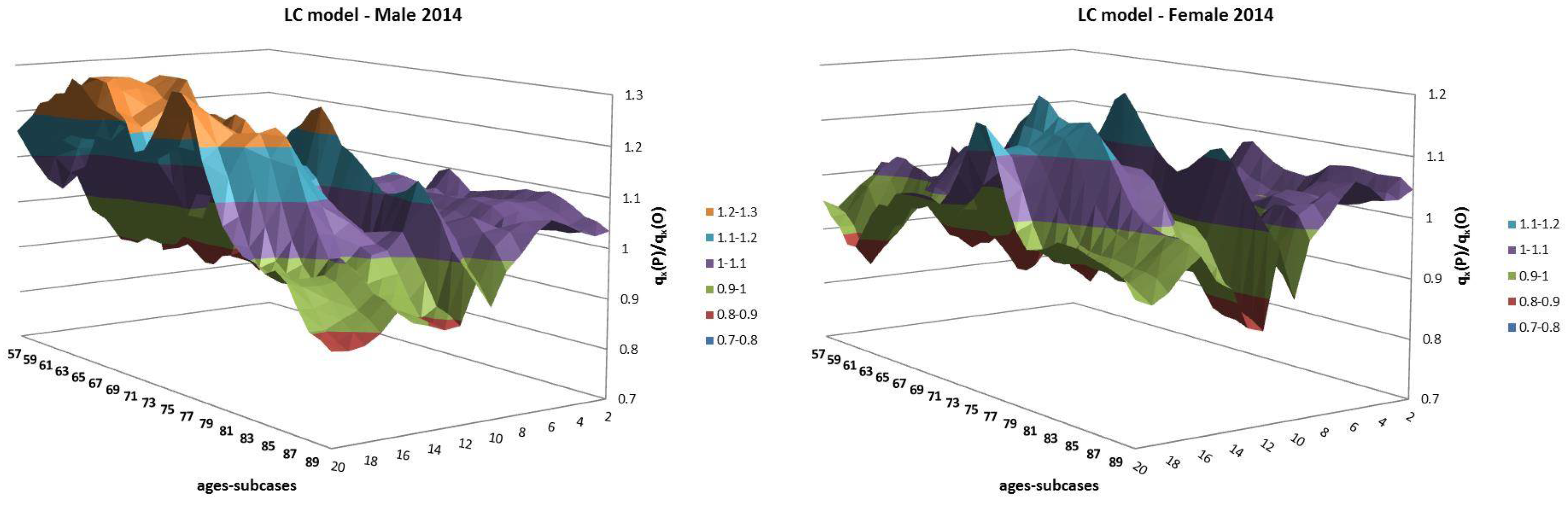
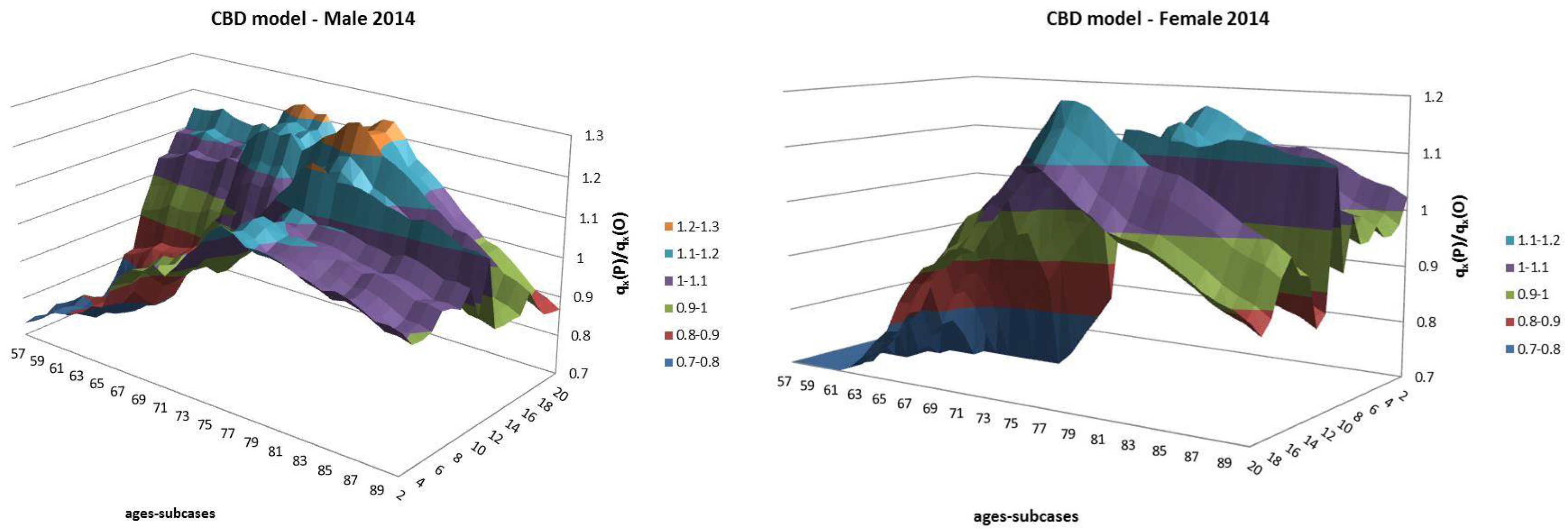
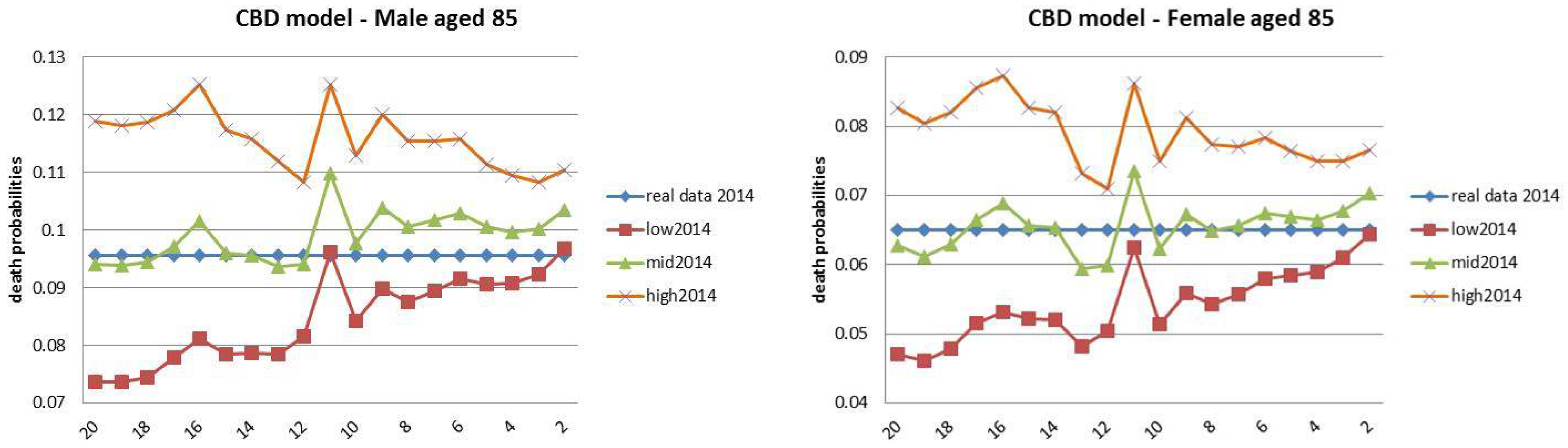
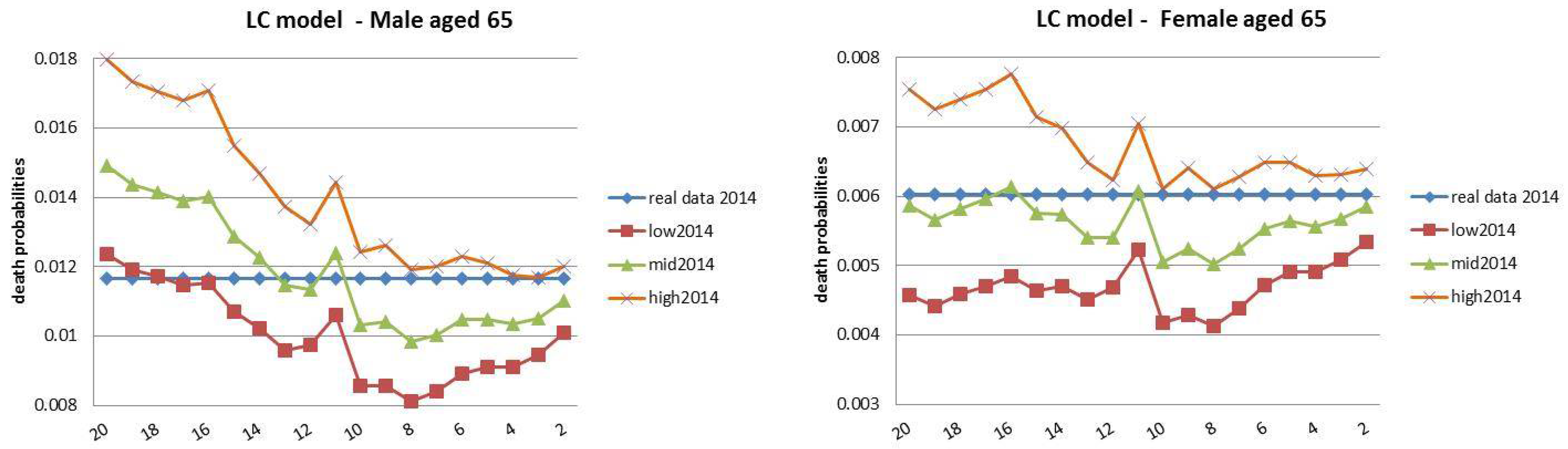
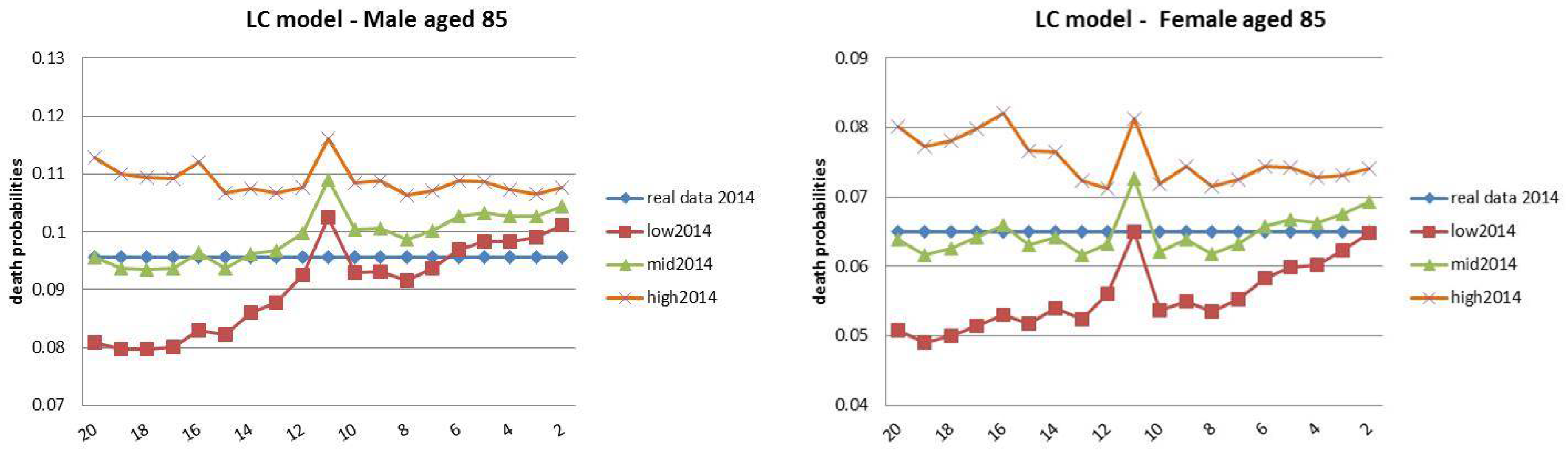
- Both models slightly suffer the cohort effect for both populations over the projection horizon (1995–2014) for the same cohort aged 77–79 in 1995 that is no longer observed from 2006. In particular, both models show an underestimated forecast for such birth cohorts on both sexes with observed values above the upper limit of the confidence interval for some ages of the cohort. This occurred particularly for males.
- The observed male for individuals aged 57–59 in 1995 and 76–78 in 2014, respectively, are often under the lower extreme of the forecast confidence interval. It seems that models have replicated the cohort effect over an homologous cohort in 1995, but since the male mortality evolution has changed consistently from 1975–1994 to 1995–2014, the two homologous cohorts (i.e., 57–59 in 1975 and 57–59 in 1995) showed different trends that lead to forecast errors. This scenario does not occur for females, since women experienced a more ordinary mortality evolution. Therefore, the homologous cohorts are similar, so the bias is not observable.
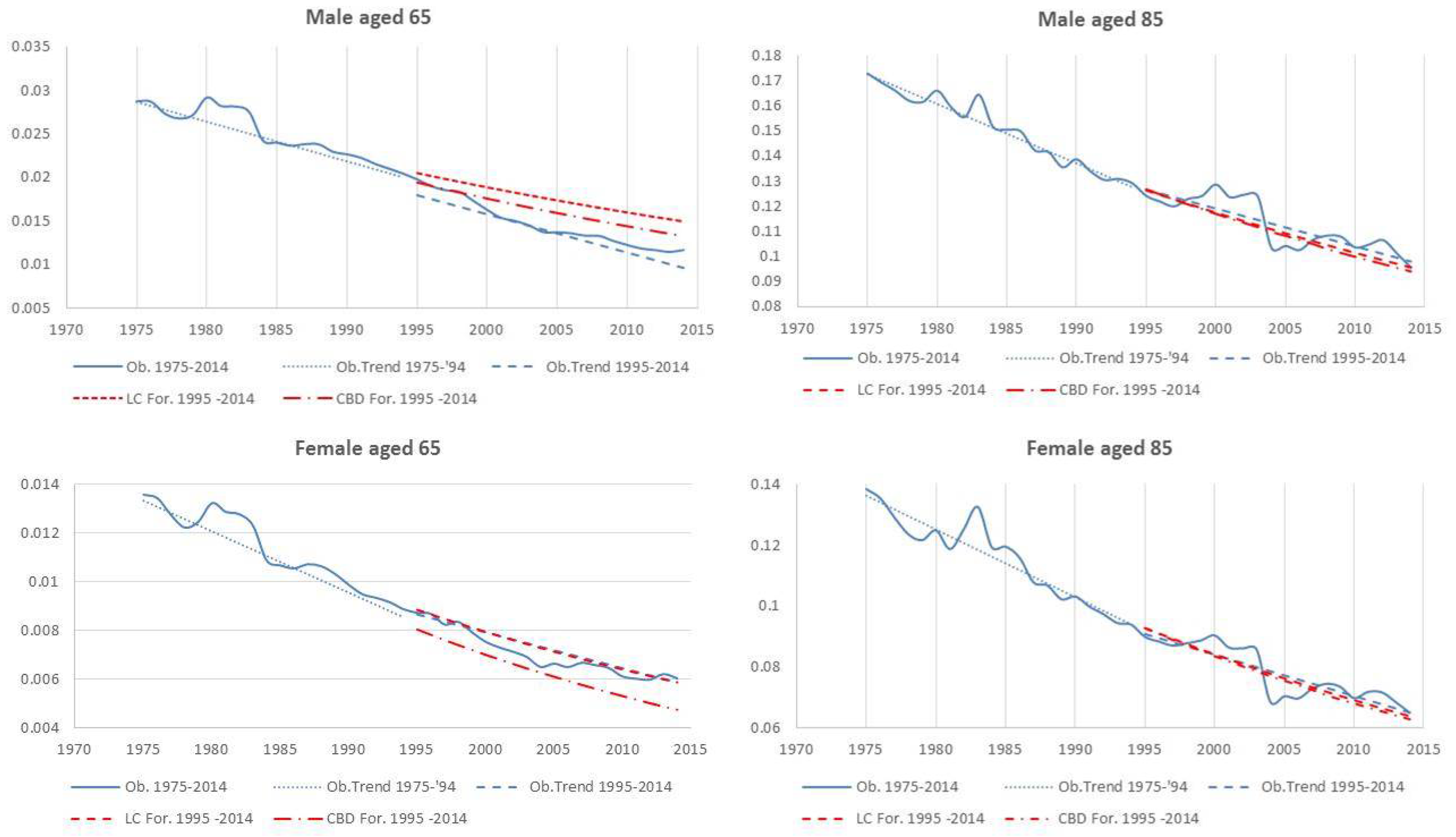
4.1. Fixed Horizon Backtest (1995–2014)
4.2. Jumping Fixed-Length Horizon Backtests
4.3. Rolling Fixed-Length Horizon Backtests
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Lee–Carter Estimation and Projection
Appendix A.1. Parameter Estimations
Appendix A.2. Parameter Projection
Appendix B. Cairns–Blake–Dowd Estimation and Projection
- is a constant 2 × 1 vector of drifts, computed as the arithmetic mean of the differenced series of estimated parameters;
- C is a constant 2 × 2 upper triangular matrix, derived by the unique Cholesky decomposition of the variance–covariance matrix of the parameters vector ; and
- is a two-dimensional standard normal random variable.
References
- ANIA. 2014. Le Basi Demografiche Per Rendite Vitalizie a 1900–2020 e a62. Technical report. Roma: Associazione Nazionale fra le Imprese Assicuratrici (ANIA). [Google Scholar]
- Avraam, Demetris, Joao Pedro de Magalhaes, and Bakhtier Vasiev. 2013. A mathematical model of mortality dynamics across the lifespan combining heterogeneity and stochastic effects. Experimental Gerontology 48: 801–11. [Google Scholar] [CrossRef] [PubMed]
- Booth, Heather, Rob Hyndman, Leonie Tickle, and Piet De Jong. 2006. Lee-carter mortality forecasting: A multi-country comparison of variants and extensions. Demographic Research 15: 289–310. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from england and wales and the united states. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Chan, Wai-Sum, Johnny Siu-Hang Li, and Jackie Li. 2014. The cbd mortality indexes: Modeling and applications. North American Actuarial Journal 18: 38–58. [Google Scholar] [CrossRef]
- Dowd, Kevin, Andrew J. G. Cairns, David Blake, Guy D Coughlan, David Epstein, and Marwa Khalaf-Allah. 2010a. Backtesting stochastic mortality models: An ex post evaluation of multiperiod-ahead density forecasts. North American Actuarial Journal 14: 281–98. [Google Scholar] [CrossRef]
- Draper, Norman R., and Harry Smith. 2014. Applied Regression Analysis. New York: John Wiley & Sons. [Google Scholar]
- Istat. 2001. Tavole di mortalità della popolazione italiana per provincia e regione di residenza. anno 1998. Roma: Servizio Popolazione Istruzione e Cultura. [Google Scholar]
- Istat. 2008. Previsioni demografiche. 1 gennaio 2007-1 gennaio 2051. Nota informativa, Popolazione. Technical report. Roma: Istat. [Google Scholar]
- Istat. 2016. Indicatori Demografici: Stime Per L’anno 2015. Technical report. Roma: Istat. [Google Scholar]
- Keyfitz, Nathan, and Hal Caswell. 2005. Applied Mathematical Demography. New York: Springer, vol. 47. [Google Scholar]
- Kullback, Solomon, and Richard A. Leibler. 1951. On information and sufficiency. The Annals of Mathematical Statistics 22: 79–86. [Google Scholar] [CrossRef]
- Lee, Ronald. 2000. The lee-carter method for forecasting mortality, with various extensions and applications. North American Actuarial Journal 4: 80–91. [Google Scholar] [CrossRef]
- Lee, Ronald, and Timothy Miller. 2001. Evaluating the performance of the lee-carter method for forecasting mortality. Demography 38: 537–49. [Google Scholar] [CrossRef] [PubMed]
- Lee, Ronald D., and Lawrence R Carter. 1992. Modeling and forecasting US mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Li, Jackie. 2010. Projections of new zealand mortality using the lee-carter model and its augmented common factor extension. New Zealand Population Review 36: 27–53. [Google Scholar]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the lee-carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [PubMed]
- Li, Ting, and James Anderson. 2013. Shaping human mortality patterns through intrinsic and extrinsic vitality processes. Demographic Research 28: 341–72. [Google Scholar] [CrossRef]
- Li, Ting, and James J Anderson. 2009. The vitality model: A way to understand population survival and demographic heterogeneity. Theoretical Population Biology 76: 118–31. [Google Scholar] [CrossRef] [PubMed]
- Loisel, Stéphane, and Daniel Serant. In the core of longevity risk: Hidden dependence in stochastic mortality models and cut-offs in prices of longevity swaps. Cahier de Recherche de l’ISFA WP2044. Working Paper. Available online: http://isfaserveur.univ-lyon1.fr/stephane.loisel/Loisel-Serant-ISFA-WP2044.pdf (accessed on 13 April 2010).
- Maccheroni, Carlo. 2014. Diverging tendencies by age in sex differentials in mortality in italy. South East Journal of Political Science (SEEJPS) 2: 42–58. [Google Scholar]
- Maccheroni, Carlo. 2016. The Actuarial Aging of Italian Veterans of World War I Born 1889-1906 and a Comparison to the Cohorts Born During the Years Immediately Following. Technical report. Torino: Department of Economics and Statistics (WP36), University of Torino. [Google Scholar]
- Mavros, George, Andrew J.G. Cairns, Torsten Kleinow, and George Streftaris. 2014. A Parsimonious Approach to Stochastic Mortality Modelling with Dependent Residuals. Technical report. Edinburgh: Citeseer. [Google Scholar]
- Pitacco, Ermanno, Michel Denuit, Steven Haberman, and Annamaria Olivieri. 2009. Modelling Longevity Dynamics for Pensions and Annuity Business. London: Oxford University Press. [Google Scholar]
- Reed, Lowell Jacob, and Margaret Merrell. 1939. A short method for constructing an abridged life table. American Journal of Epidemiology 30: 33–62. [Google Scholar] [CrossRef]
- Thatcher, A. Roger, Väinö Kannisto, and James W. Vaupel. 1998. The force of mortality at ages 80 to 120. Odense Monographs on Population Aging 5: 104–20. [Google Scholar]
- Vaupel, James W. 2010. Biodemography of human ageing. Nature 464: 536–42. [Google Scholar] [CrossRef] [PubMed]
- Whitehouse, Edward. 2007. Life-expectancy risk and pensions: Who bears the burden? Available online: http://www.oecd.org/social/soc/39469901.pdf (accessed on 5 October 2007).
| 1 | Refer to Cairns et al. (2009) for a detailed list and quantitative comparison of the principal stochastic mortality models. |
| 2 | ISTAT population projections 2011–2065: http://demo.istat.it/uniprev2011/note.html. |
| 3 | Particularly for the case of Cairns–Blake–Dowd model. |
| 4 | Data downloaded on June 2016. Source: http://demo.istat.it/tvm2016/index.php?lingua=eng. |
| 5 | For the sake of simplicity, we decided to adopt the same terminology used by Dowd et al. (2010a). |
| 6 | The variables and are the common biometric functions as described in the life tables. |
| 7 | |
| 8 | Even though the backtesting analysis will be focused on the interval of ages 57–90, here we decided to provide information also on ages lower than . In this way, we are able to present a more accurate Italian demographic scenario for the period observed. |
| 9 | The starting point for the final age interval is denoted by w. |
| 10 | We made a forecast of each year in the short-run projection window (5 years). |
| 11 | Even though the LC and CBD models do not take into account social factors in their original formulation, several other studies have considered heterogeneity and vitality factors (Li and Anderson 2009; Li and Anderson 2013). |
| 12 | For this reason, we decided to plot exclusively the dynamics, since they show a more interesting variability with respect to the parameters that, in this case, are barely distant parallel and smooth curves among backtest jumps. |
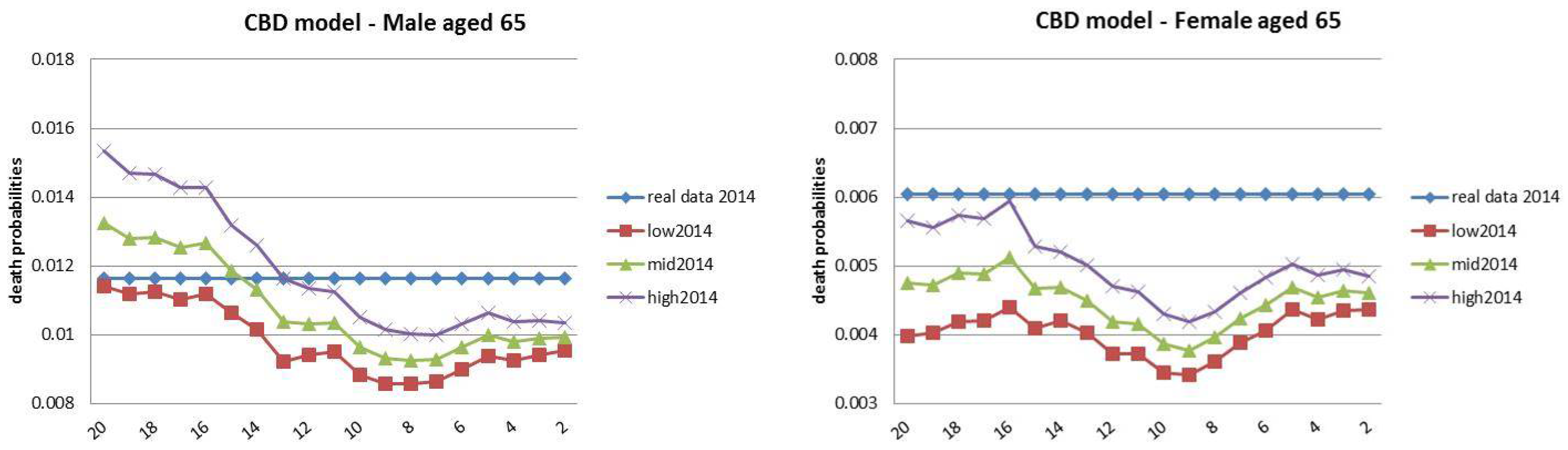
| 13 | The choice for the year 2014 was motivated by the observed regular mortality path. The 2015 mortality trend is expected to be increased, particularly at old ages (Istat 2016). |
| 14 | These represent the initial years of the 20-year-long database; i.e., 1975 refers to the estimation period 1975–1994, and so on. |
| 15 | Equation (A3) has no explicit solution, so it has to be solved numerically. |
| 16 | We used MATLAB (R2010b, The MathWorks, Inc., Natick, Massachusetts 01760 USA) for estimation and forecast. |
| 17 | We used MATLAB for estimation and forecast. |

| Italian Period Life Tables | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ages | 1975 | 1980 | 1985 | 1990 | 1995 | 2000 | 2005 | 2010 | 2014 |
| Male | |||||||||
| 50 | 0.9438 | 0.9483 | 0.9554 | 0.9583 | 0.9591 | 0.9662 | 0.9722 | 0.9755 | 0.9777 |
| 60 | 0.8406 | 0.8487 | 0.8646 | 0.8839 | 0.8951 | 0.90962 | 0.9242 | 0.9324 | 0.9376 |
| 70 | 0.6292 | 0.6409 | 0.6691 | 0.7081 | 0.7351 | 0.7732 | 0.8060 | 0.8257 | 0.8385 |
| 80 | 0.3014 | 0.3161 | 0.3539 | 0.4029 | 0.4406 | 0.4936 | 0.5434 | 0.5912 | 0.6188 |
| 90 | 0.0464 | 0.0527 | 0.0682 | 0.0954 | 0.1170 | 0.1396 | 0.1648 | 0.1996 | 0.2250 |
| 95 | 0.0080 | 0.0096 | 0.0140 | 0.0235 | 0.0318 | 0.0401 | 0.0491 | 0.0595 | 0.0743 |
| Female | |||||||||
| 50 | 0.9703 | 0.9739 | 0.9769 | 0.9785 | 0.9796 | 0.9822 | 0.9850 | 0.9865 | 0.9871 |
| 60 | 0.9194 | 0.9290 | 0.9364 | 0.9427 | 0.9473 | 0.9525 | 0.9585 | 0.9620 | 0.9639 |
| 70 | 0.8009 | 0.8168 | 0.8337 | 0.8546 | 0.8681 | 0.8828 | 0.8972 | 0.9053 | 0.9087 |
| 80 | 0.5070 | 0.5403 | 0.5814 | 0.6249 | 0.6576 | 0.69561 | 0.7322 | 0.7540 | 0.7674 |
| 90 | 0.1154 | 0.1433 | 0.1629 | 0.2141 | 0.2547 | 0.2860 | 0.3297 | 0.3653 | 0.3878 |
| 95 | 0.0226 | 0.0326 | 0.0380 | 0.0626 | 0.0830 | 0.1030 | 0.1259 | 0.1420 | 0.1654 |
| Lookback Horizon | Lookforward Horizon |
|---|---|
| 1975–1994 | 1995–1999 |
| 1980–1999 | 2000–2004 |
| 1985–2004 | 2005–2009 |
| 1990–2009 | 2010–2014 |
| Lookback | Lookforward | Lookback | Lookforward |
|---|---|---|---|
| 1975–1994 | 1995–2014 (20) | 1985–2004 | 2005-2014 (10) |
| 1976–1995 | 1996–2014 (19) | 1986–2005 | 2006–2014 (9) |
| 1977–1996 | 1997–2014 (18) | 1987–2006 | 2007–2014 (8) |
| 1978–1997 | 1998–2014 (17) | 1988–2007 | 2008–2014 (7) |
| 1979–1998 | 1999–2014 (16) | 1989–2008 | 2009–2014 (6) |
| 1980–1999 | 2000–2014 (15) | 1990–2009 | 2010–2014 (5) |
| 1981–2000 | 2001–2014 (14) | 1991–2010 | 2011–2014 (4) |
| 1982–2001 | 2002–2014 (13) | 1992–2011 | 2012–2014 (3) |
| 1983–2002 | 2003–2014 (12) | 1993–2012 | 2013–2014 (2) |
| 1984–2003 | 2004–2014 (11) |
| Fixed Horizon Backtest | ||||
|---|---|---|---|---|
| CBD model | LC model | |||
| Prediction Years | Male | Female | Male | Female |
| 1995-2014 | 0.00625 | 0.00401 | 0.00596 | 0.00274 |
| Jumping Fixed-Length Horizon Backtests | ||||
| CBD model | LC model | |||
| Prediction Years | Male | Female | Male | Female |
| 1995–1999 | 0.00321 | 0.00201 | 0.00386 | 0.00210 |
| 2000–2004 | 0.00470 | 0.00411 | 0.00532 | 0.00369 |
| 2005–2009 | 0.00373 | 0.00366 | 0.00455 | 0.00301 |
| 2010–2014 | 0.00250 | 0.00229 | 0.00299 | 0.00219 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maccheroni, C.; Nocito, S. Backtesting the Lee–Carter and the Cairns–Blake–Dowd Stochastic Mortality Models on Italian Death Rates. Risks 2017, 5, 34. https://doi.org/10.3390/risks5030034
Maccheroni C, Nocito S. Backtesting the Lee–Carter and the Cairns–Blake–Dowd Stochastic Mortality Models on Italian Death Rates. Risks. 2017; 5(3):34. https://doi.org/10.3390/risks5030034
Chicago/Turabian StyleMaccheroni, Carlo, and Samuel Nocito. 2017. "Backtesting the Lee–Carter and the Cairns–Blake–Dowd Stochastic Mortality Models on Italian Death Rates" Risks 5, no. 3: 34. https://doi.org/10.3390/risks5030034
APA StyleMaccheroni, C., & Nocito, S. (2017). Backtesting the Lee–Carter and the Cairns–Blake–Dowd Stochastic Mortality Models on Italian Death Rates. Risks, 5(3), 34. https://doi.org/10.3390/risks5030034






