Lead–Lag Relationship Using a Stop-and-Reverse-MinMax Process
Abstract
:1. Introduction
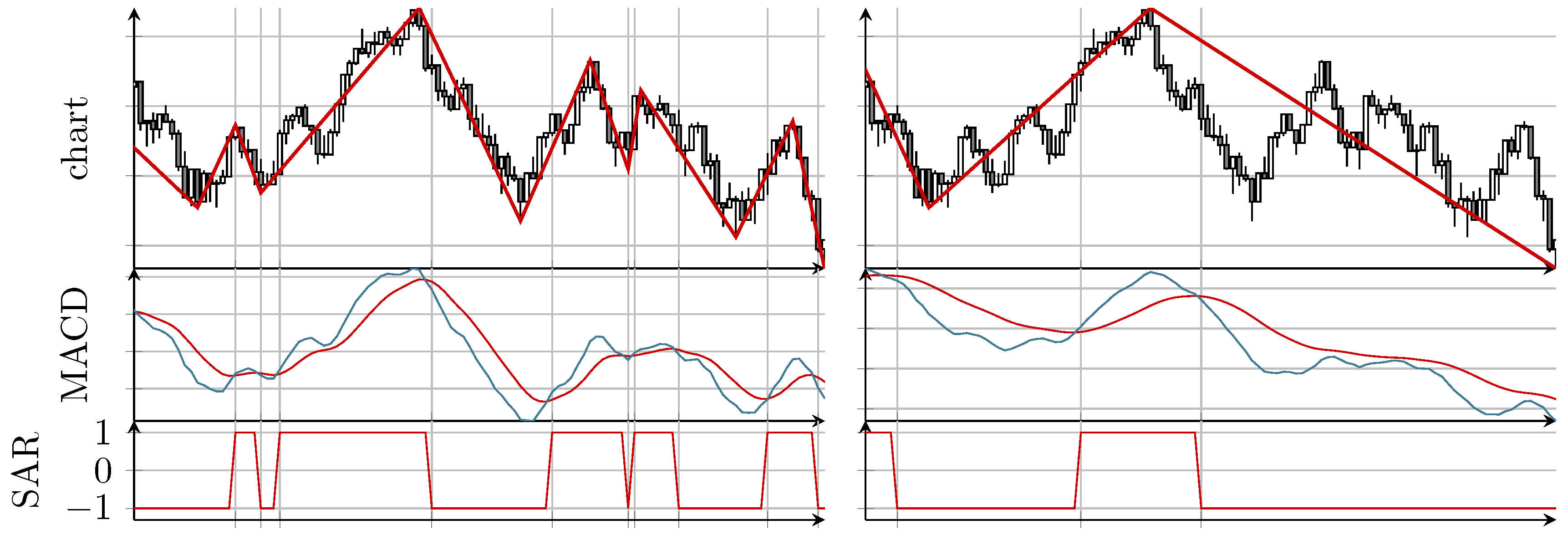
2. Method for Intermarket Analysis
- Fix the desired mean wavelength .
- Find all local extreme values and for the primary and the secondary market, respectively, such that the mean wavelengths (1) for both markets on the full data base matches , i.e., such that .
- Find such that and .For each , do the following:
- (a)
- Find such that .
- (b)
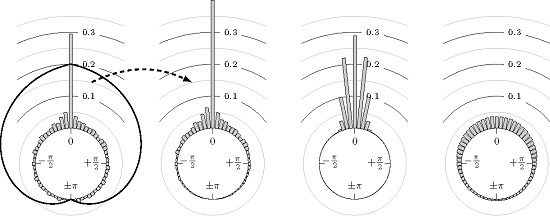
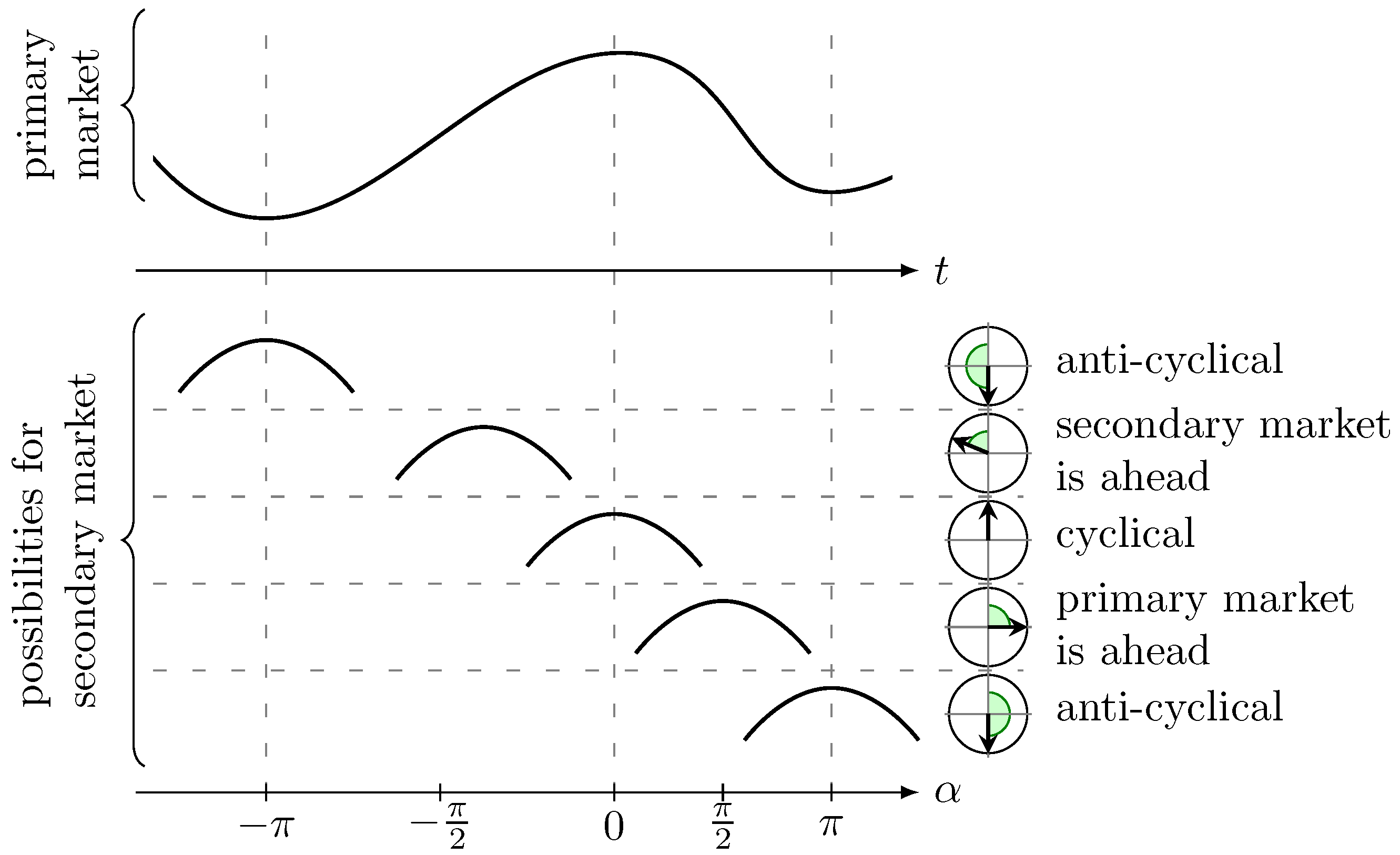
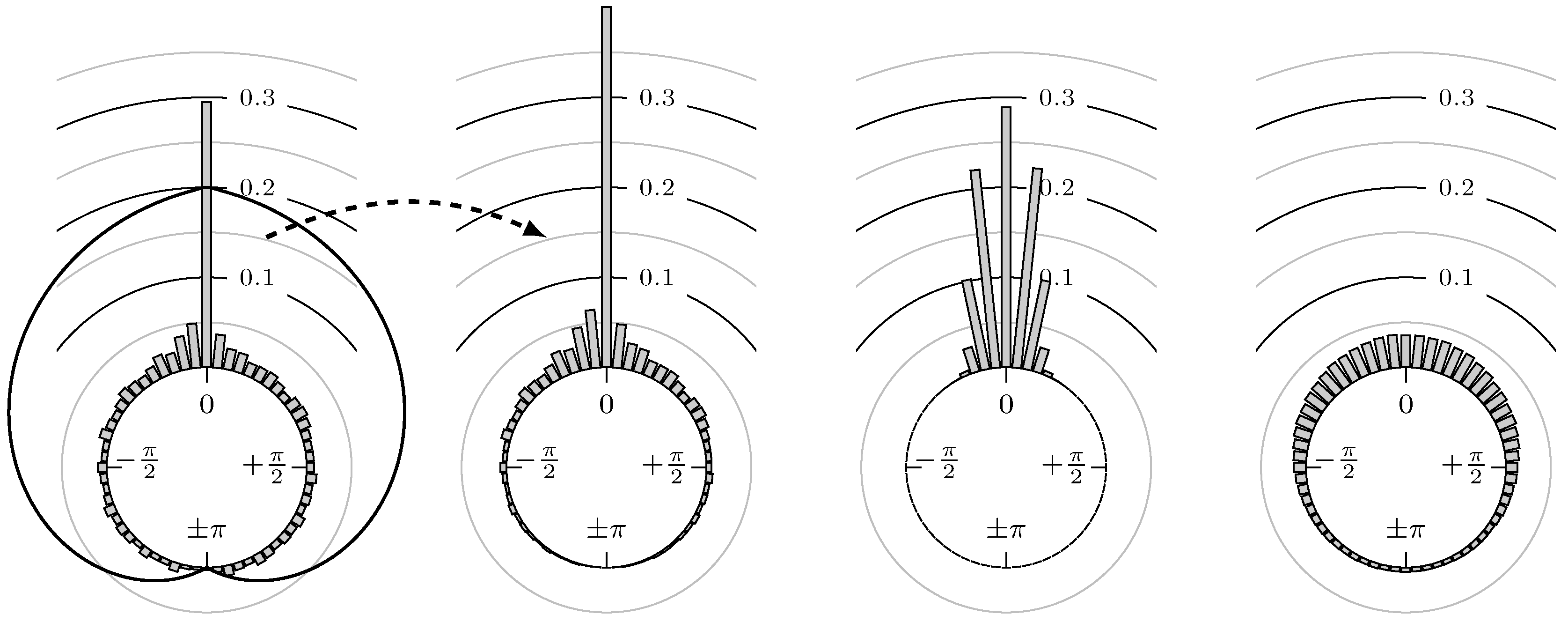
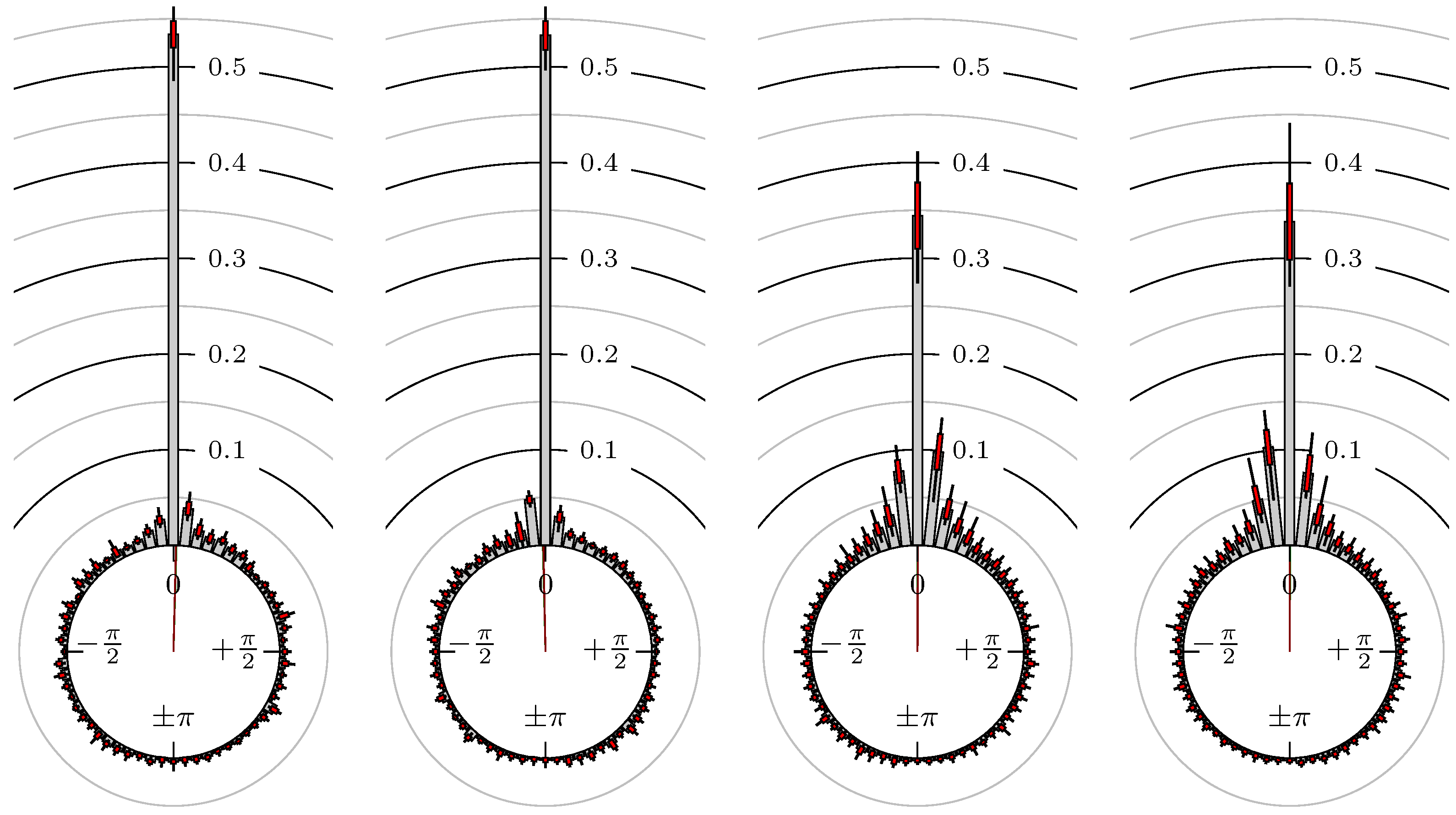
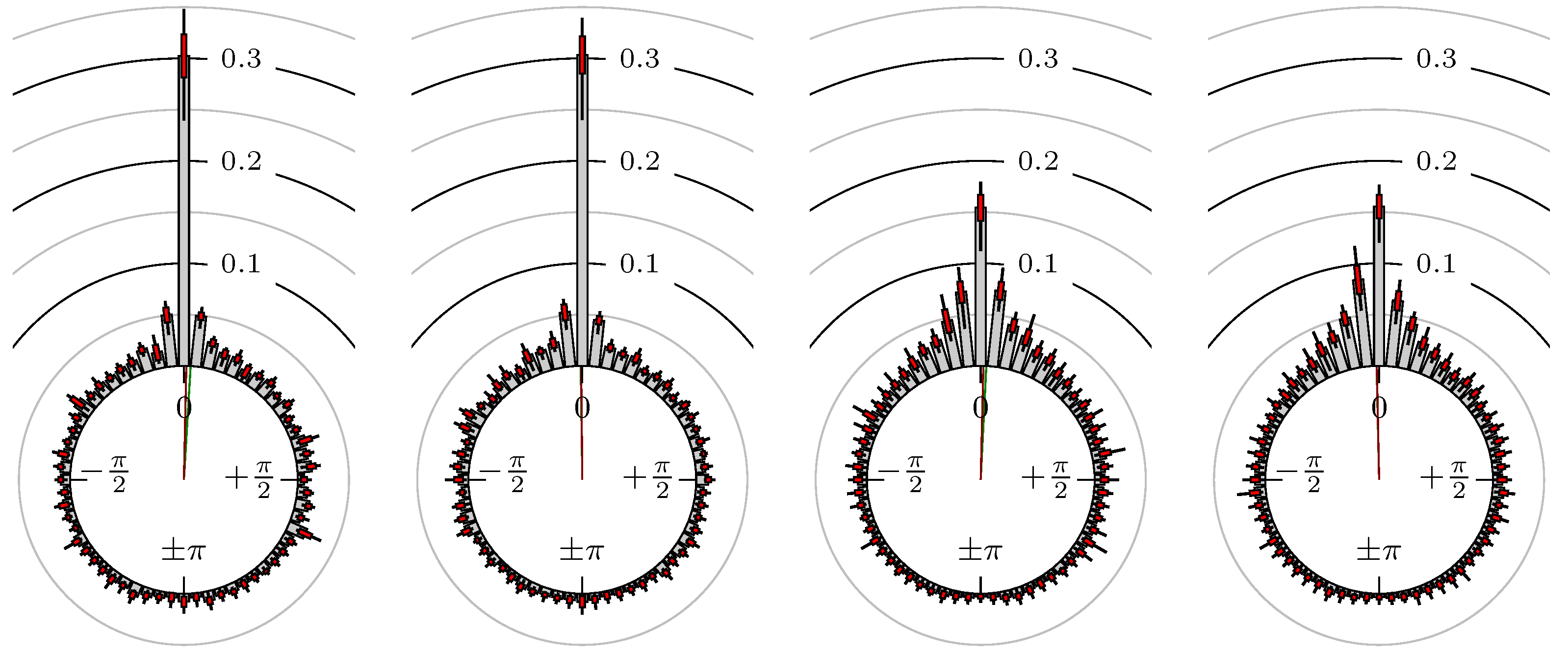
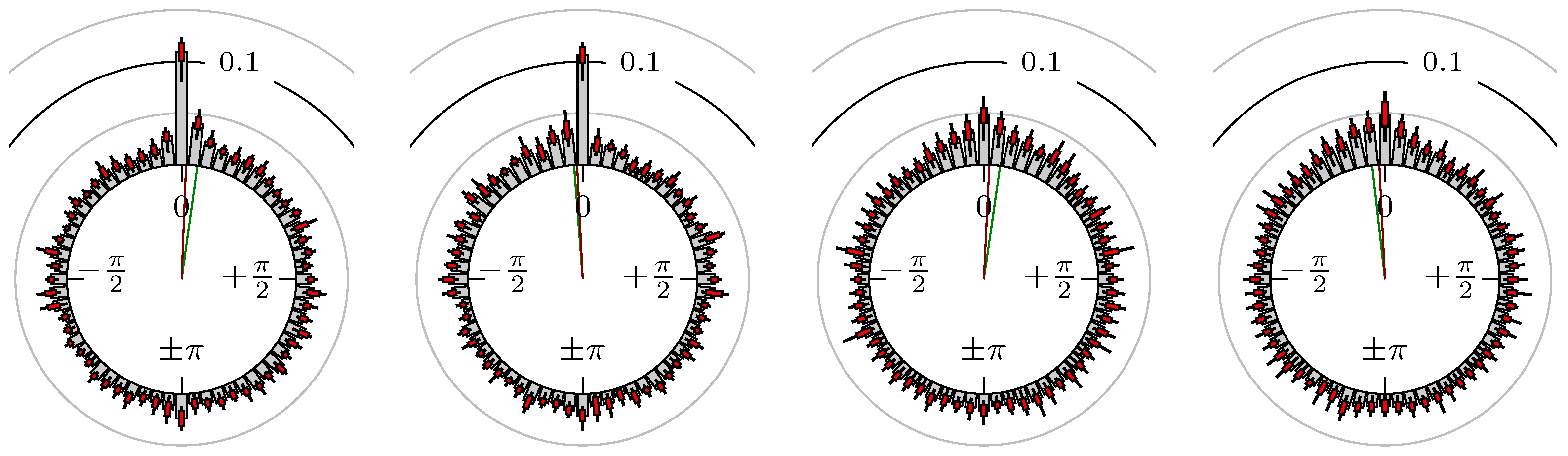
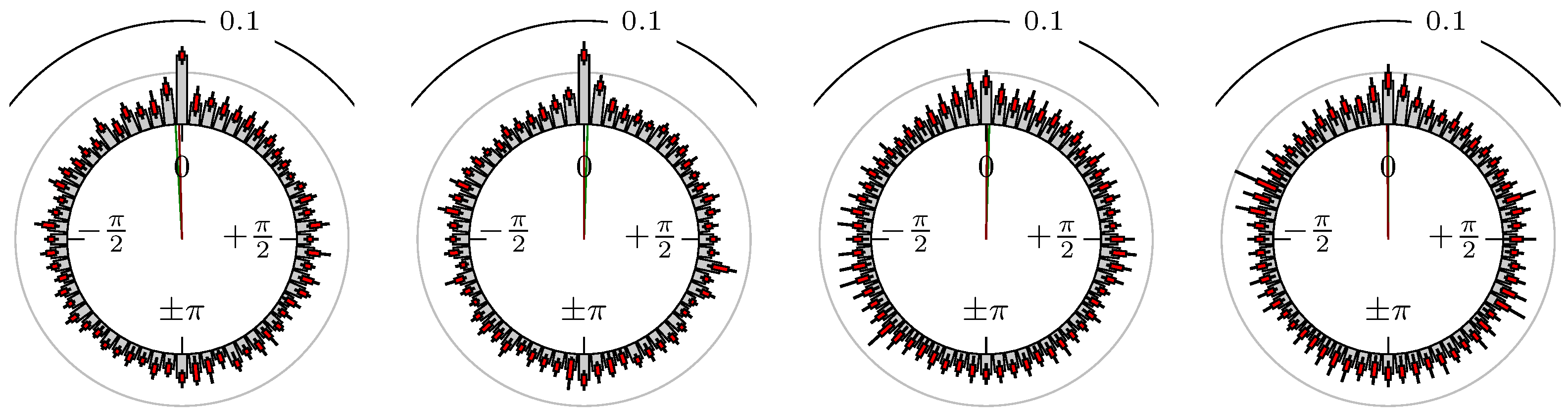
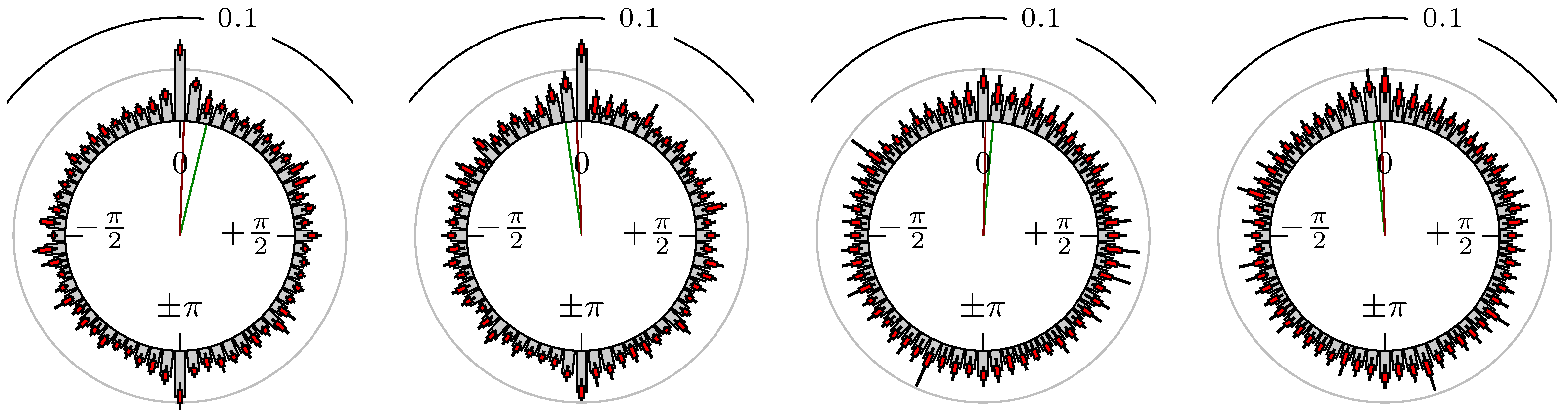
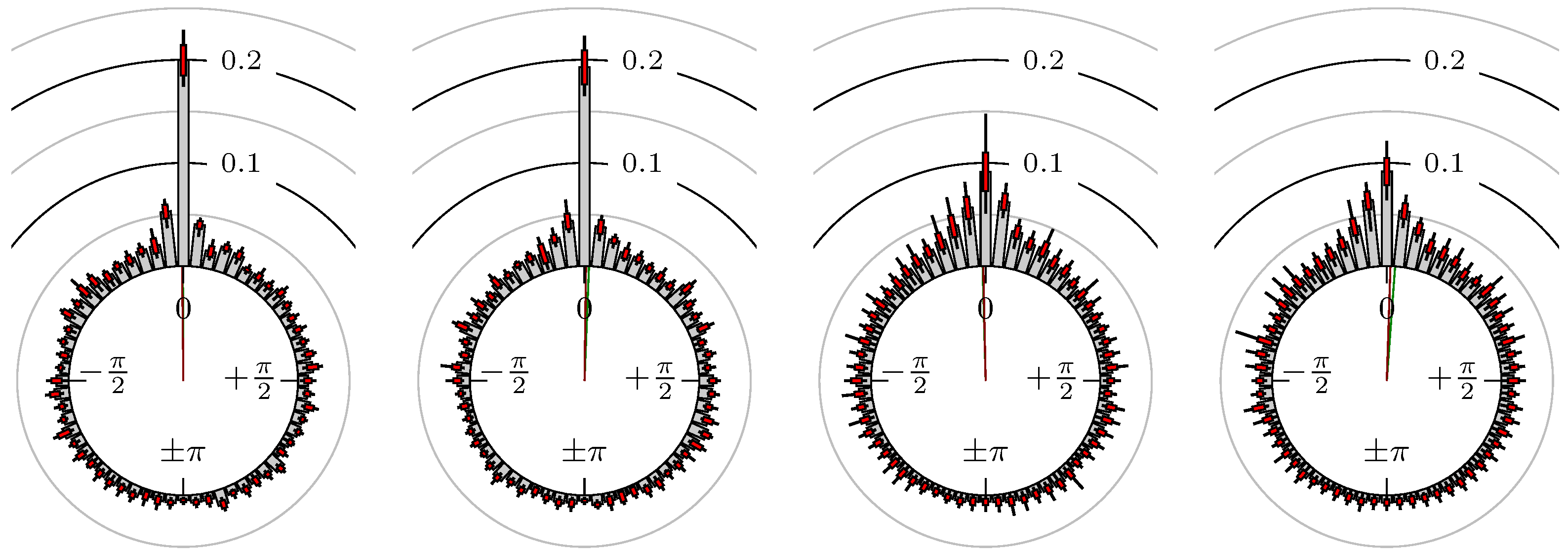
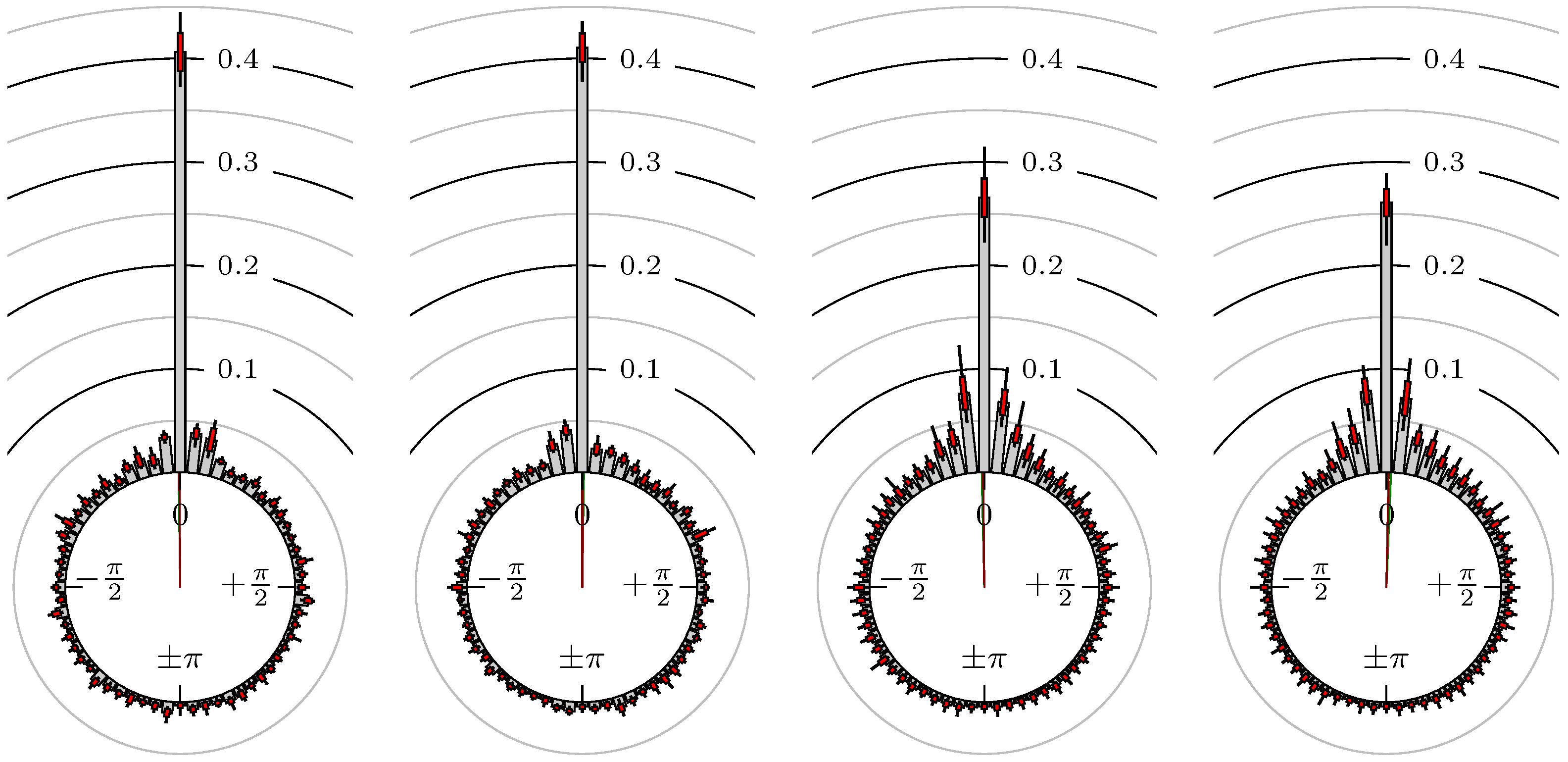
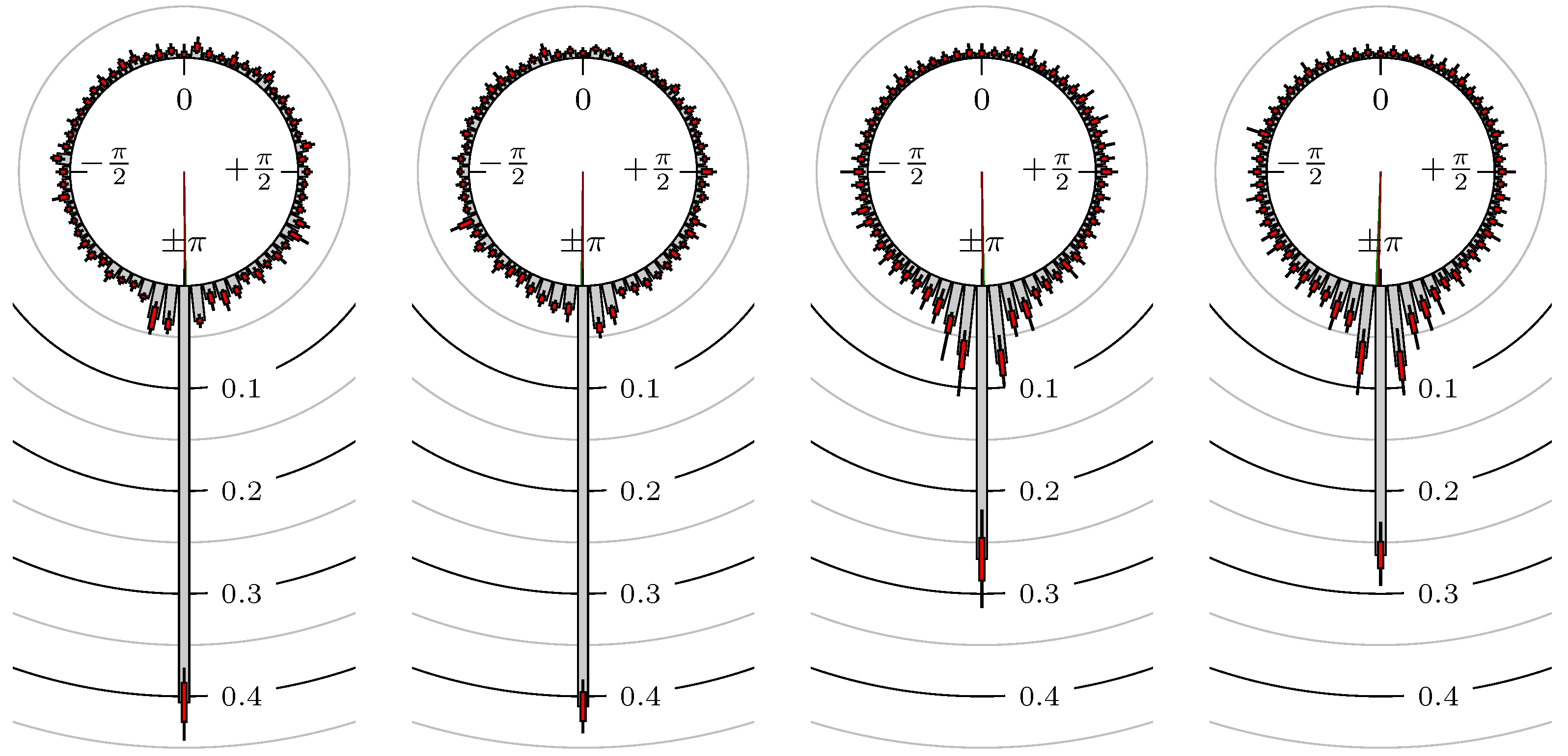
- Define the phase shift of extreme value regarding the extreme values and . Here, the linear relative distance between the corresponding extrema values, measured as an angle, is used. We setwhereFigure 3 shows some examples for the position of a maximum of the secondary market relative to some extreme values of the primary market.
- We end up with the empirical circular distribution depending on the mean wavelength .
3. Directional Statistics
3.1. Basic Quantities
3.2. Statistical Tests
3.3. Lead or Lag
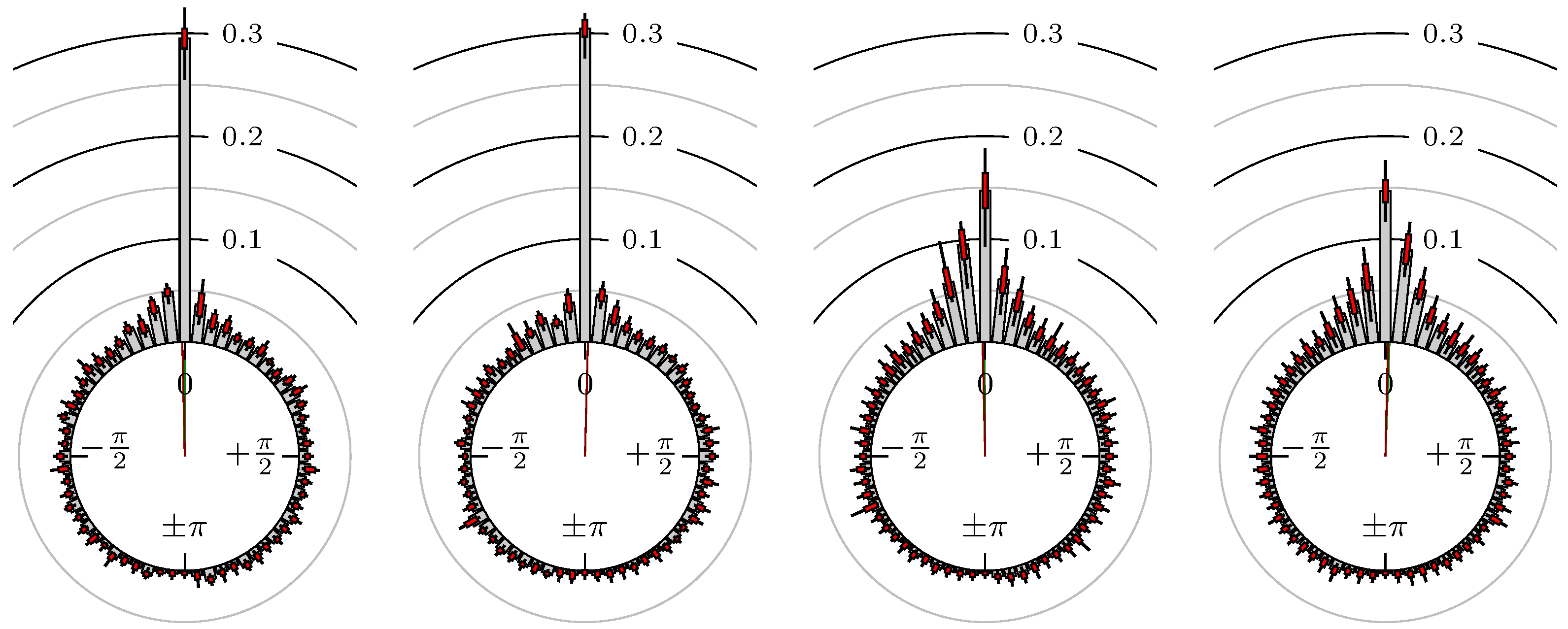
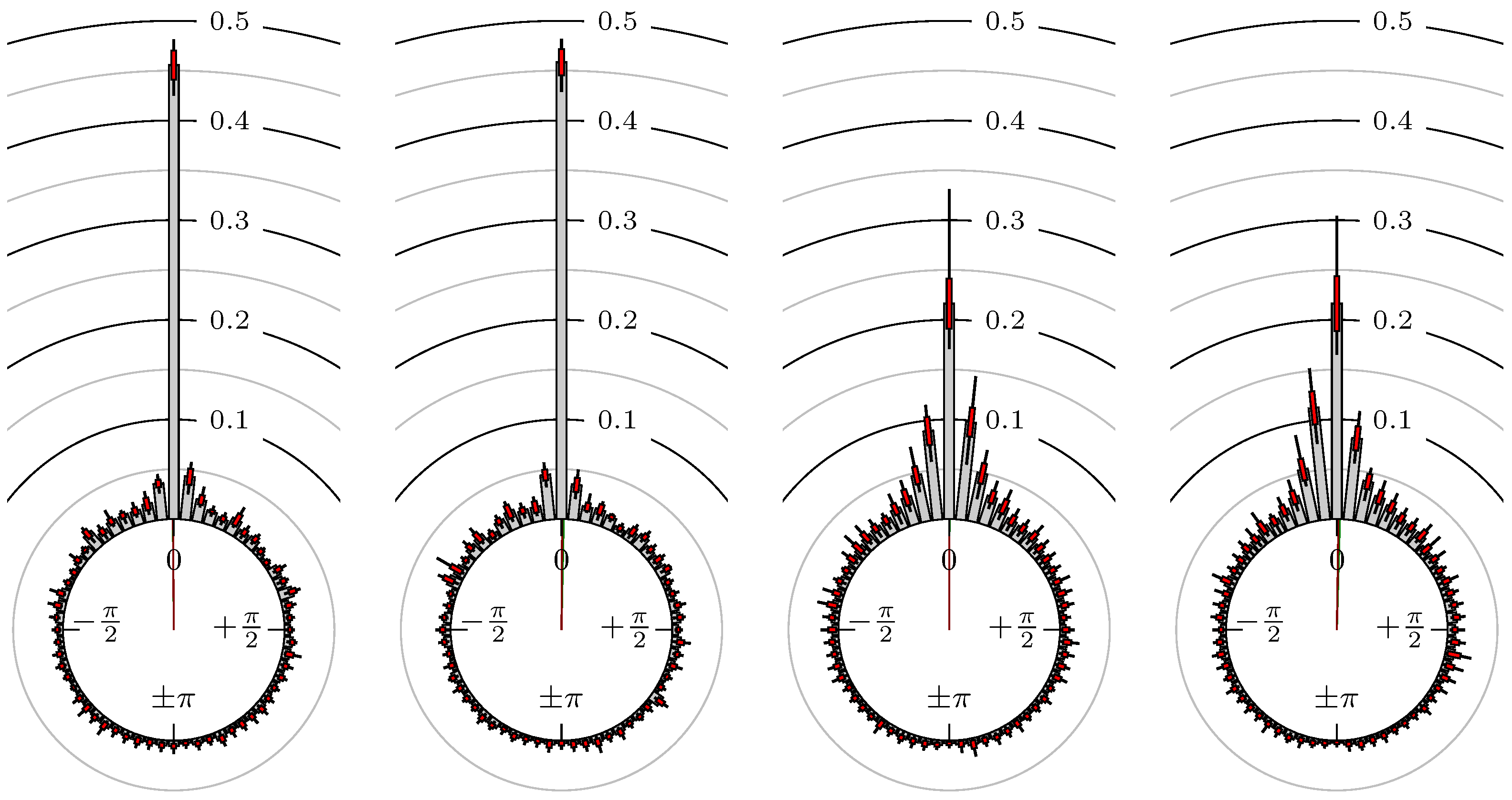
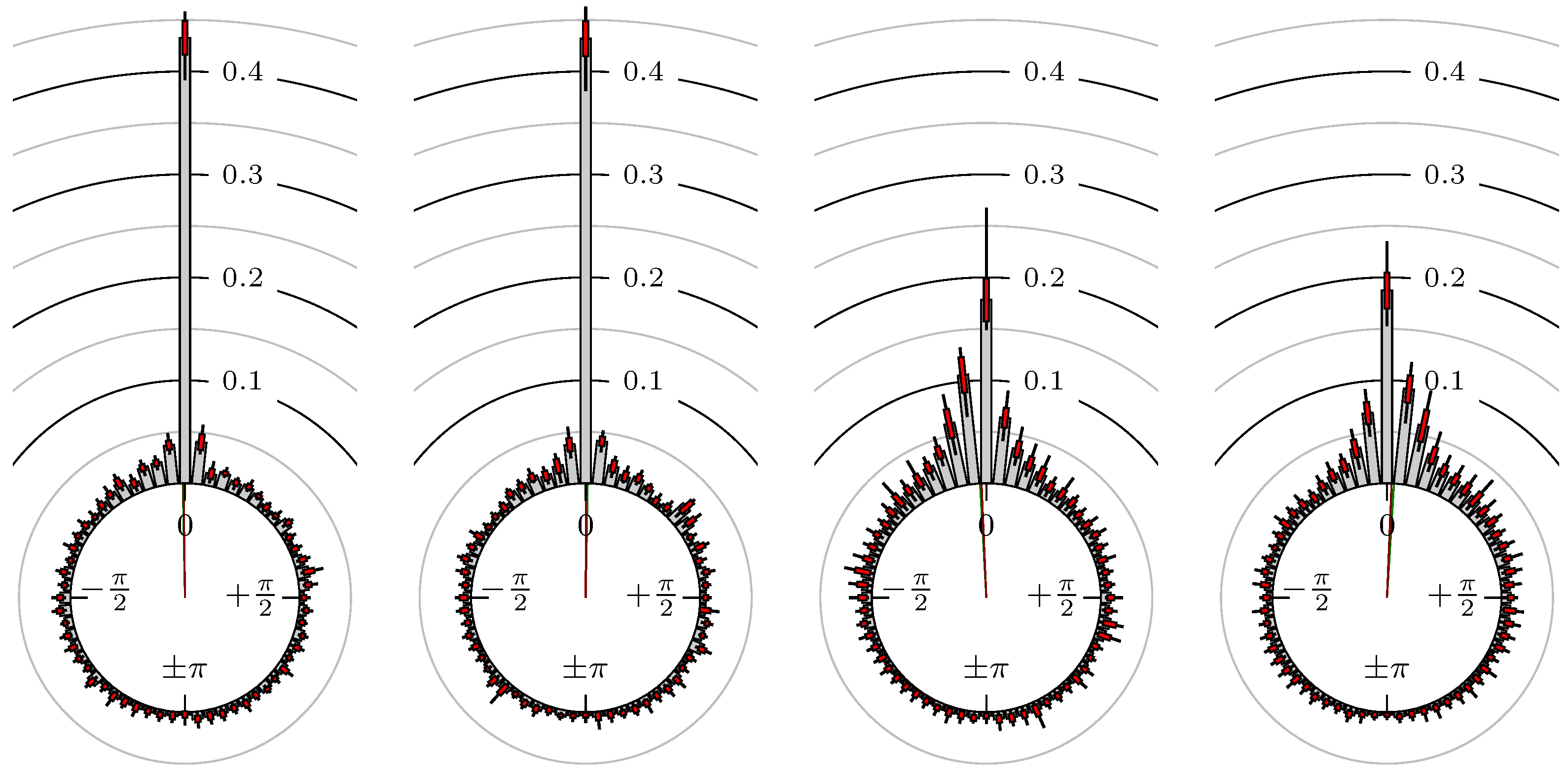
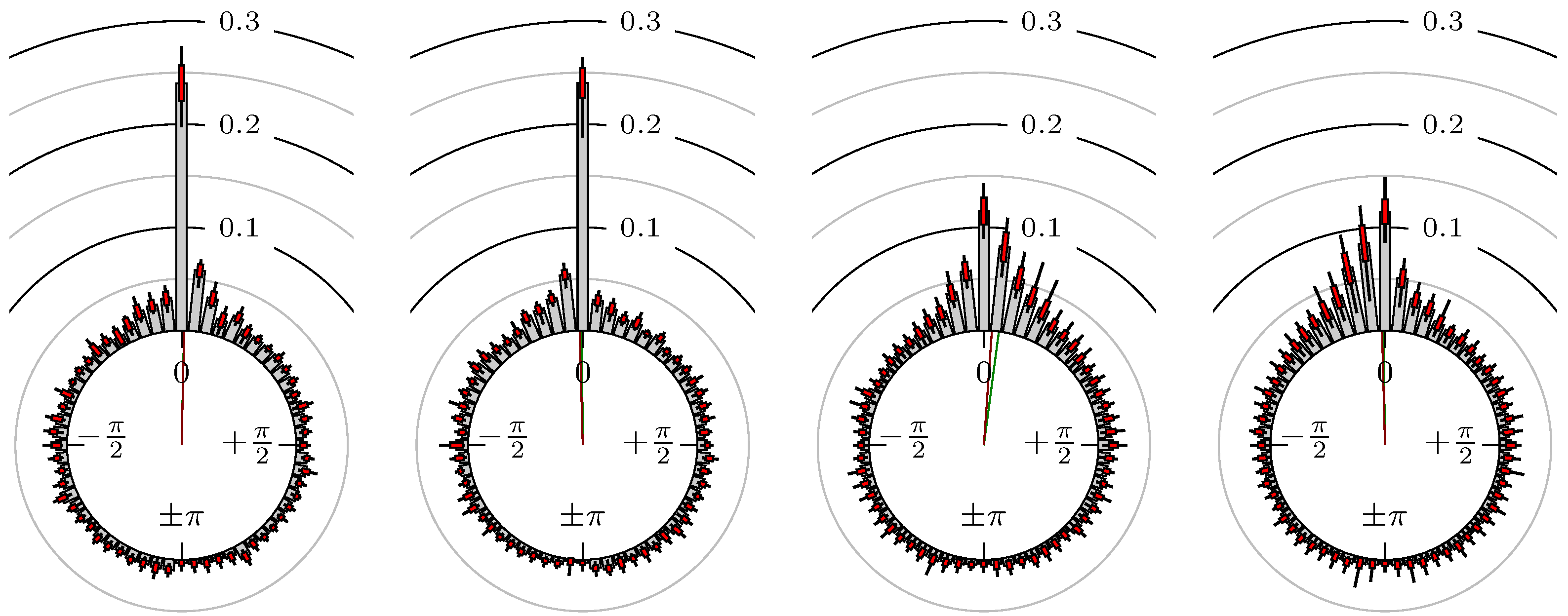
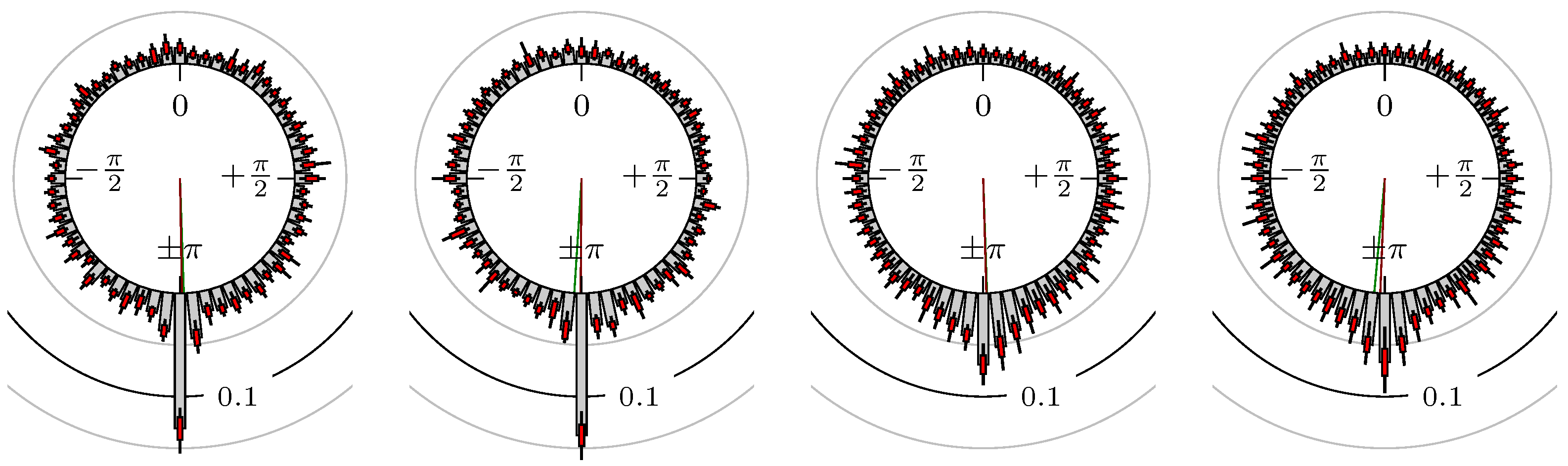
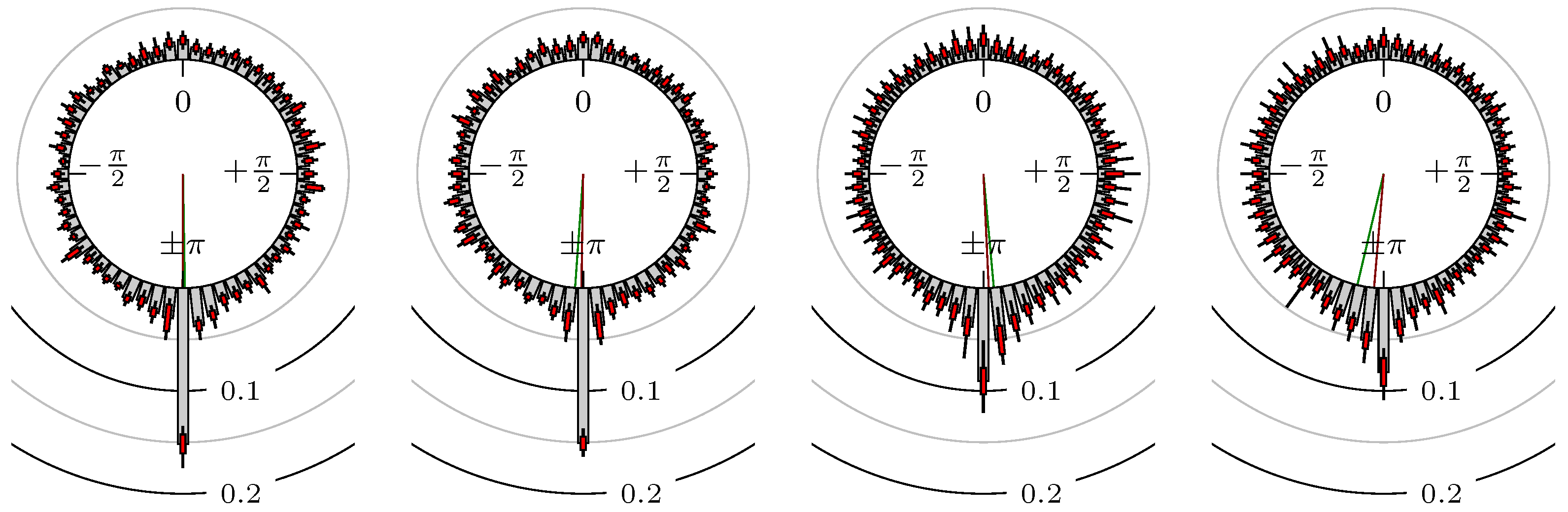
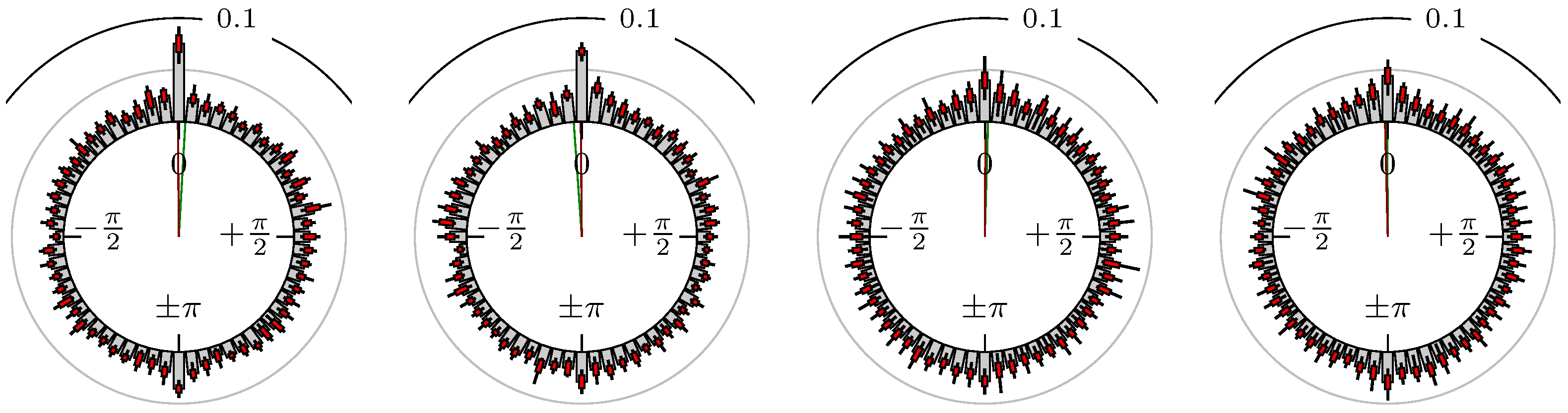
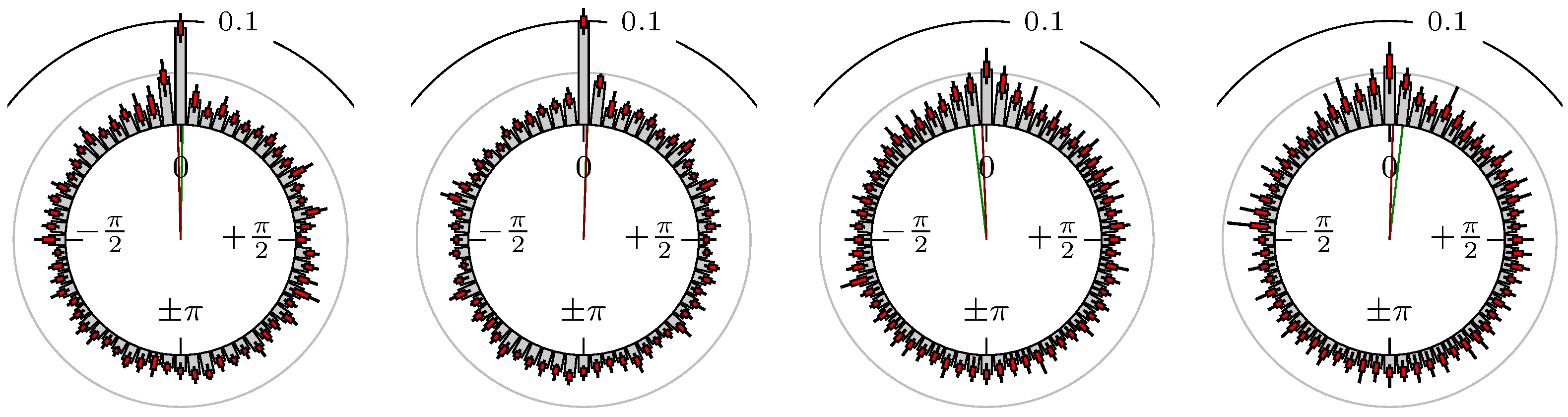
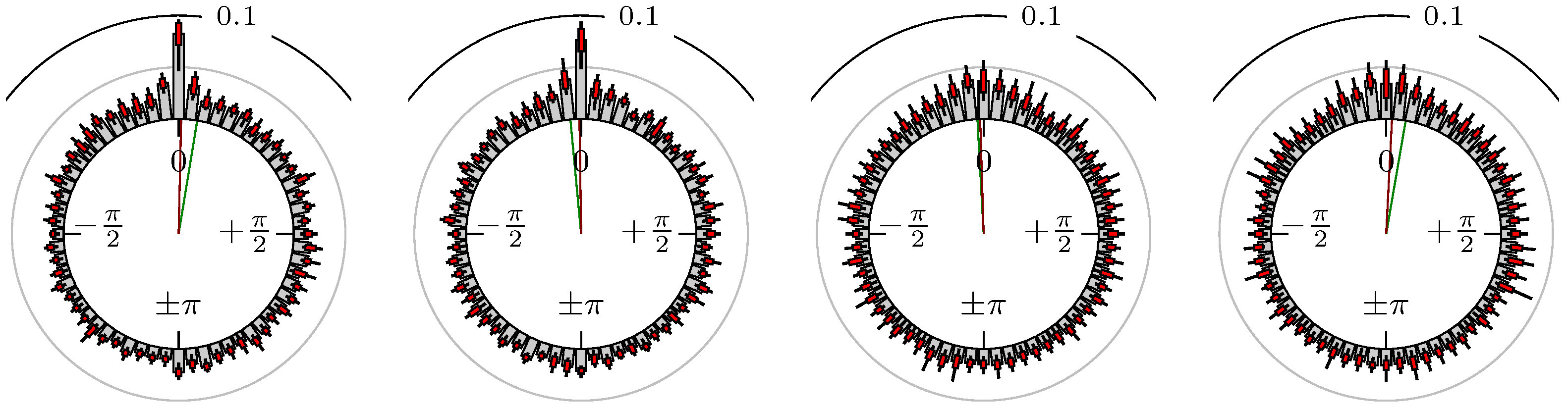
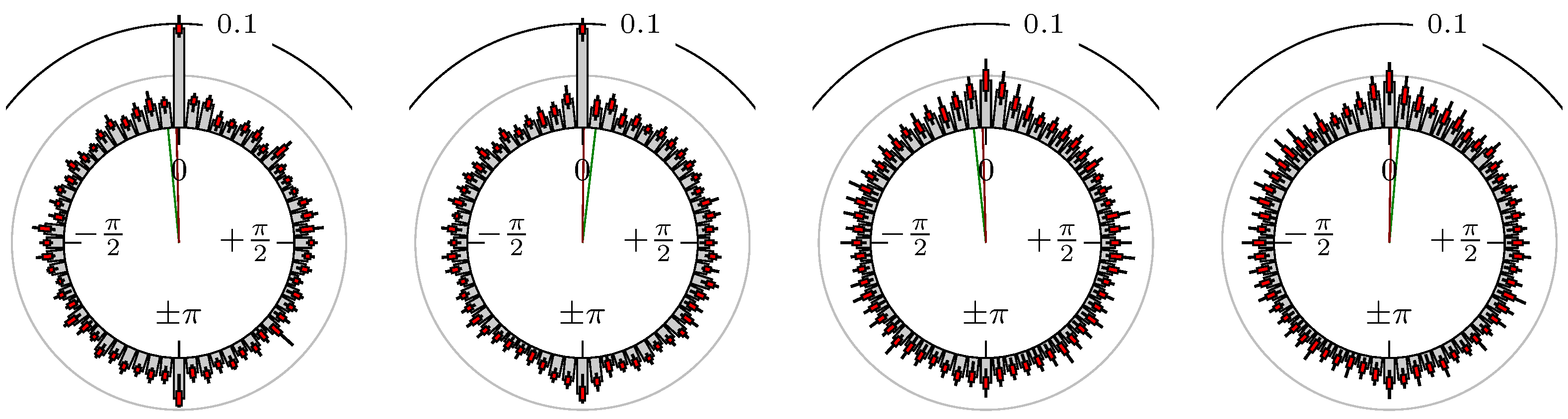
4. Empirical Study
4.1. Settings
4.2. Results
- Time of extrema: A as primary and B as secondary market.
- Time of extrema: B as primary and A as secondary market.
- Time of extrema confirmed (see Remark 4): A as primary and B as secondary market.
- Time of extrema confirmed (see Remark 4): B as primary and A as secondary market.
Time of Extrema
Confirmation Time of Extrema
All Together
5. Conclusions
Author Contributions
Conflicts of Interest
References
- S. Dajčman. “Interdependence Between Some Major European Stock Markets–A Wavelet Lead/Lag Analysis.” Prague Econ. Pap. 22 (2013): 28–49. [Google Scholar] [CrossRef]
- F. In, and S. Kim. “The Hedge Ratio and the Empirical Relationship between the Stock and Futures Markets: A New Approach Using Wavelet Analysis.” J. Bus. 79 (2006): 799–820. [Google Scholar] [CrossRef]
- S. Kim, and F. In. “The relationship between stock returns and inflation: New evidence from wavelet analysis.” J. Empir. Financ. 12 (2005): 435–444. [Google Scholar] [CrossRef]
- J.B. Ramsey, and C. Lampart. “The Decomposition of Economic Relationships by Time Scale Using Wavelets: Expenditure and Income.” Stud. Nonlinear Dyn. Econ. 3 (1998): 23–42. [Google Scholar] [CrossRef]
- J.B. Ramsey, and C. Lampart. “Decomposition of Economic Relationships by Timescale using Wavelets.” Macroecon. Dyn. 2 (1998): 49–71. [Google Scholar]
- R. Gençay, F. Selçuk, and B. Whitcher. An Introduction to Wavelets and Other Filtering Methods in Finance and Economics. New York, NY, USA: Academic Press, 2001. [Google Scholar]
- K. Chan. “Imperfect Information and Cross-Autocorrelation Among Stock Prices.” J. Financ. 48 (1993): 1211–1230. [Google Scholar] [CrossRef]
- F. de Jong, and M.W.M. Donders. “Intraday Lead-Lag Relationships Between the Futures-, Options and Stock Market.” Rev. Financ. 1 (1998): 337–359. [Google Scholar] [CrossRef]
- F. de Jong, and T. Nijman. “High frequency analysis of lead–lag relationships between financial markets.” J. Empir. Financ. 4 (1997): 259–277. [Google Scholar] [CrossRef]
- B. Égert, and E. Kočenda. “Time-varying synchronization of European stock markets.” Empir. Econ. 40 (2011): 393–407. [Google Scholar] [CrossRef]
- R. Garcia, and G. Tsafack. “Dependence structure and extreme comovements in international equity and bond markets.” J. Bank. Financ. 35 (2011): 1954–1970. [Google Scholar] [CrossRef]
- T. Iwaisako. “Stock Index Autocorrelation and Cross-autocorrelations of Size-sorted Portfolios in the Japanese Market.” Hitotsubashi J. Econ. 48 (2007): 95–112. [Google Scholar]
- H.R. Stoll, and R.E. Whaley. “The Dynamics of Stock Index and Stock Index Futures Returns.” J. Financ. Quant. Anal. 25 (1990): 441–468. [Google Scholar] [CrossRef]
- D.Y. Kenett, T. Preis, G. Gur-Gershgoren, and E. Ben-Jacob. “Quantifying meta-correlations in financial markets.” EPL (Europhys. Lett.) 99 (2012): 38001. [Google Scholar] [CrossRef]
- B. Podobnik, and H.E. Stanley. “Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Nonstationary Time Series.” Phys. Rev. Lett. 100 (2008): 084102. [Google Scholar] [CrossRef] [PubMed]
- P. Fiedor. “Information-theoretic approach to lead–lag effect on financial markets.” Eur. Phys. J. B 87 (2014): 168. [Google Scholar] [CrossRef]
- T. Aste, W. Shaw, and T. Di Matteo. “Correlation structure and dynamics in volatile markets.” New J. Phys. 12 (2010): 085009. [Google Scholar] [CrossRef]
- T. Didier, I. Love, and M.D.M. Pería. “What explains comovement in stock market returns during the 2007–2008 crisis? ” Int. J. Financ. & Econ. 17 (2012): 182–202. [Google Scholar]
- K.J. Forbes, and R. Rigobon. “No Contagion, Only Interdependence: Measuring Stock Market Comovements.” J. Financ. 57 (2002): 2223–2261. [Google Scholar] [CrossRef]
- J. Bollen, H. Mao, and X. Zeng. “Twitter mood predicts the stock market.” J. Comput. Sci. 2 (2011): 1–8. [Google Scholar] [CrossRef]
- H. Mao, S. Counts, and J. Bollen. “Predicting Financial Markets: Comparing Survey, News, Twitter and Search Engine Data.” Available online: http://arxiv.org/abs/1112.1051 (accessed on 5 December 2011).
- J.J. Murphy. Intermarket Analysis: Profiting from Global Market Relationships. Hoboken, NJ, USA: John Wiley & Sons, 2004. [Google Scholar]
- M.A. Ruggiero. Cybernetic Trading Strategies. Hoboken, NJ, USA: John Wiley & Sons, 1997. [Google Scholar]
- S. Maier-Paape. “Automatic One Two Three.” Quant. Financ. 15 (2015): 247–260. [Google Scholar] [CrossRef]
- G. Appel. Technical Analysis: Power Tools for Active Investors. Upper Saddle River, NJ, USA: Financial Times Prentice Hall, 2005. [Google Scholar]
- N.I. Fisher. Statistical Analysis of Circular Data. Cambridge, UK: Cambridge University Press, 1996. [Google Scholar]
- K.V. Mardia, and P.E. Jupp. Directional Statistics. Wiley Series in Probability and Statistics; Hoboken, NJ, USA: Wiley, 1999. [Google Scholar]
- J.H. Zar. Biostatistical Analysis, 5th ed. Upper Saddle River, NJ, USA: Pearson, 2010. [Google Scholar]
- P. Berens. “CircStat: A MATLAB Toolbox for Circular Statistics.” J. Stat. Softw. 31 (2009): 1–21. [Google Scholar] [CrossRef]
- A.W. Lo. “The Adaptive Markets Hypothesis.” J. Portf. Manag. 30 (2004): 15–29. [Google Scholar] [CrossRef]

| Stock Exchange | Financial Instrument | Short Name | Initial Date |
|---|---|---|---|
| CME eMini | S&P 500 E-mini Futures | S&P 500 | 1 January 2007 |
| CME eMini | NASDAQ 100 E-mini Futures | NASDAQ 100 | 1 January 2007 |
| ICE US | Russell 2000 Mini Futures | Russell 2000 | 8 February 2008 |
| Eurex | DAX Futures | DAX | 1 January 2007 |
| Eurex | EuroSTOXX 50 Futures | EuroSTOXX 50 | 1 January 2007 |
| Eurex | BUND Futures | BUND | 1 January 2007 |
| CBOT | 30Y U.S. Treasury Bond Futures | 30y T-Bonds | 1 January 2007 |
| COMEX | Gold Futures | Gold | 1 January 2007 |
| COMEX | Silver Futures | Silver | 1 January 2007 |
| NYMEX | Crude Oil (WTI) Future | Oil (WTI) | 1 January 2007 |
| NYMEX | Natural Gas Futures | Natural Gas | 1 January 2007 |
| Forex | EUR-USD | EUR-USD | 1 January 2007 |
| Forex | JPY-USD | JPY-USD | 1 January 2007 |
| Forex | GBP-USD | GBP-USD | 1 January 2007 |
| Forex | CHF-USD | CHF-USD | 1 January 2007 |
| prime | sec | / | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S&P 500 | DAX | 0.0044 | 0.0023 | 0.526 | −0.061 | 0.409 | 0.000 | 0 | 68999 | |||
| DAX | S&P 500 | 0.0043 | 0.0023 | 0.528 | 0.022 | 0.425 | 0.324 | 1 | 68582 | |||
| S&P 500 | NASDAQ 100 | 0.0028 | 0.0017 | 0.389 | −0.002 | 0.581 | 0.813 | 1 | 70686 | |||
| NASDAQ 100 | S&P 500 | 0.0029 | 0.0017 | 0.382 | −0.034 | 0.573 | 0.916 | 1 | 68408 | |||
| S&P 500 | Russell 2000 | 0.0035 | 0.0020 | 0.442 | 0.007 | 0.528 | 1.000 | 1 | 62104 | |||
| Russell 2000 | S&P 500 | 0.0035 | 0.0020 | 0.429 | −0.029 | 0.529 | 1.000 | 1 | 59627 | |||
| DAX | EuroSTOXX 50 | 0.0023 | 0.0014 | 0.329 | 0.005 | 0.650 | 0.003 | 1 | 70865 | |||
| EuroSTOXX 50 | DAX | 0.0023 | 0.0014 | 0.311 | 0.001 | 0.666 | 0.737 | 1 | 66871 | |||
| BUND | 30y T-Bonds | 0.0059 | 0.0028 | 0.599 | 0.021 | 0.365 | 1.000 | 1 | 57067 | |||
| 30y T-Bonds | BUND | 0.0057 | 0.0028 | 0.578 | −0.058 | 0.350 | 1.000 | 0 | 56435 | |||
| S&P 500 | 30y T-Bonds | 0.0095 | 0.0034 | 0.750 | 0.007 | 0.249 | 0.000 | 1 | 66307 | |||
| 30y T-Bonds | S&P 500 | 0.0096 | 0.0034 | 0.754 | −0.057 | 0.253 | 0.000 | 1 | 66842 | |||
| DAX | BUND | 0.0095 | 0.0033 | 0.741 | 0.032 | 0.313 | 0.000 | 0 | 56556 | |||
| BUND | DAX | 0.0106 | 0.0035 | 0.765 | −0.054 | 0.299 | 0.000 | 1 | 56563 | |||
| Gold | Silver | 0.0046 | 0.0023 | 0.555 | −0.059 | 0.403 | 1.000 | 1 | 69975 | |||
| Silver | Gold | 0.0045 | 0.0023 | 0.545 | −0.002 | 0.410 | 1.000 | 1 | 69799 | |||
| Gold | Oil (WTI) | 0.0143 | 0.0037 | 0.835 | −0.053 | 0.214 | 0.000 | 1 | 70429 | |||
| Oil (WTI) | Gold | 0.0136 | 0.0038 | 0.825 | −0.023 | 0.205 | 0.000 | 1 | 69620 | |||
| Oil (WTI) | Natural Gas | 0.0250 | 0.0043 | 0.904 | −0.005 | 0.176 | 0.000 | 1 | 70594 | |||
| Natural Gas | Oil (WTI) | 0.0254 | 0.0043 | 0.904 | −0.021 | 0.178 | 0.001 | 0 | 68257 | |||
| Gold | S&P 500 | 0.0347 | 0.0042 | 0.931 | −0.085 | 0.195 | 0.000 | 1 | 70164 | |||
| S&P 500 | Gold | 0.0314 | 0.0043 | 0.923 | 0.015 | 0.196 | 0.259 | 1 | 69463 | |||
| Gold | DAX | 0.0355 | 0.0043 | 0.932 | −0.046 | 0.195 | 0.000 | 0 | 69162 | |||
| DAX | Gold | 0.0313 | 0.0043 | 0.924 | 0.030 | 0.202 | 0.000 | 1 | 69644 | |||
| Oil (WTI) | DAX | 0.0142 | 0.0038 | 0.831 | −0.060 | 0.215 | 0.001 | 0 | 68837 | |||
| DAX | Oil (WTI) | 0.0142 | 0.0037 | 0.834 | 0.035 | 0.232 | 0.763 | 0 | 69082 | |||
| Gold | EUR-USD | 0.0141 | 0.0039 | 0.823 | −0.099 | 0.177 | 0.000 | 1 | 66762 | |||
| EUR-USD | Gold | 0.0137 | 0.0038 | 0.823 | 0.038 | 0.217 | 0.000 | 1 | 66701 | |||
| Oil (WTI) | EUR-USD | 0.0148 | 0.0041 | 0.831 | −0.090 | 0.162 | 0.000 | 1 | 66722 | |||
| EUR-USD | Oil (WTI) | 0.0156 | 0.0041 | 0.841 | 0.049 | 0.189 | 0.000 | 1 | 65848 | |||
| EUR-USD | JPY-USD | 0.0285 | 0.0042 | 0.914 | 0.027 | 0.209 | 0.236 | 1 | 66559 | |||
| JPY-USD | EUR-USD | 0.0283 | 0.0043 | 0.912 | −0.053 | 0.185 | 0.000 | 1 | 66373 | |||
| EUR-USD | GBP-USD | 0.0061 | 0.0029 | 0.626 | −0.021 | 0.319 | 0.993 | 0 | 64905 | |||
| GBP-USD | EUR-USD | 0.0064 | 0.0029 | 0.640 | −0.031 | 0.313 | 0.998 | 1 | 65248 | |||
| EUR-USD | CHF-USD | 0.0036 | 0.0020 | 0.466 | 0.006 | 0.508 | 1.000 | 1 | 67828 | |||
| CHF-USD | EUR-USD | 0.0035 | 0.0020 | 0.447 | −0.031 | 0.511 | 1.000 | 1 | 65479 |
| Prime | sec | / | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S&P 500 | DAX | 0.0046 | 0.0025 | 0.532 | −0.048 | 0.360 | 0.000 | 0 | 69063 | |||
| DAX | S&P 500 | 0.0046 | 0.0025 | 0.536 | −0.007 | 0.376 | 0.000 | 1 | 68421 | |||
| S&P 500 | NASDAQ 100 | 0.0030 | 0.0019 | 0.388 | 0.000 | 0.532 | 0.000 | 0 | 70605 | |||
| NASDAQ 100 | S&P 500 | 0.0029 | 0.0018 | 0.366 | −0.024 | 0.538 | 0.270 | 1 | 68514 | |||
| S&P 500 | Russell 2000 | 0.0038 | 0.0022 | 0.455 | 0.001 | 0.471 | 0.089 | 1 | 62015 | |||
| Russell 2000 | S&P 500 | 0.0039 | 0.0023 | 0.442 | −0.018 | 0.444 | 0.001 | 1 | 59406 | |||
| DAX | EuroSTOXX 50 | 0.0023 | 0.0015 | 0.322 | 0.015 | 0.642 | 0.000 | 0 | 70889 | |||
| EuroSTOXX 50 | DAX | 0.0023 | 0.0015 | 0.294 | −0.019 | 0.654 | 0.001 | 0 | 66896 | |||
| BUND | 30y T-Bonds | 0.0061 | 0.0030 | 0.599 | −0.047 | 0.320 | 0.119 | 1 | 57092 | |||
| 30y T-Bonds | BUND | 0.0059 | 0.0030 | 0.585 | −0.041 | 0.318 | 0.000 | 0 | 56367 | |||
| S&P 500 | 30y T-Bonds | 0.0093 | 0.0035 | 0.740 | −0.018 | 0.230 | 0.000 | 1 | 66303 | |||
| 30y T-Bonds | S&P 500 | 0.0097 | 0.0035 | 0.753 | −0.023 | 0.226 | 0.228 | 1 | 66801 | |||
| DAX | BUND | 0.0109 | 0.0036 | 0.770 | 0.012 | 0.283 | 0.000 | 1 | 56509 | |||
| BUND | DAX | 0.0118 | 0.0037 | 0.782 | −0.090 | 0.252 | 0.979 | 1 | 56632 | |||
| Gold | Silver | 0.0043 | 0.0024 | 0.515 | −0.034 | 0.379 | 0.285 | 1 | 69916 | |||
| Silver | Gold | 0.0043 | 0.0024 | 0.509 | −0.011 | 0.389 | 0.000 | 1 | 69793 | |||
| Gold | Oil (WTI) | 0.0143 | 0.0040 | 0.831 | −0.030 | 0.173 | 0.000 | 1 | 70334 | |||
| Oil (WTI) | Gold | 0.0138 | 0.0040 | 0.823 | 0.006 | 0.178 | 0.132 | 1 | 69636 | |||
| Oil (WTI) | Natural Gas | 0.0254 | 0.0045 | 0.903 | −0.002 | 0.146 | 0.000 | 0 | 70613 | |||
| Natural Gas | Oil (WTI) | 0.0253 | 0.0045 | 0.902 | −0.017 | 0.156 | 0.000 | 0 | 68277 | |||
| Gold | S&P 500 | 0.0379 | 0.0046 | 0.935 | −0.013 | 0.158 | 0.000 | 1 | 70108 | |||
| S&P 500 | Gold | 0.0362 | 0.0046 | 0.932 | 0.004 | 0.165 | 0.000 | 1 | 69458 | |||
| Gold | DAX | 0.0475 | 0.0047 | 0.948 | −0.004 | 0.167 | 0.000 | 0 | 69101 | |||
| DAX | Gold | 0.0505 | 0.0046 | 0.952 | −0.031 | 0.178 | 0.000 | 0 | 69600 | |||
| Oil (WTI) | DAX | 0.0150 | 0.0040 | 0.836 | 0.026 | 0.176 | 0.000 | 1 | 68821 | |||
| DAX | Oil (WTI) | 0.0145 | 0.0039 | 0.834 | −0.043 | 0.199 | 0.000 | 1 | 69034 | |||
| Gold | EUR-USD | 0.0125 | 0.0039 | 0.802 | −0.041 | 0.185 | 0.000 | 1 | 66695 | |||
| EUR-USD | Gold | 0.0118 | 0.0038 | 0.793 | 0.001 | 0.197 | 0.000 | 1 | 66672 | |||
| Oil (WTI) | EUR-USD | 0.0154 | 0.0043 | 0.837 | −0.012 | 0.154 | 0.000 | 1 | 66745 | |||
| EUR-USD | Oil (WTI) | 0.0169 | 0.0043 | 0.850 | −0.035 | 0.150 | 0.343 | 1 | 65812 | |||
| EUR-USD | JPY-USD | 0.0228 | 0.0043 | 0.892 | 0.023 | 0.185 | 0.000 | 1 | 66509 | |||
| JPY-USD | EUR-USD | 0.0227 | 0.0044 | 0.890 | −0.034 | 0.173 | 0.000 | 1 | 66345 | |||
| EUR-USD | GBP-USD | 0.0062 | 0.0030 | 0.622 | −0.009 | 0.288 | 0.009 | 1 | 64963 | |||
| GBP-USD | EUR-USD | 0.0065 | 0.0031 | 0.632 | −0.032 | 0.265 | 0.000 | 1 | 65228 | |||
| EUR-USD | CHF-USD | 0.0035 | 0.0020 | 0.447 | 0.021 | 0.488 | 1.000 | 1 | 67831 | |||
| CHF-USD | EUR-USD | 0.0035 | 0.0020 | 0.429 | −0.035 | 0.491 | 0.990 | 1 | 65457 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier-Paape, S.; Platen, A. Lead–Lag Relationship Using a Stop-and-Reverse-MinMax Process. Risks 2016, 4, 27. https://doi.org/10.3390/risks4030027
Maier-Paape S, Platen A. Lead–Lag Relationship Using a Stop-and-Reverse-MinMax Process. Risks. 2016; 4(3):27. https://doi.org/10.3390/risks4030027
Chicago/Turabian StyleMaier-Paape, Stanislaus, and Andreas Platen. 2016. "Lead–Lag Relationship Using a Stop-and-Reverse-MinMax Process" Risks 4, no. 3: 27. https://doi.org/10.3390/risks4030027
APA StyleMaier-Paape, S., & Platen, A. (2016). Lead–Lag Relationship Using a Stop-and-Reverse-MinMax Process. Risks, 4(3), 27. https://doi.org/10.3390/risks4030027