Community Analysis of Global Financial Markets
Abstract
:1. Introduction
2. Results
2.1. Pearson Correlation Analysis
2.2. Summary Statistics
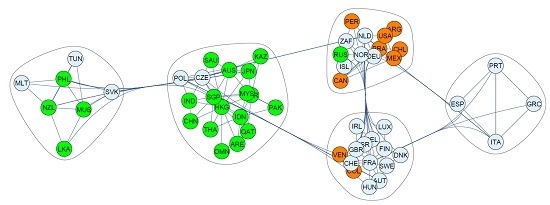
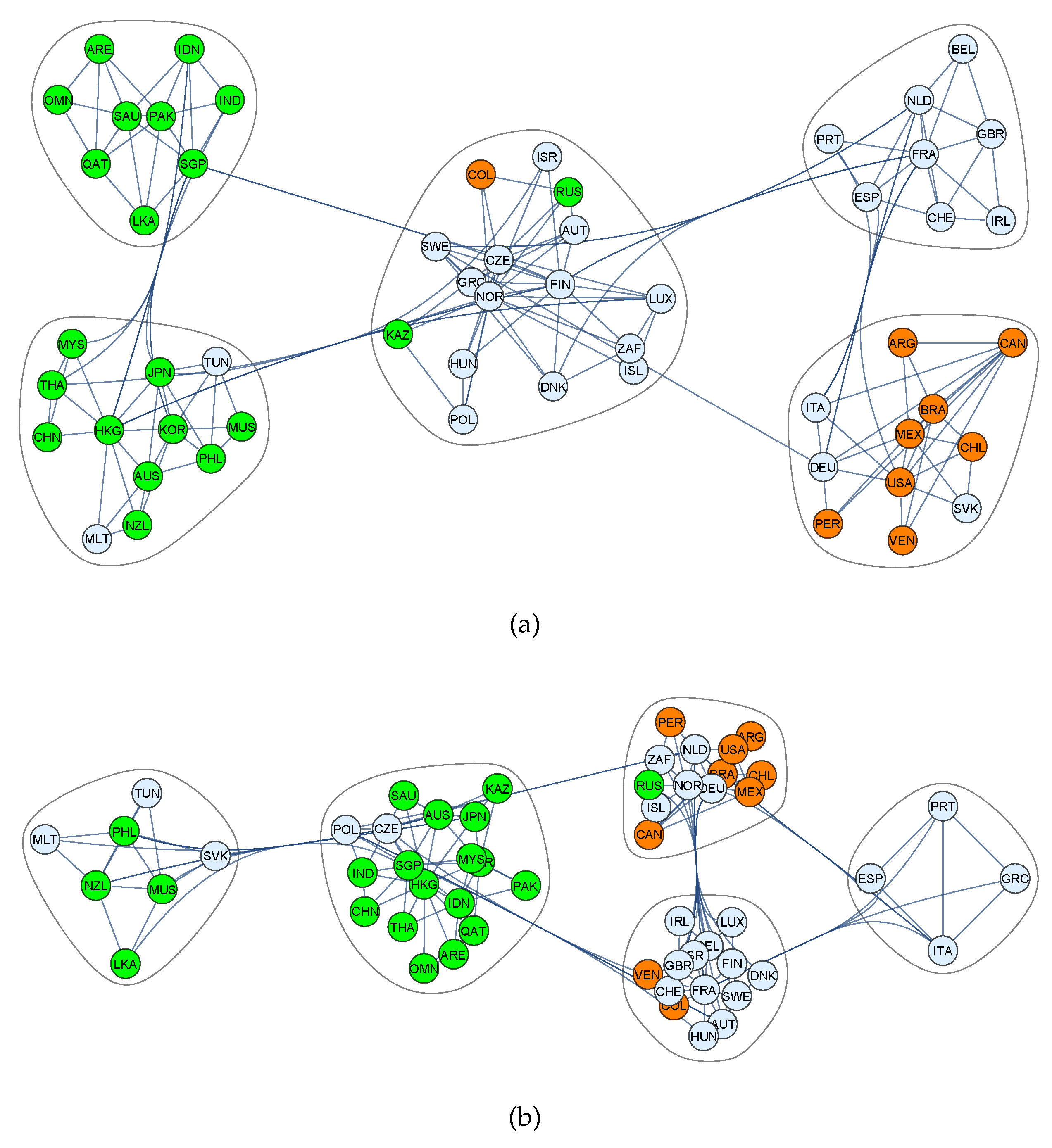
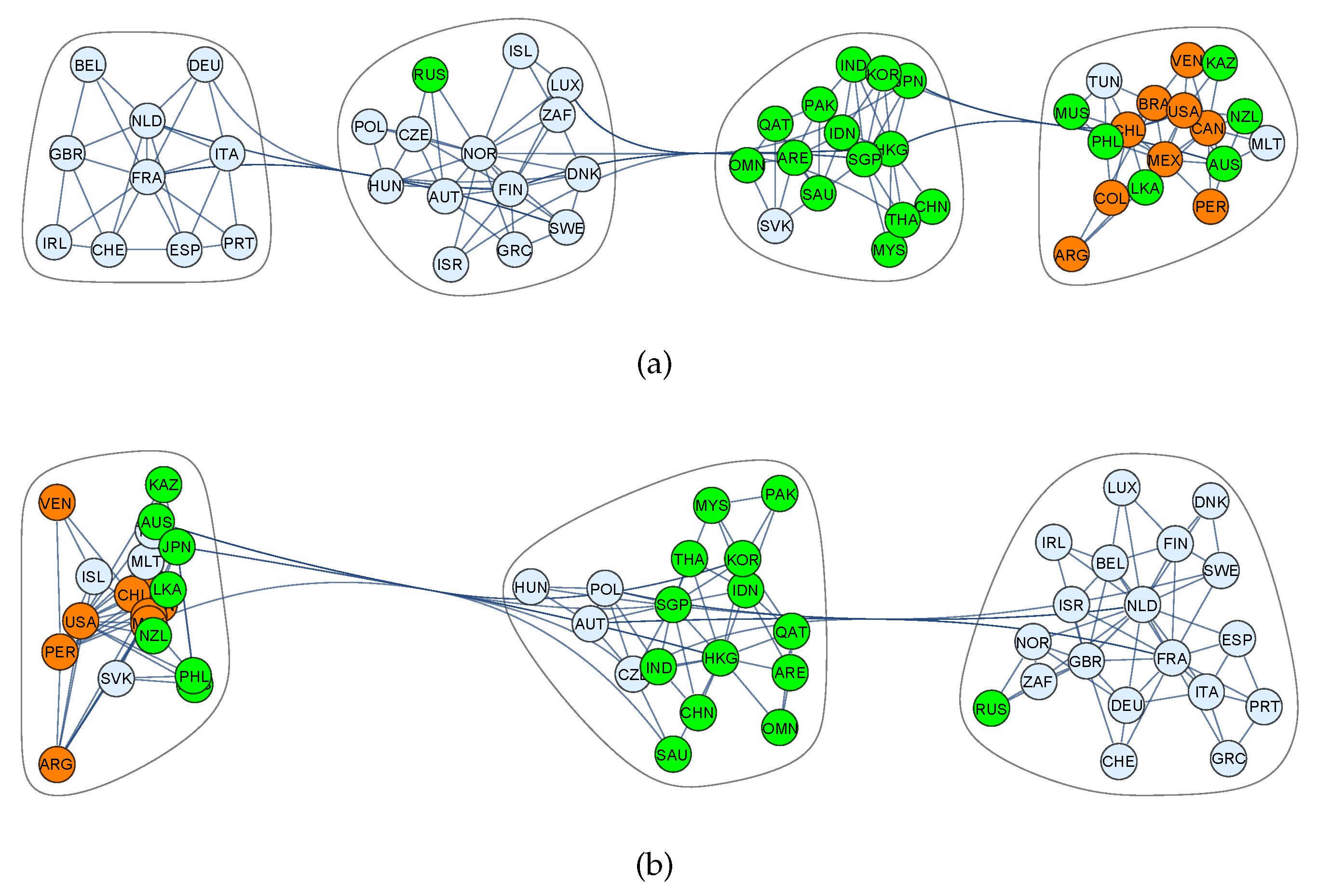
2.3. Community Formation and Cluster Analysis
2.3.1. Stock Markets
Synchronous Correlations
Lagged Correlations
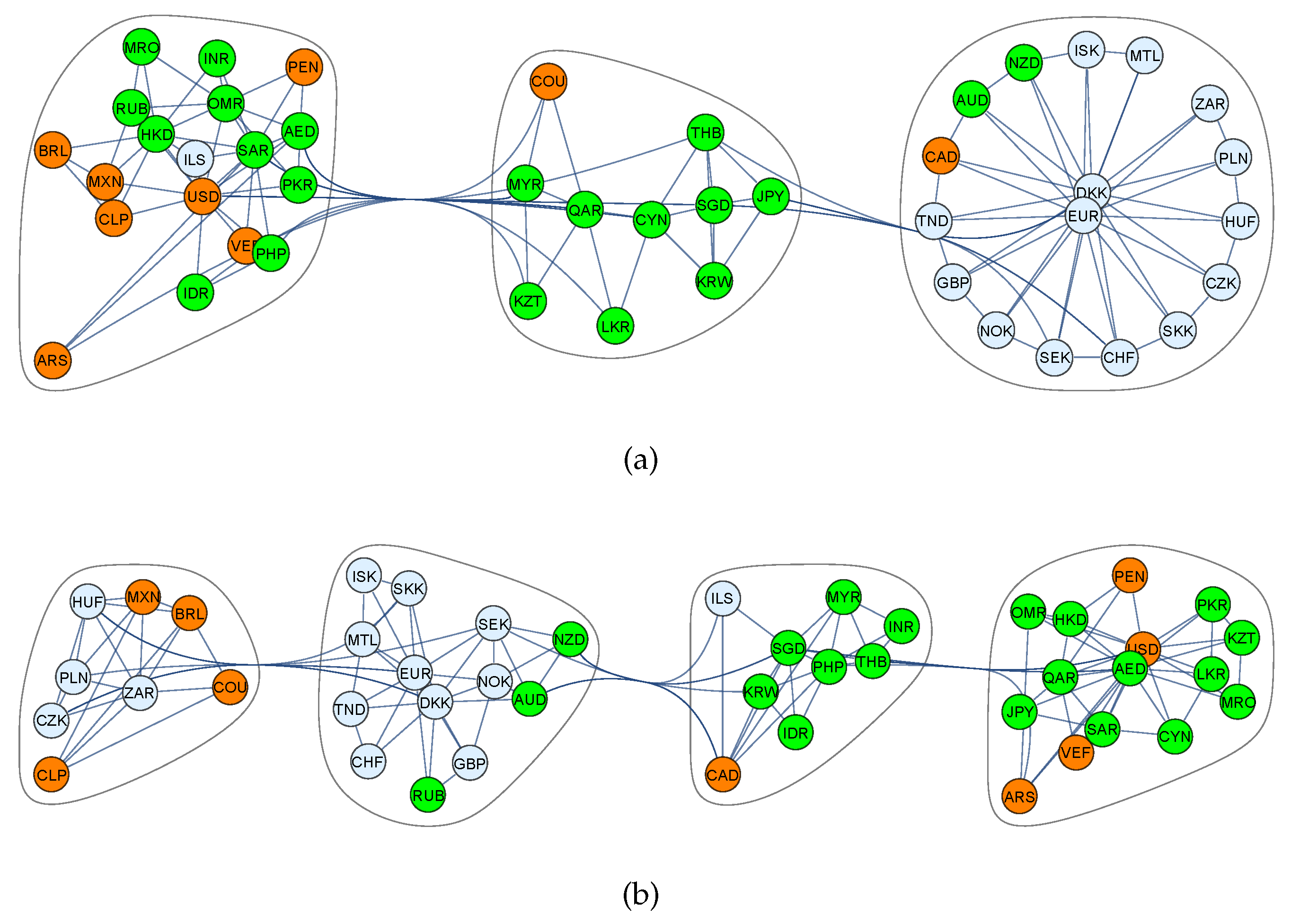
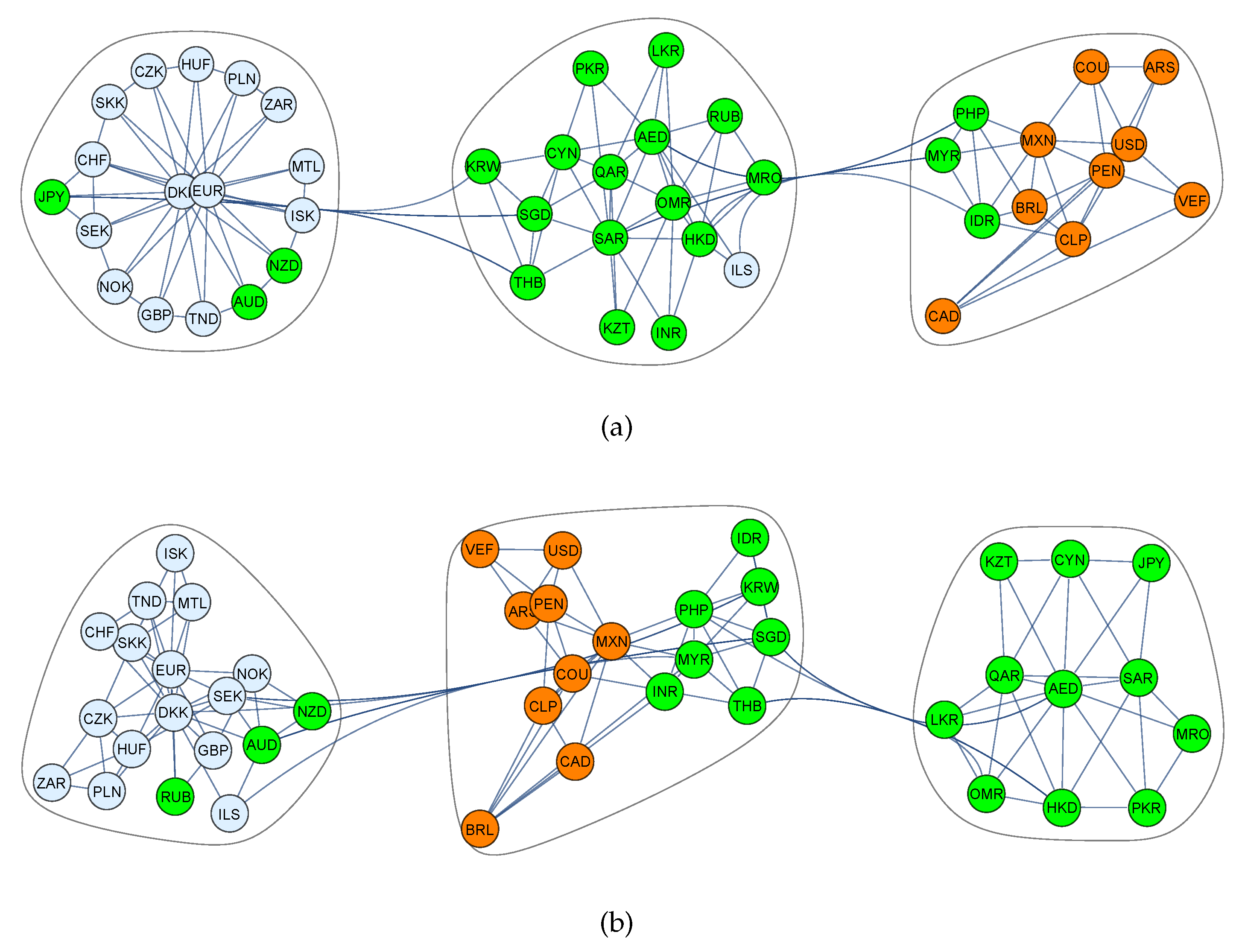
2.3.2. Foreign Exchange Markets
Synchronous Correlations
Lagged Correlations
3. Discussion
4. Materials and Methods
4.1. Data
4.2. Pearson Correlation Analysis
4.3. Analyzed Countries
| Country | Currency | Index Label | Currency Label | Country | Currency | Index Label | Currency Label |
|---|---|---|---|---|---|---|---|
| Argentina | Argentine peso | ARG | ARS | Malta | Maltese lira | MLT | MTL/EUR |
| Australia | Australian dollar | AUS | AUD | Mauritius | Mauritian rupee | MUS | MRO |
| Austria | euro | AUT | EUR | Mexico | Mexican peso | MEX | MXN |
| Belgium | euro | BEL | EUR | Netherlands | euro | NLD | EUR |
| Brazil | Brazilian real | BRA | BRL | New Zealand | New Zealand dollar | NZL | NZD |
| Canada | Canadian dollar | CAN | CAD | Norway | Norwegian krone | NOR | NOK |
| Chile | Chilean peso | CHL | CLP | Oman | Omani rial | OMN | OMR |
| China | Chinese yuan | CHN | CNY | Pakistan | Pakistani rupee | PAK | PKR |
| Colombia | Colombian peso | COL | COU | Peru | Peruvian nuevo sol | PER | PEN |
| Czech Republic | Czech koruna | CZE | CZK | Philippines | Philippine peso | PHL | PHP |
| Denmark | Danish krone | DNK | DKK | Poland | Polish zloty | POL | PLN |
| Finland | euro | FIN | EUR | Portugal | euro | PRT | EUR |
| France | euro | FRA | EUR | Qatar | Qatari riyal | QAT | QAR |
| Germany | euro | DEU | EUR | Russia | Russian ruble | RUS | RUB |
| Greece | euro | GRC | EUR | Saudi Arabia | Saudi riyal | SAU | SAR |
| Hong Kong | Hong Kong dollar | HKG | HKD | Singapore | Singapore doller | SGP | SGD |
| Hungary | Hungarian forint | HUN | HUF | Slovakia | Slovak koruna | SVK | SKK/EUR |
| Iceland | Icelandic krona | ISL | ISK | South Africa | South African rand | ZAF | ZAR |
| India | Indian rupee | IND | INR | Spain | euro | ESP | EUR |
| Indonesia | Indonesian rupiah | IDN | IDR | Sri Lanka | Sri Lankan rupee | LKA | LKR |
| Ireland | euro | IRL | EUR | Sweden | Swedish krona | SWE | SEK |
| Israel | Israel new shekel | ISR | ILS | Switzerland | Swiss franc | CHE | CHF |
| Italy | euro | ITA | EUR | Thailand | Thai baht | THA | THB |
| Japan | Japanese yen | JPN | JPY | Tunisia | Tunisian dinar | TUN | TND |
| Kazakhstan | Kazakhstani tenge | KAZ | KZT | Utd. Arab Emirates | UAE dirham | ARE | AED |
| Korea | South Korean won | KOR | KRW | United Kingdom | British pound | GBR | GBP |
| Luxembourg | euro | LUX | EUR | United States | US dollar | USA | USD |
| Malaysia | Malaysian ringgit | MYS | MYR | Venezuela | Venezuelan bolivar | VEN | VEF |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- W.L. Lin, R.F. Engle, and T. Ito. “Do Bulls and Bears Move Across Borders? International Transmission of Stock Returns and Volatility as the World Turns.” Rev. Financ. Stud. 7 (1994): 507–538. [Google Scholar] [CrossRef]
- R.D. Smith. “The spread of the credit crisis: View from a stock correlation network.” J. Korean Phys. Soc. 54 (2009): 2460–2463. [Google Scholar] [CrossRef]
- K.J. Forbes, and R. Rigobon. “No contagion, only interdependence: Measuring stock market comovements.” J. Financ. 57 (2002): 2223–2261. [Google Scholar] [CrossRef]
- T.J. Flavin, M.J. Hurley, and F. Rousseau. “Explaining stock market correlation: A gravity model approach.” Manch. Sch. 70 (2002): 87–106. [Google Scholar] [CrossRef]
- B. Solnik, C. Boucrelle, and Y. Le Fur. “International market correlation and volatility.” Financ. Anal. J. 52 (1996): 17–34. [Google Scholar] [CrossRef]
- L. Ramchand, and R. Susmel. “Volatility and cross correlation across major stock markets.” J. Empir. Financ. 5 (1998): 397–416. [Google Scholar] [CrossRef]
- B.H. Boyer, T. Kumagai, and K. Yuan. “How do crises spread? Evidence from accessible and inaccessible stock indices.” J. Financ. 61 (2006): 957–1003. [Google Scholar] [CrossRef]
- G. Bonanno, N. Vandewalle, and R.N. Mantegna. “Taxonomy of stock market indices.” Phys. Rev. E 62 (2000): R7615–R7618. [Google Scholar] [CrossRef]
- G. Bonanno, G. Caldarelli, F. Lillo, and R.N. Mantegna. “Topology of correlation-based minimal spanning trees in real and model markets.” Phys. Rev. E 68 (2003): 046130. [Google Scholar] [CrossRef] [PubMed]
- G. Bonanno, G. Caldarelli, F. Lillo, F. Miccichè, N. Vandewalle, and R.N. Mantegna. “Networks of equities in financial markets.” Eur. Phys. J. B 38 (2004): 363–371. [Google Scholar] [CrossRef]
- E. Sheedy. “Correlation in currency markets a risk-adjusted perspective.” J. Int. Financ. Mark. Inst. Money 8 (1998): 59–82. [Google Scholar] [CrossRef]
- R. Meese. “Currency fluctuations in the post-Bretton Woods era.” J. Econ. Perspect. 4 (1990): 117–134. [Google Scholar] [CrossRef]
- F. Longin, and B. Solnik. “Is the correlation in international equity returns constant: 1960–1990.” J. Int. Money Financ. 14 (1995): 3–26. [Google Scholar] [CrossRef]
- B. Arshanapalli, and J. Doukas. “International stock market linkages: Evidence from the pre-and post-October 1987 period.” J. Bank. Financ. 17 (1993): 193–208. [Google Scholar] [CrossRef]
- D.Y. Kenett, Y. Shapira, A. Madi, S. Bransburg-Zabary, G. Gur-Gershgoren, and E. Ben-Jacob. “Dynamics of stock market correlations.” AUCO Czech Econ. Rev. 4 (2010): 330–341. [Google Scholar]
- D.Y. Kenett, Y. Shapira, A. Madi, S. Bransburg-Zabary, G. Gur-Gershgoren, and E. Ben-Jacob. “Index cohesive force analysis reveals that the US market became prone to systemic collapses since 2002.” PLoS ONE 6 (2011): e19378. [Google Scholar] [CrossRef] [PubMed]
- D.Y. Kenett, M. Raddant, T. Lux, and E. Ben-Jacob. “Evolvement of uniformity and volatility in the stressed global financial village.” PLoS ONE 7 (2012): e31144. [Google Scholar] [CrossRef] [PubMed]
- J.P. Onnela, A. Chakraborti, K. Kaski, J. Kertesz, and A. Kanto. “Dynamics of market correlations: Taxonomy and portfolio analysis.” Rev. Mod. Phys. 68 (2003): 056110. [Google Scholar] [CrossRef] [PubMed]
- L. Sandoval, and I.D.P. Franca. “Correlation of financial markets in times of crisis.” Phys. A Stat. Mech. Appl. 391 (2012): 187–208. [Google Scholar] [CrossRef]
- L. Sandoval. “To lag or not to lag? How to compare indices of stock markets that operate on different times.” Phys. A Stat. Mech. Appl. 403 (2014): 227–243. [Google Scholar] [CrossRef]
- C. Curme, M. Tumminello, R.N. Mantegna, H.E. Stanley, and D.Y. Kenett. “Emergence of statistically validated financial intraday lead-lag relationships.” SSRN Electron. J. 15 (2015): 1375–1386. [Google Scholar] [CrossRef]
- T. Aste, W. Shaw, and T. Di Matteo. “Correlation structure and dynamics in volatile markets.” New J. Phys. 12 (2010): 085009. [Google Scholar] [CrossRef]
- M. Tumminello, T. Di Matteo, T. Aste, and R.N. Mantegna. “Correlation based networks of equity returns sampled at different time horizons.” Eur. Phys. J. B 55 (2007): 209–217. [Google Scholar] [CrossRef]
- R. Dornbusch, and S. Fischer. “Exchange rates and the current account.” Am. Econ. Rev. 70 (1980): 960–971. [Google Scholar]
- M. Dooley, and P. Isard. “A portfolio-balance rational-expectations model of the dollar-mark exchange rate.” J. Int. Econ. 12 (1982): 257–276. [Google Scholar] [CrossRef]
- B. Morley. “Exchange rates and stock prices: Implications for European convergence.” J. Policy Model. 24 (2002): 523–526. [Google Scholar] [CrossRef]
- C.C. Nieh, and C.F. Lee. “Dynamic relationship between stock prices and exchange rates for G-7 countries.” Q. Rev. Econ. Financ. 41 (2002): 477–490. [Google Scholar] [CrossRef]
- K.H. Bae, G.A. Karolyi, and R.M. Stulz. “A new approach to measuring financial contagion.” Rev. Financ. Stud. 16 (2003): 717–763. [Google Scholar] [CrossRef]
- L. Gagnon, and G.A. Karolyi. “Price and volatility transmission across borders.” Financ. Mark. Inst. Instrum. 15 (2006): 107–158. [Google Scholar] [CrossRef]
- L. Cappiello, and R.A. De Santis. Explaining Exchange Rate Dynamics: The Uncovered Equity Return Parity Condition. ECB Working Paper. 2005. Available online: http://ssrn.com/abstract=804924 (accessed on 19 October 2005).
- C.W. Granger, B.N. Huangb, and C.W. Yang. “A bivariate causality between stock prices and exchange rates: Evidence from recent Asianflu*.” Q. Rev. Econ. Financ. 40 (2000): 337–354. [Google Scholar] [CrossRef]
- M.S. Pan, R.C.W. Fok, and Y.A. Liu. “Dynamic linkages between exchange rates and stock prices: Evidence from East Asian markets.” Int. Rev. Econ. Financ. 16 (2007): 503–520. [Google Scholar] [CrossRef]
- C. Ning. “Dependence structure between the equity market and the foreign exchange market—A copula approach.” J. Int. Money Financ. 29 (2010): 743–759. [Google Scholar] [CrossRef]
- H. Zhao. “Dynamic relationship between exchange rate and stock price: Evidence from China.” Res. Int. Bus. Financ. 24 (2010): 103–112. [Google Scholar] [CrossRef]
- G. Katechos. “On the relationship between exchange rates and equity returns: A new approach.” J. Int. Financ. Mark. Inst. Money 21 (2011): 550–559. [Google Scholar] [CrossRef]
- C.H. Lin. “The comovement between exchange rates and stock prices in the Asian emerging markets.” Int. Rev. Econ. Financ. 22 (2012): 161–172. [Google Scholar] [CrossRef]
- L. Cohen, and A. Frazzini. “Economic links and predictable returns.” J. Financ. 63 (2008): 1977–2011. [Google Scholar] [CrossRef]
- J.H. Cochrane. “The dog that did not bark: A defense of return predictability.” Rev. Financ. Stud. 21 (2008): 1533–1575. [Google Scholar] [CrossRef]
- E.F. Fama, and K.R. French. “Dividend yields and expected stock returns.” J. Financ. Econ. 22 (1988): 3–25. [Google Scholar] [CrossRef]
- E.F. Fama, and K.R. French. “Business conditions and expected returns on stocks and bonds.” J. Financ. Econ. 25 (1989): 23–49. [Google Scholar] [CrossRef]
- I. Welch, and A. Goyal. “A comprehensive look at the empirical performance of equity premium prediction.” Rev. Financ. Stud. 21 (2008): 1455–1508. [Google Scholar] [CrossRef]
- W.E. Ferson, and C.R. Harvey. “The risk and predictability of international equity returns.” Rev. Financ. Stud. 6 (1993): 527–566. [Google Scholar] [CrossRef]
- M. Dahlquist, and H. Hasseltoft. “International bond risk premia.” J. Int. Econ. 90 (2013): 17–32. [Google Scholar] [CrossRef]
- W. Breen, L.R. Glosten, and R. Jagannathan. “Economic significance of predictable variations in stock index returns.” J. Financ. 44 (1989): 1177–1189. [Google Scholar] [CrossRef]
- C.R. Harvey. “The world price of covariance risk.” J. Financ. 46 (1991): 111–157. [Google Scholar] [CrossRef]
- G. Bekaert, R.J. Hodrick, and X. Zhang. “International stock return comovements.” J. Financ. 64 (2009): 2591–2626. [Google Scholar] [CrossRef]
- D.E. Rapach, J.K. Strauss, and G. Zhou. “International stock return predictability: What is the role of the United States? ” J. Financ. 68 (2013): 1633–1662. [Google Scholar] [CrossRef]
- A.L. Barabási, and R. Albert. “Emergence of scaling in random networks.” Science 286 (1999): 509–512. [Google Scholar] [PubMed]
- S.V. Buldyrev, R. Parshani, G. Paul, H.E. Stanley, and S. Havlin. “Catastrophic cascade of failures in interdependent networks.” Nature 464 (2010): 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- R.N. Mantegna. “Hierarchical structure in financial markets.” Eur. Phys. J. B 11 (1999): 193–197. [Google Scholar] [CrossRef]
- D.J. Watts, and S.H. Strogatz. “Collective dynamics of ‘small-world’networks.” Nature 393 (1998): 440–442. [Google Scholar] [CrossRef] [PubMed]
- R. Albert, and A.L. Barabási. “Statistical mechanics of complex networks.” Rev. Mod. Phys. 74 (2002): 47. [Google Scholar] [CrossRef]
- L.A.N. Amaral, A. Scala, M. Barthélémy, and H.E. Stanley. “Classes of small-world networks.” Proc. Natl. Acad. Sci. USA 97 (2000): 11149–11152. [Google Scholar] [CrossRef] [PubMed]
- D. Li, B. Fu, Y. Wang, G. Lu, Y. Berezin, H.E. Stanley, and S. Havlin. “Percolation transition in dynamical traffic network with evolving critical bottlenecks.” Proc. Natl. Acad. Sci. USA 112 (2015): 669–672. [Google Scholar] [CrossRef] [PubMed]
- D.Y. Kenett, T. Preis, G. Gur-Gershgoren, and E. Ben-Jacob. “Dependency network and node influence: Application to the study of financial markets.” Int. J. Bifurc. Chaos 22 (2012). [Google Scholar] [CrossRef]
- M. Billio, M. Getmansky, A.W. Lo, and L. Pelizzon. “Econometric measures of connectedness and systemic risk in the finance and insurance sectors.” J. Financ. Econ. 104 (2012): 535–559. [Google Scholar] [CrossRef]
- P. Gai, A. Haldane, and S. Kapadia. “Complexity, concentration and contagion.” J. Monet. Econ. 58 (2011): 453–470. [Google Scholar] [CrossRef]
- K. Anand, P. Gai, S. Kapadia, S. Brennan, and M. Willison. A Network Model of Financial System Resilience. Technical Report; London, UK: Bank of England, 2012. [Google Scholar]
- A.G. Haldane, and R.M. May. “Systemic risk in banking ecosystems.” Nature 469 (2011): 351–355. [Google Scholar] [CrossRef] [PubMed]
- S. Battiston, D. Delli Gatti, M. Gallegati, B. Greenwald, and J.E. Stiglitz. “Liaisons dangereuses: Increasing connectivity, risk sharing, and systemic risk.” J. Econ. Dyn. Control 36 (2012): 1121–1141. [Google Scholar] [CrossRef]
- X. Huang, I. Vodenska, S. Havlin, and H.E. Stanley. “Cascading Failures in Bi-partite Graphs: Model for Systemic Risk Propagation.” Sci. Rep. 3 (2013): 1219. [Google Scholar] [PubMed]
- F. Schweitzer, G. Fagiolo, D. Sornette, F. Vega-Redondo, and D.R. White. “Economic Networks: What do we know and what do we need to know? ” Adv. Complex Syst. 12 (2009): 407–422. [Google Scholar] [CrossRef]
- P. Glasserman, and H.P. Young. “How likely is contagion in financial networks? ” J. Bank. Financ. 50 (2015): 383–399. [Google Scholar] [CrossRef]
- D. Acemoglu, A. Ozdaglar, and A. Tahbaz-Salehi. Systemic Risk and Stability in Financial Networks. Technical Report; Cambridge, MA, USA: National Bureau of Economic Research, 2013. [Google Scholar]
- D. Acemoglu, V.M. Carvalho, A. Ozdaglar, and A. Tahbaz-Salehi. “The network origins of aggregate fluctuations.” Econometrica 80 (2012): 1977–2016. [Google Scholar] [CrossRef]
- N. Dehmamy, S.V. Buldyrev, S. Havlin, H.E. Stanley, and I. Vodenska. “A Systemic Stress Test Model in Bank-Asset Networks.” arXiv Preprint, 2014, arXiv:1410.0104. [Google Scholar]
- L. Ellis, A. Haldane, and F. Moshirian. “Systemic risk, governance and global financial stability.” J. Bank. Financ. 45 (2014): 175–181. [Google Scholar] [CrossRef]
- Bank for International Settlements. “Triennial Central Bank Survey of foreign exchange turnover in April 2013—Preliminary results released by the BIS.” 2013. Available online: http://www.bis.org/press/p130905.htm (accessed on 10 April 2016).
- M. Tumminello, T. Aste, T. Di Matteo, and R.N. Mantegna. “A tool for filtering information in complex systems.” Proc. Natl. Acad. Sci. USA 102 (2005): 10421–10426. [Google Scholar] [CrossRef] [PubMed]
- T. Di Matteo, F. Pozzi, and T. Aste. “The use of dynamical networks to detect the hierarchical organization of financial market sectors.” Eur. Phys. J. B 73 (2010): 3–11. [Google Scholar] [CrossRef]
- NYT. “The U.S. Financial Crisis Is Spreading to Europe.” Available online: http://www.nytimes.com/2008/10/01/business/worldbusiness/01global.html (accessed on 10 April 2016).
- DailyFX. “Why is the Australian Dollar Correlated to the US S&P 500? ” Available online: https://www.dailyfx.com/forex/technical/article/forex_correlations/2012/03/27/forex_correlations_australian_dollar_us_dollar.html (accessed on 10 April 2016).
- Telegraph. “BRICs attack QE and urge Western leaders to be ’responsible’.” Available online: http://www.telegraph.co.uk/finance/economics/9174292/BRICs-attack-QE-and-urge-Western-leaders-to-be-responsible.html (accessed on 10 April 2016).
- Reuters. “Timeline: China’s reforms of yuan exchange rate.” Available online: http://www.reuters.com/article/2012/04/14/us-china-yuan-timeline-idUSBRE83D03820120414 (accessed on 17 April 2015).
- BBC. “Japan government and central bank intervene to cut yen.” Available online: http://www.bbc.co.uk/news/business-14398392 (accessed on 10 April 2016).
- NBS. “Slovak Koruna Included in the ERM II.” Available online: http://www.nbs.sk/PRESS/PR051128.HTM (accessed on 17 April 2015).
- OECD. OECD Economic Surveys: Euro Area 2004. Paria, France: OECD Publishing, 2004. [Google Scholar]
- J.A. Frankel, and S.J. Wei. Is There a Currency Bloc in the Pacific? Berkeley, CA, USA: Department of Economics, University of California, 1993. [Google Scholar]
- J.A. Frankel, S.J. Wei, M. Canzoneri, and M. Goldstein. Emerging Currency Blocks. Berlin/Heidelberg, Germany: Springer, 1995. [Google Scholar]

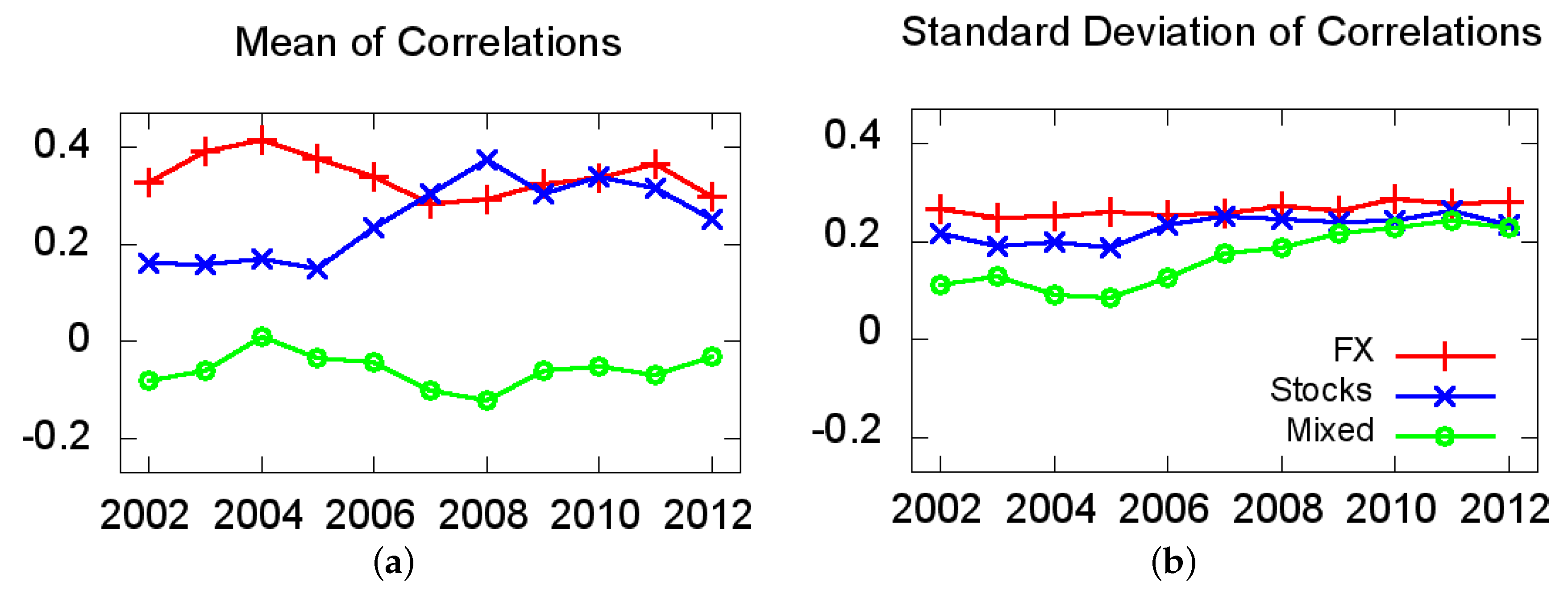
| Stocks | Currency | |||
|---|---|---|---|---|
| 2002–2006 | 2007–2012 | 2002–2006 | 2007–2012 | |
| Mean | ||||
| Standard Deviation | ||||
| Minimum | ||||
| Maximum | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vodenska, I.; Becker, A.P.; Zhou, D.; Kenett, D.Y.; Stanley, H.E.; Havlin, S. Community Analysis of Global Financial Markets. Risks 2016, 4, 13. https://doi.org/10.3390/risks4020013
Vodenska I, Becker AP, Zhou D, Kenett DY, Stanley HE, Havlin S. Community Analysis of Global Financial Markets. Risks. 2016; 4(2):13. https://doi.org/10.3390/risks4020013
Chicago/Turabian StyleVodenska, Irena, Alexander P. Becker, Di Zhou, Dror Y. Kenett, H. Eugene Stanley, and Shlomo Havlin. 2016. "Community Analysis of Global Financial Markets" Risks 4, no. 2: 13. https://doi.org/10.3390/risks4020013
APA StyleVodenska, I., Becker, A. P., Zhou, D., Kenett, D. Y., Stanley, H. E., & Havlin, S. (2016). Community Analysis of Global Financial Markets. Risks, 4(2), 13. https://doi.org/10.3390/risks4020013