Enhancing Insurer Portfolio Resilience and Capital Efficiency with Green Bonds: A Framework Combining Dynamic R-Vine Copulas and Tail-Risk Modeling

Abstract

This study develops an integrated risk modeling framework to assess capital adequacy and optimize portfolio performance for Thai life and non-life insurers. Leveraging ARMA–GJR–GARCH models with skewed Student-t innovations, extreme value theory, and dynamic R-vine copulas, the framework effectively captures volatility, tail risks, and evolving asset interdependencies. Utilizing daily data from 2014 to 2024, the models generate value-at-risk forecasts consistent with international standards such as Basel III’s 10-day 99% VaR and rolling Sharpe ratios for portfolios integrating green bonds compared to traditional asset allocations. The results demonstrate that green bonds, fixedincome instruments funding renewable energy and other environmental projects, significantly improve risk-adjusted returns and have the potential to reduce capital requirements, particularly for life insurers with long-term sustainability mandates. These findings underscore the importance of portfolio-level capital assessment and support the proactive integration of ESG considerations into supervisory investment guidelines to enhance financial resilience and align the insurance sector with Thailand’s sustainable finance agenda.

1. Introduction

Accurately modeling risk is essential for modern insurance portfolio management, particularly for life and non-life insurers operating under increasingly stringent solvency frameworks. Market volatility, shifting macroeconomic conditions, and evolving sustainability regulations require more sophisticated modeling approaches that capture tail risks and nonlinear dependencies, elements often neglected in traditional risk assessment frameworks (Bollerslev 1986; Daly 2008). For insurers, precise modeling is not merely a technical exercise; it is central to meeting capital adequacy requirements and safeguarding policyholder protection.

Insurance companies are increasingly integrating environmental, social, and governance (ESG) considerations into their investment strategies to strengthen portfolio resilience, support long-term sustainability goals, and align with evolving regulatory expectations. Among ESG instruments, green bonds have emerged as a compelling asset class, functioning like traditional bonds but with proceeds exclusively directed toward verified environmental projects such as renewable energy, energy efficiency, sustainable transport, and low-carbon infrastructure (Climate Bonds Initiative 2022). Their dual role of delivering financial returns while advancing sustainability objectives makes them attractive to insurers (Ferrer et al. 2021; Han et al. 2024; Karim et al. 2024; Park et al. 2020; Papavassiliou et al. 2025). Empirical evidence associates green bonds with improved Sharpe ratios and reduced capital charges under solvency frameworks, offering diversification benefits that reduce reliance on more volatile asset classes (Taghizadeh-Hesary et al. 2021). Their typically longer maturities and high credit quality can assist life insurers in matching long-term liabilities, while regulatory incentives and favorable capital treatment can further enhance capital efficiency and support solvency objectives (Flammer 2020; Huang and Lin 2023; Okeke et al. 2024). In Thailand, where insurers manage sizable and duration-sensitive portfolios, green bond inclusion supports both financial stability and national sustainability objectives (Fitrah and Soemitra 2022; Ramadhan 2020). Regulatory support, through instruments such as green taxonomies, targeted incentives, and integration of sustainability guidance into supervisory frameworks, is central to enabling this transition and ensuring ESG investments genuinely contribute to insurers’ strategic and financial resilience.

However, integrating green bonds also introduces risk considerations for insurers. Liquidity risks, arising from the limited secondary trading capacity in ESG instruments, can increase volatility and create mismatches between assets and liabilities (Kocaarslan 2023). Greenwashing risks, especially in jurisdictions with weaker enforcement, can lead to mispricing and reputational damage. Empirical evidence indicates that green bond issuance does not always correspond to actual environmental improvements. For example, some corporate issuers show no reduction in emissions following issuance (Leung et al. 2023), and misleading environmental claims can undermine pricing integrity in green bond markets (Zhu et al. 2025). At a broader level, adopting ESG-oriented investment models can also expose insurers to measurement errors, inconsistent rating methodologies, and evolving regulatory standards, which may complicate risk assessment and lead to unintended portfolio biases (Berg et al. 2022). These findings highlight the importance of strong disclosure standards, credible ESG frameworks, and the application of advanced risk modeling.

Advanced financial econometrics provides crucial tools for modeling the complex risks faced by insurers. The Autoregressive Moving Average Generalized Autoregressive Conditional Heteroskedasticity (ARMA–GARCH) model, especially with the Glosten–Jagannathan–Runkle (GJR) extension, is valuable for capturing volatility clustering and asymmetric shock responses (Adegboyo and Sarwar 2025; Glosten et al. 1993; Hidayana et al. 2021; Ma et al. 2024; Wei et al. 2025). The GJR–GARCH model accounts for the leverage effect, where negative shocks induce greater volatility than positive ones (Liu and Hung 2010). Financial returns often exhibit skewness and fat tails, which, if unaccounted for, can lead to the underestimation of risk. To address this, skewed Student-t innovations are widely adopted to improve value-at-risk (VaR) accuracy and better capture these distributional properties (Akanbi et al. 2025; Al-Khasawneh et al. 2025; Hansen 1994; Harvey and Siddique 1999; Lambert and Laurent 2001; Patra and Gupta 2025). However, even these enhanced models may underestimate extreme losses. Extreme value theory (EVT), particularly through the generalized Pareto distribution (GPD), enhances tail-risk modeling by focusing on exceedances beyond a high threshold (Braione and Scholtes 2016; Majumder 2018). When applied to GARCH-filtered residuals, EVT improves VaR estimation under stress conditions, which is crucial for insurers operating under solvency requirements (Chen et al. 2024; Okou and Amar 2023).

Insurers require methods that capture interdependence among assets, moving beyond univariate modeling. Correlation matrices often fail to reflect nonlinear and time-varying relationships, particularly during periods of financial distress. Copula models address this limitation by constructing flexible joint distributions. R-vine copulas are well suited to modeling complex dependency structures using sequences of bivariate copulas (Brechmann and Czado 2013). Their dynamic extensions allow dependencies to evolve over time, which is essential for capturing contagion effects and shifts in market conditions (Raza et al. 2025; Zhou and Ji 2021). When integrated with GARCH-based marginal models, this approach offers significant advantages for multivariate risk modeling. It enhances portfolio-level risk assessment and supports the design of capital-efficient, ESG-aligned investment strategies.

This study integrates ARMA–GJR–GARCH models with skewed Student-t innovations, EVT, and dynamic R-vine copulas into a unified framework tailored to insurer portfolios. Capturing volatility dynamics, tail risks, and evolving interdependencies, the framework improves VaR estimation and Sharpe ratio assessment under both normal and stressed conditions (Ahmadi et al. 2023; Han and Li 2022; Jeleskovic et al. 2024). Using daily data on Thai financial assets and green bonds from 2014 to 2024, the study evaluates VaR forecasts and rolling Sharpe ratios across optimized portfolios. The results reveal that green bond inclusion enhances insurer portfolio performance, strengthens capital adequacy, improves risk-adjusted returns through diversification, and supports alignment with Thailand’s sustainability goals. This research offers practical insights for risk practitioners and regulators in emerging markets. The proposed framework enables more accurate capital requirement calculations and supports ESG integration within supervisory investment guidelines, crucial as Thai regulatory guidance, market maturity, and sustainability commitments rapidly evolve.

While this study focuses on Thailand’s regulatory environment, the proposed framework is broadly adaptable. It aligns with international standards such as Basel III market risk measurement, including the 10-day 99% VaR, and the Fundamental Review of the Trading Book (FRTB) emphasis on tailrisk modeling. This compatibility makes the findings relevant for global insurers, banks, and regulators seeking to integrate ESG assets into capital adequacy assessments. The framework can also be applied in other emerging markets with similar regulatory structures, including ASEAN countries such as Malaysia and Singapore, offering opportunities for cross-country comparisons to assess the generalizability of results and regional ESG investment dynamics.

Based on the theoretical arguments and empirical evidence reviewed above, this study tests the following hypotheses:

H1. 

ARMA–GJR–GARCH models with skewed Student-t innovations provide accurate VaR estimates and capital requirement measures under normal market conditions.

H2. 

ARMA–GJR–GARCH models with skewed Student-t innovations combined with EVT produce more accurate VaR estimates under stress scenarios.

H3. 

When integrated with dynamic R-vine copulas for dependence modeling, green bond inclusion in insurer portfolios reduces portfolio-level capital requirements, as measured by VaR, and increases risk-adjusted returns, as measured by the Sharpe ratio.

H4. 

The magnitude of diversification and capital efficiency benefits from green bond integration, as assessed using dynamic R-vine copula portfolio modeling, differs between life and non-life insurers due to variations in liability duration and investment horizons.

The remainder of this paper is structured as follows: Section 2 describes the dataset and methodology, including model specifications and validation procedures; Section 3 presents empirical findings and discussions on VaR forecasting, backtesting, portfolio performance analysis, and limitations and future research; and Section 4 concludes with key findings and policy implications related to capital efficiency and ESG-aligned investment strategies in the Thai insurance sector.

2. Domain of Experiment and Methodology

This study analyzes a comprehensive dataset of 2869 daily observations spanning 1 January 2014, to 31 December 2024, using logarithmic returns. Logarithmic returns were calculated using the formula $r_t=\ln \left(P_t/P_{t-1}\right)$, where $P_t$ is the price at time $t,$ and $P_{t-1}$ is the price at time t $-$ 1. The dataset encompasses a variety of significant Thai financial assets: the SET index, the Dubai crude oil, the Thai bullion gold, the 3–7-year government bond index, the 7–10-year government bond index, the JPY/THB exchange rate, the property sector index, and the Bloomberg Barclays MSCI US green bond index. Data obtained from Datastream International and Bloomberg exhibit statistical properties typical of financial time series. With the exception of the exchange rate, the series display negative skewness, indicating a higher likelihood of large negative returns. High kurtosis values confirm leptokurtosis in most series, indicating a greater concentration around the mean and fatter tails than expected under normality, suggestive of increased extreme events. The Jarque–Bera (JB) test indicates that gold returns are normally distributed, unlike the other assets. The Augmented Dickey–Fuller (ADF) test results confirm that all series are stationary.

Table 1. Summary statistics for eight assets.

	SET Index	Dubai Crude Oil	Thai Bullion Gold	3–7 TTM GOV	7–10 TTM GOV	JPY/THB Exchange Rate	Property Sector Index	Bloomberg Barclays MSCI US Green Bond Index
Mean	0.00015	−0.00012	0.00028	0.00011	0.00015	−0.00012	0.00007	0.00007
Median	0.00000	0.00050	0.00003	0.00011	0.00013	−0.00017	0.00000	0.00005
Maximum	0.07656	0.18789	0.04715	0.00859	0.01651	0.04207	0.08322	0.01957
Minimum	−0.11384	−0.31530	−0.05498	−0.00947	−0.01768	−0.03333	−0.14303	−0.02087
SD	0.00878	0.02492	0.00846	0.00107	0.00230	0.00554	0.01126	0.00286
Skewness	−1.606	−0.748	−0.045	−0.509	−0.366	0.238	−1.351	−0.203
Kurtosis	24.820	13.871	3.079	10.091	6.154	4.741	20.541	4.413
JB	58,149.93	14,393.36	1.71	6134.58	1253.54	389.60	37,656.12	258.45
JB (p-value)	0.000	0.000	0.427	0.000	0.000	0.000	0.000	0.000
ADF	−13.10	−13.41	−13.54	−11.66	−12.02	−14.61	−13.42	−13.37
ADF (p-value)	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

presents the summary statistics of daily returns for all eight assets examined in this study.

2.1. Autoregressive Moving Average Glosten–Jagannathan–Runkle Generalized Autoregressive Conditional Heteroskedasticity with Skewed Student-t Innovations

This study addresses key complexities in financial time series, such as volatility clustering, fat tails, and asymmetric shock responses, across eight asset classes, including green bonds. To model individual asset dynamics, it adopts the Autoregressive Moving Average–Glosten–Jagannathan–Runkle Generalized Autoregressive Conditional Heteroskedasticity (ARMA–GJR–GARCH) model with skewed Student-t innovations, jointly modeling the conditional mean and variance of returns. Portfolios of five and six assets (including green bonds) are then constructed by maximizing the Sharpe ratio using dynamic R-vine copulas. This integrated approach offers a flexible and robust structure for volatility modeling and risk forecasting. To capture excess kurtosis and skewness common in financial return distributions, the innovation term follows the skewed Student-t distribution introduced by Hansen (1994). This distribution accounts for both fat tails and asymmetry, enhancing the precision of value-at-risk (VaR) estimates under both normal and extreme market conditions.

The GJR component is central to capturing asymmetric volatility in response to shocks, an effect often observed in financial markets. In the general ARMA(m,n)–GJR–GARCH(p,q) model, p represents the number of ARCH terms (lagged squared residuals) and asymmetry terms, while q denotes the number of GARCH terms (lagged conditional variances). Estimating mean and variance with skewed Student-t innovations, the model is given by the following:

$$\left\{\begin{array}{c}{r}_t = \mu +{{\displaystyle \sum }}_{i=1}^{\mathrm{m}}{\varnothing }_i r_{t-i}+{{\displaystyle \sum }}_{j=1}^{\mathrm{n}}{\theta }_{j }{\epsilon }_{t-j}+ {\epsilon }_t\\ {\epsilon }_t = {\sigma }_t{z}_t, z_t~Skewed-t\left(0,1,\nu ,\eta \right) \end{array}\right.$$

(1)

In this model, $r_t$ represents the return of the time series at time $t$, and $\mu$ is the constant mean. The autoregressive coefficients ${\varnothing }_i$ capture the influence of past returns (AR part of order m), while the moving average coefficients ${\theta }_{j }$ account for the impact of past shocks (MA part of order n). The innovation term ${\epsilon }_t$ represents unpredictable shocks, modeled as the product of the conditional standard deviation ${\sigma }_t$ and a shock $z_t$, which follows a skewed Student-t distribution with zero mean and unit variance.

The skewed Student-t distribution is parameterized by degrees of freedom $\nu$ > 2 to ensure finite variance and a skewness parameter $\eta \in \left(-1, 1\right)$, where $\eta =0$ corresponds to the symmetric Student-t distribution. Its density function, $f\left(z_t;\nu ,\eta \right)$, is defined as follows:

$$f\left(z_t;\nu ,\eta \right)=\left\{\begin{array}{c}bc{\left[1+{\displaystyle \frac{1}{\nu -2}}{\left({\displaystyle \frac{b{z}_t+a}{1-\eta }}\right)}^2\right]}^{-{\displaystyle \frac{\nu +1}{2}}},z_t<-{\displaystyle \frac{a}{b}}\\ bc{\left[1+{\displaystyle \frac{1}{\nu -2}}{\left({\displaystyle \frac{b{z}_t+a}{1+\eta }}\right)}^2\right]}^{-{\displaystyle \frac{\nu +1}{2}}}, z_t\ge -{\displaystyle \frac{a}{b}}\end{array}\right.$$

(2)

where constants $a, b$, and $c$ are given by the following:

$$\left\{\begin{array}{c}a=4\eta c{\displaystyle \frac{\nu -2}{\nu -1}} \\ b=\sqrt{1+3{\eta }^2-a^2} \\ c={\displaystyle \frac{\mathsf{\Gamma }\left(\frac{\nu +1}{2}\right)}{\sqrt{\pi \left(\nu -2\right)}\cdot \mathsf{\Gamma }\left(\frac{\nu }{2}\right)}} \end{array}\right.$$

(3)

The conditional variance ${\sigma }_t^2$ equation under the GJR–GARCH(p,q) specification is as follows:

$${\sigma }_t^2= \omega + {{\displaystyle \sum }}_{i=1}^{\mathrm{p}}{\alpha }_i{\epsilon }_{t-i}^2+{{\displaystyle \sum }}_{i=1}^{\mathrm{p}}{\gamma }_i{\epsilon }_{t-i}^2{I}_{\left\{{\epsilon }_{t-i<0}\right\}}+ {{\displaystyle \sum }}_{j=1}^{\mathrm{q}}{\beta }_j{\sigma }_{t-j}^2$$

(4)

The constant $\omega$ helps ensure the variance remains positive. The ARCH terms ${\alpha }_i$ represent the effects of lagged squared shocks, while the GARCH terms ${\beta }_j$ capture the persistence of volatility through lagged conditional variances. The asymmetry terms ${\gamma }_i$, together with the indicator function $I_{\left\{{\epsilon }_{t-i<0}\right\}}$, allow the model to distinguish between the effects of positive and negative shocks. This indicator equals 1 when the lagged shock is negative and 0 otherwise.

Under this specification, a positive shock contributes ${\alpha }_i{\epsilon }_{t-i}^2$ to the conditional variance, whereas a negative shock contributes $({\alpha }_i+ {\gamma }_i){\epsilon }_{t-i}^2$. A positive and statistically significant ${\gamma }_i$ indicates a leverage effect, meaning that negative shocks have a greater impact on volatility than positive shocks of the same magnitude. The GJR–GARCH model is particularly relevant for analyzing assets like green bonds, which may react asymmetrically to environmental developments or policy shifts. While the ARMA component captures serial dependence in returns, GJR–GARCH effectively models both volatility persistence and its asymmetric responses.

Model selection involved a systematic search over ARMA–GJR–GARCH specifications by varying the parameters m, n, p, and q. Each model was estimated using pseudo-maximum likelihood and validated through residual diagnostics to ensure zero mean, homoscedasticity, and no autocorrelation. The model with the lowest Akaike Information Criterion (AIC) was selected, reflecting the best trade-off between fit and simplicity.

2.2. Extreme Value Theory

In financial risk management, accurately capturing the behavior of extreme events in the distribution tails is essential for robust stress testing and the determination of adequate capital reserves. Such tail events frequently occur under volatile or stressed market conditions, making their proper modeling crucial for reliable risk assessment.

As an initial step, serial dependence and conditional heteroskedasticity in asset returns are removed by applying an ARMA(m,n)–GJR–GARCH(p,q) model with skewed Student-t innovations. The standardized residuals obtained from this filtering process are subsequently used for tail modeling.

To characterize the tail behavior of these residuals, extreme value theory (EVT), specifically the peak over threshold (POT) method, is employed. This approach focuses on the statistical properties of returns exceeding a high threshold, enabling refined estimation of tail-related risk measures such as value-at-risk (VaR) under stressed conditions (Degen and Embrechts 2008; Reiss and Thomas 2007). The effectiveness of EVT in financial applications has been extensively documented (Ayusuk and Sriboonchitta 2015; Melina et al. 2024; Benito et al. 2023; Roy 2022; Singh et al. 2013; Uluceviz 2025). The integration of the POT method with the ARMA–GJR–GARCH framework enhances the understanding of extreme market events within the context of volatility dynamics, ultimately facilitating more accurate estimation of capital requirements.

2.2.1. Peak over Threshold

To estimate one-day VaR under stressed conditions, this study applies the POT method to eight financial assets, including green bonds. Following Nortey et al. (2015), asset returns are first filtered using ARMA–GJR–GARCH models to capture time-varying volatility. Standardized residuals are then used as input for tail-risk modeling. This approach is consistent with established EVT applications in finance (Rosso 2015) and enhances the robustness of stress testing and capital requirement assessments.

Let $X$ denote a sequence of financial returns with cumulative distribution function (CDF) $F\left(x\right)$, and let $u$ be a predefined high threshold. POT focuses on the distribution of exceedances above this threshold, specifically the conditional distribution of $X$, given that $X>u$. An exceedance occurs when $X>u$. Defining the excess as $y=X-u$, the conditional distribution function $F_u\left(y\right)$ is given by the following:

$$F_u\left(y\right)=\mathrm{Pr}\left(\left(X-u\right)\le \left.y\right|X>u\right)={\displaystyle \frac{F\left(u+y\right)-F\left(u\right)}{1-F\left(u\right)}}, 0\le y\le x_F-u$$

(5)

where $x_F$ is the right endpoint of $F$.

The POT method assumes a sequence of independent and identically distributed (i.i.d.) losses $X_i$. It models the conditional excess distribution $F_u\left(y\right)$ for values exceeding the threshold $u$ (Magnou 2017). As noted by Gharib et al. (2017), such exceedances are often modeled using the generalized Pareto distribution (GPD), which is well suited for capturing extreme tail risk and is critical in stress testing and VaR estimation (Basu 2011). The GPD is widely used in finance to model low probability events (Sharpe and Juarez 2019).

Following the ARMA–GJR–GARCH modeling, the next step is to characterize the distribution of extreme values for each asset. The goal is to find a suitable parametric distribution to model $F_u\left(y\right)$, with threshold $u$ chosen to ensure that excesses are well-approximated by the GPD. Given the sensitivity of GPD quantiles to threshold choice (Benito et al. 2023), a sample mean excess function can be used to determine the threshold (Nurhadi 2016). Accurate tail modeling is particularly critical in this study, as it involves financial assets such as green bonds. Underestimating risk for these assets could lead to significant misjudgments.

The foundational results of Balkema and De Haan (1974) and Pickands (1975) show that, for a sufficiently high threshold, $u$, the distribution of exceedances converges to the GPD:

$$G_{\xi ,\beta }\left(y\right)=\left\{\begin{array}{c}1-{\left(1+ \xi {\displaystyle \frac{y}{\beta }}\right)}^{-{\displaystyle \frac{1}{\xi }}} if \xi \ne 0 \\ 1- e^{-{\displaystyle \frac{y}{\beta }}} if \xi =0 \end{array}\right.$$

(6)

where $\xi$ and $\beta$ represent the shape and scale parameters, respectively. The GPD’s flexibility enables it to model different tail behaviors −$\xi >0$, heavy-tailed distributions (e.g., Pareto Type I); −$\xi \to 0,$ exponential distribution; and $\xi <0$, bounded, short-tailed distributions (e.g., Pareto Type II).

2.2.2. Estimation of Value-at-Risk

Traditional risk measures often fail to adequately capture the dynamics of financial time series during extreme market conditions (Omari et al. 2020). EVT provides a robust framework for modeling the tails of distributions, making it especially valuable for estimating VaR (Zhang and Zhang 2016).

Given that the exceedances over a sufficiently high threshold, $u$, converge in distribution to the GPD, the CDF for values above $u$ can be expressed as follows:

$$F\left(x\right)=\left[1-F\left(u\right)\right]F_u\left(y\right)+F\left(u\right), X>u$$

(7)

where $F_u\left(y\right)$ is the distribution of exceedances $y=X-u$, given $X>u$.

With the GPD approximation substituted for $F_u\left(y\right)$, the tail of $F\left(x\right)$ becomes the following:

$$F\left(x\right)=\left[1-F\left(u\right)\right]G_{\xi ,\beta }\left(x-u\right)+F\left(u\right), X>u$$

(8)

The empirical estimator of the tail distribution is then as follows:

$$\widehat{F}\left(x\right)=1-{\displaystyle \frac{N_u}{n}}{\left(1+\widehat{\xi }{\displaystyle \frac{\left(x-u\right)}{\widehat{\beta }}}\right)}^{-{\displaystyle \frac{1}{\widehat{\xi }}}}, X>u$$

(9)

where $n$ is the total number of observations, $N_u$ is the number of exceedances above the threshold $u$, and $\widehat{\xi }$ and $\widehat{\beta }$ are the maximum likelihood estimates of the shape and scale parameters, respectively.

To compute the unconditional VaR at a confidence level $q>F\left(u\right)$, Equation (9) can be inverted to obtain the following:

$${\mathrm{VaR}}_q=u+{\displaystyle \frac{\widehat{\beta }}{\widehat{\xi }}}\left[{\left({\displaystyle \frac{n}{N_u}}\left(1-q\right)\right)}^{-\widehat{\xi }}-1\right]$$

(10)

This formula provides the estimated VaR at quantile $q$, incorporating the tail behavior beyond the threshold $u$. The POT approach under EVT is particularly suited for modeling such tail risks in financial stress testing.

2.3. Dynamic R-Vine Copulas: Capturing Time-Varying Dependencies

This section introduces the dynamic Regular vine (R-vine) copula model to capture evolving dependence structures among financial assets. Unlike static copulas, the dynamic R-vine framework reflects time-varying interdependencies, which are essential for modeling volatility clustering and asymmetric co-movements in financial markets (Zhou and Ji 2021). R-vine copulas, introduced by Bedford and Cooke (2001, 2002), decompose high-dimensional dependence into structured pairs of bivariate copulas, enabling flexibility and modularity. They outperform traditional copulas in representing conditional and asymmetric dependencies.

The Student-t copula is used due to its ability to capture symmetric tail dependence, critical for modeling joint extreme events like market crashes. Unlike the Gaussian copula, it incorporates both correlation ($\rho$) and degrees of freedom ($\nu$) parameters, enhancing its relevance in capital adequacy and risk management. In the dynamic copula framework, copula parameters evolve over time using a rolling-window maximum likelihood estimation (MLE) method. The model recalibrates copula parameters over a moving window of observations, instead of specifying a time-series process. This approach allows each bivariate pair to exhibit unique, time-varying dependence patterns (Yang et al. 2021), enabling a granular and adaptive representation of joint dynamics.

In this study, the modeling process begins by estimating marginal distributions using ARMA–GJR–GARCH models with skewed Student-t innovations (see Section 2.1). Standardized residuals from each model are tested to ensure they are i.i.d., a prerequisite for copula modeling (Brechmann and Czado 2013). These residuals are then transformed via the probability integral transform to produce uniform margins for the R-vine copulas. To capture time-varying dependence, copula parameters are subsequently estimated using a rolling-window approach.

2.3.1. Sklar’s Theorem and the Dynamic R-Vine Framework

Sklar’s (1959) theorem underpins copula theory by decoupling marginal distributions from their joint dependence structure. For asset returns at time $t$, the joint distribution $H_t\left(r_{1,t}, r_{2,t},\dots ,r_{d,t} \right)$ is expressed as follows:

$$H_t\left(r_{1,t}, r_{2,t},\dots ,r_{d,t} \right) =C_t\left(F_{1,t}\left(r_{1,t}\right), \dots ,F_{d,t}\left(r_{d,t}\right);{\theta }_t\right)$$

(11)

where $F_{i,t}\left(r_{i,t}\right)$ represents the time-varying marginal CDF of asset $i$ at time $t$, and ${\theta }_t$ denotes the vector of time-varying copula parameters.

2.3.2. R-Vine Copula Structure and Hierarchical Decomposition

The R-vine copula decomposes the joint copula density $c_t\left(u_{1,t}, \dots , u_{d,t}\right)$ into a product of conditional bivariate copulas as follows:

$$c_t\left(u_{1,t}, \dots , u_{d,t}\right)={{\displaystyle \prod }}_{k=1}^{d-1}{{\displaystyle \prod }}_{e\in E_k}{c}_{j_e,\left.l_e\right|D_e}(F\left(\left.u_{j_e,t}\right|u_{D_e,t}\right),F\left(\left.u_{l_e,t}\right|u_{D_e,t}\right);{\theta }_{\left.j_e,l_e\right|D_e,t})$$

(12)

Each term $c_{j_e,\left.l_e\right|D_e}\left(\cdot \right)$ denotes a bivariate copula density for variables $j_e$ and $l_e$, conditional on the set $D_e$, where ${\theta }_{\left.j_e,l_e\right|D_e,t}$ is the time-varying copula parameter at time $t$. Here, $E_k$ represents the set of edges in tree $k$ of the vine structure, and $F\left(\left.u_{j_e,t}\right|u_{D_e,t}\right)$ and $F\left(\left.u_{l_e,t}\right|u_{D_e,t}\right)$ are conditional distribution functions computed recursively.

The hierarchical structure is encoded in a sequence of trees $V_t=\left(T_{1,t},T_{2,t}, \dots , T_{d-1,t}\right)$, where each tree $T_{k,t}$ is constructed from edges in $T_{k-1,t}$, and all trees obey the proximity condition to ensure model validity. The proximity condition requires that, for each tree $T_{k,t}$, an edge can be formed only between nodes that share a common node in the previous tree $T_{k-1,t}$, thereby ensuring consistent conditional dependence modeling. This hierarchical structure enables tailored modeling of both pairwise and conditional dependencies, enhancing the flexibility and accuracy of multivariate dependence representation (Bedford and Cooke 2001, 2002).

2.3.3. Copula Family

All bivariate copulas used in the R-vine structure are specified as bivariate Student-t copulas due to their ability to capture symmetric tail dependence, which is crucial in modeling joint extreme market movements. The Student-t copula with correlation parameter $\rho$ and degrees of freedom $\nu$ is defined as follows:

$$C_{\rho ,\nu }^t\left(u_1,u_2\right)=t_{\rho ,\nu }\left(t_{\nu }^{-1}\left(u_1\right),t_{\nu }^{-1}\left(u_2\right)\right)$$

(13)

where $t_{\nu }^{-1}\left(\cdot \right)$ is the inverse CDF (quantile function) of the univariate Student-t distribution with $\nu$ degrees of freedom, and $t_{\rho ,\nu }\left(\cdot ,\cdot \right)$ is the CDF of the bivariate Student-t distribution with correlation $\rho$ and degrees of freedom $\nu$.

The corresponding copula density function is as follows:

$$c_{\rho ,\nu }^t\left(u_1,u_2\right)= {\displaystyle \frac{f_{\rho ,\nu }\left(t_{\nu }^{-1}\left(u_1\right),t_{\nu }^{-1}\left(u_2\right)\right)}{f_{\nu }\left(t_{\nu }^{-1}\left(u_1\right)\right)\cdot f_{\nu }\left(t_{\nu }^{-1}\left(u_2\right)\right)}}$$

(14)

where $f_{\rho ,\nu }\left(\cdot ,\cdot \right)$ is the bivariate Student-t density, and $f_{\nu }\left(\cdot \right)$ is the univariate Student-t density. These properties enable the Student-t copula to jointly model extreme outcomes in both tails of the distribution, making it particularly suitable for financial risk modeling, including VaR forecasts and capital adequacy analyses, as discussed in the empirical section (Demarta and McNeil 2005).

2.3.4. Kendall’s Tau and Tail Dependence

To initialize and evaluate dependencies within the R-vine framework, Kendall’s tau is used for its robustness and its direct relationship with copula parameters. For a bivariate copula $C\left(u_1,u_2\right)$, Kendall’s tau $\left(\tau \right)$ defined as follows:

$$\tau =4{{\displaystyle \int }}_0^1{{\displaystyle \int }}_0^{1}C\left(u_1,u_2\right)·c\left(u_1,u_2\right)\mathrm{d}{u}_{1}d{u}_2-1$$

(15)

where $c\left(u_1,u_2\right)$ is the copula density, assuming it exists.

To further assess the likelihood of joint extreme events, upper and lower tail dependence coefficients, ${\lambda }_U$ and ${\lambda }_L$, are defined as follows:

$${\lambda }_U=\underset{t\to 1^{-}}{lim}{\displaystyle \frac{1-2t+C\left(t,t\right)}{1-t}} \mathrm{and} {\lambda }_L= \underset{t\to 0^{+}}{lim}{\displaystyle \frac{C\left(t,t\right)}{t}}$$

(16)

The Student-t copula employed in this study exhibits symmetric, non-zero tail dependence, offering robustness in modeling extreme co-movements (Joe 2014; Nelsen 2006).

2.3.5. Estimation of Time-Varying Copula Parameters

To capture the evolving dependence structure among financial assets, time-varying copula parameters ${\theta }_t$ are estimated using a rolling-window MLE. At each time point, $t$, the copula parameters are estimated over a moving window of size $W$ (e.g., 2269 trading days). The local log-likelihood function at time $t$ is defined as follows:

$$L\left({\theta }_t\right)={\displaystyle \sum }_{k=1}^{d-1}{\displaystyle \sum }_{e\in E_k}{\displaystyle \sum }_{s=t-W+1}^{t}log\left[c_{j_e,\left.l_e\right|D_e}\left(F\left(\left.u_{j_e,s}\right|u_{D_e,s}\right),F\left(\left.u_{l_e,s}\right|u_{D_e,s}\right);{\theta }_{\left.j_e,l_e\right|D_e,s}\right)\right]$$

(17)

where $c_{j_e,\left.l_e\right|D_e}\left(\cdot ,·;\theta \right)$ is the bivariate copula density for edge $e$ in tree $k$, parameterized by $\theta$; ${\theta }_{\left.j_e,l_e\right|D_e,s}$ denotes the copula parameter vector at time $s$ for the conditional pair $\left(j_e,l_e|D_e\right)$; $E_k$ denotes the set of edges in tree $k$ of the vine structure; and $F\left(\left.u_{j_e,s}\right|u_{D_e,s}\right)$ and $F\left(\left.u_{l_e,s}\right|u_{D_e,s}\right)$ are the recursively computed conditional marginal distributions of the pseudo-observations (see Section 2.3.2).

This framework can accommodate various copula families, including Gaussian, Clayton, Gumbel, Frank, and Student-t, with selection based on information criteria such as AIC or Bayesian Information Criterion (BIC).

If the Student-t copula is selected for a given bivariate pair, the log-likelihood function becomes the following:

$$L\left({\theta }_t\right)={\displaystyle \sum }_{k=1}^{d-1}{\displaystyle \sum }_{e\in E_k}{\displaystyle \sum }_{s=t-W+1}^{t}log\left[c_t\left(F\left(\left.u_{j_e,s}\right|u_{D_e,s}\right),F\left(\left.u_{l_e,s}\right|u_{D_e,s}\right);{\rho }_{\left.j_e,l_e\right|D_e,s},{\nu }_{\left.j_e,l_e\right|D_e,s}\right)\right]$$

(18)

where the following applies: ${\rho }_{\left.j_e,l_e\right|D_e,s}$ is the time-varying correlation parameter; ${\nu }_{\left.j_e,l_e\right|D_e,s}$ is the degrees of freedom; $c_t\left(\cdot ,\cdot ,\rho ,\nu \right)$ is the bivariate Student-t copula density function, defined in Section 2.3.3; and the conditional marginals $F\left(\left.u_{j_e,s}\right|u_{D_e,s}\right)$ and $F\left(\left.u_{l_e,s}\right|u_{D_e,s}\right)$ are computed recursively, as before. This methodological framework and estimation strategy closely follow the approaches of Aas et al. (2009) and Brechmann and Czado (2013).

2.3.6. Model Selection and Vine Structure

The vine structure is selected using the Dißmann et al. (2013) algorithm, which uses empirical Kendall’s tau and AIC to guide pair-copula selection and tree construction. While the flexible R-vine is the default, a D-vine may be chosen when a natural economic ordering exists. This data-driven approach ensures both statistical fit and economic interpretability.

2.4. Forecasting Method

This study adopts a rolling-window approach with a fixed size of 2269 daily observations to estimate ARMA–GJR–GARCH, ARMA–GJR–GARCH–EVT, and dynamic R-vine copula models. At each step, the window advances by one day to re-estimate parameters and produce one-step-ahead forecasts. The marginal models generate forecasts of conditional means and variances for all eight assets. Based on these forecasts, two types of portfolios comprising $d$ assets, where $d$ = 5 and 6 (with the six-asset portfolio including a green bond), are constructed from the full set of eight. Concurrently, the dynamic R-vine copula is estimated using standardized residuals, and S pseudo-random samples are drawn via inverse Rosenblatt sampling to simulate joint returns. These simulations yield time-varying forecasts of portfolio means and covariances, dynamically updating the risk and return structure over 600 out-of-sample observations.

The 600-day window, representing approximately 20% of the total sample, was selected for out-of-sample analysis to ensure a sufficient period for backtesting performance while preserving estimation stability. While this fixed length is consistent with common practices in financial forecasting, future research could examine alternative window sizes to assess the robustness of model performance across different sample lengths.

2.5. Value-at-Risk Measures

This section introduces the value-at-risk (VaR) framework used to quantify potential portfolio losses under normal market conditions. VaR estimates are based on ARMA–GJR–GARCH and ARMA–GJR–GARCH–EVT forecasts, together with simulations from a dynamic R-vine copula, forming the basis for forward-looking risk and capital adequacy assessment.

This study deliberately selects specific VaR forecasting horizons to address both regulatory mandates and insurers’ practical risk management needs. The ten-day VaR aligns with international regulatory standards for market risk capital, notably Basel III, a benchmark influencing insurance solvency frameworks like the OIC’s. This horizon is critical for assessing capital adequacy and ensuring long-term financial resilience. Concurrently, the one-day VaR captures short-term market fluctuations, essential for daily risk monitoring, internal operational limits, and immediate liquidity management. Together, these two horizons provide a comprehensive view of risk, spanning day-to-day operational management to regulatory capital planning, thereby directly addressing insurers’ liquidity and solvency requirements.

In this study, VaR values are reported as the left-tail quantiles of returns, where negative values indicate potential losses at the specified confidence level. For consistency, all numerical results in tables are reported as negative values in line with the loss-sign convention, whereas the discussion in the text refers to the absolute magnitude of VaR when comparing risk levels.

2.5.1. ARMA–GJR–GARCH VaR (with Skewed Student-t)

To quantify market risk, one-day-ahead VaR estimates are obtained from the conditional mean and variance forecasts produced via the ARMA–GJR–GARCH model. Let ${\mu }_{t+1}$ and ${\sigma }_{t+1}^2$ denote the conditional mean and variance of asset returns at time $t+1$. Assuming the standardized residuals follow a skewed Student-t distribution (Hansen 1994), the VaR at confidence level $1-\alpha$ (left-tail probability $\alpha$) is computed as follows:

$${\mathrm{VaR}}_{t+1}^{\alpha }={\mu }_{t+1}+{\sigma }_{t+1}{q}_{\alpha , skewed-t}$$

(19)

where ${\mathrm{VaR}}_{t+1}^{\alpha }$ is the VaR for the next period $t+1$ at a confidence level of $\alpha$, ${\mu }_{t+1}$ is the conditional mean return forecast from the ARMA model for the next period $t+1$, ${\sigma }_{t+1}$ is the conditional standard deviation forecast from the GJR–GARCH model for the next period $t+1$, and $q_{\alpha , skewed-t}$ is the $\alpha$-quantile of the standardized skewed Student’s t-distribution with estimated skewness $\left(\eta \right)$ and degrees of freedom $\left(\nu \right)$ parameters. A 95% confidence level is applied for one-day VaR, in line with Thai regulations. For ten-day VaR, consistent with Basel’s 99% confidence level, a rolling-window generates 10 one-step-ahead forecasts from the ARMA–GJR–GARCH model.

2.5.2. ARMA–GJR–GARCH–EVT VaR

To estimate one-day-ahead VaR under stressed conditions, this study combines ARMA–GJR–GARCH filtering with EVT. Returns are first modeled using ARMA–GJR–GARCH with skewed Student-t innovations, and the resulting standardized residuals are fitted using the POT method with a GPD to capture tail extremes. To assess capital requirements during market stress, the one-day VaR at time $t+1$ is estimated at a 97.5% confidence level. This tail-focused approach enhances risk quantification by better modeling the distribution of extreme losses. The one-day VaR at time $t+1$ derived from the conditional EVT model is given by the following:

$${\mathrm{VaR}}_{t+1}^{\alpha }={\mu }_{t+1}+ {\sigma }_{t+1}\left[u+{\displaystyle \frac{\widehat{\beta }}{\widehat{\xi }}}\left[{\left({\displaystyle \frac{n}{N_u}}\left(1-\alpha \right)\right)}^{-\widehat{\xi }}-1\right]\right]$$

(20)

where the following applies: ${\mu }_{t+1}$ and ${\sigma }_{t+1}$ are the one-step-ahead forecasts of the conditional mean and standard deviation, respectively; $n$ is the total number of observations; $N_u$ is the number of observations exceeding the threshold $u$; and $\widehat{\xi }$ and $\widehat{\beta }$ are the estimated shape and scale parameters. This two-stage filtering and tail-modeling framework follows the extreme value approach of McNeil and Frey (2000).

2.5.3. Dynamic R-Vine Copula VaR

To estimate VaR under evolving market conditions, this study applies a dynamic R-vine copula to model time-varying dependencies among portfolios of five and six assets, each modeled using ARMA–GJR–GARCH with skewed Student-t innovations. The one-day portfolio VaR at a confidence level $\alpha$ is computed using a Monte Carlo simulation. At each time, $t$, a set of $S$ pseudo-random return vectors, ${\left\{r_{t+1}^{\left(s\right)}\right\}}_{s=1}^S$, is generated from the dynamic R-vine copula, conditioned on the current marginal forecasts. Each $r_{t+1}^{\left(s\right)}$ represents the $s^{th}$ simulated return vector drawn from the copula model. The simulated portfolio returns are then computed as follows:

$$R_{t+1}^{\left(s\right)}=w^T{r}_{t+1}^{\left(s\right)}$$

(21)

where $w$ is the vector of portfolio weights. The empirical $\alpha$-quantile of the simulated portfolio returns ${\left\{R_{t+1}^{\left(s\right)}\right\}}_{s=1}^S$ provides the one-day portfolio VaR estimate at time $t+1$:

$${\mathrm{VaR}}_{t+1}^{\alpha }=Quantil{e}_{\alpha }\left({\left\{R_{t+1}^{\left(s\right)}\right\}}_{s=1}^S\right)$$

(22)

where $Quantil{e}_{\alpha }$ denotes the empirical quantile at level $\alpha$, capturing left-tail portfolio risk. This simulation-based dynamic copula framework builds on the methodology developed by Aas et al. (2009) and Brechmann and Czado (2013).

This study constructs four portfolios—two for life insurers and two for non-life insurers—each comprising five conventional assets or six assets including green bonds. All portfolios are designed with two key objectives: duration matching, to align asset durations with insurer liabilities, and Sharpe ratio maximization, to optimize risk-adjusted returns. The combined use of VaR and Sharpe ratio metrics follows recent green bond portfolio research that demonstrates how ESG asset inclusion can improve risk-adjusted returns and reduce capital charges in regulated insurance environments (Han et al. 2024; Karim et al. 2024; Papavassiliou et al. 2025). Using the optimal weights, the one-day 95% VaR is estimated via a dynamic R-vine copula, which captures time-varying dependencies and non-Gaussian features. These estimates serve as proxies for capital requirements. Comparing five- and six-asset portfolios for both life and non-life insurers allows this study to assess whether green bond inclusion reduces capital needs and improves Sharpe ratios under evolving market conditions, consistent with Markowitz’s (1952) portfolio theory, adapted to the regulatory and liability constraints of the insurance sector.

2.6. Backtesting

Backtesting evaluates the accuracy of VaR models by comparing predicted losses with actual outcomes. This study applies two widely used methods: Kupiec’s unconditional coverage test and Christoffersen’s conditional coverage test, which assess model reliability from different perspectives (Ziggel et al. 2014). These model validation techniques follow recent applications in GARCH–EVT VaR forecasting contexts, such as applications in the Chinese banking sector and in Thailand’s financial markets (Chen et al. 2023; Likitratcharoen and Suwannamalik 2024).

2.6.1. Kupiec’s Unconditional Coverage Test

Kupiec’s test assesses whether the observed number of VaR exceedances aligns with the expected frequency implied by the model’s confidence level (Kupiec 1995). Let $N$ be the number of exceedances over $T$ trading days, and let $\alpha$ be the probability of an exceedance, dictated by the confidence level of the VaR model. Under the null hypothesis $H_0$, $N$ follows a binomial distribution with parameters $\left(T,\alpha \right)$. The likelihood ratio test statistic is calculated as follows:

$$L{R}_{UC}=-2\ln \left[{\displaystyle \frac{{\left(1-\alpha \right)}^{T-N}{\left(\alpha \right)}^N}{{\left(1-\frac{N}{T}\right)}^{T-N} {\left(\frac{N}{T}\right)}^N}} \right] \sim {\chi }_{1 }^2$$

(23)

If the calculated $L{R}_{UC}$ exceeds the critical value from the chi-squared distribution with 1 degree of freedom, the null hypothesis is rejected. This indicates that the model’s predicted exceedance frequency is inaccurate and may either underestimate or overestimate risk.

2.6.2. Christoffersen’s Conditional Coverage Test

While Kupiec’s test evaluates whether the overall frequency of VaR exceedances conforms to the model’s confidence level, it does not consider the timing or sequence of those exceedances. Christoffersen’s conditional coverage test addresses this limitation by assessing whether exceedances are independently distributed over time (Christoffersen 1998). The null hypothesis states that the likelihood of an exceedance on day $t+1$ is unaffected by whether one occurred on day $t$. To test this, the number of transitions between exceedance states across consecutive days is recorded. Specifically, $n_{ij}$ represents the number of transitions from state $i$ on day $t$ to state $j$ on day $t+1$, where $i$ and $j$ can be either 0 (no exceedance) or 1 (exceedance). This structure enables the estimation of conditional probabilities to determine whether exceedances occur independently over time. Based on these transitions, the following conditional probabilities are defined:

$${\pi }_{01}=P\left(I_{t+1}=1|I_t=0\right) =\mathrm{Pr}\left(Exceedance tomorrow | No exceedance today\right)$$

(24)

$${\pi }_{11}=P\left(I_{t+1}=1|I_t=1\right)=\mathrm{Pr}\left(Exceedance tomorrow | Exceedance today\right)$$

(25)

Under the assumption of independence, ${\pi }_{01}$ and ${\pi }_{11}$ should be equal and approximately equal to $\alpha$, the VaR model’s stated exceedance probability.

Christoffersen’s test uses a likelihood ratio statistic to compare the likelihood of the observed data under the independence assumption with the likelihood without this constraint:

$$L{R}_{CC}=2ln\left[{\left(1-{\pi }_{01}\right)}^{n_{00}}{\pi }_{01}^{n_{01}}{\left(1-{\pi }_{11}\right)}^{n_{10}}{\pi }_{11}^{n_{11}}\right]-2ln\left[{\left(1-\alpha \right)}^{T-N}{\alpha }^N\right] ~ {\chi }_2^2$$

(26)

where $N$ is the total number of exceedances in a sample of $T$ observations. If the $L{R}_{CC}$ statistic exceeds the critical value from the chi-squared distribution with two degrees of freedom, the null of independence is rejected. This indicates clustered exceedances and potential shortcomings in the VaR model.

2.7. Software Implementation

The models were implemented in R, leveraging libraries such as the tseries package to test the hypothesis of stationarity, the rugarch package to construct and estimate univariate GARCH models, the POT, ismev, and extRemes packages to perform extreme value theory (EVT) analyses, and the VineCopula package to model and estimate R-vine copula structures.

3. Empirical Results and Discussions

This section details the empirical findings of the study, beginning with the estimation results of the ARMA–GJR–GARCH models incorporating a skewed Student-t distribution for each of the eight assets: the SET index, the Dubai crude oil, the Thai bullion gold, the 3–7-year government bond index, the 7–10-year government bond index, the JPY/THB exchange rate, the property sector index, and the Bloomberg Barclays MSCI US green bond index. Subsequently, the analysis transitions to the ARMA–GJR–GARCH–EVT model, which leverages extreme value theory to model tail risk. Finally, the dynamic R-vine copula model is employed to evaluate dynamic correlations among the assets and their subsequent impact on portfolio VaR. The results for each model are discussed in detail, highlighting key findings and their implications for risk management within the Thai insurance industry.

3.1. ARMA–GJR–GARCH Estimation (with Skewed Student-t Distribution)

Table 2. Parameter estimation results of the ARMA–GJR–GARCH model (with skewed Student-t distribution).

Model	SET Index	Dubai Crude Oil	Thai Bullion Gold	3–7 TTM GOV	7–10 TTM GOV	JPY/THB Exchange Rate	Property Sector Index	Bloomberg Barclays MSCI US Green Bond Index
Mu (p-value)	1.45 × 10−4 (0.3180)	−3.75 × 10−6 (0.7511)	1.25 × 10−4 (0.3861)	1.13 × 10−4 (0.0000 ***)	1.13 × 10−4 (0.0003 ***)	−1.08 × 10−4 (0.2746)	−6.00 × 10−4 (0.0000 ***)	1.06 × 10−4 (0.0064 ***)
ar(1) (p-value)	−0.3985 (0.0000 ***)	−0.3621 (0.0000 ***)	−0.0863 (0.0000 ***)	0.6992 (0.0000 ***)	0.1954 (0.0000 ***)	−0.9976 (0.0000 ***)	0.0680 (0.0000 ***)	−0.0637 (0.0027 ***)
ar(2) (p-value)	0.2656 (0.0000 ***)	−1.0109 (0.0000 ***)		−0.9695 (0.0000 ***)			0.0599 (0.0000 ***)
ar(3) (p-value)	0.9411 (0.0000 ***)	−0.0531 (0.0000 ***)		0.2143 (0.0000 ***)			0.9025 (0.0000 ***)
ar(4) (p-value)							0.0157 (0.0000 ***)
ar(5) (p-value)							−0.0527 (0.0000 ***)
ma(1) (p-value)	0.4124 (0.0000 ***)	0.3101 (0.0000 ***)		−0.4425 (0.0021 ***)		0.9944 (0.0021 ***)	−0.0852 (0.0000 ***)
ma(2) (p-value)	−0.2468 (0.0000 ***)	1.0071 (0.0000 ***)		0.8271 (0.0000 ***)			−0.0263 (0.0000 ***)
ma(3) (p-value)	−0.9351 (0.0000 ***)						−0.8970 (0.0000 ***)
omega (p-value)	8.81 × 10−7 (0.0800 *)	5.99 × 10−6 (0.0242 **)	9.62 × 10−7 (0.0650 *)	8.42 × 10−9 (0.9801)	6.84 × 10−8 (0.8500)	9.40 × 10−7 (0.4100)	3.0010−6 (0.0672 *)	9.87 × 10−8 (0.7638)
alpha1 (p-value)	0.0155 (0.0039 ***)	0.0709 (0.0000 ***)	0.0669 (0.0000 ***)	0.0673 (0.0002 ***)	0.1357 (0.0000 ***)	0.0987 (0.0010 ***)	0.0177 (0.0010 ***)	0.069050 (0.0000 ***)
beta1 (p-value)	0.9201 (0.0000 ***)	0.8922 (0.0000 ***)	0.9417 (0.0000 ***)	0.9186 (0.0000 ***)	0.8857 (0.0000 ***)	0.8980 (0.0000 ***)	0.9065 (0.0000 ***)	0.918404 (0.0000 ***)
gamma 1	0.1087 (0.0000 ***)	0.0742 (0.0012 ***)	−0.0408 (0.0024 ***)	−0.0054 (0.6760)	−0.0451 (0.0447 **)	−0.0594 (0.0049 ***)	0.0858 (0.0049 ***)	−0.0091 (0.5132)
skew	0.9074 (0.0000 ***)	0.8939 (0.0000 ***)	1.0267 (0.0000 ***)	0.9698 (0.0000 ***)	0.9922 (0.0000 ***)	1.0269 (0.0000 ***)	0.9167 (0.0000 ***)	0.9103 (0.0000 ***)
shape	4.5028 (0.0000 ***)	4.7935 (0.0000 ***)	4.9194 (0.0000 ***)	4.6552 (0.0000 ***)	4.0896 (0.0000 ***)	5.6768 (0.0000 ***)	4.6055 (0.0000 ***)	6.8252 (0.0000 ***)
AIC	−7.0677	−4.9339	−6.8785	−11.391	−9.6517	−7.7985	−6.5029	−9.4954
Ljung–Box Test (p-value)	6.6342 (0.2318)	1.4770 (0.9574)	1.8907 (0.9176)	1.0713 (0.9831)	1.4362 (0.9606)	1.4830 (0.9570)	10.3583 (0.0420 **)	2.5347 (0.8326)
ARCH–LM Test (p-value)	7.2680 (0.07601)	1.5889 (0.8034)	1.9305 (0.7320)	1.3349 (0.8538)	1.0280 (0.9089)	0.0899 (0.9995)	12.6000 (0.0045 ***)	1.6175 (0.7975)

Note: *** significant at 0.01, ** significant at 0.05, * significant at 0.1.

presents the in-sample parameter estimates derived from the selected ARMA–GJR–GARCH models, employing a skewed Student-t distribution, for each asset. Model selection, guided by the AIC, resulted in distinct ARMA orders for different assets. The results show that ARMA(3,3)–GJR–GARCH(1,1) for the SET, ARMA(3,2)–GJR–GARCH(1,1) for the crude oil, ARMA(1,0)–GJR–GARCH(1,1) for the gold, ARMA(3,2)–GJR–GARCH(1,1) for the 3–7-year government bond, ARMA(1,0)–GJR–GARCH(1,1) for the 7–10-year government bond, ARMA(1,1)–GJR–GARCH(1,1) for the exchange rate, ARMA(5,3)–GJR–GARCH(1,1) for the property, and ARMA(1,0)–GJR–GARCH(1,1) for the green bond. The diverse ARMA orders suggest varying degrees of short-term dependencies in the return series of the assets.

A consistent observation across all assets is the presence of significant volatility clustering, evidenced by the near-unity sum of the ARCH and GARCH coefficients in the selected models. This reinforces the necessity of employing time-varying volatility models for effective risk management. Furthermore, the statistically significant and positive coefficients of lagged squared returns confirm strong ARCH effects, and the significant coefficients on the lagged conditional variance confirm strong GARCH effects, indicating that both past shock and past volatility information are critical for forecasting future volatility. These findings align with previous research that has documented persistent volatility in both developed and emerging markets (Floros 2007; Lin et al. 2020). This study builds upon these findings by demonstrating the applicability of GARCH models, specifically the GJR–GARCH, for capturing volatility dynamics relevant to investment risk management for insurers within the Thai insurance industry.

The GJR–GARCH specification captures asymmetries in volatility responses to shocks via the gamma coefficient. Most assets displayed statistically significant gamma estimates, though the sign and magnitude varied. A positive gamma, as seen in the SET, the crude oil, and the property, implies a leverage effect, where negative shocks increase volatility more than positive ones. A negative and significant gamma, observed in the gold, the 7–10-year government bond, and the exchange rate, aligns with the inverse leverage effect, where positive shocks have a stronger impact on volatility. In contrast, the 3–7-year government bond and the green bond had negative but statistically insignificant gamma estimates, indicating no discernible asymmetric effect for these assets. Moreover, the statistically significant skewness and shape parameters support the use of the skewed Student-t distribution, which accommodates both asymmetry and excess kurtosis in the standardized residuals. This specification improves model fit and yields more realistic volatility and risk estimates (Nugroho et al. 2021).

Diagnostic tests, including the Ljung–Box test on standardized squared residuals and the ARCH–LM test, generally support the adequacy of the selected ARMA–GJR–GARCH models for capturing volatility dynamics, as most assets exhibit no significant autocorrelation or residual ARCH effects (p-values > 0.05). An exception is the property, for which the Ljung–Box test indicates mild autocorrelation at higher lags, and the ARCH–LM test reveals significant residual ARCH effects. While such autocorrelation may be tolerable, the persistence of this heteroskedasticity suggests that additional modeling is needed to fully capture extreme volatility behavior.

Although the ARMA–GJR–GARCH model effectively captures time-varying volatility and asymmetric responses to shocks, it may fall short in modeling extreme tail events in this sector. To address this limitation, the next section introduces an EVT framework, which complements the GARCH model by explicitly focusing on the distribution of extreme returns. This two-stage approach enhances the ability to assess tail-related risks and improves the reliability of value-at-risk (VaR) estimates for risk management in the Thai insurance sector. By incorporating EVT, the model is better equipped to capture recent and extreme fluctuations in returns, thereby producing more accurate VaR forecasts across a range of confidence levels.

3.2. ARMA–GJR–GARCH–EVT Estimation for Tail-Risk Assessment

Accurate tailrisk modeling is crucial for capital adequacy, especially during market downturns. To enhance tail-risk estimation, this study integrates the ARMA–GJR–GARCH model with EVT, focusing on the left tail due to observed negative skewness and potential downside risk. The framework incorporates the skewed Student-t distribution to account for key stylized facts in financial time series such as asymmetry and leptokurtosis, inadequately captured by models assuming normality (Huang and Chinhamu 2014). By modeling asymmetric volatility via the GJR–GARCH structure and capturing skewness and excess kurtosis through skewed Student-t innovations, the approach offers a more nuanced and realistic representation of volatility and tail behavior.

After estimating the conditional mean and variance using the ARMA–GJR–GARCH specification, the POT approach from EVT is applied to model extreme losses in the standardized residuals. Selecting an appropriate threshold is a critical step: if set too low, non-extreme observations may be included, distorting tail estimates; if too high, the number of exceedances may be too small, increasing estimation variance and reducing reliability (Coles 2001). In line with the recent literature (Eita and Djemo 2022; Huang et al. 2017; Li 2017; McNeil and Frey 2000), this study adopted the 93rd-percentile as the threshold level. Lower thresholds, such as the 90th percentile, may include non-extreme observations that distort the GPD fit, while higher thresholds, such as the 95th, yield too few exceedances for stable estimation. At the chosen threshold, the sample averages 159 exceedances across asset classes, offering sufficient data for reliable modeling. For reference, the average number of exceedances was 227 at the 90th percentile and 114 at the 95th, supporting the 93rd percentile as an effective trade-off between stability and tail focus. This higher threshold is particularly suitable for stress testing in regulatory and solvency contexts that demand a focus on rare but impactful losses.

Across all asset classes, the selected threshold yields an average of approximately 159 exceedances, providing a stable sample size for tail modeling. Despite differences in absolute threshold values, the consistent exceedance count supports the robustness of the chosen threshold. As shown in

Table 3. Parameter estimation results of the ARMA–GJR–GARCH–EVT model.

	u	Nu	AIC	$\mathit{\beta }$ (Lower, Upper)	Standard $\mathbf{Error} \mathbf{of} \mathit{\beta }$	$\mathit{\xi }$ (Lower, Upper)	Standard $\mathbf{Error} \mathbf{of} \mathit{\xi }$	Distribution	KS Test
SET Index ARMA(3,3)–GJR–GARCH(1,1)	1.4735	159	223.150	0.6838 (0.5382, 0.8295)	0.0743	0.0755 (−0.0716, 0.2216)	0.0745	exponential	0.4553
Dubai Crude Oil ARMA(3,2)–GJR–GARCH(1,1)	1.4096	159	227.495	0.6464 (0.4938, 0.7990)	0.07779	0.1454 (−0.0337, 0.3245)	0.0914	exponential	0.9946
Thai Bullion Gold ARMA(1,0)–GJR–GARCH(1,1)	1.3811	159	161.983	0.5389 (0.4060, 0.6718)	0.0678	0.1213 (−0.0712, 0.3138)	0.0982	exponential	0.6723
3–7 TTM GOV ARMA(3,2)–GJR–GARCH(1,1)	1.4691	159	243.778	0.6979 (0.5128, 0.8829)	0.0944	0.1200 (−0.0957, 0.3357)	0.1101	exponential	0.3579
7–10 TTM GOV ARMA(1,0)–GJR–GARCH(1,1)	1.3433	159	211.324	0.7825 (0.6090, 0.9560)	0.0885	−0.0965 (−0.2553, 0.0624)	0.0810	exponential	0.8511
JPY/THB Exchange Rate ARMA(1,1)–GJR–GARCH(1,1)	1.3525	159	156.536	0.5445 (0.4181, 0.6710)	0.0645	0.0938 (−0.0794, 0.2670)	0.0884	exponential	0.9075
Property Sector Index ARMA(5,3)–GJR–GARCH(1,1)	1.3803	159	234.215	0.6320 (0.4805, 0.7835)	0.0773	0.1891 (0.0042, 0.3739)	0.0943	pareto	0.9991
Bloomberg Barclays MSCI US Green Bond Index ARMA(1,0)–GJR–GARCH(1,1)	1.4300	159	181.911	0.6146 (0.4806, 0.7485)	0.0683	0.0526 (−0.1003, 0.2056)	0.0780	exponential	0.9475

, the estimated shape parameter ($\xi$) is close to zero for most asset classes, suggesting that their tails are wellapproximated by an exponential distribution. However, the property exhibits distinctly heavier tails, with a positive and statistically significant shape parameter; this implies a Pareto-type distribution and greater exposure to extreme downside risk. The Kolmogorov–Smirnov goodness-of-fit test supports these findings, with p-values above 0.05 for the exponential fit in most cases, while a heavier-tailed model provides a better fit for the property. These results confirm the effectiveness of the ARMA–GJR–GARCH–EVT framework in capturing heterogeneous tail risks across asset classes, which is vital for robust investment risk assessment.

This is particularly important in light of Section 3.1, where the property exhibited residual ARCH effects even after modeling with ARMA–GJR–GARCH and skewed Student-t distribution. The incorporation of EVT directly addresses these residual tail risks by explicitly modeling extreme losses that conventional GARCH structures may not fully capture. The ARMA–GJR–GARCH–EVT framework is thus employed specifically to estimate capital requirements under stress scenarios, focusing on the extreme downside risks faced by insurers.

Notably, the findings underscore the inadequacy of assuming normally distributed returns, as such assumptions can substantially underestimate capital requirements for Thai insurers during market stress, especially given the fat tails and skewness typical of financial return distributions. The GJR–GARCH component captures the asymmetric volatility response to negative shocks, a well-documented phenomenon in financial markets, while the ARMA component accounts for autocorrelation in return series. This two-stage modeling framework improves the accuracy of VaR estimates and facilitates more prudent and risk-sensitive capital allocation.

In the next section, the analysis is extended by incorporating dynamic dependence structures through R-vine copulas, enabling realistic modeling of time-varying and nonlinear relationships across asset classes in a diversified investment environment.

3.3. R-Vine Copula Estimation

This section presents empirical results from R-vine copula models for life and non-life insurer portfolios. Building on the ARMA–GJR–GARCH marginal models discussed in Section 3.1, the analysis captures nonlinear and asymmetric dependencies among financial assets and evaluates the impact of green bond inclusion on diversification, capital adequacy, and risk-adjusted returns. R-vine copulas with Student-t pairings effectively model tail dependencies, critical for portfolio risk management across diverse financial assets in extreme markets.

3.3.1. Portfolio Analysis for Life Insurers

This subsection presents R-vine copula results for life insurer portfolios, comparing a five-asset baseline with a six-asset version that includes green bonds. Both portfolios are optimized for the Sharpe ratio, meet capital requirements, and align with life insurers’ long-term liabilities. The analysis evaluates whether green bond inclusion enhances diversification, reduces tail risk, and improves overall portfolio performance.

The results of the copula estimations are summarized in

Table 4. R-vine copula estimation for life insurers.

D-Vine Copula Estimation for the Five-Asset Portfolio
	Copula  $\mathit{C}\left(\mathbf{\cdot }\right)$	Edge  ${\mathit{E}}_{\mathit{i}}$	Parameter 1  $\mathit{\rho }$	Parameter 2  $\nu$	Tau  $\mathit{\tau }$	Lower Tail  ${\mathit{\lambda }}_{\mathbf{1}}$	Upper Tail  ${\mathit{\lambda }}_{\mathbf{2}}$
Tree 1	t	1,3	0.98	19.96	0.87	0.64	0.64
	t	2,4	0.82	10.59	0.62	0.31	0.31
	t	5,1	−0.91	8.91	−0.72	0.00	0.00
	t	5,2	0.95	3.38	0.80	0.75	0.75
Tree 2	t	5,3|1	−0.65	7.55	−0.45	0.00	0.00
	t	5,4|2	0.46	5.83	0.31	0.16	0.16
	t	2,1|5	−0.03	30.00	−0.02	0.00	0.00
Tree 3	t	2,3|5,1	−0.32	13.77	−0.20	0.00	0.00
	t	1,4|5,2	−0.79	7.20	−0.58	0.00	0.00
Tree 4	t	4,3|2,5,1	0.14	18.69	0.09	0.00	0.00
Log-likelihood		7733.54
AIC		−15,427.08
BIC		−15,312.54
D-vine Copula Estimation for the Six-Asset Portfolio
	Copula $\mathit{C}\left(\mathbf{\cdot }\right)$	Edge  ${\mathit{E}}_{\mathit{i}}$	Parameter1  $\mathit{\rho }$	Parameter2  $\mathit{\nu }$	Tau  $\mathit{\tau }$	Lower Tail  ${\mathit{\lambda }}_{\mathbf{1}}$	Upper Tail  ${\mathit{\lambda }}_{\mathbf{2}}$
Tree 1	t	1,3	0.98	19.96	0.87	0.64	0.64
	t	2,4	0.82	10.59	0.62	0.31	0.31
	t	5,1	−0.91	8.91	−0.72	0.00	0.00
	t	6,2	0.93	6.04	0.75	0.62	0.62
	t	6,5	0.92	8.99	0.74	0.53	0.53
Tree 2	t	5,3|1	−0.65	7.55	−0.45	0.00	0.00
	t	6,4|2	−0.32	10.62	−0.21	0.00	0.00
	t	6,1|5	0.50	8.08	0.34	0.12	0.12
	t	5,2|6	0.67	5.15	0.47	0.31	0.31
Tree 3	t	6,3|5,1	−0.38	15.69	−0.25	0.00	0.00
	t	5,4|6,2	0.61	5.40	0.42	0.26	0.26
	t	2,1|6,5	−0.29	13.39	−0.18	0.00	0.00
Tree 4	t	2,3|6,5,1	−0.14	23.76	−0.09	0.00	0.00
	t	1,4|5,6,2	−0.69	8.01	−0.49	0.00	0.00
Tree 5	t	4,3|2,6,5,1	0.09	19.54	0.06	0.00	0.00
Log-likelihood		9545.86
AIC		−19,031.73
BIC		−18,859.92

. Both configurations use D-vine Student-t copulas, crucial for managing extreme market risks by capturing nonlinear, asymmetric, and tail-dependent relationships. The upper panel of Table 4 presents the five-asset portfolio, comprising the SET index (1), the Thai bullion gold (2), the property sector index (3), the 7–10-year government bond index (4), and the JPY/THB exchange rate (5). The strongest unconditional dependence is observed between the SET and the property ($\tau$ = 0.87), reflecting equity market concentration. A strong positive dependence between the gold and the exchange rate ($\tau$ = 0.80, ${\lambda }_1$ = ${\lambda }_2$ = 0.75) reflects safe-haven behavior, while a notable negative dependence between the SET and the exchange rate ($\tau$ = −0.72) suggests diversification potential. As the R-vine structure progresses, tail dependence and conditional relationships weaken, indicating that extreme co-movements are concentrated among a few key asset pairs. The estimated degrees of freedom ($\nu$) range from 3.38 to 30, reflecting varying tail heaviness across the dependence structure. Overall, the five-asset model exhibits strong statistical performance, with the log-likelihood at 7733.54, the AIC at −15,427.08, and the BIC at −15,312.54, forming a robust baseline for evaluating the added value of green bond inclusion in the six-asset configuration.

The lower panel of Table 4 presents the six-asset portfolio, which includes the Bloomberg Barclays MSCI US green bond index (6). The green bond significantly alters the dependence structure. In Tree 1, the green bond exhibits strong unconditional positive dependence with the gold ($\tau$ = 0.75) and the exchange rate ($\tau$ = 0.74), along with substantial symmetric tail dependence (${\lambda }_1$ = ${\lambda }_2$ = 0.62 and 0.53, respectively), positioning them alongside traditional safe-haven assets and reinforcing their stabilizing role during market stress. In higher-order trees, the green bond displays moderate to weak conditional dependencies, such as a modest positive link with the SET ($\tau$ = 0.34), a weak negative association with the 7–10-year government bond ($\tau$ = −0.21), and a slightly stronger negative relationship with the property ($\tau$ = −0.25). These relationships suggest that the green bond provides differentiated exposure to macroeconomic risks and may help mediate cross-asset risk transmission. By Tree 5, dependencies are negligible, highlighting their role in diffusing residual co-movement. Statistically, the six-asset model outperforms the five-asset configuration, with the log-likelihood of 9545.86, the AIC of −19,031.73, and the BIC of −18,859.92. These improvements indicate that green bonds enrich the dependence structure, enhance diversification, and strengthen tail-risk modeling. This clearly supports capital-efficient and resilient portfolio design aligned with sustainability-oriented investment objectives.

Table 5. Optimal portfolio weights based on Sharpe ratio maximization for life insurers.

Optimal Portfolio Weights Based on Sharpe Ratio Maximization for the Five-Asset Portfolio
Asset	SET Index	Thai Bullion Gold	PropertySector Index	7–10 TTM GOV		JPY/THB Exchange Rate
Weight	0.30	0.05	0.05	0.50		0.10
Optimal Portfolio Weights Based on Sharpe Ratio Maximization for the Six-Asset Portfolio
Asset	SET Index	Thai Bullion Gold	Property Sector Index	7–10 TTM GOV	JPY/THB Exchange Rate	Bloomberg Barclays MSCI US Green Bond Index
Weight	0.20	0.05	0.10	0.50	0.05	0.10

presents the optimal portfolio weights for life insurers under Sharpe ratio maximization, comparing a traditional five-asset configuration with a six-asset portfolio that includes the green bond. In the five-asset portfolio, the 7–10-year government bond receives the highest allocation (50%) due to its low volatility and strong duration-matching benefits. The SET accounts for 30%, while the gold and the property are each allocated 5%. The exchange rate receives a 10% weight, offering diversification and safe-haven characteristics. The introduction of the green bond in the six-asset portfolio reshapes the asset mix while preserving portfolio stability. The 7–10-year government bond remains at 50%, while the SET is reduced to 20%. The green bond and the property are each allocated 10%, with the gold and the exchange rate maintaining their 5% weights. This reallocation underscores green bonds’ contribution to diversification and resilience, while supporting ESG-aligned objectives.

These optimized in-sample weights provide a baseline for the subsequent dynamic analysis. The next step evaluates time-varying portfolio performance using 600-day rolling-window forecasts of VaR and the Sharpe ratio for life insurers.

3.3.2. Portfolio Analysis for Non-Life Insurers

This subsection presents R-vine copula results for non-life insurer portfolios, built using the same Sharpe ratio optimization and duration-matching approach as applied to life insurers. Due to their shorter-duration liabilities, non-life insurers require greater sensitivity to liquidity and volatility. While return optimization remains relevant, capital preservation and regulatory compliance take precedence.

Two portfolios are analyzed: a five-asset baseline and a six-asset version including green bonds. The five-asset portfolio uses a D-vine structure, while the six-asset R-vine captures increased interdependencies with green bond inclusion. Both utilize Student-t copulas to model nonlinear, asymmetric, tail-dependent relationships, crucial under market stress. The upper panel of

Table 6. R-vine copula estimation for non-life insurers.

D-vine Copula Estimation for the Five-Asset Portfolio
	Copula  $\mathit{C}\left(\mathbf{\cdot }\right)$	Edge  ${\mathit{E}}_{\mathit{i}}$	Parameter 1  $\mathit{\rho }$	Parameter 2  $\mathit{\nu }$	Tau  $\mathit{\tau }$	Lower Tail  ${\mathit{\lambda }}_{\mathbf{1}}$	Upper Tail  ${\mathit{\lambda }}_{\mathbf{2}}$
Tree 1	t	1,3	0.98	20.16	0.87	0.64	0.64
	t	2,4	−0.82	12.52	−0.61	0.00	0.00
	t	5,1	−0.91	8.93	−0.72	0.00	0.00
	t	5,2	−0.97	3.95	−0.83	0.00	0.00
Tree 2	t	5,3|1	−0.65	7.55	−0.45	0.00	0.00
	t	5,4|2	0.16	12.37	0.11	0.01	0.01
	t	2,1|5	0.32	14.47	−0.21	0.01	0.01
Tree 3	t	2,3|5,1	0.33	13.44	0.21	0.02	0.02
	t	1,4|5,2	−0.81	6.31	−0.60	0.00	0.00
Tree 4	t	4,3|2,5,1	0.22	10.50	0.14	0.00	0.00
Log-likelihood		8037.66
AIC		−16,035.31
BIC		−15,920.77
R-vine Copula Estimation for the Six-Asset Portfolio
	Copula  $\mathit{C}\left(\mathbf{\cdot }\right)$	Edge  ${\mathit{E}}_{\mathit{i}}$	Parameter1  $\mathit{\rho }$	Parameter2  $\mathit{\nu }$	Tau  $\mathit{\tau }$	Lower Tail  ${\mathit{\lambda }}_{\mathbf{1}}$	Upper Tail  ${\mathit{\lambda }}_{\mathbf{2}}$
Tree 1	t	1,3	0.98	20.16	0.87	0.64	0.64
	t	5,1	−0.91	8.93	−0.72	0.00	0.00
	t	5,2	−0.97	3.95	−0.83	0.00	0.00
	t	6,4	−0.92	4.71	−0.74	0.00	0.00
	t	6,5	0.92	8.93	0.74	0.54	0.54
Tree 2	t	5,3|1	−0.65	7.55	−0.45	0.00	0.00
	t	2,1|5	0.32	14.47	0.21	0.01	0.01
	t	6,2|5	−0.28	10.77	−0.18	0.00	0.00
	t	5,4|6	0.24	15.45	0.15	0.01	0.01
Tree 3	t	2,3|5,1	0.33	13.44	0.21	0.02	0.02
	t	6,1|2,5	0.62	11.48	0.42	0.11	0.11
	t	4,2|6,5	0.07	30.00	0.05	0.00	0.00
Tree 4	t	6,3|2,5,1	−0.26	26.47	−0.17	0.00	0.00
	t	4,1|6,2,5	−0.44	17.91	−0.29	0.00	0.00
Tree 5	t	4,3|6,2,5,1	0.32	17.94	0.20	0.01	0.01
Log-likelihood		9797.16
AIC		−19,534.31
BIC		−19,362.50

presents the five-asset portfolio, comprising the SET index (1), the Dubai crude oil (2), the property sector index (3), the 3–7-year government bond index (4), and the JPY/THB exchange rate (5). The D-vine structure reveals the strongest unconditional dependence between the SET and the property ($\tau$ = 0.87, ${\lambda }_1$ = ${\lambda }_2$ = 0.64), reflecting high co-movement within the equity market. Notable negative dependencies are observed between the exchange rate and both the SET ($\tau$ = −0.72) and the crude oil ($\tau$ = −0.83), highlighting the diversification potential of currency exposure. A moderate negative relationship between the crude oil and the 3–7-year government bond ($\tau$ = −0.61) suggests opposing responses to macroeconomic shocks such as inflation or interest rate changes. As the vine progresses, dependencies weaken. For instance, Tree 3 reports a weak positive link between the crude oil and the property ($\tau$ = 0.21) and a moderately negative relationship between the SET and the 3–7-year government bond ($\tau$ = −0.60), indicating differentiated behavior under stress. Tail dependence is concentrated in the first tree. The model demonstrates strong statistical performance, with the log-likelihood of 8037.66, the AIC of −16,035.31, and the BIC of −15,920.77.

The lower panel of Table 6 presents the six-asset portfolio, incorporating the Bloomberg Barclays MSCI US green bond index (6). With increased interdependencies, a general R-vine structure is adopted. In Tree 1, the green bond exhibits strong positive dependence with the exchange rate ($\tau$ = 0.74, ${\lambda }_1$ = ${\lambda }_2$ = 0.54) and a strong negative dependence with the 3–7-year government bond ($\tau$ = −0.74), indicating their potential as a hedge against interest-rate-sensitive assets. In higher-order trees, the green bond shows moderate conditional dependence with the SET ($\tau$ = 0.42) and weak negative relationships with the property ($\tau$ = −0.17) and the crude oil ($\tau$ = −0.18), suggesting differentiated macroeconomic exposure. The six-asset model improves the statistical fit, with the log-likelihood of 9797.16, the AIC of −19,534.31, and the BIC of −19,362.50. These results confirm that green bonds enhance the dependence structure, improve diversification, and contribute to tail-risk mitigation. This supports the construction of capital-efficient and resilient portfolios for non-life insurers while aligning with sustainable investment strategies (Abakah et al. 2022).

Table 7. Optimal portfolio weights based on Sharpe ratio maximization for non-life insurers.

Optimal Portfolio Weights Based on Sharpe Ratio Maximization for the Five-Asset Portfolio
Asset	SET Index	Dubai Crude Oil	Property Sector Index	7–10 TTM GOV		JPY/THB Exchange Rate
Weight	0.05	0.05	0.05	0.55		0.30
Optimal Portfolio Weights Based on Sharpe Ratio Maximization for the Six-Asset Portfolio
Asset	SET Index	Dubai Crude Oil	Property Sector Index	7–10 TTM GOV	JPY/THB Exchange Rate	Bloomberg Barclays MSCI US Green Bond Index
Weight	0.10	0.05	0.05	0.40	0.30	0.10

presents the optimal portfolio weights for non-life insurers under Sharpe ratio maximization, comparing a traditional five-asset configuration with a six-asset portfolio that includes green bonds. In the five-asset portfolio, the 3–7-year government bond receives the highest allocation (55%), reflecting its role as low-risk, liquid instrument aligned with non-life insurers’ short-duration liabilities. The exchange rate accounts for 30%, offering diversification and safe-haven benefits under volatile conditions. The remaining 15% is equally distributed across the SET, the crude oil, and the property, reflecting measured exposure to higher-volatility assets. In the six-asset portfolio, green bond inclusion reshapes the allocation while preserving the conservative structure. The 3–7-year government bond is reduced to 40%, while the green bond is allocated 10%, highlighting their role in enhancing stability and supporting ESG mandates. The exchange rate remains at 30%, the SET increases to 10%, and the crude oil and the property retain 5% each. This reallocation reflects a strategic response to the risk–return dynamics introduced via green bonds and supports capital efficiency under regulation-sensitive investment policies.

Consistent with the life insurer analysis, these in-sample weights are used as inputs for a 600-day rolling-window estimation. This dynamic approach captures the evolving risk–return profile of non-life insurer portfolios through forecasts of VaR and the Sharpe ratio.

3.4. Value-at-Risk Backtesting

This section evaluates the predictive performance of the VaR forecasts using two established backtesting procedures: the Kupiec unconditional coverage test and the Christoffersen conditional coverage test. Backtesting serves as a critical validation step, assessing whether the VaR estimates adequately capture potential losses and comply with solvency capital requirements (Smolović et al. 2017). The analysis employs a rolling-window estimation approach, as described in Section 2.4, to generate 600 daily out-of-sample VaR forecasts for each model under review.

Three modeling frameworks are evaluated across different confidence levels and horizons. (1) ARMA–GJR–GARCH with skewed Student-t innovations: Captures volatility clustering, asymmetric responses, and fat-tailed return distributions. It provides one-day-ahead VaR forecasts at the 95% confidence level, consistent with the requirement of the Thai OIC, and ten-day-ahead forecasts at the 99% level, aligned with Basel standards. These estimates reflect the capital buffers that life and non-life insurers are required to hold at specified confidence levels under financial solvency frameworks. (2) ARMA–GJR–GARCH–EVT hybrid model: Combines conditional volatility modeling with EVT to improve tail-risk estimation, especially under extreme market conditions. It generates one-day-ahead VaR forecasts at the 97.5% confidence level, a threshold commonly used in insurance sector stress testing (Paraschiv et al. 2020), offering more conservative and robust estimates for capital adequacy. (3) Dynamic R-vine copula model: Captures time-varying, nonlinear dependencies among asset returns. Dynamically estimated copula parameters are used to forecast one-day-ahead VaR at the 95% confidence level and to compute Sharpe ratios based on optimized weights for life and non-life insurer portfolios.

3.4.1. ARMA–GJR–GARCH Model (with Skewed Student-t Innovations) and ARMA–GJR–GARCH–EVT Performance

This subsection presents backtesting results for two VaR forecasting models: the ARMA–GJR–GARCH with skewed Student-t innovations and its tail-risk-enhanced extension incorporating EVT. Both models are estimated using a 600-day rollingwindow and evaluated using the Kupiec unconditional coverage and Christoffersen conditional coverage tests to ensure forecast reliability for regulatory compliance and capital adequacy.

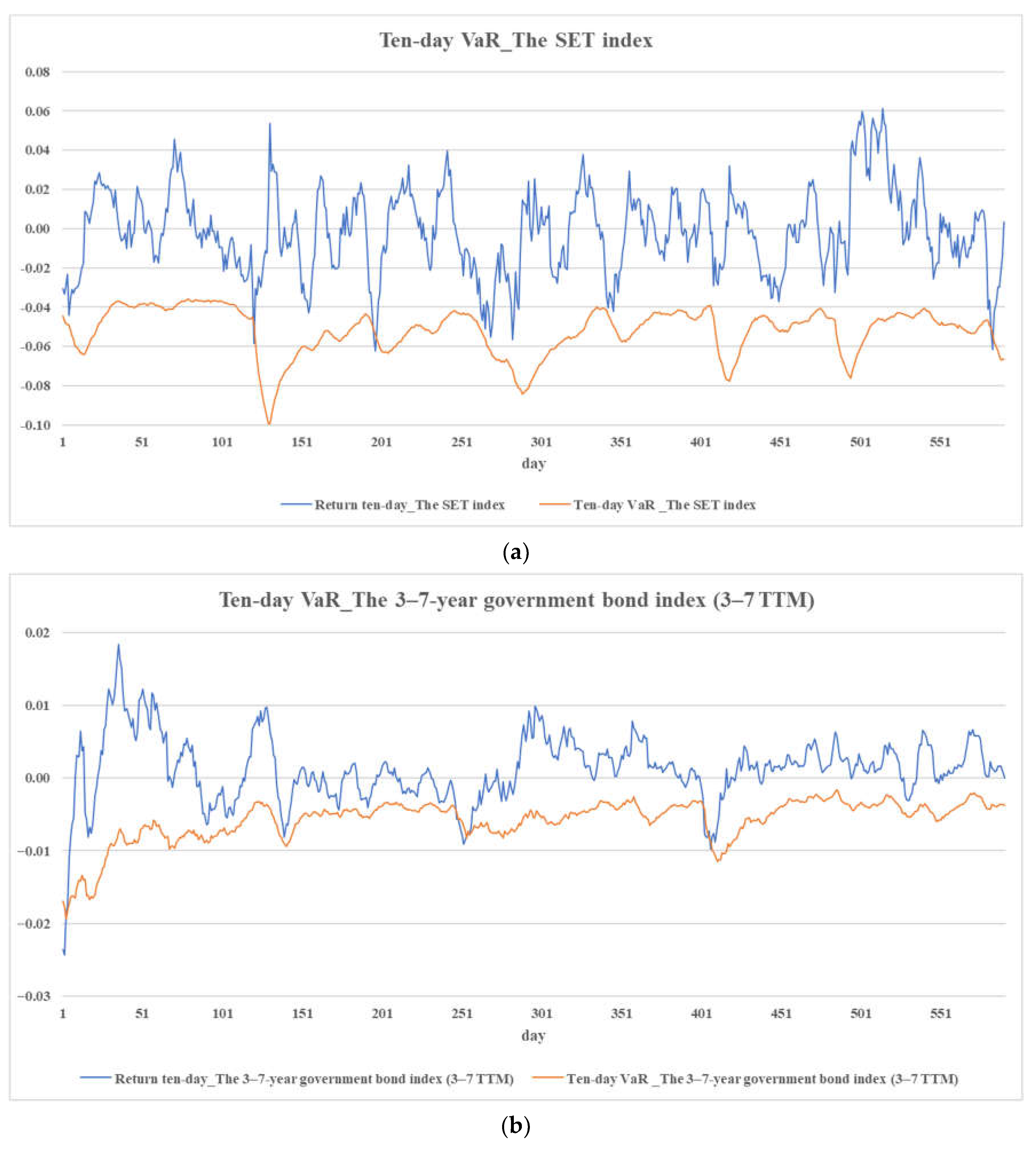
The ARMA–GJR–GARCH model generates one-day-ahead VaR forecasts at the 95% confidence level and ten-day-ahead forecasts at the 99% level. It effectively captures asymmetric volatility and fat tails, producing accurate forecasts for most assets. As shown in

Table 8. One-day-ahead VaR and ten-day-ahead VaR backtesting: ARMA–GJR–GARCH model (with skewed Student-t innovations) performance.

Asset Model	SET Index ARMA(3,3) –GJR–GARCH (1,1)	Dubai Crude Oil ARMA(3,2) –GJR–GARCH (1,1)	Thai Bullion Gold ARMA(1,0) –GJR–GARCH (1,1)	3–7 TTM GOV ARMA(3,2) –GJR–GARCH (1,1)	7–10 TTM GOV ARMA(1,0) –GJR–GARCH (1,1)	JPY/THB Exchange Rate ARMA(1,1) –GJR–GARCH (1,1)	Property Sector Index ARMA(5,3) –GJR–GARCH (1,1)	Bloomberg Barclays MSCI US Green Bond Index ARMA(1,0) –GJR–GARCH (1,1)
Average One-day-ahead VaR at 95%	−1.16%	−3.38%	−1.34%	−0.14%	−0.31%	−0.94%	−1.49%	−0.65%
Observed Exceedance Rate	4.17%	5.17%	4.00%	5.17%	3.50%	4.50%	3.83%	5.50%
Kupiec Test	0.928	0.035	1.352	0.035	3.161	0.326	1.863	0.306
Kupiec’s p-value	0.335	0.852	0.245	0.852	0.075 *	0.568	0.172	0.580
Christoffersen Test	0.912	0.327	1.182	0.140	4.764	0.361	1.855	0.337
Christoffersen’s p-value	0.634	0.849	0.554	0.932	0.092 *	0.835	0.395	0.845
Average ten-day-ahead VaR at 99%	−5.19%	−14.93%	−5.92%	−0.58%	−1.34%	−4.29%	−6.70%	−2.86%
Observed Exceedance Rate	0.85%	0.17%	0.85%	2.03%	1.52%	0.51%	0.68%	0.68%
Kupiec Test	0.149	6.308	0.149	4.882	1.407	1.766	0.703	0.703
Kupiec’s p-value	0.699	0.012 **	0.699	0.027 **	0.236	0.184	0.402	0.402
Christoffersen Test	4.035	4.958	3.594	3.546	0.960	4.958	4.035	5.452
Christoffersen’s p-value	0.133	0.084 *	0.139	0.170	0.618	0.084 *	0.133	0.065 *

Note: ** significant at 0.05, * significant at 0.1.

and Figure 1 and Figure 2, most assets pass both backtests. Minor exceptions include the 7–10-year government bond, with p-values below 0.1, suggesting mild underestimation of risk. For the ten-day-ahead horizon, Kupiec test violations are observed for the crude oil and the 3–7-year government bond, while the Christoffersen test flags the crude oil, the exchange rate, and the green bond, indicating areas for improvement.

To enhance tail-risk estimation, the ARMA–GJR–GARCH–EVT model forecasts one-day-ahead VaR at the 97.5% confidence level.

Table 9. One-day-ahead VaR backtesting: ARMA–GJR–GARCH–EVT model performance.

Asset Model	SET Index ARMA(3,3) –GJR–GARCH (1,1)–EVT	Dubai Crude Oil ARMA(3,2) –GJR–GARCH (1,1)–EVT	Thai Bullion Gold ARMA(1,0) –GJR–GARCH (1,1)–EVT	3–7 TTM GOV ARMA(3,2) –GJR–GARCH (1,1)–EVT	7–10 TTM GOV ARMA(1,0) –GJR–GARCH (1,1)–EVT	JPY/THB Exchange Rate ARMA(1,1) –GJR–GARCH (1,1)–EVT	Property Sector Index ARMA(5,3) –GJR–GARCH (1,1)–EVT	Bloomberg Barclays MSCI US Green Bond Index ARMA(1,0) –GJR–GARCH (1,1)–EVT
Average One-day-ahead VaR at 97.5%	−1.56%	−4.46%	−1.64%	−0.21%	−0.43%	−1.09%	−1.91%	−0.84%
Observed Exceedance Rate	2.00%	2.00%	2.67%	2.00%	2.33%	3.67%	1.83%	2.83%
Kupiec Test	0.660	0.660	0.067	0.660	0.070	2.936	1.204	0.262
Kupiec’s p-value	0.417	0.417	0.796	0.417	0.791	0.087 *	0.273	0.609
Christoffersen Test	2.809	1.989	0.612	6.608	1.359	2.389	3.838	2.605
Christoffersen p-value	0.245	0.370	0.736	0.037 **	0.507	0.303	0.147	0.272

Note: ** significant at 0.05, * significant at 0.1.

and Figure 3 present results that demonstrate strong model performance, with exceedance rates generally aligning with expectations. Notable exceptions include the exchange rate (Kupiec p-value of 0.087) and the 3–7-year government bond (Christoffersen p-value of 0.037), indicating some inconsistency in the timing of exceedances.

The green bond exhibits one-day-ahead VaR magnitudes of 0.65% under the ARMA–GJR–GARCH model and 0.84% under the EVT-enhanced specification. These values are greater than those of the 3–7-year (0.14%, 0.21%) and the 7–10-year (0.31%, 0.43%) Thai sovereign bonds but remain lower than the SET (1.16%, 1.56%). Compared to other asset classes, the green bond also demonstrates lower risk than the crude oil (3.38%, 4.46%), the gold (1.34%, 1.64%), the exchange rate (0.94%, 1.09%), and the property sector (1.49%, 1.91%). Over a ten-day-ahead horizon at the 99% confidence level, the green bond’s VaR magnitude is 2.86%, exceeding those of the 3–7-year (0.58%) and the 7–10-year (1.34%) government bonds but remaining below riskier assets such as the SET (5.19%), gold (5.92%), and crude oil (14.93%).

Despite some discrepancies, both models provide valuable insights. The ARMA–GJR–GARCH model is well suited to routine risk monitoring, while its EVT-enhanced extension improves reliability under stressed market conditions. One-day-ahead VaR magnitudes from the GARCH model range from 0.14% to 3.38%, and ten-day-ahead estimates range from 0.58% to 14.93%. The SET’s average ten-day-ahead VaR magnitude is 5.19%, exceeding the typical range in developed markets (Degiannakis et al. 2014), supporting the case for localized capital adequacy standards. The EVT model yields higher one-day-ahead VaR magnitudes—from 0.21% to 4.46%—and shows the SET at 1.56%, below the 2.60–3.99% range observed in developed economies (Echaust and Just 2020), indicating differences in volatility or capital regulation.

The relatively higher VaR magnitude of the green bond in this study, compared to conventional Thai government bonds, suggests that it may not appear to be a lower-risk asset when considered in isolation. This contrasts with findings from developed markets, such as Liaw (2020), which describe a “greenium” effect, characterized by lower yields and reduced perceived risk driven by sustained ESG demand. However, such results are typically reported within the same market, credit tier, or issuer type. In contrast, this study compares an international green bond with Thai sovereign bonds, representing a cross-jurisdictional and cross-credit-category assessment. The elevated VaR magnitude observed for green bonds may, therefore, reflect differences in market structure, issuer composition, duration exposure, and currency denomination, rather than a true absence of the greenium effect.

While the green bond may not appear lower risk than Thai government bonds on a standalone basis, it exhibits lower capital requirements than other asset classes discussed earlier. Its predominantly negative dependence with other assets, as revealed by the R-vine copula analysis, suggests potential diversification benefits. The next subsection examines this potential by evaluating portfolio-level risk and return through rollingwindow Sharpe ratios and VaR forecasts.

3.4.2. Performance Evaluation of the Dynamic R-Vine Copula Model: Rolling-Window Sharpe Ratios and VaR Forecasts

This section assesses the dynamic R-vine copula model’s performance in forecasting one-day-ahead VaR at the 95% confidence level and calculating Sharpe ratios using a 600-day rolling-window. The model combines ARMA–GJR–GARCH marginal models with skewed Student-t innovations and a dynamic copula to capture time-varying, asymmetric dependencies among assets. This approach is valuable for insurers managing portfolio risk in volatile markets while aligning investments with solvency and sustainability goals. Unlike univariate models, R-vine copulas capture evolving nonlinear interdependencies, making them suitable for life and non-life insurers with distinct asset-liability management and risk-adjusted return objectives.

Table 10. Performance comparison of R-vine copula models: Sharpe ratio and VaR backtesting.

	Portfolio Type	Average Sharpe Ratio	% of Windows with Higher Sharpe Ratio	Average One-Day-Ahead VaR (95%)	% of Windows with Lower One-Day-Ahead VaR
Life insurer portfolios	Five-Asset Portfolio	−0.0432	19.50%	−0.1576%	39.67%
	Six-Asset Portfolio	0.0063	80.50%	−0.1428%	60.33%
Non-life insurer portfolios	Five-Asset Portfolio	−0.0928	39.33%	−0.1004%	66.17%
	Six-Asset Portfolio	−0.0441	60.67%	−0.1264%	33.83%

presents rolling performance results for life and non-life portfolios with and without green bonds. For life insurers, green bond inclusion significantly enhances portfolio efficiency. The average Sharpe ratio rises from −0.0432 to 0.0063, while the average one-day-ahead VaR magnitude decreases from 0.1576% to 0.1428%, indicating both enhanced risk-adjusted returns and lower capital requirements. The six-asset portfolio achieves a higher Sharpe ratio in 80.50% of rolling windows and records a lower VaR magnitude in 60.33%, demonstrating meaningful diversification benefits. These findings align with those of Iglesias-Casal et al. (2025) and Gupta et al. (2025), supporting the role of green bonds as dual contributors to portfolio performance and solvency for life insurers. Although the improvement in the average Sharpe ratio is numerically modest, even marginal increases can be economically meaningful in a regulatory context where small changes in capital efficiency may affect risk budgets, reserve requirements, or portfolio allocation decisions. Moreover, the consistent outperformance across a majority of rolling windows underscores the reliability of diversification benefits over time.

For non-life insurers, the six-asset portfolio delivers a moderate improvement in the average Sharpe ratio, increasing from −0.0928 to −0.0441. Additionally, 60.67% of rolling windows exhibit higher Sharpe ratios, underscoring the presence of diversification benefits. However, this performance gain is accompanied by a slight rise in downside risk, as the average one-day-ahead VaR magnitude increases from 0.1004% to 0.1264%. For insurers that prioritize short-term liquidity and volatility control, the trade-off may still be justifiable, particularly for those with a higher risk appetite who are seeking enhanced returns. These findings align with Jareño et al. (2024), reinforcing that ESG-focused assets can enhance portfolio dynamics even when risk reduction is not uniform.

In summary, the dynamic R-vine copula model demonstrates that green bonds fundamentally alter inter-asset relationships, boosting portfolio efficiency, especially for life insurers, despite their higher standalone VaR. This restructuring reduces tail risk, improves Sharpe ratios for both life and non-life insurers, and lowers portfolio-level VaR, notably for life insurers. These findings align with those of Mensi et al. (2022), who highlight the effectiveness of copula-based models in capturing dynamic co-movements under market volatility. The results also support Tsoukala and Tsiotas’s (2021) emphasis on integrating ESG assets into complex financial systems. These benefits are more pronounced for life insurers, whose long-term investment horizons and solvency-driven mandates make them especially responsive to diversification gains. While Bouri et al. (2023) and Pham and Nguyen (2022) report green bond vulnerabilities to oil price volatility, policy uncertainty, and limited hedging capacity, the current findings highlight the importance of evaluating ESG assets through a dependence-aware, multivariate framework. Although the extent of benefit varies by insurer type, green bond integration supports both portfolio stability and ESG-aligned performance when assessed using advanced models such as dynamic copulas, which are able to capture nonlinear dependencies. These results, which clarify the nuanced role of green bonds in insurance portfolio construction, are further synthesized in the concluding section.

3.5. Limitations and Future Research

While this study has presented a robust framework for assessing capital requirements and optimizing insurer portfolios with green bonds, several limitations clarify the scope of its findings. The Sharpe ratio optimization was conducted under idealized conditions, excluding real-world complexities such as transaction costs and liquidity constraints. Although widely adopted in empirical finance to benchmark theoretical portfolio performance and explore risk–return trade-offs, incorporating market frictions would improve the realism and practical applicability of the results.

To enhance relevance for institutional investors, future research could integrate liquidity-adjusted performance measures or optimization strategies that explicitly account for transaction costs and operational constraints. Such enhancements would better align the framework with the investment environments and regulatory conditions faced by insurers.

Forecasting accuracy could also be improved by exploring alternative GARCH-family models (e.g., EGARCH, TGARCH, or GJR-GARCH-M) or regime-switching frameworks to better capture market asymmetries and structural shifts. Integrating EVT–copula models may strengthen tail-dependence modeling under extreme conditions, while advanced distributions such as generalized hyperbolic or finite mixtures could more precisely capture skewness and fat tails. Although this study employs Student-t copulas to capture symmetric tail dependence, future research could consider other copula families, such as Clayton or Gumbel, to explore asymmetric dependence structures. These extensions would reinforce insurer risk management and support adaptive, sustainability-aligned investment strategies.

The geographic scope of this study is limited to Thailand. Extending the framework to cross-country comparisons would help assess external validity and capture regional differences in insurer behavior, ESG policy integration, and market development. Comparative studies across ASEAN markets, such as Malaysia or Singapore, could further contextualize the findings and enhance generalizability.

Beyond methodological considerations, practical implementation challenges remain. In emerging markets such as Thailand, limited availability of detailed green bond data, particularly at the issuer or project level, may constrain modeling precision and performance evaluation. Due to the short history and illiquidity of the local green bond market, this study uses the Bloomberg Barclays MSCI US green bond index as a proxy for ESG-aligned fixed-income exposure. While this global benchmark may not fully reflect local market characteristics, its use aligns with current OIC regulations, which allow insurers to allocate up to 30% of portfolios to international investments. As the Thai green bond market matures and longer time series become available, future research could incorporate local green bond instruments to enhance contextual relevance and modeling fidelity. Additionally, supervisory authorities may face capacity constraints when applying advanced techniques such as dynamic copulas or integrating ESG considerations.

4. Conclusions

This study presents a robust framework for assessing capital requirements and optimizing insurer portfolios, particularly those that include green bonds, through advanced risk modeling. By integrating ARMA–GJR–GARCH models with skewed Student-t innovations, extreme value theory, and dynamic R-vine copulas, the methodology captures essential risk features such as volatility clustering, tail risk, and time-varying dependencies. This approach is well suited for regulatory stress testing and solvency assessment, offering a comprehensive perspective under both normal and adverse market conditions. These advanced models can support regulators in establishing appropriate capital requirements by providing more accurate risk evaluations. Backtesting results further validate the models’ effectiveness and support their application in proactive risk oversight and regulatory supervision.

The analysis reveals that the risk level associated with green bonds is lower than that of more volatile asset classes such as equities, oil, property, gold, and exchange rates. Incorporating green bonds into diversified insurer portfolios enhances risk-adjusted returns by increasing Sharpe ratios and reducing portfolio-level value-at-risk, in most rolling periods, which may improve capital efficiency. These findings underscore the importance of evaluating capital requirements at the portfolio level, rather than focusing solely on individual assets. These benefits are especially evident among life insurers, whose long-term horizons and solvency mandates align with the characteristics of green bonds. While non-life insurers also experience diversification benefits, their shorter risk horizons require more careful consideration. As ESG-aligned instruments, green bonds offer insurers a pathway to strengthen financial resilience while supporting national sustainability priorities.

While the empirical focus of this study is on Thailand’s OIC solvency rules, the proposed framework aligns with international regulatory standards, including Basel III’s market risk measurement and the Fundamental Review of the Trading Book (FRTB)’s emphasis on tail-risk modeling. The dynamic R-vine copula approach, together with the GARCH–EVT framework, could complement Basel III and FRTB stress-testing practices for insurers with global exposures, particularly in jurisdictions integrating ESG factors into capital requirements. This compatibility underscores the framework’s potential for application in global insurance and banking risk management, making the findings relevant to analysts, regulators, and policymakers beyond Thailand. By strengthening regulatory guidance in this way, regulators can not only enhance insurers’ financial resilience and potentially reduce capital charges under the Office of Insurance Commission of Thailand regulatory frameworks, but also actively steer the insurance sector towards supporting Thailand’s sustainable finance agenda and commitments under the United Nations Sustainable Development Goals (SDGs).