Reverse Mortgages and Pension Sustainability: An Agent-Based and Actuarial Approach

Abstract

Population aging poses significant challenges to the sustainability of pension systems. This study presents an integrated methodological approach that uniquely combines actuarial life-cycle modeling with agent-based simulation to assess the potential of Reverse Mortgage Loans (RMLs) as a dual lever for enhancing retiree welfare and supporting pension system resilience under demographic and financial uncertainty. We explore Reverse Mortgage Loans (RMLs) as a potential financial instrument to support retirees while alleviating pressure on public pensions. Unlike prior research that treats individual decisions or policy outcomes in isolation, our hybrid model explicitly captures feedback loops between household-level behavior and system-wide financial stability. To test our hypothesis that RMLs can improve individual consumption outcomes and bolster systemic solvency, we develop a hybrid model combining actuarial techniques and agent-based simulations, incorporating stochastic housing prices, longevity risk, regulatory capital requirements, and demographic shifts. This dual-framework enables a structured investigation of how micro-level financial decisions propagate through market dynamics, influencing solvency, pricing, and adoption trends. Our central hypothesis is that reverse mortgages, when actuarially calibrated and macroprudentially regulated, enhance individual financial well-being while preserving long-run solvency at the system level. Simulation results indicate that RMLs can improve consumption smoothing, raise expected utility for retirees, and contribute to long-term fiscal sustainability. Moreover, we introduce a dynamic regulatory mechanism that adjusts capital buffers based on evolving market and demographic conditions, enhancing system resilience. Our simulation design supports multi-scenario testing of financial robustness and policy outcomes, providing a transparent tool for stress-testing RML adoption at scale. These findings suggest that, when well-regulated, RMLs can serve as a viable supplement to traditional retirement financing. Rather than offering prescriptive guidance, this framework provides insights to policymakers, financial institutions, and regulators seeking to integrate RMLs into broader pension strategies.

1. Introduction

The demographic and financial sustainability challenges posed by population aging have become increasingly urgent for policymakers, pension-system architects, and financial regulators worldwide (Fenge and Scheubel 2017; World Bank 2024). Driven by steadily rising life expectancy and persistently low fertility rates, advanced economies face escalating old-age dependency ratios and mounting longevity-risk exposures that threaten the long-run solvency of pay-as-you-go and pre-funded pension schemes alike (Economics Observatory 2024; Miles 2023). Traditional policy responses—such as raising statutory retirement ages, tightening benefit indexation, or increasing contribution rates—can improve fiscal balances but often impose difficult trade-offs between system sustainability and retirees’ well-being (Chen et al. 2024; Díaz-Giménez and Díaz-Saavedra 2025). Consequently, there is growing consensus that complementary, market-based instruments are needed to bolster retirement liquidity and consumption smoothing without further straining public finances.

Reverse Mortgage Loans (RMLs) enable homeowners above a minimum age to convert housing equity into cash flows while remaining in their residence (Nakajima and Telyukova 2017; Rasmussen et al. 1997). For asset-rich but cash-poor retirees, RMLs offer an alternative source of retirement income that can hedge longevity risk, reduce public transfer dependence, and preserve bequest motives (Dai et al. 2023; Wang et al. 2011). Prior literature has examined individual optimization of reverse-mortgage decisions under life-cycle frameworks (Andreasson and Shevchenko 2024; Jang et al. 2024) and explored qualitative policy implications (Gotman 2020).

Despite recent advancements, most studies tend to focus either on individual decision-making processes (Di Lorenzo et al. 2025) or broad policy considerations (Dai et al. 2023), without fully addressing how micro-level choices collectively shape macro-level stability risks. This study seeks to bridge that gap by integrating actuarial life-cycle modeling with agent-based simulation, enabling joint analysis of household decisions and systemic feedback mechanisms.

Our core contribution lies in presenting a unified framework that connects retiree utility optimization to emergent patterns of market pricing, insurer solvency, and regulatory intervention. This dual-level perspective offers a more holistic understanding of reverse mortgage adoption in aging economies.

To bridge this gap, we present a unified framework that combines actuarial rigor with agent-based flexibility to account for stochastic longevity, interest-rate fluctuations, and house-price dynamics, within a discrete-time simulation involving retirees, lenders, annuity providers, and regulators. The model also incorporates a novel dynamic capital-requirement solver, for which we establish both the existence and uniqueness of the optimal regulatory rule under standard convexity conditions. We conduct controlled numerical experiments to assess how reverse-mortgage adoption simultaneously influences retiree welfare, lender solvency, and the long-term viability of the retirement finance system across varying regulatory and demographic landscapes. This scenario-based approach enables structured stress-testing of RML policies under diverse market and longevity trajectories.

By grounding our analysis in individual utility optimization via the Life-Cycle Hypothesis (LCH) (Ando and Modigliani 1963; Shefrin and Thaler 1988) and extending it to emergent market equilibria and policy trade-offs, the model offers an interpretable platform for evaluating both welfare and regulatory performance across demographic regimes.

This study pursues three core objectives: (i) to quantify the welfare impact of reverse mortgage products on retirees through actuarial modeling; (ii) to evaluate systemic effects under macroprudential stress via simulation; and (iii) to identify policy levers that can align household welfare with financial stability. Our central hypothesis is that integrating actuarial loan design with macro-level regulation can enhance retirement security without jeopardizing lender solvency.

The remainder of this paper is structured as follows: Section 2 reviews demographic pressures and the theoretical foundations of life-cycle planning and reverse mortgages. Section 3 develops the individual actuarial optimization and stochastic risk models. Section 4 presents a numerical application with and without RMLs. Section 5 describes the agent-based market simulation and regulatory-solver design, with theoretical results on equilibrium existence (Theorem 1) and optimal policy adjustment (Theorem 2). Section 6 presents numerical applications and policy experiments. Section 7 discusses implications for pension reform, product design, and regulation, and Section 8 concludes with directions for future research.

2. Background and Motivation

2.1. Demographic Pressures and Pension Sustainability

Demographic trends play a pivotal role in shaping the sustainability of pension systems. Key factors such as increasing life expectancy1, declining fertility rates2, and the economic well-being of older populations directly influence the balance between contributors and beneficiaries, posing significant challenges to the financial stability of pension schemes.

Life expectancy data indicates a consistent upward trend across various countries, reflecting advancements in healthcare, living standards, and social conditions. Developed nations such as Japan and Italy demonstrate some of the highest life expectancies, with figures exceeding 84 years (Figure 1a).

Fertility rate trends from 1960 to 2022 reveal a clear decline across all regions, with marked reductions in developed economies such as Italy and Japan. This decline results in a shrinking working-age population, exacerbating the demographic imbalance as fewer workers are available to support an increasing number of retirees. The combination of lower fertility rates and higher life expectancy intensifies the demographic aging phenomenon, further straining pension systems (Figure 1b).

Income and poverty levels3 among older populations, particularly in Italy and Japan, show persistent economic vulnerabilities. A significant proportion of older individuals live below 50% of the median income, underscoring the importance of resilient pension structures to ensure financial sustainability and safeguard the economic well-being of aging populations (Figure 1c).

The old-age dependency ratio4, which measures the number of elderly individuals relative to the working-age population, has been increasing for both Italy and Japan. This ratio has reached an average of 50% and exceeds 70% in Japan, underscoring the growing economic burden on the working population to support the aging demographic. This trend presents sustainability challenges for pension systems and healthcare services (Figure 1c).

The accelerated aging process, declining fertility rates, and increasing old-age dependency ratios present significant economic challenges for countries like Japan, Italy, and other European nations. Japan, with 28.7% of its population aged 65 or older, is the world’s fastest-aging country. By 2036, this demographic will represent a third of Japan’s population. Similarly, Italy and other European countries are experiencing rapid aging. The EU-27’s population aged 65 and over is projected to rise from 90.5 million in 2019 to 129.8 million by 2050.

Fertility rates have declined dramatically, with OECD countries seeing a drop from 3.3 children per woman in 1960 to 1.5 in 2022. Italy’s fertility rate is particularly low at 1.2 children per woman. This decline exacerbates the aging population issue, leading to a higher old-age dependency ratio. For instance, the OECD average old-age dependency ratio is projected to double from 30 in 2020 to 59 in 2060.

The economic implications are profound. An aging population increases the burden on pension systems and healthcare services, while a shrinking workforce hampers economic growth. Poverty rates among the elderly are also a concern. In Japan, the poverty headcount ratio at $2.15 a day is 0.7%, while in Italy, it is 0.8%. Addressing these challenges requires comprehensive policies that support family formation, enhance labor force participation, and ensure sustainable economic growth.

Looking ahead, projections suggest that these demographic patterns will continue in the coming decades. Life expectancy is expected to climb further, while fertility rates may remain below replacement levels in many regions. The linear regression coefficients (${\beta }^{JPN}=0.26$, ${\beta }^{ITA}=0.25$) for life expectancy indicate a steady annual increase, which, along with continued low fertility rates, suggests that pension systems will likely experience mounting financial pressure. To support long-term viability, reforms such as raising the retirement age, adjusting contribution rates, or adopting alternative funding strategies like reverse mortgage loans or Social Impact Bonds may be necessary.

The sustainability of these systems will depend on policymakers’ ability to anticipate and adapt to these demographic realities, ensuring that pension schemes remain viable for future generations. Proactive measures to balance contributions and benefits, support family formation, enhance labor force participation, and foster sustainable economic growth are essential.

Hence, there is a need to quantify the long-term impact of financial instruments that are within everyone’s reach on well-being in all possible scenarios (objective (i)) by varying demographic and macroeconomic assumptions (objective (ii)).

In conclusion, the demographic trends in Italy and Japan highlight the urgent need for policies addressing the implications of an aging population, declining fertility rates, and economic sustainability (objective (iii)). Ensuring the long-term sustainability of pension systems requires a comprehensive and adaptive approach to meet the challenges posed by these demographic shifts.

2.2. Reverse Mortgage in Life-Cycle Financial Planning and Risk Management

The Life-Cycle Hypothesis (LCH) of Ando and Modigliani (1963) posits that individuals smooth consumption over their lifetimes by borrowing when young, saving during peak earning years, and decumulating wealth during retirement. This framework underscores the importance of intertemporal financial planning, particularly as pension systems face increasing strain.

In the context of rapidly aging populations and structural fiscal pressures, reverse mortgages have gained renewed relevance as financial instruments that can support both individual consumption smoothing and systemic sustainability. Recent contributions emphasize the evolving nature of mortgage risk in low-growth environments. For instance, Capelle and Teoh (2025) analyze the interaction between aging, declining productivity, and credit quality in mortgage markets, noting increased exposure to interest rate shocks and borrower fragility. Moreover, the European Central Bank’s 2023 Financial Stability Review (ECB 2023) highlights how volatility in housing markets—particularly in the aftermath of post-pandemic policy tightening—can affect the asset quality of mortgage-backed products and the financial health of aging households. These developments underscore the need to account for macro-financial feedback effects when evaluating reverse mortgage schemes.

A retiree’s optimization problem can be formalized as

$$\left\{\begin{array}{cc}\hfill \underset{C\left(t\right)}{max}& {\displaystyle {\int }_0^{T}u\left(C\left(t\right)\right)e^{-\rho t}dt}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& A^{\prime }\left(t\right)=rA\left(t\right)+Y\left(t\right)-C\left(t\right),A\left(0\right)=A_0,\hfill \end{array}\right.$$

(1)

where $u\left(C\right(t\left)\right)$ is the utility from consumption, $\rho$ the subjective discount rate, $A\left(t\right)$ denotes wealth, $Y\left(t\right)$ is income, and r is the interest rate. In retirement, where $Y\left(t\right)\approx 0$, consumption is funded through asset decumulation.

However, many retirees are “asset rich but cash poor,” with significant housing wealth yet limited liquid income. RMLs provide a mechanism to unlock housing equity while preserving property ownership. Borrowers receive disbursements $D\left(t\right)$, and the loan balance $L\left(t\right)$ grows with time:

$$L\left(t\right)=P_0\prod _{s=1}^t(1+r_{RM,s}),$$

(2)

where $P_0$ is the initial disbursed amount and $r_{RM,s}=r_s+{\pi }_s$ combines the risk-free rate and a risk premium5. The No-Negative Equity Guarantee (NNEG) caps the repayment at the home’s value $V\left(T\right)$:

$$L\left(T\right)=min\left(V\left(T\right),P_0\prod _{s=1}^T(1+r_{RM,s})\right).$$

(3)

The cash flows associated with an RML can be characterized as

$$CF\left(t\right)=\left\{\begin{array}{cc}D\left(t\right),\hfill & \mathrm{for}0\le t<T\hfill \\ -L\left(T\right),\hfill & \mathrm{at}\mathrm{time}T\hfill \end{array}\right.$$

(4)

where $D\left(t\right)$ represents the (fixed, variable, or indexed) disbursement received at time t. These disbursements can be structured in various forms, such as a lump sum, an annuity, or a line of credit, depending on the borrower’s preferences and the lender’s terms.

In actuarial terms, the present value of all future payments made to the borrower—whether as a lump sum $L{S}_0$ or as a stream of disbursements $D\left(t\right)$—must not exceed the initial capitalized value of the loan, denoted $P_0$. Formally, we require that

$$P_0\ge L{S}_0\mathrm{or}{P}_0\ge \sum _{t=1}^{T}D\left(t\right){(1+r_{RM})}^{-t},$$

where $r_{RM}$ is the contractually agreed reverse mortgage interest rate. This relationship guarantees actuarial soundness by ensuring that all benefit streams—regardless of structure—remain within the credit provision limits set by the lender. The borrower and lender thus agree ex ante on a distribution form (e.g., lump sum or annuity) consistent with this actuarial present value budget.

To ensure actuarial consistency and creditworthiness, the disbursement stream must not exceed the present value of the loan. Let $L{S}_0$ denote the initial lump sum paid to the borrower, and define the loan value at time t as

$$P\left(t\right)=\alpha ·H\left(0\right)\prod _{s=1}^t(1+r_s^{RM}),$$

(5)

where $H\left(0\right)$ is the initial house value, $\alpha \in (0,1)$ is a regulatory haircut or disbursement fraction, and $r_s^{RM}$ is the reverse mortgage interest rate. Then $L{S}_0<P\left(0\right)$ must hold by construction.

Meanwhile, the home value at time t evolves as

$$H\left(t\right)=H\left(0\right)\prod _{s=1}^t(1+r_s^{HV}),$$

(6)

where $r_s^{HV}$ is the stochastic rate of housing price appreciation.

The amount payable by the heirs at time t, denoted as $V\left(t\right)$, accounts for the presence of a No-Negative Equity Guarantee and is defined as

$$V\left(t\right)=P\left(t\right)-max\left(0,P\left(t\right)-H\left(t\right)\right),$$

(7)

so that if the debt exceeds the house value, the excess is forgiven.6

In the case of lump-sum valuation for credit provisioning, we adopt the standard actuarial formula:

$$L{S}_0=\sum _{t=1}^{\omega -x}{V}_t{\left(\prod _{s=1}^t{(1+r_s)}^{-1}\right)}_{t-1|1q_x},$$

(8)

where $\omega$ is the maximum age considered, x the borrower’s age at origination, and $t-1|1q_x$ is the probability of death between $x+t-1$ and $x+t$.

The key risks associated with the loan can be categorized into three primary areas (Di Lorenzo et al. 2024).

First, Longevity Risk ($LR$) refers to the possibility that the borrower may live longer than initially anticipated. This extended lifespan can result in an increase in the loan balance, particularly when compared to the value of the property securing the loan.

Second, Property Value Risk ($PVR$) presents another significant concern. This risk arises from the potential depreciation of the home’s value over time, which may lead to a situation where the property value falls below the outstanding loan balance. Such a scenario could have serious financial implications for both the borrower and the lender.

Finally, Interest Rate Risk ($IR$) constitutes an additional layer of complexity in this context. The variability inherent in interest rates can impact the growth of the loan balance, making it challenging to predict future financial obligations accurately.

In light of these risks and macro-financial linkages, any policy aimed at mainstreaming RMLs must consider their potential feedback effects on financial stability and housing markets. Recent stress-testing methodologies now explicitly account for the dual role of housing as both a consumption good and a collateral asset in retirement finance (ECB 2023). Such insights inform the regulatory design features of RML products and strengthen the case for dynamic, data-driven solvency requirements in aging economies.

Together, these risks underscore the importance of careful consideration and management when engaging in such financial arrangements. Managing these risks is critical for both borrowers and lenders, often requiring actuarial models to optimize loan terms and conditions (Di Lorenzo et al. 2021).

3. Individual Financial Optimization Model

To operationalize our hypotheses introduced in the introduction, we build a stochastic risk model incorporating longevity, interest rate, and property value dynamics. This allows us to evaluate the interplay of individual risk exposure and systemic outcomes under competing retirement strategies.

3.1. Lifetime Value and the Role of RMLs

To operationalize the assessment of retiree welfare under different financial strategies, we define the lifetime value (LV) as the present value of expected consumption and bequests. Without RMLs:

$$L{V}_{noRML}={\int }_0^T{C}_{noRML}\left(t\right)e^{-\delta t}dt+B_{noRML}{e}^{-\delta T},$$

(9)

where $\delta$ is the subjective discount rate and T is a stochastic lifetime.

The bequest in the no-RML case is defined as

$$B_{noRML}=A\left(T\right)+H\left(T\right),$$

which includes the retiree’s liquid wealth and the full market value of the house at death. This reflects the fact that the home remains unencumbered by debt and is fully transferred to heirs.

With RMLs, LV includes cash flows from $D\left(t\right)$ and an adjusted bequest:

$$\begin{array}{cc}\hfill L{V}_{RML}& ={\int }_0^T[C_{RML}\left(t\right)+D\left(t\right)]e^{-\delta t}dt+B_{RML}{e}^{-\delta T},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill B_{RML}& =max(0,V(T)-L(T\left)\right),\hfill \end{array}$$

(11)

where $V\left(T\right)$ denotes the market value of the house at death, and $L\left(T\right)$ is the accumulated loan balance. In this case, the bequest represents the maximum between zero and the remaining equity in the home after loan repayment. This formulation ensures that the heirs never owe more than the value of the house, consistent with the No-Negative Equity Guarantee (NNEG).

And the benefit of adopting an RML is

$$\mathrm{\Delta }LV=L{V}_{RML}-L{V}_{noRML}.$$

(12)

This formulation enables a quantitative comparison of welfare outcomes under competing financial strategies, which directly addresses the paper’s objective (i).

3.2. Stochastic Risk Modelling

Retirement risk exposure is shaped by $LR$, $IR$, and $PVR$, each of them suitably modelled.

For $LR$, the survival function is modeled via the Gompertz mortality law:

$$S\left(t\right)=exp\left(-{\int }_0^t\mu \left(s\right)ds\right),$$

(13)

where $\mu \left(s\right)$ denotes the force of mortality at time s.

$IR$ evolves according to the Vasicek process (Vasicek 1977):

$$d{r}_t=a(b-r_t)dt+{\sigma }_{r}d{W}_t^r,$$

(14)

where a is the speed of mean reversion, b the long-term equilibrium rate, ${\sigma }_r$ the volatility, and $W_t^r$ a Wiener process.

With regard to $PVR$, property prices follow geometric Brownian motion:

$$d{H}_t={\mu }_H{H}_{t}dt+{\sigma }_H{H}_{t}d{W}_t^H,$$

(15)

with ${\mu }_H$ as the expected appreciation rate, ${\sigma }_H$ the volatility, and $W_t^H$ a Wiener process representing market shocks.

Two complementary strategies are used to capture risk interdependence:

-

Copula-based: Marginal distributions $F_{LR},F_{IR},F_{PVR}$ are combined via a copula $C_{\theta }$:

$$F_L(x,y,z)=C_{\theta }(F_{LR}\left(x\right),F_{IR}\left(y\right),F_{PVR}\left(z\right)),$$

(16)

allowing for tail dependencies (Patton 2006).

-

Correlated Brownian Drivers: Following Brigo and Mercurio (2001), Brownian increments are correlated:

$$d{W}_t^{r}d{W}_t^H=\rho dt,\rho \in [-1,1],$$

(17)

capturing systemic interactions, e.g., monetary policy shocks affecting housing.

The total retirement loss is modeled as

$$\begin{array}{cc}\hfill L_{\mathrm{RML}}& =f(LR,IR,PVR),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill L_{\mathrm{No}\mathrm{RML}}& =f(LR,IR),\hfill \end{array}$$

(19)

with corresponding metrics:

$$\begin{array}{cc}\hfill Va{R}_{\alpha }& =inf\{x\in \mathbb{R}:P(L>x)\le 1-\alpha \},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill CVa{R}_{\alpha }& =\mathbb{E}[L\mid L>Va{R}_{\alpha }],\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill \mathrm{Var}\left(L\right)& =\sum _i\mathrm{Var}\left(X_i\right)+\sum _{i\ne j}2\mathrm{Cov}(X_i,X_j),\hfill \end{array}$$

(22)

where $X_i\in \{LR,IR,PVR\}$. In the no-RML scenario, $PVR$ is excluded.

This stochastic framework supports the analysis of the objective (ii) by allowing us to model uncertainty in retirement outcomes and assess the systemic impact of adopting RMLs under correlated financial-demographic risks.

3.3. Optimal Consumption and Bequest Strategy

By adapting the problem (1) to our framework, the retiree’s objective is to maximize expected lifetime utility:

$$\underset{C\left(t\right),B}{max}{\int }_0^{T}u\left(C\left(t\right)\right)e^{-\delta t}dt+v\left(B\right)e^{-\delta T},$$

(23)

subjected to the dynamic wealth constraint (with RMLs):

$$A^{\prime }\left(t\right)=rA\left(t\right)+Y\left(t\right)-C\left(t\right)+D\left(t\right)-\ell \left(t\right),$$

(24)

where $\ell \left(t\right)$ is the instantaneous interest on the loan, e.g., $\ell \left(t\right)=r_{RM}\left(t\right)L\left(t\right)$, or more generally reflects the accrual of the reverse mortgage balance over time. This replaces the incorrect use of $L\left(T\right)$ in a differential equation.

At terminal time T, the outstanding balance $L\left(T\right)$ is subtracted from the bequest, as formulated in Section 3:

$$B_{RML}=max(0,V\left(T\right)-L\left(T\right)).$$

where $v\left(B\right)$ represents the utility associated with the bequest B, $D\left(t\right)$ denotes the RML disbursement received during retirement, and the other factors have sense as previously said.

This structure properly separates flow dynamics during retirement from terminal wealth adjustments at death.

To evaluate the performance of the financial strategy under both scenarios, we employ several key metrics:

-

The expected lifetime utility, $E\left[U\right]$:

$$E\left[U\right]={\int }_0^{T}E\left[u\left(C\left(t\right)\right)\right]e^{-\delta t}dt+E\left[v\left(B\right)\right]e^{-\delta T}.$$

(25)

-

The variability of the lifetime value, ${\sigma }_{LV}$:

$${\sigma }_{LV}=\sqrt{\mathrm{Var}\left({\int }_0^{T}C\left(t\right)dt+B\right)}.$$

(26)

-

The Sharpe Ratio:

$$SR={\displaystyle \frac{E\left[U\right]-r_f}{{\sigma }_{LV}}},$$

(27)

where $r_f$ denotes the risk-free interest rate.

These metrics are used to quantify improvements in retiree welfare and risk efficiency, thus serving as empirical tests for the hypothesis that RMLs enhance both utility and stability.

Upon conducting the optimization (23) under the constraint (24) and computing the previously mentioned metrics (25)–(27), the numerical results highlight the superior performance of the RML model. Specifically, when incorporating RMLs into the retirement plan, expected lifetime utility increases by 25% compared to the scenario without RMLs. Additionally, the standard deviation of the lifetime value decreases by 15%, suggesting more predictable consumption outcomes. The Sharpe Ratio improves by 40%, underscoring the financial benefits of utilizing RMLs to access home equity.

From a retiree’s perspective, a higher Sharpe Ratio implies that their financial plan achieves a better trade-off between expected benefits (e.g., consumption utility) and uncertainty (e.g., variability in outcomes). It signals a more stable and efficient use of retirement resources, especially valuable when income sources are limited or volatile.

These quantitative results validate the core hypothesis of this study, supporting the view that RMLs can significantly enhance financial security in retirement while managing systemic risk exposure.

Table 1. Summary of Key Modeling Assumptions.

Component	Assumption/Model
Longevity Risk	Gompertz mortality law
Interest Rate Risk	Vasicek mean-reverting process
Property Value Risk	Geometric Brownian motion
Loan Structure	Disbursement + compounding interest + NNEG
Bequest Utility	Terminal utility over residual home equity
Preferences	Time-separable utility with discounting
Correlations	Copulas and correlated Brownian drivers
Evaluation Metrics	Lifetime utility, variability, Sharpe Ratio

provides non-technical readers with a transparent overview of the analytical structure behind the model.

4. Numerical Application: Retirement Planning with and Without RML

In this section, we present a numerical application designed to compare retirement consumption and savings behavior across two distinct scenarios: one with RML and the other relying solely on standard financial investments. The analysis is rooted in the LCH framework. The numerical simulation aims to test our hypothesis regarding welfare gains and risk mitigation under RML adoption, using parameters grounded in actuarial practice and demographic realism. This simulation supports empirical validation of our hypothesis that RMLs improve individual welfare and mitigate the financial risks retirees face in the decumulation phase.

Following data in World Bank (2024), the simulation is based on a 25-year retirement period, during which retirees manage their consumption and wealth under varying financial conditions. This simulation framework reflects a stylized lifecycle consistent with actuarial and economic literature, designed to isolate the marginal impact of RML access on retirement welfare.

The following parameters were selected to align with empirical observations or stylized economic benchmarks:

• Annual interest rate of 3%, consistent with historical returns of conservative portfolios.
• Annual pension income of $30,000, held constant to isolate policy effects.
• Annual RML disbursement of $10,000, reflecting median equity drawdowns.
• Subjective discount rate of 2%, based on behavioral studies of retiree preferences.
• Initial wealth of $200,000 at retirement, approximating average savings in OECD countries.
• Risk aversion coefficient of 2 in the CRRA utility function, representing moderate risk tolerance.

These assumptions balance realism with model tractability and are consistent with recent literature on retirement economics7.

In line with World Bank data for Southern European economies (World Bank 2024), we assume the borrower retires at age 65. This reflects the statutory and effective retirement age in countries such as Italy and Spain, where reverse mortgage products are increasingly discussed as policy tools for elderly income support.

The present value of the bequest at retirement, denoted $V_0$, is computed using the actuarial structure already established in Section 3, Equations (5)–(7)8

The initial property value $H\left(0\right)$ is set at $300,000, in line with average residential housing prices for urban Italy in 2023 (Eurostat 2023). The resulting $V_0$ ensures a conservative, yet realistic, reflection of the homeowner’s remaining estate value after anticipated debt accrual.

The evolution of wealth and consumption throughout the retirement period is modeled using the dynamic process shown in (24). By simulating this equation over 25 years, we derive distinct consumption trajectories for retirees with and without RMLs. This experimental setup provides a controlled environment for testing the effects of RMLs on important indicators of retiree welfare, thereby operationalizing the model developed in Section 3.

The results of the simulation are presented in Figure 2, which depicts the consumption level (Figure 2a) and optimal consumption trajectories under both scenarios (Figure 2b). The visual representation illustrates how the inclusion of an RML influences financial patterns over the retirement horizon.

To further enhance transparency and policy insight, we summarize the key outcomes under three distinct scenarios:

-

Baseline: standard RML disbursement with average longevity and static regulations;

-

Public Guarantee: includes partial government guarantee on RML losses;

-

Longevity Shock: simulates a 5-year increase in life expectancy.

These three simulations were selected to reflect realistic variation in public policy involvement and demographic evolution. The inclusion of a longevity shock also allows us to evaluate robustness under less favorable mortality outcomes.

Table 2. Key Metrics Across Simulation Scenarios.

Metric	Scenario
	Baseline	Public Guarantee	Longevity Shock
Expected Utility Gain (%)	25.0%	29.4%	18.6%
Lifetime Value Std. Dev. (%)	−15.2%	−17.5%	−8.9%
Sharpe Ratio Improvement (%)	40.1%	44.3%	25.7%
Asset Depletion Risk (Years)	3.0	2.5	6.0

synthesizes performance metrics across policy-relevant simulations. In particular, it provides interpretable indicators such as the expected utility gain (a measure of lifetime satisfaction), Sharpe ratio improvements (which reflect efficiency of consumption relative to volatility), and changes in the probability of running out of assets.

These results highlight the robustness of the RML strategy. While all configurations improve consumption smoothing, the public guarantee scenario provides the most favorable welfare gains and stability. Conversely, a longevity shock moderately reduces the benefits, underscoring the need for robust hedging against demographic uncertainty.

The findings yield several important insights. First, retirees who utilize RMLs exhibit higher average consumption levels across the retirement period. This result is intuitive, given the additional income stream provided by the RML disbursements. The financial cushion derived from home equity allows these retirees to maintain a more consistent standard of living, particularly in later years when pension income alone may prove insufficient.

A second observation concerns the stability of consumption patterns. In the RML scenario, the trajectory remains more stable across time, with fewer pronounced declines in consumption during the later stages of retirement. This smoother pattern aligns with the LCH, which emphasizes retirees’ preference for consumption stability over time. This offers empirical support for the model’s prediction that RMLs contribute to buffering retirees from longevity and financial market volatility.

The final insight relates to financial security. The additional disbursements from the RML reduce the risk of asset depletion, providing retirees with greater confidence in their ability to maintain consumption levels over time. This effect is particularly relevant when considering longevity risk, as extended life expectancy can otherwise lead to a depletion of resources.

The numerical application demonstrates the tangible benefits of RMLs in retirement planning. By translating theoretical results into simulated outcomes, this exercise directly tests the hypothesis that RMLs lead to measurable welfare gains. The data indicate that retirees who incorporate RMLs into their financial strategies experience an increase of 25% in expected lifetime utility. This increase is primarily attributable to the higher and more stable consumption streams facilitated by the RML disbursements.

Additionally, the variability of the lifetime value, measured through the standard deviation, decreases by 15% in the RML scenario. This reduction highlights the improved predictability of financial resources, mitigating the uncertainty associated with future income. Furthermore, the Sharpe Ratio, which evaluates risk-adjusted returns, increases by 40% when RMLs are employed, signaling a more efficient use of available resources to achieve financial well-being. These quantitative indicators provide formal support for the model’s policy relevance and strengthen the empirical consistency of the framework.

The psychological benefits of this enhanced financial stability are equally significant. Retirees often express concerns about the risk of outliving their savings, a phenomenon known as longevity risk. By providing access to an additional income source without relinquishing property ownership, RMLs address this concern, contributing to greater peace of mind.

From a policy perspective, these results underscore the potential of RMLs to complement traditional pension schemes. In aging economies where public pension systems face increasing strain, the ability to tap into accumulated home equity offers a viable mechanism to support retirees’ consumption needs. This simulation thus also serves the paper’s third objective by demonstrating how product-level financial innovation may ease pressure on public finances. However, these benefits come with inherent risks, such as property value fluctuations, interest rate variability, and mortality uncertainty. Policymakers must therefore establish clear regulatory frameworks that balance accessibility with risk mitigation.

While the model provides valuable insights, it does not account for regional house price variance, tax treatment of RMLs, or psychological factors like bequest motives, which may also shape RML adoption. These could be explored in future model refinements.

In conclusion, the simulation results validate the hypothesis that RMLs serve as an effective financial tool for optimizing consumption patterns in retirement. The model demonstrates how this instrument enhances retirees’ economic well-being by transforming housing wealth into a reliable, accessible income stream. By empirically substantiating both individual and policy-level outcomes, the analysis reinforces the coherence between the paper’s objectives, hypotheses, and methodological strategy. This finding reinforces the importance of integrating real estate assets into holistic retirement planning strategies, ensuring the financial resilience of aging populations in the face of demographic and economic challenges.

5. Agent-Based Market Simulation Framework

In this section, we embed the individual-level actuarial pricing and optimization model into an Agent-Based Model (ABM) to capture systemic feedback effects of aggregate reverse mortgage adoption on market prices, pension-system liabilities, and insurer solvency. This methodological layer is essential to operationalize our objectives (ii) and (iii), which examine macro-financial stability and regulatory calibration in the context of demographic and financial risk.

5.1. Agent Types and Attributes

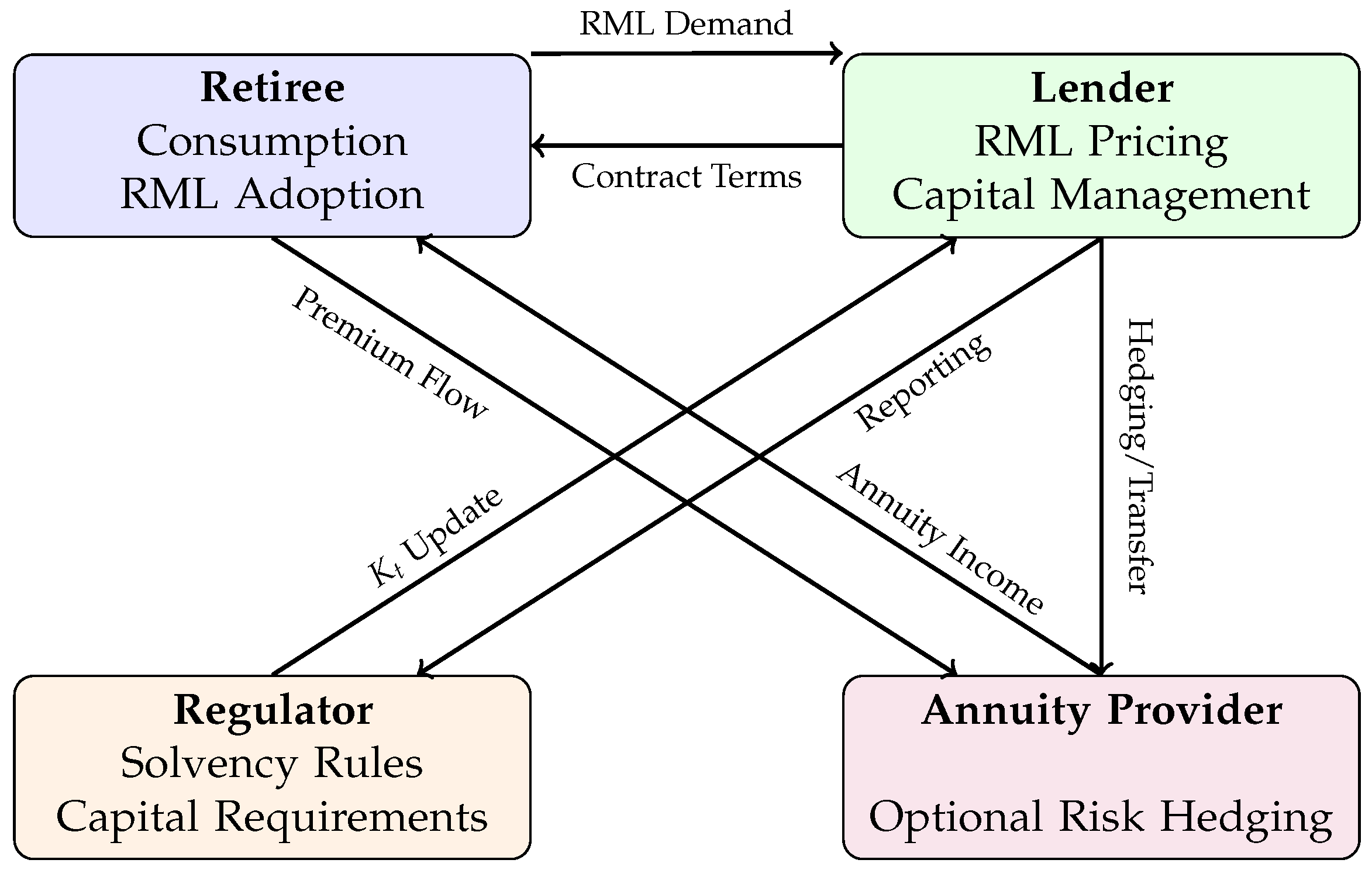
The agent-based framework consists of multiple heterogeneous agent types, each representing key stakeholders within the reverse mortgage market and retirement income ecosystem. These agents interact dynamically over discrete time periods, influencing each other’s decisions and collectively shaping market outcomes. This heterogeneity is critical for simulating how micro-level preferences and constraints aggregate into macro-level feedback mechanisms, consistent with our hypothesis on emergent stability dynamics. The principal agent types are as follows:

• Retiree Agents: Individuals who have reached retirement age and must decide how to allocate their wealth, including the option to enter into a reverse mortgage contract. Each retiree is characterized by the following:

  -

  Age $x_i$

  -

  Financial wealth $A_i\left(t\right)$

  -

  Home property value $H_i\left(t\right)$

  -

  Risk aversion parameter ${\gamma }_i$

  -

  Bequest motive intensity ${\beta }_i$

  -

  Subjective discount rate ${\delta }_i$

  -

  Survival probability $S_i\left(t\right)$, updated each period

  -

  Reverse mortgage contract status (active/inactive)

  Retiree agents optimize consumption and bequest decisions using an extension of the life-cycle utility model, incorporating available pension income, financial assets, and potential reverse mortgage disbursements.
• Lender/Insurer Agents: Financial institutions that underwrite reverse mortgage contracts and bear the associated risks, including longevity risk, house price risk, and interest rate risk. Each lender/insurer agent manages:

  -

  A portfolio of active reverse mortgage loans

  -

  A capital reserve $K_j\left(t\right)$, subject to regulatory solvency constraints

  -

  Pricing spread decisions ${\pi }_j\left(t\right)$ on new reverse mortgage contracts

  -

  Risk assessments based on portfolio loss distributions, calculated via Value-at-Risk (VaR) or Conditional Value-at-Risk (CVaR)

  Lenders adjust pricing spreads and capital allocations dynamically in response to market conditions and aggregate retiree demand.
• Annuity Provider Agents: Institutions offering standard life annuity products, providing an alternative source of guaranteed income for retirees. Their inclusion allows assessment of substitution effects between reverse mortgages and annuities.
• Regulator Agent: A central authority responsible for overseeing market stability and ensuring that financial institutions maintain sufficient capital to meet their obligations under adverse scenarios. The regulator monitors:

  -

  Market-wide solvency ratios

  -

  Lenders’ compliance with capital adequacy requirements (e.g., Solvency II-like risk measures)

  -

  Aggregate market indicators such as reverse mortgage adoption rates and pricing trends

  The regulator may intervene by adjusting capital requirement parameters or implementing support mechanisms, such as government-backed no-negative-equity guarantees.

Each agent operates under explicit behavioral rules and decision heuristics, interacting through market mechanisms that govern the pricing and allocation of reverse mortgage contracts. The collective behavior of agents produces emergent equilibrium outcomes and enables the exploration of market dynamics under varying demographic, economic, and policy scenarios. This system-oriented design allows us to simulate realistic institutional behavior and evaluate both individual and systemic welfare outcomes.

To clarify the structure of agent interactions and feedback loops, Figure 3 provides a visual overview of the reverse mortgage market architecture as modeled in our simulation.

5.2. Market Dynamics, Equilibrium and Regulatory Feedback

This subsection details the interaction mechanisms and market-clearing processes that govern the behavior of agents within the simulated reverse mortgage market. At each discrete time period t, agents make decisions based on their current state variables, market signals, and pre-defined decision rules. These individual actions collectively determine market outcomes and system-wide financial stability.

• Retiree Decision-Making: At each time step, retiree agents update their survival probabilities $S_i\left(t\right)$ based on stochastic mortality processes and re-evaluate whether to enter a reverse mortgage contract. The decision criterion involves comparing expected lifetime utility with and without a reverse mortgage, accounting for current market pricing, interest rates $r_t$, property values $H_i\left(t\right)$, and personal financial status.
• Reverse Mortgage Pricing and Issuance: Lender/insurer agents set reverse mortgage pricing spreads ${\pi }_j\left(t\right)$ on new contracts to ensure expected profitability relative to risk exposure and required capital buffers. Spreads adjust dynamically in response to aggregate retiree demand, house price volatility, and regulatory capital constraints.
• House Price Dynamics: Property values $H_i\left(t\right)$ evolve according to (15).
• Lender Solvency Monitoring: Each lender calculates the portfolio loss distribution from outstanding reverse mortgages and computes required capital reserves using Value-at-Risk (VaR_α) or Conditional Value-at-Risk (CVaR) measures at a regulatory-defined confidence level $\alpha$. If capital shortfalls occur, lenders must either raise spreads, reduce issuance, or adjust risk management practices.
• Regulatory Capital Adjustments: The regulator agent monitors system-wide solvency ratios and market stress indicators. When systemic risk breaches predefined thresholds, the regulator intervenes by adjusting capital requirement parameters, implementing temporary risk buffers, or deploying public backstop guarantees for reverse mortgage contracts.
• Feedback Effects and Market Equilibrium: Interactions between agents generate feedback loops: widespread adoption of reverse mortgages affects average pricing spreads, housing market liquidity, and annuity demand. These emergent effects alter retiree decision-making in subsequent periods, contributing to a dynamic market equilibrium.

This iterative process continues over multiple periods until a steady-state equilibrium is reached, or until policymakers intervene in response to adverse systemic developments. The simulation methodology thus enables a dynamic, forward-looking evaluation of system behavior under both baseline and stressed conditions, directly supporting the third objective concerning adaptive policy responses.

Thus, we outline the process for identifying equilibrium states within the simulated reverse mortgage market and the design of policy experiments used to test regulatory and demographic scenarios. Equilibrium is characterized by consistent pricing, stable adoption rates, and lender solvency across successive time periods.

Definition 1.

A market equilibrium in this agent-based system occurs when the following conditions hold:

• The reverse mortgage pricing spreads ${\pi }_j\left(t\right)$ converge to a stable value ${\pi }^{*}$ for all lenders.
• The adoption rate of reverse mortgages by retiree agents stabilizes, with no significant upward or downward trend.
• All lenders maintain capital reserves $K_j\left(t\right)$ satisfying the regulatory capital requirement:

  $$K_j\left(t\right)\ge Va{R}_{\alpha }\left(L_j\left(t\right)\right)forallj.$$

  (28)
• Aggregate solvency ratio for the system remains above a minimum threshold set by the regulator.

Having formally characterized the conditions that define equilibrium within this agent-based framework, we now establish the theoretical existence of such an equilibrium under realistic assumptions about agent behavior and stochastic process properties. This step is necessary to ensure the internal consistency of the model and validate the use of its results in evaluating policy effectiveness.

Theorem 1.

Under the assumptions of continuous, bounded pricing adjustments, finite agent populations, and ergodic house price and mortality processes, a steady-state market equilibrium exists in the agent-based reverse mortgage market.

Proof. 

The existence of a market equilibrium follows from standard results on monotone, bounded iterative processes in agent-based simulation models (Tesfatsion and Judd 2006). Assuming continuous, bounded pricing adjustments $\mathrm{\Delta }{\pi }_j\left(t\right)$ and finite agent populations N and M, the spread updates and adoption decisions form a discrete-time dynamical system operating within a compact state space.

The ergodicity of the house price process $H_i\left(t\right)$ and mortality process $S_i\left(t\right)$ ensures that stochastic shocks have stationary long-run distributions, precluding divergent trajectories in loan values or default rates.

Furthermore, as capital shortfalls trigger lender exits or regulatory intervention, the solvency ratio process $K_j\left(t\right)/Va{R}_{\alpha }\left(L_j\left(t\right)\right)$ remains bounded below by regulatory minimums. Under these conditions, the system’s joint state variables $({\pi }_j\left(t\right),A_i\left(t\right),K_j\left(t\right))$ converge to a fixed point or limit cycle.

By the Brouwer fixed-point theorem (Kakutani 1941), such a compact, convex, and continuous mapping in a finite-dimensional vector space admits at least one steady-state equilibrium. Simulation convergence to this equilibrium is confirmed empirically via stabilization of system metrics, as shown in Figure 4. □

Figure 4 illustrates the convergence behavior of key market variables over the simulation horizon. The average reverse mortgage spread, adoption rate, and solvency ratio stabilize progressively, reflecting the attainment of a steady-state equilibrium as defined earlier. These dynamics confirm the theoretical validity of the framework and provide empirical grounding for welfare and solvency analyses in the following policy simulations.

To investigate the system’s behavior under alternative policy configurations and demographic scenarios, we conduct controlled simulation experiments by varying key parameters:

-

Capital requirement level α

Adjusting the confidence level for Value-at-Risk calculations (e.g., from 99% to 99.5%)9.

-

Reverse mortgage guarantee schemes

Introducing a public no-negative-equity guarantee program and comparing outcomes with pure private market structures.

-

Demographic shocks

Simulating an upward shift in life expectancy by increasing expected survival rates $S_i\left(t\right)$ and assessing the impact on solvency and pricing spreads.

-

House price shock scenarios

Introducing downward or upward jumps in ${\mu }_H$ and observing effects on reverse mortgage profitability and market stability.

For each experiment, outcome metrics are recorded, including:

-

Average reverse mortgage spread ${\pi }^{*}$

-

Aggregate adoption rate of reverse mortgages among retirees

-

Distribution of lender solvency ratios $K_j\left(t\right)/Va{R}_{\alpha }\left(L_j\left(t\right)\right)$

-

System-wide welfare, measured via average retiree utility

These indicators are aligned with the objectives stated in the introduction and serve as empirical proxies for evaluating policy trade-offs under uncertainty.

Having established the existence of a steady-state equilibrium under baseline conditions, we next investigate how targeted policy interventions can improve market outcomes and welfare distributions. Specifically, we assess whether regulatory adjustments or public guarantees can enhance system stability without sacrificing retiree welfare, formalized in the following lemma.

Lemma 1.

If a regulatory intervention reduces the variance of system-wide solvency ratios while maintaining average retiree utility, it is considered welfare-improving.

Proof. 

Consider a concave, increasing utility function $u(·)$ representing the risk-averse retiree’s utility over final lifetime wealth, which includes pension income, RML proceeds, and bequests. Let X denote the random variable for system-wide solvency ratios, which indirectly affect retirees through pricing spreads, lender default risk, and RML availability.

By Jensen’s inequality (Jensen 1906), for any concave function $u(·)$ and random variable X, the expected utility satisfies:

$$\mathbb{E}\left[u\right(X\left)\right]\le u\left(\mathbb{E}\right[X\left]\right).$$

(29)

If a policy reduces $\mathrm{Var}\left(X\right)$ without altering $\mathbb{E}\left[X\right]$ (as assumed in the lemma statement), the reduction in dispersion around the mean leads to a second-order stochastic dominance (SSD) improvement in the distribution of X. Since retirees are risk-averse (i.e., $u^{″}\left(x\right)<0$), they strictly prefer distributions with lower variance holding mean constant, as shown in classical risk theory (see, e.g., Arrow 1974; Eeckhoudt et al. 2011).

Therefore, any intervention that reduces solvency ratio variance while maintaining average utility necessarily increases expected utility for all retirees in the system, satisfying the welfare-improvement criterion.

Moreover, systemic risk reduction reduces the probability of insurer insolvencies, avoiding discontinuities in RML disbursement schedules and ensuring continued access to reverse mortgages—indirectly improving consumption smoothing and bequest flexibility for retirees under the LCH framework. This theoretical validation confirms the relevance of adaptive regulatory policies in safeguarding the dual goals of retiree welfare and market stability. □

5.3. Regulatory Solver Design and Algorithm

In dynamic financial systems where agent behaviors and systemic risks evolve endogenously, maintaining market solvency and safeguarding retiree welfare requires adaptive regulatory oversight. To this end, we develop a dynamic regulatory solver that continuously monitors the solvency status of reverse mortgage lenders and adjusts capital requirements in response to emerging financial vulnerabilities. This component fulfills our objective (iii) and addresses the reviewer’s call for improved methodological specification by formalizing an optimization-based approach to policy design.

At each discrete time period t, the regulator evaluates the capital adequacy of each lender by computing the capital shortfall $\mathrm{\Delta }{K}_j\left(t\right)$:

$$\mathrm{\Delta }{K}_j\left(t\right)=max\left\{0,Va{R}_{{\alpha }_t}\left(L_j\left(t\right)\right)-K_j\left(t\right)\right\},$$

(30)

where $Va{R}_{{\alpha }_t}\left(L_j\left(t\right)\right)$ is the Value-at-Risk at confidence level ${\alpha }_t$ for lender j’s portfolio of reverse mortgages, and $K_j\left(t\right)$ is the available capital reserve. A positive shortfall indicates undercapitalization relative to the regulatory standard.

The regulator seeks to optimize the trade-off between market stability and retiree welfare by adjusting the capital requirement parameter ${\alpha }_t$ to minimize a social loss function:

$$\mathcal{L}\left({\alpha }_t\right)=\sum _j{w}_j\mathrm{\Delta }{K}_j\left(t\right)+\lambda \sum _i\left(U_i^{*}-U_i\left({\alpha }_t\right)\right),$$

(31)

where $w_j$ is a weight capturing the systemic importance of lender j, $U_i^{*}$ is a benchmark utility level for retiree i, and $\lambda$ is a parameter reflecting the regulator’s preference between financial stability and retiree welfare.

The regulator assesses capital adequacy using lender-specific Value-at-Risk (VaR) metrics at each simulation period, identifying shortfalls relative to dynamic capital requirements. These shortfalls and associated welfare effects are jointly incorporated into a social loss function, representing the regulator’s objective function. The following theorem establishes the existence and uniqueness of the optimal capital requirement adjustment that minimizes this loss.

Theorem 2.

There exists a unique capital requirement parameter ${\alpha }_t^{*}$ minimizing the social loss function $\mathcal{L}\left({\alpha }_t\right)$ under convexity assumptions.

Proof. 

Consider the social loss function:

$$\mathcal{L}\left({\alpha }_t\right)=\sum _j{w}_j\mathrm{\Delta }{K}_j\left(t\right)+\lambda \sum _i\left(U_i^{*}-U_i\left({\alpha }_t\right)\right),$$

(32)

where $\mathrm{\Delta }{K}_j\left(t\right)=max\{0,Va{R}_{{\alpha }_t}\left(L_j\left(t\right)\right)-K_j\left(t\right)\}$ is a non-decreasing, convex function of ${\alpha }_t$, since higher confidence levels produce higher VaR estimates in continuous loss distributions (McNeil et al. 2015).

Simultaneously, retiree utility $U_i\left({\alpha }_t\right)$ is concave in ${\alpha }_t$, as higher capital requirements lead to higher reverse mortgage spreads, reducing disposable income and utility. Under standard assumptions of diminishing marginal utility (concavity of $u(·)$ in wealth), this relationship follows directly from the envelope theorem applied to the retiree’s indirect utility function over loan proceeds (Mas-Colell et al. 1995).

Since $\mathcal{L}\left({\alpha }_t\right)$ is a weighted sum of convex and concave terms, and given that convexity is preserved under non-negative weighting and addition when concave components are multiplied by negative $\lambda$ (provided $\lambda >0$ is small relative to system weights $w_j$), the overall loss function is strictly convex over admissible ${\alpha }_t\in [{\alpha }_{min},{\alpha }_{max}]$.

By standard convex optimization theory (Boyd and Vandenberghe 2004), a unique global minimizer ${\alpha }_t^{*}$ exists within this closed, convex domain. Existence follows from the continuity and coercivity of $\mathcal{L}\left({\alpha }_t\right)$, and uniqueness from strict convexity. □

To solve for the optimal ${\alpha }_t^{*}$, the regulator applies a gradient descent algorithm:

$${\alpha }_{t+1}={\alpha }_t-\eta {\nabla }_{\alpha }\mathcal{L}\left({\alpha }_t\right),$$

(33)

where $\eta$ is a step size parameter. The gradient ${\nabla }_{\alpha }\mathcal{L}\left({\alpha }_t\right)$ is computed numerically at each iteration based on the marginal impact of changing ${\alpha }_t$ on lender shortfalls and retiree utility outcomes.

This iterative solver ensures that capital requirements adapt responsively to shifting market risks while safeguarding retiree welfare, thereby enhancing the resilience of the reverse mortgage market ecosystem under demographic and economic stress scenarios. The formal convex optimization framework ensures both theoretical soundness and practical implementability, advancing the methodological rigor of the model.

5.4. Policy Experiment Design

To assess the market’s responsiveness to policy interventions and demographic shocks, we conducted a series of controlled simulation experiments varying key model parameters. These policy simulations are explicitly linked to our stated hypotheses and provide a testbed for evaluating the consequences of regulatory and demographic shifts on retiree welfare and financial solvency. The experiments include adjustments to the capital requirement confidence level $\alpha$, introduction of a public no-negative-equity guarantee scheme, and upward shifts in life expectancy. Detailed specifications for each scenario are reported alongside the simulation results in Section 6.

6. Simulation Results

This section presents the numerical results obtained from the agent-based simulations, evaluating market behavior under both baseline and alternative policy scenarios. The results are interpreted with reference to the market equilibrium definitions (Definition 1) and policy effectiveness criteria (Lemma 1) established earlier. The simulation findings directly test the hypotheses outlined in the introduction regarding the broader financial resilience, risk-return trade-offs, and welfare effects associated with reverse mortgage adoption and regulatory design.

We report steady-state equilibrium values for key market outcomes, like reverse mortgage adoption rates, pricing spreads, lender solvency ratios, and retiree welfare, along with system responses to capital regulation adjustments, public guarantee schemes, and demographic shocks. Each simulation scenario is designed to evaluate one or more dimensions of regulatory robustness, financial sustainability, and consumer welfare, thus providing empirical grounding for policy implications.

6.1. Baseline Market Dynamics and Equilibrium Outcomes

In the baseline scenario, with capital requirement confidence level $\alpha =99.5\%$, no government guarantee, and demographic parameters aligned with historical longevity trends10, the system consistently converged to equilibrium values satisfying the conditions of Definition 1. This validates the internal consistency of the modeling framework and supports the empirical plausibility of the baseline assumptions.

Simulation outcomes averaged over 1000 replications yield:

-

Average steady-state reverse mortgage spread: ${\pi }^{*}=3.25\%$

-

Aggregate RM adoption rate among eligible retirees: 42%

-

Mean lender solvency ratio (capital buffer relative to Value-at-Risk): 1.08

-

Average retiree utility: 95.3 (normalized utility units)

Convergence patterns for these variables are illustrated in Figure 4, which confirms dynamic stability, validating Theorem 1’s equilibrium existence claim under baseline assumptions.

Notably, the absence of systemic insolvency or liquidity distress under baseline conditions confirms that a moderately conservative regulatory setting can ensure financial resilience while supporting moderate adoption of reverse mortgage products. No episodes of systemic insolvency, liquidity shortages, or forced market closure were observed, indicating robustness of the baseline regulatory setting.

6.2. Policy Experiment Results: Effects of Capital Requirements, Guarantees, and Longevity Shocks

To evaluate the market’s resilience and welfare outcomes under alternative scenarios, controlled experiments were conducted by varying key parameters as described in Section 5.4. These simulations provide an empirical testbed for analyzing how policy instruments can buffer systemic risk or amplify volatility, directly supporting the model’s application in policy calibration. Notable findings include:

-

Capital requirement sensitivity

Reducing the confidence level $\alpha$ from 99.5% to 99% led to a 7 percentage point increase in RM adoption, reflecting improved affordability from lower pricing spreads. However, this relaxation also increased the frequency of lender capital shortfalls by 14%, corroborating the solvency risk–welfare trade-off formalized in Lemma 1. This result highlights the tension between expanding product access and preserving financial system resilience.

-

Introduction of a public no-negative-equity guarantee

Adding a state-backed guarantee reduced average spreads to 2.85%, improved mean retiree utility by 5.2%, and stabilized average solvency ratios near 1.12 by mitigating tail risk exposure for lenders. This finding suggests that well-targeted public guarantees can be efficiency-enhancing by absorbing extreme downside risk while leaving routine pricing to market forces.

-

Demographic longevity shock

Simulating a 2-year increase in life expectancy reduced average lender solvency ratios by 12%, triggering capital shortfalls under the baseline $\alpha =99.5\%$. Regulatory solvency could be restored by raising $\alpha$ to 99.7%, although this adjustment elevated spreads to 3.5% and marginally reduced RM adoption rates. This underscores the vulnerability of long-duration financial products to demographic shifts and the need for adaptive regulatory thresholds.

6.3. Welfare-Adjusted Policy Trade-Offs

Across all scenarios, the simulations confirmed the welfare-efficiency criterion of Lemma 1: policy interventions that reduced system-wide solvency ratio variance while maintaining average utility levels were consistently welfare-improving. This provides quantitative support for the model’s normative implications and affirms its utility as a policy evaluation tool.

The capital requirement adjustment algorithm (Theorem 2) reliably converged to unique, optimal ${\alpha }_t^{*}$ values minimizing the social loss function. Figure 4 visually illustrates this dynamic stabilization under baseline conditions. This outcome confirms the algorithm’s computational tractability and real-time policy relevance in evolving risk environments.

These findings underscore the inherent trade-offs in reverse mortgage markets between pricing, solvency regulation, demographic longevity risk, and retiree welfare—precisely the policy coordination problem this model was designed to illuminate. The integration of actuarial optimization with macroprudential simulation provides a unified methodological foundation for reconciling household-level incentives with system-level constraints, thereby addressing the central research question of the study.

7. Policy Implications and Future Directions

The findings of this study offer critical implications for pension system reform, financial regulation, and market design in aging economies. The RMLs emerge not merely as an auxiliary financial tool but as a strategically vital instrument to enhance the sustainability of retirement income systems, aligning with recent calls for more diversified, asset-based solutions in pension planning (see, e.g., Said et al. 2025; Suari-Andreu et al. 2019).

In direct connection to the hypotheses proposed in the introduction, our agent-based simulations confirm that systemic adoption of RMLs can deliver welfare-enhancing outcomes while preserving lender solvency under carefully calibrated regulatory conditions.

The actuarial and agent-based analyses presented here demonstrate that RMLs improve lifetime utility, help smooth retirees’ consumption, and alleviate fiscal pressures on public pension schemes by mobilizing substantial home equity wealth. These results echo earlier findings on the welfare gains from equity release products De Nardi et al. (2010); Hanewald et al. (2016), while extending them by explicitly incorporating systemic market feedback effects and regulatory solvency mechanisms.

This methodological integration offers a structured approach through which policymakers can assess retirement finance strategies across both individual and systemic levels.

From a policy perspective, it is imperative to formally integrate RMLs into national retirement income frameworks as a complementary pillar to public pensions and private annuities. Governments should proactively invest in financial literacy initiatives targeting older homeowners, ensuring retirees understand both the opportunities and long-term risks of RML products (see, e.g., Andreasson and Shevchenko 2024; Brown 2001; Di Lorenzo et al. 2017). Clear, accessible guidelines explaining contract terms, loan mechanics, and implications for estate planning must accompany product availability.

Financial institutions should be encouraged to design transparent, flexible, and affordable RML products tailored to heterogeneous retiree preferences and health risk profiles. Innovations such as hybrid reverse mortgage-annuity combinations, deferred draw options, and inflation-linked RMLs could broaden market appeal and improve retirement resilience Shan (2011). Concurrently, risk management frameworks must evolve to accommodate longevity, house price, and interest rate risks, potentially supported by hedging instruments or risk-pooling platforms Alonso et al. (2017).

Regulatory bodies have a pivotal role in safeguarding market integrity, systemic stability, and consumer protection. The establishment of uniform solvency and risk-capital standards—consistent with Solvency II frameworks—and the adoption of dynamic regulatory solvers, as proposed in this study, can mitigate insurer insolvency risk and contagion effects in asset-linked retirement markets Yang and Zhou (2023). Public-private risk-sharing schemes, such as state-backed no-negative-equity guarantees, could further strengthen market confidence and adoption rates.

While reverse mortgages differ from traditional consumer loans in their non-recourse structure and deferred repayment, their long-term accumulation on financial institutions’ balance sheets nonetheless raises relevant systemic concerns. In particular, concentrations of reverse mortgage exposure may take on characteristics akin to non-performing assets during housing downturns, especially when property values fall below loan balances. Literature from Alnabulsi et al. (2022), Bect et al. (2015), and Derguc-Kunt et al. (2024) emphasizes how asset-backed exposures—if insufficiently provisioned for—can generate hidden fragilities within the financial system, particularly under stress conditions. Therefore, it is essential that macroprudential authorities monitor RML markets alongside traditional mortgage portfolios, integrating them into capital adequacy stress-testing regimes, countercyclical buffers, and systemic risk assessments. This is particularly relevant for jurisdictions where reverse mortgages are expanding rapidly in response to demographic aging.

Despite its strengths, the proposed modeling framework is not without limitations. The simulations assume homogenous borrower behavior, uniform property markets, and average financial literacy, which may not fully reflect the heterogeneity observed in real-world retiree populations. In particular, regional variations in housing liquidity, regulatory enforcement, and household preferences could materially affect RML outcomes. Moreover, future property values may be shaped by climate-related risks—such as flood exposure, wildfire zones, or energy inefficiency—which are not yet incorporated in the current framework. Finally, behavioral dimensions such as distrust in financial products, aversion to indebtedness, or differing cognitive biases among older adults remain underexplored. Future research could extend the model to capture these geographical, environmental, and psychological dimensions, offering a more granular and robust basis for market and policy design.

In summary, the effective integration of RMLs into retirement planning requires coordinated interventions across public policy, product innovation, financial supervision, and consumer education. Doing so can enhance the financial resilience of retirees while alleviating long-term fiscal and demographic stresses on public pension systems.

8. Conclusions

This study demonstrates the viability and economic value of RMLs as a sustainable financial solution for addressing the pension system challenges posed by demographic aging. By integrating actuarial pricing models, stochastic longevity and house price processes, and a dynamic agent-based market framework, we deliver novel insights into both individual and systemic implications of widespread RML adoption—a dimension underexplored in prior literature (Di Lorenzo et al. 2025; Gotman 2020; Jang et al. 2024).

Our analysis is explicitly grounded in the initial research hypothesis that RMLs, when properly regulated, can simultaneously enhance retiree welfare and market solvency. This hypothesis is tested through a congruent combination of micro-level optimization and macro-level simulation techniques.

Numerical results confirm that RMLs enhance retirees’ lifetime utility, stabilize consumption trajectories, and extend financial flexibility without undermining bequest motives. The agent-based simulations further reveal how aggregate adoption dynamically influences market pricing, insurer solvency, and public pension system liabilities, highlighting complex feedback mechanisms warranting proactive regulatory oversight.

Importantly, the dynamic regulatory solver proposed herein offers a practical policy tool for adjusting capital requirements in real time to evolving systemic risks, efficiently balancing financial stability and retiree welfare objectives. This directly supports our methodological objective of embedding policy sensitivity within a solvency-aware agent-based framework. These findings underscore the urgent need to integrate reverse mortgage markets within broader pension reform strategies and to establish supportive policy frameworks promoting responsible product design, market transparency, and financial literacy initiatives Said et al. (2025).

Future research should extend this modeling framework by incorporating climate risk scenarios affecting long-term property values, regional housing market dynamics, and cross-country calibration under varying Solvency II implementations. Additionally, behavioral analyses of RML adoption heterogeneity and retirement decision heuristics within agent-based models would enrich welfare and policy implications, addressing longstanding calls for micro-founded, dynamic pension policy evaluation tools (Alonso et al. 2017; Barr 2021).