Effects of Traditional Reinsurance on Demographic Risk Under the Solvency II Framework
Abstract
1. Introduction
2. Preliminaries
3. The General Framework
- 1.
- Gross premiums are collected at the beginning of each year, at time , for every policyholder who is still alive.
- 2.
- Acquisition expenses are fully paid at the inception of the contract (i.e., ), while management expenses are paid at the beginning of each period, at time , provided the policyholder is still alive.
- 3.
- Death benefits due to beneficiaries for claims occurring within the period are paid at the end of the time interval, i.e., at time .
4. The Cohort Valuation Portfolio
- Step 1 Choice of financial instruments.According to Formula (9), the distinct timing of cash flows necessitates separate consideration of inflows and outflows at time t. Each can be replicated using respective portfolios of financial instruments. We consider a cohort of term insurance policies with constant capital and fixed annual premiums. At each time t, the inflows and outflows are replicated using ZCBs, denoted as and .
- Step 2 Determination of the number of portfolio shares to replicate cash flows.Once the financial instruments are selected, we determine the quantity of each required to replicate the future cash flows :
- Step 3 The accounting principle used to value financial instruments.Each financial instrument is valued according to the selected accounting principle. In this paper, we adopt a fair value approach under the Solvency II framework, meaning that each instrument is valued at its current market price. We denote this accounting principle by , with , and define the accounting value of the cash flows as:Introducing the prices of the financial instruments, we have:
5. Demographic Risk and Solvency
5.1. The Model Framework
5.2. The Idiosyncratic Risk
5.3. Characteristics of Demographic-Idiosyncratic Risk
6. Managing Demographic Risk and Reinsurance Strategy
- 1.
- The primary insurer bears the full cost of acquisition and management expenses.
- 2.
- The price of the reinsurance contract is implicitly determined by the reinsurer, with the commission percentage determining the reinsurance fee.
- 3.
- The commission is paid by the reinsurer to the primary insurer at the beginning of each year.
6.1. Surplus Reinsurance
6.2. Quota-Share Reinsurance
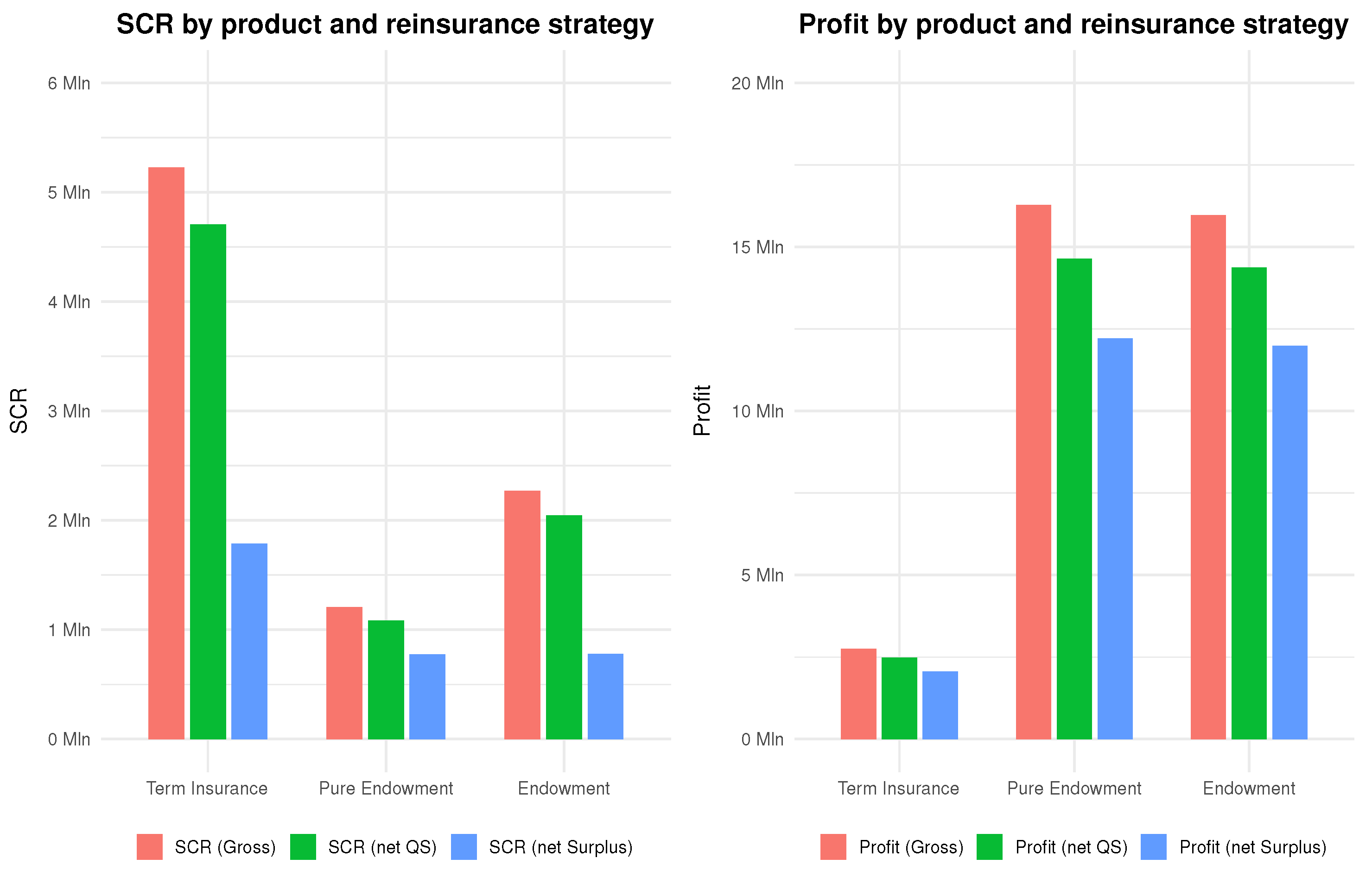
7. Numerical Analysis
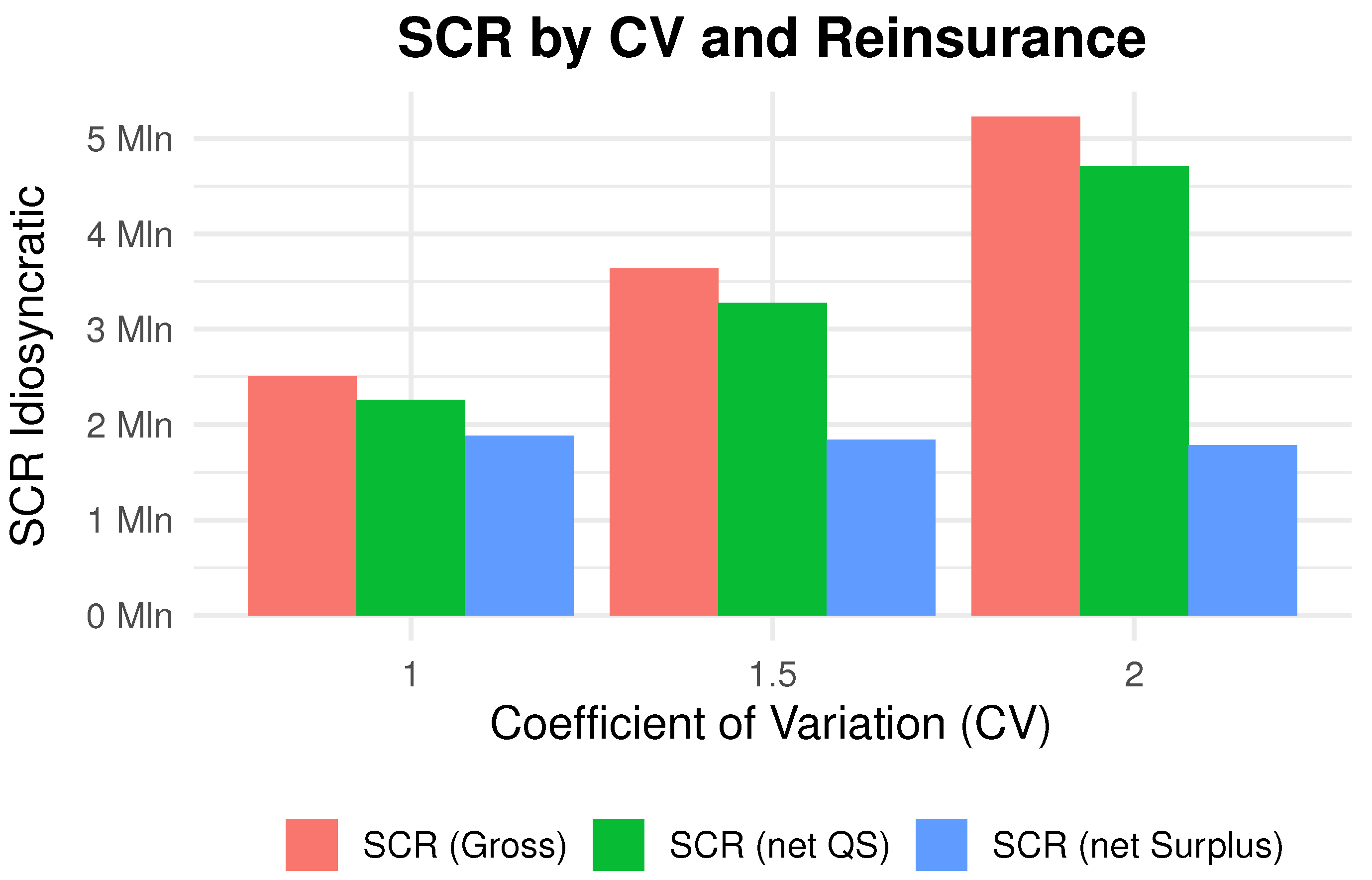
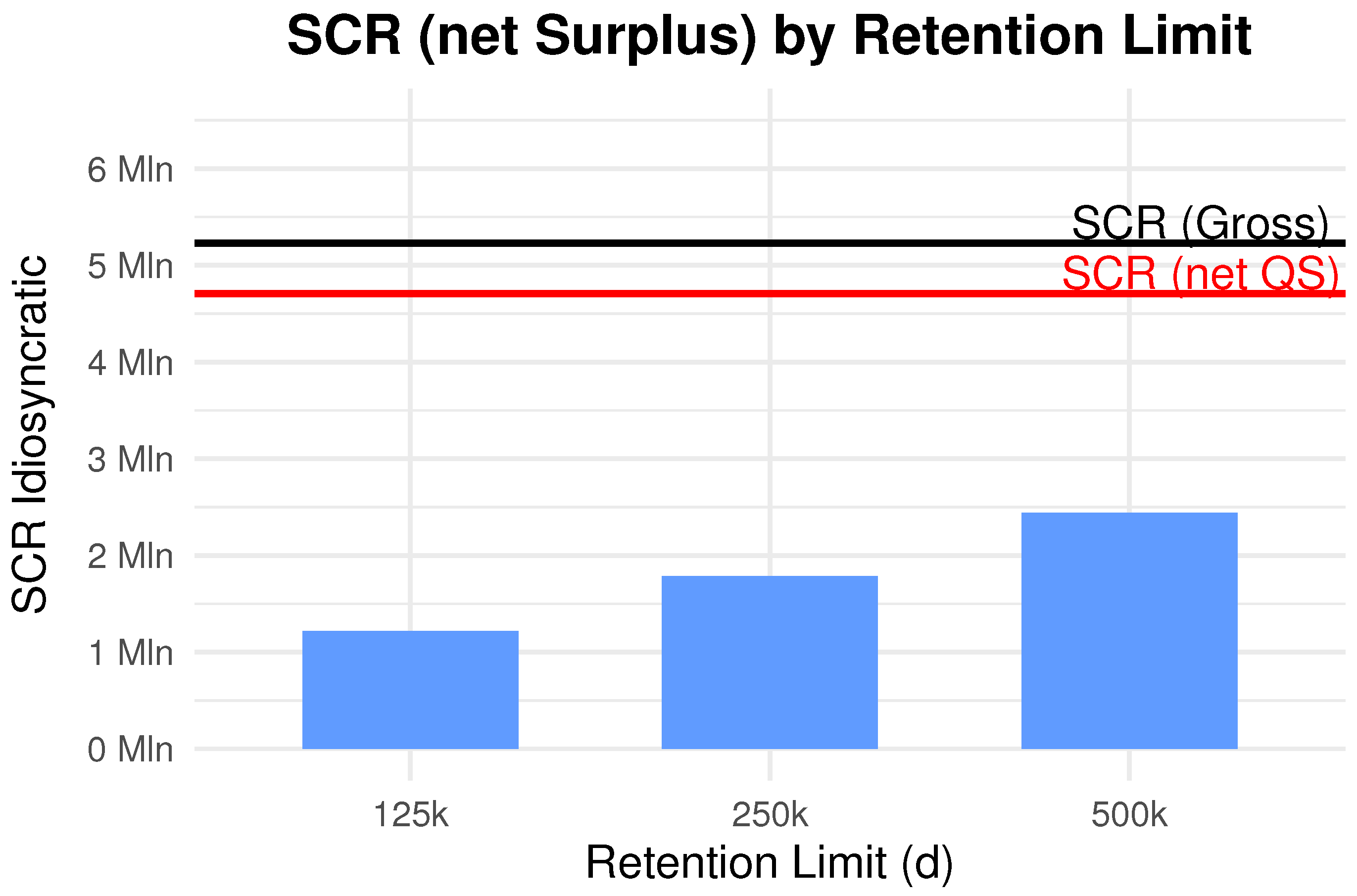
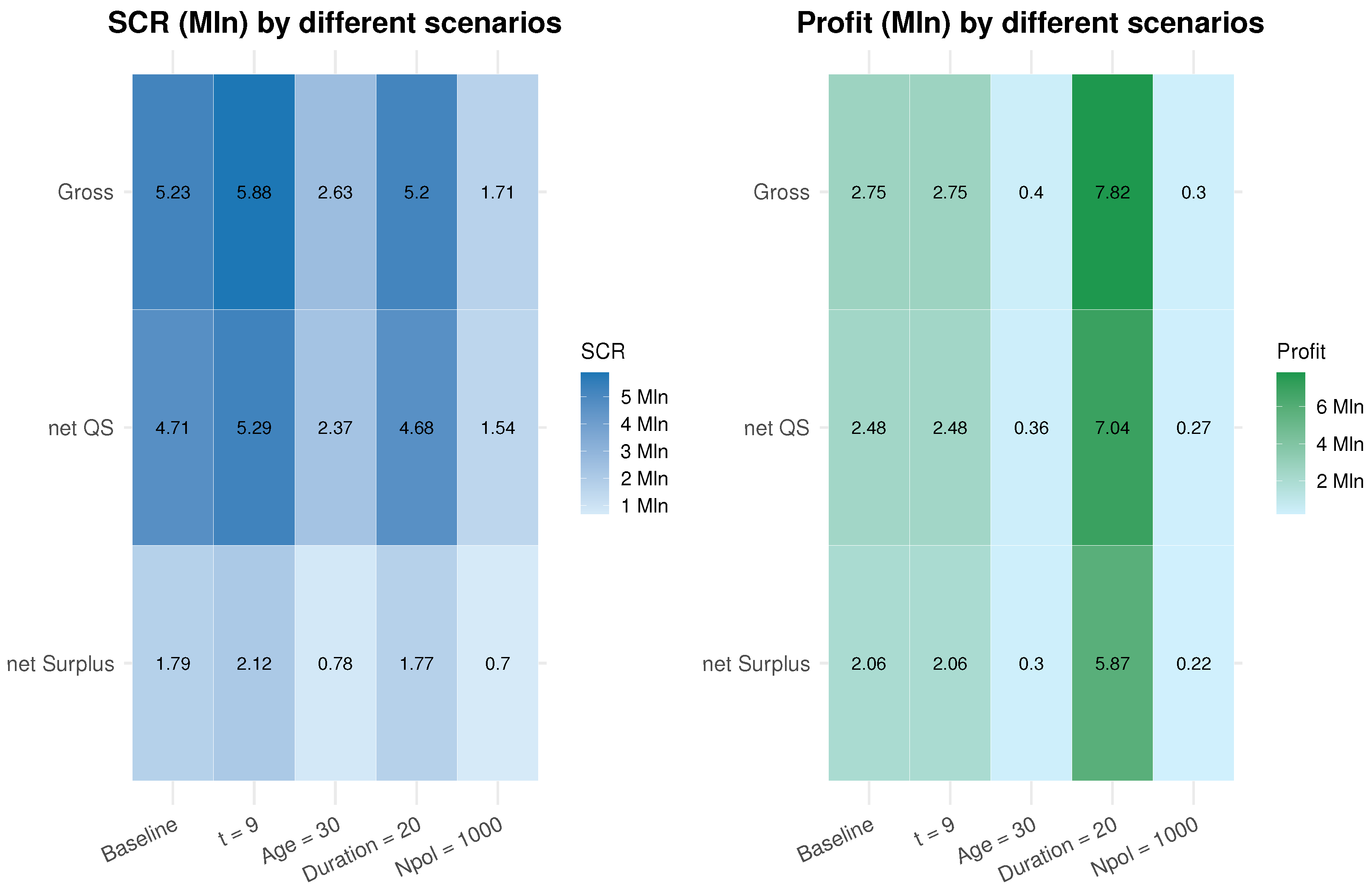
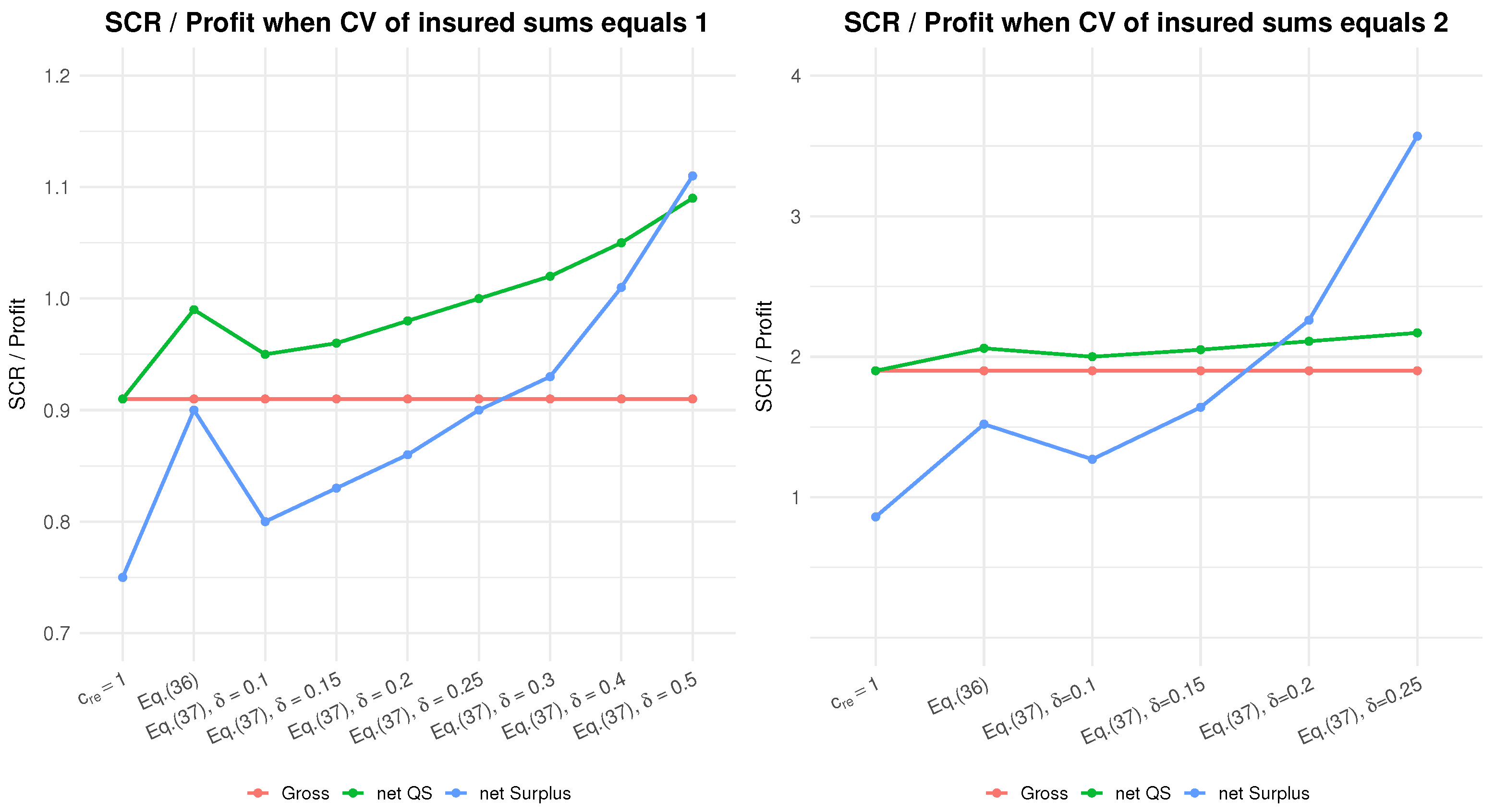
7.1. Simulation Parameters and Preliminary Analysis
7.2. Baseline Analysis and Sensitivities
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Claims Development Result for Idiosyncratic Risk
Appendix B. Moments of the Claims Development Result for Idiosyncratic Risk
Appendix B.1. Deterministic Parameter
Appendix B.2. Stochastic Parameter
Appendix C. Claims Development Result with Reinsurance
Appendix C.1. Surplus Reinsurance
Appendix C.2. Quota-Share Reinsurance
| 1 | Random variables are indicated with capital letters, deterministic values with lowercase letters, and vectors and matrices in bold. |
| 2 | This notation is taken from (Wüthrich et al. 2010). |
| 3 | The superscript L in stands for Life. |
| 4 | From now on, the superscripts M and A will refer to management and acquisition, respectively. |
| 5 | Details on how the expense loadings are determined are provided in Section 4. |
| 6 | We clarify that is a function taking the value 1 if , and 0 otherwise. |
| 7 | By contrast, for an endowment policy we should distinguish the two cases: for it takes values , while for , it is equal to 1. |
| 8 | The superscripts B, D in and stand, respectively, for benefit and death. |
| 9 | With second-order assumptions or second-order technical bases we refer to the expected realizations, without any prudence included in the valuation. They do not contain any margin and consist of the Best Estimate with respect to the insured population, often called experience basis (see, e.g., Bowers et al. 1997; Olivieri and Pitacco 2015). |
| 10 | The same relation holds for , which, for each , are i.i.d. Bernoulli random variables described by a -measurable random parameter , with expected value equal to the second-order annual survival probability, , of a policyholder aged x at inception. |
| 11 | The deflator is defined as the ratio between first-order and second-order annual probabilities. |
| 12 | In the definition of the Cohort VaPo protected in Formula (13), the value of financial instruments is determined using the market-consistent accounting principle . |
| 13 | These formulas apply to a cohort with constant annual premiums over the duration of the contract. |
| 14 | The superscript E in stands for expenses. |
| 15 | Under local accounting principles is also referred to as the Zillmer Reserve. |
| 16 | According to Solvency II, the Best Estimate includes all future cash inflows and outflows. |
| 17 | By “predefined”, we mean either that the sum insured is determined in advance or that the mechanism governing the evolution of benefits is clearly specified. |
| 18 | An expanded version of Formula (27) is provided in Appendix C.1. |
| 19 | The expanded version of Formula (33) is provided in Appendix C.2. |
| 20 | A detailed description of the procedure used for obtaining the is provided in Appendix C.2. |
| 21 | Because may differ for each policyholder in the cohort, the mgf of cannot be modeled as a binomial distribution without oversimplifying the variability in the sum insured. |
References
- Albrecher, Hansjörg, Jan Beirlant, and Jozef L. Teugels. 2017. Reinsurance: Actuarial and Statistical Aspects. Hoboken: John Wiley & Sons. [Google Scholar]
- Bacinello, Anna Rita. 2001. Fair Pricing of Life Insurance Participating Policies with a Minimum Interest Rate Guaranteed. ASTIN Bulletin: The Journal of the IAA 31: 275–97. [Google Scholar] [CrossRef]
- Barigou, Karim, and Łukasz Delong. 2022. Pricing Equity-Linked Life Insurance Contracts with Multiple Risk Factors by Neural Networks. Journal of Computational and Applied Mathematics 404: 113922. [Google Scholar] [CrossRef]
- Barigou, Karim, Ze Chen, and Jan Dhaene. 2019. Fair Dynamic Valuation of Insurance Liabilities: Merging Actuarial Judgement with Market- and Time-Consistency. Insurance: Mathematics and Economics 88: 19–29. [Google Scholar] [CrossRef]
- Besson, Jean-Luc, Michel M. Dacorogna, Paolo de Martin, Michael Kastenholz, and Michael Moller. 2009. How Much Capital Does a Reinsurance Need? The Geneva Papers on Risk and Insurance—Issues and Practice 34: 159–74. [Google Scholar] [CrossRef]
- Bowers, Newton L., Hans U. Gerber, James C. Hickman, Donald A. Jones, and Cecil J. Nesbitt. 1997. Actuarial Mathematics, 2nd ed. Schaumburg: Society of Actuaries. [Google Scholar]
- Brennan, Michael J., and Eduardo S. Schwartz. 1976. The Pricing of Equity-Linked Life Insurance Policies with an Asset Value Guarantee. Journal of Financial Economics 3: 195–213. [Google Scholar] [CrossRef]
- Brennan, Michael J., and Eduardo S. Schwartz. 1979. Alternative Investment Strategies for the Issuers of Equity-Linked Life Insurance Policies with an Asset Value Guarantee. Journal of Business 52: 63–93. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson Log-Bilinear Regression Approach to the Construction of Projected Life Tables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar]
- Chi, Yichun, X. Sheldon Lin, and Ken Seng Tan. 2017. Optimal Reinsurance under the Risk-Adjusted Value of an Insurer’s Liability and an Economic Reinsurance Premium Principle. North American Actuarial Journal 21: 417–32. [Google Scholar] [CrossRef]
- Clemente, Gian Paolo, Francesco Della Corte, and Nino Savelli. 2022. A Stochastic Model for Capital Requirement Assessment for Mortality and Longevity Risk, Focusing on Idiosyncratic and Trend Components. Annals of Actuarial Science 16: 527–46. [Google Scholar] [CrossRef]
- Clemente, Gian Paolo, Francesco Della Corte, and Nino Savelli. 2024a. An Undertaking-Specific Approach to Address Diversifiable Demographic Risk within the Solvency II Framework. Decisions in Economics and Finance. [Google Scholar] [CrossRef]
- Clemente, Gian Paolo, Francesco Della Corte, Nino Savelli, and Diego Zappa. 2024b. Market-Consistent Valuation and Capital Assessment for Demographic Risk in Life Insurance: A Cohort Approach. North American Actuarial Journal 29: 1–25. [Google Scholar] [CrossRef]
- Dacorogna, Michel. 2018. A Change of Paradigm for the Insurance Industry. Annals of Actuarial Science 12: 211–32. [Google Scholar] [CrossRef]
- Deelstra, Griselda, Pierre Devolder, Kossi Gnameho, and Peter Hieber. 2020. Valuation of Hybrid Financial and Actuarial Products in Life Insurance by a Novel Three-Step Method. ASTIN Bulletin: The Journal of the IAA 50: 709–42. [Google Scholar] [CrossRef]
- European Parliament and Council. 2009. Directive 2009/138/EC of the European Parliament and of the Council of 25 November 2009 on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance (Solvency II). Official Journal of the European Union. Available online: https://eur-lex.europa.eu/eli/dir/2009/138/oj/eng (accessed on 20 September 2025).
- European Parliament and Council. 2014. Commission Delegated Regulation (EU) 2015/35. Luxembourg: European Parliament and Council. [Google Scholar]
- Hanbali, Hamza, Michel Denuit, Jan Dhaene, and Julien Trufin. 2019. A Dynamic Equivalence Principle for Systematic Longevity Risk Management. Insurance: Mathematics and Economics 86: 158–67. [Google Scholar]
- Lee, Ronald. 2000. The Lee–Carter Method for Forecasting Mortality, with Various Extensions and Applications. North American Actuarial Journal 4: 80–91. [Google Scholar] [CrossRef]
- Malamud, Semyon, Eugene Trubowitz, and Mario V. Wüthrich. 2008. Market-Consistent Pricing of Insurance Products. ASTIN Bulletin: The Journal of the IAA 38: 483–526. [Google Scholar] [CrossRef]
- Meyricke, Ramona, and Michael Sherris. 2014. Longevity Risk, Cost of Capital and Hedging for Life Insurers under Solvency II. Insurance: Mathematics and Economics 55: 147–55. [Google Scholar]
- Milevsky, Moshe A., S. David Promislow, and Virginia R. Young. 2006. Killing the Law of Large Numbers: Mortality Risk Premiums and the Sharpe Ratio. Journal of Risk and Insurance 73: 673–86. [Google Scholar] [CrossRef]
- Møller, Thomas. 1998. Risk-Minimizing Hedging Strategies for Unit-Linked Life Insurance Contracts. ASTIN Bulletin: The Journal of the IAA 28: 17–47. [Google Scholar] [CrossRef]
- Møller, Thomas. 2002. On Valuation and Risk Management at the Interface of Insurance and Finance. British Actuarial Journal 8: 787–827. [Google Scholar] [CrossRef]
- Olivieri, Annamaria, and Ermanno Pitacco. 2015. Introduction to Insurance Mathematics: Technical and Financial Features of Risk Transfers. Cham: Springer. [Google Scholar]
- R Core Team. 2023. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Savelli, Nino, and Gian Paolo Clemente. 2013. A Risk-Theory Model to Assess the Capital Requirement for Mortality and Longevity Risk. Journal of Interdisciplinary Mathematics 16: 397–429. [Google Scholar] [CrossRef]
- Villegas, Andrés M., Vladimir K. Kaishev, and Pietro Millossovich. 2018. StMoMo: An R Package for Stochastic Mortality Modeling. R Package Version 0.5.2. Journal of Statistical Software 84: 1–38. [Google Scholar] [CrossRef]
- Wüthrich, Mario V., Hans Bühlmann, and Hansjörg Furrer. 2010. Market-Consistent Actuarial Valuation. Cham: Springer, vol. 2. [Google Scholar]
- Yang, Shuai, and Kenneth Q. Zhou. 2023. On Risk Management of Mortality and Longevity Capital Requirement: A Predictive Simulation Approach. Risks 11: 206. [Google Scholar] [CrossRef]

| Symbol | Cash Flow | Definition | When Are They Paid? |
|---|---|---|---|
| Sum insured paid out at the end of the year in which death occurs | 1, 2, …, n | ||
| Anticipated acquisition expenses paid out at inception | 0 | ||
| Anticipated management expenses paid out at the beginning of each year | 0, 1, …, | ||
| Anticipated pure premiums collected at the beginning of each year | 0, 1, …, | ||
| Anticipated acquisition expense loadings collected at the beginning of each year | 0, 1, …, | ||
| Anticipated management expense loadings collected at the beginning of each year | 0, 1, …, |
| Parameter | Value |
|---|---|
| Number of policyholders at inception, | 10,000 |
| Average sum insured at inception, | 100,000 |
| Coefficient of variation of the sum insured, | 0 |
| Cohort policyholders’ age, x | 50 |
| Contract duration, n | 10 |
| Valuation time, t | 5 |
| Second-order demographic base | Lee-Carter model, applied to data of the Italian population (age range: 0–100, time range: 2000–2021) |
| Risk-free rate curve | EIOPA curve at the end of year 2024 |
| First-order demographic base | Second-order stressed by 10% |
| Technical rate | 2% |
| Acquisition expenses paid at inception as a percentage of the insured sums, | 1% |
| Annual management expenses as a percentage of the insured sums, | 0.1% |
| Retained percentage Quota-Share reinsurance, | 0.9 |
| Retention limit Surplus reinsurance, d | 90,000 |
| Commission rate, | 1 |
| Number of simulations, M | 10,000,000 |
| Statistic | Gross Reinsurance | Net of Quota-Share | Net of Surplus |
|---|---|---|---|
| Best Estimate at time 0 | −2750.62 | −2475.56 | −2475.56 |
| Standard deviation | 593.14 | 534.08 | 534.08 |
| Skewness | −0.20 | −0.20 | −0.20 |
| SCR (VaR at 99.5%) | 1665.77 | 1499.91 | 1499.91 |
| SCR (ES at 99%) | 1749.94 | 1575.70 | 1575.70 |
| SCR (ES at 99.5%) | 1936.44 | 1743.62 | 1743.62 |
| Statistic | Gross Reinsurance | Net of Quota-Share | Net of Surplus |
|---|---|---|---|
| Best Estimate at time 0 | −2750.62 | −2475.56 | −2063.92 |
| Standard deviation | 1292.48 | 1164.24 | 620.64 |
| Skewness | −1.39 | −1.39 | −0.34 |
| SCR (VaR at 99.5%) | 5226.89 | 4706.45 | 1785.05 |
| SCR (ES at 99%) | 5517.91 | 4968.49 | 1858.70 |
| SCR (ES at 99.5%) | 6282.10 | 5656.58 | 2040.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchessi, E.; Clemente, G.P.; Della Corte, F.; Savelli, N. Effects of Traditional Reinsurance on Demographic Risk Under the Solvency II Framework. Risks 2025, 13, 203. https://doi.org/10.3390/risks13100203
Bianchessi E, Clemente GP, Della Corte F, Savelli N. Effects of Traditional Reinsurance on Demographic Risk Under the Solvency II Framework. Risks. 2025; 13(10):203. https://doi.org/10.3390/risks13100203
Chicago/Turabian StyleBianchessi, Emily, Gian Paolo Clemente, Francesco Della Corte, and Nino Savelli. 2025. "Effects of Traditional Reinsurance on Demographic Risk Under the Solvency II Framework" Risks 13, no. 10: 203. https://doi.org/10.3390/risks13100203
APA StyleBianchessi, E., Clemente, G. P., Della Corte, F., & Savelli, N. (2025). Effects of Traditional Reinsurance on Demographic Risk Under the Solvency II Framework. Risks, 13(10), 203. https://doi.org/10.3390/risks13100203







