Multi-Timescale Recurrent Neural Networks Beat Rough Volatility for Intraday Volatility Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Recurrent Neural Networks with Multiple Timescales
2.2. Volatility Prediction
2.3. Architecture and Hyperparameters
3. Results
3.1. Average Loss
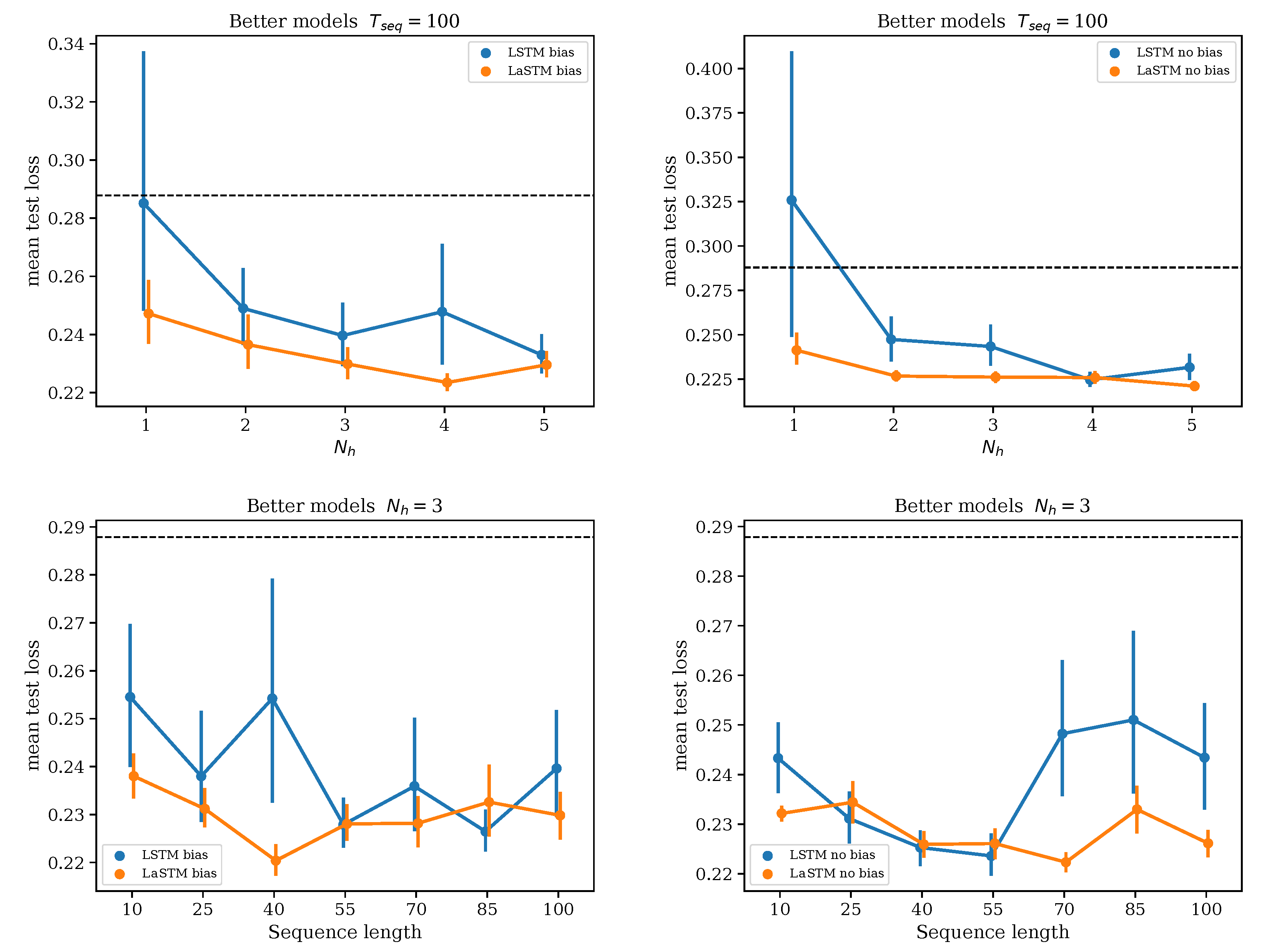
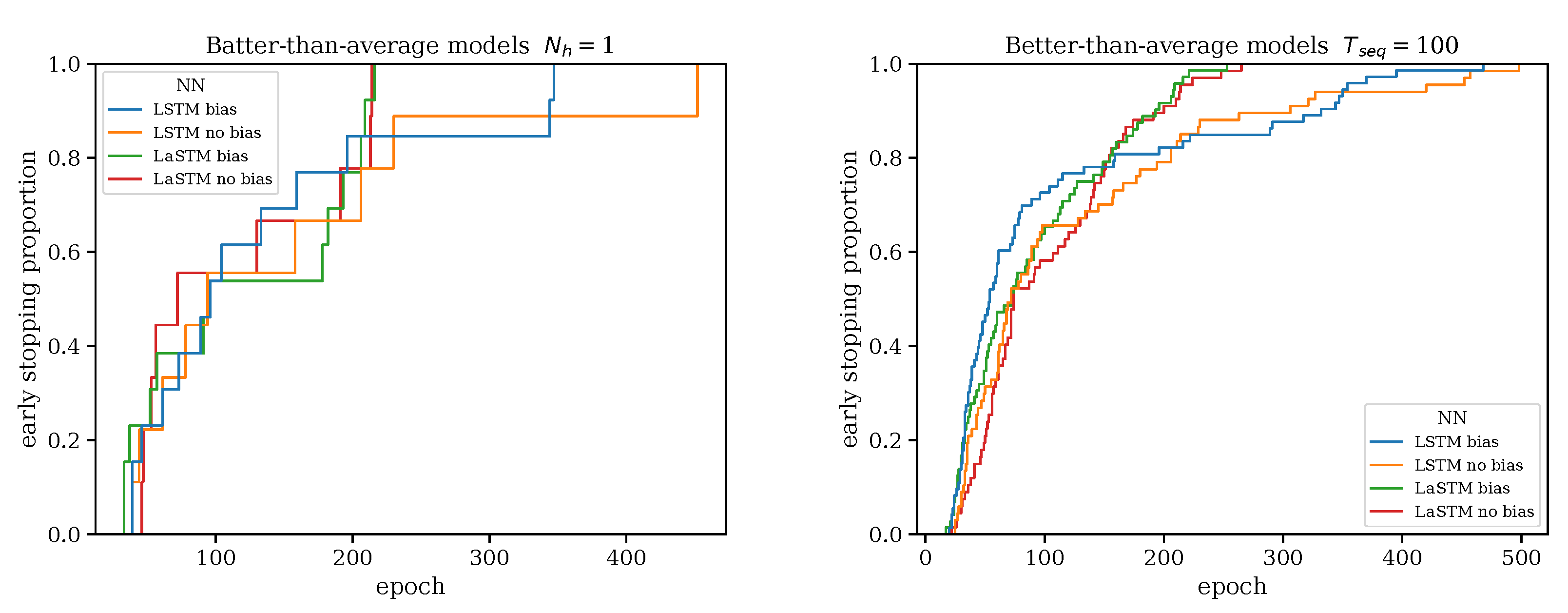
3.2. Keeping the Better Models
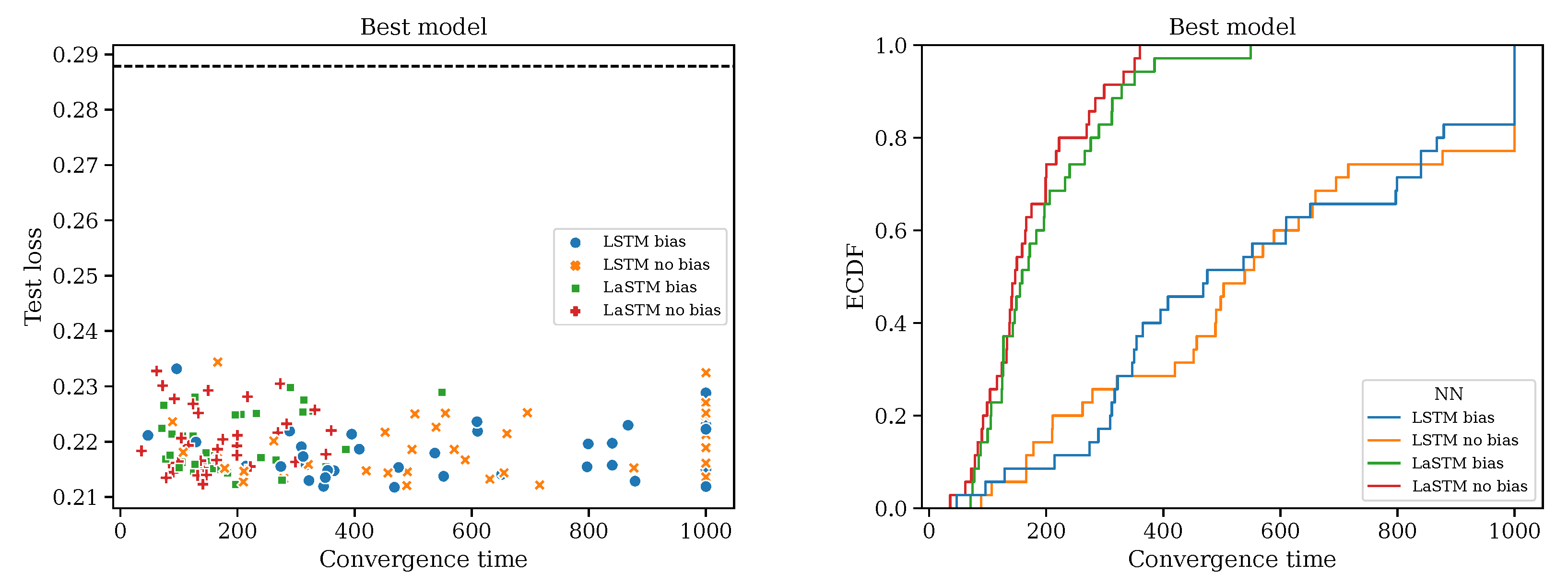
3.3. Best Model
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | AEX, AORD, BFX, BSESN, BVLG, BVSP, DJI, FCHI, FTMIB, FTSE, GDAXI, GSPTSE, HSI, IBEX, IXIC, KS11, KSE, MXX, N225, NSEI, OMXC20, OMXHPI, OMXSPI, OSEAX, RUT, SMSI, SPX, SSEC, SSMI, STI, STOXX50E. |
References
- Barndorff-Nielsen, Ole E., Peter Reinhard Hansen, Asger Lunde, and Neil Shephard. 2008. Designing realized kernels to measure the ex post variation of equity prices in the presence of noise. Econometrica 76: 1481–536. [Google Scholar]
- Bochud, Thierry, and Damien Challet. 2007. Optimal approximations of power laws with exponentials: Application to volatility models with long memory. Quantitative Finance 7: 585–89. [Google Scholar] [CrossRef]
- Challet, Damien, and Robin Stinchcombe. 2001. Analyzing and modeling 1 + 1d markets. Physica A: Statistical Mechanics and Its Applications 300: 285–99. [Google Scholar] [CrossRef]
- Cho, Kyunghyun, Bart van Merrienboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. 2014. Learning phrase representations using rnn encoder–decoder for statistical machine translation. Paper Presented at the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, October 25–29; Cedarville: Association for Computational Linguistics, p. 1724. [Google Scholar]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223. [Google Scholar] [CrossRef]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 174–96. [Google Scholar] [CrossRef]
- Dixon, Matthew, and Justin London. 2021. Financial forecasting with α-RNNs: A time series modeling approach. Frontiers in Applied Mathematics and Statistics 6: 551138. [Google Scholar] [CrossRef]
- Filipović, Damir, and Amir Khalilzadeh. 2021. Machine Learning for Predicting Stock Return Volatility. Swiss Finance Institute Research Paper. Zürich: Swiss Finance Institute, pp. 21–95. [Google Scholar]
- Ganesh, Prakhar, and Puneet Rakheja. 2018. Vlstm: Very long short-term memory networks for high-frequency trading. arXiv arXiv:1809.01506. [Google Scholar]
- Gatheral, Jim. 2016. Rough Volatility with Python. Available online: https://tpq.io/p/rough_volatility_with_python.html (accessed on 14 May 2024).
- Gatheral, Jim, Thibault Jaisson, and Mathieu Rosenbaum. 2018. Volatility is rough. Quantitative Finance 18: 933–49. [Google Scholar] [CrossRef]
- Gers, Felix A., Jürgen Schmidhuber, and Fred Cummins. 2000. Learning to forget: Continual prediction with LSTM. Neural Computation 12: 2451–71. [Google Scholar] [CrossRef] [PubMed]
- Guyon, Julien, and Jordan Lekeufack. 2023. Volatility is (mostly) path-dependent. Quantitative Finance 23: 1221–58. [Google Scholar] [CrossRef]
- Heber, Gerd, Asger Lunde, Neil Shephard, and Kevin Sheppard. 2022. Oxford-Man Institute’s Realized Library. Available online: https://realized.oxford-man.ox.ac.uk/ (accessed on 18 February 2021).
- Kim, Ha Young, and Chang Hyun Won. 2018. Forecasting the volatility of stock price index: A hybrid model integrating lstm with multiple GARCH-type models. Expert Systems with Applications 103: 25–37. [Google Scholar] [CrossRef]
- Lillo, Fabrizio, and J. Doyne Farmer. 2004. The long memory of the efficient market. Studies in Nonlinear Dynamics & Econometrics 8: 1–27. [Google Scholar] [CrossRef]
- Ohno, Kentaro, and Atsutoshi Kumagai. 2021. Recurrent neural networks for learning long-term temporal dependencies with reanalysis of time scale representation. Paper Presented at the 2021 IEEE International Conference on Big Knowledge (ICBK), Auckland, New Zealand, December 7–8; pp. 182–89. [Google Scholar]
- Palma, Wilfredo. 2007. Long-Memory Time Series: Theory and Methods. Hoboken: John Wiley & Sons. [Google Scholar]
- Palminteri, Stefano, Germain Lefebvre, Emma J Kilford, and Sarah-Jayne Blakemore. 2017. Confirmation bias in human reinforcement learning: Evidence from counterfactual feedback processing. PLoS Computational Biology 13: e1005684. [Google Scholar] [CrossRef] [PubMed]
- Resagk, Christian, Ronald du Puits, André Thess, Felix V Dolzhansky, Siegfried Grossmann, Francisco Fontenele Araujo, and Detlef Lohse. 2006. Oscillations of the large scale wind in turbulent thermal convection. Physics of Fluids 18: 095105. [Google Scholar] [CrossRef]
- Robinson, Peter M. 2003. Advanced Texts in Econometrics. In Time Series with Long Memory. Oxford: Oxford University Press. [Google Scholar]
- Rosenbaum, Mathieu, and Jianfei Zhang. 2021. Deep calibration of the quadratic rough heston model. arXiv arXiv:2107.01611. [Google Scholar]
- Rosenbaum, Mathieu, and Jianfei Zhang. 2022. On the universality of the volatility formation process: When machine learning and rough volatility agree. arXiv arXiv:2206.14114. [Google Scholar] [CrossRef]
- Thuerey, Nils, Philipp Holl, Maximilian Mueller, Patrick Schnell, Felix Trost, and Kiwon Um. 2021. Physics-based Deep Learning. arXiv arXiv:2109.05237. [Google Scholar]
- Zhao, Jingyu, Feiqing Huang, Jia Lv, Yanjie Duan, Zhen Qin, Guodong Li, and Guangjian Tian. 2020. Do RNN and LSTM have long memory? Paper Presented at the International Conference on Machine Learning, Online, July 13–18; pp. 11365–75. [Google Scholar]
- Zumbach, Gilles. 2010. Volatility conditional on price trends. Quantitative Finance 10: 431–42. [Google Scholar] [CrossRef]
- Zumbach, Gilles. 2015. Cross-sectional universalities in financial time series. Quantitative Finance 15: 1901–12. [Google Scholar] [CrossRef]
- Zumbach, Gilles, and Paul Lynch. 2001. Heterogeneous volatility cascade in financial markets. Physica A: Statistical Mechanics and Its Applications 298: 521–29. [Google Scholar] [CrossRef]


| Architecture | Bias | Test Loss Average | Test Loss Std Dev. |
|---|---|---|---|
| rough vol. | 0.288 | 0.015 | |
| LSTM | yes | 0.241 | 0.032 |
| LSTM | no | 0.245 | 0.057 |
| LaSTM | yes | 0.232 | 0.017 |
| LaSTM | no | 0.230 | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Challet, D.; Ragel, V. Multi-Timescale Recurrent Neural Networks Beat Rough Volatility for Intraday Volatility Prediction. Risks 2024, 12, 84. https://doi.org/10.3390/risks12060084
Challet D, Ragel V. Multi-Timescale Recurrent Neural Networks Beat Rough Volatility for Intraday Volatility Prediction. Risks. 2024; 12(6):84. https://doi.org/10.3390/risks12060084
Chicago/Turabian StyleChallet, Damien, and Vincent Ragel. 2024. "Multi-Timescale Recurrent Neural Networks Beat Rough Volatility for Intraday Volatility Prediction" Risks 12, no. 6: 84. https://doi.org/10.3390/risks12060084
APA StyleChallet, D., & Ragel, V. (2024). Multi-Timescale Recurrent Neural Networks Beat Rough Volatility for Intraday Volatility Prediction. Risks, 12(6), 84. https://doi.org/10.3390/risks12060084






