The SEV-SV Model—Applications in Portfolio Optimization
Abstract
1. Introduction
- We define a new, richer model capturing both stochastic elasticity of volatility and stochastic volatility.
- We study two sub-models arising from the way in which the OU process relates to the elasticity of volatility . We use estimates of the 4/2 model as per (Cheng and Escobar-Anel 2021) and estimates for the SEV as per (Kim et al. 2015) for further analyses.
- In closed-form optimal investment, we find optimal wealth and value function for a risk-averse investor within expected utility theory, for two choices of prices of risk (MPR). Our setting is different from that of (Gao 2010).
- We show the impact of the new parameters, namely , and , on the optimal allocation. For this, we select and fix the paths of the processes representing states of the market, i.e., increasing prices (bull market), a decreasing path (bear market), and stable prices (normal market conditions).
- We also compare the solution in the absence of SV to separate the effects of SEV from those of SV.
2. Material and Methods: Model Formulation and Properties
- = 0, , and —The celebrated SV Heston model (Heston 1993).
- , , and —The SV 3/2 model (Heston 1997).
- , , and —The SV stochastic volatility model (Grasselli 2017).
- , , , and —The constant elasticity of variance (CEV) model (see Cox 1975; Cox and Ross 1976).
- , , , and —The stochastic elasticity of variance (SEV) model (see Kim et al. 2014)
- and —The E-CEV model of (Gao 2010) and a particular case of the generalized SABR model in (Lions and Musiela 2007).
3. Results: Portfolio Problem and Solution
- Assume and hold. The value function (17) can be represented aswhere and are given bywith auxiliary parameters , , and , where . Then, the optimal strategy is given bywith defined by functions (5) and (6).Furthermore, the optimal wealth has the following dynamics under measurewith initial wealth .
- Furthermore, the optimal wealth has the following dynamics under real-world measurewith initial wealth .
4. Results: Numerical Setting
4.1. Parameter Value Selection
- Values for the 4/2-related parameters , , in the SEV-4/2 modelOur model combines two models—the SEV and 4/2 models. The hybrid structure not only possesses new features but also inherits some characteristics of each of the two models. The parameters, , a, b, , , , and are inherited from the 4/2 model, and their estimates were already obtained by (Cheng and Escobar-Anel 2021). Table 1 displays these parameter values.
- Values for the SEV-related parameters , , in the SEV-4/2 modelWe consider two approaches for these parameters based on the two bound functions f (see Equations (5) and (6)) connecting and .
- 2.1
- For the Gaussian function, we propose values of , , and for a baseline case and two other cases as follows in Table 2.
- 2.2
- For the Arctan function, we match the SEV part of our model to the SEV part of (Kim et al. 2015). Here, we call the SEV model in (Kim et al. 2015) as Kim’s model. To distinguish the parameters from our model’s parameters, we use a subscript K to denote parameters from Kim’s model. Let us recall that the stock price process can be expressed by the stochastic differential equation (SDE) in Kim’s model as follows:under a risk-neutral measure, where (interest rate) and (volatility coefficient) are positive constants, is a nonnegative stochastic process, and is a standard Brownian motion. Let (i.e., ) for convenience, and suppose that follows an Ornstein–Uhlenbeck process given by the solution to the SDE:where , , and are constants. From Figure 1 in (Kim et al. 2015), we know that the estimates of are . In addition, using the properties of OU processes, for we haveNow, with our model and notation, we getGiven the non-linear nature of f, we first perform a Taylor approximation for around . That is,Next, we match the properties of our approximated process and those of Kim’s process:Using formulae (31)–(33) yields , , and . Due to , it follows thatThus, for the Arctan function, we could propose values of , , and associated with Kim’s model for a new baseline case and two other cases, as listed in Table 3 below:
4.2. Model Discretization and Simulation
5. Results: Analysis of Optimal Investment Strategies
5.1. Sensitivity to the Interaction of SEV and SV Processes
- Gaussian function analysis. The figures in this analysis can be found in Appendix A.3.1.
- (a)
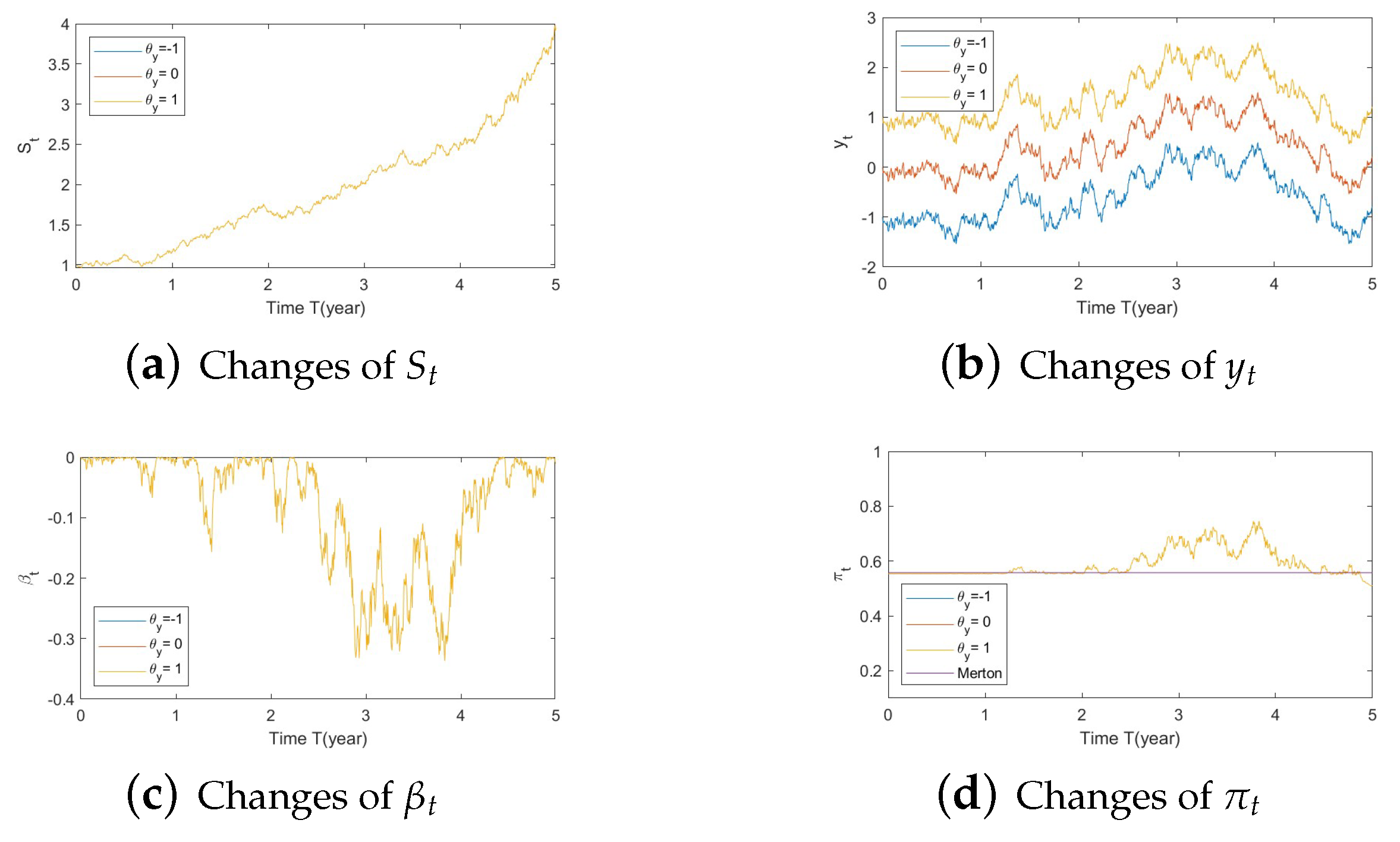
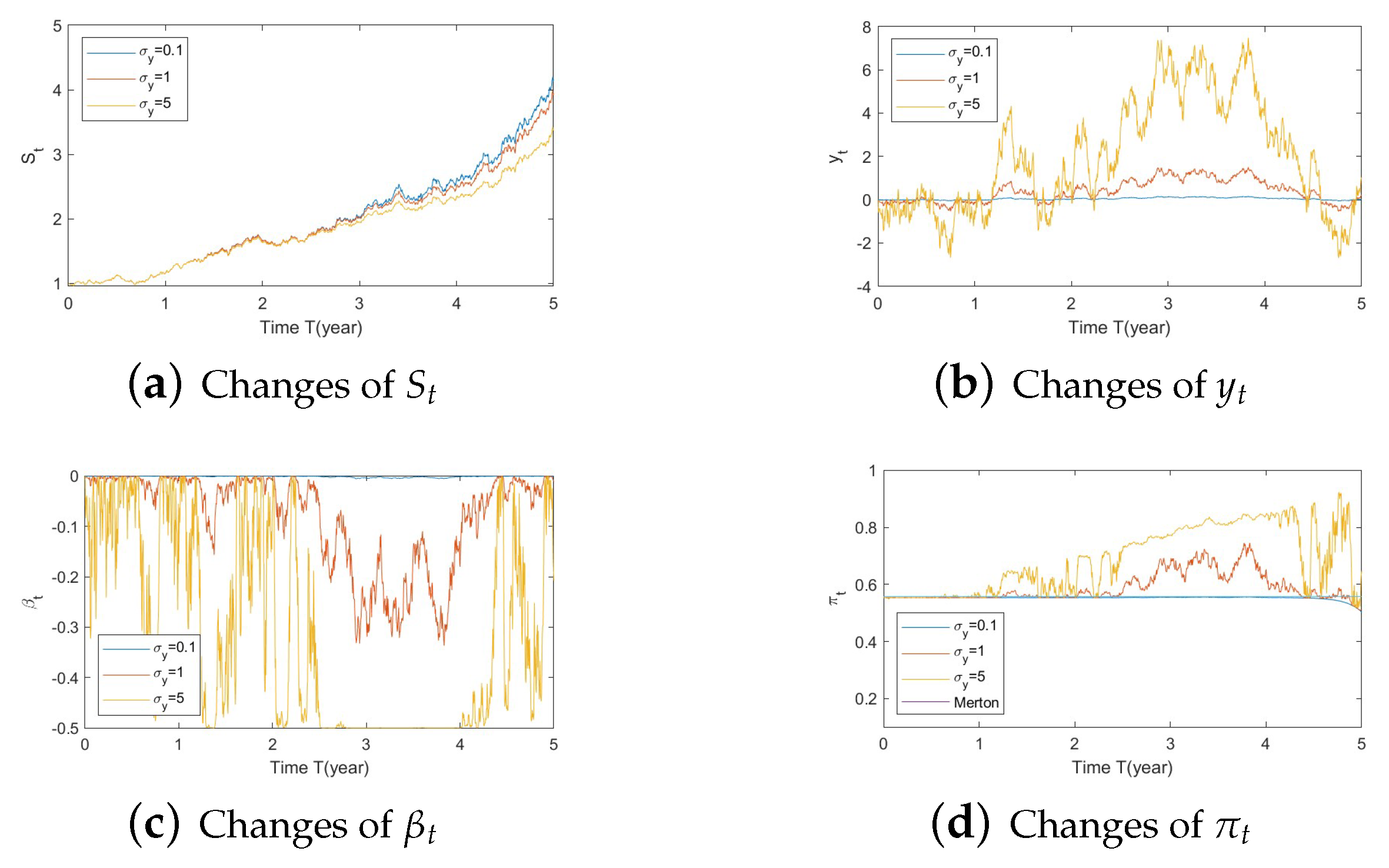
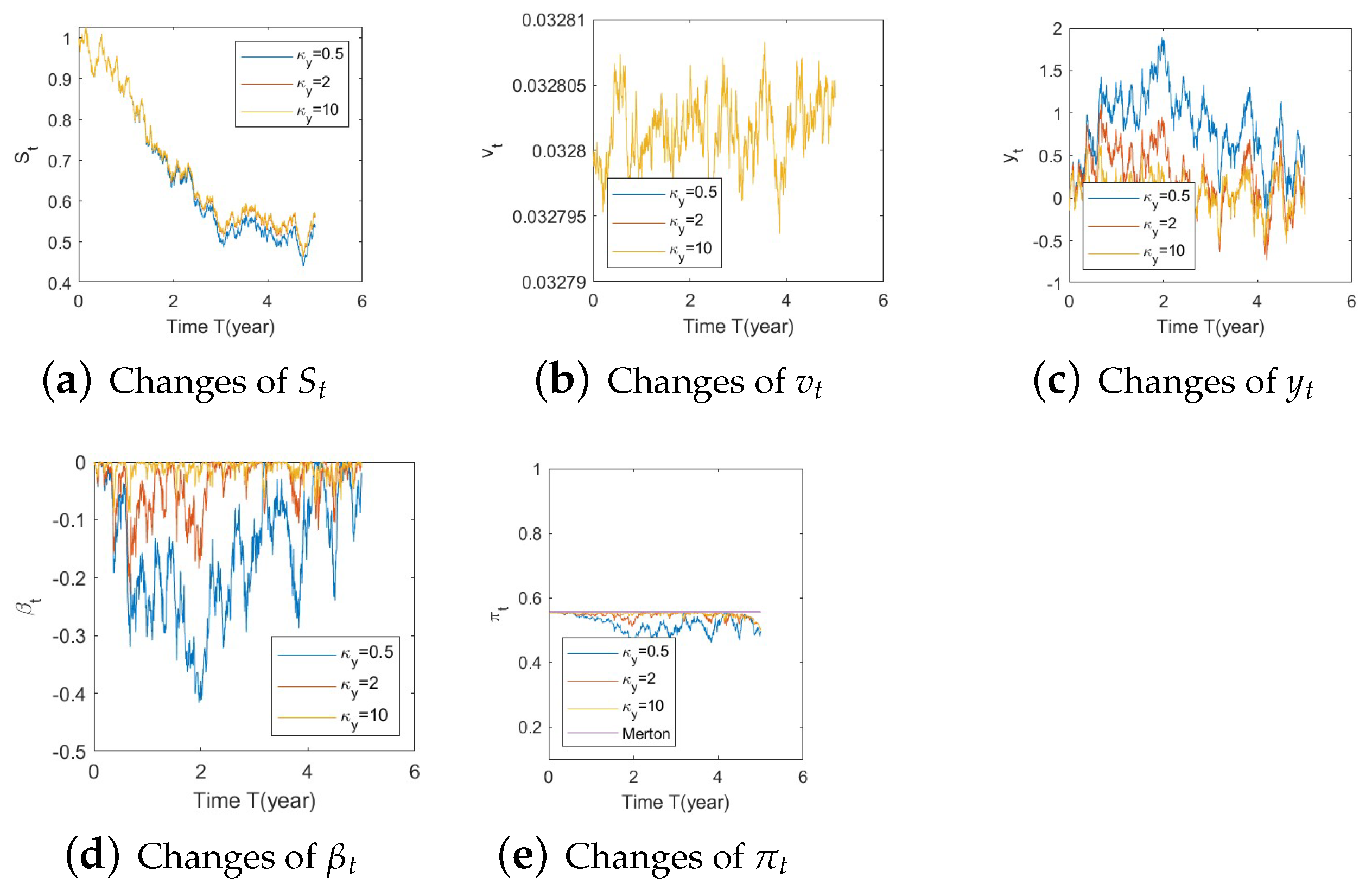
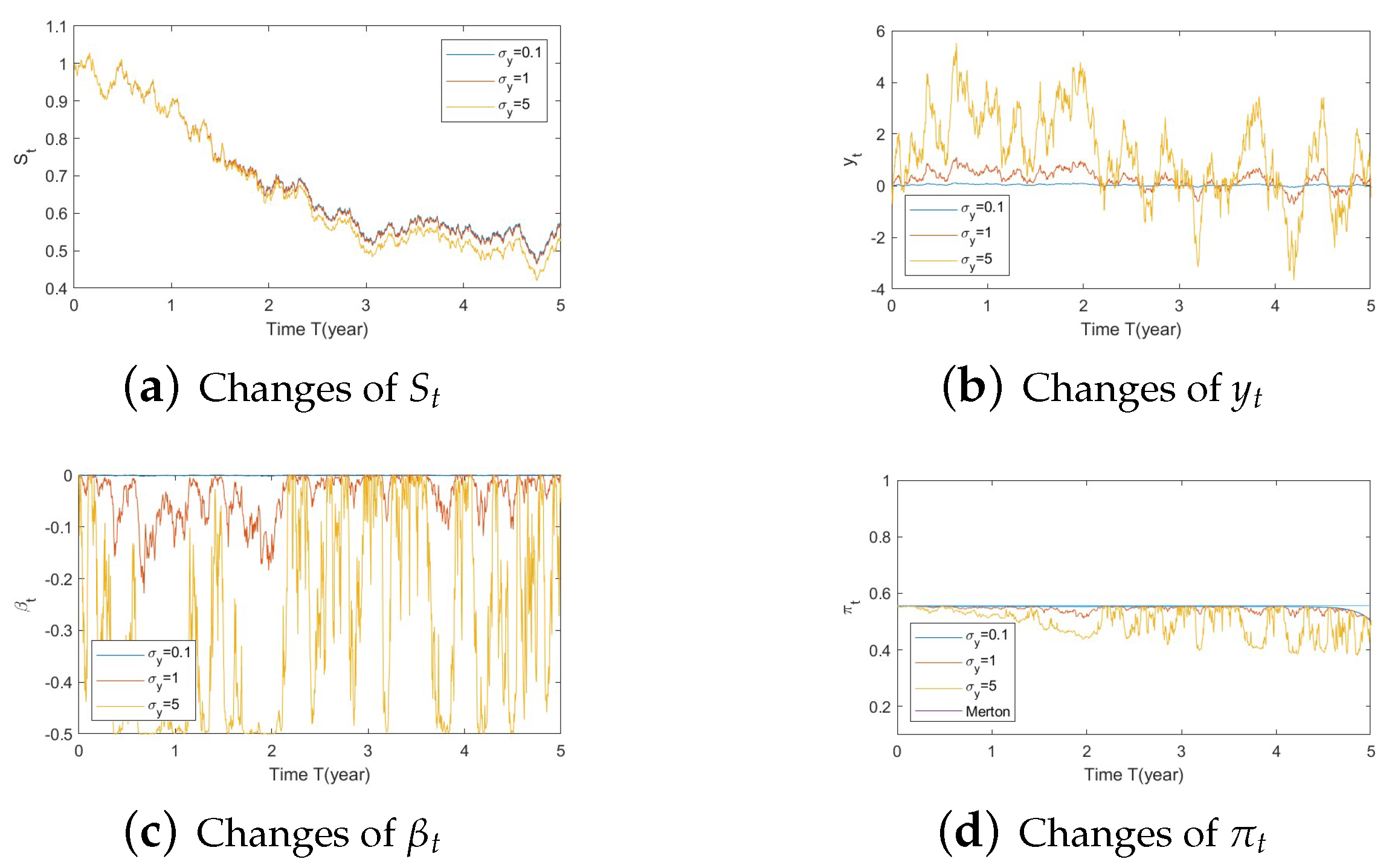
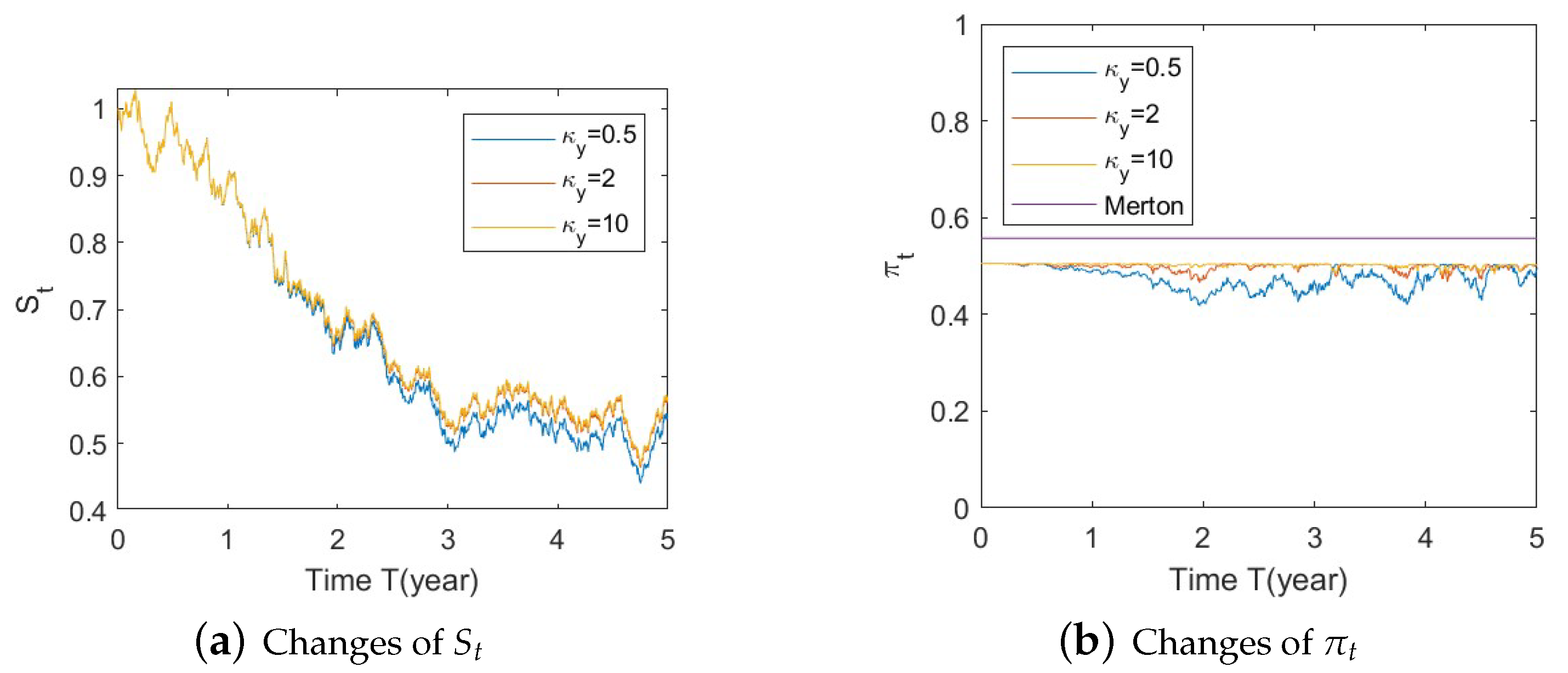
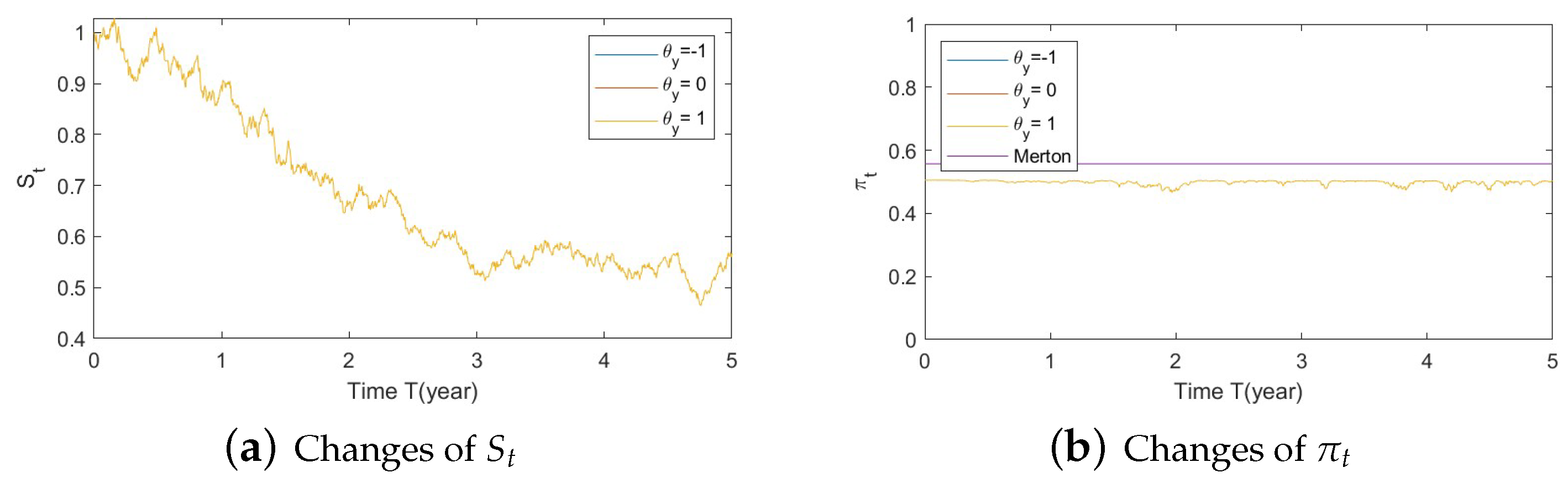
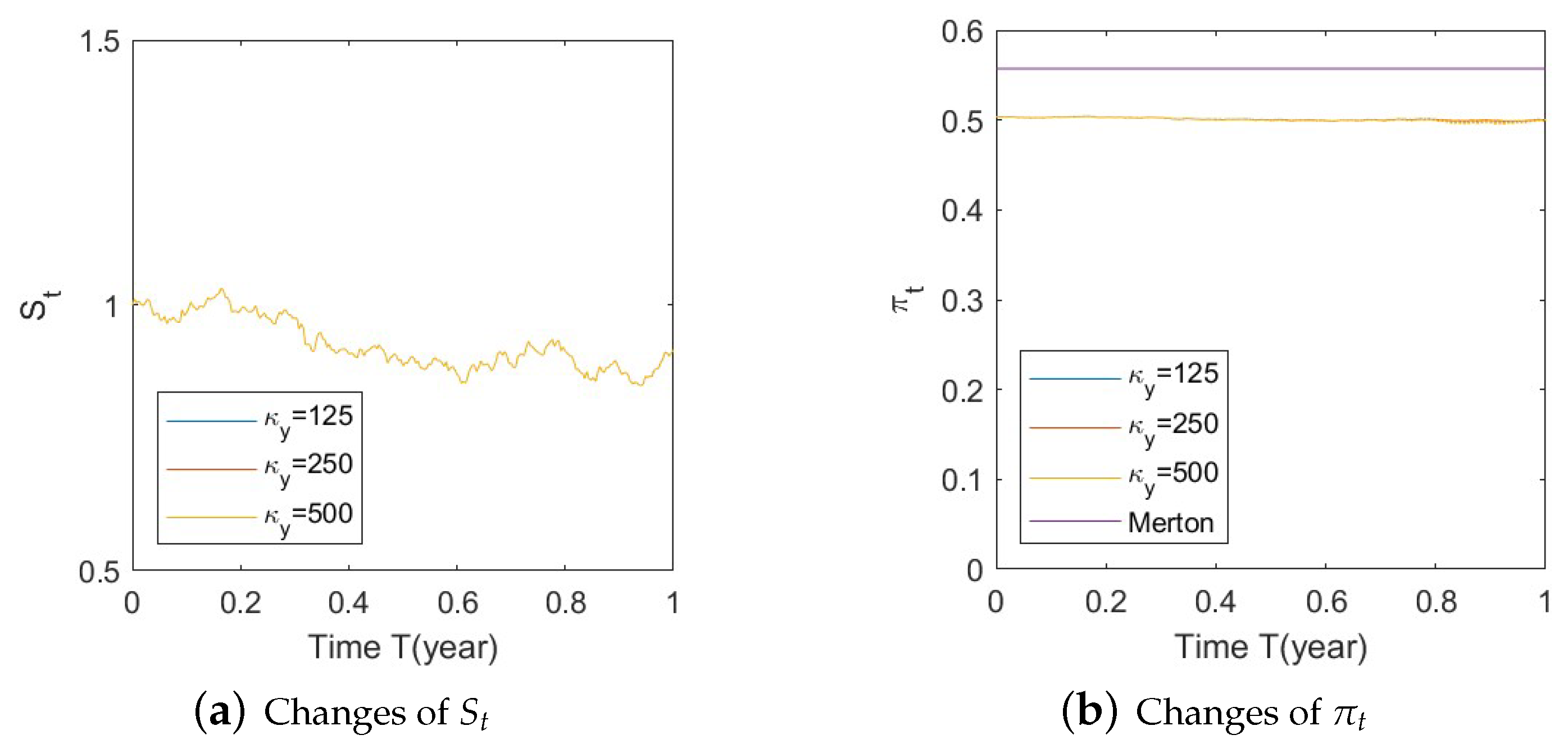
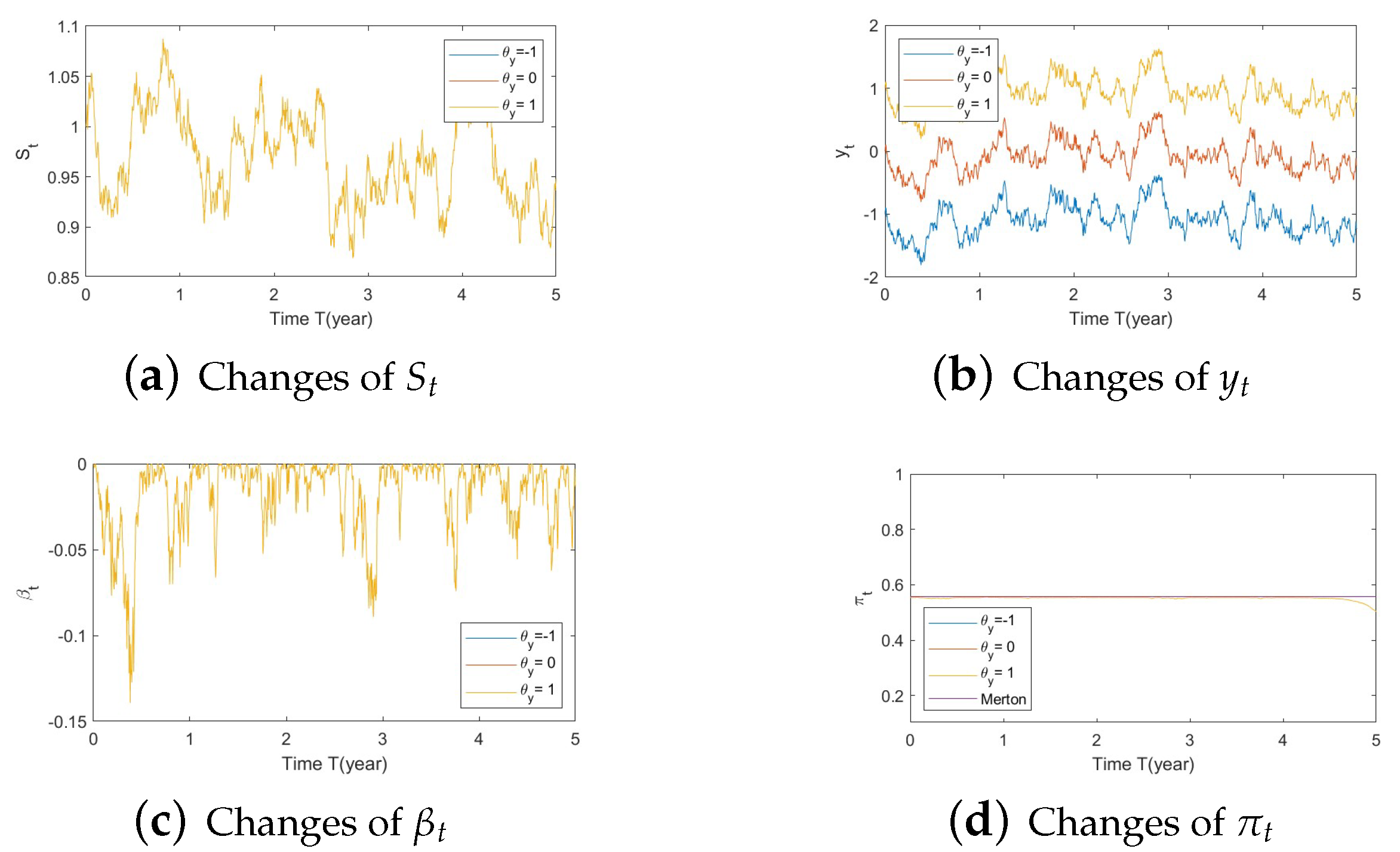
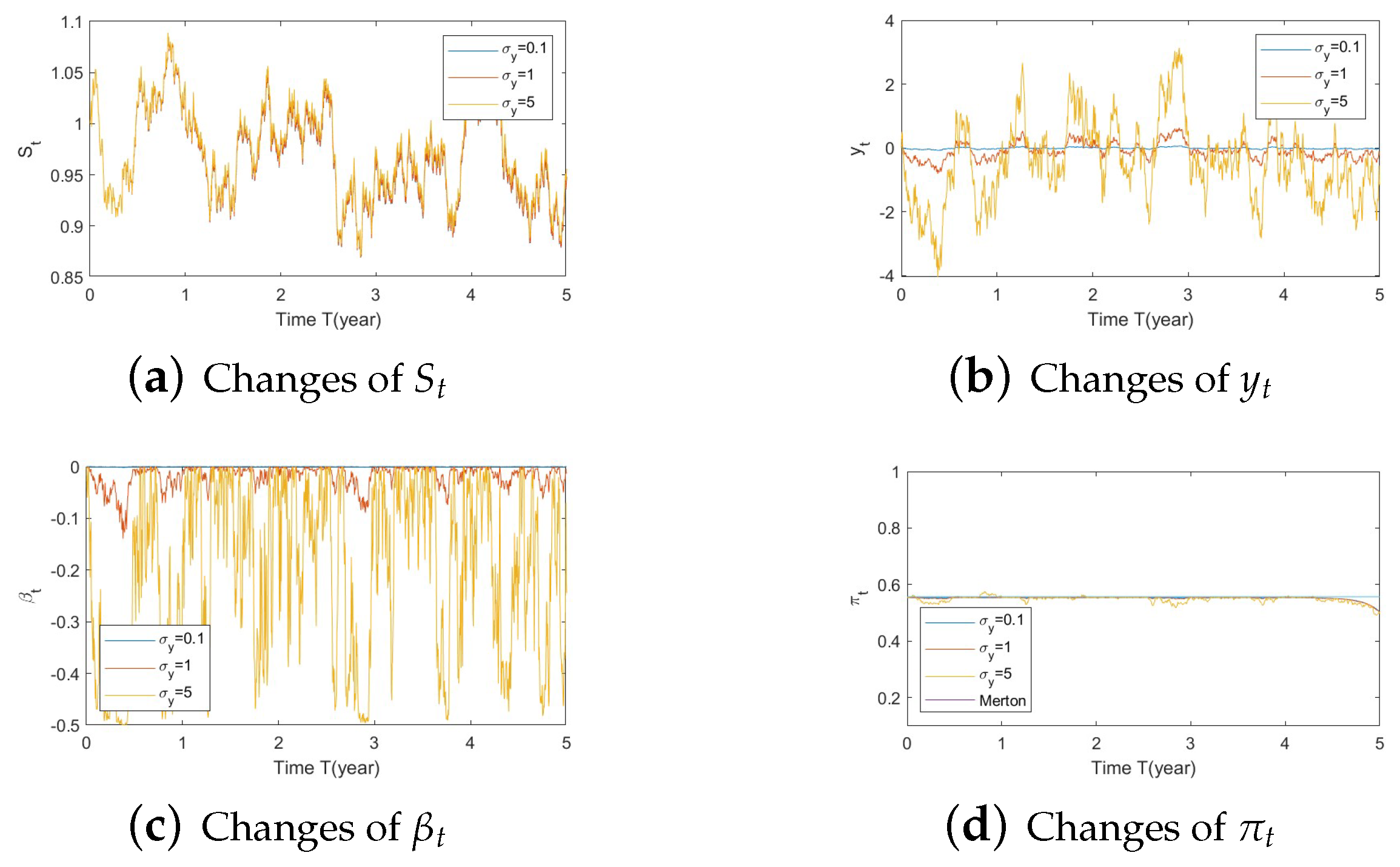
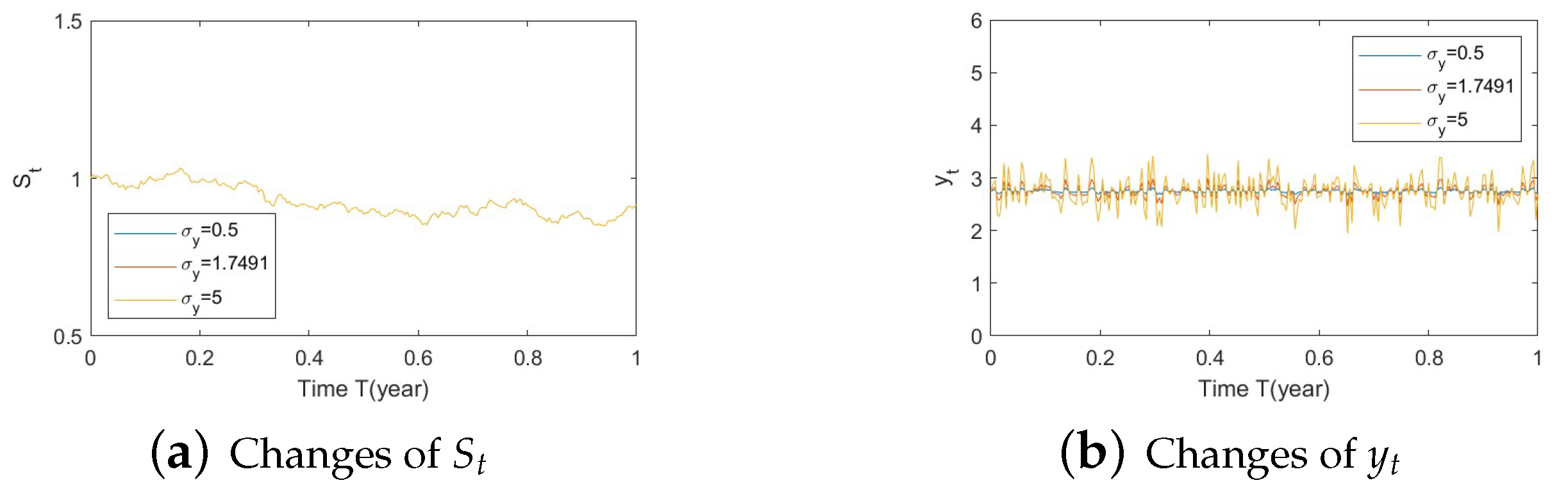
- Bull market conditions.The first three figures (Figure A1, Figure A2 and Figure A3 in Appendix A.3.1) illustrate the impact of parameters on the factors and the optimal stock allocation under the bull market path.We first study the impact of on the optimal stock allocation. We select three different values for : {0.5, 2, 10}. Figure A1a shows the behavior of the bull market path for the stock under these choices of . As anticipated, in such a bull market, a slower speed of reversion for generates more variation in and hence lower, more negative values (Figure A1d), leading to lower stock prices (compared with a faster reversion).Figure A1b shows no impact of parameters on as expected, while Figure A1c,d confirm the changes in speed of reversion for and , respectively.The optimal stock allocation in Figure A1e demonstrates a similar behavior as : a slower mean reversion of allocation for that quickens as increases. A decrease in the speed of reversion leads to (1) larger fluctuation on the optimal allocation due to larger fluctuations in and (2) more aggressive investment due to more negative values for . Interestingly, the more aggressive investments are a result of not only higher stock prices but also a more negative elasticity of volatility (), which result from a slower speed of reversion in .Figure A2 focuses on the impact of three different : {−1, 0, 1}. Figure A2a reports the changes in the bull market path for the stock price. Due to the assumption , changes in create a shift on the mean reverting level of (Figure A2b), which is further cancelled out by the function in the transformation from to , leading to no changes in (Figure A2c) and therefore no impact on stock prices (Figure A2a). This parameter is also disconnected from . Figure A2c,d indicate that variations in away from 0 (i.e., lower, more negative values) lead to more aggressive stock allocations.Figure A3 targets the influence of , {0.1, 1, 5}, on optimal stock allocation for the bull market path. In this case, a larger volatility has a similar effect as a slower speed of reversion. Therefore, it creates larger variations on (Figure A3d), e.g., lower, more negative values and hence lower stock prices (Figure A3a). This leads to similar implications in terms of optimal stock allocation (Figure A3e): the higher , the more aggressive the investments in the stock price (even though stock prices would be lower in this bull market, Figure A3a).In summary, the consistent pattern among all these figures (bull market) is that larger deviations of from 0 lead to more aggressive stock allocations; these variations can be incited by larger values of and smaller values of . This phenomenon can be explained, in financial terms, by observing that a more negative beta implies smaller volatilities, which, combined with an increase in stock prices (bull market), lead to excellent market conditions and therefore more aggressive stock allocations.
- (b)
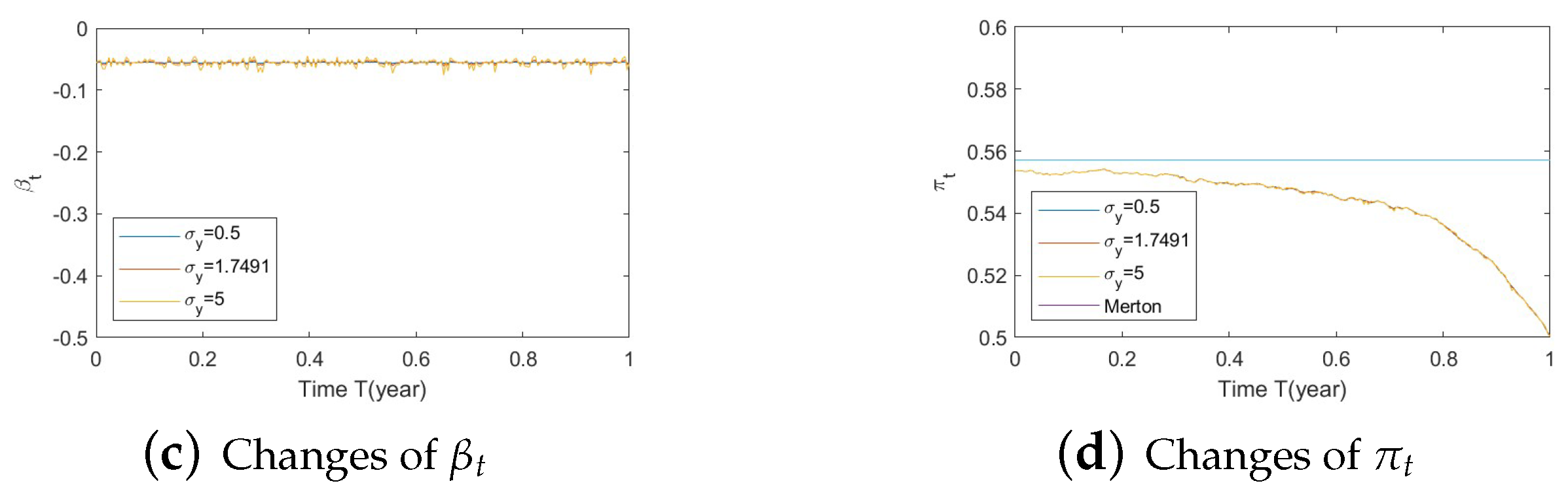
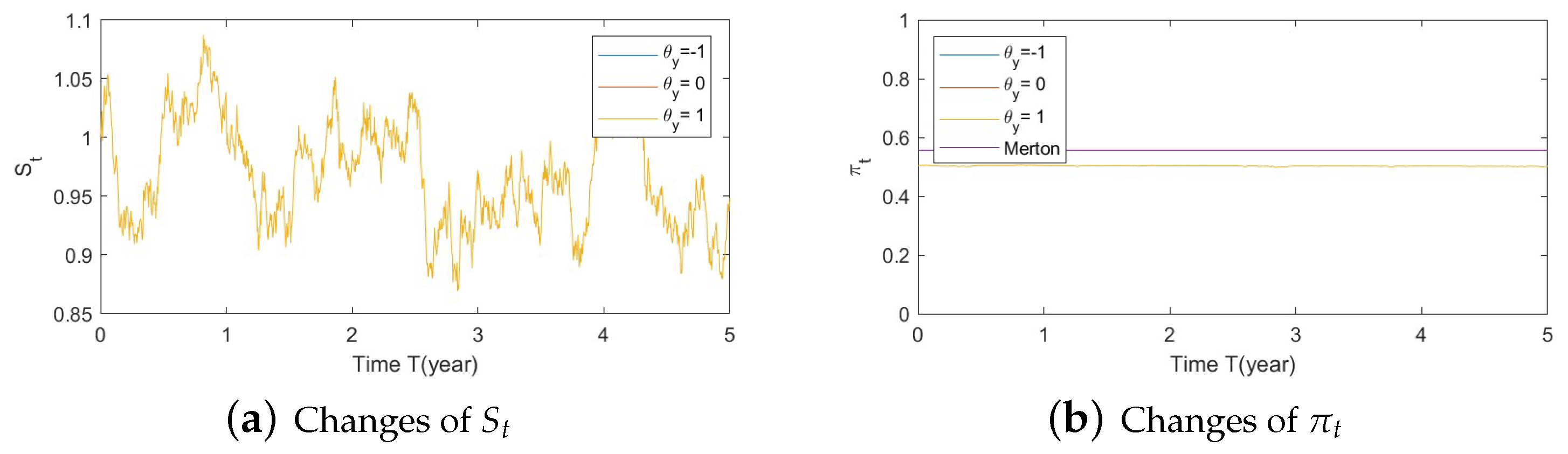
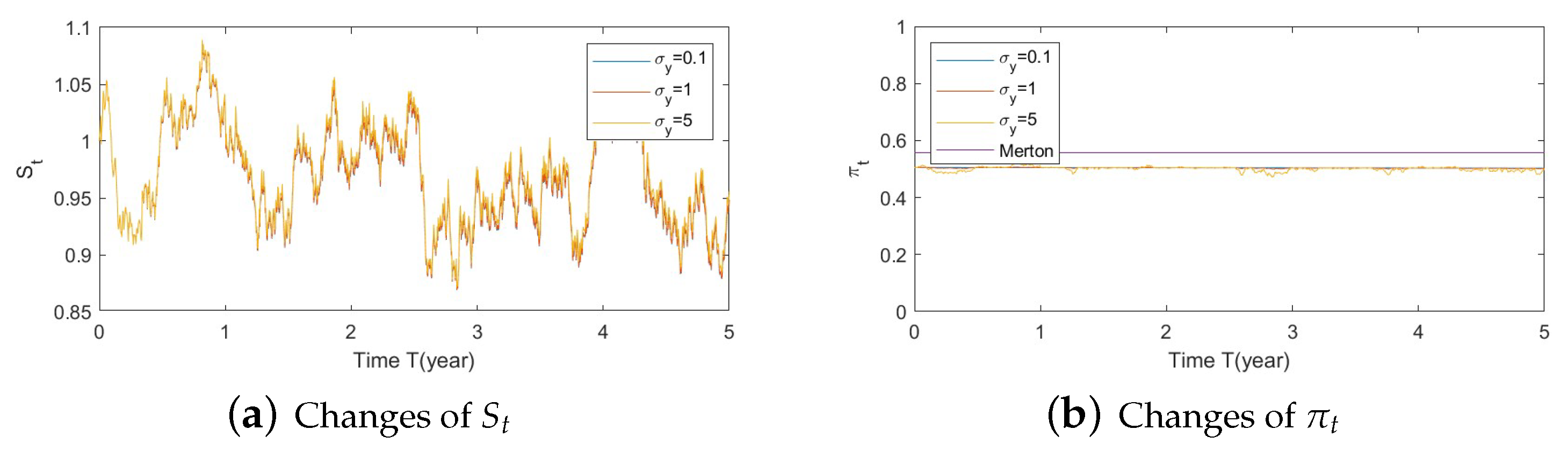
- Bear market conditions.The detailed analysis presented above can be extended concisely to the case of the bear market (Figure A4, Figure A5 and Figure A6 for , , and , respectively). Here, larger deviations of (away from 0) combined with a downturn in prices (bear market) lead to a more conservative stock allocation. The variation in is more pronounced with larger values of or smaller values of . In financial terms, this suggests that lower stock prices combined with larger volatilities lead to more conservative risky allocations.
- (c)
- Normal market conditions.The case of normal market conditions (Figure A7, Figure A8 and Figure A9 for , , and , respectively) behaves as expected. That is, allocations could increase or decrease depending on small fluctuations in prices and beta, with no clear pattern in terms of aggressive/conservative behavior. As anticipated, causes larger fluctuations in optimal allocation, with a smaller impact by and no impact of . The sharp downward movement in allocations in these figures toward the end of the horizon (from year 4 to 5) is due to the impact of the SV component (not observable in the figures in Section 5.2). This means that the SV component plays a larger role under normal market conditions than it does under bull and bear conditions.
- Arctan function analysis. The figures in this analysis can be found in Appendix A.3.2.
- (a)
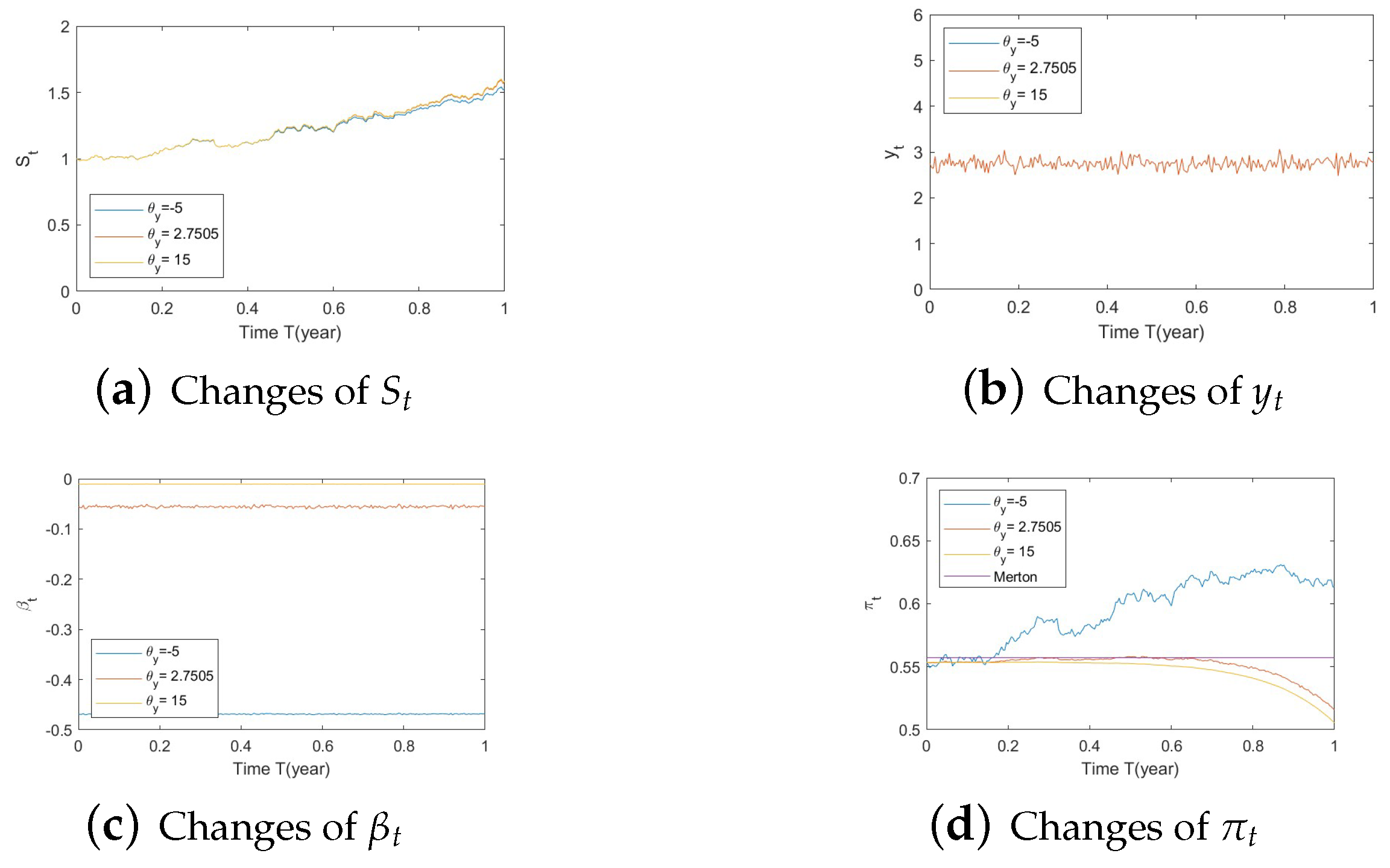
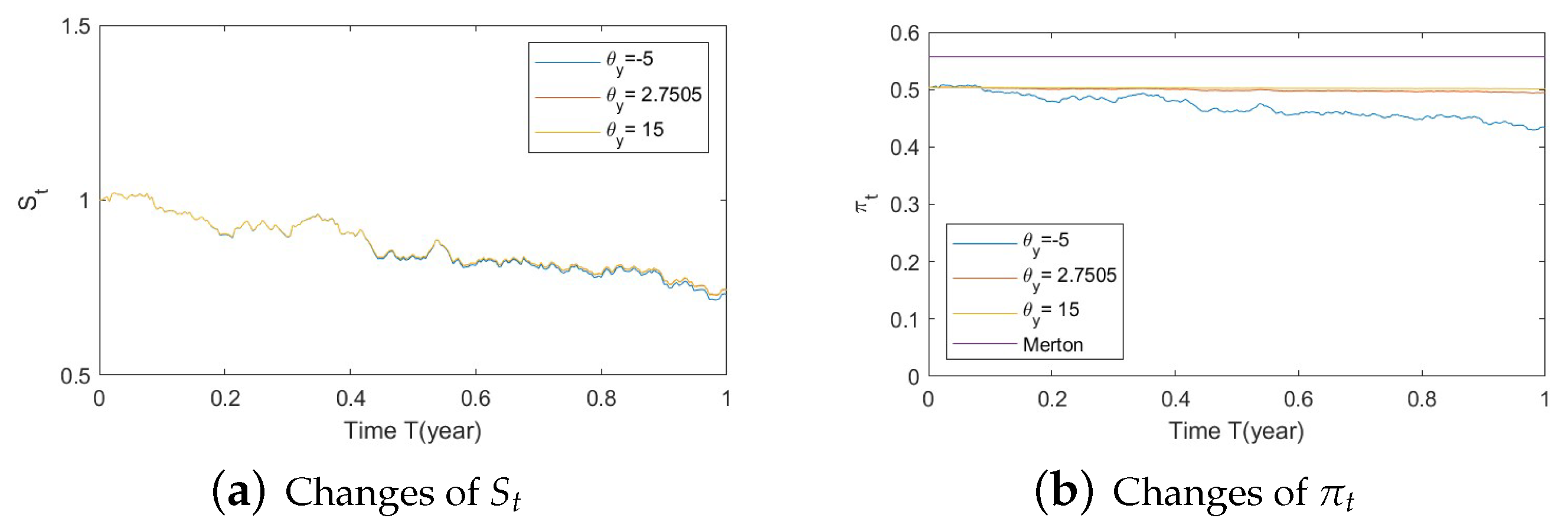
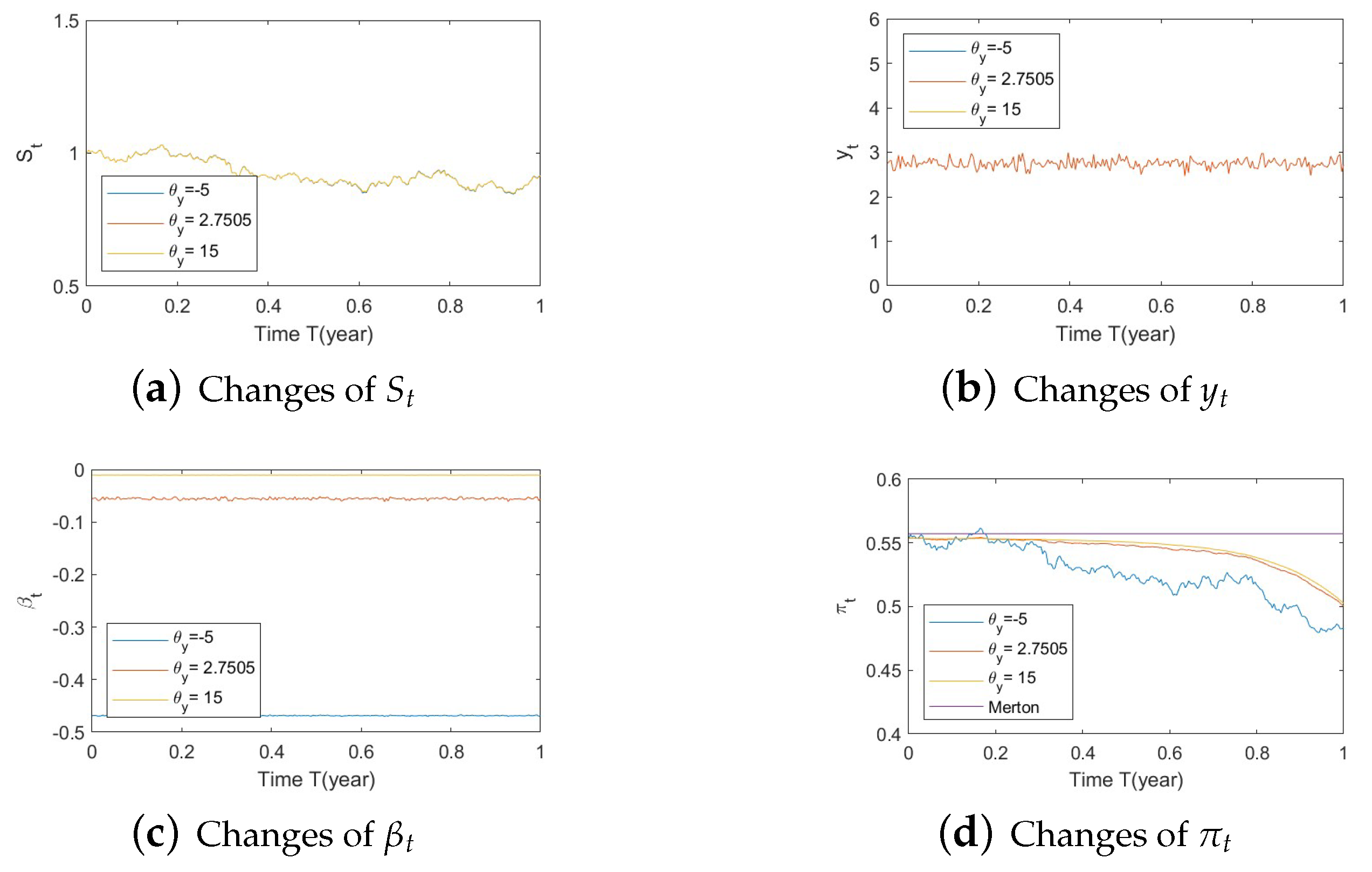
- Bull market conditions.Figure A10, Figure A11 and Figure A12 illustrate the impact of parameters on the factors and the optimal stock allocation under the bull market path. We first study the impact of on the optimal stock allocation. We select three different values for . In this section, we present on the main observations.Figure A10a indicates no impact of on the behavior of the stock . This is because inherits the mean-reverting nature of via the Arctan function, which behaves almost linearly around the mean-reverting level. Figure A10c,d confirm the changes in speed of reversion for and , respectively.The optimal stock allocation, as depicted Figure A10e, shows a similar behavior to that of . An increase in the speed of reversion leads to larger fluctuations on the optimal allocation due to larger fluctuations in . The range of the fluctuation is small and mostly impacted by the SV component due to the sharp downward movement toward the end of the horizon.Figure A11 depicts the impact of . Changes in create significant shifts on the elasticity of volatility in Figure A11c, leading to lower stock prices in Figure A11a. These large changes in impact the optimal stock allocation, as shown in Figure A11d. A smaller long-term mean leads to a more negative and more aggressive optimal allocations. Interestingly, the more aggressive investments are not a result of higher stock prices but rather a more negative elasticity of volatility ().Figure A12 focuses on the impact of . Figure A12b,c confirm the changes in volatility for and , respectively. The latter shows very small variations on (Figure A12c) and therefore no impact on stock prices (Figure A12a). All of the above lead to almost no impact on the optimal allocation for various volatilities . Similarly to above, here the main impact stems from the SV component, as evidenced by the downward movement.In summary, on the one hand, changes in and have almost no impact on the optimal allocation, as the main source of influence is the SV component. On the other hand, the long-term mean plays a key role: the more negative it is, the more aggressive the stock allocations become. This phenomenon can be explained, in financial terms, as follows: a more negative implies smaller volatilities, which, combined with an increase in stock prices (bull market), lead to excellent market conditions and hence more aggressive stock allocations.
- (b)
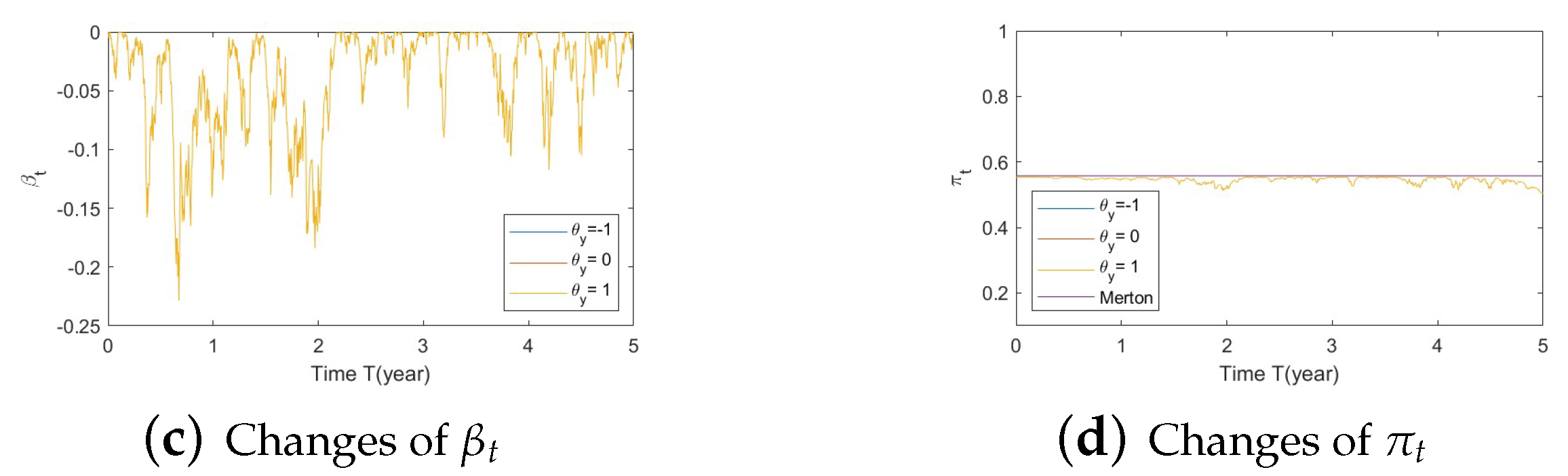
- Bear market conditions.The detailed analysis presented above can be extended concisely to the case of the bear market (Figure A13, Figure A14 and Figure A15 for , , and , respectively). First of all, optimal allocation remain insensitive to changes in and . Secondly, larger deviations of (away from 0), which happens for large negative values of , combined with a downturn in prices (bear market) lead to a more conservative stock allocation. In financial terms, this tells us that lower stock prices combined with larger volatilities lead to more conservative risky allocations.
- (c)
- Normal market conditions.The case of normal market conditions (Figure A16, Figure A17 and Figure A18 for , , and , respectively), behaves as expected and similarly to the bear and bull cases in terms of and .However, here, we also observe that the smaller the , the farther the deviation of from zero and hence the less aggressive the investment strategy. This means normal market conditions behave like bear market conditions in terms of the impact of parameters.
5.2. Sensitivity in the Absence of the SV Process
- Gaussian function analysis. The figures in this analysis can be found in Appendix A.4.1.
- (a)
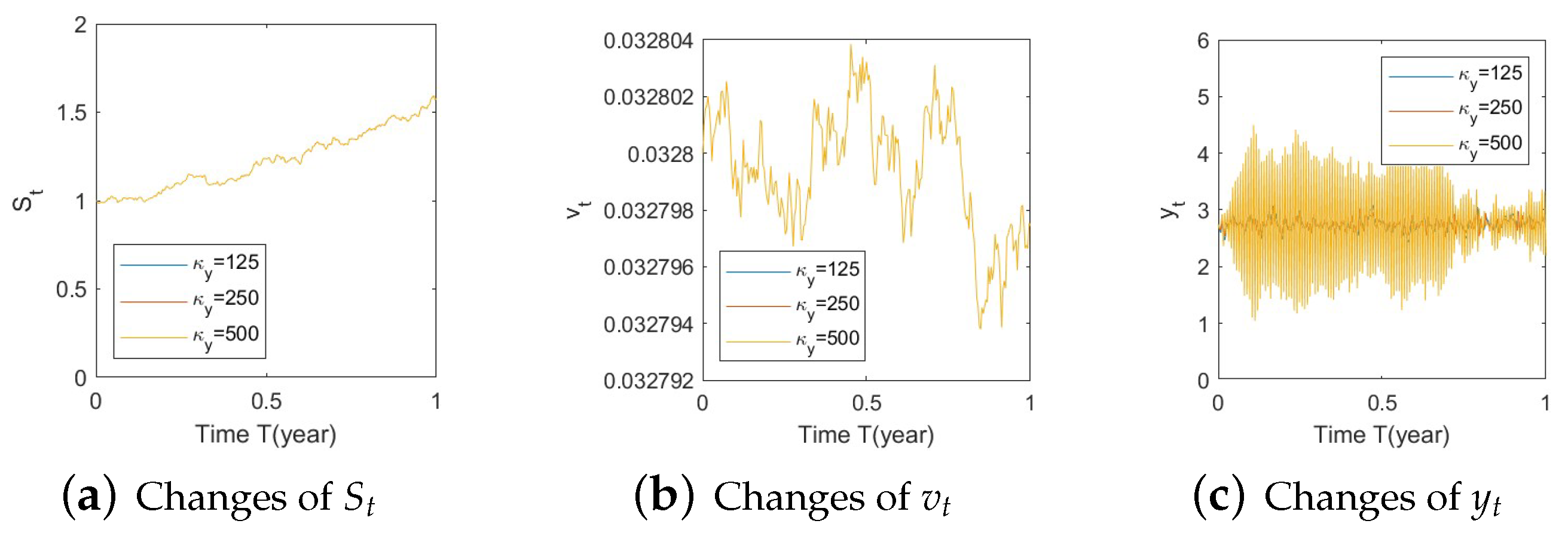
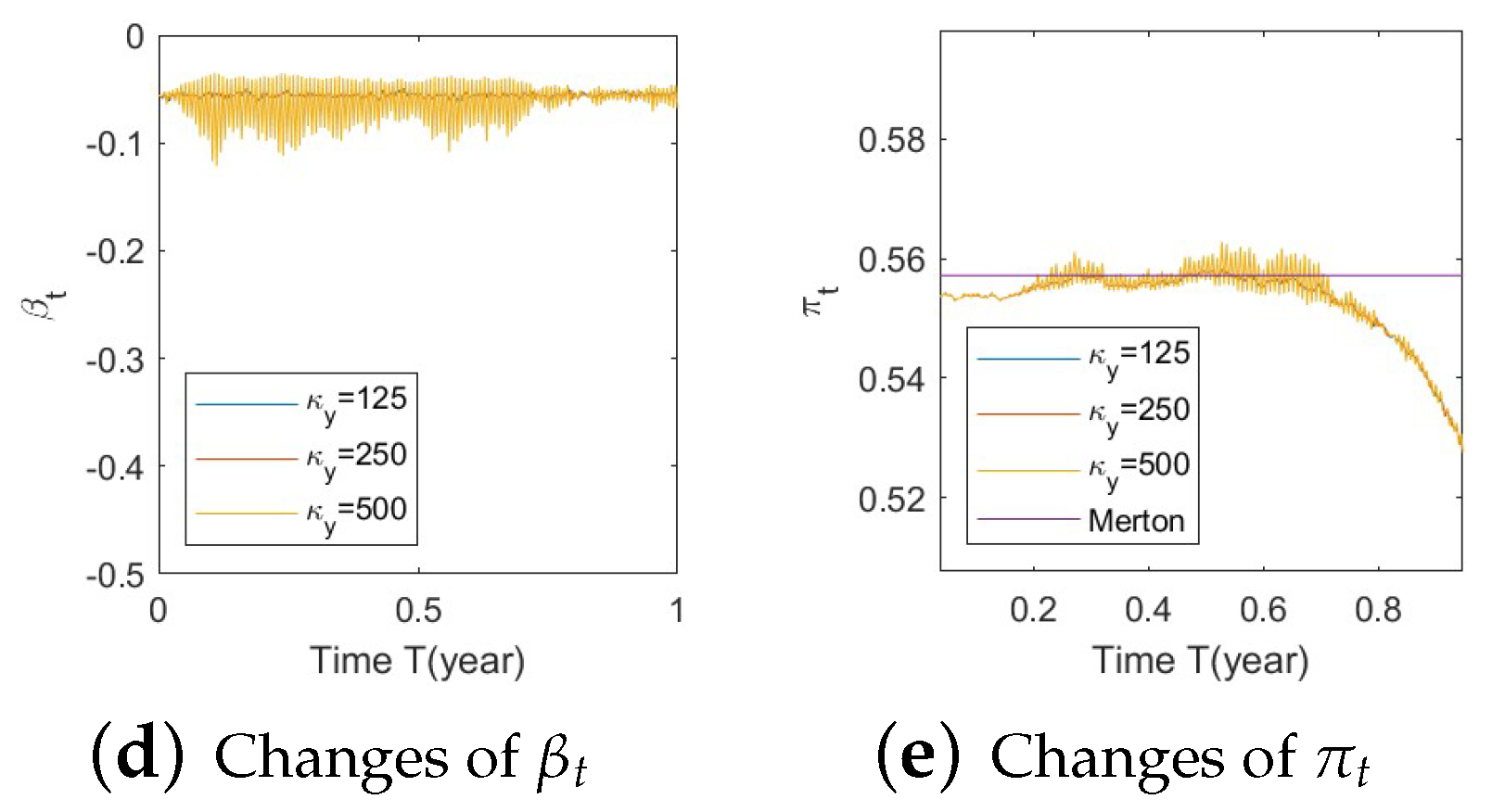
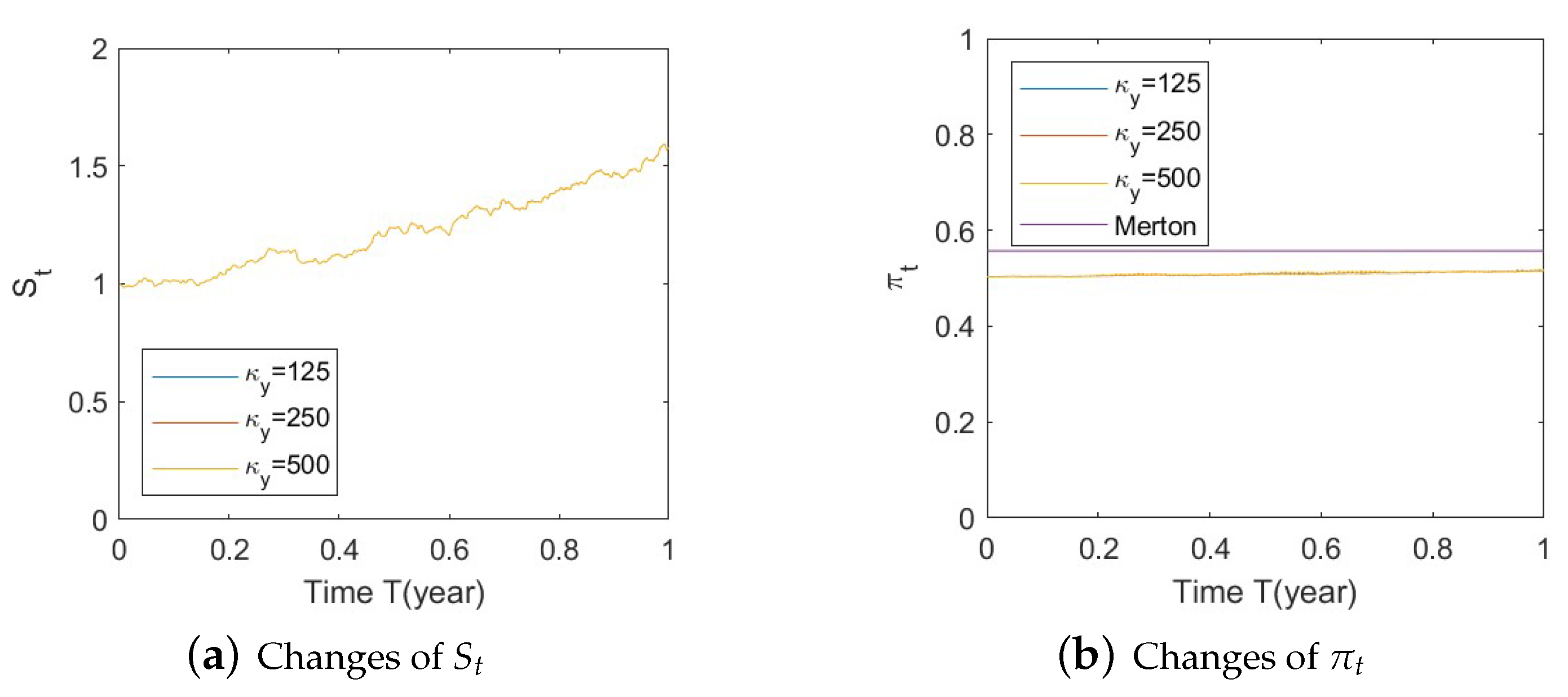
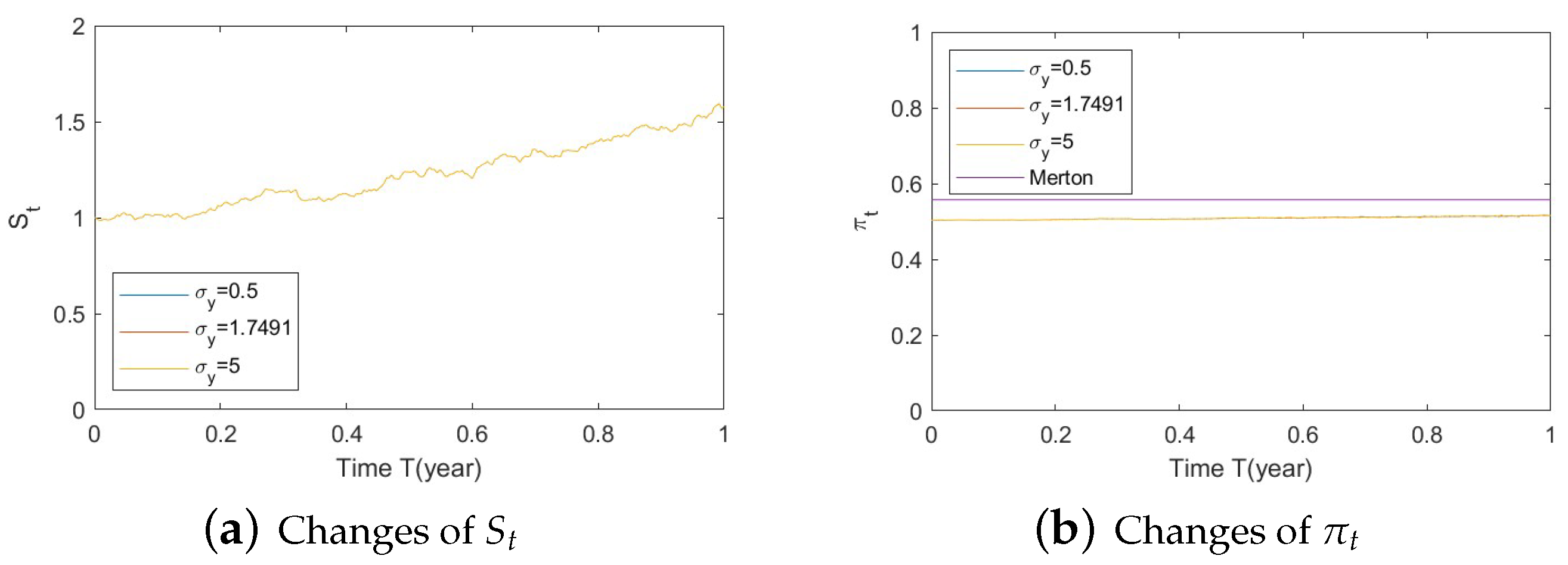
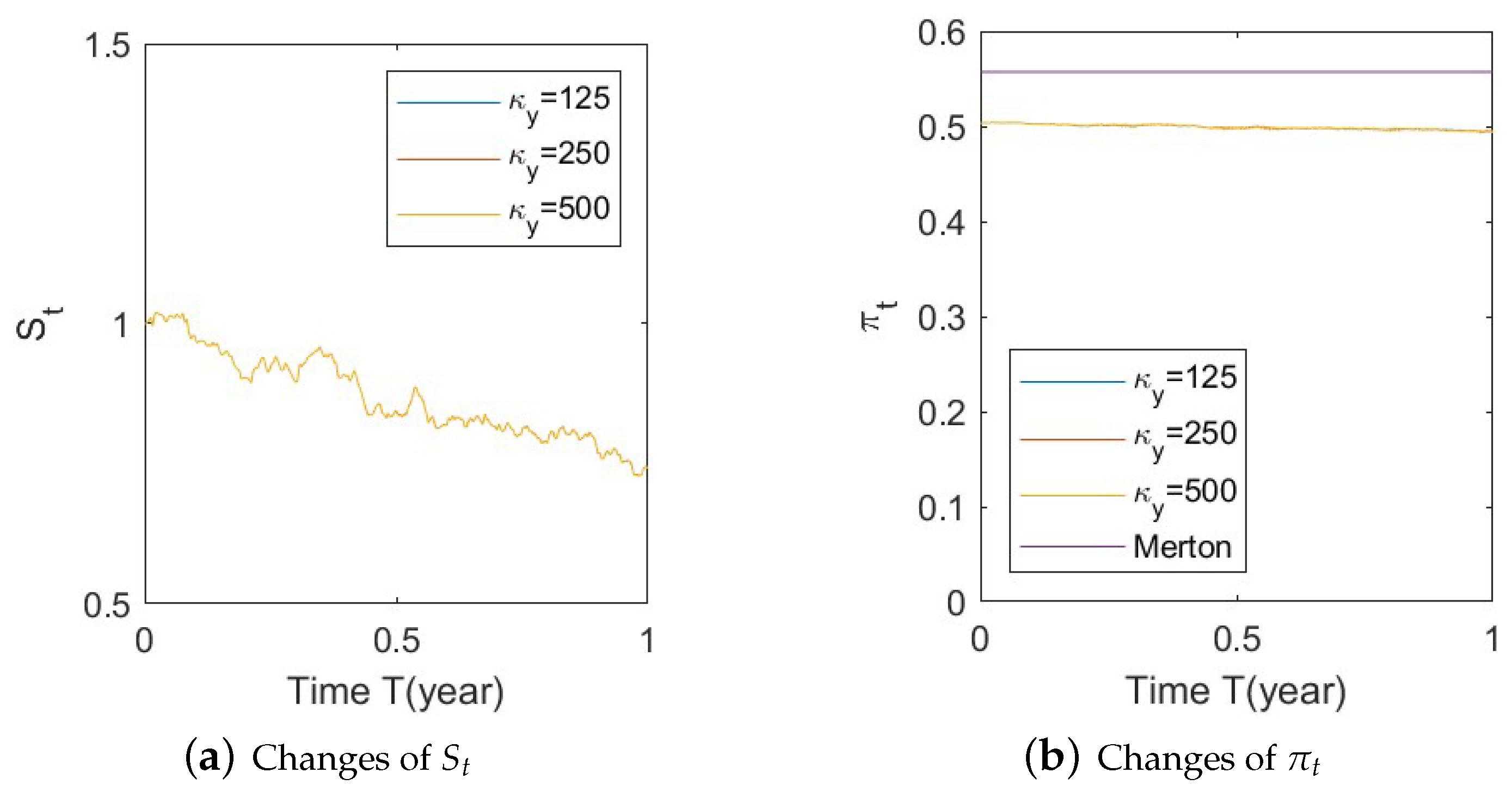
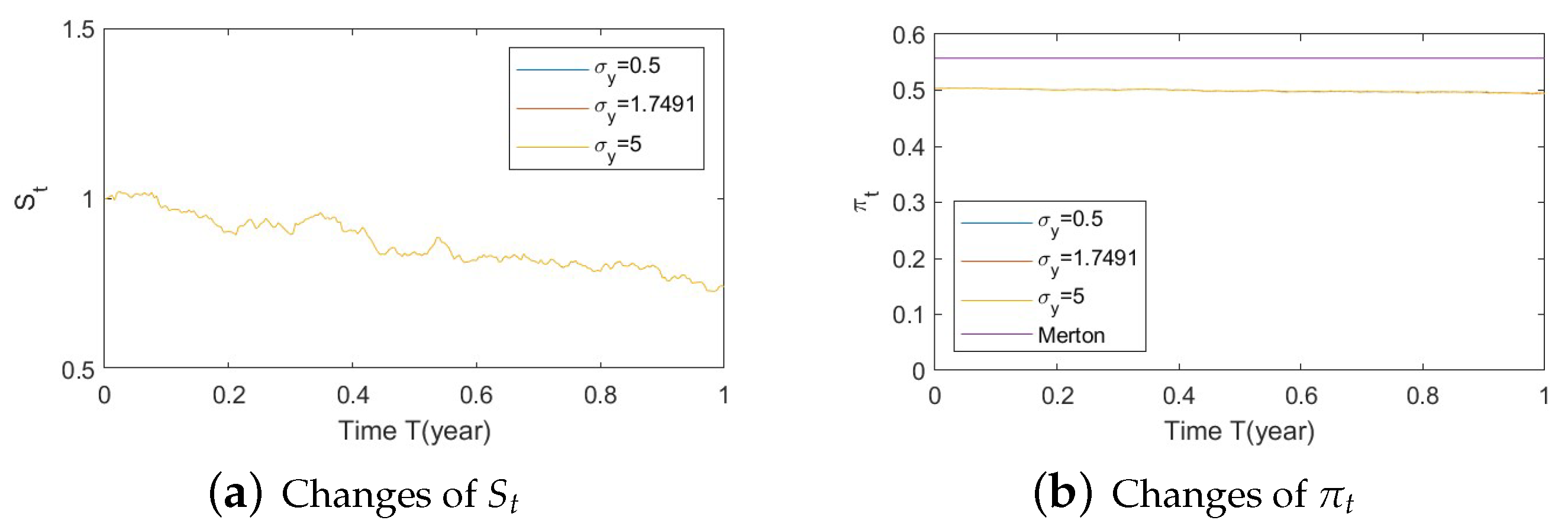
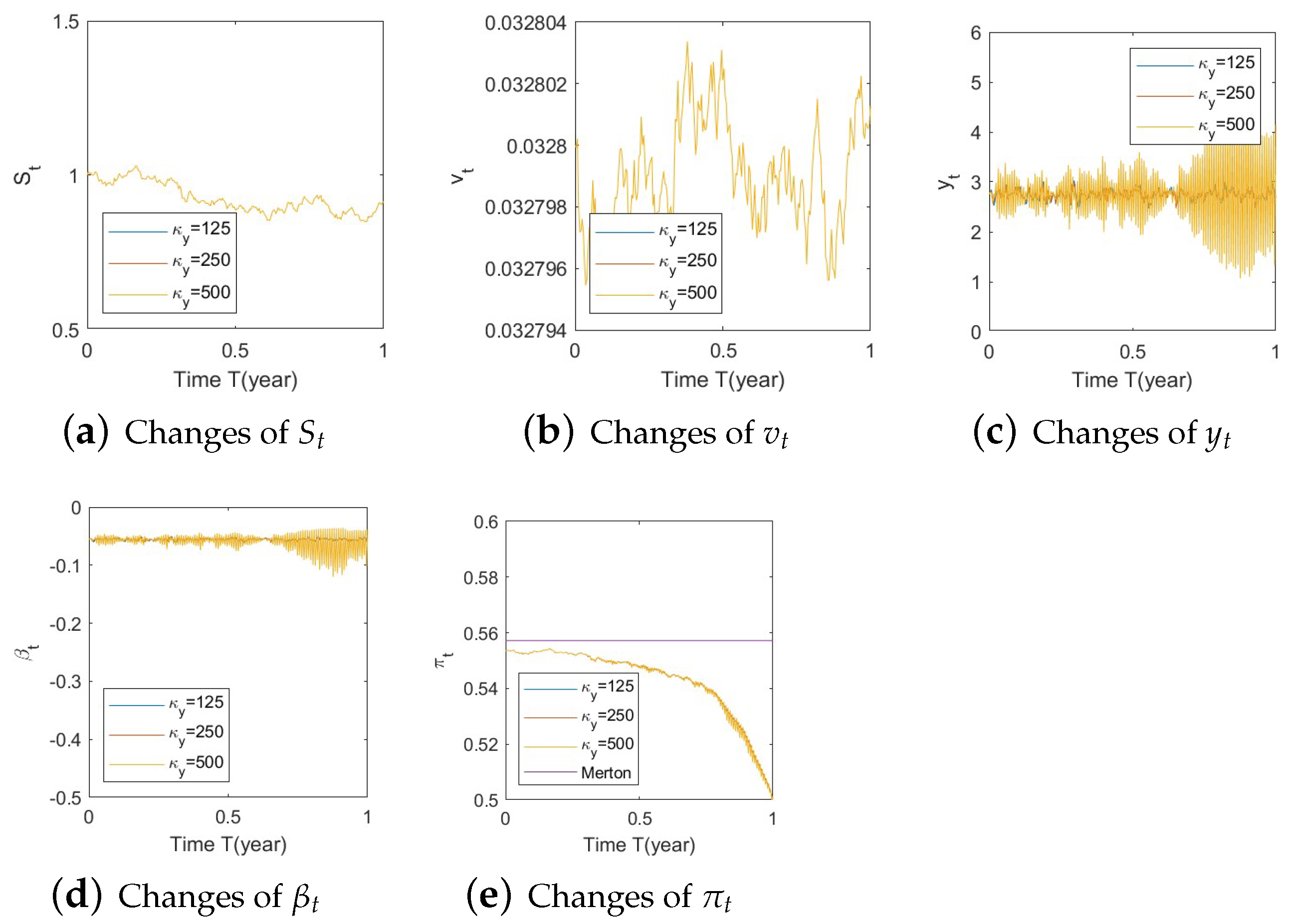
- Bull market conditions.Figure A19, Figure A20 and Figure A21 in Appendix A.4.1 illustrate the impact of parameters on the stock price and the optimal stock allocation under the bull market path. Since the order of parameters and values is the same as in Section 5.1, we will not repeat the details here.Compared to Section 5.1–1(a), Figure A19a shows a similar behavior of the bull market path for the stock under various as the interaction of the SEV and SV processes, which highlights the low impact of the SV part on the stock behavior. The optimal stock allocation, depicted in Figure A19b, presents a similar behavior as that in Section 5.1–1(a). However, the slight difference is that the curve of optimal allocations has a small shift towards conservative allocations due to the absence of the SV component. The allocation becomes less aggressive than that in Section 5.1–1(a).Figure A20 demonstrates the impact of . The behaviors of and optimal allocation are similar to those in Section 5.1– 1(a). Again, the curve of optimal allocations has a small shift towards conservative allocations due to the absence of the SV component.Figure A21 depicts the influence of on optimal stock allocation. The lack of the SV component creates a small shift towards conservative allocations.The major difference in the absence of the SV component is that we observe minimum impact on , and the curve of optimal allocations is similar in shape but has a small shift towards conservative allocations.
- (b)
- Bear market conditions.The analysis presented above can be extended to the case of bear market for , , and (Figure A22, Figure A23 and Figure A24, respectively, in Appendix A.4.1). Here, we observe the same behavior as presented for the Gaussian function with SEV and SV (Section 5.1–1(b)): larger deviations of (away from 0) combined with a downturn in prices (bear market) lead to a more conservative stock allocation. The variation in is more pronounced with larger values in or smaller values in . In addition, the sharp down turn in optimal allocations at the end of year 5 is corrected when the SV component is eliminated.
- (c)
- Normal market conditions.The case of normal market conditions (Figure A25, Figure A26 and Figure A27 for , , and respectively) behaves as in the corresponding Section 5.1–1(c). The key observation is that the sharp downward movement in allocations in these figures toward the end of the horizon (from year 4 to 5) is corrected in the absence of the SV component. This means that the SV component plays a larger role under normal market conditions than it does under bull and bear conditions.
- Arctan function analysis. The figures in this analysis can be found in Appendix A.4.2.
- (a)
- Bull market conditions.Figure A28, Figure A29 and Figure A30 illustrate the impact of parameters on the factors and the optimal stock allocation under the bull market path. The order of parameters and values is the same as in Section 5.1 and Section 5.2, so we will not repeat the details here.We first analyze the impact of . The behavior of is similar to that in Section 5.1–2(a), but the optimal stock allocation (Figure A28b) shows a significantly different behavior than in Section 5.1–2(a). As fluctuations on the optimal allocation are mostly impacted by the SV component, almost no fluctuations occur in this case. The sharp downside movement toward the end of the horizon has also disappeared.Figure A29 depicts the impact of . Similar behaviors are observed as those in Section 5.1–2(a) for various . Additionally, due to the lack of the SV component, almost no fluctuations occur in optimal allocation, and the sharp downside movement toward the end of the horizon observed in Section 5.1–2(a) is corrected.Figure A30 illustrate on the impact of , which is minimal on stock prices and on the optimal allocation. Again, due to the lack of the SV component, the downward movement of allocations in Section 5.1–2(a) disappears.In summary, only has some impact on the optimal allocation, and the sharp downside movements toward the end of the horizon are corrected in all cases.
- (b)
- Bear market conditions.The bear market analysis is illustrated in Figure A31, Figure A32 and Figure A33. Here also, optimal allocation remains insensitive to changes in and . Larger deviations of (away from 0) occur for large negative values of , which combined with a downturn in prices (bear market), lead to a more conservative stock allocation. In the absence of the SV component, the fluctuations in optimal allocations are very small, and the sharp downside movement toward the end of the horizon, as in Section 5.1–2(b), is also eliminated.
- (c)
- Normal market conditions.The case of normal market conditions is depicted in Figure A34, Figure A35 and Figure A36. This behaves as in the corresponding Section 5.1–2(c). More interestingly, in the absence of the SV component, the fluctuations in optimal allocations are very small, and, as expected, the sharp downside movement toward the end of the horizon disappears.
6. Conclusions, Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SEV | Stochastic elasticity volatility |
| GBM | Geometric Brownian motion |
| CEV | Constant elasticity of variance |
| EUT | Expected utility theory |
| SV | Stochastic volatility |
Appendix A. Proofs and Figures
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. SEV-SV Analysis
Appendix A.3.1. Figures of Gaussian Function Analysis
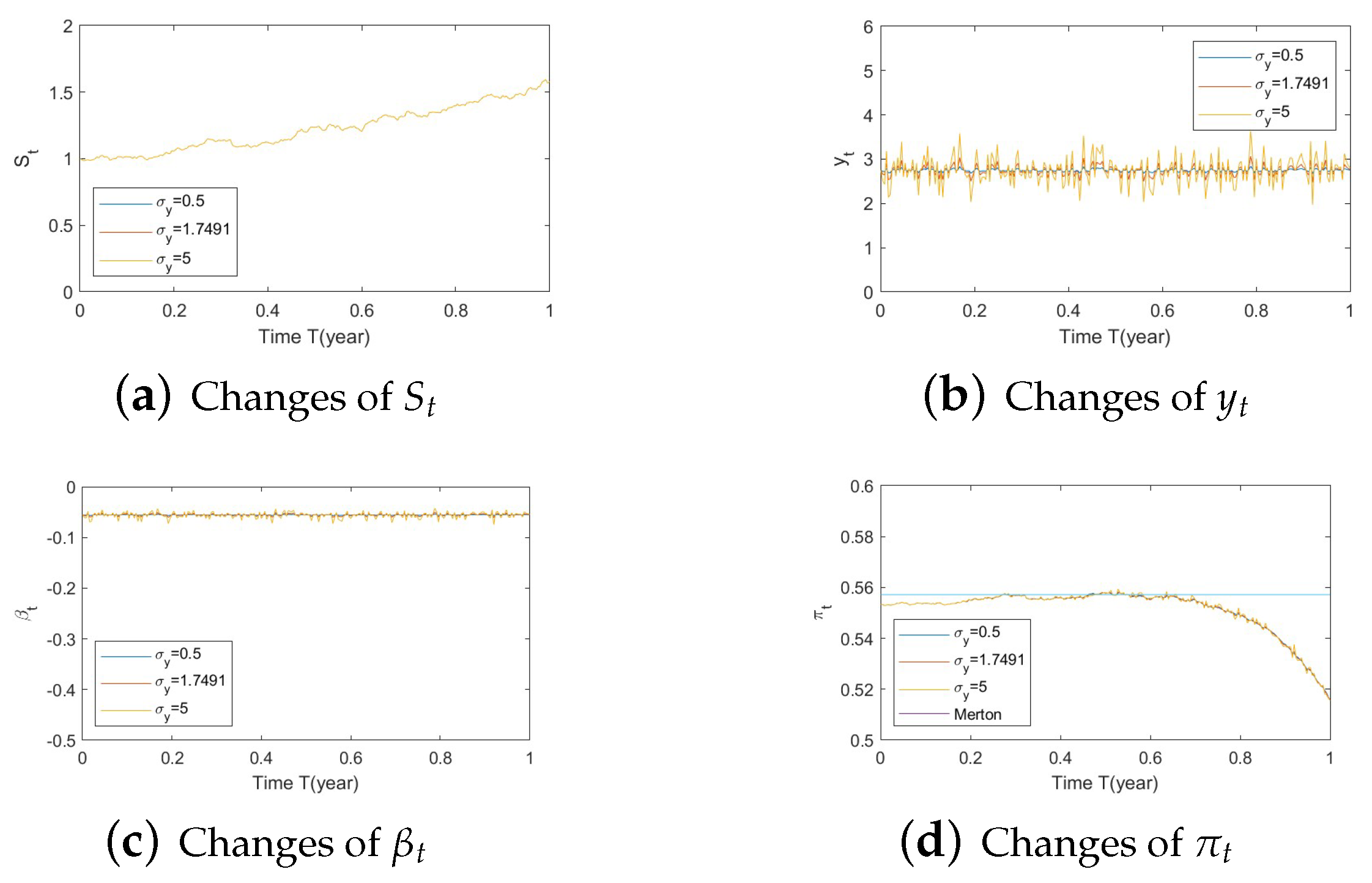
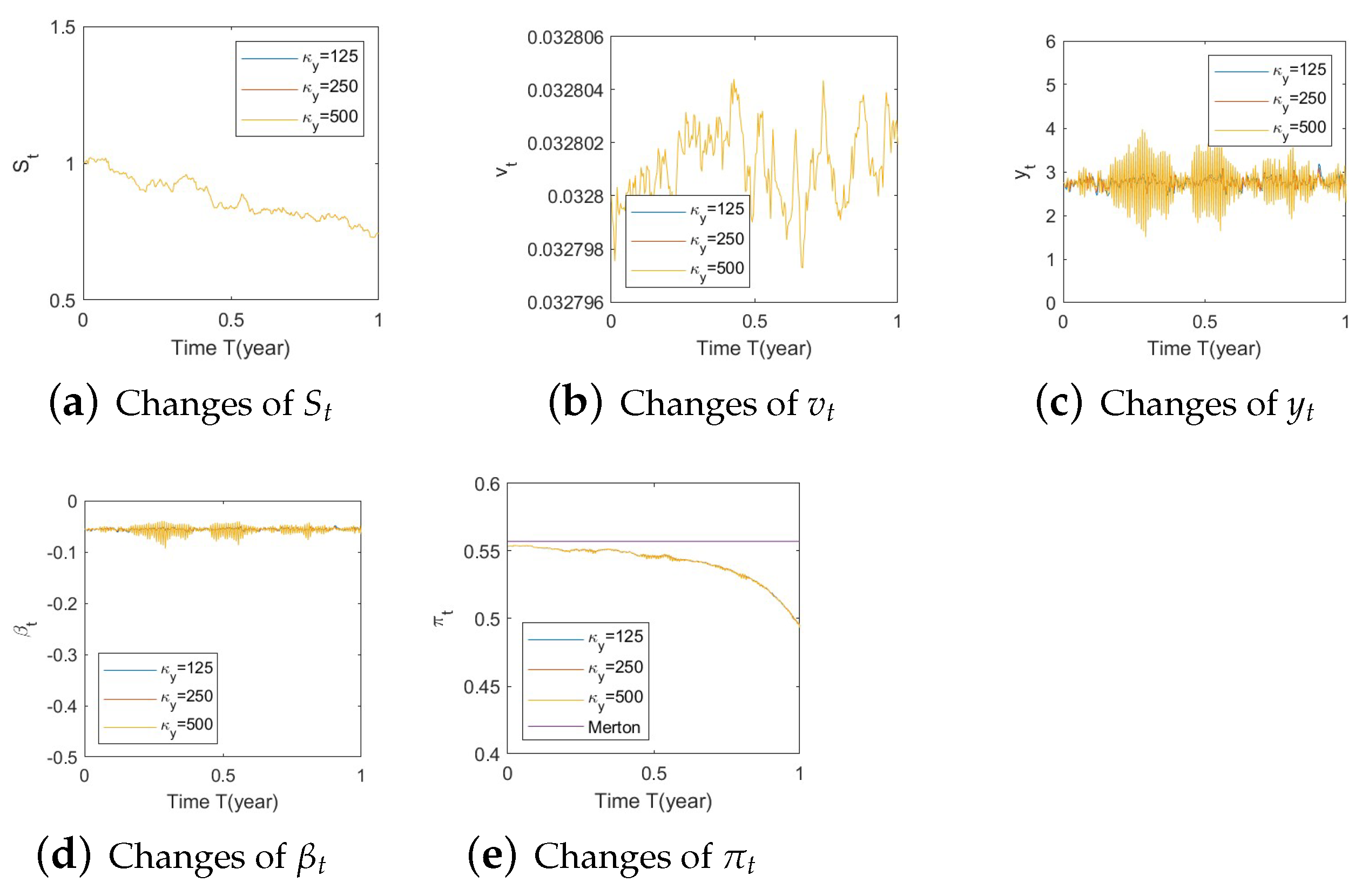
- Bull market conditions (Figure A1, Figure A2 and Figure A3):Figure A1. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A1. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A2. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A2. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A3. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A3. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .
- Bear market conditions (Figure A4, Figure A5 and Figure A6):Figure A4. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A4. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A5. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying θy(e.g., θy = −1, 0, 1).Figure A5. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying θy(e.g., θy = −1, 0, 1).Figure A6. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A6. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .
- Normal market conditions (Figure A7, Figure A8 and Figure A9):Figure A7. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A7. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .
Appendix A.3.2. Figures of Arctan Function Analysis
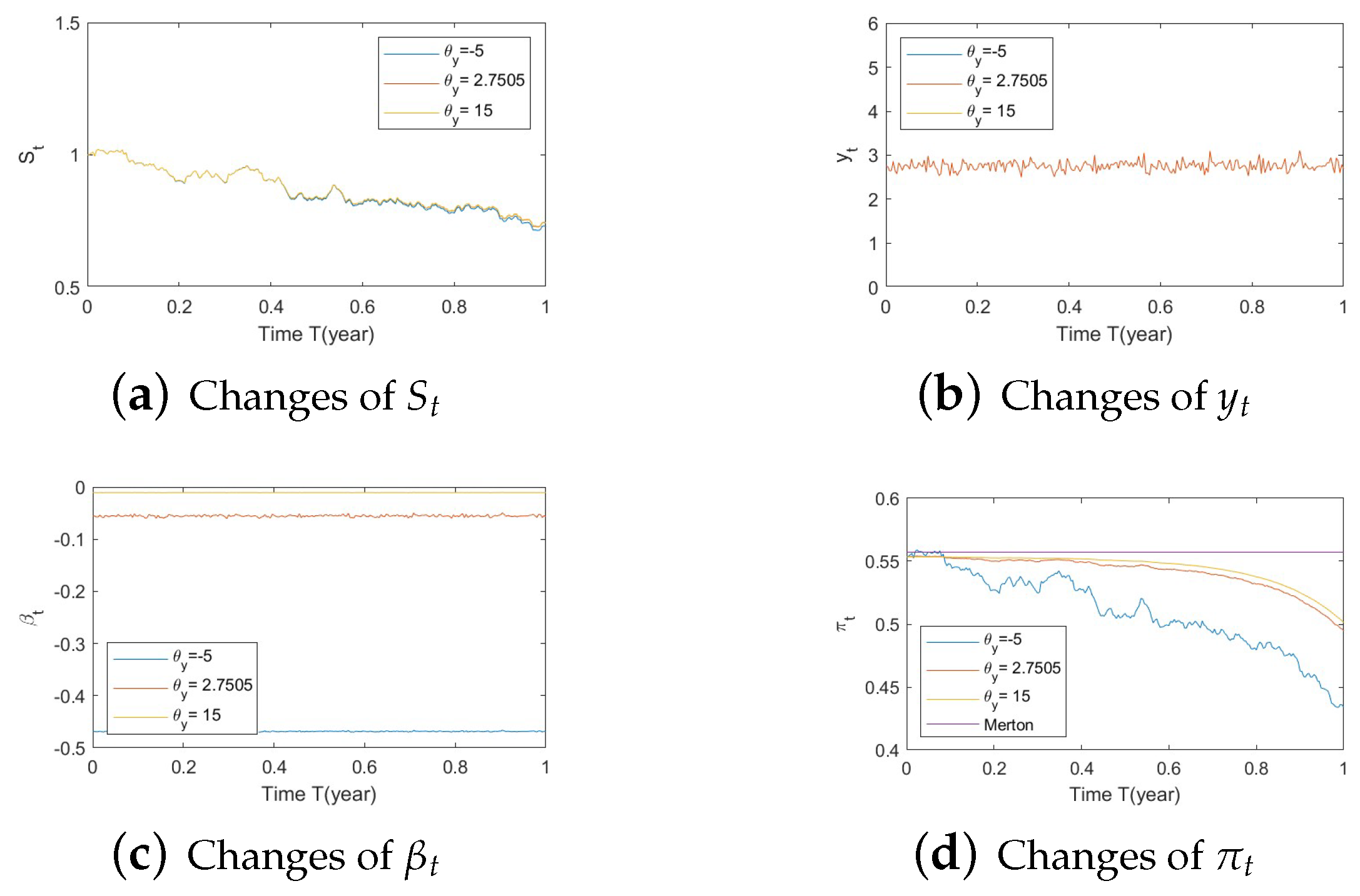
- Bull market conditions (Figure A10, Figure A11 and Figure A12):Figure A10. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A10. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A11. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying θy(e.g., θy = −5, 2.7505, 15).Figure A11. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying θy(e.g., θy = −5, 2.7505, 15).Figure A12. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A12. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .
- Bear market conditions (Figure A13, Figure A14 and Figure A15):Figure A13. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A13. Illustrate the impact on (a) stock prices, (b) driver of volatility, (c) driver of elasticity, (d) elasticity of volatility, and (e) optimal stock allocations when varying the speed of reversion, .Figure A14. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A14. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A15. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .Figure A15. Illustrate the impact on (a) stock prices, (b) driver of elasticity, (c) elasticity of volatility, and (d) optimal stock allocations when varying .
Appendix A.4. SEV Analysis
Appendix A.4.1. Figures of Gaussian Function Analysis
- 1.
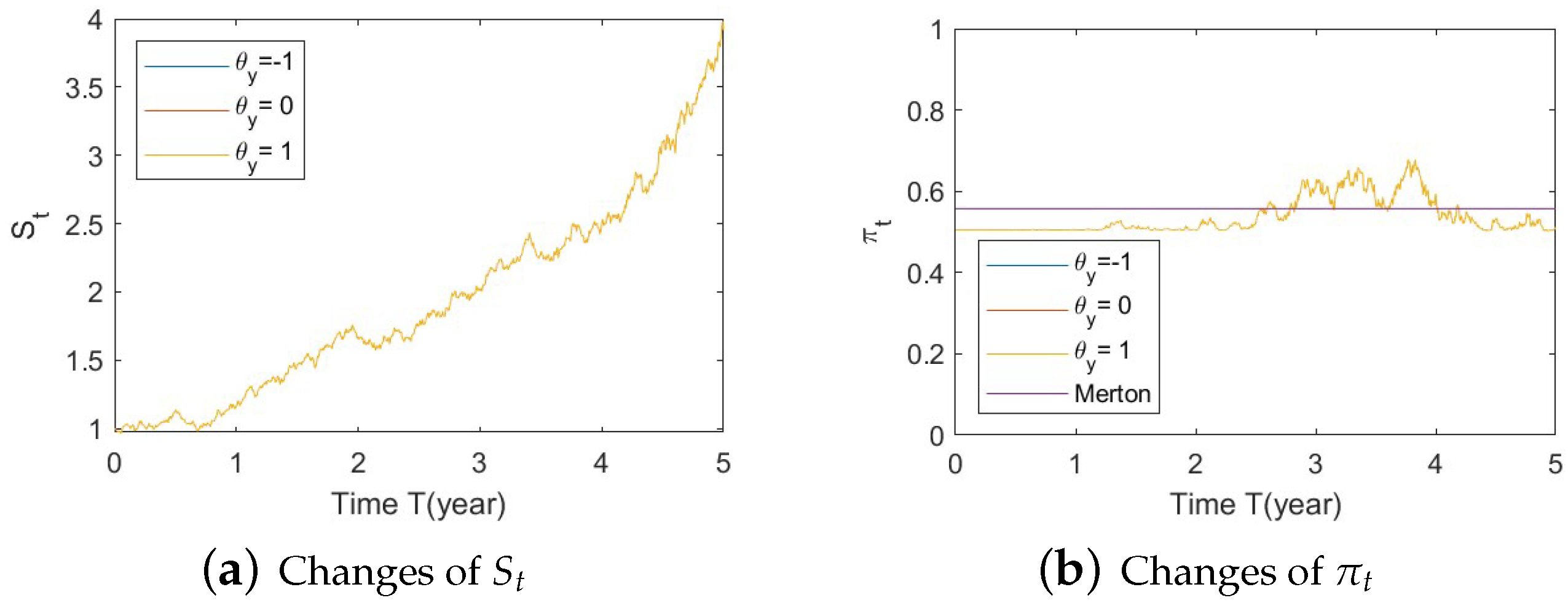
- Bull market conditions (Figure A19, Figure A20 and Figure A21):Figure A19. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion .Figure A19. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion .Figure A20. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying θy(e.g., θy = −1, 0, 1).Figure A20. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying θy(e.g., θy = −1, 0, 1).Figure A21. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A21. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .
- 2.
- Bear market conditions (Figure A22, Figure A23 and Figure A24):Figure A22. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion .Figure A22. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion .Figure A23. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A23. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A24. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A24. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .
- 3.

Appendix A.4.2. Figures of Arctan Function Analysis
- 1.
- Bull market conditions (Figure A28, Figure A29 and Figure A30):Figure A28. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion, .Figure A28. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion, .Figure A29. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A29. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A30. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A30. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .
- 2.
- Bear market conditions (Figure A31, Figure A32 and Figure A33):Figure A31. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion, .Figure A31. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion, .Figure A32. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A32. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A33. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A33. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .
- 3.
- Normal market conditions (Figure A34, Figure A35 and Figure A36):Figure A34. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion, .Figure A34. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying the speed of reversion, .Figure A35. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A35. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A36. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .Figure A36. Illustrate the impact on (a) stock prices and (b) optimal stock allocations when varying .
| 1 | In principle, an incomplete market setting permits infinitely many risk-neutral measures, nonetheless investors can select one using options in an approach called market completion. |
| 2 | This provides necessary conditions. |
References
- Beckers, Stan. 1980. The constant elasticity of variance model and its implications for option pricing. The Journal of Finance 35: 661–73. [Google Scholar] [CrossRef]
- Boguslavskaya, Elena, and Dmitry Muravey. 2016. An explicit solution for optimal investment in heston model. Theory of Probability & Its Applications 60: 679–88. [Google Scholar]
- Cao, Jiling, Jeong-Hoon Kim, and Wenjun Zhang. 2021. Pricing variance swaps under hybrid cev and stochastic volatility. Journal of Computational and Applied Mathematics 386: 113220. [Google Scholar] [CrossRef]
- Chacko, George, and Luis M. Viceira. 2005. Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets. The Review of Financial Studies 18: 1369–402. [Google Scholar] [CrossRef]
- Cheng, Yuyang, and Marcos Escobar-Anel. 2021. Optimal investment strategy in the family of 4/2 stochatic volatility models. Quantitative Finance 21: 1723–51. [Google Scholar] [CrossRef]
- Cheng, Yuyang, and Marcos Escobar-Anel. 2022. A class of portfolio optimization solvable problems. Finance Research Letters, 103373. [Google Scholar] [CrossRef]
- Choi, Sun-Yong, Jean-Pierre Fouque, and Jeong-Hoon Kim. 2013. Option pricing under hybrid stochastic and local volatility. Quantitative Finance 13: 1157–65. [Google Scholar] [CrossRef]
- Cox, John. 1975. Notes on Option Pricing I: Constant Elasticity of Variance Diffusions. Unpublished note, Stanford University, Graduate School of Business, Stanford, CA, USA. [Google Scholar]
- Cox, John C. 1996. The constant elasticity of variance option pricing model. Journal of Portfolio Management 23: 15–17. [Google Scholar] [CrossRef]
- Cox, John C., and Stephen A. Ross. 1976. The valuation of options for alternative stochastic processes. Journal of Financial Economics 3: 145–66. [Google Scholar]
- Cui, Zhenyu, J. Lars Kirkby, and Duy Nguyen. 2017a. Equity-linked annuity pricing with cliquet-style guarantees in regime-switching and stochastic volatility models with jumps. Insurance: Mathematics and Economics 74: 46–62. [Google Scholar]
- Cui, Zhenyu, J. Lars Kirkby, and Duy Nguyen. 2017b. A general framework for discretely sampled realized variance derivatives in stochastic volatility models with jumps. European Journal of Operational Research 262: 381–400. [Google Scholar] [CrossRef]
- Cui, Zhenyu, J. Lars Kirkby, and Duy Nguyen. 2018. A general valuation framework for sabr and stochastic local volatility models. SIAM Journal on Financial Mathematics 9: 520–63. [Google Scholar] [CrossRef]
- Davydov, Dmitry, and Vadim Linetsky. 2001. The valuation and hedging of barrier and lookback options under the cev process. Management Science 47: 949–65. [Google Scholar]
- Emanuel, David C., and James D. MacBeth. 1982. Further results on the constant elasticity of variance call option pricing model. Journal of Financial and Quantitative Analysis 17: 533–54. [Google Scholar] [CrossRef]
- Gao, Jianwei. 2009. Optimal portfolios for dc pension plans under a cev model. Insurance: Mathematics and Economics 44: 479–90. [Google Scholar]
- Gao, Jianwei. 2010. An extended cev model and the legendre transform–dual–asymptotic solutions for annuity contracts. Insurance: Mathematics and Economics 46: 511–30. [Google Scholar] [CrossRef]
- Ghysels, Eric, Andrew C. Harvey, and Eric Renault. 1996. 5 stochastic volatility. Handbook of Statistics 14: 119–91. [Google Scholar]
- Grasselli, Martino. 2017. The 4/2 stochastic volatility model: A unified approach for the heston and the 3/2 model. Mathematical Finance 27: 1013–34. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 2001. The specification of conditional expectations. Journal of Empirical Finance 8: 573–637. [Google Scholar] [CrossRef]
- Heston, Steven L. 1993. A closed-form solution for options with stochastic volatility with applications to bond and currency options. The Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Heston, Steven L. 1997. A Simple New Formula for Options with Stochastic Volatility. St. Louis: Washington University in St. Louis. [Google Scholar]
- Kim, Jeong-Hoon, Jungwoo Lee, Song-Ping Zhu, and Seok-Hyon Yu. 2014. A multiscale correction to the black–scholes formula. Applied Stochastic Models in Business and Industry 36: 753–65. [Google Scholar]
- Kim, Jeong-Hoon, Ji-Hun Yoon, Jungwoo Lee, and Sun-Yong Choi. 2015. On the stochastic elasticity of variance diffusions. Economic Modelling 51: 263–68. [Google Scholar] [CrossRef]
- Kraft, Holger. 2005. Optimal portfolios and heston’s stochastic volatility model: An explicit solution for power utility. Quantitative Finance 5: 303–13. [Google Scholar] [CrossRef]
- Lions, P.-L., and Marek Musiela. 2007. Correlations and bounds for stochastic volatility models. Annales De L’Institut Henri Poincaré C, Analyse Non Linéaire 24: 1–16. [Google Scholar] [CrossRef]
- Lo, Chi Fai, P. H. Yuen, and Cho-Hoi Hui. 2000. Constant elasticity of variance option pricing model with time-dependent parameters. International Journal of Theoretical and Applied Finance 3: 661–74. [Google Scholar] [CrossRef]
- Lord, Roger, Remmert Koekkoek, and Dick Van Dijk. 2010. A comparison of biased simulation schemes for stochastic volatility models. Quantitative Finance 10: 177–194. [Google Scholar] [CrossRef]
- MacBeth, James D., and Larry J. Merville. 1980. Tests of the black-scholes and cox call option valuation models. The Journal of Finance 35: 285–301. [Google Scholar] [CrossRef]
- Merton, Robert C. 1969. Lifetime portfolio selection under uncertainty: The continuous-time case. The review of Economics and Statistics 51: 247–57. [Google Scholar] [CrossRef]
- Platen, E. 1997. A Non-Linear Stochastic Volatility Model. Financial Mathematics Research Report No. FMRR 005-97. Canberra: Center for Financial Mathematics, Australian National Universite. [Google Scholar]
- Yuen, K. C., H. Yang, and K. L. Chu. 2001. Estimation in the constant elasticity of variance model. British Actuarial Journal 7: 275–92. [Google Scholar] [CrossRef]
| Parameters | 4/2 Model | Merton |
|---|---|---|
| 7.3479 | - | |
| 0.0328 | ||
| 0.6612 | - | |
| 0.9051 | - | |
| 0.0023 | - | |
| −0.7689 | - | |
| 2.9428 | 3.3431 | |
| Theoretical leverage () | −0.76889 | - |
| Parameters | Baseline | Case 1 | Case 2 |
|---|---|---|---|
| 2 | 0.5 | 10 | |
| 0 | −1 | 1 | |
| 1 | 0.1 | 5 |
| Parameters | Baseline | Case 1 | Case 2 |
|---|---|---|---|
| 250 | 125 | 500 | |
| 2.7505 | −5 | 15 | |
| 1.7491 | 0.5 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escobar-Anel, M.; Fan, W. The SEV-SV Model—Applications in Portfolio Optimization. Risks 2023, 11, 30. https://doi.org/10.3390/risks11020030
Escobar-Anel M, Fan W. The SEV-SV Model—Applications in Portfolio Optimization. Risks. 2023; 11(2):30. https://doi.org/10.3390/risks11020030
Chicago/Turabian StyleEscobar-Anel, Marcos, and Weili Fan. 2023. "The SEV-SV Model—Applications in Portfolio Optimization" Risks 11, no. 2: 30. https://doi.org/10.3390/risks11020030
APA StyleEscobar-Anel, M., & Fan, W. (2023). The SEV-SV Model—Applications in Portfolio Optimization. Risks, 11(2), 30. https://doi.org/10.3390/risks11020030