1. Introduction
Many portfolio managers purchase risk-bearing allocations of assets in order to maximize returns while reducing risk, with proceeds reinvested in the portfolio. For example, one popular strategy involves selecting a calibrated portfolio allocation of specific assets according to an objective function and constraints, followed by periodic rebalancing, i.e., by selling those assets whose market value has grown past their target percentage of the portfolio’s total value and purchasing those that have fallen behind.
Maeso and Martellini (
2020) provide empirical evidence on the effectiveness of this approach over strictly “buy-and-hold” strategies, irrespective of prior estimates and objective function specifications that might bias portfolio construction. Evaluation of the performance of such strategies emphasizes the returns basis on a risky portfolio, while the quantity basis of individual securities provides control variables for management.
This approach is rather different from the vast majority of research on financial derivatives. This is clearly illustrated by the seminal work of
Black and Scholes (
1973) and
Merton (
1973) (BSM, hereafter), and the large body of literature it inspired (for some early contributions see, for example,
Cox et al. 1979,
1985;
Madan et al. 1989;
Merton 1998). This literature establishes the central role of the BSM approach in addressing questions concerning the behavior of contingent claims, derivatives, options, and related constructs.
The BSM approach focuses on valuation and risk-management in the cash basis. Option contracts have well-defined values at specific times or states of the world, which are a function of the underlying variables specified in the contract, such as the price of a given stock. In order to understand the behavior of the values of option contracts, behavior of underlying stock prices is specified, which provides a mechanism for linking fluctuations in the value of an option to fluctuations in the prices of the underlying stock.
In the BSM framework, stochastic elements are eliminated through dynamic hedging, by considering a specific weighted portfolio of an option and an underlying stock. Since such portfolios are riskless under BSM assumptions, the values of their constituents are determined by what might be obtained by investing the portfolio in a risk-free asset. Should equivalence fail, a trader might extract from the difference an instantaneous risk-free profit, an arbitrage, thereby restoring the BSM relation. In the absence of arbitrage, the values of option contracts and other contingent claims can be computed from this fixed relation, which takes the form of a deterministic partial differential equation.
Over the years, the BSM framework has received its share of criticisms. Many question fundamental model assumptions, such as liquidity (see, for example,
Schönbucher and Wilmott 2000), market completeness (see, for example,
Dumas and Lyasoff 2012), and transaction costs (see, for example,
Dewynne et al. 1994;
Leland 1985;
Kennedy et al. 2009). In addition, the assumption of mesokurtosis has created a significant debate among both practitioners and theoreticians (see, for example,
Haug and Taleb 2014).
Others have attempted to resolve some of the above criticisms and noted empirical incongruities, such as the implied volatility smile and surface, by expanding structural assumptions concerning the behavior of the underlying asset price.
Heston (
1993), for example, employs a stochastic volatility framework in order to value bond and currency options.
Heston and Nandi (
1997) derive a closed-form solution should volatility display GARCH properties.
Kennedy et al. (
2009) attempt to incorporate jump diffusions in the underlying with transaction costs.
This paper differs from this literature in that it attempts to place the BSM approach in a more general market framework while retaining its remaining core assumptions. It focuses on the implicit and unstated assumption that, in contrast with standard market structure, there is no feedback between the value of options and their underlying stock price. In order to relax this BSM assumption, we introduce the alternative assumption of a complete market network with bidirectional continuous-time exchange dynamics, thereby extending the original BSM formulation. Assuming the existence of a complete market network and attempting to derive a comparable delta-hedging formula within this framework is shown to lead to a contradiction, raising important concerns about the applicability of the BSM approach in liquid markets. At the same time, additional option strategies beyond BSM are revealed to be available when modeling a complete market context. Our approach also recognizes and speaks to the fact that most portfolio managers purchase risk-bearing allocations of assets in order to attempt to maximize returns while reducing risk, with proceeds reinvested in the portfolio.
This paper is organized as follows.
Section 2 derives the basic BSM as a reference point.
Section 3 introduces assumption implicit in the BSM framework and assesses its reasonableness and possible implications.
Section 4 relaxes this assumption and derives the equivalent of the BSM under a more general and practically relevant market network. Finally,
Section 5 discusses some potential implications and applications of the results.
3. Black–Scholes–Merton: An Implicit Assumption
3.1. The Implicit Assumption
The derivation of the central BSM equation, as in (13), implicitly makes an additional assumption, which precludes the price of an option relative to the price of its underlying stock from entering into the option valuation process. The implicit assumption postulates the absence of feedback between variables, , and . Instead, there is a unidirectional causal chain (.
This implicit assumption means that the BSM approach ignores some aspects of the actual market structure and of the economic incentives of market participants. As the valuations of options contracts are functions of the underlying stock, amidst no-arbitrage arguments, it ignores the fact that the two may be substitutes for the agents whose interactions determine their prices. As such, this assumption has remained largely unaddressed (for an exception involving partial feedback effects from the volume of trading, see
Schönbucher and Wilmott 2000).
By contrast, the nature of exchange provides a mechanism for traders to select the asset basis most relevant to their strategies and to convert their performance metrics accordingly. The appropriate choice of basis will vary by trader and strategy. However, BSM only measures portfolio behavior in a single currency numeraire basis. This could become relevant should speculators or arbitrage-seekers using various other bases enter the BSM universe, seeking risk-adjusted excess returns or employing other trading approaches.
For example,
Merton (
1971) demonstrates that continuous rebalancing to original portfolio weights is the optimal strategy for risk-bearing, risk-averse investors. Since this cannot take place in practice, due to the restrictions of discrete time,
Maeso and Martellini (
2020) empirically examine the discrete-time rebalancing premium on a monthly basis and find performance that clearly exceeds the benchmark “buy-and-hold” strategy. This relates directly to option-pricing behavior. Indeed, it is possible to view the discretely implemented BSM delta-hedging strategy as a form of time-varying rebalancing itself. As such, gains attributed to arbitrage strategies may actually be the product of the rebalancing premium phenomenon.
Although seen as an arbitrage strategy, BSM-rebalancing carries the risk that the arbitrageur’s estimate of present and future volatility is incorrect. In this case, the implicit BSM assumption preventing relative price levels from affecting option prices may no longer be innocuous. A rational investor will want to evaluate risk along with relative costs and projected returns in dynamic strategies along with any other possible risk-bearing trading approaches.
As a model framework, the implicit BSM assumption limits available market network connections. It implies that all portfolio adjustments by traders occur according to the solution to the BSM partial differential equation, the final and boundary conditions of which are derived from legal stipulations of the contract alone. Within a universe comprised entirely of arbitrageurs seeking gains in the currency basis, there are no speculators attempting to find risk-adjusted excess return opportunities by alternative strategies, nor are there arbitrageurs in other numeraire bases. In reality, and could easily compete for capital allocations.
3.2. Market Networks and Non-Contractual Exchange Behavior
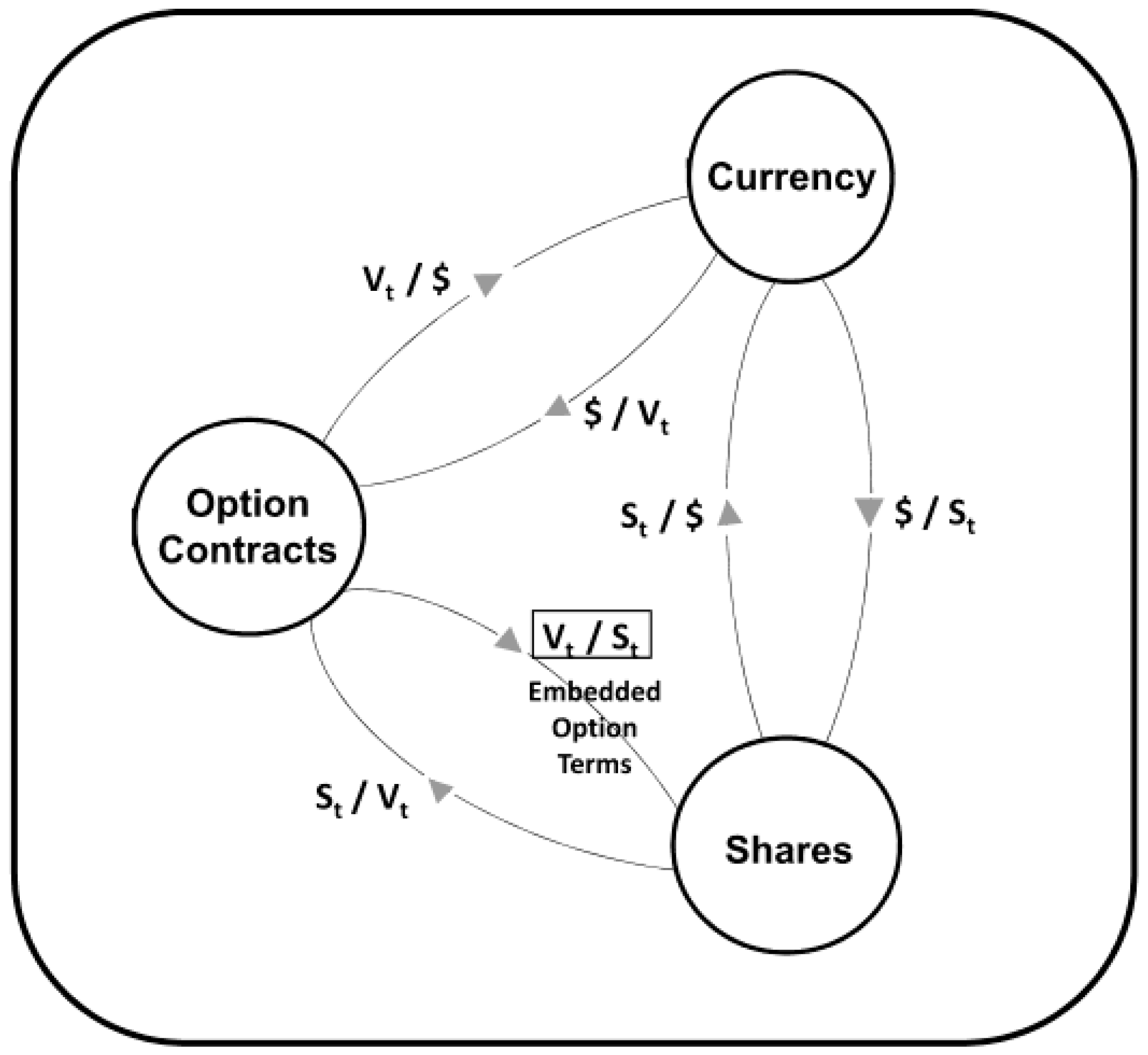
The BSM approach focuses on trading strategies between the numeraire and the stock, and the numeraire and the option, separately. In doing so, it neglects a fundamental opportunity provided by the market structure. Specifically, the option and stock may also be exchanged for one another. Although some traders exchange directly, the price ratios in the numeraire, / and /, provide the exchange rates necessary to perform this operation through the numeraire. This property of exchange is endowed by the market itself. It is an implicit embedded conversion option, which is not described in the contract.
In practice, if one has reason to believe that will rise relative to , one may want to use anticipated profits from the leveraged upward movement of to acquire more of the underlying than could be obtained otherwise. This potential opportunity certainly applies to near-the-money options, where percentage changes in the price of the underlying stock typically translate into much greater percentage changes in the value of an option, a leverage effect known as “gearing.” To apply this strategy, one purchases the option at the initial price in hopes of greater relative (not absolute) price appreciation, then converts the option to stock by selling it (rather than exercising it) and uses the proceeds to invest in more shares of the stock.
As a practical matter, market structure produces a potential asymmetry between returns in the numeraire basis and returns in the shares basis, as well as a failure of BSM to account for fluctuations in the value of the implicit embedded option. For all risk-bearing asset managers, the implicit option constitutes an additional means to acquire the underlying asset, and fluctuations in option prices may provide a strategy to do so on more favorable terms than immediate direct purchases. Addressing this necessitates the modeling of all rates of exchange in the network. For example, suppose that a European call option is priced at USD 0.25 on given stock, which is priced at USD 1, producing an exchange rate of 0.25 shares per option contract. For convenience, we refer to the value of the option in the shares basis as the shares-per-option value. If the stock price rises to USD 1.10 and the option price rises to USD 0.30 as a result, the option will have gained 20% in USD value and the stock will have gained 10% in USD value, but the shares-per-option value will have risen 9%. Even though the implicit embedded early-exercise option endowed by the market has risen in value, BSM will not incorporate these gains into the option’s value. Alternatively, if the stock price falls to USD 0.90 and the option price falls to USD 0.20 as a result, the option will have lost 20% in USD value and the stock will have lost 10% in USD value, but the shares-per-option value will have lost 11%. These fluctuations in shares-per-option values, which affect the value of the embedded option, are not accounted for in the original BSM approach.
If all assets may be exchanged for one another, the state of the market at a given time may be represented as a complete directed graph, one in which all nodes are connected with one another and in which edge connections are bidirectional. Each asset, including the numeraire, may be represented by a unique node in the graph. Rates of exchange between assets are directionally dependent attributes of edge connections between nodes representing their respective assets. While the exchange opportunity we identify produces a complete directed graph—see
Figure 1, the analysis of BSM produces a different, more limited market network—see
Figure 2.
The distinction is especially relevant to those whose option purchases are ultimately devoted to taking long or short positions within the underlying portfolio they manage. For such managers, options are not merely a potential arbitrage opportunity, but a means to a very specific end. Since BSM assumes that no such arbitrage exists in the first place, BSM itself points to the importance of this constituency. Accordingly, one might expect that rational traders should want to monitor such exchange rates carefully.
The perspectives of these managers are, generally, absent in the no-arbitrage derivatives literature. Yet, to most fund managers, arbitrage cash flows would be materially no different than influxes of new capital for investment. Ultimately, such managers are responsible for investing the capital entrusted to them in positions that will yield higher returns than the risk-free rate. While arbitrage profits would clearly be desirable, they would ultimately only be a means to the end of asset acquisition. As a result, it makes sense to consider seriously the perspective of the asset allocator who views at least one primary function of the option contract as simply providing a mechanism to assume positions in the underlying security.
4. Black–Scholes–Merton: Relaxing the Implicit Assumption
4.1. Formalizing the Hedge Portfolio
The new risk factor that needs to be hedged must be measured in the shares basis. This reflects the reality that many portfolio managers ultimately regard holdings in the currency basis as a means to the end of acquiring positions in assets which, properly balanced, will conceivably lead to superior returns with less risk than a given benchmark.
With this perspective, risk-free profits in one numeraire alone are insufficient to attract trader interest. Opportunity cost across assets must also be considered. If a trading strategy facilitates the acquisition of a fixed amount of currency, while asset prices move such that fewer assets may be obtained after the strategy is implemented, the opportunity cost of the strategy will make it unattractive to such managers. To accommodate this, we apply the BSM analysis in a way that allows for the consideration of the terms of exchange between the non-currency assets, rather than a single fixed numeraire.
To formalize the statement of the portfolio and the exchange conversion factor, let and . By definition, is the price of the underlying stock in units of the option, while is the price of the option in units of shares of the underlying stock. As such, assumes the role of in the portfolio representation, yielding the number of shares for which the option may be implicitly exchanged. Both and vary stochastically. This risk affects the terms faced by the option holders should they exercise the implicit embedded option. At the same time, the portfolio manager may choose to hold an amount of the currency numeraire. For the sake of simplicity, we assume units are a single USD and so the numeraire may be exchanged for shares of the stock.
For hedging this conversion risk factor, the portfolio should be expressed in terms of a consistent numeraire, specifically, shares of the stock itself. Accordingly, the modified representation of the delta-hedged portfolio employed by BSM, the equivalent of (9), mapped into the shares basis, becomes
where
is the per share purchasing power of the currency numeraire,
is the per share purchasing power of the option, and
is the amount of the cash numeraire held.
is given by
4.2. In Search of the Optimal Financial Strategy
Since (14) is measured in the shares basis, the risk presented by the fluctuating terms of exchange provided by the implicit embedded option and the reciprocal of the stock price must be represented by a continuous-time random process measured in the same basis. In order to provide a perfect hedge in both the currency and shares bases, fluctuations in both the stock price and the new terms of exchange need to be accounted for. For simplicity, we model risk in the shares basis rather than the currency basis.
Since the dynamics of
are derivable from a specification for
, we begin with
. Let
be a continuous-time stochastic contribution. Following BSM, let
This determines the functional form with which hedging will occur in the shares basis, and it will be the path by which option and stock prices may be directly recovered.
The specification in (16) has several advantages. It is parsimonious, it mirrors BSM, and it seems to be a rather minimal baseline requirement for hedging any more complex specification. If , the deterministic trend component could be heuristically nudged away from zero and infinity. At the same time, at least approaching limits of zero and infinity are potential consequences of extremes of the exchange ratios. In the currency numeraire basis, should the price of the option fall below the quantization provided by units of the numeraire, it would appear to be zero. This would result in a divergence of toward infinity, which this model accommodates.
This specification for exchange ratio dynamics differs from what would be derived had one started with (4), describing stock price changes in the currency numeraire, and (8), describing the resulting option price changes in the currency numeraire and cross-effects. The process of invoking (4) to produce (8) presumes the existence of . If the new risk dimension is unhedgeable, this deterministic definition would not hold.
The term
may be derived from Itô’s Lemma, which initially yields
Calculating the relevant partial derivatives produces
and
. Ignoring terms smaller than
dt,
, mirroring its counterpart in BSM. Inserting these and the specification for
into the above yields
which simplifies to
It is important to observe that (16) and (19) both describe geometric Brownian motions. This means that we could have specified either or first, and the functional form of the resulting dynamic process would be unaffected.
In like manner, we may derive the stochastic dynamics of
from (4). Noting that
,
and
, by Itô’s Lemma,
which provides the continuous-time fluctuation in the per share purchasing power of one unit of the currency numeraire. Substituting
into (19), it is possible to express terms in the potentially hedged portfolio in the shares basis in terms of option and stock prices, as in BSM. This yields
Now, we specify the dynamics for
by inserting (21) and (20) into (14),
This may be simplified as
4.3. Hedging Impossibility
It is possible now to address the issue of whether or not one can hedge the purchasing power of the portfolio (14) while at the same time keeping the prices of the stock and the option strictly positive. These terms are necessary so that the dynamics in (8) do not encounter a sink at , which would make further analysis trivial.
Suppose that the purchasing power of the portfolio is hedgeable. In that case, we can eliminate
by solving for
. This produces the quantity of the currency numeraire held to hedge option price fluctuations,
which, when inserted into (23), produces the analog of (11).
If a risk-free interest rate,
r, paid in quantity of shares, existed, we could derive the equivalent of (13) from (25) for the shares basis. This results in the relation
Subtracting the right-hand side and eliminating
dt provides the equivalent of (13) for the shares basis, with the implicit embedded option now structurally recognized:
Unlike (13), (27) is not a partial differential equation. This is a consequence of explicitly recognizing the structural relationships provided by the implicit embedded option, which makes partial derivatives in the shares basis readily computable. This also makes any proof by contradiction more accessible. Factoring out
from each term, it may be seen that
Of course, no risk-free interest rate, r, exists in the shares basis, although if and only if hedging is possible, r could serve as a proxy for a deterministic, hedged growth rate from a given dynamic strategy. Regardless, if (28) is able to yield nonzero deterministic values for the option in the currency or shares basis, we may reasonably assume that the multiplier on the right of in (28) is nonzero for any scenario of interest. If the multiplier were zero, then from (28), we would conclude that the conversion rate is an entirely free variable, and the risk in the portfolio cannot be dynamically hedged.
Secondarily, from a practitioner’s perspective, every term in the multiplier other than
r is continuous and must be estimated by some process. Any such set of estimators must be associated with a continuous probability density function in which the probability of a single fixed value is by definition equal to zero. This means that, as a practical matter,
Dividing both sides of (28) by the multiplier yields
At this point, several paths lead to serious logical contradictions or to violations of the terms of hedgeability. For example, assuming
trivially produces
Were (31) to be satisfied, it would produce a collapse of the implicit exchange relationship between the stock and the option. Were (25) still valid and able to be derived from a dynamic specification, we would find that , meaning that no holdings exist in the currency basis. We would also observe that , rendering the portfolio described in (18) and (25) valueless. In other words, if the purchasing power of the cash and option portfolio is hedgeable, then the option is worthless.
As a result, it may be concluded that the assumption of hedgeability in the shares basis fails. Moreover, the implication of (31), that the value of the option equals zero, stands in stark contrast to the predictions of BSM. So long as the underlying has nonzero volatility, BSM always predicts that an option will have a positive arbitrage-free value.
5. Concluding Remarks
For almost half a century, option pricing theory has relied heavily on the seminal dynamic hedging and replication arguments set forth by the BSM approach. These arguments presume a restricted subset of the market network, a subset over which any resulting dynamics are constrained to unfold. This paper focuses on what may occur when the BSM approach is extended to a more practically relevant general market network. Specifically, we consider explicitly an implicit option embedded in all option contracts, one that arises from the nature of the market itself. This implicit option is exercised by selling the option to which it is attached and exchanging it for another asset according to relative price ratios. The effect of this is to add an early-exercise conversion provision that provides option holders an additional means to enter positions in underlying assets.
For the holder of a call option, the underlying may be acquired either by exercising the option according to the terms of the contract or by exchanging the option for shares in the underlying. This allows the holder of a put option to enter a long position in the underlying by exchanging the put option for a certain number of shares of the underlying, which reveals the put option to contain an inherent exotic call provision on the underlying. Significantly, this exotic call provision may be exercised at any point prior to expiry. Alternatively, the holder of a put option may exercise the contract terms of the option in order to take a negative position in the underlying. For example, as the price of the underlying stock decreases, the price of a put option will typically rise, ceteris paribus. This means that the put option may be used to purchase more shares of the underlying asset than a given call option may have made possible, even though the put contract itself only expressly facilitates entering a negative position.
As a result of the early exercise properties of the implicit embedded option, certain additional consequences necessarily follow. For example, the nature of the added embedded exotic call provision with early exercise interferes with adherence to some classically assumed relations for European options, such as put-call parity. This arises because it is impossible to guarantee replication of the payoff diagram at expiry in all bases.
Adapting the problem structure to the terms of the embedded option, the portfolio hedged in the original BSM framework is unhedgeable within the resulting market network of assets and exchange rates. This leads to a breakdown in deterministic option pricing approaches, as well as in popular risk-management metrics for options that are widely employed by portfolio managers and regulatory institutions.
By integrating a complete market network structure into the BSM analysis of option hedging, several issues become apparent. The strategy provided by the implicit conversion property of any asset in a market network removes the ability of the BSM approaches to provide -hedging, resulting in a stochastic portfolio. Without the ability to derive a deterministic partial differential equation for what once seemed to be hedged portfolio dynamics, contract terms themselves become irrelevant to the hedging problem. Moreover, the “Greeks” used in risk-management are derived from the terms , , and , all of which require a deterministic partial differential equation.
At the same time, the exercise highlights the fundamental objective of the portfolio manager—to acquire positions in underlying assets, using whatever means seem most appropriate. In fact, this pursuit of returns in assets subject to risk is implied by the no-arbitrage assumption of BSM. The results demonstrate that, under these assumptions, the goal of increasing share acquisition cannot be achieved without some assumption of risk. For investors with the proper risk tolerances, the resulting dynamics for the unhedgeable portfolio may provide a means of indirectly acquiring shares. Such investors would purchase the option expressly in hopes of converting it to stock through the implicit mechanism granted by the market itself. If the resulting exchange rate between the derivative and underlying trends strongly and stably in a favorable direction, the option may be a risky but strategically optimal shortcut to greater share acquisition.
As noted earlier, the results herein constitute a marked departure from dynamic replication-based valuation approaches introduced by BSM and those works that descend from it. While these assert deterministic contingent claim valuations, predicated upon variations of optimal control theory over subspaces of market networks, the present work highlights unhedgeable non-contractual characteristics endowed to the same contingent claims by complete market networks. This yields a failure of dynamic replication-based determinism. In this sense, the work not only echoes model performance criticisms raised in
Haug and Taleb (
2014), but it offers an additional explanation for such failures. Constructively, it both provides a bridge between existing option pricing theory and the rich literature that attempts to optimally manage risky portfolios of assets, as exemplified in
Maeso and Martellini (
2020). The establishment of this connection invites portfolio management applications of innovative new decision-making methodologies which may incorporate subjective as well as objective probabilities, such as the Entropy Decision Risk Model (EDRM) of
Monroe et al. (
2020).
These findings present a challenge to existing dynamic-replication-based valuation and risk-management approaches. However, answering this challenge remains a task for future research, using methodologies that are not reliant upon replication and which recognize the perils of assuming deterministic solutions to the valuation of contingent claims within completely connected market networks and subnetworks. Promising techniques include approaches employing econometric estimation of supply and demand structures, prospect theory, and Bayesian approaches which accommodate parameter updating due to fluctuations in market sentiment. In particular, restoring the role of option prices to their essential position, as opposed to replacing them with BSM-implied volatilities, should catalyze material theoretical and empirical advances. It should also be noted that the completely connected market networks described herein are inapplicable to situations involving highly illiquid markets, although future research might be conducted using random graphs to describe intermittently liquid subnetworks.