1. Introduction
Demographic changes have been caused by many factors. On the one hand, the developments and progress in medicine and the improved living conditions have extended life expectancy. On the other hand, the birth rate has been systematically decreasing. The consequence of these phenomena is the rapid increase in the over-65 population. In 2019, the percentage of people in this age group reached about 20.3% of the total European population (
Eurostat 2020b). This group has become the fastest-growing segment of the population. It would not be an exaggeration to say that the world is turning grey.
The declining birth rate and increasing longevity worldwide have contributed to significant changes in the population’s makeup and affected many branches of the economy, especially the labour and medical service markets. An increase in the elderly dependency ratio overburdens the work-age population. This indicates that in the future, pensions’ funding gap will be a significant social problem. Moreover, the burden on health care triggered by the expenditures for the 65 and over population is becoming a large problem due to deteriorating health conditions, the presence of chronic diseases, and the need to provide long-term care for this social group. Ensuring financial security and health services to such a large elderly population is becoming a big challenge (
Chen et al. 2021).
Aging implies changes in financial behaviour and the perception of many aspects of life, as well as the deterioration of health. Older adults’ life satisfaction depends on such factors as their pensions, social support, and ability for self-care. Overall health and financial worries are significantly associated with life satisfaction (
Borg et al. 2006,
2008). Therefore, it is also a crucial issue to provide financial peace and treatment options for the elderly (
Korenman et al. 2021).
Many members of society, including retirees, own apartments or homes that they do not want to sell. On average, 70 % of people own their own properties in European Union (EU) countries (
Eurostat 2020a); in Poland, this figure reaches almost 84 %, in Hungary almost 90 %, and in Romania over 95 %. Therefore, financial institutions in different countries have introduced equity release contracts for the retired (
Hanewald et al. 2016), which provide an additional income in exchange for surrendering their real estates. Many variants of these contracts are available in European countries (also in Poland). The largest European market for equity release contracts is the United Kingdom (UK) market (
Shao et al. 2015), while the largest world markets are the United States of America and Australia (
Lee and Shi 2021).
Many studies and debates focus on equity release contracts. It is suggested that the housing equity of elderly homeowners may provide significant financial resources. The authors of the paper by (
Mullings and Hamnett 1992) examined the participation of elderly persons in equity release schemes. In the article by (
Toussaint and Elsinga 2009), attitudes toward the use of housing equity in several EU countries are examined. Based on 2005 data, researchers have observed that respondents used housing equity in various ways to help plan their finances. Since 2005, more people are aware that a possible method for funding the expenses associated with old age is through the use of equity release contracts (
Marciniuk et al. 2020). Retirees are asset-rich and cash-poor; therefore, their housing wealth can be used to supplement their retirement income. Thus, the equity release contract is socially significant (
IFoA 2019). The authors of the article (
Sharma et al. 2020) point to various schemes for approaching equity release contracts, such as focussing on government subsidies for contracts. They conclude that the focus of government policy on equity release to tackle the challenges of an aging population is misplaced. However, treating equity release as an additional private source of income has many benefits.
In the richer countries of the world, an increase in demand for medical services has been observed. This increase is caused not only by demographic changes, such as the phenomenon of an aging population, but also by the occurrence of civilization diseases and technological progress in medicine. These additional factors result in increased health care expenses; consequently, it is impossible to provide high-level medical services without a mechanism of co-financing by patients. Two basic forms of co-payment can be considered: private payments, i.e., out of pocket expenditures, or private health insurance. Private health insurance can ensure access to additional funding, especially for critical or chronic illnesses. The funds obtained from this type of insurance can be used to improve the quality of life and treatment standards even in places where the state finances medical care. However, not everyone can afford to buy this insurance. Therefore, it has been necessary to introduce financial products combining different types of contracts (e.g., life insurance or equity release) with health insurance. Additional contracts are a source of financing the health insurance premium. The paper by (
Webber 1993) presents an example of the financial contract, which meets the healthcare costs of the elderly. The authors emphasize that a major demand for the new products have been created by demographic changes, more widespread homeownership, and other political and cultural changes. A rapidly expanding market for products providing finance and healthcare for the elderly was observed, and its analysis indicates that the aged care insurance is both feasible and welfare-enhancing (
Paolucci et al. 2015). Contracts that combine with critical health insurance are described in many papers. An example of a contract with life insurance is examined in the papers by (
Dębicka and Zmyślona 2018,
2019). The second example, considering a contract combined with a reverse annuity contract is described in article (
Dębicka et al. 2015), which discusses an individual contract and one for a married couple (
Zmyślona and Marciniuk 2020). In the two mentioned articles, home equity release products combined with dread disease insurance are promoted as a potential solution to long-term care costs for the elderly.
The aim of this paper is to present two variants of these contracts, the first for both spouses and the second is a combination of two separate contracts for the wife and the husband. In
Section 2, we describe the theoretical background of the contracts, and the multiplied Markov models are applied. Two varieties of contract with their cash flows are presented in
Section 3. In
Section 4, we analyse and compare the cash flows related to both options. The analysis results suggest the contract version affects the amount of cash flows connected to the reverse annuity contract and the dread disease insurance benefits, depending on the financial needs, health status, and spouses’ age. The construction of the presented model is original. It is a continuation of the research conducted by the authors of the current work. Firstly, the individual model described in (
Dębicka et al. 2015) was generalized to the marital model. In addition, the model was extended to include health benefit payments in two states (not only at the moment of diagnosis but also when the health condition worsens). Secondly, all analyses are performed based on the authors’ own life expectancy tables for lung cancer patients in the critical stage described in (
Dębicka and Zmyślona 2016,
2019). Finally, all calculations are performed based on original computer programs in MATLAB.
2. Contract Combining Reverse Annuity with Critical Health Insurance
The new product consists of two elements, namely, the reverse annuity contract and the dread disease insurance. One of the equity release forms similar to the home reversion scheme is the reverse annuity contract (
Marciniuk et al. 2020). The benefits derived from the new product can help improve the living conditions and the quality of life for the elderly as well as provide additional financial resources in case of a critical illness. The construction of this kind of contract is based on a model that describes an extended lifetime considering the risk of morbidity, severe disease, and life expectancy in the case of the critical stage.
Usually, both spouses are property owners and so the joint further lifetime of the wife and the husband should be considered. The spouses, who want to contract reverse annuity, receive a lifetime annuity in exchange for surrendering their real estate to a company. We consider two kinds of cash flows; the first group is connected with the reverse annuity contract. We distinguish a single premium and annuity benefits. This premium is not actually paid. It depends on the percentage
of real estate value. In the considered contract, the annuity benefits are paid with the option of selecting the last-surviving status (
Marciniuk et al. 2020). This status means that the annuity benefits are paid every year while at least one of the spouses is alive and healthy. The annuity benefits depend on the pensioner’s age and his/her further life expectancy and the value of the real estate W.
The second kind of cash flow concerns critical disease insurance. The survival time in case of falling ill with a severe disease depends on its course. We consider the health insurance premium that is paid every year that the insured party is healthy and alive. This insurance premium is paid as a percentage of the reverse annuity benefits. The health insurance benefits are firstly paid in case of a diagnosis. Moreover, the contract enables a benefit payment in the situation of deterioration of a patient’s condition. This is important because the deterioration of health conditions in the case of a critical illness involves the necessity of care in the terminal state. The end-of-life heath expenditures are often huge. In many cases, families caring for terminally ill patients require financial support. For this reason, mild and critical health conditions are distinguished. In the critical stage the fatality rates grow rapidly, which decreases the probability of survival year by year. The analysis of the joint cash flows connected with the reverse annuity contract and health insurance requires the introduction of a multistate model, which is built separately for both spouses.
We have distinguished the following steps:
First step: Equity release—in exchange for surrendering their real estate, the clients at the retirement age receive a lifetime annuity (they do not pay a cash premium for that); the level of this theoretical annuity is computed in relation to the value of the house.
Second step: from the theoretical annuity, a portion is paid to the insurer to finance health insurance; the remaining portion is paid in cash to the annuitant as a lifetime annuity (level 1).
Third step: in case of a mild stage illness, the annuitant does not have to pay the health premium and therefore receives an annuity (level 2) equal to the initial theoretical annuity; at the moment of a diagnosis, additional benefits are paid through health insurance.
Fourth step: in case of the critical stage of an illness; an additional single benefit financed by health insurance is paid to the client (level 3).
2.1. Multistate Markov Models
The multistate model is described by the state space
and a set of direct transitions between states T of the state space, where
denotes a direct transition from state
i to
j . All the possible insured risk events up until the end of the contract can be described by this model (
Pitacco 2014;
Dhaene et al. 2017;
Haberman and Pitacco 2018).
We consider the Markov model in which the stationary Markov chain is described as a
discrete-time process . The model describes the state and its changes for the contract at time .
The construction of a contract combining the reverse annuity and dread disease insurance enables the introduction of two models. The first one is related to the reverse annuity contract and the latter with health insurance. The model connected with the reverse annuity contract considers only two states:
The model connected with health insurance considers the course of a dread disease. Thus, the following states are distinguished (
Zmyślona and Marciniuk 2020):
the insured is alive and healthy;
the insured became mildly ill during the last year;
the insured has been mildly ill for at least one year;
the insured became critically ill during the last year;
the insured has been critically ill for at least one year;
the insured is dead (D—dead).
We assume that an insured could survive in the critical stages of illness during
h years, and for that reason the fifth stage is extended by the introduction of states
,
,…,
. The Markov model has a lack of memory; therefore, the presented model is extended by one additional state denoted by the number 3. This state describes a case when the insured fell mildly ill during the year. The multistate model related to the critical health insurance is presented in
Figure 1 (
Zmyślona and Marciniuk 2020). The circles present the states, and the arcs describe the direct transitions between the states.
2.2. The Probability Structure of the Model
The probabilistic structure of the multistate model for the considered contract is given by the transition probability matrix
. We denote the elements of matrix
by
. We define the following nonzero transition probabilities matrix for a person initially aged
x (during the time interval [
x +
k,
x +
k + 1)) connected with the model for the reverse annuity contract
where
stands for the probability of surviving denoted as
and
represents the probability of death denoted as
. Considering the sex of the insured requires the introduction of two separate matrixes
and
, where
denotes the initial age of a woman and
the initial age of a man.
The transition probabilities matrix connected with the multistate model related to critical health insurance is given by
The transition probabilities matrixes in the female and male populations are denoted by and , respectively.
The formulas for these elements are obtained based on the methodology of the multistate life table (increment-decrement table). The descriptions of the formulation and estimation processes are described in (
Dębicka and Zmyślona 2016,
2019). These elements depend on the following population rates:
—the probability of death;
—the dread disease mortality rate;
—the dread disease incidence rate (the morbidity rate);
—the percentage of patients diagnosed in the critical stage;
—the probability of health deterioration to the critical state;
—the fatality rate in the population of the critically ill.
The above first three values are calculated for the whole population and the remaining three for the patient population.
The formulas for the elements of the matrixes
are presented in
Table 1 (
Dębicka and Zmyślona 2016,
2019). The matrix formulas for the male
population are obtained analogously to those for the female population.
3. Two Version of Combining Contract
A property is usually owned by both spouses, so the contract should be concluded by both a husband and a wife. The spouses may sign either one marriage contract for which they will receive one annuity benefit, or two individual contracts, in which two annuity benefits are paid independently. In each of the abovementioned cases, health insurance benefits are paid independently for the husband and the wife. Both solutions have advantages and disadvantages and provide a varied number of benefits. The choice of the type of contract will have an impact on the formation and differentiation of the reverse annuity and health insurance benefits.
3.1. Marriage Contract
The spouses sign one contract in which, in exchange for surrendering their rights to the property, they receive an annuity for life. A percentage
of the real value of the property
W funds the benefit. Then, they pay two separate premiums for private health insurance. The funds designated for paying health insurance form a part of the annuity premium. We define
as the reverse annuity parameter. This parameter describes the percentage of the paid annuity. The remaining part
describes the health insurance premium. The impact of this parameter on the benefits is described in (
Zmyślona and Marciniuk 2020). The annuity benefit is paid in advance for both spouses at the beginning of the year, if at least one of the spouses is alive.
The cash flows connected with the marriage version of the model are obtained in three steps. In the first step, the annuity benefits are calculated based on the multiple state Markov model, which describes the further lifetime of a couple. It consists of 4 states (1—both spouses are alive, 2—the wife is dead, 3—the husband is dead, and 4—both spouses are dead).
Let
and
be the probabilities of the remaining process
at states
, for
. The matrixes describing the process duration in each state are shown in
Table 2 for the wife and the husband.
The transition probability matrix for the 4-state Markov model (for a marriage) is defined as the following Hadamard product
where
x denotes the age of the wife and
y the age of the husband. An element of matrix (2) equals the following product
for each
i and
j.
The course of the process is described by the matrix D. This matrix is defined as the following formula
where
denotes the initial distribution vector,
, where
is the state number and
is a contract duration.
This course takes into consideration both spouses’ survival times.
The annuity benefit is determined by means of the following formula (
Dębicka et al. 2022)
where
denotes a discounting factor, which relates to the interest rate. The auxiliary vectors are used, where
,
and
I is an identity matrix with n+1 rows and columns. In this case,
N = 2. The formula for the reverse annuity contract benefit in the classical notation is presented in (e.g.,
Marciniuk et al. 2020).
In the second step, the health insurance benefits are estimated. The health insurance premium is separately payable for the husband and wife. The further lifetime of a couple is described by the model presented in
Figure 1. The part of the pension allocated to the payment of health insurance is divided between the spouses proportionally to the
R parameter, which denotes a fraction of the men in the population who fall ill with the disease that is subject to dread disease insurance within a year. This parameter determines the risk of morbidity connected with a critical disease in the population of men. The decomposition of the annuity benefit is represented by the formula
. Thus, the annual health insurance premium is given by the following formulas: for a husband
and for a wife
. The health premiums are paid separately by the spouses for when they are healthy. Health insurance benefits are paid individually to the spouses depending on their health condition (at the moment of the diagnosis of a critical illness and in the event of deterioration of health), for a wife
and for a husband
. The formula for calculating the value of the health benefits is given by (compare
Appendix A)
Matrix D, describing the probability structure, is calculated on the basis of the matrix of transition probabilities given by (2) for the husband and wife separately. Thus, the number of columns in matrix D is reduced to N. The matrix of all premiums paid during the term of the contract is denoted as . The matrix equals 1 in the second and the fourth columns.
In summary, during the duration of the contract, spouses receive the following benefits:
(Both spouses are healthy);
(The husband is healthy; the wife is ill or dead);
(The husband is ill or dead; the wife is healthy);
(The husband has become sick or his health has worsened; the wife is healthy);
(The husband is healthy; the wife has become sick or her health has worsened);
(The husband has become sick or his health has worsened; the wife is sick or dead);
(The husband is sick or dead; the wife has become sick or her health has worsened);
(The spouses have both become sick or their health has worsened).
Therefore, the spouses receive annuity benefits reduced by the health insurance premium (if they are healthy). In the event of a diagnosis or a deterioration of their health state(s), the spouses receive health insurance benefits individually. From the moment the diagnosis is made, the spouse does not pay the health insurance premium.
3.2. Two Individual Contracts
An individual version of the contract implies that a married couple signs two separate contracts. In this case, the premiums and benefits connected with health insurance and the reverse annuity contract are paid separately. The benefits of the reverse annuity contract are financed and determined based on the part of the property value owned by a given spouse (usually 50%) and is equal to . The annuity benefits are calculated separately for a husband and for a wife . The sum of the annuity benefits in an individual version is higher than the annuity benefit paid under the marriage contract. However, in the individual case, the annuity benefits are paid independently to each of the spouses only until their death. Thus, in the event of the death of one of the spouses, the surviving partner will be deprived of the part of the dead spouse.
Within individual contracts, the spouses may separately determine a part of an annuity benefit, which will be spent on the health insurance premium by setting the value of the reverse annuity parameter . Therefore, the amounts of the health insurance premium are equal to and for a husband and a wife, respectively. In the next step, the health insurance benefits are estimated for a husband and a wife .
The cash flows related to the individual version of the contract are separately modelled for a husband and a wife. The probability structure describing the further lifetime of a wife is denoted by , whereas for a husband it is denoted by (compare (2)).
The benefits are obtained separately for individual models for a wife and a husband in three steps. In the first step, the annuity benefits are obtained separately on the basis of the further lifetime for a wife and a husband using the following formula (compare
Dębicka and Marciniuk 2014)
which is calculated separately for a husband and a wife. The matrix
D is obtained on the basis of the transition probability matrix given by (1) separately for the spouses.
In the second step, the health insurance benefits are obtained using the model described in
Figure 1. The health insurance benefits are calculated in a similar way as in the case of a marriage version of the contract using the Formula (6).
During two individual contracts, the spouses receive the following benefits:
(Both spouses are healthy);
(The husband is healthy; the wife is ill);
(The husband is healthy; the wife is dead);
(The husband is ill; the wife is healthy);
(The husband is dead; the wife is healthy);
(The husband has become sick or his health has worsened; the wife is healthy);
(The husband is healthy; the wife has become sick or her health has worsened);
(The husband has become sick or his health has worsened; the wife is sick);
(The husband has become sick or his health has worsened; the wife is dead);
(The husband is sick; the wife has become sick or her health has worsened);
(The husband is dead; the wife has become sick or her health has worsened);
(The spouses have become sick or their health has worsened).
The spouses receive annuity benefits reduced by the health insurance premium (if they are alive and healthy). The death of a spouse deprives the living partner of a part of their pension. Payments of dread disease insurance benefits are made in the event of the diagnosis of a serious illness or deterioration of the health state. From the moment the diagnosis is made, the spouse does not pay the health insurance premium.
4. Results
The retirees’ family, economic, and health conditions determine their financial needs. The state of their health of has an important impact on their financial resources. Simultaneously, the elderly often have limited funds to buy an insurance policy against the risk of a dread disease. Therefore, the described contract may be an alternative to obtaining additional pensioner’s income and funds for treatment and palliative care in the case of a dread disease.
A sample of numerical examples using two variants of the equity release contract is presented in this section. In the marriage variant, it is assumed that a married couple has a property valued at W. Together, they decide to sign the marriage reverse annuity and spend the percentage of on withdrawing from both of their dread disease insurance plans. In the individual variant, the spouses also have a property valued at the same sum W. They decide to sign the individual reverse annuity contracts for 0.5W and allocate the percentage of to buy dread disease insurance from their part of the benefit payment. In this case, they have two separate contracts.
The empirical examples are based on actual data. The examples concern the risk of lung cancer mortality and the morbidity of the Lower Silesia population (one of Poland’s voivodeships). The calculations are made separately for male and female groups based on datasets provided by the National Cancer Registry for the Lower Silesia Region (
Wojciechowska and Didikowska 2014) and the Lower Silesia Department of the National Health Fund (the public payer in Poland). The available, unpublished data covers the period between 2006 and 2011. The transition probabilities matrixes are obtained from the life expectancy tables described in the (
Dębicka and Zmyślona 2016). The maximum survival time in a critical condition was 4 years. A critical stage entails diagnosis with distant metastases or an inoperable life-threatening tumour (
Dębicka and Zmyślona 2019).
Let
x denote a woman’s age and
y denote a man’s age. The percentage of a real value of property
and the real value of a property is 100,000 euro. This assumption allows for the easy rescaling of the results obtained in case of different property prices. The discounting factor
v, which is calculated from formula
, is closely connected with the analysed period of the disease and a constant long-term interest rate
i = 0.0579. The interest rate
i was estimated on the basis of actual Polish market data based on the yield to maturity on the fixed interest bonds and Treasury bills from 2008 (
Zmyślona and Marciniuk 2020). The percentage of men who fall ill with lung cancer in 2008, denoted by
R, equals 0.691. We consider couples aged 65, 70, 75, 80, and 85, as well as mixed-age couples. We analyse a case when
which means that 1% of the annuity is intended for paying the premium. It is obvious that the levels of the premium may vary (
Zmyślona and Marciniuk 2020). Annual marriage reverse annuity payments, single benefit payments of illness insurance, which could be paid twice, and premiums in euros are calculated using self-developed programs written in MATLAB.
Table 3 presents all cash flows in both variants.
In both variants, an increase in all the benefits was observed. This growth is positively correlated with the spouses’ age. Women pay lower premiums because the incidence of lung cancer is lower in the female population. Consequently, the critical illness insurance benefit is significantly higher for females than for the male population. It is obvious that in case of another disease the relation may be opposite. The percentage of the morbidity rate under consideration R determines the distribution of the premium. In the marriage variant, the total benefit payment of the equity release is lower than the same benefit in the individual variant. The differences in the benefit payments increase with the rise in the spouses’ age and reach almost 30% for x = y = 85. The same relationship is observable for illness benefits; however, women pay an almost two-fold higher premium in the second option, thus receiving twice as much payment. This shows that women could pay half the premium for this particular disease, which means , to receive the same chronic illness benefit payment. The critical illness insurance payment for men is comparable in both cases. This is due to the fact that the premium is divided according to the morbidity risk in the marriage contract. In both variants, the spouses receive a reverse annuity as a yearly payment, and they can allow themselves to buy critical illness insurance. The annuity income is not significantly reduced because the level of the annual premium is very low. Whereas the health insurance benefit allows for the acquirement of significant financial resources for health care, treatment, and improvement of the quality of life in the case of dread disease.
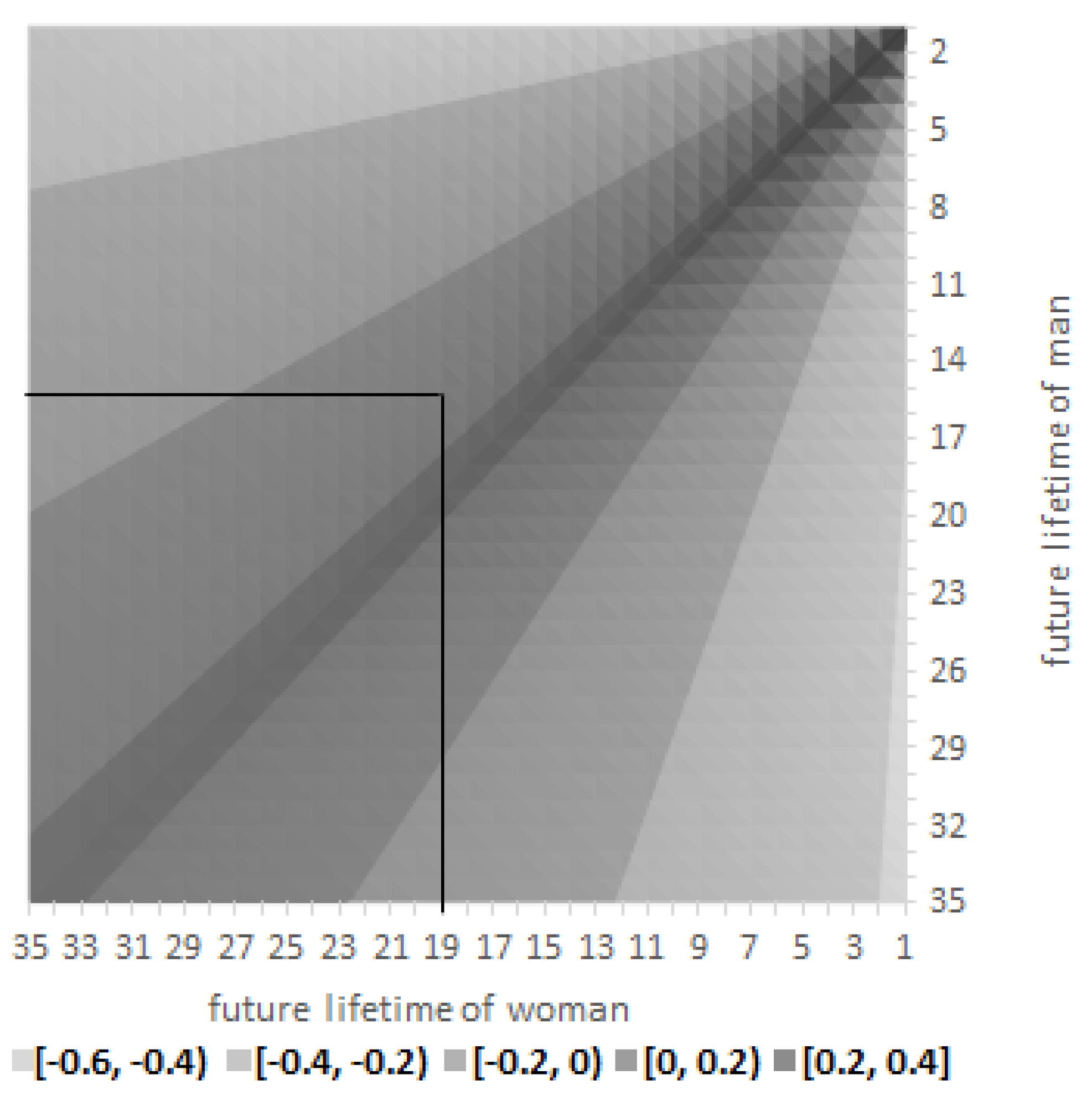
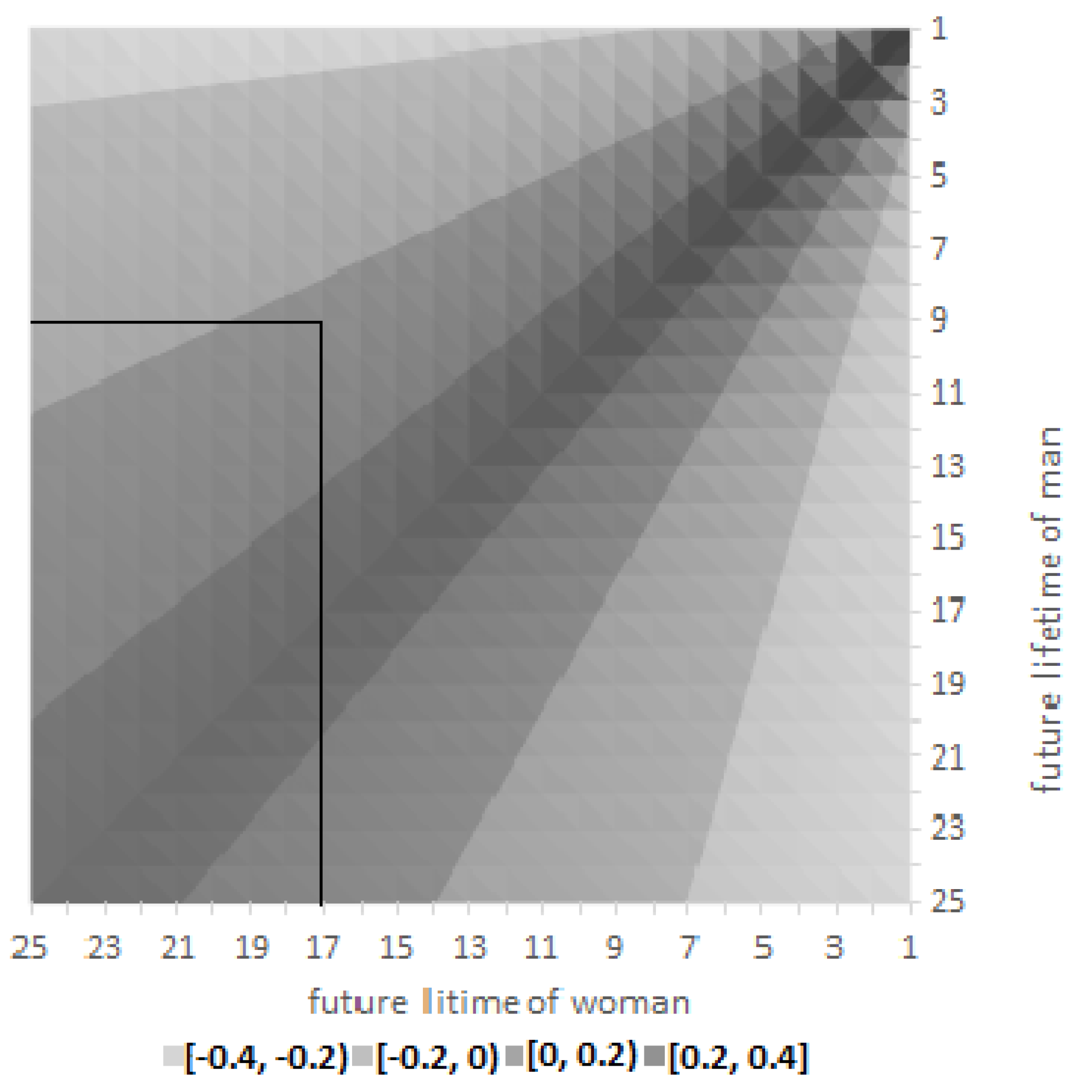
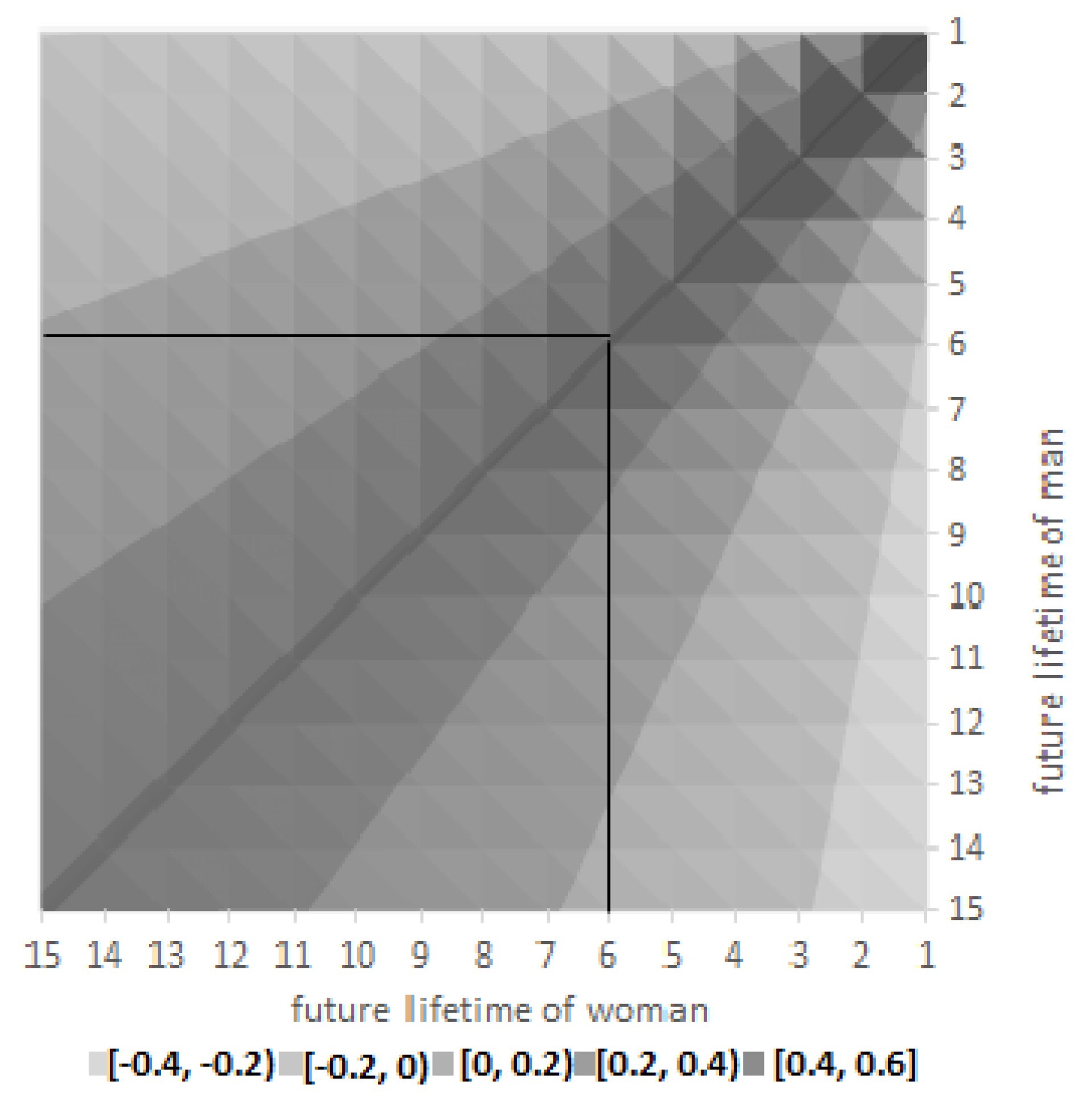
As shown by the above analysis, it can be assumed that the second variant is more favourable for the spouses. Therefore, let us analyse the relative increases in the number of total benefits payments received by spouses at 65, 75, and 85 years depending on their further life expectancy, which is presented in
Figure 2,
Figure 3 and
Figure 4.
The dark colours indicate positive differences, i.e., a higher total benefit in the second variant. Lighter colours represent negative differences, which means a higher total payment in the first option. The graphs also show lines that illustrate the future life expectancy of people at the considered age. The future life expectancy of a 65, 75, and 85-year-old woman is 19.04, 16.54, and 6.05 years, respectively, and for men of the same age it is 14.73, 9.22, and 5.2 years, respectively.
It is visible that the similar age of the spouses’ death determines the total benefit of the equity release contract, increasing up to 40%, and results in a higher dread disease insurance payment in the event of sickness. This means that the second variant of the contract is more favourable for spouses. When one of the spouses dies earlier than the other, and the second spouse lives a long time, the first variant is more beneficial. This can especially be observed for women, who become widows more often than men, and receive a higher marital annuity, even by over 40%. However, when the husband additionally suffers from a serious illness, in the considered case of lung cancer, the health insurance benefit is of a similar amount. The lower left rectangle shows situations when the spouses live longer than their future life expectancy. Then, the probability of receiving a higher benefit increases. When spouses are at 65, the higher payments of the second variant of the contract occur in 40.7% of cases, of which 61.3% concerns a situation when spouses live above their future life expectancy. These numbers increase with the rise in the spouses’ age. The second variant’s higher benefit occurs in 50.9% and 63.1% when spouses are at 75 and 85 years, respectively. Of these situations, 72.3% are placed in the left lower rectangle.
The spouses are not very often at the same age; therefore,
Table 4 and
Table 5 present the amount of the annuity and health insurance benefits in both variants for spouses of various ages. An exemplary five-year age difference between the spouses was assumed.
It is evident that the reverse annuity payments increase alongside the rise in the spouses’ age in both cases. However, the benefits are higher in the second variant. The difference in both benefits increases for younger women and decreases for older women as the men’s age increases. For example, when x = 65 and y = 85, the benefit is over 95% higher, and when men become older, it is only 41.2% higher, but it is still huge. It is not difficult to notice that the payment is lower for a younger wife and an older husband than contrariwise. In the case of men, age has a higher impact on the benefit. This relates to the fact that men live shorter lives than women.
The critical illness insurance payment for women is almost always twice as high in the second variant. Wives do not share the premium for this insurance with husbands. This benefit does not depend on the age of the second spouse in the second case. For a younger husband and an older wife, the dread disease insurance payment is higher in the first contract; thus, it is more favourable for men.
5. Discussion and Conclusions
The article presents two variants of a contract that is a combination of an equity release and critical illness insurance. This new proposition could protect against the effects of longevity. The contractual cash flow and different scenarios were analysed. It cannot be clearly stated which of these contracts is better. Assuming a pessimistic variant, when both spouses fall ill and die quickly, neither option will be beneficial, although they will receive the health insurance benefit payment. If one spouse dies earlier and the other lives healthily longer than the life expectancy, then the marriage variant is more favourable. On the other hand, assuming an optimistic version, when both spouses live together in good health for a long time, particularly above the life expectancy, the individual variant is definitely a better choice. Of course, when concluding a contract, most people do not consider the risk of death. The knowledge of the genetic burden concerning a critical illness can help to more adequately adjust the client’s contract. It was shown that both contracts offer high benefits payments, but for women, who become widows more often, the marriage contract is more beneficial. The calculations show a very significant gender impact on the amount of the benefits. In the considered examples, net premiums and net benefits were presented. All the contracts have additional costs. Combining arrangements into one lowers the costs; hence, the first variant seems to be a cheaper option than buying individual policies.
The introduction of critical illness insurance into the contract has caused two important constraints for the presented model. Firstly, the limited critical illness survival time (a four-year period for lung cancer as described in the studied example) enforced the application of the periodic life tables. Secondly, since an estimation of the relationship between cancer risk for both the spouses seems impossible, we have assumed independence between the spouses’ life expectancies. A justification of the possibility of such an assumption of independence is presented in (
Zmyślona and Marciniuk 2020).
The studied contracts could be used as part of longevity risk management policies as they provide an instrument of incentive for the retirees to use housing resources to improve their living conditions. In case of a dread disease, additional funds are likely to improve the quality of life during the treatment. The two variants of contracts, marriage and individual, could help pensioners to manage their home budget.