Financial Technical Indicator and Algorithmic Trading Strategy Based on Machine Learning and Alternative Data
Abstract
1. Introduction
2. Technical Analysis Indicators and Machine Learning Algorithms
2.1. Technical Analysis Indicators
- 1.
- The Simple Moving Average (SMA), which is the sample mean of the close daily prices over a specific time interval (see Ellis and Parbery 2005, for more details). Therefore, to assess the short-, medium-, and long-term price directions, we include in our analysis SMA for 7, 80, and 160 days, respectively.
- 2.
- 3.
- 4.
- The Donchian Channel (DC) is used to detect strong price movements, looking for either a candlestick breaking the upper ceiling (for bullish movements) or the lower floor (for bearish ones).
- 1.
- The Average Directional Index (ADI) measures the trend’s strength but without telling us whether the movement is up or down. The ADI ranges from 0 to 100, and a value above 25 points out the fact that the trend of the price company is strong enough for being traded.
- 2.
- The Momentum Indicator (MOM) is an anticipatory indicator that measures the rate of the rise or fall of stock prices (see Thomsett 2019, and references therein).
2.2. Extreme Gradient Boosting and Light Gradient Boosted Machine Algorithms
- It computes second-order gradients to understand the direction of gradients themselves.
- It uses , regularizations and tree pruning to prevent overfitting.
- It parallelizes on your own machine for improving the velocity of the computations.
- 1.
- How can we find a good tree structure?
- 2.
- How can we assign prediction scores?
- Assign the data point x to a leaf by q.
- Assign the corresponding score on the -th leaf to the data point.
- 1.
- How do we choose the feature split?
- 2.
- When do we stop the split?
- is the value of the left leaf;
- is the value of the right leaf;
- is the objective of the previous leaf;
- is the parameter which controls the number of leaves (i.e., the complexity of the algorithm).
3. Materials and Methods
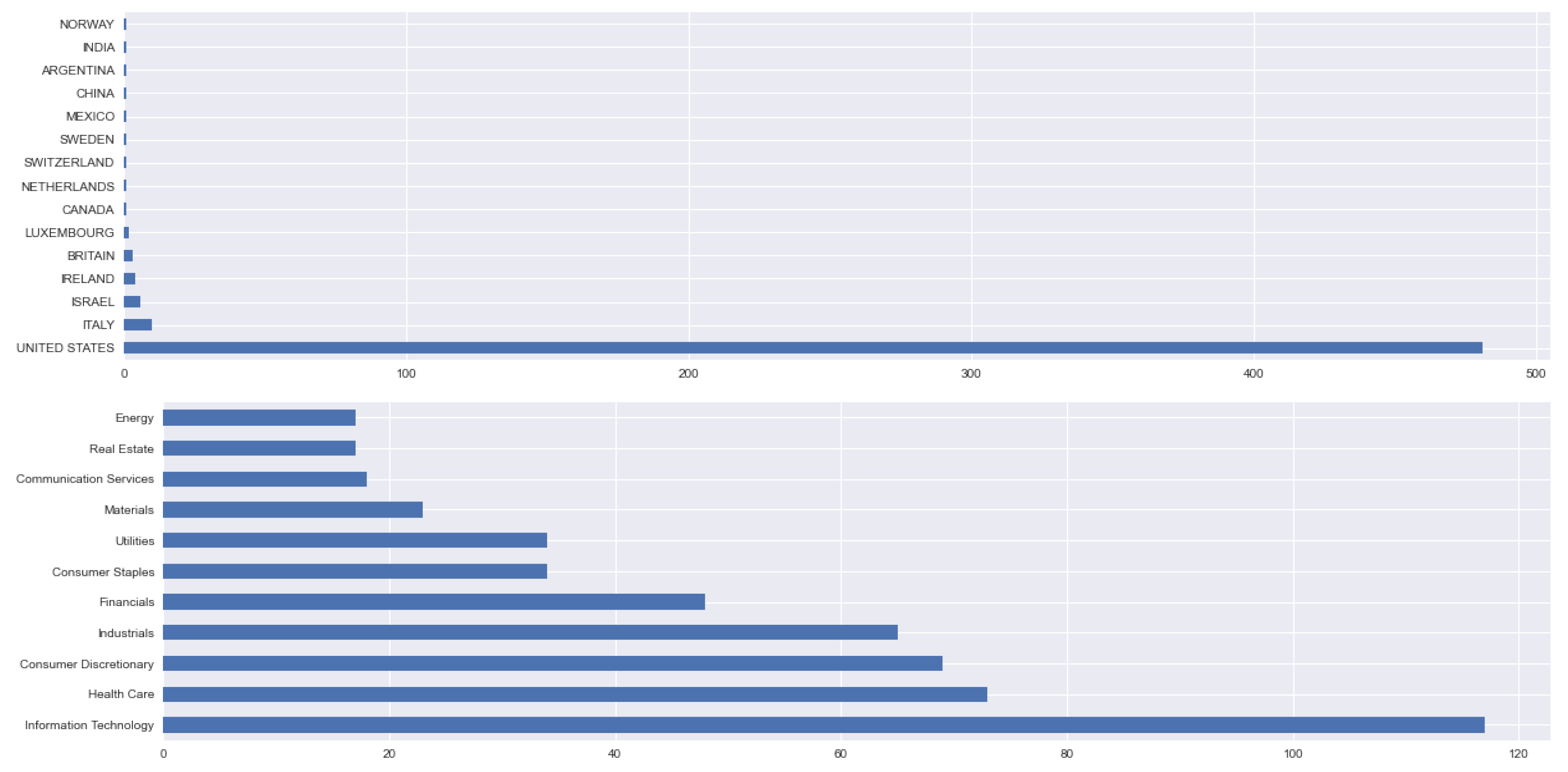
3.1. Dataset
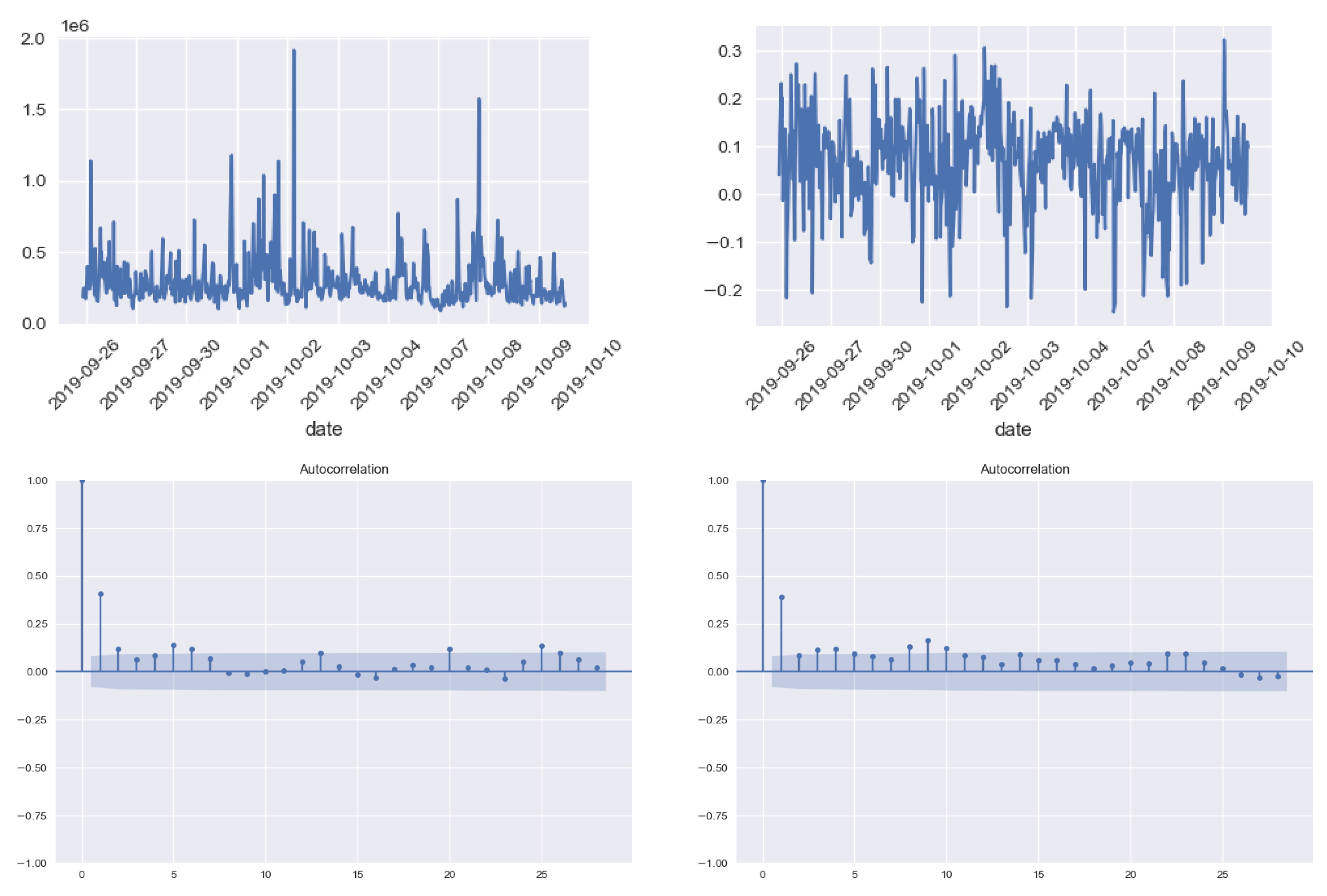
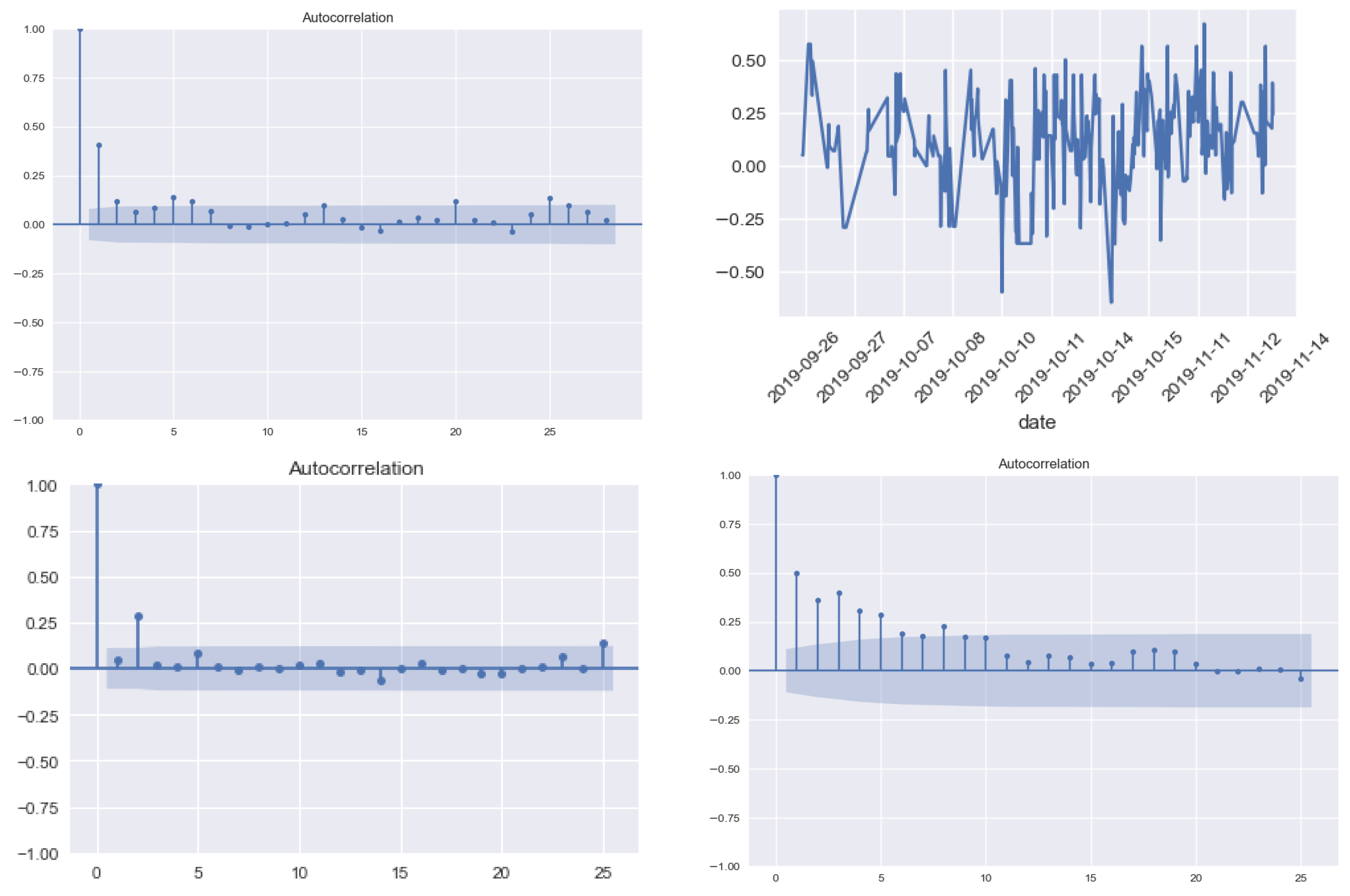
3.2. Popularity and Sentiment Metrics
- Company Digital Popularity measures the level of diffusion of a digital signal on the web. It is obtained by aggregating the diffusion metrics of the news mentioning the company and can take only positive values. The diffusion metric of a news article is quantified by taking into account the number of times the link is shared on social media and also the relevance of the company inside the text. It basically measures how popular a company/stock is among investors.
- Company Sentiment measures the user’s perception concerning the company and can take values in the interval [−1, 1], boundaries included. The sentiment metric of the company on a specific date is represented by a weighted average of the sentiment scores of all news mentioning the company, where the weight is the popularity of the articles.
Popularity and Sentiment Analysis for the Most and the Least Capitalized Companies
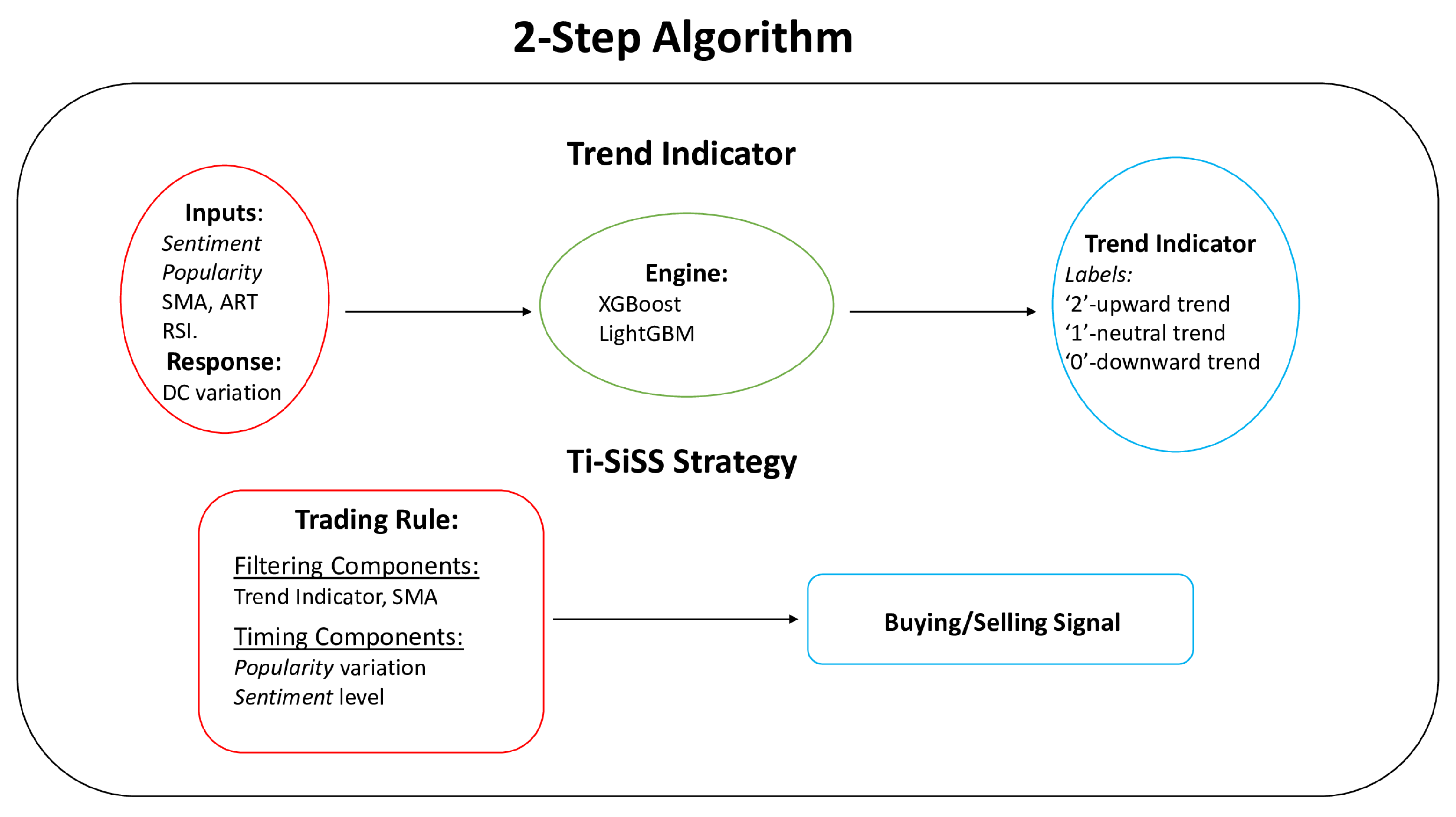
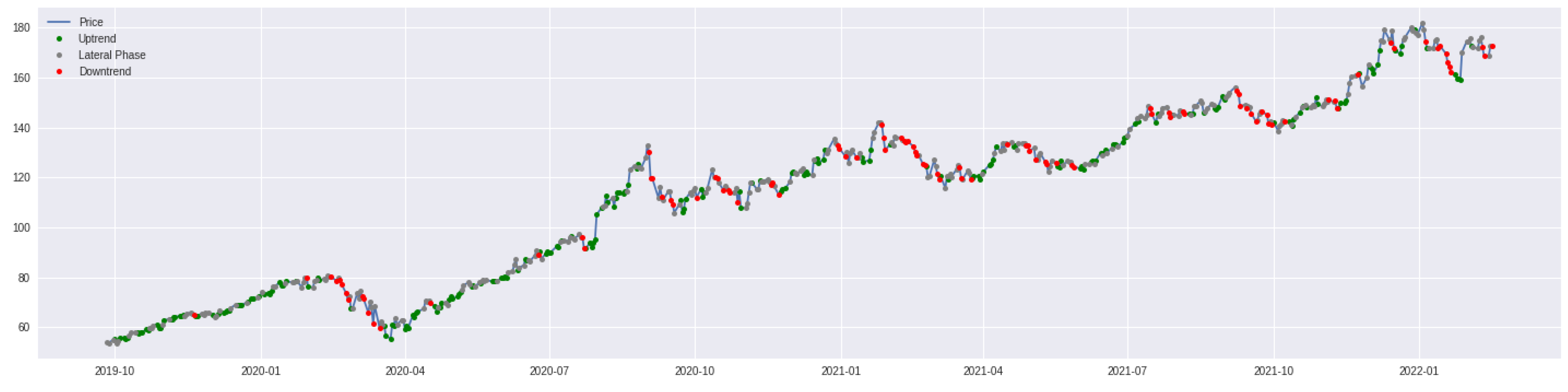
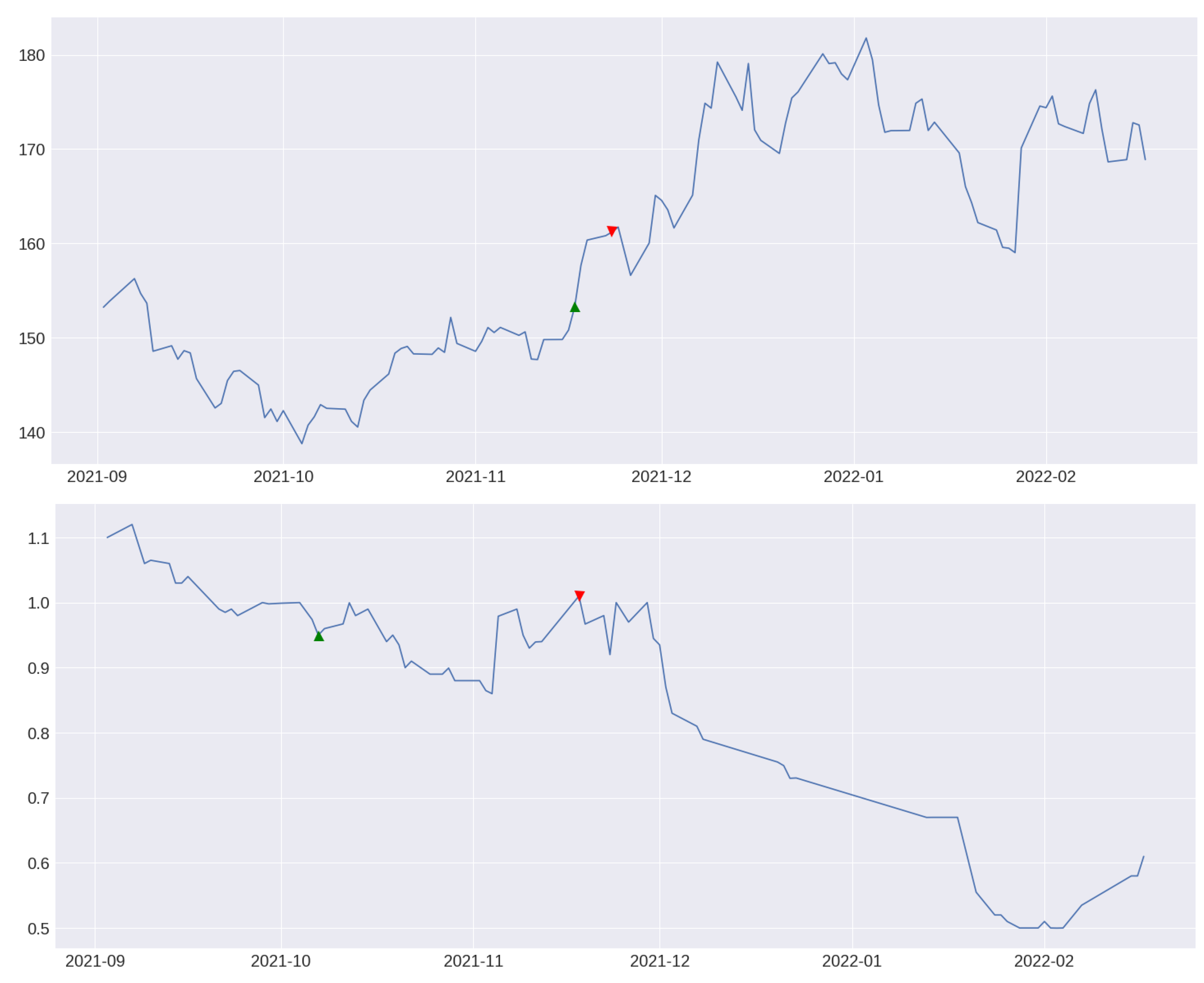
3.3. Trend Indicator
3.3.1. Preprocessing Phase
3.3.2. Trend Indicator Creation through Python
- n_estimators: (50, 100, 200, 300, 500, 1000, 2000).
- learning_rate: (0.05, 0.10, 0.15, 0.2, 0.25, 0.3).
- objective: (multi:softprob, ’multi:softmax).
- : (0, 0.1, 0.2, 0.3, 0.5, 1).
- max_depth: (5, 10, 15, 20, 25, 30, 50, 100).
learning_rate= 0.15,gamma= 0,max_depth= 10,random state= 0)
- n_estimators: (50, 100, 200, 300, 500, 1000, 2000).
- learning_rate: (0.05, 0.10, 0.15, 0.2, 0.25, 0.3).
- max_depth: (5, 10, 15, 20, 50, 100).
- subsample_for_bin: (5.000, 10.000, 100.000, 200.000, 300.000, 500.000).
- min_split_gain: (0, 0.1, 0.3, 0.5, 1).
0.3,max_depth= 15,subsample_for_bin= 200,000,min_split_gain= 0,random
state= 123)
- 1.
- Use the entire training set for train the model.
- 2.
- Use the trained model to make predictions for the entire test set.
- 3.
- Extract and save the first prediction (i.e., the prediction of tomorrow).
- 4.
- Add the first data point of the test set to the training set.
- 5.
- Go back to step 1 and continue until there are no more data points in the test set.
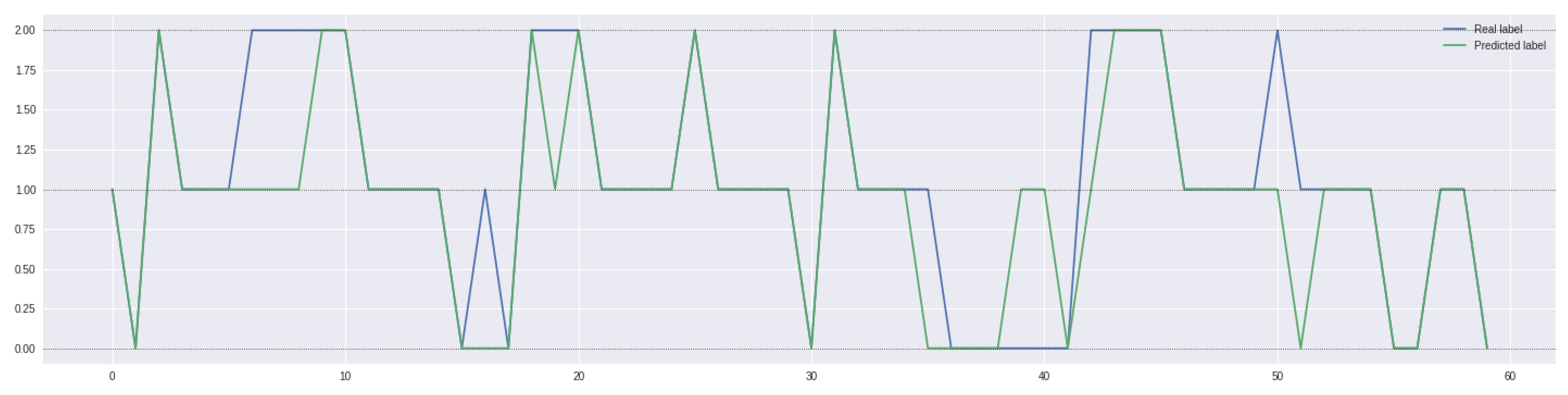
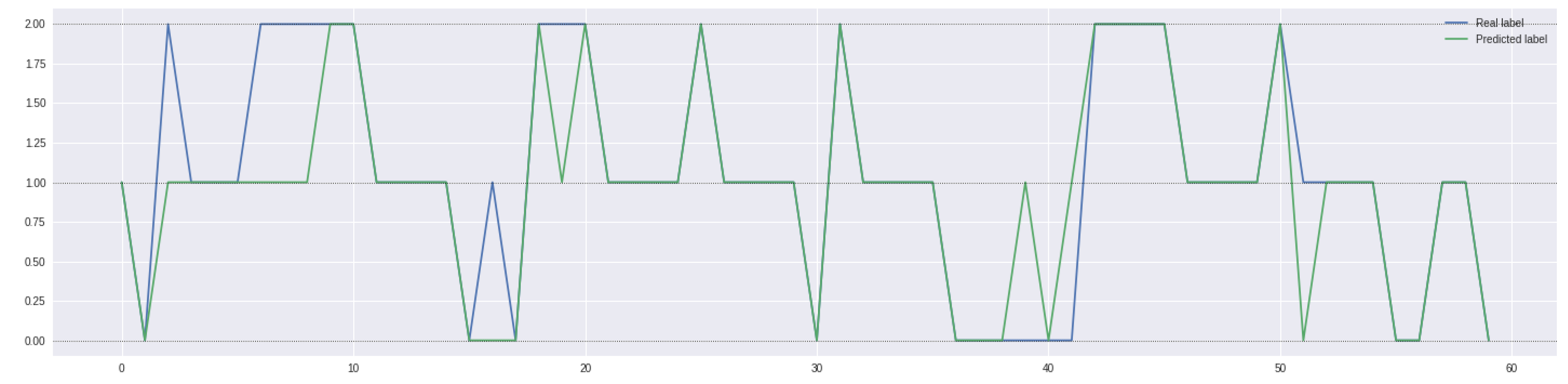
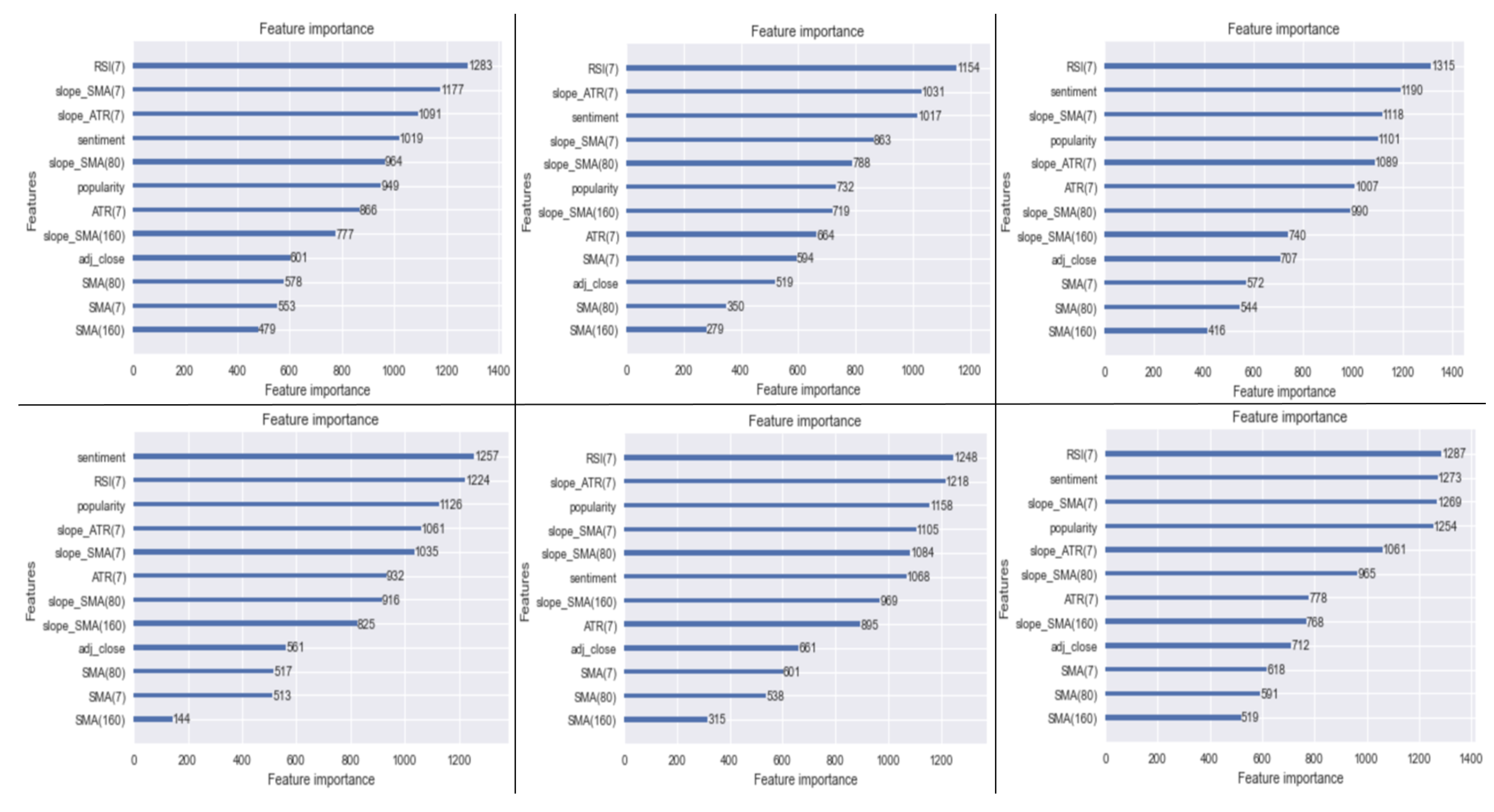
3.3.3. Model Selection and Results
- Model 1: model with all the inputs; closing price, sentiment and its variations, popularity and its variations, SMA(7) and its slope, SMA(80) and its slope, SMA(160) and its slope, ART(7) and its slope, RSI(7) and its slope, Labels.
- Model 2: model with all the inputs except for the point value of the simple moving averages (but maintaining their slopes); closing price, sentiment and its variations, popularity and its variations, SMA(7)’s slope, SMA(80)’s slope, SMA(160)’s slope, ART(7) and its slope, RSI(7) and its slope, Labels.
- Model 3: model with all the inputs except for the point value of the simple moving averages (but maintaining their slopes) and the variations of sentiment and popularity; closing price, sentiment, popularity, SMA(7)’s slope, SMA(80)’s slope, SMA(160)’s slope, ART(7) and its slope, RSI(7) and its slope, Labels.
- Model 4: model with all the inputs except for the variations of sentiment/popularity; closing price, sentiment, popularity, SMA(7) and its slope, SMA(80) and its slope, SMA(160) and its slope, ART(7) and its slope, RSI(7) and its slope, Labels.
- Model 5: model with all the inputs except for any value related to the metrics; closing price, SMA(7) and its slope, SMA(80) and its slope, SMA(160) and its slope, ART(7) and its slope, RSI(7) and its slope, Labels.
- 1.
- One, representing the case in which the model predicts an ongoing price trend (either positive or negative) and the actual value is a sideways phase (and vice versa);
- 2.
- Another, in which the model predicts an ongoing price trend (either positive or negative) and the actual value is the exact opposite situation.
- Created through the machine learning model LightGBM;
- Embedded within a rolling algorithm;
- Capable of reaching an average accuracy of 53.64% (much greater than the threshold of 33%);
- Alternative-data strongly dependent.
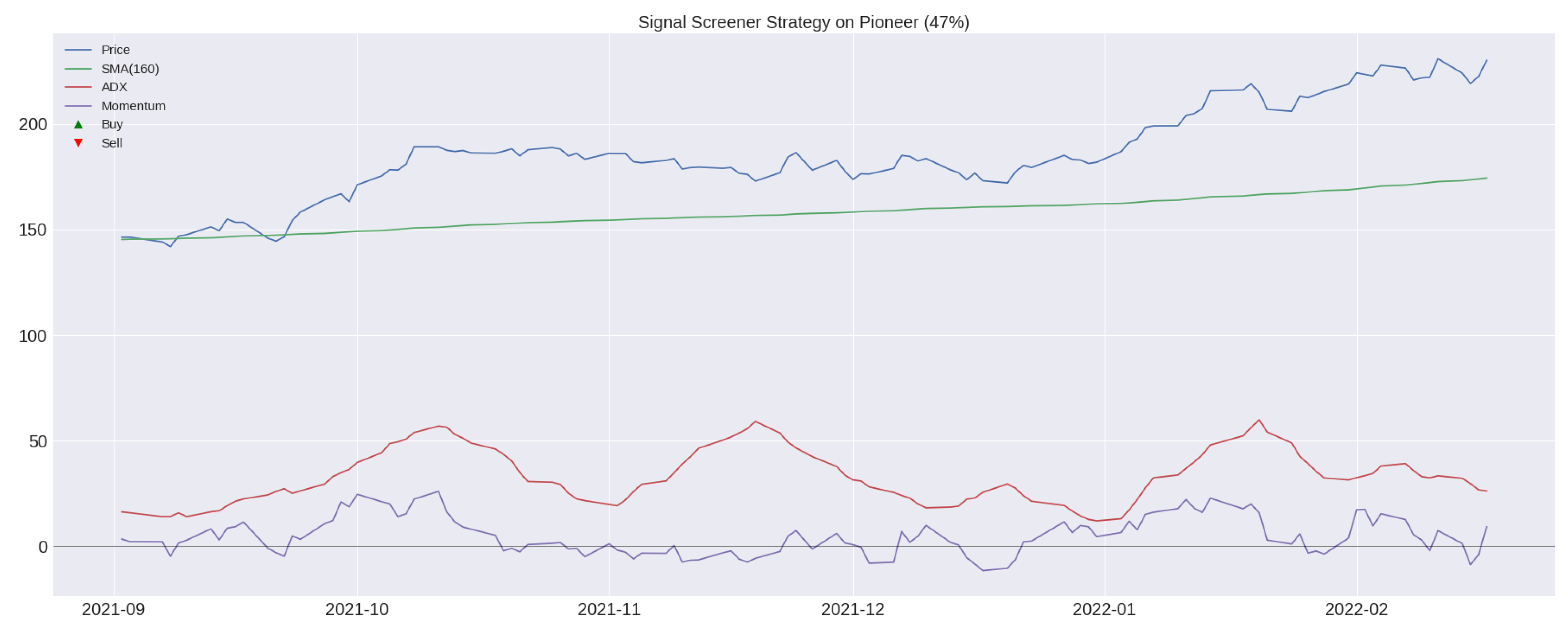
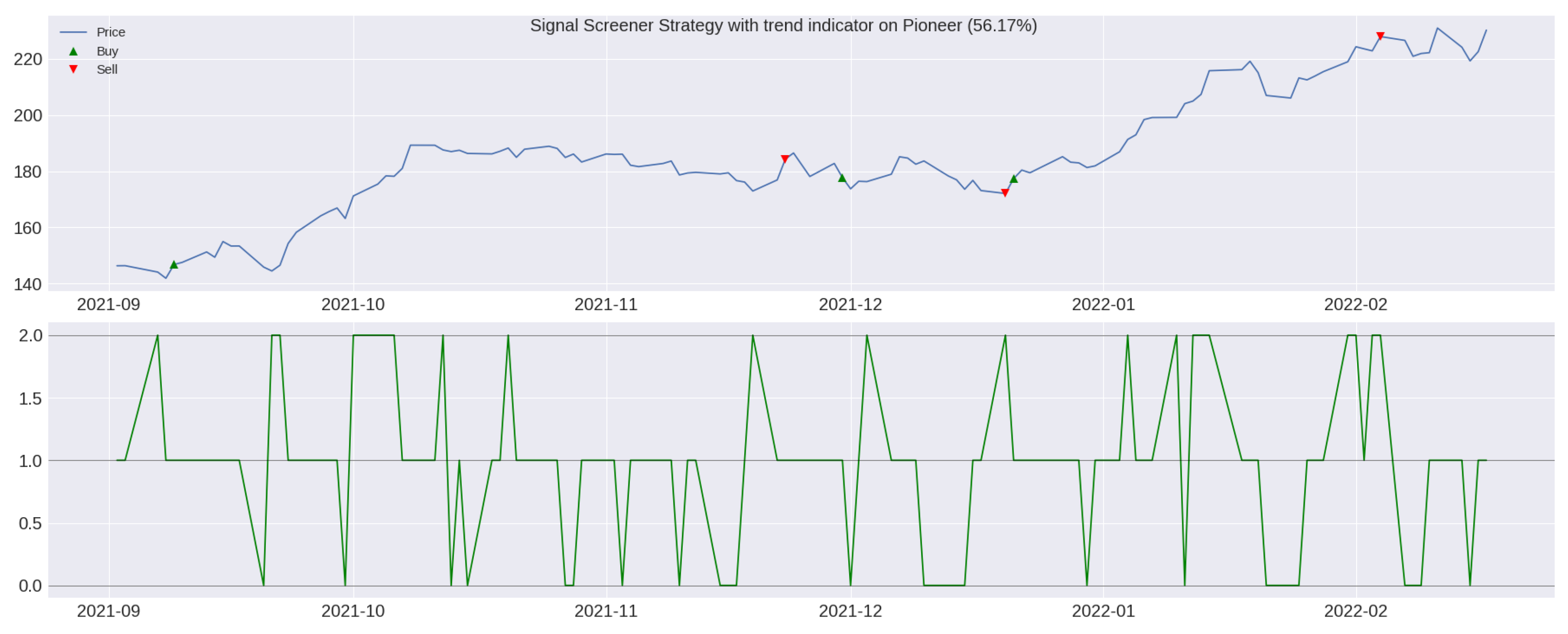
3.4. Algorithmic Trading Strategy: TI-SiSS
Gross and Net Profit Analysis for a TI-SiSS Strategy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm A1 Trend indicator for a single security. |
| Input: adjusted close price, adjusted high price, adjusted low price, sentiment, popularity |
| Output: Dataframe with the security names and the corresponding returns |
Required Packages: pandas, pandas_ta, lightgbm
|
| Algorithm A2 Trend indicator for multiple securities into a MultiIndex DataFrame. | |
| Input: adjusted close price, adjusted high price, adjusted low price, sentiment, popularity Output: Dataframe with the security names and the corresponding returns Required Packages: pandas, pandas_ta, lightgbm Other requirements: the identifier (here called FIGI) of each security must be the first index, while the time series of dates must be the second index | |
| import pandas as pd | |
| 2: | import pandas_ta as ta |
| from lightgbm import LGBMClassifier | |
| 4: | |
| MANDATORY_COLUMNS = [’adj_close’, ’adj_high’, ’adj_low’] | |
| 6: | functionlabeling(x): |
| out = None | |
| 8: | if ((x is not None) and (x > 0)) then: |
| out = 2 | |
| 10: | else if ((x is not None) and (x < 0)) then: |
| out = 0 | |
| 12: | else if ((x is not None) and (x == 0)) then: |
| out = 1 | |
| 14: | end if |
| return out | |
| 16: | end function |
| 18: | function check_columns_name(dataset:pd.DataFrame) → bool: |
| list_cols = dataset.columns | |
| 20: | return set(SISS_MANDATORY_COLUMNS).issubset(list_cols) |
| end function | |
| 22: | function Trend_Indicator_for_MultIndex(dataset:pd.DataFrame, Donchian_periods:int, test_percentage:float): |
| dataset = dataset.copy() | |
| 24: | check = check_columns_name(dataset=dataset) |
| if not check then: | |
| 26: | raise Exception(f"Dataset is not correct! It must contain the columns called as follows: MANDATORY_COLUMNS ") |
| else: | |
| 28: | for figi in dataset.index.get_level_values(0).unique() do: |
| donchian = ta.donchian(dataset.loc[(figi, slice(None)), ’adj_low’], dataset.loc[(figi, slice(None)), ’adj_high’], lower_length=Donchian_periods, upper_length= Donchian_periods).dropna() | |
| 30: | donchian_up = donchian[f’DCU_Donchian_periods_Donchian_periods’] |
| donchian_pct = donchian_up.pct_change() | |
| 32: | donchian_right_size = donchian_up.tolist() |
| [donchian_right_size.append(None) for _ in range(Donchian_periods-1)] | |
| 34: | dataset.loc[(figi, slice(None)), ’Donchian channel’] = donchian_right_size |
| donchian_pct_right_size = donchian_pct.tolist() | |
| 36: | [donchian_pct_right_size.append(None) for _ in range(Donchian_periods-1)] |
| dataset.loc[(figi, slice(None)), ’Donchian change’] = donchian_pct_right_size | |
| 38: | dataset.loc[(figi, slice(None)), "Labels"] = dataset.loc[(figi, slice(None)), "Donchian change"].apply(labeling).dropna() |
| end for | |
| 40: | dataset = dataset.dropna() |
| del dataset["adj_high"] | |
| 42: | del dataset["adj_low"] |
| del dataset["Donchian channel"] | |
| 44: | del dataset["Donchian change"] |
| LGBM_model = LGBMClassifier(objective=’softmax’, n_estimators=300, learning_rate=0.3, max_depth = 15, subsample_for_bin= 200,000, min_split_gain= 0, random_state=123) | |
| 46: | for num, figii in enumerate(dataset.index.get_level_values(0).unique()) do: |
| test_size = int(len(dataset.loc[(figii,slice(None)), ’adj_close’])*0.2) | |
| 48: | Y = dataset.loc[(figii,slice(None)), ’Labels’].shift(-1) |
| X = dataset.loc[(figii,slice(None))] | |
| 50: | test_predictions = [] |
| for i in range(test_size): do: | |
| 52: | x_train = X[:(-test_size+i)] |
| y_train = Y[:(-test_size+i)] | |
| 54: | x_test = X[(-test_size+i):] |
| LGBM_model.fit(x_train, y_train) | |
| 56: | pred_test = LGBM_model.predict(x_test) |
| test_predictions.append(pred_test[0]) | |
| 58: | end for |
| array_of_predictions = [] | |
| 60: | [array_of_predictions.append(None) for _ in range(len(X[:(-test_size)]))] |
| array_of_predictions.extend(test_predictions) | |
| 62: | dataset.loc[(figii,slice(None)), ’Trend_Predictions’] = array_of_predictions |
| end for | |
| 64: | end if |
| return dataset, LGBM_model | |
| 66: | end function |
| Algorithm A3 TI-SiSS. | |
| Input: adjusted close price, sentiment, popularity, company names and Trend Indicator’s predictions Output: Dataframe with the security names and the corresponding returns Required Packages: pandas, numpy, talib, linregress | |
| import pandas as pd import numpy as np | |
| 3: | import talib |
| from scipy.stats import linregress | |
| 6: | TI_SISS_MANDATORY_COLUMNS = [’adj_close’, ’popularity’, ’sentiment’, ’company_name’, ’Trend_Predictions’] |
| functionti_siss_check_columns_name(dataset:pd.DataFrame) → bool: | |
| list_cols = dataset.columns | |
| 9: | return set(SISS_MANDATORY_COLUMNS).issubset(list_cols) |
| end function | |
| 12: | function get_slope(array): |
| y = np.array(array) | |
| x = np.arange(len(y)) | |
| 15: | slope, intercept, r_value, p_value, std_err = linregress(x,y) |
| return slope | |
| end function | |
| 18: | |
| functionTI_SiSS(stock: pd.DataFrame, backrollingN: float) → pd.DataFrame: | |
| check = ti_siss_check_columns_name(dataset=stock) | |
| 21: | if not check then: |
| raise Exception(f"Dataset is not correct! It must contain the columns called as follows: TI_SISS_MANDATORY_COLUMNS ") | |
| else: | |
| 24: | stock[’popularity_variation’] = stock[’popularity’].pct_change() |
| stock[’sentiment_variation’] = stock[’sentiment’].pct_change() | |
| stock[’popularity_variation’] = stock[’popularity_variation’].replace(np.inf, 10,000,0000) | |
| 27: | stock[’sentiment_variation’] = stock[’sentiment_variation’].replace(np.inf, 100,000,000) |
| stock[’pop_SMA(7)’] = talib.SMA(stock[’popularity’], backrollingN) | |
| stock[’SMA(160)’] = talib.SMA(stock[’adj_close’], 160) | |
| 30: | stock[’slope_SMA(160)’] = stock[’SMA(160)’].rolling(window=backrollingN).apply(get_slope, raw=True) |
| stock = stock.dropna() | |
| stock[’entry_long’] = 0 | |
| 33: | stock[’close_long’] = 0 |
| stock[’positions’] = None | |
| 36: | for i, date in enumerate(stock.index) do: |
| pop_day_before = stock[’popularity’][i-1] | |
| if ((stock[’slope_SMA(160)’][i]>0) and (stock[’Trend_Predictions’][i] is not None) and (stock[’Trend_Predictions’][i]>=1)) then: | |
| 39: | dpv = stock[’popularity’][i] |
| sma7 = stock[’pop_SMA(7)’][i] | |
| pop_var = ((dpv - pop_day_before)/abs(pop_day_before))*100 | |
| 42: | sent = stock[’sentiment’][i] |
| if ((dpv>sma7) and (pop_var>100) and (sent>0.05)) then: | |
| stock[’entry_long’][i] = 1 | |
| 45: | else if (dpv>sma7) and (pop_var>100) and (sent<(-0.05)) then: |
| stock[’close_long’][i] = 1 | |
| end if | |
| 48: | end if |
| end for | |
| end if | |
| 51: | log_returns = [] |
| close_index = -1 | |
| for g, val in enumerate(stock.index) do: | |
| 54: | if ((g > 14) and (stock[’entry_long’][g] == 1) and (g > close_index)) then: |
| open_long_price = stock[’adj_close’][g] | |
| flag_closed = False | |
| 57: | for j, elem in enumerate(stock.index[(g+1):]) do: |
| if (stock[’close_long’][g+1+j] == 1) then: | |
| close_index = g+1+j | |
| 60: | close_long_price = stock[’adj_close’][close_index] |
| flag_closing = True | |
| break | |
| 63: | end if |
| end for | |
| if flag_closing: then: | |
| 66: | stock[’positions’][g] = 1 |
| stock[’positions’][g+1+j] = 0 | |
| single_trade_log_ret = np.log(close_long_price/open_long_price) | |
| 69: | log_returns.append(single_trade_log_ret) |
| end if | |
| end if | |
| 72: | end for |
| sum_all_log_ret = sum(log_returns) | |
| performance = (np.exp(sum_all_log_ret) - 1)*100 | |
| 75: | return performance |
| end function | |
| Algorithm A4 SiSS. | |
| Input: adjusted close price, adjusted high price, adjusted low price, sentiment, popularity and company names Output: Dataframe with the security names and the corresponding returns Required Packages: pandas, numpy, talib, linregress | |
| import pandas as pd | |
| import numpy as np | |
| import talib | |
| 4: | from scipy.stats import linregress |
| SISS_MANDATORY_COLUMNS = [’adj_close’, ’adj_high’, ’adj_low’, ’popularity’, ’sentiment’] | |
| 8: | |
| function siss_check_columns_name(dataset:pd.DataFrame) → bool: | |
| list_cols = dataset.columns | |
| return set(SISS_MANDATORY_COLUMNS).issubset(list_cols) | |
| 12: | end function |
| functionget_slope(array): | |
| y = np.array(array) | |
| 16: | x = np.arange(len(y)) |
| slope, intercept, r_value, p_value, std_err = linregress(x,y) | |
| return slope | |
| end function | |
| 20: | |
| functionSiSS(stock:pd.Dataframe, backrollingN:float) → pd.DataFrame: | |
| check = siss_check_columns_name(dataset=stock) | |
| if not check then: | |
| 24: | raise Exception(f"Dataset is not correct! It must contain the columns called as follows: SISS_MANDATORY_COLUMNS ") |
| else: | |
| stock[’popularity_variation’] = stock[’popularity’].pct_change() | |
| stock[’sentiment_variation’] = stock[’sentiment’].pct_change() | |
| 28: | stock[’popularity_variation’] = stock[’popularity_variation’].replace(np.inf, 100,000,000) |
| stock[’sentiment_variation’] = stock[’sentiment_variation’].replace(np.inf, 100,000,000) | |
| stock[’pop_SMA(7)’] = talib.SMA(stock[’popularity’], backrollingN) | |
| stock[’ADX’] = talib.ADX(stock[’adj_high’], stock[’adj_low’], stock[’adj_close’], timeperiod= backrollingN) | |
| 32: | stock[’slope_ADX’] = stock[’ADX’].rolling(window=backrollingN).apply(get_slope, raw=True) |
| stock[’Momentum’] = talib.MOM(stock[’adj_close’], timeperiod=backrollingN) | |
| stock[’SMA(160)’] = talib.SMA(stock[’adj_close’], 160) | |
| stock[’slope_SMA(160)’] = stock[’SMA(160)’].rolling(window=backrollingN).apply(get_slope, raw=True) | |
| 36: | stock = stock.dropna() |
| stock[’entry_long’] = 0 | |
| stock[’close_long’] = 0 | |
| stock[’positions’] = None | |
| 40: | for i, date in enumerate(stock.index) do: |
| pop_previous_day = stock[’popularity’][i-1] | |
| sum_momentum = stock[’Momentum’][i-7:i].sum() | |
| if ((stock[’slope_SMA(160)’][i]>0) and (stock[’slope_ADX’][i]>0) and (sum_momentum > 3)) then: | |
| 44: | dpv = stock[’popularity’][i] |
| sma7 = stock[’pop_SMA(7)’][i] | |
| pop_var = ((dpv - pop_previous_day)/abs(pop_previous_day))*100 | |
| sent = stock[’sentiment’][i] | |
| 48: | if ((dpv>sma7) and (pop_var>100) and (sent>0.05)) then: |
| stock[’entry_long’][i] = 1 | |
| else if ((dpv>sma7) and (pop_var>100) and (sent<(-0.05))) then: | |
| stock[’close_long’][i] = 1 | |
| 52: | end if |
| end if | |
| end for | |
| end if | |
| 56: | log_returns = [] |
| close_long_index = -1 | |
| for g, val in enumerate(stock.index) do: | |
| if ((g > 14) and (stock[’entry_long’][g] == 1) and (g > close_long_index)) then: | |
| 60: | open_long_price = stock[’adj_close’][g] |
| flag_close = False | |
| for j, elem in enumerate(stock.index[(g+1):]) do: | |
| if (stock[’close_long’][g+1+j] == 1) then: | |
| 64: | close_long_index = g+1+j |
| close_long_price = stock[’adj_close’][close_long_index] | |
| flag_close = True | |
| break | |
| 68: | end if |
| end for | |
| if flag_close then: | |
| stock[’positions’][g] = 1 | |
| 72: | stock[’positions’][g+1+j] = 0 |
| single_trade_log_ret = np.log(close_long_price/open_long_price) | |
| log_returns.append(single_trade_log_ret) | |
| end if | |
| 76: | end if |
| end for | |
| sum_all_log_ret = sum(log_returns) | |
| performance = (np.exp(sum_all_log_ret) - 1)*100 | |
| 80: | return performance |
| end function | |
| 1 | Italian firm specialized in the usage of AI in financial world. Website: accessed on 1 January 2022 https://finscience.com/it/. |
| 2 | Sentiment and Popularity were first published on 25 September 2019 and, for this reason, we are not able to take into account previous time-frames. |
| 3 | Some assets were included in the dataset after 25 September 2019. |
References
- Achelis, Steven B. 2001. Technical Analysis from A to Z, 1st ed. New York: McGraw Hill. [Google Scholar]
- Allen, Franklin, and Risto Karjalainen. 1999. Using genetic algorithms to find technical trading rules. Journal of Financial Economics 51: 245–71. [Google Scholar] [CrossRef]
- Ballings, Michel, Dirk Van den Poel, Nathalie Hespeels, and Ruben Gryp. 2015. Evaluating multiple classifiers for stock price direction prediction. Expert Systems with Applications 42: 7046–56. [Google Scholar] [CrossRef]
- Barucci, Emilio, Michele Bonollo, Federico Poli, and Edit Rroji. 2021. A machine learning algorithm for stock picking built on information based outliers. Expert Systems with Applications 184: 115497. [Google Scholar] [CrossRef]
- Bollen, Johan, Huina Mao, and Xiaojun Zeng. 2011. Twitter mood predicts the stock market. Journal of Computational Science 2: 1–8. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. Xgboost: A scalable tree boosting system. Paper presented at 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17. [Google Scholar]
- Chong, Eunsuk, Chulwoo Han, and Frank C. Park. 2017. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Systems with Applications 83: 187–205. [Google Scholar] [CrossRef]
- Duz Tan, Selin, and Oktay Tas. 2021. Social media sentiment in international stock returns and trading activity. Journal of Behavioral Finance 22: 221–34. [Google Scholar] [CrossRef]
- Ellis, Craig A., and Simon A. Parbery. 2005. Is smarter better? A comparison of adaptive, and simple moving average trading strategies. Research in International Business and Finance 19: 399–411. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Jaquart, Patrick, David Dann, and Carl Martin. 2020. Machine learning for bitcoin pricing—A structured literature review. Paper presented at WI 2020 Proceedings, Potsdam, Germany, March 8–11; Berlin: GITO Verlag, pp. 174–88. [Google Scholar]
- Ke, Guolin, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie-Yan Liu. 2017. Lightgbm: A highly efficient gradient boosting decision tree. Paper presented at 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, December 4–9. [Google Scholar]
- Lee, Ming-Chi. 2009. Using support vector machine with a hybrid feature selection method to the stock trend prediction. Expert Systems with Applications 36: 10896–904. [Google Scholar] [CrossRef]
- Levy, Robert A. 1967. Relative strength as a criterion for investment selection. The Journal of Finance 22: 595–610. [Google Scholar] [CrossRef]
- LightGBm. 2022. Python Package. Available online: https://lightgbm.readthedocs.io/en/v3.3.2/ (accessed on 10 October 2022).
- Thomsett, Michael C. 2019. Momentum Oscillators: Duration and Speed of a Trend. In Practical Trend Analysis: Applying Signals and Indicators to Improve Trade Timing, 2nd ed. Berlin: De Gruyter. [Google Scholar]
- XGBoost. 2022. Python Package. Available online: https://xgboost.readthedocs.io/en/stable/python/index.html (accessed on 3 November 2022).
- Yang, Steve Y., Sheung Yin Kevin Mo, Anqi Liu, and Andrei A. Kirilenko. 2017. Genetic programming optimization for a sentiment feedback strength based trading strategy. Neurocomputing 264: 29–41. [Google Scholar] [CrossRef]
| Stock | Mrk. Cap. (bn) | Max/Min Pop. | Max/Min Sent. | Mean | S.D. | Skew. | Kurt. | MDD |
|---|---|---|---|---|---|---|---|---|
| Apple | 2260 | / | 0.32/−0.25 | 0.022 | −0.246 | 6.000 | −70.5% | |
| Microsoft | 1710 | / | 0.30/−0.21 | 0.021 | −0.465 | 10.662 | −61.6% | |
| UnitedHealth | 467 | /8.650 | 0.64/−0.64 | 0.021 | −0.653 | 15.298 | −62.4 % | |
| J&J | 422 | /196 | 0.52/−0.49 | 0.014 | −0.017 | 8.343 | −40.0% | |
| Exxon | 412 | /432 | 0.49/−0.59 | 0.025 | −0.098 | 4.286 | −66.2% | |
| Tejon Ranch | 3.844 | 9304/0 | 0.72/−0.69 | 0.027 | 0.529 | 6.924 | −37.1% | |
| Entravision | 3.482 | 1808/0 | 0.85/−0.66 | 0.044 | 2.974 | −87.6% | ||
| Community Health | 2.802 | /0 | 0.76/−0.66 | 0.057 | 0.469 | 4.039 | −85.5% | |
| Provident Financial | 1.035 | /0 | 0.96/−0.66 | 0.029 | −0.364 | 10.233 | −48.2% | |
| Jones Soda | 0.286 | 3244/0 | 0.67/−0.64 | 0.070 | 0.584 | 6.887 | −90.9% |
| Stat. | Apple | Jones | ||
|---|---|---|---|---|
| Pop. | Sent. | Pop. | Sent. | |
| Mean | 0.072 | 96.844 | 0.010 | |
| St.Dev. | 0.095 | 267.536 | 0.242 | |
| Skew. | 3.437 | −0.579 | 6.765 | −0.447 |
| Kurt. | 20.309 | 0.852 | 66.113 | 0.002 |
| XGBoost | LightGBM | |
|---|---|---|
| Tot. Stocks | 527 | 527 |
| N. Stocks < 33% | 8 | 10 |
| N. Stocks > 33% | 519 | 517 |
| Average accuracy | 53.95% | 53.64% |
| Running time | 6:15 h | 3:30 h |
| SiSS | TI-SiSS |
|---|---|
| Slope SMA(160) > 0 | Slope SMA(160) > 0 |
| Slope ADX Line > 0 | Trend Indicator ≥ 1 |
| Momentum > 0 |
| Buy | Sell |
|---|---|
| SiSS | TI-SiSS | |
|---|---|---|
| Tot. stocks | 527 | 527 |
| N. stocks with trades | 134 | 309 |
| N. stocks with positive returns | 104 | 207 |
| N. stocks with negative returns | 30 | 102 |
| Variance of returns | 55.3% | 84.02% |
| Average return | 1.98% | 3.12% |
| Operations | Apple | Microsoft | United Health | J&J | Exxon | |
| 1st | Buying | 100 | 100 | 100 | 100 | 100 |
| 2nd | Selling | 105.160 | 110.076 | 99.799 | 104.850 | 104.717 |
| 3rd | Buying | - | - | - | 104.850 | - |
| 4th | Selling | - | - | - | 106.886 | - |
| MDD | 0 | −7.500% | −0.201% | −3.791% | −0.488% | |
| Tejon | Entravision | Community Health | Provident | Jones | ||
| 1st | Buying | 100 | 100 | 100 | 100 | 100 |
| 2nd | Selling | 99.406 | 109.144 | 85.868 | 97.844 | 106.316 |
| 3rd | Buying | 99.406 | 109.144 | 85.868 | 97.844 | - |
| 4th | Selling | 99.138 | 104.626 | 116.883 | 99.668 | - |
| MDD | −9.302% | −25.926% | −25% | −5.392% | −13.333% |
| Operations | Apple | Microsoft | United Health | J&J | Exxon | |
| 1st | Buying | 100 | 100 | 100 | 100 | 100 |
| 2nd | Selling | 104.108 | 108.975 | 98.802 | 103.801 | 103.670 |
| 3rd | Buying | - | - | - | 102.763 | - |
| 4th | Selling | - | - | - | 103.708 | - |
| Tejon | Entravision | Community Health | Provident | Jones | ||
| 1st | Buying | 100 | 100 | 100 | 100 | 100 |
| 2nd | Selling | 98.412 | 108.053 | 85.009 | 96.865 | 105.253 |
| 3rd | Buying | 97.428 | 106.972 | 84.159 | 95.897 | - |
| 4th | Selling | 96.193 | 101.518 | 114.411 | 96.798 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frattini, A.; Bianchini, I.; Garzonio, A.; Mercuri, L. Financial Technical Indicator and Algorithmic Trading Strategy Based on Machine Learning and Alternative Data. Risks 2022, 10, 225. https://doi.org/10.3390/risks10120225
Frattini A, Bianchini I, Garzonio A, Mercuri L. Financial Technical Indicator and Algorithmic Trading Strategy Based on Machine Learning and Alternative Data. Risks. 2022; 10(12):225. https://doi.org/10.3390/risks10120225
Chicago/Turabian StyleFrattini, Andrea, Ilaria Bianchini, Alessio Garzonio, and Lorenzo Mercuri. 2022. "Financial Technical Indicator and Algorithmic Trading Strategy Based on Machine Learning and Alternative Data" Risks 10, no. 12: 225. https://doi.org/10.3390/risks10120225
APA StyleFrattini, A., Bianchini, I., Garzonio, A., & Mercuri, L. (2022). Financial Technical Indicator and Algorithmic Trading Strategy Based on Machine Learning and Alternative Data. Risks, 10(12), 225. https://doi.org/10.3390/risks10120225






