A Generalized Linear Mixed Model for Data Breaches and Its Application in Cyber Insurance
Abstract
1. Introduction
2. Chronology of Data Breaches from PRC Dataset
2.1. Data Description
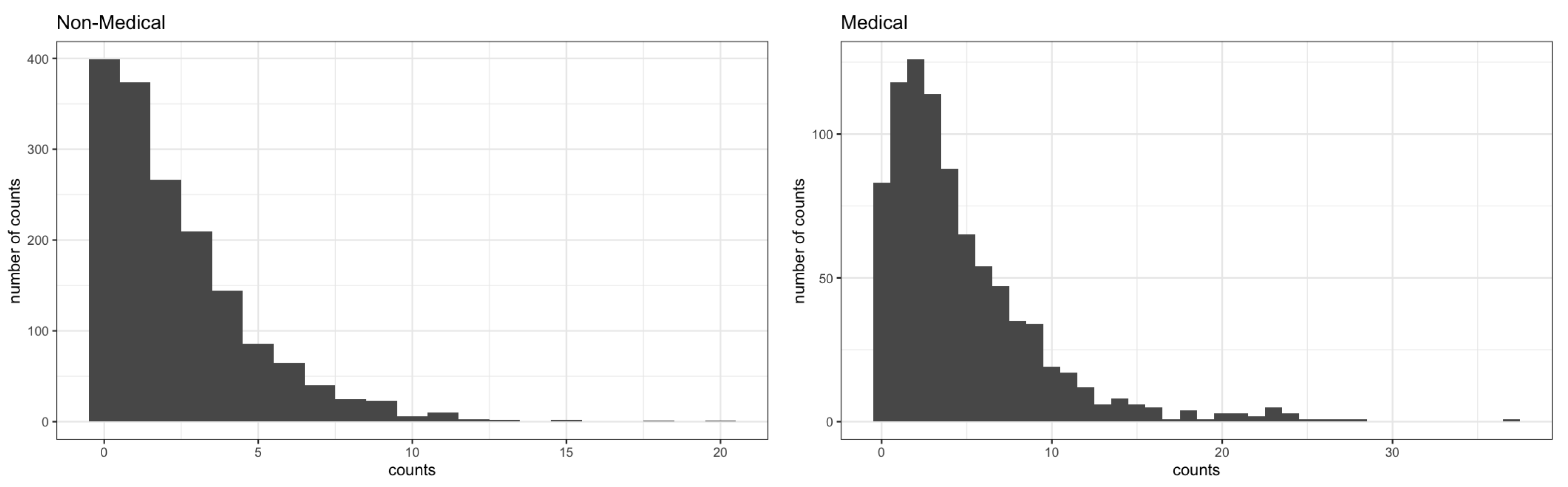
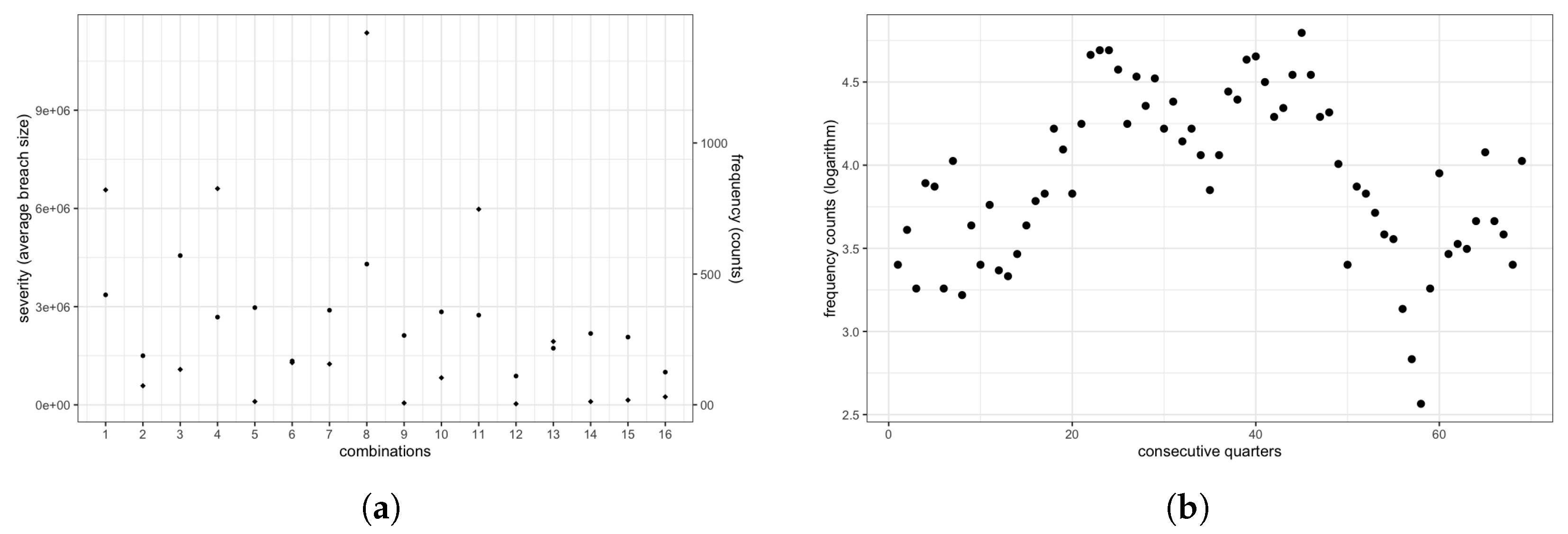
2.2. Empirical Data Analysis
3. Generalized Linear Mixed Model for Data Breaches
3.1. Model Formulation
3.2. Parameter Inference under Bayesian Framework
3.2.1. Prior and Posterior Distribution
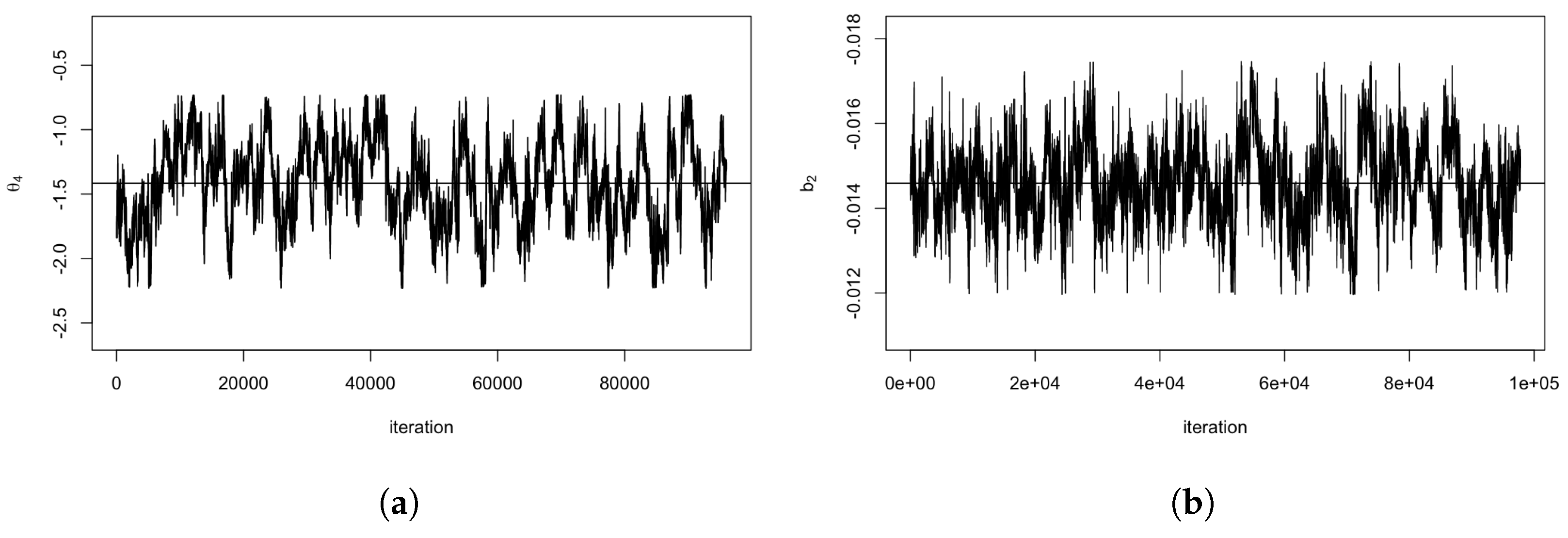
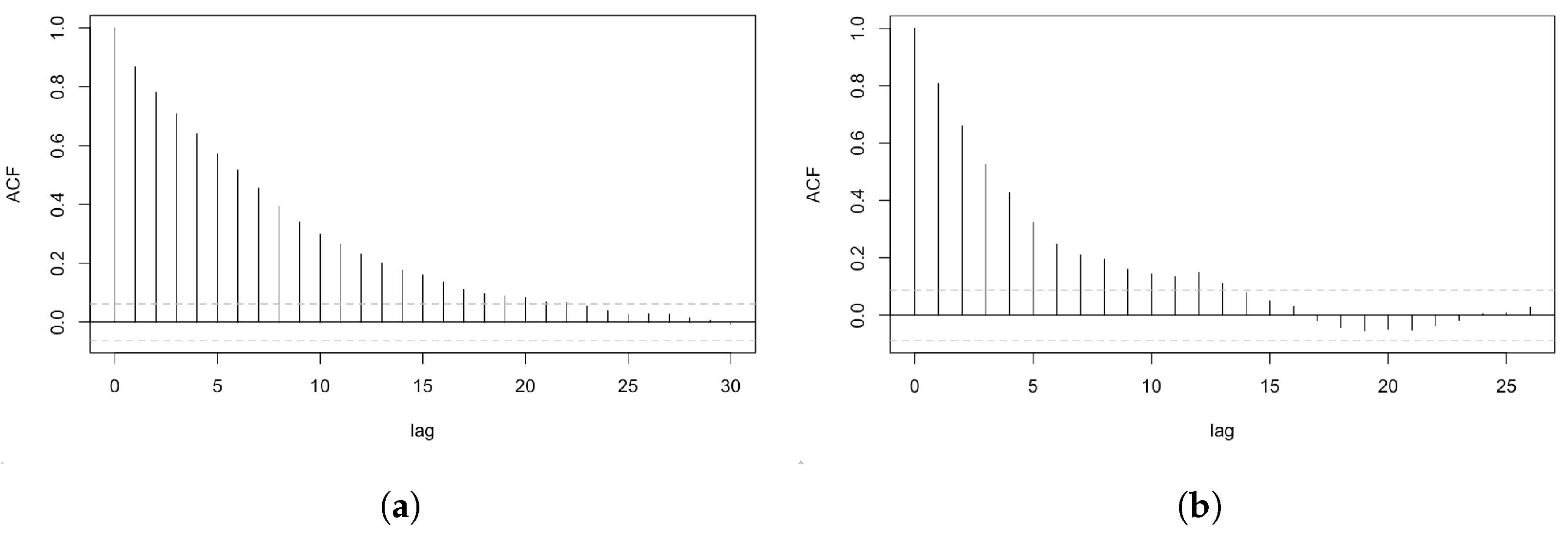
3.2.2. Markov Chain Monte Carlo for Parameter Estimations
- Sample from full conditional distribution (4):
- (a)
- Compute and from , where
- (b)
- Sample .
- Sample from full conditional distribution (5):
- (a)
- Compute from , where
- (b)
- Sample .
- Obtain maximum likelihood estimate of from the conditional log-likelihood function (6), given .
- Generate .
- Compute the acceptance ratiowhere and .
- Sample . Set to if , or to if .
- Update , given , under our regression model given by (1) using the maximum likelihood algorithm.
4. Analysis of Frequencies of Data Breaches
4.1. Specification of Priors and Parameters
4.2. Posterior Results and Diagnoses
5. Simulation Study and Validation Test
6. Practical Implications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Posterior Estimation of Variance–Covariance Matrix
| 1 | Unknown types of breach and business have been eliminated due to their incomplete information. |
| 2 | . |
| 3 | Since the available range of PRC dataset is from 2001 to 2018, here next quarter could be the next quarter after latest available data. |
References
- Antonio, Katrien, and Jan Beirlant. 2007. Actuarial statistics with generalized linear mixed models. Insurance: Mathematics and Economics 40: 58–76. [Google Scholar] [CrossRef]
- BBC News. 2021. US Companies Hit by ‘Colossal’ Cyber-Attack. Available online: https://www.bbc.com/news/world-us-canada-57703836 (accessed on 1 October 2022).
- Bessy-Roland, Yannick, Alexandre Boumezoued, and Caroline Hillairet. 2021. Multivariate hawkes process for cyber insurance. Annals of Actuarial Science 15: 14–39. [Google Scholar] [CrossRef]
- Bozdogan, Hamparsum. 1987. Model selection and akaike’s information criterion (aic): The general theory and its analytical extensions. Psychometrika 52: 345–70. [Google Scholar] [CrossRef]
- Breslow, Norman E., and David G. Clayton. 1993. Approximate inference in generalized linear mixed models. Journal of the American statistical Association 88: 9–25. [Google Scholar]
- Brooks, Stephen P., and Andrew Gelman. 1998. General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics 7: 434–55. [Google Scholar]
- Carfora, Maria Francesca, and Albina Orlando. 2019. Quantile based risk measures in cyber security. Papar presented at 2019 International Conference on Cyber Situational Awareness, Data Analytics And Assessment (Cyber SA), Oxford, UK, June 3–4; pp. 1–4. [Google Scholar]
- Casella, George, and Edward I. George. 1992. Explaining the gibbs sampler. The American Statistician 46: 167–74. [Google Scholar]
- Chatfield, Christopher, and Alexander J. Collins. 2018. Introduction to Multivariate Analysis. London: Routledge. [Google Scholar]
- Chib, Siddhartha, and Edward Greenberg. 1995. Understanding the metropolis-hastings algorithm. The American Statistician 49: 327–35. [Google Scholar]
- Cowles, Mary Kathryn, and Bradley P. Carlin. 1996. Markov chain monte carlo convergence diagnostics: A comparative review. Journal of the American Statistical Association 91: 883–904. [Google Scholar] [CrossRef]
- Data Accountability and Trust Act. 2019. Available online: https://www.congress.gov/bill/116th-congress/house-bill/1282 (accessed on 1 October 2022).
- Data Security and Breach Notification Act. 2015. Available online: https://www.congress.gov/bill/114th-congress/house-bill/1770 (accessed on 1 October 2022).
- Dempster, Arthur P. 1968. A generalization of bayesian inference. Journal of the Royal Statistical Society: Series B (Methodological) 30: 205–32. [Google Scholar]
- Edwards, Benjamin, Steven Hofmeyr, and Stephanie Forrest. 2016. Hype and heavy tails: A closer look at data breaches. Journal of Cybersecurity 2: 3–14. [Google Scholar] [CrossRef]
- Eling, Martin. 2020. Cyber risk research in business and actuarial science. European Actuarial Journal 10: 303–33. [Google Scholar] [CrossRef]
- Eling, Martin, and Kwangmin Jung. 2018. Copula approaches for modeling cross-sectional dependence of data breach losses. Insurance: Mathematics and Economics 82: 167–80. [Google Scholar] [CrossRef]
- Eling, Martin, and Nicola Loperfido. 2017. Data breaches: Goodness of fit, pricing, and risk measurement. Insurance: Mathematics and Economics 75: 126–36. [Google Scholar] [CrossRef]
- Fahrenwaldt, Matthias A., Stefan Weber, and Kerstin Weske. 2018. Pricing of cyber insurance contracts in a network model. ASTIN Bulletin: The Journal of the IAA 48: 1175–218. [Google Scholar] [CrossRef]
- Farkas, Sébastien, Olivier Lopez, and Maud Thomas. 2021. Cyber claim analysis using generalized pareto regression trees with applications to insurance. Insurance: Mathematics and Economics 98: 92–105. [Google Scholar] [CrossRef]
- FBI. 2000. Internet Crime Complaint Center (IC3). Available online: https://www.fbi.gov/investigate/cyber (accessed on 1 October 2022).
- Gamerman, Dani, and Hedibert F. Lopes. 2006. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. Boca Raton: CRC Press. [Google Scholar]
- Garrido, José, and Jun Zhou. 2009. Full credibility with generalized linear and mixed models. ASTIN Bulletin: The Journal of the IAA 39: 61–80. [Google Scholar] [CrossRef]
- Geman, Stuart, and Donald Geman. 1984. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence PAMI- 6: 721–41. [Google Scholar] [CrossRef]
- Gilks, Walter R. 1996. Introducing markov chain monte carlo. In Markov Chain Monte Carlo in Practice. London: Routledge. [Google Scholar]
- Gordon, Lawrence A., and Martin P. Loeb. 2002. The economics of information security investment. ACM Transactions on Information and System Security (TISSEC) 5: 438–57. [Google Scholar] [CrossRef]
- Hastings, W. Keith. 1970. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Oxford: Oxford University Press. [Google Scholar]
- Hilbe, Joseph M. 2011. Negative Binomial Regression. Cambridge: Cambridge University Press. [Google Scholar]
- Hoff, Peter D. 2009. A First Course in Bayesian Statistical Methods. Berlin and Heidelberg: Springer, vol. 580. [Google Scholar]
- IBM. 2021. Security Cost of Data Breach Report. Available online: https://www.ibm.com/downloads/cas/ojdvqgry (accessed on 1 October 2022).
- Internet Crime Report. 2020. Available online: https://www.ic3.gov/media/pdf/annualreport/2020{_}ic3report.pdf (accessed on 1 October 2022).
- Jacobs, Jay. 2014. Analyzing Ponemon Cost of Data Breach. Available online: http://datadrivensecurity.info/blog/posts/2014/dec/ponemon/ (accessed on 28 September 2022).
- Jain, Anil K., M. Narasimha Murty, and Patrick J. Flynn. 1999. Data clustering: A review. ACM Computing Surveys (CSUR) 31: 264–23. [Google Scholar] [CrossRef]
- Jeong, Himchan, Emiliano A. Valdez, Jae Youn Ahn, and Sojung Park. 2021. Generalized linear mixed models for dependent compound risk models. Variance 14: 1–18. [Google Scholar] [CrossRef]
- Jevtić, Petar, and Nicolas Lanchier. 2020. Dynamic structural percolation model of loss distribution for cyber risk of small and medium-sized enterprises for tree-based lan topology. Insurance: Mathematics and Economics 91: 209–23. [Google Scholar] [CrossRef]
- Joe, Harry, and Rong Zhu. 2005. Generalized poisson distribution: The property of mixture of poisson and comparison with negative binomial distribution. Biometrical Journal: Journal of Mathematical Methods in Biosciences 47: 219–29. [Google Scholar] [CrossRef] [PubMed]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2012. Loss Models: From Data to Decisions. Hoboken: John Wiley & Sons, vol. 715. [Google Scholar]
- Kshetri, Nir. 2020. The evolution of cyber-insurance industry and market: An institutional analysis. Telecommunications Policy 44: 102007. [Google Scholar] [CrossRef]
- Maillart, Thomas, and Didier Sornette. 2010. Heavy-tailed distribution of cyber-risks. The European Physical Journal B 75: 357–64. [Google Scholar] [CrossRef]
- Mazzoccoli, Alessandro, and Maurizio Naldi. 2020. Robustness of optimal investment decisions in mixed insurance/investment cyber risk management. Risk Analysis 40: 550–64. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, Charles E. 2006. Generalized linear mixed models. In Encyclopedia of Environmetrics. Hoboken: John Wiley & Sons, vol. 2. [Google Scholar]
- McCulloch, Charles E., and Shayle R. Searle. 2004. Generalized, Linear, and Mixed Models. Hoboken: John Wiley & Sons. [Google Scholar]
- Metropolis, Nicholas, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, and Edward Teller. 1953. Equation of state calculations by fast computing machines. The Journal of Chemical Physics 21: 1087–92. [Google Scholar] [CrossRef]
- Metropolis, Nicholas, and Stanislaw Ulam. 1949. The monte carlo method. Journal of the American Statistical Association 44: 335–41. [Google Scholar] [CrossRef]
- Mosier, Charles I. 1951. I. problems and designs of cross-validation 1. Educational and Psychological Measurement 11: 5–11. [Google Scholar] [CrossRef]
- NAIC. 2020. National Association of Insurance Commissioners Report on the Cybersecurity Insurance Market. Available online: https://www.insurancejournal.com/app/uploads/2021/11/naic-cyber_insurance-report-2020.pdf (accessed on 1 October 2022).
- Pal, Ranjan, Leana Golubchik, Konstantinos Psounis, and Pan Hui. 2017. Security pricing as enabler of cyber-insurance a first look at differentiated pricing markets. IEEE Transactions on Dependable and Secure Computing 16: 358–72. [Google Scholar] [CrossRef]
- Piegorsch, Walter W. 1990. Maximum likelihood estimation for the negative binomial dispersion parameter. Biometrics 46: 863–67. [Google Scholar] [CrossRef]
- Pinheiro, José C., and Edward C. Chao. 2006. Efficient laplacian and adaptive gaussian quadrature algorithms for multilevel generalized linear mixed models. Journal of Computational and Graphical Statistics 15: 58–81. [Google Scholar] [CrossRef]
- PRC. 2019. Privacy Rights Clearinghouse Chronology of Data Breaches. Available online: https://privacyrights.org/data-breaches (accessed on 1 October 2022).
- Rathee, Avisha. 2020. Data breaches in healthcare: A case study. CYBERNOMICS 2: 25–29. [Google Scholar]
- Raudenbush, Stephen W., Meng-Li Yang, and Matheos Yosef. 2000. Maximum likelihood for generalized linear models with nested random effects via high-order, multivariate laplace approximation. Journal of computational and Graphical Statistics 9: 141–57. [Google Scholar]
- Rudolph, Max J. 2022. 15th Annual Survey of Emerging Risks. Available online: https://www.casact.org/sites/default/files/2022-08/15th-survey-emerging-risks.pdf (accessed on 1 October 2022).
- Schall, Robert. 1991. Estimation in generalized linear models with random effects. Biometrika 78: 719–27. [Google Scholar] [CrossRef]
- Schnell, Werner. 2020. Does Cyber Risk Pose a Systemic Threat to the Insurance Industry? Working Paper. Available online: https://www.alexandria.unisg.ch/260003/ (accessed on 1 October 2022).
- Smith, Adrian F. M., and Gareth O. Roberts. 1993. Bayesian computation via the gibbs sampler and related markov chain monte carlo methods. Journal of the Royal Statistical Society: Series B (Methodological) 55: 3–23. [Google Scholar] [CrossRef]
- Stroup, Walter W. 2012. Generalized Linear Mixed Models: Modern Concepts, Methods and Applications. Boca Raton: CRC Press. [Google Scholar]
- Tierney, Luke. 1994. Markov chains for exploring posterior distributions. the Annals of Statistics 22: 1701–728. [Google Scholar] [CrossRef]
- Tse, Yiu-Kuen. 2009. Nonlife Actuarial Models: Theory, Methods and Evaluation. Cambridge: Cambridge University Press. [Google Scholar]
- Werner, Geoff, and Claudine Modlin. 2010. Basic Ratemaking. Arlington: Casualty Actuarial Society, vol. 4, pp. 1–320. [Google Scholar]
- Wheatley, Spencer, Thomas Maillart, and Didier Sornette. 2016. The extreme risk of personal data breaches and the erosion of privacy. The European Physical Journal B 89: 1–12. [Google Scholar] [CrossRef]
- Wolfinger, Russ, and Michael O’connell. 1993. Generalized linear mixed models a pseudo-likelihood approach. Journal of statistical Computation and Simulation 48: 233–43. [Google Scholar] [CrossRef]
- Xie, Xiaoying, Charles Lee, and Martin Eling. 2020. Cyber insurance offering and performance: An analysis of the us cyber insurance market. The Geneva Papers on Risk and Insurance-Issues and Practice 45: 690–736. [Google Scholar] [CrossRef]
- Xu, Maochao, Kristin M. Schweitzer, Raymond M. Bateman, and Shouhuai Xu. 2018. Modeling and predicting cyber hacking breaches. IEEE Transactions on Information Forensics and Security 13: 2856–871. [Google Scholar] [CrossRef]
- Young, Derek, Juan Lopez, Jr., Mason Rice, Benjamin Ramsey, and Robert McTasney. 2016. A framework for incorporating insurance in critical infrastructure cyber risk strategies. International Journal of Critical Infrastructure Protection 14: 43–57. [Google Scholar] [CrossRef]

| Chronology Legend Labels | Statistical Inputs | |
|---|---|---|
| CARD | Fraud Involving Debit and Credit Cards | External |
| HACK | Hacked by an Outside Party or Infected by Malware | |
| INSD | Insider | Internal |
| PHYS | Physical Paper Documents | |
| PORT | Portable Device | |
| STAT | Stationary Computer Loss | |
| DISC | Other Disclosure | |
| UNKN | Not Enough Information about Breach | – |
| BSF | Businesses (Financial and Insurance Services) | Businesses |
| BSR | Businesses (Retail/Merchant including Online Retail) | |
| BSO | Businesses (Other) | |
| EDU | Educational Institutions | Non-Businesses |
| GOV | Government and Military | |
| NGO | Nonprofits | |
| UNKN | Not Enough Information about Breach | – |
| Entity Type | Minimum | Maximum | Mean | Median | Variance | Proportion of Zeros |
|---|---|---|---|---|---|---|
| Non-Medical | 0 | 20 | 2.277 | 2 | 6.014 | 0.267 |
| Medical | 0 | 37 | 4.762 | 3 | 22.274 | 0.096 |
| Entity Type | Non-Medical | Medical |
|---|---|---|
| Poisson | 7617 | 5947 |
| Negative Binomial | 6739 | 4552 |
| Zero-inflated Poisson | 7165 | 5657 |
| Zero-inflated Negative Binomial | 6941 | 4555 |
| Parameter | Distribution | Starting Value |
|---|---|---|
| ; | ||
| ine | ; |
| Regressor | Symbol | Mean | Standard Error | 95% HPD Interval | |
|---|---|---|---|---|---|
| South | 1.2536 | 0.0015 | 0.4053 | 2.2278 | |
| West | 2.2002 | 0.0011 | 1.4898 | 2.9617 | |
| Northeast | 0.7115 | 0.0011 | 0.0141 | 1.3812 | |
| ine Internal | −1.4176 | 0.0011 | −2.0852 | −0.8232 | |
| ine Non-Business | −0.2181 | 0.0011 | −0.9858 | 0.3756 | |
| ine Ave-Size | −0.1699 | 0.0001 | −0.2322 | −0.1103 | |
| ine | 0.5892 | 0.5355 | 0.6997 | ||
| Regressor | Parameter | True Values | Estimated Mean | Relative Error |
|---|---|---|---|---|
| South | 1.2536 | 1.2018 | −0.0413 | |
| West | 2.2002 | 2.2524 | 0.0237 | |
| Northeast | 0.7115 | 0.7429 | 0.0442 | |
| ine Int. | −1.4176 | −1.5368 | 0.0841 | |
| ine Non-Bus. | −0.2181 | −0.2335 | 0.0708 | |
| ine Ave-Size | −0.1699 | −0.1742 | 0.0255 | |
| ine | 0.5892 | 0.5809 | −0.0141 | |
| −0.0267 | ||||
| −0.0161 |
| Partition | Training Set | Test Set | ||
|---|---|---|---|---|
| Model | Poisson | Negative Binomial | GLMM | GLMM |
| Location | Business Type | Deductible | Max. Coverage | Estimated Loss |
|---|---|---|---|---|
| Northeast | Business | - | - | USD 197,891 |
| USD 10,000 | - | USD 188,469 | ||
| - | USD 1M | USD 197,891 | ||
| USD 10,000 | USD 1M | USD 188,469 | ||
| Non-Business | - | - | USD 2,283,023 | |
| USD 10,000 | - | USD 2,273,881 | ||
| - | USD 1M | USD 1,164,335 | ||
| USD 10,000 | USD 1M | USD 1,162,902 | ||
| West | Business | - | - | USD 1,408,541 |
| USD 10,000 | - | USD 1,398,568 | ||
| - | USD 1M | USD 1,264,013 | ||
| USD 10,000 | USD 1M | USD 1,260,245 | ||
| Non-Business | - | - | USD 14,661,661 | |
| USD 10,000 | - | USD 14,651,699 | ||
| - | USD 1M | USD 1,680,241 | ||
| USD 10,000 | USD 1M | USD 1,680,149 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Lu, Y. A Generalized Linear Mixed Model for Data Breaches and Its Application in Cyber Insurance. Risks 2022, 10, 224. https://doi.org/10.3390/risks10120224
Sun M, Lu Y. A Generalized Linear Mixed Model for Data Breaches and Its Application in Cyber Insurance. Risks. 2022; 10(12):224. https://doi.org/10.3390/risks10120224
Chicago/Turabian StyleSun, Meng, and Yi Lu. 2022. "A Generalized Linear Mixed Model for Data Breaches and Its Application in Cyber Insurance" Risks 10, no. 12: 224. https://doi.org/10.3390/risks10120224
APA StyleSun, M., & Lu, Y. (2022). A Generalized Linear Mixed Model for Data Breaches and Its Application in Cyber Insurance. Risks, 10(12), 224. https://doi.org/10.3390/risks10120224





