Optimal Dynamic Portfolio with Mean-CVaR Criterion

Abstract

Value-at-risk (VaR) and conditional value-at-risk (CVaR) are popular risk measures from academic, industrial and regulatory perspectives. The problem of minimizing CVaR is theoretically known to be of a Neyman–Pearson type binary solution. We add a constraint on expected return to investigate the mean-CVaR portfolio selection problem in a dynamic setting: the investor is faced with a Markowitz type of risk reward problem at the final horizon, where variance as a measure of risk is replaced by CVaR. Based on the complete market assumption, we give an analytical solution in general. The novelty of our solution is that it is no longer the Neyman–Pearson type, in which the final optimal portfolio takes only two values. Instead, in the case in which the portfolio value is required to be bounded from above, the optimal solution takes three values; while in the case in which there is no upper bound, the optimal investment portfolio does not exist, though a three-level portfolio still provides a sub-optimal solution.

1. Introduction

The portfolio selection problem published by Markowitz [1] in 1952 is formulated as an optimization problem in a one-period static setting with the objective of maximizing expected return, subject to the constraint of variance being bounded from above. In 2005, Bielecki et al. [2] published the solution to this problem in a dynamic complete market setting. In both cases, the measure of risk of the portfolio is chosen as variance and the risk-reward problem is understood as the “mean-variance” problem.

Much research has been done in developing risk measures that focus on extreme events in the tail distribution where the portfolio loss occurs (variance does not differentiate loss or gain), and quantile-based models have thus far become the most popular choice. Among those, conditional value-at-risk (CVaR), developed by Rockafellar and Uryasev [3,4], also known as expected shortfall by Acerbi and Tasche [5], has become a prominent candidate to replace variance in the portfolio selection problem. On the theoretical side, CVaR is a “coherent risk measure”, a term coined by Artzner et al. [6,7] in pursuit of an axiomatic approach for defining properties that a ‘good’ risk measure should possess. On the practical side, the convex representation of CVaR from Rockafellar and Uryasev [3] opened the door for convex optimization for the mean-CVaR problem and gave it vast advantage in implementation. In a one-period static setting, Rockafellar and Uryasev [3] demonstrated how linear programming can be used to solve the mean-CVaR problem, making it a convincing alternative to the Markowitz [1] mean-variance concept.

The work of Rockafellar and Uryasev [3] has raised huge interest for extending this approach. Acerbi and Simonetti [8] and Adam et al. [9] generalized CVaR to a spectral risk measure in a static setting. A spectral risk measure is also known as weighted value-at-risk (WVaR) by Cherny [10], who, in turn, studied its optimization problem. Ruszczynski and Shapiro [11] revised CVaR into a multi-step dynamic risk measure, namely the “conditional risk mapping for CVaR”, and solved the corresponding mean-CVaR problem using Rockafellar and Uryasev’s [3] technique for each time step. When expected return is replaced by expected utility, the utility-CVaR portfolio optimization problem is often studied in a continuous-time dynamic setting; see Gandy [12] and Zheng [13]. More recently, the issue of robust implementation is dealt with in Quaranta and Zaffaroni [14], Gotoh et al. [15], Huang et al. [16] and El Karoui et al. [17]. Research on systemic risk that involves CVaR can be found in Acharya et al. [18], Chen et al. [19] and Adrian and Brunnermeier [20].

To the best of our knowledge, no complete characterization of a solution has been done for the mean-CVaR problem in a continuous-time dynamic setting. Similar to Bielecki et al. [2], we reduce the problem to a combination of a static optimization problem and a hedging problem with the complete market assumption. Our main contribution is that in solving the static optimization problem, we find a complete characterization, whose nature is different than what is known in the literature. As a pure CVaR minimization problem without the expected return constraint, Sekine [21], Li and Xu [22] and Melnikov and Smirnov [23] found the optimal solution to be binary. This is confirmed to be true for more general law-invariant risk (preference) measure minimization by Schied [24] and He and Zhou [25]. The key to finding the solution that is binary is the association of the mean-CVaR problem with the Neyman–Pearson problem. We observe in Section 2.1 that the stochastic part of CVaR minimization can be transformed into shortfall risk minimization using the representation (CVaR is the Fenchel–Legendre dual of the expected shortfall) given by Rockafellar and Uryasev [3]. Föllmer and Leukert [26] characterized the solution to the latter problem in a general semimartingale complete market model to be binary, where they have demonstrated its close relationship to the Neyman–Pearson problem of hypothesis testing between the risk neutral probability measure, $\tilde{P}$, and the physical probability measure, P.

Adding the expected return constraint to WVaR minimization (CVaR is a particular case of WVaR), Cherny [10] found conditions under which the solution to the mean-WVaR problem was still binary and conditions under which the solution does not exist. In this paper, we discuss all cases for solving the mean-CVaR problem depending on a combination of two criteria: the level of the Radon–Nikodým derivative, $\frac{d\tilde{P}}{dP}$, relative to the confidence level of the risk measure; and the level of the return requirement. More specifically, when the portfolio is uniformly bounded from above and below, we find the optimal solution to be nonexistent or binary in some cases and, more interestingly, take three values in the most important case (see Case 4 of Theorem 3.15). When the portfolio is unbounded from above, in most cases (see Case 2 and 4 in Theorem 3.17), the solution is nonexistent, while portfolios of three levels still give sub-optimal solutions. Since the new solution we find can take not only the upper or the lower bound, but also a level in between, it can be viewed in part as a generalization of the binary solution for the Neyman–Pearson problem with an additional constraint on expectation.

This paper is organized as follows. Section 2 formulates the dynamic portfolio selection problem and compares the structure of the binary solution and the three-level solution, with an application of exact calculation in the Black–Scholes model. Section 3 details the analytic solution in general, where the proofs are delayed to the Appendix. Section 4 lists possible future work.

2. The Structure of the Optimal Portfolio

2.1. Main Problem

Let $(\Omega ,\mathcal{F},{\left(\mathcal{F}\right)}_{0\le t\le T},P)$ be a filtered probability space that satisfies the usual conditions, where ${\mathcal{F}}_0$ is trivial and ${\mathcal{F}}_T=\mathcal{F}$. The market model consists of $d+1$ tradable assets: one riskless asset (money market account) and d risky assets (stock). Suppose the risk-free interest rate, r, is a constant and the stock, $S_t$, is a d-dimensional real-valued locally-bounded semimartingale process. Let the number of shares invested in the risky asset, ${\xi }_t$, be a d-dimensional predictable process, such that the stochastic integral with respect to $S_t$ is well-defined. Then, the value of a self-financing portfolio, $X_t$, evolves according to the dynamics:

$$d{X}_t={\xi }_{t}d{S}_t+r(X_t-{\xi }_t{S}_t)dt,X_0=x_0$$

Here, ${\xi }_{t}d{S}_t$ and ${\xi }_t{S}_t$ are interpreted as inner products if the risky asset is multidimensional $d>1$. The portfolio selection problem is to find the best strategy, ${\left({\xi }_t\right)}_{0\le t\le T}$, to minimize the conditional value-at-risk (CVaR) of the final portfolio value, $X_T$, at confidence level $0<\lambda <1$, while requiring the expected value to remain above a constant z.1 In addition, we require uniform lower bound $x_d$ and upper bound $x_u$ on the value of the portfolio over time, such that $-\infty <x_d<x_0<x_u\le \infty$. Therefore, our main dynamic problem is:

$$\begin{array}{cc}& \underset{{\xi }_t}{inf}CVa{R}_{\lambda }\left(X_T\right)\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \text{subject}\text{to}& E\left[X_T\right]\ge z,x_d\le X_t\le x_{u}a.s.\forall t\in [0,T]\hfill \end{array}$$

Note that the no-bankruptcy condition can be imposed by setting the lower bound to be $x_d=0$, and the portfolio value can be unbounded from above by taking the upper bound as $x_u=\infty$. Our solution will be based on the following complete market assumption.

Assumption 2.1 There is no free lunch with vanishing risk (as defined in Delbaen and Schachermayer [27]), and the market model is complete with a unique equivalent local martingale measure, $\tilde{P}$, such that the Radon–Nikodým derivative, $\frac{d\tilde{P}}{dP}$, has a continuous distribution.

Under the above assumption, any $\mathcal{F}$-measurable random variable can be replicated by a dynamic portfolio. Thus, the dynamic optimization problem Equation (1) can be reduced to: first, find the optimal solution, $X^{**}$, to the main static problem:

$$\begin{array}{cc}& \underset{X\in \mathcal{F}}{inf}CVa{R}_{\lambda }\left(X\right)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \text{subject}\text{to}& E\left[X\right]\ge z,\tilde{E}\left[X\right]=x_r,x_d\le X\le x_{u}a.s.\hfill \end{array}$$

if it exists, and then, find the dynamic strategy that replicates the $\mathcal{F}$-measurable random variable, $X^{**}$. Here, the expectations, E and $\tilde{E}$, are taken under the physical probability measure, P, and the risk neutral probability measure, $\tilde{P}$, respectively. Constant $x_r=x_0{e}^{rT}$ is assumed to satisfy $-\infty <x_d<x_0\le x_r<x_u\le \infty$, and the additional capital constraint $\tilde{E}\left[X\right]=x_r$ is the key to making sure that the optimal solution can be replicated by a dynamic self-financing strategy with initial capital $x_0$.

Using the equivalence between the conditional value-at-risk and the Fenchel–Legendre dual of the expected shortfall derived in Rockafellar and Uryasev [3]:

$$CVa{R}_{\lambda }\left(X\right)=\frac{1}{\lambda }\underset{x\in \mathbb{R}}{inf}\left(E\left[{(x-X)}^{+}\right]-\lambda x\right),\forall \lambda \in (0,1)$$

(3)

the CVaR optimization problem Equation (2) can be reduced to an expected shortfall optimization problem, which we name the two-constraint problem:

• Step 1: minimization of expected shortfall

  $$\begin{array}{ccc}& v\left(x\right)=\underset{X\in \mathcal{F}}{inf}E\left[{(x-X)}^{+}\right]\hfill & \end{array}$$

  (4)

  $$\begin{array}{ccc}\hfill \text{subject}\text{to}& E\left[X\right]\ge z,\hfill & \hfill \left(\text{return}\text{constraint}\right)\end{array}$$

  $$\begin{array}{ccc}& \tilde{E}\left[X\right]=x_r,\hfill & \hfill \left(\text{capital}\text{constraint}\right)\end{array}$$

  $$\begin{array}{cc}& x_d\le X\le x_{u}a.s.\hfill \end{array}$$
• Step 2: minimization of conditional value-at-risk

  $$\underset{X\in \mathcal{F}}{inf}CVa{R}_{\lambda }\left(X\right)=\frac{1}{\lambda }\underset{x\in \mathbb{R}}{inf}\left(v\left(x\right)-\lambda x\right)$$

  (5)

To compare our solution to existing ones in the literature, we also name an auxiliary problem, which simply minimizes the conditional value-at-risk without the return constraint, the one-constraint problem: Step 1 in Equation (4) is replaced by:

• Step 1: minimization of expected shortfall

  $$\begin{array}{ccc}& v\left(x\right)=\underset{X\in \mathcal{F}}{inf}E\left[{(x-X)}^{+}\right]\hfill & \end{array}$$

  (6)

  $$\begin{array}{ccc}\hfill \text{subject}\text{to}& \tilde{E}\left[X\right]=x_r,\hfill & \hfill \left(\text{capital}\text{constraint}\right)\end{array}$$

  $$\begin{array}{cc}& x_d\le X\le x_{u}a.s.\hfill \end{array}$$

Step 2 in Equation (5) remains the same.

2.2. Main Result

This subsection is devoted to a conceptual comparison between the solutions to the one-constraint problem and the two-constraint problem. The solution to the expected shortfall minimization problem in Step 1 of the one-constraint problem is found by Föllmer and Leukert [26] under Assumption 2.1 to be binary in nature:

$$X\left(x\right)=x_d{\mathbb{I}}_A+x{\mathbb{I}}_{A^c},\text{for}{x}_d<x<x_u$$

(7)

where ${\mathbb{I}}_{·}\left(\omega \right)$ is the indicator function and set A is defined as the collection of states where the Radon–Nikodým derivative is above a threshold, $\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>a\right\}$. This particular structure, in which the optimal solution, $X\left(x\right)$, takes only two values, namely, the lower bound, $x_d$, and x, is intuitively clear once the problems of minimizing expected shortfall and hypothesis testing between P and $\tilde{P}$ are connected in Föllmer and Leukert [26], the later being well-known to possess a binary solution by the Neyman–Pearson Lemma. There are various ways to prove the optimality. Other than the Neyman–Pearson approach, it can be viewed as the solution from a convex duality perspective; see Theorem 1.19 in Xu [29]. In addition, a simplified version to the proof of Proposition 3.14 gives a direct method using the Lagrange multiplier for convex optimization.

The solution to Step 2 of one-constraint problem and, thus, to the main problems in Equations (1) and (2), as a pure risk minimization problem without the return constraint is given in Schied [24], Sekine [21] and Li and Xu [22]. Since Step 2 only involves minimization over a real-valued number, x, the binary structure is preserved through this step. Under some technical conditions, the solution to Step 2 of the one-constraint problem is shown by Li and Xu [22] (Theorem 2.10 and Remark 2.11) to be:

$$\begin{array}{ccc}\hfill X^{*}& =x_d{\mathbb{I}}_{A^{*}}+x^{*}{\mathbb{I}}_{A^{*c}},\hfill & \hfill \text{(two-line}\text{configuration)}\end{array}$$

(8)

$$\begin{array}{cc}\hfill CVa{R}_{\lambda }\left(X^{*}\right)& =-x_r+\frac{1}{\lambda }(x^{*}-x_d)\left(P\left(A^{*}\right)-\lambda \tilde{P}\left(A^{*}\right)\right)\hfill \end{array}$$

(9)

where $(a^{*},x^{*})$ is the solution to the capital constraint ($\tilde{E}\left[X\left(x\right)\right]=x_r$) in Step 1 and the first order Euler condition ($v^{\prime }\left(x\right)=0$) in Step 2:

$$\begin{array}{ccc}\hfill x_d\tilde{P}\left(A\right)+x\tilde{P}\left(A^c\right)& =x_r,\hfill & \hfill \text{(capital}\text{constraint)}\end{array}$$

(10)

$$\begin{array}{ccc}\hfill P\left(A\right)+\frac{\tilde{P}\left(A^c\right)}{a}-\lambda & =0.\hfill & \hfill \text{(first}\text{order}\text{Euler}\text{condition)}\end{array}$$

(11)

A static portfolio holding only the riskless asset will yield a constant portfolio value, $X\equiv x_r$, with $CVaR\left(X\right)=-x_r$. The diversification by dynamically managing the exposure to risky assets decreases the risk of the overall portfolio by an amount shown in Equation (9). One interesting observation is that the optimal portfolio exists regardless of whether the upper bound on the portfolio is finite $x_u<\infty$ or not $x_u=\infty$. This conclusion will change drastically as we add the return constraint to the optimization problem.

The main result of this paper is to show that the optimal solution to the two-constraint problem and, thus, main problem Equation (1) and Equation (2), does not have a Neyman–Pearson type of binary solution, which we call two-line configuration in Equation (8); instead, it has a three-line configuration. Proposition 3.14 and Theorem 3.15 prove that, when the upper bound is finite $x_u<\infty$, and under some technical conditions, the solution to Step 2 of the two-constraint problem turns out to be:

$$\begin{array}{ccc}\hfill X^{**}& =x_d{\mathbb{I}}_{A^{**}}+x^{**}{\mathbb{I}}_{B^{**}}+x_u{\mathbb{I}}_{D^{**}},\hfill & \hfill \text{(three-line}\text{configuration)}\end{array}$$

(12)

$$\begin{array}{cc}\hfill CVa{R}_{\lambda }\left(X_T^{**}\right)& =\frac{1}{\lambda }\left((x^{**}-x_d)P\left(A^{**}\right)-\lambda x^{**}\right)\hfill \end{array}$$

(13)

where $(a^{**},b^{**},x^{**})$ is the solution to the capital constraint and the first order Euler condition, plus the additional return constraint ($E\left[X\right(x\left)\right]=z$):

$$\begin{array}{ccc}\hfill x_{d}P\left(A\right)+xP\left(B\right)+x_{u}P\left(D\right)& =z,\hfill & \hfill \text{(return}\text{constraint)}\end{array}$$

(14)

$$\begin{array}{ccc}\hfill x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)& =x_r,\hfill & \hfill \text{(capital}\text{constraint)}\end{array}$$

(15)

$$\begin{array}{ccc}\hfill P\left(A\right)+\frac{\tilde{P}\left(B\right)-bP\left(B\right)}{a-b}-\lambda & =0.\hfill & \hfill \text{(first}\text{order}\text{Euler}\text{condition)}\end{array}$$

(16)

The sets in Equations (14)–(16) are defined by different levels of the Radon–Nikodým derivative:

$$A=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>a\right\},B=\left\{\omega \in \Omega :b\le \frac{d\tilde{P}}{dP}\left(\omega \right)\le a\right\},D=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)<b\right\}$$

When the upper bound is infinite $x_u=\infty$, Theorem 3.17 shows that the solution for the optimal portfolio is no longer a three-line configuration. It can be pure money market account investment (one-line), binary (two-line) or very likely nonexistent. In the last case, the infimum of the CVaR can still be computed, and a sequence of three-line configuration portfolios can be found with their CVaR converging to the infimum.

2.3. Example: Exact Calculation in the Black–Scholes Model

We show the closed-form calculation of the three-line configuration presented in Equations (12)–(16), as well as the corresponding optimal dynamic strategy in the benchmark Black–Scholes Model. Suppose an agent is trading between a money market account with interest rate r and one stock2 that follows geometric Brownian motion $d{S}_t=\mu S_{t}dt+\sigma S_{t}d{W}_t$ with instantaneous rate of return μ, volatility σ and initial stock price $S_0$. The endowment starts at $x_0$, and bankruptcy is prohibited at any time, $x_d=0$, before the final horizon, T. The optimal portfolio, $X^{*}$, in Equation (8) for the one constraint problem is a binary option $X^{*}=x^{*}{\mathbb{I}}_{A^{*c}}$ with expected return $z^{*}\stackrel{\Delta }{=}E\left[X^{*}\right]$. The expected terminal value, $E\left[X_T\right]$, is required to be above a fixed level z to satisfy the return constraint. When z is low, namely, $z\le z^{*}$, the return constraint is non-binding, and obviously the two-line configuration, $X^{*}$, is optimal. Let $\overline{z}$ be the highest expected value achievable by any self-financing portfolio starting with initial capital $x_0$ (see Definition 3.2 and Lemma 3.3). When the return requirement becomes meaningful, i.e., $z\in (z^{*},\overline{z}]$, the three-line configuration, $X^{**}$, provided by Equation (12), becomes optimal.

Since the Radon–Nikodým derivative, $\frac{d\tilde{P}}{dP}$, is a scaled power function of the final stock price, which has a log-normal distribution, the probabilities in Equations (14)–(16) can be computed in closed-form:

$$\begin{array}{cccc}\hfill P\left(A\right)& =N(-\frac{\theta \sqrt{T}}{2}-\frac{lna}{\theta \sqrt{T}}),\hfill & \hfill P\left(D\right)=1-N(-\frac{\theta \sqrt{T}}{2}-\frac{lnb}{\theta \sqrt{T}}),& P\left(B\right)=1-P\left(A\right)-P\left(D\right)\hfill \\ \hfill \tilde{P}\left(A\right)& =N(\frac{\theta \sqrt{T}}{2}-\frac{lna}{\theta \sqrt{T}}),\hfill & \hfill \tilde{P}\left(D\right)=1-N(\frac{\theta \sqrt{T}}{2}-\frac{lnb}{\theta \sqrt{T}}),& \tilde{P}\left(B\right)=1-\tilde{P}\left(A\right)-\tilde{P}\left(D\right)\hfill \end{array}$$

where $\theta =\frac{\mu -r}{\sigma }$ and $N(·)$ is the cumulative distribution function of a standard normal random variable. From these, the solution, $(a^{**},b^{**},x^{**})$, to Equations (15) and (16) can be found numerically and, thus, the $X^{**}$ from Equation (12). The formulae3 for the dynamic value of the optimal portfolio, $X_t^{**}$, the corresponding dynamic hedging strategy, ${\xi }_t^{**}$4, and the associated final minimal risk, $CVa{R}_{\lambda }\left(X_T^{**}\right)$, are:

$$\begin{array}{cc}\hfill X_t^{**}& =e^{-r(T-t)}[x^{**}N\left(d_{+}(a^{**},S_t,t)\right)+x_{d}N\left(d_{-}(a^{**},S_t,t)\right)]\hfill \\ & +e^{-r(T-t)}[x^{**}N\left(d_{-}(b^{**},S_t,t)\right)+x_{u}N\left(d_{+}(b^{**},S_t,t)\right)]-e^{r(T-t)}{x}^{**}\hfill \\ \hfill {\xi }_t^{**}& =\frac{x^{**}-x_d}{\sigma S_t\sqrt{2\pi (T-t)}}{e}^{-r(T-t)-\frac{d_{-}^2(a^{**},S_t,t)}{2}}+\frac{x^{**}-x_u}{\sigma S_t\sqrt{2\pi (T-t)}}{e}^{-r(T-t)-\frac{d_{+}^2(b^{**},S_t,t)}{2}}\hfill \\ \hfill CVa{R}_{\lambda }\left(X_T^{**}\right)& =\frac{1}{\lambda }\left((x^{**}-x_d)P\left(A^{**}\right)-\lambda x^{**}\right)\hfill \end{array}$$

where we define: $d_{-}(a,s,t)=\frac{1}{\theta \sqrt{T-t}}[-lna+\frac{\theta }{\sigma }(\frac{\mu +r-{\sigma }^2}{2}t-ln\frac{s}{S_0})+\frac{{\theta }^2}{2}(T-t)]$ and $d_{+}(a,s,t)=-d_{-}(a,s,t).$

Numerical results comparing the minimal risk for various levels of upper-bound $x_u$ and return constraint z are summarized in Table 1. As expected, the upper bound on the portfolio value, $x_u$, has no impact on the one-constraint problem, as $(x^{*},a^{*})$ and $CVa{R}_{\lambda }\left(X_T^{*}\right)$ are optimal whenever $x_u\ge x^{*}$. On the contrary, in the two-constraint problem, the stricter the return requirement, z, the more the three-line configuration, $X^{**}$, deviates from the two-line configuration, $X^{*}$. Stricter return requirement (higher z) implies higher minimal risk $CVa{R}_{\lambda }\left(X_T^{**}\right)$; while a less strict upper bound (higher $x_u$) decreases minimal risk $CVa{R}_{\lambda }\left(X_T^{**}\right)$. Notably, under certain conditions in Theorem 3.17, for all levels of return $z\in (z^{*},\overline{z}]$, when $x_u\to \infty$, $CVa{R}_{\lambda }\left(X_T^{**}\right)$ approaches $CVa{R}_{\lambda }\left(X_T^{*}\right)$, as the optimal solution ceases to exist in the limiting case.

Table 1. Black–Scholes example for one-constraint (pure CVaR minimization) and two-constraint (mean-CVaR optimization) problems with parameters: $r=5\%$, $\mu =0.2$, $\sigma =0.1$, $S_0=10$, $T=2$, $x_0=10$, $x_d=0$, $\lambda =5\%$. Consequently, $z^{*}=18.8742$ and $\overline{z}=28.8866$.

One-Constraint Problem				Two-Constraint Problem
$x_u$	30	50		$x_u$	30	30	50
				z	20	25	25
$x^{*}$	19.0670	19.0670		$x^{**}$	19.1258	19.5734	19.1434
$a^{*}$	14.5304	14.5304		$a^{**}$	14.3765	12.5785	14.1677
				$b^{**}$	0.0068	0.1326	0.0172
$CVa{R}_{5\%}\left(X_T^{*}\right)$	−15.2118	−15.2118		$CVa{R}_{5\%}\left(X_T^{**}\right)$	−15.2067	−14.8405	−15.1483

Table 1. Black–Scholes example for one-constraint (pure CVaR minimization) and two-constraint (mean-CVaR optimization) problems with parameters: $r=5\%$, $\mu =0.2$, $\sigma =0.1$, $S_0=10$, $T=2$, $x_0=10$, $x_d=0$, $\lambda =5\%$. Consequently, $z^{*}=18.8742$ and $\overline{z}=28.8866$.

One-Constraint Problem				Two-Constraint Problem
$x_u$	30	50		$x_u$	30	30	50
				z	20	25	25
$x^{*}$	19.0670	19.0670		$x^{**}$	19.1258	19.5734	19.1434
$a^{*}$	14.5304	14.5304		$a^{**}$	14.3765	12.5785	14.1677
				$b^{**}$	0.0068	0.1326	0.0172
$CVa{R}_{5\%}\left(X_T^{*}\right)$	−15.2118	−15.2118		$CVa{R}_{5\%}\left(X_T^{**}\right)$	−15.2067	−14.8405	−15.1483

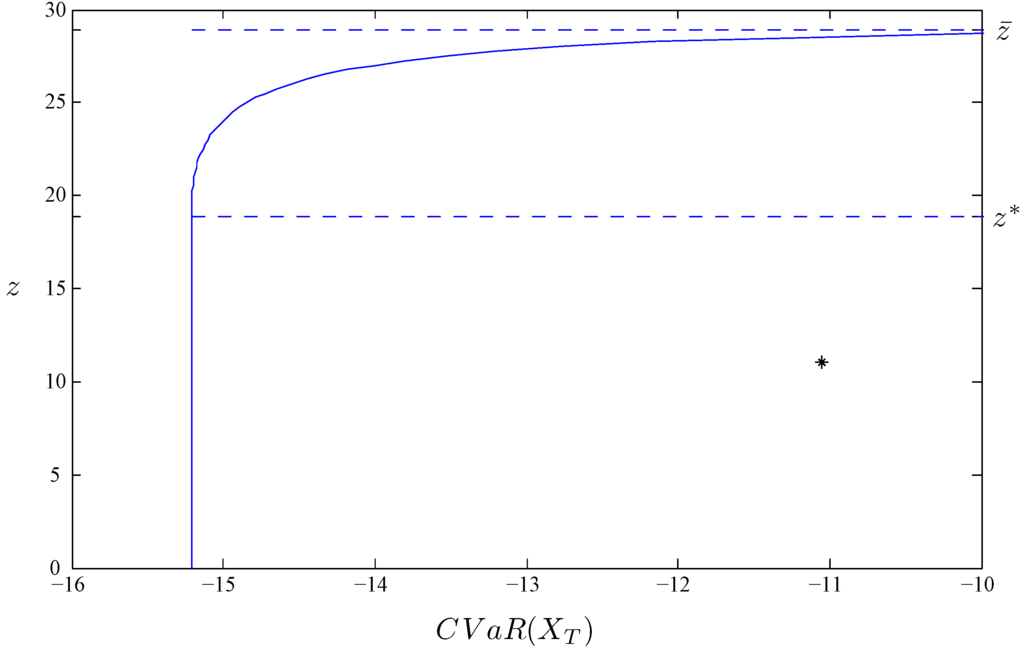
Figure 1. Efficient frontier for mean-CVaR portfolio selection.

Figure 1. Efficient frontier for mean-CVaR portfolio selection.

Figure 1 plots the efficient frontier of the above mean-CVaR portfolio selection problem with fixed upper bound $x_u=30$. The curve between return level $z^{*}$ and $\overline{z}$ are the mean-CVaR efficient portfolio from various three-line configurations, while the straight line is the same mean-CVaR efficient two-line configuration when the return constraint is non-binding. The star positioned at $(-x_r,x_r)=(-11.0517,11.0517)$, where $x_r=x_0{e}^{rT}$, corresponds to the portfolio that invests purely in the money market account. In contrast to its position on the traditional capital market Line (the efficient frontier for a mean-variance portfolio selection problem), the pure money market account portfolio is no longer efficient in the mean-CVaR portfolio selection problem.

3. Analytical Solution to the Portfolio Selection Problem

Under Assumption 2.1, the solution to the main mean-CVaR optimization problem Equation (2), i.e., the two-constraint problem Equations (4) and (5), will be discussed in two separate cases where the upper bound for the portfolio value is finite or infinite. The main results are stated in Theorem 3.15 and Theorem 3.17, respectively. To create a flow showing clearly how the optimal solutions are related to the two-line and three-line configurations, all proofs will be delayed to the Appendix.

3.1. Case $x_u<\infty$: Finite Upper Bound

We first define the general three-line configuration and its degenerate two-line configurations. Recall from Section 2.2 the definitions of the sets, $A,B,D$, are:

$$A=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>a\right\},B=\left\{\omega \in \Omega :b\le \frac{d\tilde{P}}{dP}\left(\omega \right)\le a\right\},D=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)<b\right\}$$

(17)

Definition 3.1 Suppose $x\in [x_d,x_u]$.

1. 

Any three-line configuration has the structure $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$.

2. 

The two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$ is associated with the above definition in the case $a=\infty$, $B=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)\ge b\right\}$ and $D=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)<b\right\}$.

The two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$ s associated with the above definition in the case $b=0$, $A=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>a\right\}$, and $B=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)\le a\right\}$.

The two-line configuration $X=x_d{\mathbb{I}}_A+x_u{\mathbb{I}}_D$ is associated with the above definition in the case $a=b$, $A=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>a\right\}$, and $D=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)<a\right\}$.

Moreover:

1. 

General constraints are the capital constraint and the equality part of the expected return constraint for a three-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$:

$$\begin{array}{cc}& E\left[X\right]=x_{d}P\left(A\right)+xP\left(B\right)+x_{u}P\left(D\right)=z\hfill \\ & \tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r\hfill \end{array}$$

2. 

Degenerated Constraints 1 are the capital constraint and the equality part of the expected return constraint for a two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$:

$$\begin{array}{cc}& E\left[X\right]=xP\left(B\right)+x_{u}P\left(D\right)=z\hfill \\ & \tilde{E}\left[X\right]=x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r\hfill \end{array}$$

Degenerated Constraints 2 are the capital constraint and the equality part of the expected return constraint for a two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$:

$$\begin{array}{cc}& E\left[X\right]=x_{d}P\left(A\right)+xP\left(B\right)=z\hfill \\ & \tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)=x_r\hfill \end{array}$$

Degenerated Constraints 3 are the capital constraint and the equality part of the expected return constraint for a two-line configuration $X=x_d{\mathbb{I}}_A+x_u{\mathbb{I}}_D$:

$$\begin{array}{cc}& E\left[X\right]=x_{d}P\left(A\right)+x_{u}P\left(D\right)=z\hfill \\ & \tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x_u\tilde{P}\left(D\right)=x_r\hfill \end{array}$$

Note that Degenerated Constraints 1 correspond to the general constraints when $a=\infty$; Degenerated Constraints 2 correspond to the general constraints when $b=0$; and Degenerated Constraints 3 correspond to the general constraints when $a=b$.

We use the two-line configuration $X=x_d{\mathbb{I}}_A+x_u{\mathbb{I}}_D$, where the value of the random variable, X, takes either the upper or the lower bound, as well as its capital constraint to define the ‘bar-system’ from which we calculate the highest achievable return.

Definition 3.2 (The bar-system) For fixed $-\infty <x_d<x_r<x_u<\infty$, let $\overline{a}$ be a solution to the capital constraint $\tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x_u\tilde{P}\left(D\right)=x_r$ in Degenerated Constraints 3 for the two-line configuration $X=x_d{\mathbb{I}}_A+x_u{\mathbb{I}}_D$. In the bar-system, $\overline{A}$, $\overline{D}$ and $\overline{X}$ are associated with the constant, $\overline{a}$, in the sense $\overline{X}=x_d{\mathbb{I}}_{\overline{A}}+x_u{\mathbb{I}}_{\overline{D}}$, where $\overline{A}=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>\overline{a}\right\}$ and $\overline{D}=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)<\overline{a}\right\}$. Define the expected return of the bar-system as $\overline{z}=E\left[\overline{X}\right]=x_{d}P\left(\overline{A}\right)+x_{u}P\left(\overline{D}\right)$.

Lemma 3.3 $\overline{z}$ is the highest expected return that can be obtained by a self-financing portfolio with initial capital $x_0$, whose value is bounded between $x_d$ and $x_u$:

$$\overline{z}=\underset{X\in \mathcal{F}}{max}E\left[X\right]s.t.\tilde{E}\left[X\right]=x_r=x_0{e}^{rT},x_d\le X\le x_{u}a.s.$$

In the following lemma, we vary the x value in the two-line configurations $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$ and $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$, while maintaining the capital constraints, respectively. We observe their expected returns to vary between values $x_r$ and $\overline{z}$ in a monotone and continuous fashion.

Lemma 3.4 For fixed $-\infty <x_d<x_r<x_u<\infty$.

1. 

Given any $x\in [x_d,x_r]$, let b be a solution to the capital constraint $\tilde{E}\left[X\right]=x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r$ in Degenerated Constraints 1 for the two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$. Define the expected return of the resulting two-line configuration as $z\left(x\right)=E\left[X\right]=xP\left(B\right)+x_{u}P\left(D\right)$.5 Then $z\left(x\right)$ is a continuous function of x and decreases from $\overline{z}$ to $x_r$ as x increases from $x_d$ to $x_r$.

2. 

Given any $x\in [x_r,x_u]$, let a be a solution to the capital constraint $\tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)=x_r$ in Degenerated Constraints 2 for the two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$. Define the expected return of the resulting two-line configuration as $z\left(x\right)=E\left[X\right]=x_{d}P\left(A\right)+xP\left(B\right)$. Then, $z\left(x\right)$ is a continuous function of x and increases from $x_r$ to $\overline{z}$ as x increases from $x_r$ to $x_u$.

From now on, we will concern ourselves with requirements on the expected return in the interval, $z\in [x_r,\overline{z}]$, because, on one side, Lemma 3.3 ensures that there are no feasible solutions to main problem Equation (2) if we require an expected return higher than $\overline{z}$. On the other side, Lemma 3.3, Lemma 3.4 and Theorem 3.11 lead to the conclusion that a return constraint where $z\in (-\infty ,x_r)$ is too weak to differentiate the two-constraint problem from the one-constraint problem, as their optimal solutions concur.

Definition 3.5 For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in [x_r,\overline{z}]$, define $x_{z1}$ and $x_{z2}$ to be the corresponding x value for two-line configurations $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$ and $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$ that satisfy Degenerated Constraints 1 and Degenerated Constraints 2 , respectively.

Definition 3.5 implies when we fix the level of expected return, z, we can find two particular feasible solutions: $X=x_{z1}{\mathbb{I}}_B+x_u{\mathbb{I}}_D$, satisfying $\tilde{E}\left[X\right]=x_{z1}\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r$ and $E\left[X\right]=x_{z1}P\left(B\right)+x_{u}P\left(D\right)=z$; and $X=x_d{\mathbb{I}}_A+x_{z2}{\mathbb{I}}_B$, satisfying $\tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x_{z2}\tilde{P}\left(B\right)=x_r$ and $E\left[X\right]=x_{d}P\left(A\right)+x_{z2}P\left(B\right)=z$. The values, $x_{z1}$ and $x_{z2}$, are well defined, because Lemma 3.4 guarantees $z\left(x\right)$ to be an invertible function in both cases. We summarize in the following lemma whether the two-line configurations satisfying the capital constraints meet or fail the return constraint as x ranges over its domain, $[x_d,x_u]$, for the two-line and three-line configurations in Definition 3.1.

Lemma 3.6 For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in [x_r,\overline{z}]$.

1. 

If we fix $x\in [x_d,x_{z1}]$, the two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$, which satisfies the capital constraint $\tilde{E}\left[X\right]=x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r$ in Degenerated Constraints 1, satisfies the expected return constraint: $E\left[X\right]=xP\left(B\right)+x_{u}P\left(D\right)\ge z$;

2. 

If we fix $x\in (x_{z1},x_r]$, the two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$, which satisfies the capital constraint $\tilde{E}\left[X\right]=x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r$ in Degenerated Constraints 1, fails the expected return constraint: $E\left[X\right]=xP\left(B\right)+x_{u}P\left(D\right)<z$;

3. 

If we fix $x\in [x_r,x_{z2})$, the two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$, which satisfies the capital constraint $\tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)=x_r$ in Degenerated Constraints 2, fails the expected return constraint: $E\left[X\right]=xP\left(B\right)+x_{u}P\left(D\right)<z$;

4. 

If we fix $x\in [x_{z2},x_u]$, the two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$, which satisfies the capital constraint $\tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)=x_r$ in Degenerated Constraints 2, satisfies the expected return constraint: $E\left[X\right]=xP\left(B\right)+x_{u}P\left(D\right)\ge z$.

We turn our attention to solving Step 1 of the two-constraint problem (4):

Step 1: minimization of expected shortfall:

$$\begin{array}{ccc}& v\left(x\right)=\underset{X\in \mathcal{F}}{inf}E\left[{(x-X)}^{+}\right]\hfill & \\ \hfill \text{subject}\text{to}& E\left[X\right]\ge z,\hfill & \hfill \text{(return}\text{constraint}\text{)}\\ & \tilde{E}\left[X\right]=x_r,\hfill & \hfill \text{(capital}\text{constraint}\text{)}\\ & x_d\le X\le x_{u}a.s.\hfill \end{array}$$

Notice that a solution is called for any given real number, x, independent of the return level, z, or capital level $x_r$. From Lemma 3.6 and the fact that the two-line configurations are optimal solutions to Step 1 of the one-constraint problem (see Theorem 3.11), we can immediately draw the following conclusion.

Proposition 3.7 For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in [x_r,\overline{z}]$.

1. 

If we fix $x\in [x_d,x_{z1}]$, then there exists a two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$ which is the optimal solution to Step 1 of the two-constraint problem;

2. 

If we fix $x\in [x_{z2},x_u]$, then there exists a two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$, which is the optimal solution to Step 1 of the two-constraint problem.

When $x\in (x_{z1},x_{z2})$, Lemma 3.6 shows that the two-line configurations, which satisfy the capital constraints ($\tilde{E}\left[X\right]=x_r$) do not generate high enough expected return ($E\left[X\right]<z$) to be feasible anymore. It turns out that a novel solution of the three-line configuration is the answer: it can be shown to be both feasible and optimal.

Lemma 3.8 For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in [x_r,\overline{z}]$. Given any $x\in (x_{z1},x_{z2})$, let the pair of numbers, $(a,b)\in {\mathbb{R}}^2$ ($b\le a$), be a solution to the capital constraint $\tilde{E}\left[X\right]=x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)=x_r$ in the general constraints for the three-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$. Define the expected return of the resulting three-line configuration as $z(a,b)=E\left[X\right]=x_{d}P\left(A\right)+xP\left(B\right)+x_{u}P\left(D\right)$. Then, $z(a,b)$ is a continuous function, which decreases from $\overline{z}$ to a number below z:

1. 

When $a=b=\overline{a}$ from Definition 3.2 of a bar-system, the three-line configuration degenerates to $X=\overline{X}$ and $z(\overline{a},\overline{a})=E\left[\overline{X}\right]=\overline{z}$.

2. 

When $b<\overline{a}$ and $a>\overline{a}$, $z(a,b)$ decreases continuously as b decreases and a increases.

3. 

In the extreme case when $a=\infty$, the three-line configuration becomes the two-line configuration $X=x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$; in the extreme case when $b=0$, the three-line configuration becomes the two-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B$. In either case, the expected value is below z by Lemma 3.6.

Proposition 3.9 For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in [x_r,\overline{z}]$. If we fix $x\in (x_{z1},x_{z2})$, then there exists a three-line configuration $X=x_d{\mathbb{I}}_A+x{\mathbb{I}}_B+x_u{\mathbb{I}}_D$ that satisfies the general constraints, which is the optimal solution to Step 1 of the two-constraint problem.

Combining Proposition 3.7 and Proposition 3.9, we arrive at the following result on the optimality of the three-line configuration.

Theorem 3.10 (Solution to Step 1: Minimization of Expected Shortfall)

For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in [x_r,\overline{z}]$. $X\left(x\right)$ and the corresponding value function, $v\left(x\right)$, described below, are optimal solutions to Step 1: minimization of expected shortfall of the two-constraint problem:

• $x\in (-\infty ,x_d]$: $X\left(x\right)=$ any random variable with values in $[x_d,x_u]$ satisfying both the capital constraint $\tilde{E}\left[X\left(x\right)\right]=x_r$ and the return constraint $E\left[X\right(x\left)\right]\ge z$. $v\left(x\right)=0.$
• $x\in [x_d,x_{z1}]$: $X\left(x\right)=$ any random variable with values in $[x,x_u]$ satisfying both the capital constraint $\tilde{E}\left[X\left(x\right)\right]=x_r$ and the return constraint $E\left[X\right(x\left)\right]\ge z$. $v\left(x\right)=0.$
• $x\in (x_{z1},x_{z2})$: $X\left(x\right)=x_d{\mathbb{I}}_{A_x}+x{\mathbb{I}}_{B_x}+x_u{\mathbb{I}}_{D_x}$, where $A_x,B_x,D_x$ are determined by $a_x$ and $b_x$ as in (17) satisfying the general constraints: $\tilde{E}\left[X\left(x\right)\right]=x_r$ and $E\left[X\right(x\left)\right]=z$. $v\left(x\right)=(x-x_d)P\left(A_x\right).$
• $x\in [x_{z2},x_u]$: $X\left(x\right)=x_d{\mathbb{I}}_{A_x}+x{\mathbb{I}}_{B_x}$, where $A_x,B_x$ are determined by $a_x$ as in Definition 3.1 satisfying both the capital constraint $\tilde{E}\left[X\left(x\right)\right]=x_r$ and the return constraint $E\left[X\right(x\left)\right]\ge z$. $v\left(x\right)=(x-x_d)P\left(A_x\right).$
• $x\in [x_u,\infty )$: $X\left(x\right)=x_d{\mathbb{I}}_{\overline{A}}+x_u{\mathbb{I}}_{\overline{B}}=\overline{X}$, where $\overline{A},\overline{B}$ are associated to $\overline{a}$ as in Definition 3.2 satisfying both the capital constraint $\tilde{E}\left[X\left(x\right)\right]=x_r$ and the return constraint $E\left[X\left(x\right)\right]=\overline{z}\ge z$. $v\left(x\right)=(x-x_d)P\left(\overline{A}\right)+(x-x_u)P\left(\overline{B}\right).$

To solve Step 2 of the two-constraint problem Equation (5) and, thus, the main problem Equation (2), we need to minimize

$$\frac{1}{\lambda }\underset{x\in \mathbb{R}}{inf}(v\left(x\right)-\lambda x),$$

where $v\left(x\right)$ has been computed in Theorem 3.10. Depending on the z level in the return constraint being lenient or strict, the solution is sometimes obtained by the two-line configuration, which is optimal to the one-constraint problem and other times obtained by a true three-line configuration. To proceed in this direction, we recall the solution to the one-constraint problem from Li and Xu [22].

Theorem 3.11 (Theorem 2.10 and Remark 2.11 in Li and Xu [22] when $x_u<\infty$)

1. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$. $X=x_r$ is the optimal solution to Step 2: minimization of conditional value-at-risk of the one-constraint problem, and the associated minimal risk is:

$$CVaR\left(X\right)=-x_r$$

2 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$.

• If $\frac{1}{\overline{a}}\le \frac{\lambda -P\left(\overline{A}\right)}{1-\tilde{P}\left(\overline{A}\right)}$ (see Definition 3.2 for the bar-system), then $\overline{X}=x_d{\mathbb{I}}_{\overline{A}}+x_u{\mathbb{I}}_{\overline{D}}$ is the optimal solution to Step 2: minimization of conditional value-at-risk of the one-constraint problem, and the associated minimal risk is:

  $$CVaR\left(\overline{X}\right)=-x_r+\frac{1}{\lambda }(x_u-x_d)(P\left(\overline{A}\right)-\lambda \tilde{P}\left(\overline{A}\right))$$
• Otherwise, let $a^{*}$ be the solution to the equation $\frac{1}{a}=\frac{\lambda -P\left(A\right)}{1-\tilde{P}\left(A\right)}$. Associate sets $A^{*}=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)>a^{*}\right\}$ and $B^{*}=\left\{\omega \in \Omega :\frac{d\tilde{P}}{dP}\left(\omega \right)\le a^{*}\right\}$ to level $a^{*}$. Define $x^{*}=\frac{x_r-x_d\tilde{P}\left(A^{*}\right)}{1-\tilde{P}\left(A^{*}\right)}$, so that configuration

  $$X^{*}=x_d{\mathbb{I}}_{A^{*}}+x^{*}{\mathbb{I}}_{B^{*}}$$

  satisfies the capital constraint $\tilde{E}\left[X^{*}\right]=x_d\tilde{P}\left(A^{*}\right)+x^{*}\tilde{P}\left(B^{*}\right)=x_r$.6, and the associated minimal risk is:

  $$CVaR\left(X^{*}\right)=-x_r+\frac{1}{\lambda }(x^{*}-x_d)(P\left(A^{*}\right)-\lambda \tilde{P}\left(A^{*}\right))$$

Definition 3.12 In part 2 of Theorem 3.11, define $z^{*}=\overline{z}$ in the first case when $\frac{1}{\overline{a}}\le \frac{\lambda -P\left(\overline{A}\right)}{1-\tilde{P}\left(\overline{A}\right)}$; define $z^{*}=E\left[X^{*}\right]$ in the second case when $\frac{1}{\overline{a}}>\frac{\lambda -P\left(\overline{A}\right)}{1-\tilde{P}\left(\overline{A}\right)}$.

We see that when z is smaller than $z^{*}$, the binary solutions, $X^{*}$ and $\overline{X}$, provided in Theorem 3.11 are indeed the optimal solutions to Step 2 of the two-constraint problem. However, when z is greater than $z^{*}$, these two-line configurations are no longer feasible in the two-constraint problem. We now show that the three-line configuration is not only feasible, but also optimal. First, we establish the convexity of the objective function and its continuity in a Lemma.

Lemma 3.13 $v\left(x\right)$ is a convex function for $x\in \mathbb{R}$ and, thus, continuous.

Proposition 3.14 For fixed $-\infty <x_d<x_r<x_u<\infty$ and a fixed level $z\in (z^{*},\overline{z}]$.

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$. The solution, $(a^{**},b^{**},x^{**})$ (and, consequently, $A^{**},B^{**}$ and $D^{**}$), to the equations:

$$\begin{array}{ccc}\hfill x_{d}P\left(A\right)+xP\left(B\right)+x_{u}P\left(D\right)& =z,\hfill & \hfill \left(\text{return}\text{constraint}\right)\\ \hfill x_d\tilde{P}\left(A\right)+x\tilde{P}\left(B\right)+x_u\tilde{P}\left(D\right)& =x_r,\hfill & \hfill \left(\text{capital}\text{constraint}\right)\\ \hfill P\left(A\right)+\frac{\tilde{P}\left(B\right)-bP\left(B\right)}{a-b}-\lambda & =0,\hfill & \hfill \left(\text{first}\text{order}\text{Euler}\text{condition}\right)\end{array}$$

exists. $X^{**}=x_d{\mathbb{I}}_{A^{**}}+x^{**}{\mathbb{I}}_{B^{**}}+x_u{\mathbb{I}}_{D^{**}}$ (what we call the ‘double-star system’) is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

$$CVaR\left(X^{**}\right)=\frac{1}{\lambda }\left((x^{**}-x_d)P\left(A^{**}\right)-\lambda x^{**}\right)$$

Putting together Proposition 3.14 with Theorem 3.11, we arrive at the main theorem of this paper.

Theorem 3.15 (Minimization of conditional value-at-risk when $x_u<\infty$)

For fixed $-\infty <x_d<x_r<x_u<\infty$.

1. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$ and $z=x_r$. The pure money market account investment $X=x_r$ is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

$$CVaR\left(X\right)=-x_r$$

2. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$ and $z\in (x_r,\overline{z}]$. The optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem does not exist, and the minimal risk is:

$$CVaR\left(X\right)=-x_r$$

3. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$ and $z\in [x_r,z^{*}]$ (see Definition 3.12 for $z^{*}$).

• If $\frac{1}{\overline{a}}\le \frac{\lambda -P\left(\overline{A}\right)}{1-\tilde{P}\left(\overline{A}\right)}$ (see Definition 3.2), then the bar-system $\overline{X}=x_d{\mathbb{I}}_{\overline{A}}+x_u{\mathbb{I}}_{\overline{D}}$ is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

  $$CVaR\left(\overline{X}\right)=-x_r+\frac{1}{\lambda }(x_u-x_d)(P\left(\overline{A}\right)-\lambda \tilde{P}\left(\overline{A}\right))$$
• Otherwise, the star-system $X^{*}=x_d{\mathbb{I}}_{A^{*}}+x^{*}{\mathbb{I}}_{B^{*}}$ defined in Theorem 3.11 is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

  $$CVaR\left(X^{*}\right)=-x_r+\frac{1}{\lambda }(x^{*}-x_d)(P\left(A^{*}\right)-\lambda \tilde{P}\left(A^{*}\right))$$

(4)

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$ and $z\in (z^{*},\overline{z}]$. The double-star-system $X^{**}=x_d{\mathbb{I}}_{A^{**}}+x^{**}{\mathbb{I}}_{B^{**}}+x_u{\mathbb{I}}_{D^{**}}$ defined in Proposition 3.14 is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

$$CVaR\left(X^{**}\right)=\frac{1}{\lambda }\left((x^{**}-x_d)P\left(A^{**}\right)-\lambda x^{**}\right)$$

We observe that the pure money market account investment is rarely optimal. When the Radon–Nikodým derivative is bounded above by the reciprocal of the confidence level of the risk measure ($ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$), a condition not satisfied in the Black–Scholes Model, the solution does not exist unless the return requirement coincides with the risk-free rate. When the Radon–Nikodým derivative exceeds $\frac{1}{\lambda }$ with positive probability and the return constraint is low, $z\in [x_r,z^{*}]$, the two-line configuration, which is optimal to the $CVaR$ minimization problem without the return constraint, is also the optimal to the mean-CVaR problem. However, in the more interesting case in which the return constraint is materially high, $z\in (z^{*},\overline{z}]$, the optimal three-line-configuration sometimes takes the value of the upper bound, $x_u$, to raise the expected return at the cost of the minimal risk, which will be at a higher level. This analysis complies with the numerical example shown in Section 2.3.

3.2. Case $x_u=\infty$: No Upper Bound

We first restate the solution to the one-constraint problem from Li and Xu [22] in the current context: when $x_u=\infty$, where we interpret $\overline{A}=\Omega$ and $\overline{z}=\infty$.

Theorem 3.16 (Theorem 2.10 and Remark 2.11 in Li and Xu [22] when $x_u=\infty$)

1. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$. The pure money market account investment $X=x_r$ is the optimal solution to Step 2: minimization of conditional value-at-risk of the one-constraint problem, and the associated minimal risk is:

$$CVaR\left(X\right)=-x_r$$

2. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$. The star-system $X^{*}=x_d{\mathbb{I}}_{A^{*}}+x^{*}{\mathbb{I}}_{B^{*}}$ defined in Theorem 3.11 is the optimal solution to Step 2: minimization of conditional value-at-risk of the one-constraint problem, and the associated minimal risk is:

$$CVaR\left(X^{*}\right)=-x_r+\frac{1}{\lambda }(x^{*}-x_d)(P\left(A^{*}\right)-\lambda \tilde{P}\left(A^{*}\right))$$

We observe that although there is no upper bound for the portfolio value, the optimal solution remains bounded from above, and the minimal $CVaR$ is bounded from below. The problem of purely minimizing $CVaR$ risk of a self-financing portfolio (bounded below by $x_d$ to exclude arbitrage) from initial capital, $x_0$, is feasible in the sense that the risk will not approach $-\infty$, and the minimal risk is achieved by an optimal portfolio. When we add substantial return constraint to the $CVaR$ minimization problem, although the minimal risk can still be calculated in the most important case (Case 4 in Theorem 3.17), it is truly an infimum and not a minimum, thus it can be approximated closely by a sub-optimal portfolio, but not achieved by an optimal portfolio.

Theorem 3.17 (Minimization of Conditional Value-At-Risk When $x_u=\infty$)

For fixed $-\infty <x_d<x_r<x_u=\infty$.

1. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$ and $z=x_r$. The pure money market account investment $X=x_r$ is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

$$CVaR\left(X\right)=-x_r$$

2. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}\le \frac{1}{\lambda }$ and $z\in (x_r,\infty )$. The optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem does not exist, and the minimal risk is:

$$CVaR\left(X\right)=-x_r$$

3. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$ and $z\in [x_r,z^{*}]$. The star-system $X^{*}=x_d{\mathbb{I}}_{A^{*}}+x^{*}{\mathbb{I}}_{B^{*}}$ defined in Theorem 3.11 is the optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem, and the associated minimal risk is:

$$CVaR\left(X^{*}\right)=-x_r+\frac{1}{\lambda }(x^{*}-x_d)(P\left(A^{*}\right)-\lambda \tilde{P}\left(A^{*}\right))$$

4. 

Suppose $ess\; sup\frac{d\tilde{P}}{dP}>\frac{1}{\lambda }$ and $z\in (z^{*},\infty )$. The optimal solution to Step 2: minimization of conditional value-at-risk of the two-constraint problem does not exist, and the minimal risk is:

$$CVaR\left(X^{*}\right)=-x_r+\frac{1}{\lambda }(x^{*}-x_d)(P\left(A^{*}\right)-\lambda \tilde{P}\left(A^{*}\right))$$

Remark 3.18 From the proof of the above theorem in the Appendix, we note that in Case 4, we can always find a three-line configuration as a sub-optimal solution, i.e., there exists for every $ϵ>0$ a corresponding portfolio $X_{ϵ}=x_d{\mathbb{I}}_{A_{ϵ}}+x_{ϵ}{\mathbb{I}}_{B_{ϵ}}+{\alpha }_{ϵ}{\mathbb{I}}_{D_{ϵ}}$, which satisfies the general constraints and produces a $CVaR$ level close to the lower bound: $CVaR\left(X_{ϵ}\right)\le CVaR\left(X^{*}\right)+ϵ.$

4. Future Work

The second part of Assumption 2.1, namely the Radon–Nikodým derivative, $\frac{d\tilde{P}}{dP}$, having a continuous distribution, is imposed for the simplification it brings to the presentation in the main theorems. Further work can be done when this assumption is weakened. We expect that the main results should still hold, albeit in a more complicated form.7 It will also be interesting to extend the closed-form solution for mean-CVaR minimization by replacing CVaR with law-invariant convex risk measures in general. Another direction will be to employ dynamic risk measures into the current setting.

Although in this paper we focus on the complete market solution, to solve the problem in an incomplete market setting, which includes stochastic volatility or jump models, the exact hedging argument via the martingale representation theorem that translates the dynamic problem Equation (1) into the static problem Equation (2) has to be replaced by a super-hedging argument via the optional decomposition developed by Kramkov [30] and Föllmer and Kabanov [31]. The detail is similar to the process carried out for shortfall risk minimization in Föllmer and Leukert [26], convex risk minimization in Rudloff [32] and law-invariant risk preference in He and Zhou [25]. The curious question is: Will the three-line configuration remain optimal?