Optimal Deterministic Investment Strategies for Insurers
Abstract
:1. Introduction
2. The Model
3. Transformation of MV to an Ordinary Stochastic Control Problem
4. Solution of MV for a Classical Adapted Investor
5. MV Problem for an Investor with Deterministic Investment Strategies
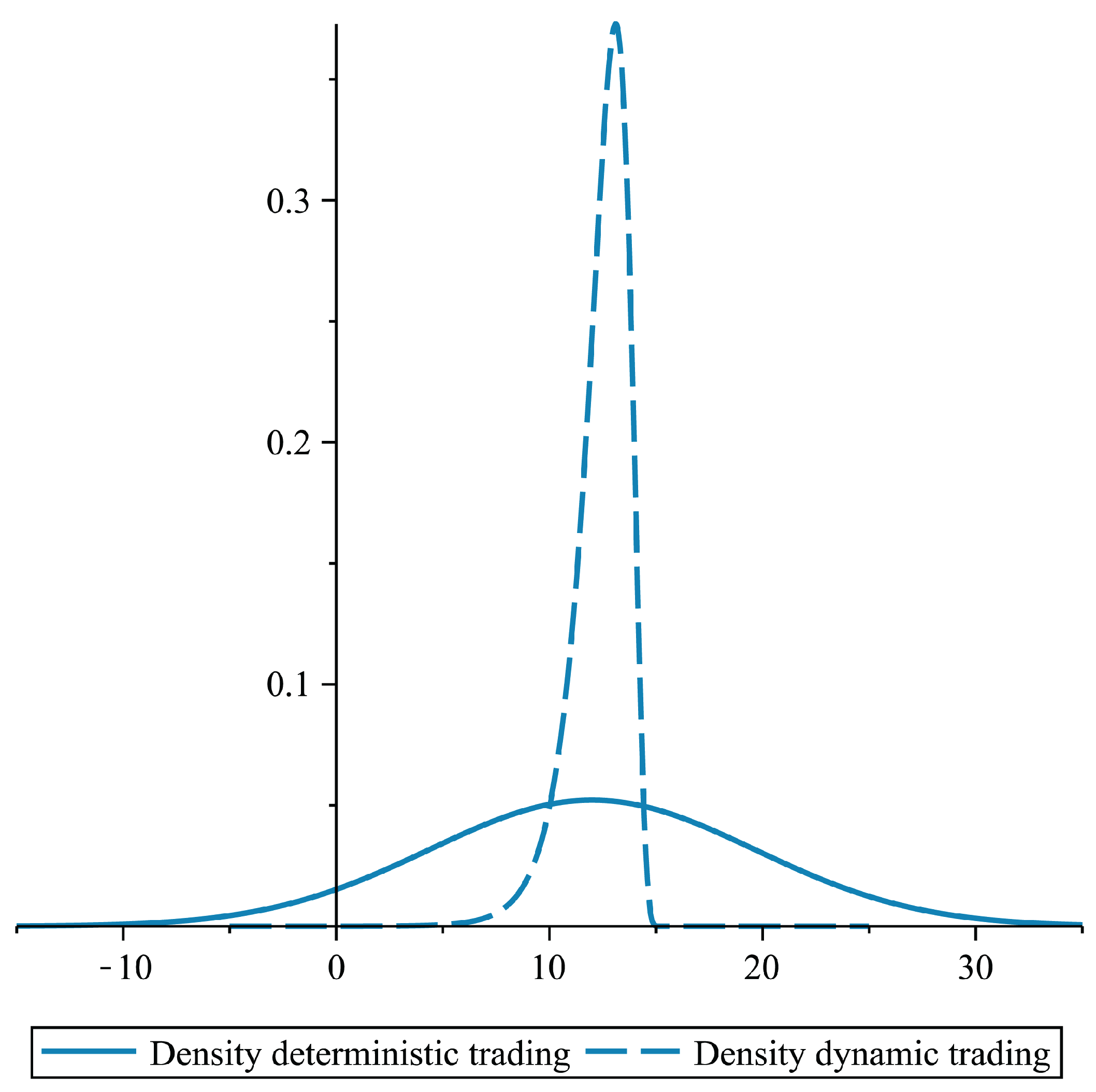
6. More General Mean-Risk Problems and Other Optimization Criteria
6.1. More General Mean-Risk Problems
6.2. Maximizing Exponential Utility of Terminal Wealth
6.3. Minimizing the Probability of Ruin
7. Problems with Lévy Processes
8. Conclusions
Conflicts of Interest
References
- M. Christiansen, and M. Steffensen. “Deterministic mean-variance-optimal consumption and investment.” Stochastics 85 (2013): 620–636. [Google Scholar] [CrossRef]
- S. Browne. “Optimal investment policies for a firm with a random risk process: Exponential utility and minimizing the probability of ruin.” Math. Oper. Res. 20 (1995): 937–958. [Google Scholar] [CrossRef]
- Y. Zeng, and Z. Li. “Optimal time-consistent investment and reinsurance policies for mean-variance insurers.” Insur. Math. Econom. 49 (2011): 145–154. [Google Scholar] [CrossRef]
- W.H. Fleming, and H.M. Soner. Controlled Markov Processes and Viscosity Solutions. New York, NY, USA: Springer, 2006. [Google Scholar]
- X.Y. Zhou, and D. Li. “Continuous-time mean-variance portfolio selection: A stochastic LQ framework.” Appl. Math. Optim. 42 (2000): 19–33. [Google Scholar] [CrossRef]
- P. Antolin, S. Payet, and J. Yermo. “Assessing default investment strategies in defined contribution pension plans.” OECD J.: Financ. Mark. Trends 1 (2010): 1–29. [Google Scholar]
- R. Korn, and S. Trautmann. “Continuous-time portfolio optimization under terminal wealth constraints.” ZOR—Math. Methods Oper. Res. 42 (1995): 69–92. [Google Scholar] [CrossRef]
- D. Li, and W.L. Ng. “Optimal dynamic portfolio selection: Multiperiod mean-variance formulation.” Math. Financ. 10 (2000): 387–406. [Google Scholar] [CrossRef]
- Ł. Delong, and R. Gerrard. “Mean-variance portfolio selection for a non-life insurance company.” Math. Methods Oper. Res. 66 (2007): 339–367. [Google Scholar]
- W. Guo, and C. Xu. “Optimal portfolio selection when stock prices follow a jump-diffusion process.” Math. Methods Oper. Res. 60 (2004): 485–496. [Google Scholar] [CrossRef]
- N. Bäuerle, and A. Blatter. “Optimal control and dependence modeling of insurance portfolios with Lévy dynamics.” Insur. Math. Econom. 48 (2011): 398–405. [Google Scholar] [CrossRef]
- B. Øksendal, and A. Sulem. Applied Stochastic Control of Jump Diffusions. Berlin, Germany: Springer, 2007. [Google Scholar]
- N. Bäuerle. “Benchmark and mean-variance problems for insurers.” Math. Methods Oper. Res. 62 (2005): 159–165. [Google Scholar] [CrossRef]
- O.S. Alp, and R. Korn. “Continuous-time mean-variance portfolios: A comparison.” Optimization 62 (2013): 961–973. [Google Scholar] [CrossRef]
- S. Basak, and G. Chabakauri. “Dynamic mean-variance asset allocation.” Rev. Financ. 23 (2010): 2970–3016. [Google Scholar] [CrossRef]
- E.M. Kryger, and M. Stefensen. “Some Solvable Portfolio Problems With Quadratic and Collective Objectives.” 2010. Available online at http://ssrn.com/abstract=1577265 (accessed on 1 October 2013).
- N. Bäuerle, and U. Rieder. Markov Decision Processes With Applications to Finance. Heidelberg, Germany: Springer, 2011. [Google Scholar]
- J. Yong, and X.Y. Zhou. Stochastic Controls. New York, NY, USA: Springer, 1999. [Google Scholar]
- G. Chamberlain. “A characterization of the distributions that imply mean variance utility functions.” JET 29 (1983): 185–201. [Google Scholar] [CrossRef]
- H. Levy, and H.M. Markowitz. “Approximating expected utility by a function of mean and variance.” Am. Econ. Rev. 69 (1979): 308–317. [Google Scholar]
- N. Bäuerle, and E. Bayraktar. “A note on applications of stochastic ordering to control problems in insurance and finance.” Stochastics, 2013. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bäuerle, N.; Rieder, U. Optimal Deterministic Investment Strategies for Insurers. Risks 2013, 1, 101-118. https://doi.org/10.3390/risks1030101
Bäuerle N, Rieder U. Optimal Deterministic Investment Strategies for Insurers. Risks. 2013; 1(3):101-118. https://doi.org/10.3390/risks1030101
Chicago/Turabian StyleBäuerle, Nicole, and Ulrich Rieder. 2013. "Optimal Deterministic Investment Strategies for Insurers" Risks 1, no. 3: 101-118. https://doi.org/10.3390/risks1030101
APA StyleBäuerle, N., & Rieder, U. (2013). Optimal Deterministic Investment Strategies for Insurers. Risks, 1(3), 101-118. https://doi.org/10.3390/risks1030101



