Elemental Feature Extraction from Historical Pigments Through X-Ray Fluorescence Spectroscopy and Unsupervised Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Pigment Dataset
2.2. XRF Measurements
2.3. Methodology
2.3.1. Data Pre-Processing
2.3.2. Multivariate Statistical Analysis
3. Results and Discussion
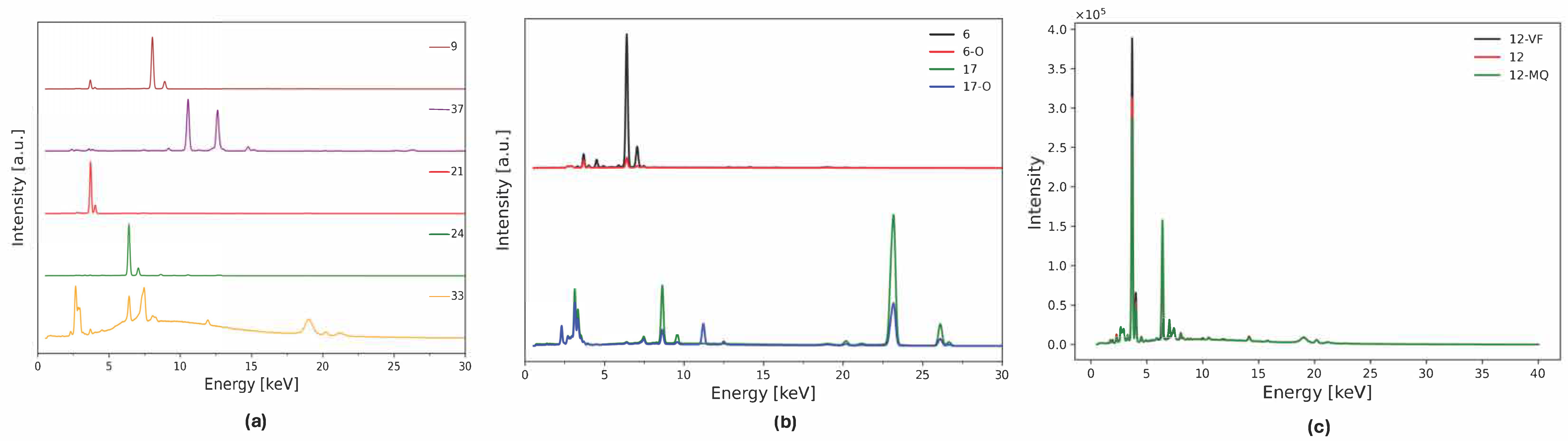
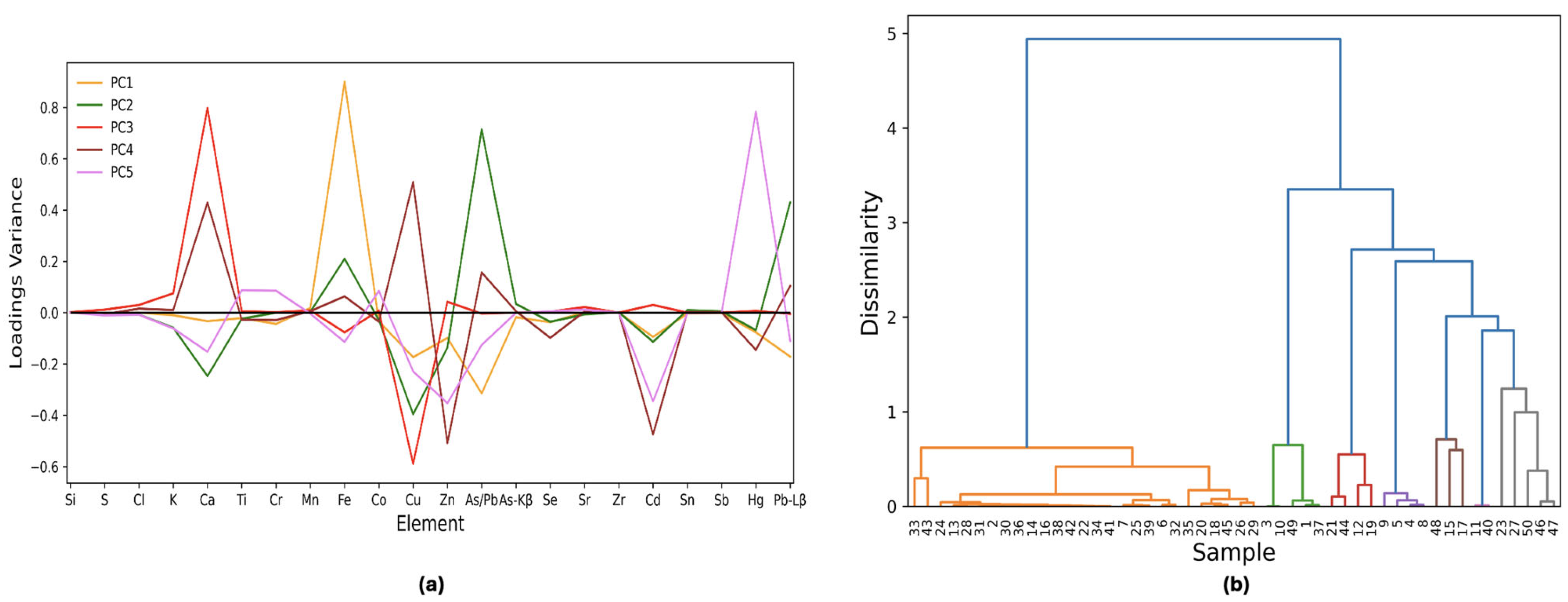
3.1. Machine Learning Applied to the Semiquantitative Dataset
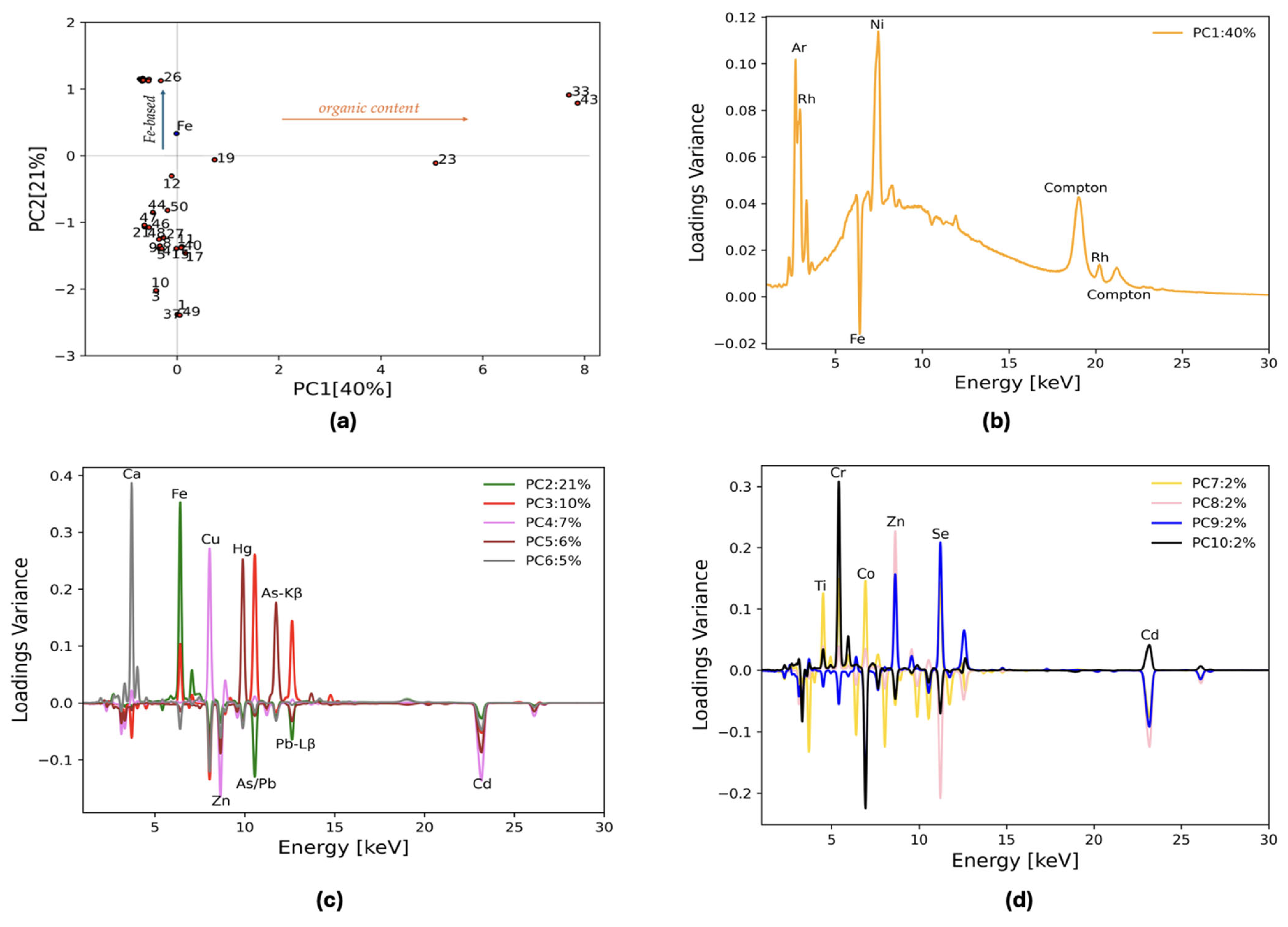
3.2. Machine Learning Approach Applied to the Raw Dataset
3.3. Validation Matrix
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coccato, A.; Caggiani, M.C. An overview of Principal Components Analysis approaches in Raman studies of cultural heritage materials. J. Raman Spectrosc. 2024, 55, 125. [Google Scholar] [CrossRef]
- Alfeld, M.; Viguerie, L.D. Recent developments in spectroscopic imaging techniques for historical paintings—A review. Spectrochim. Acta Part B At. Spectrosc. 2017, 136, 81–105. [Google Scholar] [CrossRef]
- Harth, A. X-ray fluorescence (XRF) on painted heritage objects: A review using topic modeling. Herit. Sci. 2024, 12, 17. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Z.; Liu, X. Spectroscopic Techniques for Identifying Pigments in Polychrome Cultural Relics. Coatings. 2025, 15, 20. [Google Scholar] [CrossRef]
- Moretti, P.; Zumbühl, S.; Caruso, O.; Gammaldi, N.; Iazurlo, P.; Piqué, F. The Characterization of the Materials Used by Gino Severini in his 20th C Wall Paintings at Semsales in Switzerland. Appl. Sci. 2021, 11, 9161. [Google Scholar] [CrossRef]
- Zuena, M.; Pensabene Buemi, L.; Nodari, L.; Subelytė, G.; Stringari, L.; Campanella, B.; Lorenzetti, G.; Palleschi, V.; Tomasin, P.; Legnaioli, S. Portrait of an artist at work: Exploring Max Ernst’s surrealist techniques. Herit. Sci. 2022, 10, 139. [Google Scholar] [CrossRef]
- Molari, R.; Appoloni, C.R. Pigment analysis in four paintings by Vincent van Gogh by portable X-ray fluorescence (pXRF). Radiat. Phys. Chem. 2021, 181, 109336. [Google Scholar] [CrossRef]
- Zhang, L.; Song, Z.; Zuo, S.; Hou, F.; Chen, S. Precise in-situ detection of inorganic pigments in ancient architectural color paintings by HH-XRF. Herit. Sci. 2023, 11, 230. [Google Scholar] [CrossRef]
- Klisińska-Kopacz, A.; Frączek, P.; Obarzanowski, M.; Czop, J. Non-Invasive Study of Pigment Palette Used by Olga Boznańska Investigated with Analytical Imaging, XRF, and FTIR Spectroscopy. Heritage 2023, 6, 1429–1443. [Google Scholar] [CrossRef]
- Pimenta, A.; Felix, V.; Oliveira, M.; Andrade, M.; Oliveira, M.; Freitas, R. Investigating Brazilian Paintings from the 19th Century by MA-XRF. Quantum Beam Sci. 2023, 7, 9. [Google Scholar] [CrossRef]
- Nardes, R.C.; Popelka-Filcoff, R.; Robertson, J.D.; Glascock, M.; Descantes, C. Analysis of the pigments in two modern Egyptian papyri using XRF technique. Braz. J. Radiat. Sci. 2021, 9, 1–16. [Google Scholar] [CrossRef]
- Mzyk, Z.; Baranowska, I.; Mzyk, J. Research on grain size effect in XRF analysis of pelletized samples. X-Ray Spectrom. 2002, 31, 39–46. [Google Scholar] [CrossRef]
- Nuchdang, S.; Niyomsat, T.; Pitiphatharabun, S.; Sukhummek, B.; Leelanupat, O.; Rattanaphra, D. Effect of grain size and moisture content on major and minor elements concentrations using portable X-ray fluorescence. J. Phys. Conf. Ser. 2018, 1144, 012060. [Google Scholar] [CrossRef]
- Shaltout, A.A.; Welz, B.; Ibrahim, M.A. Influence of the grain size on the quality of standardless WDXRF analysis of river Nile sediments. Microchem. J. 2011, 99, 356–363. [Google Scholar] [CrossRef]
- Erlandson, J.M.; Robertson, J.D.; Descantes, C. Geochemical Analysis of Eight Red Ochres from Western North America. Am. Antiq. 1999, 64, 517–526. [Google Scholar] [CrossRef]
- Popelka-Filcoff, R.S.; Robertson, J.D.; Glascock, M.D.; Descantes, C. Trace element characterization of ochre from geological sources. J. Radioanal. Nucl. Chem. 2007, 272, 17–27. [Google Scholar] [CrossRef]
- Fontana, D.; Alberghina, M.F.; Barracoa, R.; Basilec, S.; Tranchina, L.; Brai, M.; Gueli, A.; Troja, S.O. Historical pigments characterisation by quantitative X-ray fluorescence. J. Cult. Herit. 2014, 15, 266–274. [Google Scholar] [CrossRef]
- Izzo, F.C.; Berg, K.J.V.B.; Keulen, H.V.; Ferriani, B.; Zendri, E. Modern Oil Paints—Formulations, Organic Additives and Degradation: Some Case Studies. Issues Contemp. Oil Paint. 2014, 75–104. [Google Scholar] [CrossRef]
- Izzo, F.C.; Balliana, E.; Pinton, F.; Zendri, E. A preliminary study of the composition of commercial oil, acrylic and vinyl paints and their behaviour after accelerated ageing conditions. Conserv. Sci. Cult. Herit. 2014, 14, 353–369. [Google Scholar]
- Towarek, A.; Halicz, L.; Matwin, S.; Wagner, B. Machine learning in analytical chemistry for cultural heritage: A comprehensive review. J. Cult. Herit. 2024, 70, 64–70. [Google Scholar] [CrossRef]
- Andric, V.; Kvascev, G.; Cvetanovic, M.; Cvetanovic, M.; Stojanovic, S.; Bacanin, N.; Gajic-Kvascev, M. Deep learning assisted XRF spectra classification. Sci. Rep. 2024, 14, 3666. [Google Scholar] [CrossRef] [PubMed]
- Arjonilla, P.; Domínguez-Vidal, A.; Domene, R.R.; Gómez, E.C.; Torre-López, M.J.D.L.; Ayora-Cañada, M.J. Characterization of Wall Paintings of the Harem Court in the Alhambra Monumental Ensemble: Advantages and Limitations of In Situ Analysis. Molecules 2022, 27, 1490. [Google Scholar] [CrossRef] [PubMed]
- Uzunoğlu, Z.; Yılmaz, D.; Şahin, Y. Quantitative x-ray spectrometric analysis with peak to Compton ratios. Radiat. Phys. Chem. 2015, 112, 189–194. [Google Scholar] [CrossRef]
- Festa, G.; Scatigno, C.; Armetta, F.; Saladino, M.L.; Ciaramitaro, V.; Nardo, V.M.; Ponterio, R.C. Chemometric Tools to Point Out Benchmarks and Chromophores in Pigments through Spectroscopic Data Analyses. Molecules 2022, 27, 163. [Google Scholar] [CrossRef]
- Renda, V.; Nardo, V.M.; Anastasio, G.; Caponetti, E.; Vasi, C.S.; Saladino, M.L.; Armetta, F.; Trusso, S.; Ponterio, R.C. A multivariate statistical approach of X-ray fluorescence characterization of a large collection of reverse glass paintings. Spectrochim. Acta Part B At. Spectrosc. 2019, 159, 105655. [Google Scholar] [CrossRef]
- García-Florentino, C.; Maguregui, M.; Morillas, H.; Marcaida, I.; Madariaga, J.M. A fast in situ non-invasive approach to classify mortars from a construction of high historical value. Microchem. J. 2017, 133, 104–113. [Google Scholar] [CrossRef]
- Cortea, I.M.; Ghervase, L.; Rădvan, R.; Serițan, G. Assessment of Easily Accessible Spectroscopic Techniques Coupled with Multivariate Analysis for the Qualitative Characterization and Differentiation of Earth Pigments of Various Provenance. Minerals 2022, 12, 755. [Google Scholar] [CrossRef]
- Amadori, M.L.; Poldi, G.; Germinario, G.; Arduini, J.; Mengacci, V. Spectroscopic and Imaging Analyses on Easel Paintings by Giovanni Santi. Appl. Sci. 2023, 13, 3581. [Google Scholar] [CrossRef]
- Sherman, J. The theoretical derivation of fluorescent X-ray intensities from mixtures. Spectrochim. Acta. 1955, 7, 283–306. [Google Scholar] [CrossRef]
- Rousseau, R.M. Corrections for matrix effects in X-ray fluorescence analysis—A tutorial. Spectrochim. Acta Part B At. Spectrosc. 2006, 61, 759–777. [Google Scholar] [CrossRef]
- Scatigno, C.; Teodonio, L.; Rocco, E.D.; Festa, G. Spectroscopic Benchmarks by Machine Learning as Discriminant Analysis for Unconventional Italian Pictorialism Photography. Polymers 2024, 16, 1850. [Google Scholar] [CrossRef]
- Armetta, F.; Saladino, M.L.; Martinelli, M.C.; Vilardo, R.; Anastasio, G.; Trusso, S.; Nardo, V.M.; Giuffrida, D.; Ponterio, R.C. Improved chemometric approach for XRF data treatment: Application to the reverse glass paintings from the Lipari collection. RSC Adv. 2023, 13, 4495–4503. [Google Scholar] [CrossRef]
- Sciutto, G.; Oliveri, P.; Prati, S.; Quaranta, M.; Bersani, S.; Mazzeo, R. An advanced multivariate approach for processing X-ray fluorescence spectral and hyperspectral data from non-invasive in situ analyses on painted surfaces. Anal. Chim. Acta. 2012, 752, 30–38. [Google Scholar] [CrossRef]
- Capobianco, G.; Pelosi, C.; Agresti, G.; Bonifazi, G.; Santamaria, U.; Serrant, S. X-ray fluorescence investigation on yellow pigments based on lead, tin and antimony through the comparison between laboratory and portable instruments. J. Cult. Herit. 2018, 29, 19–29. [Google Scholar] [CrossRef]
- Cortea, I.M.; Chiroşca, A.; Angheluţă, L.M.; Seriţan, G. INFRA-ART: An Open Access Spectral Library of Art-related Materials as a Digital Support Tool for Cultural Heritage Science. J. Comput. Cult. Herit. 2023, 40, 11. Available online: https://infraart.inoe.ro/ (accessed on 19 June 2025). [CrossRef]
- Habashi, F. Pigments through the Ages. Interceram-Int. Ceram. Rev. 2016, 65, 4–5. [Google Scholar] [CrossRef]
- Švarcová, S.; Hradil, D.; Hradilová, J.; Čermáková, Z. Pigments—Copper-based greens and blues. Archaeol Anthr. Sci. 2021, 13, 190. [Google Scholar] [CrossRef]
- Barnett, J.R.; Miller, S.; Pearce, E. Colour and art: A brief history of pigments. Opt. Laser Technol. 2006, 38, 445–453. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliverio, I.; Scatigno, C.; Festa, G. Elemental Feature Extraction from Historical Pigments Through X-Ray Fluorescence Spectroscopy and Unsupervised Machine Learning. Chemosensors 2025, 13, 314. https://doi.org/10.3390/chemosensors13080314
Oliverio I, Scatigno C, Festa G. Elemental Feature Extraction from Historical Pigments Through X-Ray Fluorescence Spectroscopy and Unsupervised Machine Learning. Chemosensors. 2025; 13(8):314. https://doi.org/10.3390/chemosensors13080314
Chicago/Turabian StyleOliverio, Ivan, Claudia Scatigno, and Giulia Festa. 2025. "Elemental Feature Extraction from Historical Pigments Through X-Ray Fluorescence Spectroscopy and Unsupervised Machine Learning" Chemosensors 13, no. 8: 314. https://doi.org/10.3390/chemosensors13080314
APA StyleOliverio, I., Scatigno, C., & Festa, G. (2025). Elemental Feature Extraction from Historical Pigments Through X-Ray Fluorescence Spectroscopy and Unsupervised Machine Learning. Chemosensors, 13(8), 314. https://doi.org/10.3390/chemosensors13080314






