Analytical Study of the Detection Model for Sulphate Saline Soil Based on Mid-Infrared Spectrometry
Abstract
1. Introduction
2. Materials and Methods
2.1. Spiking Treatments and Sample Preparation
2.2. Data Preprocessing and Spectral Measurements
- (1)
- Savitzky–Golay filtering (SG)
- (2)
- Baseline
- (3)
- Standard normal variate transform (SNV)
- (4)
- Multiplicative scatter correction (MSC)
- (5)
- Derivative
2.3. Outliers Rejection and Identification of Key Wavelengths
2.4. Models Used in Spectral Data Processing
2.5. Model Performance Criteria
3. Results
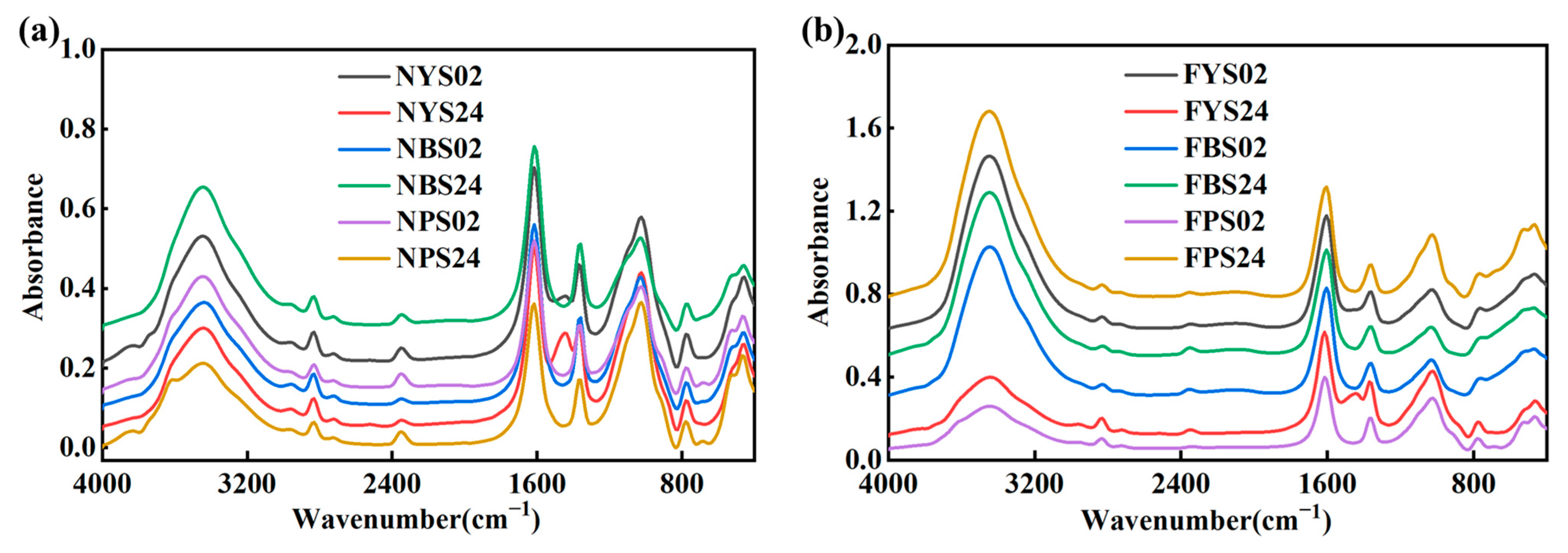
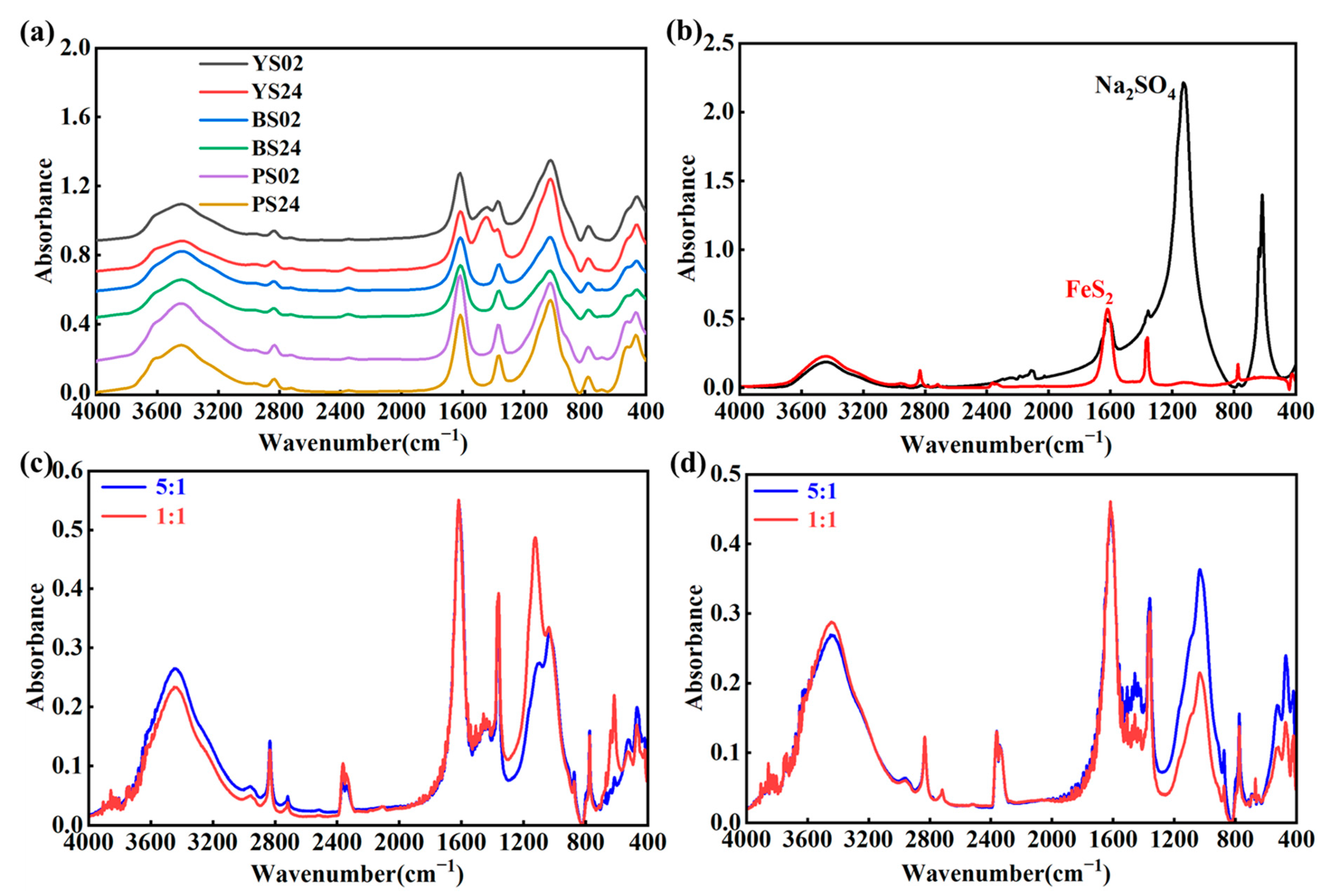
3.1. Spectral Features
3.2. Data Preprocessing
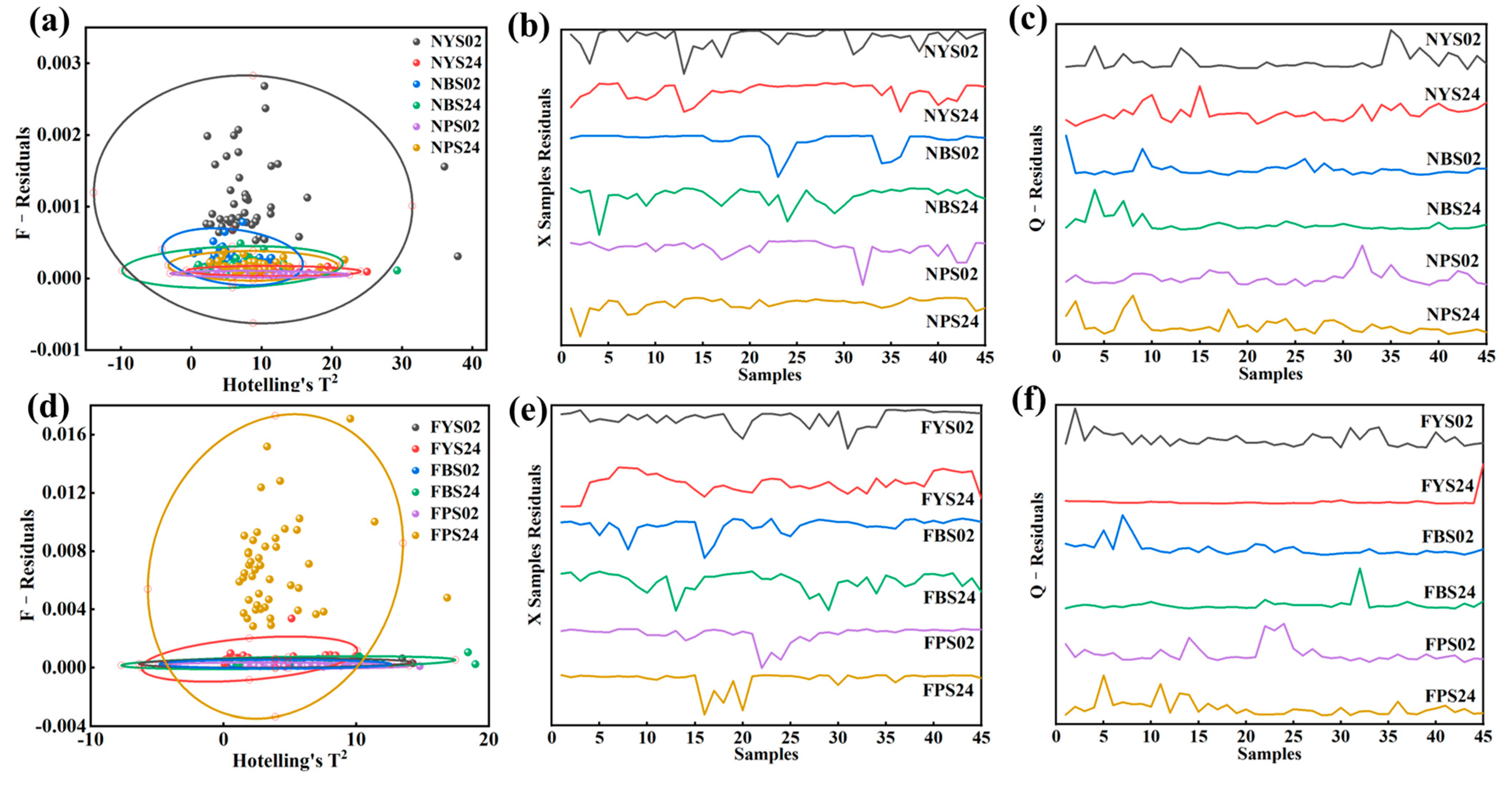
3.3. Outlier Rejection
3.4. Identification of Key Wavelengths
3.5. Establishment and Validation of Regression Models
3.5.1. Regression Modeling of Soluble Salts
3.5.2. Regression Modeling of Sulfide
4. Discussion
4.1. Interpretation of Mid-Infrared Spectra
4.2. Comparison of Chemometrics Methods with Deep Learning Methods
4.3. Excellent Performance of MLR
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Radha, B.; Sunitha, N.C.; Sah, R.P.; Tp, M.A.; Krishna, G.; Umesh, D.K.; Thomas, S.; Anilkumar, C.; Upadhyay, S.; Kumar, A. Physiological and molecular implications of multiple abiotic stresses on yield and quality of rice. Front. Plant Sci. 2023, 13, 996514. [Google Scholar] [CrossRef] [PubMed]
- Hopmans, J.W.; Qureshi, A.; Kisekka, I.; Munns, R.; Grattan, S.; Rengasamy, P.; Ben-Gal, A.; Assouline, S.; Javaux, M.; Minhas, P. Critical knowledge gaps and research priorities in global soil salinity. Adv. Agron. 2021, 169, 1–191. [Google Scholar]
- Santhanam, M.; Cohen, M.D.; Olek, J. Sulfate attack research—Whither now? Cem. Concr. Res. 2001, 31, 845–851. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, L.; Yu, W.; Yang, Y.; Teng, H.; Shi, Z. Improving TMPA 3B43 V7 data sets using land-surface characteristics and ground observations on the Qinghai–Tibet Plateau. IEEE Geosci. Remote Sens. Lett. 2018, 15, 178–182. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Yu, D.; Ma, X.; Zhang, Z.; Ge, X.; Teng, D.; Li, X.; Liang, J.; Lizaga, I. Capability of Sentinel-2 MSI data for monitoring and mapping of soil salinity in dry and wet seasons in the Ebinur Lake region, Xinjiang, China. Geoderma 2019, 353, 172–187. [Google Scholar] [CrossRef]
- Wang, N.; Xue, J.; Peng, J.; Biswas, A.; He, Y.; Shi, Z. Integrating remote sensing and landscape characteristics to estimate soil salinity using machine learning methods: A case study from Southern Xinjiang, China. Remote Sens. 2020, 12, 4118. [Google Scholar] [CrossRef]
- Dent, D.; Pons, L. A world perspective on acid sulphate soils. Geoderma 1995, 67, 263–276. [Google Scholar] [CrossRef]
- Fanning, D.S.; Rabenhorst, M.C.; Fitzpatrick, R.W. Historical developments in the understanding of acid sulfate soils. Geoderma 2017, 308, 191–206. [Google Scholar] [CrossRef]
- Nelson, M.D.; Riitters, K.H.; Coulston, J.W.; Domke, G.M.; Greenfield, E.J.; Langner, L.L.; Nowak, D.J.; O’Dea, C.B.; Oswalt, S.N.; Reeves, M.C.; et al. Defining the United States land base: A technical document supporting the USDA Forest Service 2020 RPA assessment. Gen. Tech. Rep. NRS-191 2020, 191, 1–70. [Google Scholar]
- Douglas, R.; Nawar, S.; Alamar, M.C.; Coulon, F.; Mouazen, A.M. Almost 25 years of chromatographic and spectroscopic analytical method development for petroleum hydrocarbons analysis in soil and sediment: State-of-the-art, progress and trends. Crit. Rev. Environ. Sci. Technol. 2017, 47, 1497–1527. [Google Scholar] [CrossRef]
- Siesler, H.W.; Ozaki, Y.; Kawata, S.; Heise, H.M. Near-Infrared Spectroscopy: Principles, Instruments, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Barra, I.; Haefele, S.M.; Sakrabani, R.; Kebede, F. Soil spectroscopy with the use of chemometrics, machine learning and pre-processing techniques in soil diagnosis: Recent advances—A review. TrAC Trends Anal. Chem. 2021, 135, 116166. [Google Scholar] [CrossRef]
- Helfenstein, A.; Baumann, P.; Viscarra Rossel, R.; Gubler, A.; Oechslin, S.; Six, J. Quantifying soil carbon in temperate peatlands using a mid-IR soil spectral library. Soil 2021, 7, 193–215. [Google Scholar] [CrossRef]
- Xing, Z.; Du, C.; Tian, K.; Ma, F.; Shen, Y.; Zhou, J. Application of FTIR-PAS and Raman spectroscopies for the determination of organic matter in farmland soils. Talanta 2016, 158, 262–269. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Zhang, T.; Sun, Y.; Tang, H.; Li, H. A hybrid variable selection method based on wavelet transform and mean impact value for calorific value determination of coal using laser-induced breakdown spectroscopy and kernel extreme learning machine. Spectrochim. Acta Part B At. Spectrosc. 2019, 154, 75–81. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, X.; Zhang, Y.; Qi, Z.; Zhang, H.; Xu, Z. Mapping multi-depth soil salinity using remote sensing-enabled machine learning in the yellow river delta, China. Remote Sens. 2023, 15, 5640. [Google Scholar] [CrossRef]
- Lotfollahi, L.; Delavar, M.A.; Biswas, A.; Fatehi, S.; Scholten, T. Spectral prediction of soil salinity and alkalinity indicators using visible, near-, and mid-infrared spectroscopy. J. Environ. Manag. 2023, 345, 118854. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Shi, Z.; Li, B.; Sun, F.; Miao, T.; Shi, Z.; Chen, S.; Yang, M.; Ji, W. Prediction of soil properties in a field in typical black soil areas using in situ MIR spectra and its comparison with vis-NIR spectra. Remote Sens. 2023, 15, 2053. [Google Scholar] [CrossRef]
- Canero, F.M.; Rodriguez-Galiano, V.; Aragones, D. Machine Learning and Feature Selection for soil spectroscopy. An evaluation of Random Forest wrappers to predict soil organic matter, clay, and carbonates. Heliyon 2024, 10, e30228. [Google Scholar] [CrossRef]
- Zhan, D.; Liu, Y.; Yang, W.; Lu, M.; Song, Y. Spatial variability of soil salinity in coastal saline-alkali farmlands: A novel approach integrating a stacked model with the reconstructed in-situ hyperspectral feature. Comput. Electron. Agric. 2025, 235, 110376. [Google Scholar] [CrossRef]
- dos Santos, E.P.; Moreira, M.C.; Fernandes-Filho, E.I.; Demattê, J.A.M.; Santos, U.J.D.; Moura-Bueno, J.M.; Cruz, R.R.P.; da Silva, D.D.; de Sá Barreto Sampaio, E.V. Integrating satellite radar vegetation indices and environmental descriptors with visible-infrared soil spectroscopy improved organic carbon prediction in soils of semi-arid Brazil. Geoderma 2025, 457, 117288. [Google Scholar] [CrossRef]
- Xia, Y.; Cheng, X.; Hu, X. Soil organic matter content prediction in tobacco fields based on hyperspectral remote sensing and generative adversarial network data augmentation. Comput. Electron. Agric. 2025, 233, 110164. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Lieber, C.A.; Mahadevan-Jansen, A. Automated method for subtraction of fluorescence from biological Raman spectra. Appl. Spectrosc. 2003, 57, 1363–1367. [Google Scholar] [CrossRef]
- Barnes, R.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Geladi, P.; MacDougall, D.; Martens, H. Linearization and scatter-correction for near-infrared reflectance spectra of meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Rinnan, Å.; Van Den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Mehmood, T. Hotelling T2 based variable selection in partial least squares regression. Chemom. Intell. Lab. Syst. 2016, 154, 23–28. [Google Scholar] [CrossRef]
- Connelly, L.M. Introduction to Analysis of Variance (ANOVA). Medsurg Nursing. 2021, 30, 3. [Google Scholar] [CrossRef]
- Chen, J. A residual-based approach to validate Q-matrix specifications. Appl. Psychol. Meas. 2017, 41, 277–293. [Google Scholar] [CrossRef]
- Ma, Y.; Roudier, P.; Kumar, K.; Palmada, T.; Grealish, G.; Carrick, S.; Lilburne, L.; Triantafilis, J. A soil spectral library of New Zealand. Geoderma Reg. 2023, 35, e00726. [Google Scholar] [CrossRef]
- Mevik, B.H.; Wehrens, R. The pls package: Principal component and partial least squares regression in R. J. Stat. Softw. 2007, 18, 1–23. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Forrester, S.T.; Grocke, S.F.; Fitzpatrick, R.W.; McLaughlin, M.J. The use of mid-infrared diffuse reflectance spectroscopy for acid sulfate soil analysis. Sci. Total Environ. 2019, 646, 1489–1502. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, I.; Lin, K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar]
- Williams, P.; Thompson, B. BY NEAR INFRARED REFLECTANCE SPECTROSCOPY (NRS). Cereal Chem. 1978, 55, 1014–1037. [Google Scholar]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Fründ, H.-C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T.; Ben-Dor, E.; Brown, D.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Li, X.; Fan, P.; Qiu, H.; Liu, Y. Optimizing soil carbon content prediction performance by multi-band feature fusion based on visible near-infrared spectroscopy. J. Soils Sediments 2024, 24, 1333–1347. [Google Scholar] [CrossRef]
- Engel, J.; Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Downey, G.; Blanchet, L.; Buydens, L.M. Breaking with trends in pre-processing? TrAC Trends Anal. Chem. 2013, 50, 96–106. [Google Scholar] [CrossRef]
- Xiaobo, Z.; Jiewen, Z.; Povey, M.J.; Holmes, M.; Hanpin, M. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef]
- Hezel, A.T.; Ross, S. Forbidden transitions in the infra-red spectra of tetrahedral anions—III. Spectra-structure correlations in perchlorates, sulphates and phosphates of the formula MXO4. Spectrochim. Acta 1966, 22, 1949–1961. [Google Scholar] [CrossRef]
- Grodzicki, A.; Piszczek, P. A new interpretation of abnormal shift of water molecules’ bending vibration frequencies in kieserite family monohydrates. J. Mol. Struct. 1998, 443, 141–147. [Google Scholar] [CrossRef]
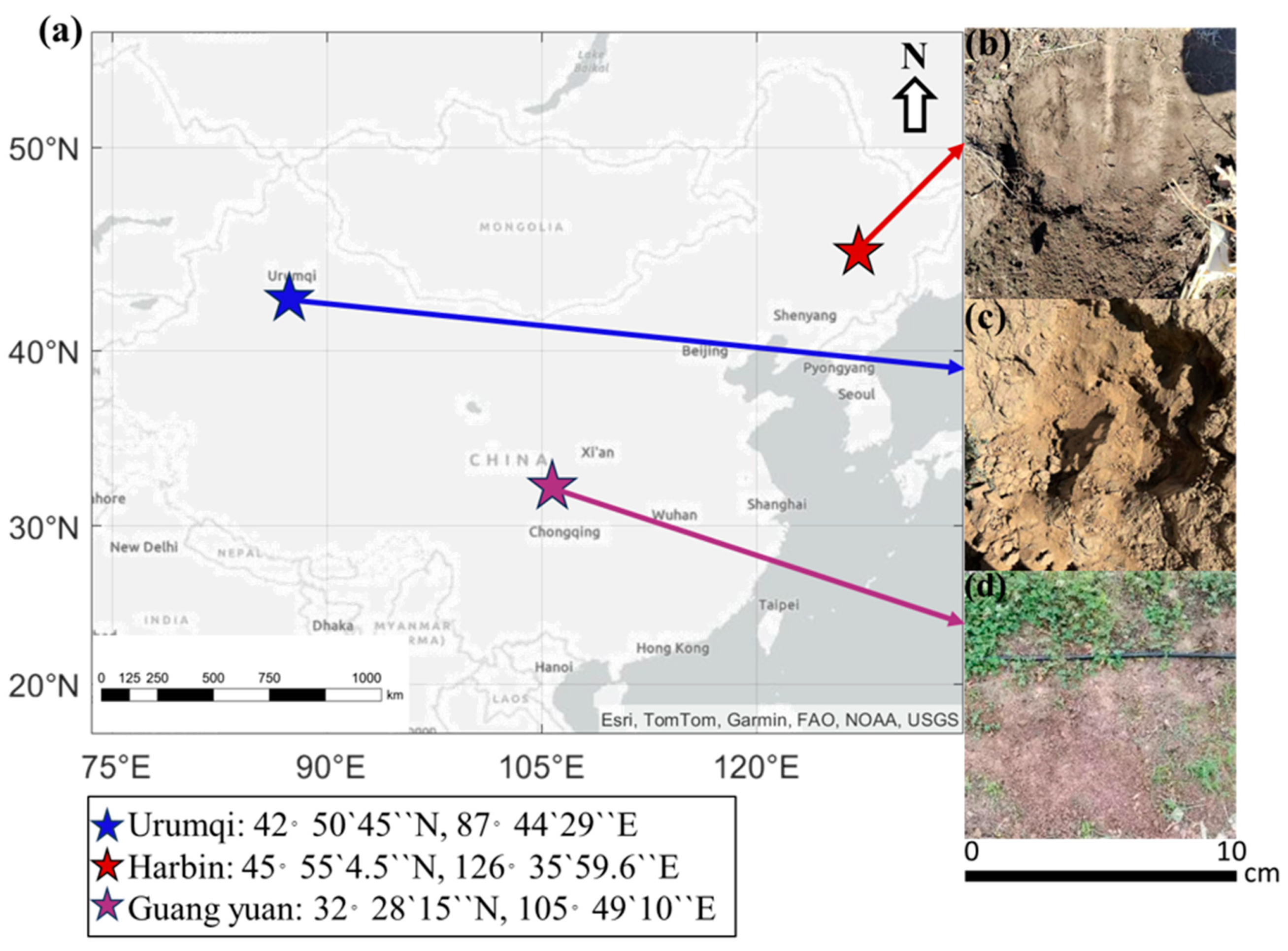

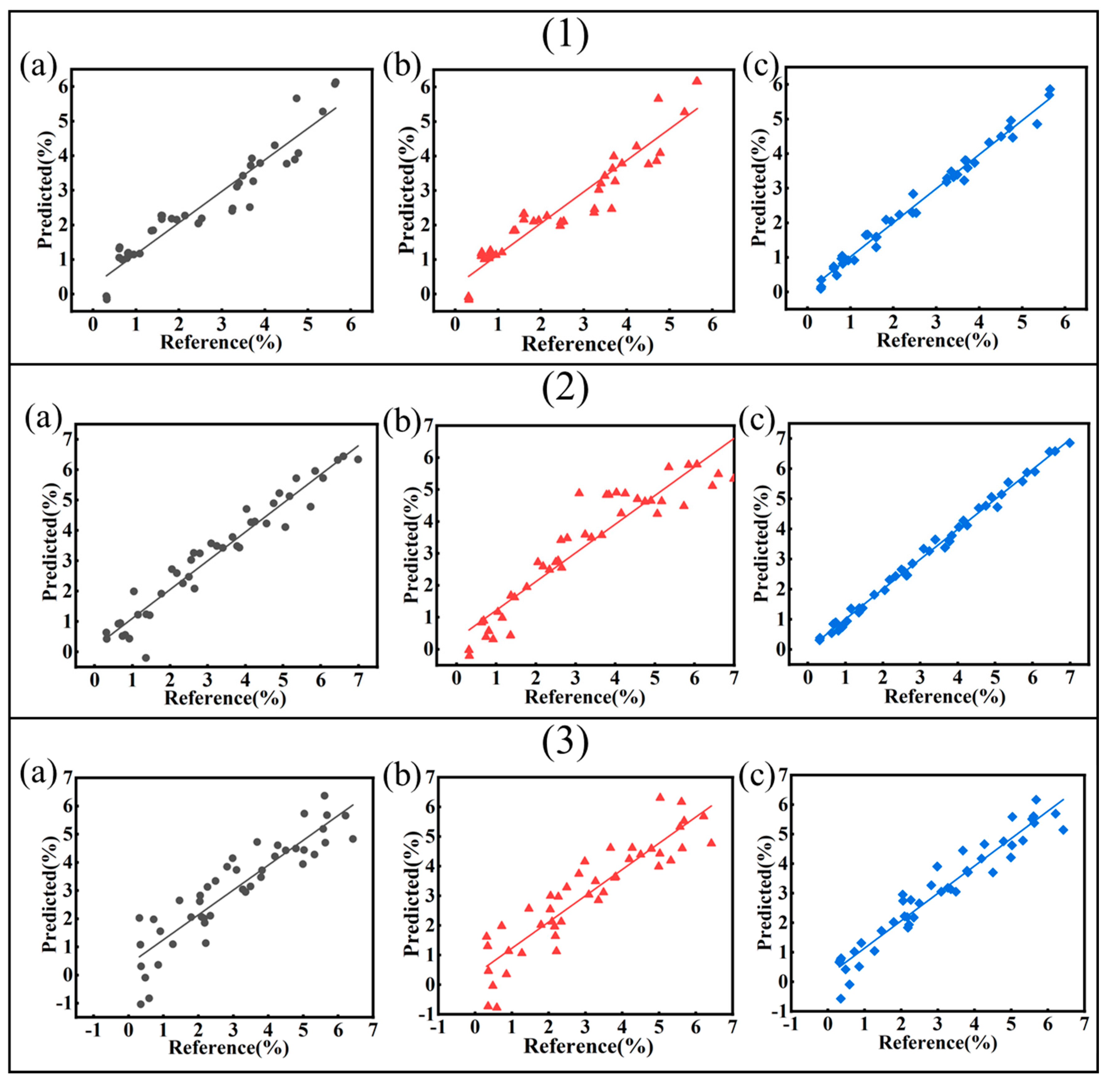
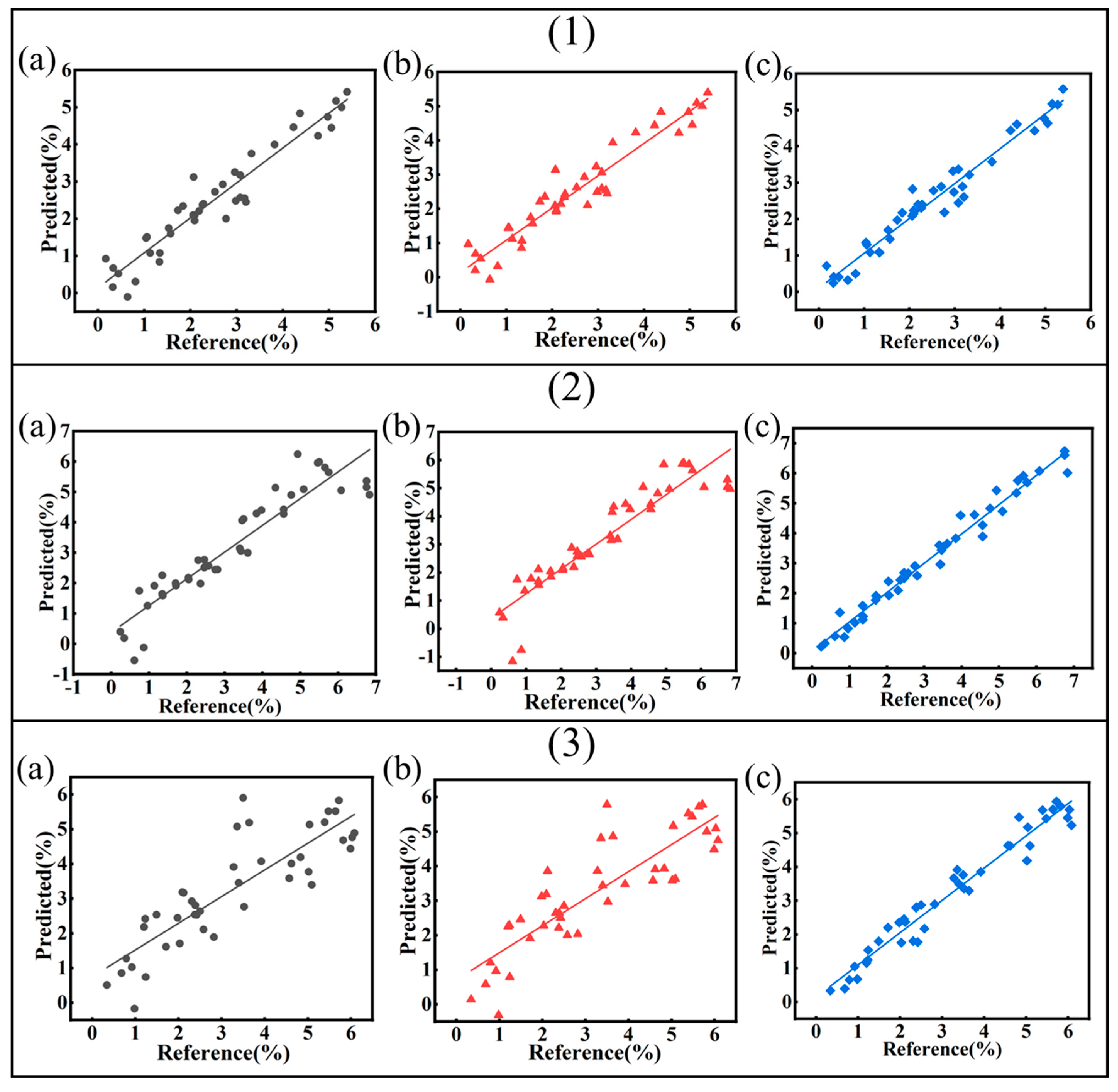

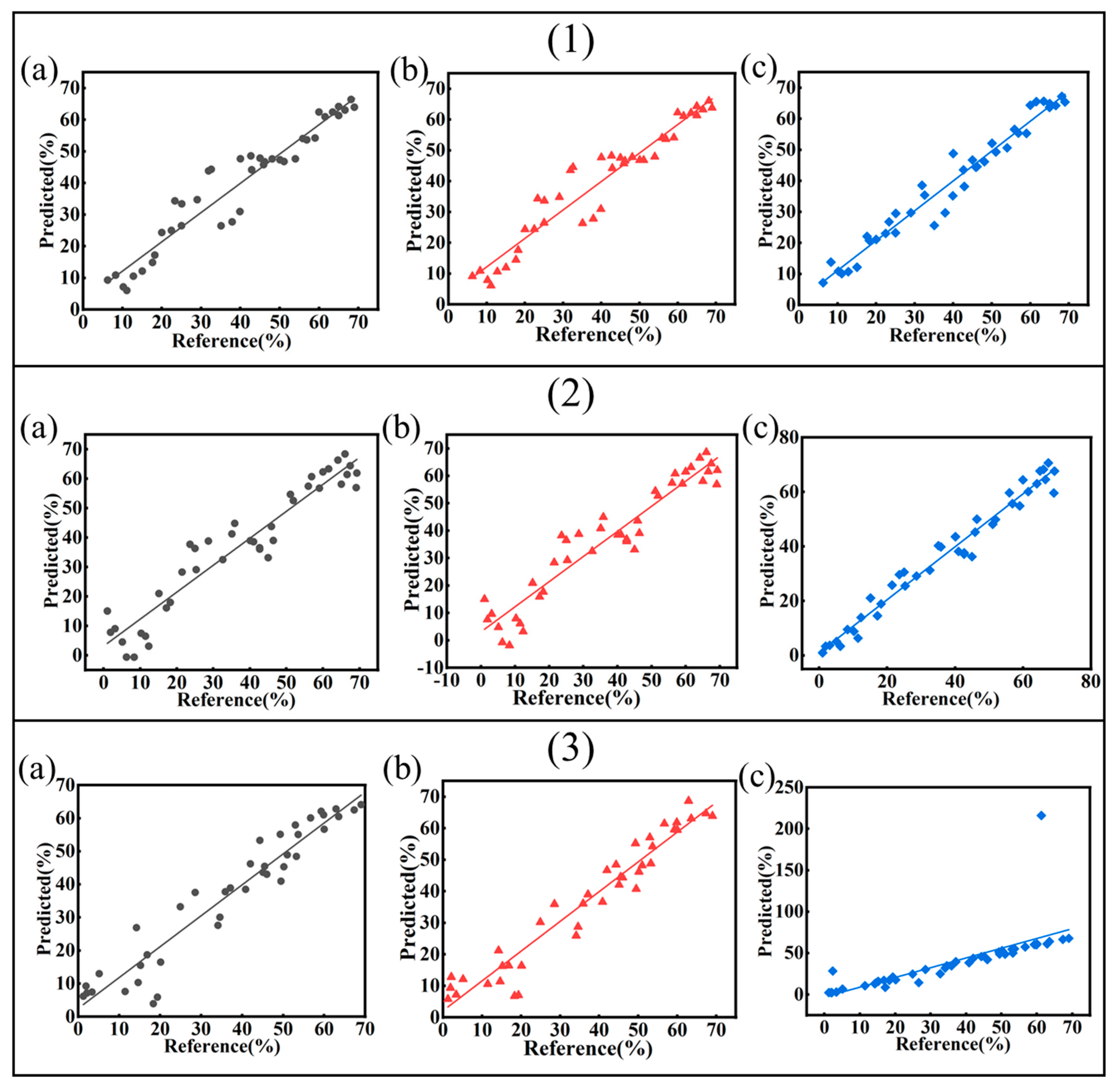
| Abbreviation | Source | Latitude and Longitude | Depths/cm | SO42−/mg/kg | Cl−/mg/kg | pH |
|---|---|---|---|---|---|---|
| YS02 | Urumqi City, Xinjiang Uyghur Autonomous Region, China | 42°50′45″ N 87°44′29″ E | 0–20 | 99.40 | 51.2 | 9.41 |
| YS24 | 20–40 | 129.21 | 64.82 | 9.66 | ||
| BS02 | Harbin, Heilongjiang Province, China | 45°55′4.5″ N 126°35′59.6″ E | 0–20 | 93.78 | 19.84 | 7.20 |
| BS24 | 20–40 | 104.32 | 36.82 | 7.01 | ||
| PS02 | Guang Yuan, Sichuan Province, China | 32°28′15″ N 105°49′10″ E | 0–20 | 53.23 | 16.44 | 8.55 |
| PS24 | 20–40 | 50.02 | 14.13 | 8.65 |
| Soil Group | Pretreatment Method | Factors | Train | Test | ||
|---|---|---|---|---|---|---|
| RMSEC | RMSEP | |||||
| NYS02 | MSC | 8 | 0.9720 | 0.0028 | 0.9306 | 0.0045 |
| NYS24 | F-D | 12 | 0.9909 | 0.0013 | 0.9526 | 0.0033 |
| FYS02 | S-D | 4 | 0.9544 | 0.045 | 0.9396 | 0.054 |
| FYS24 | S-D | 2 | 0.9378 | 0.053 | 0.9320 | 0.056 |
| NBS02 | F-D | 6 | 0.9585 | 0.0039 | 0.9409 | 0.004 |
| NBS24 | S-G | 4 | 0.9622 | 0.0037 | 0.9252 | 0.0053 |
| FBS02 | S-D | 4 | 0.9604 | 0.042 | 0.9402 | 0.053 |
| FBS24 | F-D | 5 | 0.9614 | 0.041 | 0.9437 | 0.052 |
| NPS02 | S-D | 10 | 0.9856 | 0.0021 | 0.9374 | 0.0046 |
| NPS24 | F-D | 9 | 0.9736 | 0.0029 | 0.9111 | 0.0058 |
| FPS02 | S-D | 5 | 0.9768 | 0.032 | 0.9673 | 0.039 |
| FPS24 | Baseline | 4 | 0.9558 | 0.043 | 0.9432 | 0.050 |
| Soil Group | Hotelling’s T2 Method | X-Sample ANOVA | Q-Residual Analysis |
|---|---|---|---|
| NYS02 | 42, 43 | 13 | 35 |
| NYS24 | 15, 38 | 13, 36 | 15 |
| NBS02 | 1 | 23 | 1, 9 |
| NBS24 | 1, 4 | 4 | 4, 7 |
| NPS02 | 32 | 32 | 32 |
| NPS24 | 1 | 2 | 2, 8 |
| FYS02 | 2, 3 | 31 | 2 |
| FYS24 | 4, 45 | 1, 2, 3 | 45 |
| FBS02 | 7 | 8, 16 | 7 |
| FBS24 | 21, 32 | 13, 29 | 32 |
| FPS02 | 38 | 22, 23, 24 | 22, 23, 24 |
| FPS24 | 5, 45 | 16, 20 | 5, 11 |
| Soil Group | Important Wavelengths (cm−1) | Model Wavelengths (cm−1) |
|---|---|---|
| NYS02 | 622 cm−1, 1069–1258 cm−1, 1537 cm−1, 1693 cm−1, 3735 cm−1 | 1069–1258 cm−1 |
| NYS24 | 589 cm−1, 1046 cm−1, 1102 cm−1, 1615 cm−1, 3433 cm−1 | 1002–1124 cm−1 |
| NBS02 | 600 cm−1, 656 cm−1, 1102 cm−1, 1180 cm−1 | 901–1281 cm−1 |
| NBS24 | 622 cm−1, 1124 cm−1,1381 cm−1, 1426 cm−1 | 991–1292 cm−1 |
| NPS02 | 578 cm−1, 622 cm−1, 689 cm−1, 745 cm−1, 1381 cm−1, 2381 cm−1, 2865 cm−1 | 567–734 cm−1 |
| NPS24 | 600 cm−1, 656 cm−1, 2351 cm−1, 2356 cm−1 | 511–734 cm−1 |
| FYS02 | 834 cm−1, 1024 cm−1 | 957–1069 cm−1 |
| FYS24 | 455 cm−1, 834 cm−1, 946 cm−1, 1024 cm−1, 1359 cm−1, 1437 cm−1 | 946–1069 cm−1 |
| FBS02 | 790 cm−1, 834 cm−1, 1046 cm−1, 1080 cm−1 | 790–1091 cm−1 |
| FBS24 | 801 cm−1, 857 cm−1, 1002 cm−1 | 779–1057 cm−1 |
| FPS02 | 834 cm−1, 890 cm−1, 979 cm−1, 2351 cm−1, 2396 cm−1 | 790–1091 cm−1 |
| FPS24 | 455 cm−1, 890–1247 cm−1, 1593 cm−1 | 890–1247 cm−1 |
| Soil Group | Regression Model | Factors | Training | Validation | ||||
|---|---|---|---|---|---|---|---|---|
| RMSEC | RMSEP | RPD | RPIQ | |||||
| NYS02 | MSC-PLSR | 3 | 0.9164 | 0.0046 | 0.9103 | 0.0050 | 3.52 | 5.52 |
| MSC-PCR | 3 | 0.9160 | 0.0047 | 0.9108 | 0.0051 | 3.19 | 5.42 | |
| MSC-MLR | - | 0.9856 | 0.0026 | 0.9832 | 0.0020 | 8.44 | 14.32 | |
| NYS24 | FD-PLSR | 7 | 0.9483 | 0.0033 | 0.9231 | 0.0042 | 3.53 | 4.46 |
| FD-PCR | 7 | 0.9471 | 0.0034 | 0.9209 | 0.0042 | 3.51 | 4.43 | |
| FD-MLR | - | 0.9583 | 0.0036 | 0.9535 | 0.0030 | 4.96 | 6.26 | |
| NBS02 | FD-PLSR | 6 | 0.9649 | 0.0035 | 0.9440 | 0.0047 | 4.03 | 7.05 |
| FD-PCR | 4 | 0.8997 | 0.0060 | 0.8777 | 0.0067 | 2.86 | 5.01 | |
| FD-MLR | - | 0.9941 | 0.0038 | 0.9396 | 0.0045 | 13.24 | 23.17 | |
| NBS24 | SG-PLSR | 3 | 0.9013 | 0.0059 | 0.8770 | 0.0068 | 2.79 | 4.46 |
| SG-PCR | 4 | 0.8916 | 0.0062 | 0.8605 | 0.0072 | 2.64 | 4.21 | |
| SG-MLR | - | 0.9766 | 0.0051 | 0.9192 | 0.0051 | 6.62 | 10.59 | |
| NPS02 | SD-PLSR | 9 | 0.8954 | 0.0058 | 0.8233 | 0.0078 | 2.33 | 3.84 |
| SD-PCR | 9 | 0.8974 | 0.0058 | 0.8277 | 0.0076 | 2.41 | 3.97 | |
| SD-MLR | - | 0.9280 | 0.0060 | 0.9274 | 0.0048 | 3.77 | 6.20 | |
| NPS24 | FD-PLSR | 3 | 0.7923 | 0.0079 | 0.7438 | 0.0090 | 1.94 | 3.34 |
| FD-PCR | 5 | 0.8157 | 0.0074 | 0.7390 | 0.0089 | 1.96 | 3.38 | |
| FD-MLR | - | 0.9555 | 0.0053 | 0.9388 | 0.0041 | 4.80 | 8.28 | |
| Soil Group | Regression Model | Factors | Training | Validation | ||||
|---|---|---|---|---|---|---|---|---|
| RMSEC | RMSEP | RPD | RPIQ | |||||
| FYS02 | SD-PLSR | 3 | 0.9009 | 0.065 | 0.8865 | 0.072 | 2.89 | 4.98 |
| SD-PCR | 3 | 0.8979 | 0.066 | 0.8765 | 0.071 | 2.93 | 5.04 | |
| SD-MLR | - | 0.9304 | 0.066 | 0.9275 | 0.053 | 3.84 | 6.61 | |
| FYS24 | SD-PLSR | 1 | 0.9277 | 0.050 | 0.9260 | 0.053 | 3.61 | 6.30 |
| SD-PCR | 1 | 0.9277 | 0.050 | 0.9262 | 0.052 | 3.63 | 6.32 | |
| SD-MLR | - | 0.9620 | 0.044 | 0.3825 | 0.14 | 5.20 | 9.06 | |
| FBS02 | SD-PLSR | 6 | 0.9365 | 0.053 | 0.8865 | 0.072 | 2.97 | 5.10 |
| SD-PCR | 7 | 0.9046 | 0.065 | 0.8745 | 0.075 | 2.86 | 4.90 | |
| SD-MLR | - | 0.9809 | 0.052 | 0.9540 | 0.044 | 7.32 | 12.55 | |
| FBS24 | FD-PLSR | 2 | 0.9204 | 0.061 | 0.9137 | 0.065 | 3.37 | 6.18 |
| FD-PCR | 2 | 0.9199 | 0.062 | 0.9097 | 0.066 | 3.33 | 6.11 | |
| FD-MLR | - | 0.9712 | 0.063 | 0.9590 | 0.042 | 5.97 | 10.94 | |
| FPS02 | FD-PLSR | 2 | 0.9573 | 0.044 | 0.9503 | 0.049 | 4.44 | 7.97 |
| FD-PCR | 3 | 0.9577 | 0.044 | 0.9508 | 0.048 | 4.52 | 8.12 | |
| FD-MLR | - | 0.9949 | 0.028 | 0.9848 | 0.025 | 14.20 | 25.48 | |
| FPS24 | Baseline-PLSR | 5 | 0.9445 | 0.048 | 0.9206 | 0.058 | 3.51 | 6.03 |
| Baseline-PCR | 6 | 0.9517 | 0.044 | 0.9363 | 0.053 | 3.88 | 6.67 | |
| Baseline-MLR | - | 0.9939 | 0.040 | 0.5217 | 0.23 | 0.88 | 1.52 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Huang, Y.; Li, S.; Zhao, J.; Liu, W.; Li, H.; Cui, Q.; Bai, R. Analytical Study of the Detection Model for Sulphate Saline Soil Based on Mid-Infrared Spectrometry. Chemosensors 2025, 13, 173. https://doi.org/10.3390/chemosensors13050173
Wei H, Huang Y, Li S, Zhao J, Liu W, Li H, Cui Q, Bai R. Analytical Study of the Detection Model for Sulphate Saline Soil Based on Mid-Infrared Spectrometry. Chemosensors. 2025; 13(5):173. https://doi.org/10.3390/chemosensors13050173
Chicago/Turabian StyleWei, Hanyu, Yong Huang, Sining Li, Jingzhuo Zhao, Wen Liu, Huan Li, Qiushuang Cui, and Ruyun Bai. 2025. "Analytical Study of the Detection Model for Sulphate Saline Soil Based on Mid-Infrared Spectrometry" Chemosensors 13, no. 5: 173. https://doi.org/10.3390/chemosensors13050173
APA StyleWei, H., Huang, Y., Li, S., Zhao, J., Liu, W., Li, H., Cui, Q., & Bai, R. (2025). Analytical Study of the Detection Model for Sulphate Saline Soil Based on Mid-Infrared Spectrometry. Chemosensors, 13(5), 173. https://doi.org/10.3390/chemosensors13050173





