High-Temperature-Sensing Smart Bolt Based on Indium Tin Oxide/In2O3 Thin-Film Thermocouples with Nickel-Based Single-Crystal Superalloy via Screen Printing
Abstract
:1. Introduction
2. Materials and Methods
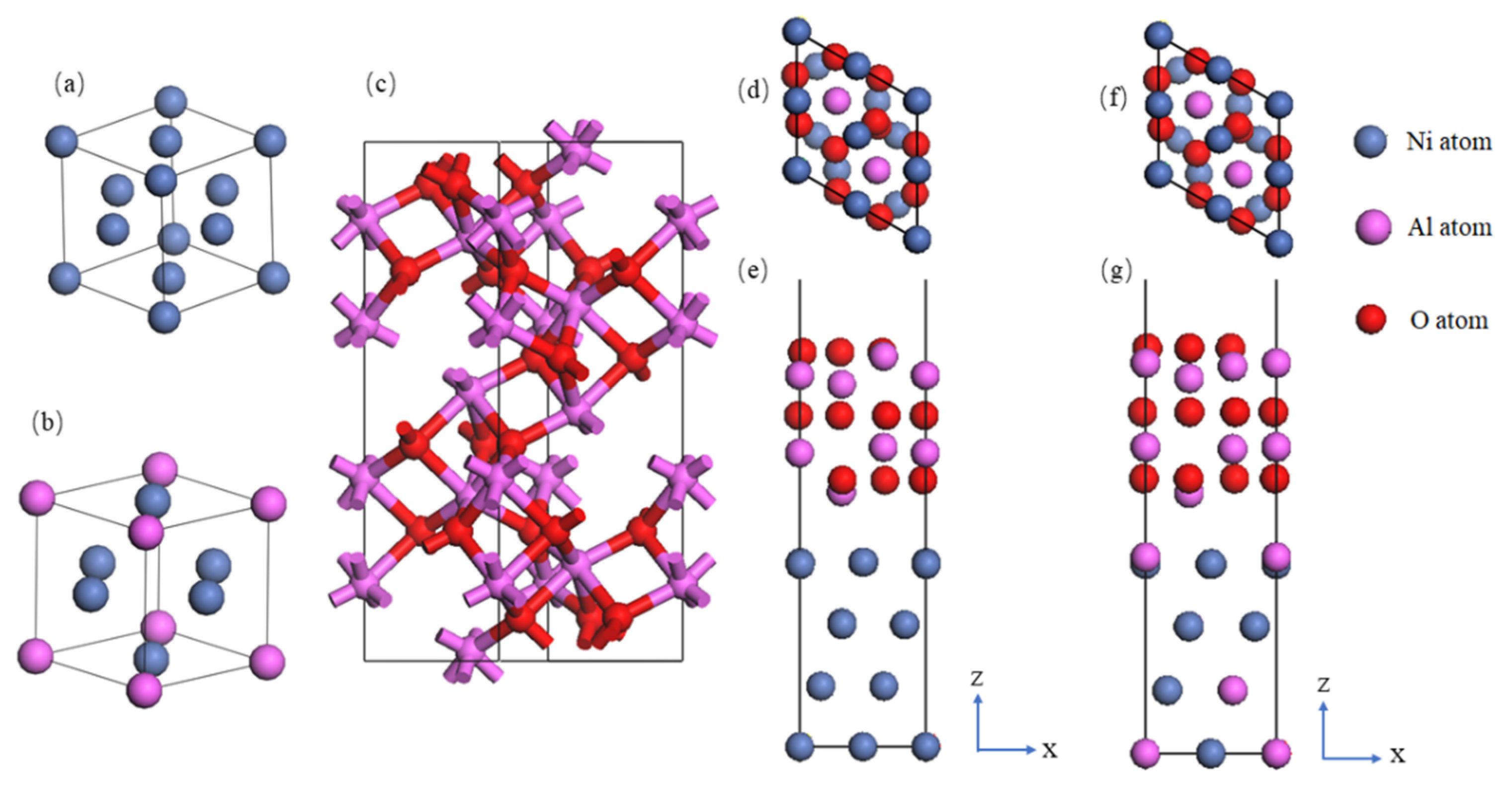
2.1. First-Principles Calculation of Ni-Based Alloys and Insulating Layers
2.2. Finite Element Analysis (FEA) of the Thermal Stress
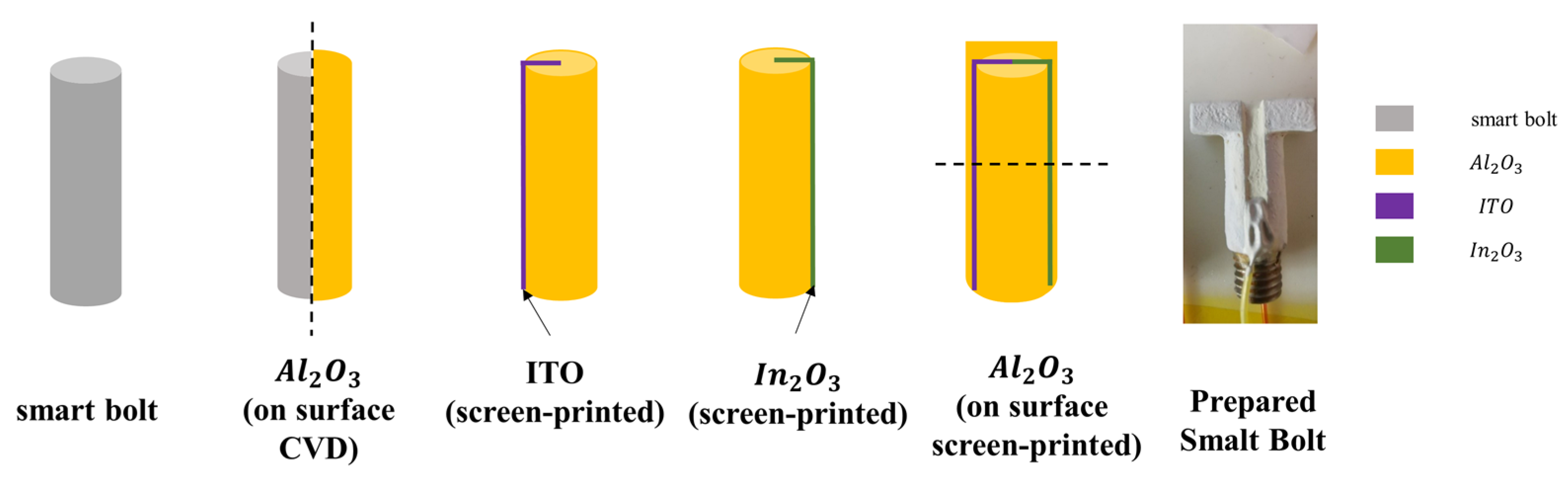
2.3. Sample Preparation and Measurements
3. Results
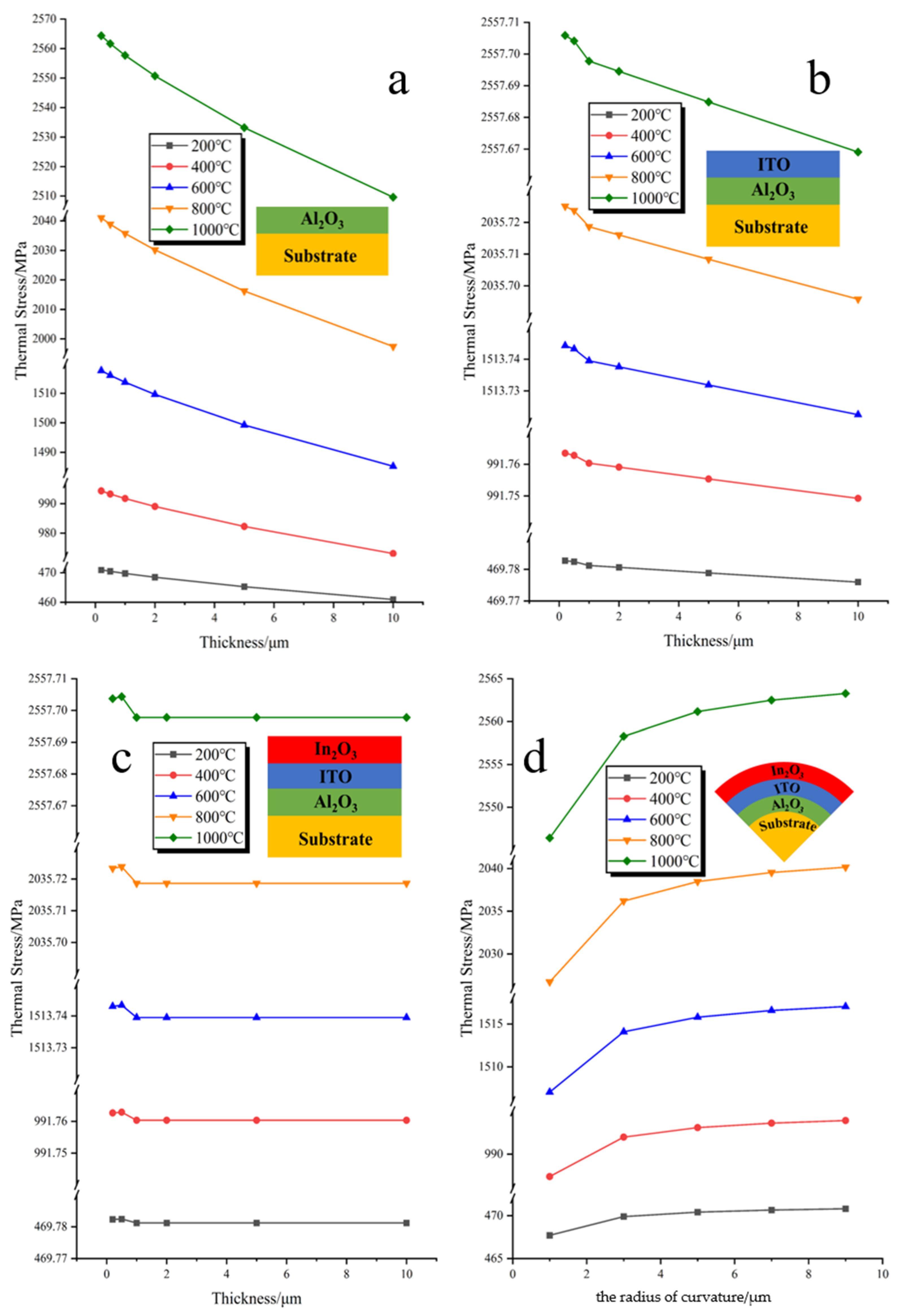
3.1. Simulation Analysis and Design
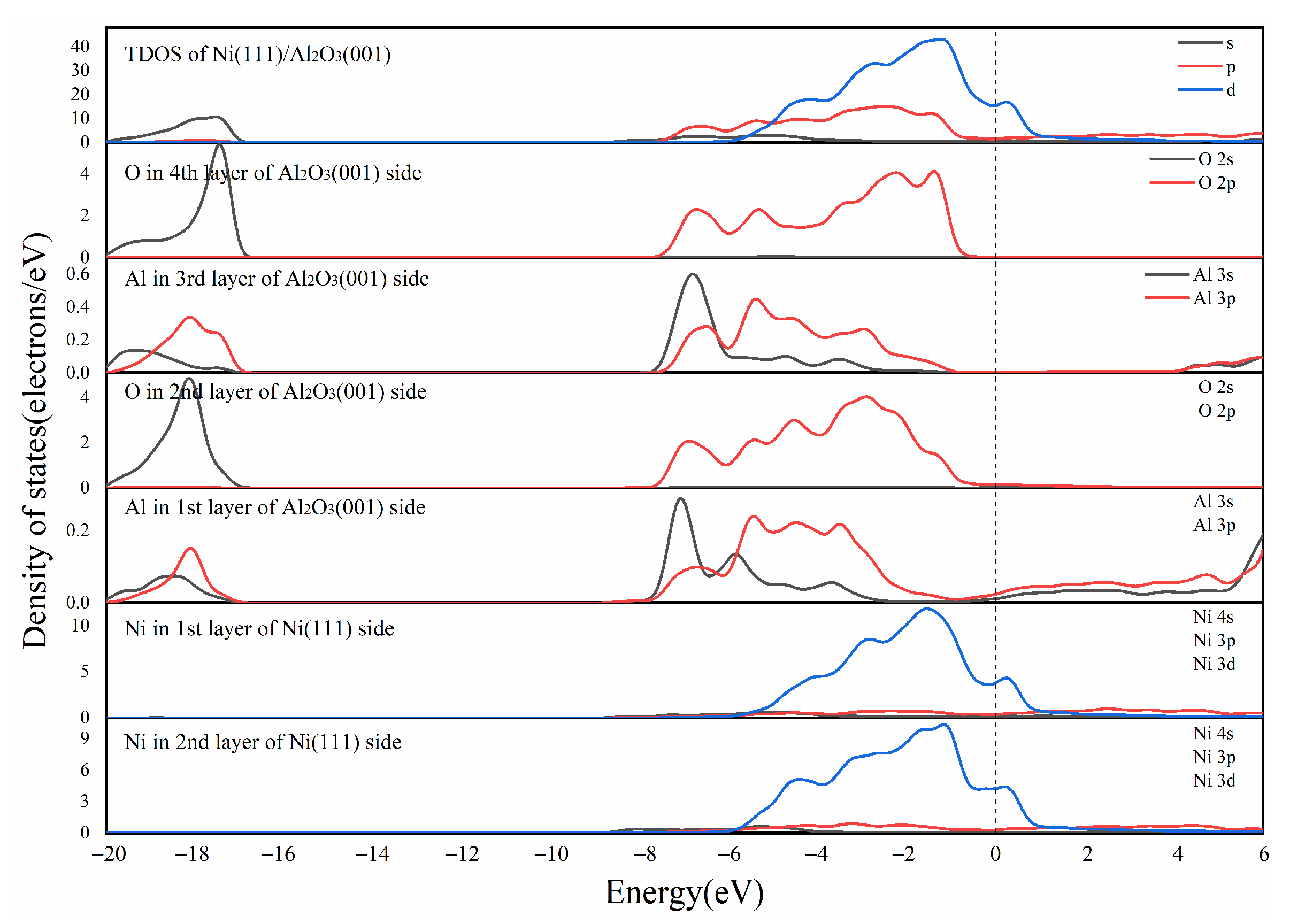
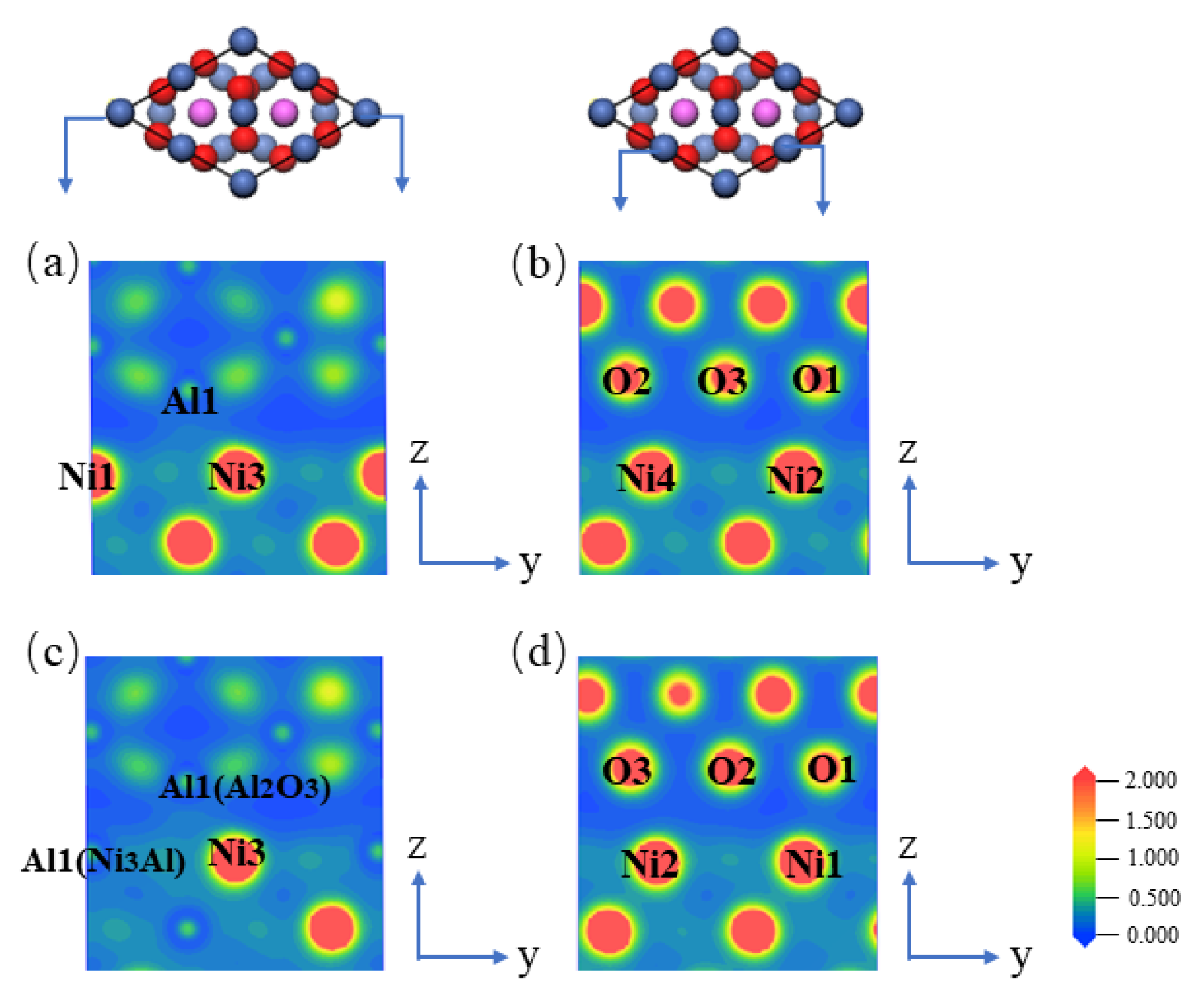
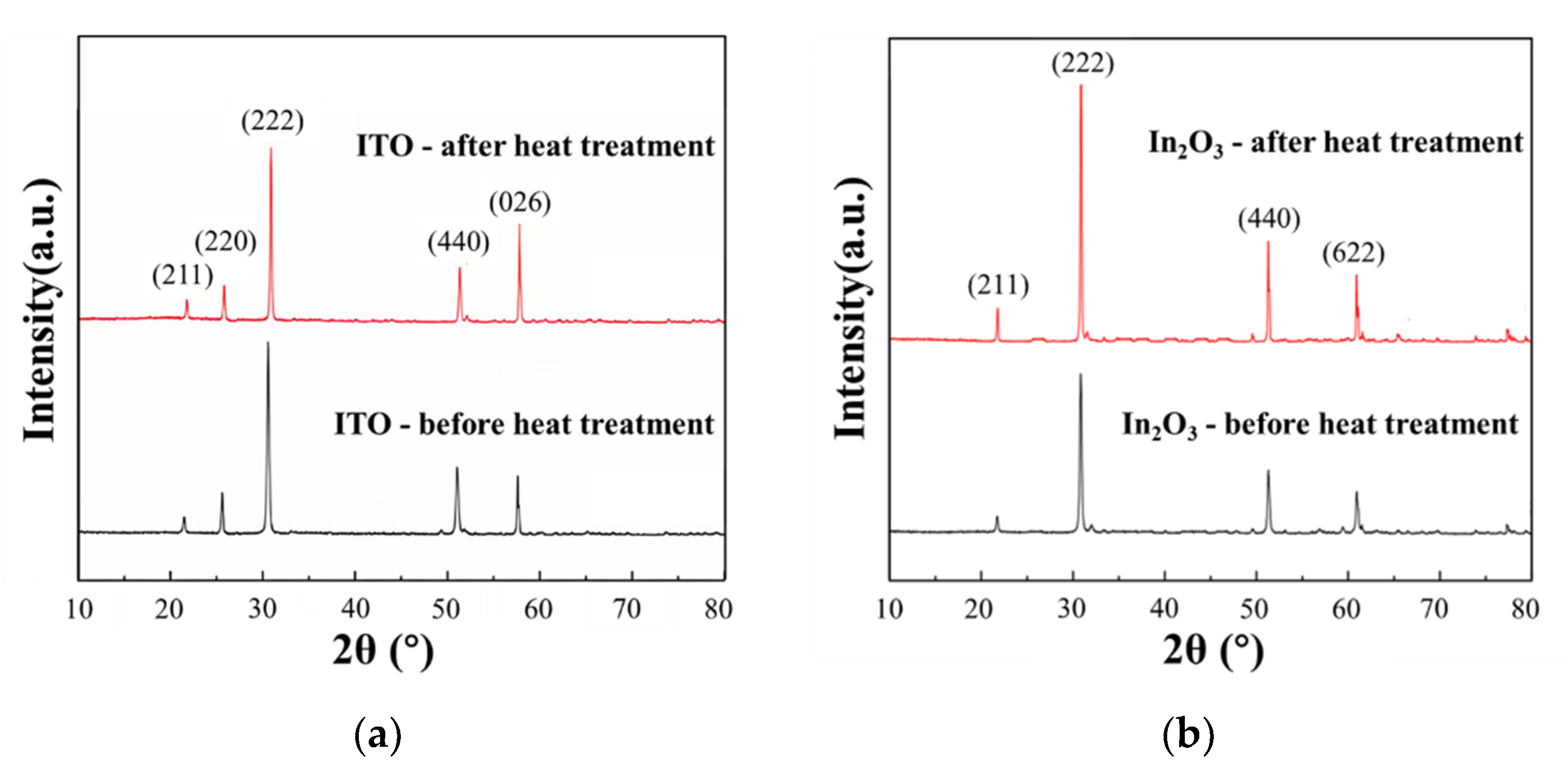
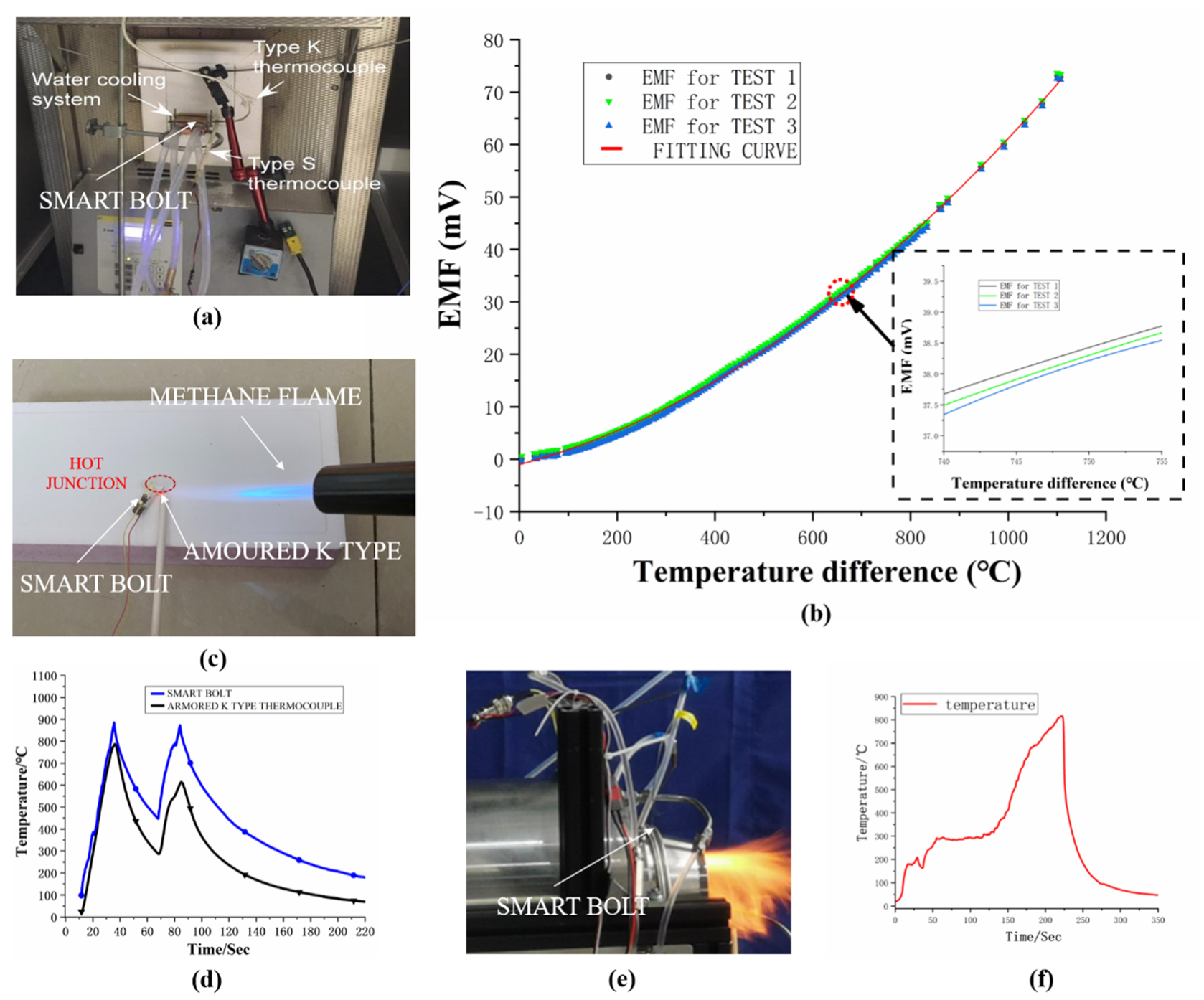
3.2. Microscopic and Thermoelectric Characteristics
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, J.; Yang, Y.; Zhao, J.; Li, H. The measure method of surface temperature in aero-engine. Meas. Technol. 2008, 28, 46–48. [Google Scholar]
- Liu, Q.M.; Huang, S.Z.; Liu, J.; Zhang, C.Q.; Fang, R.L.; Pei, H.P. Progress and Application of High Temperature Structural Materials on Aero-Engine. Gas Turbine Exp. Res. 2014, 27, 27–31. [Google Scholar]
- Jin, X.H.; Ma, B.H.; Qiu, T.; Deng, J.J.; Luo, J.; Yuan, W.Z.; Le, J.L.; Han, Y.Y. ITO thin film thermocouple for dynamic inner wall temperature measurement of supersonic combustion. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Zhang, J.; Mei, G.; Xie, Z.; Zhao, S.M. A Fast Response Sensor for Continuously Measuring Molten Steel Temperature. ISIJ Int. 2018, 58, 1453–1458. [Google Scholar] [CrossRef] [Green Version]
- Marr, M.A.; Wallace, J.S.; Chandra, S.; Pershin, L.; Mostaghimi, J. A fast response thermocouple for internal combustion engine surface temperature measurements. Exp. Thermal. Fluid Sci. 2010, 34, 183–189. [Google Scholar] [CrossRef]
- Martin, L.C. Testing of Thin Film Thermocouples in Rocket Engine Environments. In Advanced Earth-to-Orbit Propulsion Technology 1994; NASA CP–3282; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Uchida, K.; Takahashi, S.; Harii, K.; Ieda, J.; Koshibae, W.; Ando, K.; Maekawa, S.; Saitoh, E. Observation of the spin Seebeck effect. Nature 2008, 455, 778–781. [Google Scholar] [CrossRef] [PubMed]
- Gregory, O.J.; You, T. Ceramic temperature sensors for harsh environments. IEEE Sens. J. 2005, 5, 833–838. [Google Scholar] [CrossRef]
- Richards, L.A.; Ogata, G. Thermocouple for Vapor Pressure Measurement in Biological and Soil Systems at High Humidity. Science 1958, 128, 1089–1090. [Google Scholar] [CrossRef]
- Majumdar, A.; Lai, J.; Chandrachood, M.; Nakabeppu, O.; Wu, Y.; Shi, Z. Thermal imaging by atomic force microscopy using thermocouple cantilever probes. Rev. Sci. Instrum. 1995, 66, 3584–3592. [Google Scholar] [CrossRef]
- Basti, A.; Obikawa, T.; Shinozuka, J. Tools with built-in thin film thermocouple sensors for monitoring cutting temperature. Int. J. Mach. Tools Manuf. 2007, 47, 793–798. [Google Scholar] [CrossRef]
- Aniolek, G.E.; Gregory, O.J. Thin Film Thermocouples for Advanced Ceramic gas Turbine Engines. Surf. Coat. Technol. 1994, 68, 70–75. [Google Scholar] [CrossRef]
- Afridi, M.; Montgomery, C.; Cooper-Balis, E.; Semancik, S.; Kreider, K.G.; Geist, J. Micro hotplate temperature sensor calibration and bist. J. Res. Natl. Inst. Stand. Technol. 2011, 116, 827–838. [Google Scholar] [CrossRef] [PubMed]
- Qiang, W.; Zhang, J.B.; Shao, J.; Chen, P.; Ding, G.; Duan, L. Preparation and performance of high temperature thin film sensors. Sens. Microsyst. 2016, 35, 33–35. [Google Scholar]
- Rivera, K.; Muth, T.; Rhoat, J. Novel temperature sensors for SiC–SiC CMC engine components. J. Mater. Res. 2017, 32, 3319–3325. [Google Scholar] [CrossRef]
- Yakaboylu, G.A.; Pillai, R.C.; Sabolsky, K. MoSi2-and WSi2-based embedded ceramic composite thermocouples for high-temperature and harsh-environment sensing. Sens. Actuators A: Phys. 2018, 272, 139–152. [Google Scholar] [CrossRef]
- Rivera, K.; Gregory, O.J. ITO: SiC Ceramic Matrix Composite Thermocouples for Engine Components. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Zhang, Z.K.; Tian, B.; Cheng, G.; Liu, Z.; Liu, J.; Zhang, B.; Lei, J.; Zhao, N.; Han, F.; Fang, X.; et al. Influences of RF Magnetron Sputtering Power and Gas Flow Rate on a High Conductivity and Low Drift Rate of Tungsten-Rhenium Thin-Film Thermocouples. Nanomaterials 2022, 12, 1120. [Google Scholar] [CrossRef]
- Jiang, Y.; Wei, Y.; Smith, J.R.; Hutchinson, J.W.; Evans, A. First principles based predictions of the toughness of a metal/oxide interface. Int. J. Mater. Res. 2010, 101, 8–15. [Google Scholar] [CrossRef] [Green Version]
- Ozfidan, I.; Chen, K.; Fu, M. Effects of additives and impurity on the adhesive behavior of the NiAl (110)/Al2O3 (0001) Interface: An ab initio study. Metall. Mater. Trans. A 2011, 42, 4126–4136. [Google Scholar] [CrossRef]
- Bao, Z.; Guo, X.; Shang, F. An atomistic investigation into the nature of fracture of Ni/Al2O3 interface with yttrium dopant under tension. Eng. Fract. Mech. 2015, 150, 239–247. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Z.; Song, G. Monitoring of multi-bolt connection looseness using entropy-based active sensing and genetic algorithm-based least square support vector machine. Mech. Syst. Signal Process. 2020, 136, 106507. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Kong, Q.; Song, G. Percussion-based bolt looseness monitoring using intrinsic multiscale entropy analysis and BP neural network. Smart Mater. Struct. 2019, 28, 125001. [Google Scholar] [CrossRef]
- Tian, B.; Liu, Y.; Zhang, Z.K.; Zhao, L.B.; Liu, Z.J.; Shi, P.; Lin, Q.; Mao, Q.; Lu, D.; Jiang, Z. WRe26-In2O3 probe-type thin film thermocouples applied to high temperature measurement. Rev. Sci. Instrum. 2020, 7, 91. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.J.; Zhang, L.W.; Hui, L.; Jin, X.H.; Ma, B.H. Indium Tin Oxide Thin-Film Thermocouple Probe Based on Sapphire Microrod. Sensors 2020, 20, 1289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Mattsson, A.E.; Schultz, P.A.; Desjarlais, M.P.; Mattsson, T.R.; Leung, K. Designing meaningful density functional theory calculations in materials science—A primer. Model. Simul. Mater. Sci. Eng. 2004, 13, R1. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Laasonen, K.; Pasquarello, A.; Car, R.; Lee, C.; Vanderbilt, D. Car-Parrinello molecular dynamics with Vanderbilt ultrasoft pseudopotentials. Phys. Rev. B 1993, 47, 10142. [Google Scholar] [CrossRef]
- Yu, X.F.; Tian, S.G.; Wang, M.G.; Zhang, S.; Lu, X.; Cui, S. Creep behaviors and effect factors of single crystal nickel-base superalloys. Mater. Sci. Eng. A 2009, 499, 352–359. [Google Scholar]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Lejaeghere, K.; Van Speybroeck, V.; Van Oost, G.; Cottenier, S. Error estimates for solid-state density-functional theory predictions: An overview by means of the ground-state elemental crystals. Crit. Rev. Solid State Mater. Sci. 2014, 39, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Barzilai, J.; Borwein, J.M. Two-point step size gradient methods. IMA J. Numer. Anal. 1988, 8, 141–148. [Google Scholar] [CrossRef]
- Ellis, D.E.; Guenzburger, D. The discrete variational method in density functional theory and its applications to large molecules and solid-state systems. In Advances in Quantum Chemistry; Academic Press: Cambridge, MA, USA, 1999; Volume 34, pp. 51–141. [Google Scholar]
- Zhou, T.T.; Huang, C.Z.; Yi, M.D. First-principle calculation of Al2O3 (012)/SiC (310) interface model. In Materials Science Forum; Trans Tech Publications Ltd.: Zurich, Switzerland, 2017; Volume 896, pp. 120–127. [Google Scholar]
- Segall, M.D.; Shah, R.; Pickard, C.J.; Payne, M.C. Population analysis of plane-wave electronic structure calculations of bulk materials. Phys. Rev. B 1996, 54, 16317. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| System | Method | a (Å) | c (Å) | Space Group | |
|---|---|---|---|---|---|
| Al2O3 | Present | GGA–PBE | 4.808 | 13.122 | R-3C |
| Expt | 4.759 | 12.991 | R-3C | ||
| Ni | Present | GGA–PBE | 3.522 | 3.522 | FM-3M |
| Expt | 3.544 | 3.544 | FM-3M | ||
| Ni3Al | Present | GGA–PBE | 3.569 | 3.569 | PM-3M |
| Expt | 3.568 | 5.568 | PM-3M |
| Material | Poisson’s Ratio | Young’s Modulus (GPa) | Coefficient of Thermal Expansion (10−6/K) |
|---|---|---|---|
| Ni-based single-crystal superalloy | 0.30 | 210 | 9.10 |
| Al2O3 | 0.29 | 390 | 7.70 |
| ITO | 0.35 | 200 | 6.37 |
| In2O3 | 0.30 | 150 | 6.50 |
| Bond | Population | Bond Length (Å) | |
|---|---|---|---|
| Ni(111)/Al2O3(001) | Al1–Ni2 | 0.08 | 2.74 |
| Al1–Ni4 | 0.07 | 2.75 | |
| Al1–Ni3 | 0.07 | 2.76 | |
| O2–Ni4 | 0.03 | 2.86 | |
| O3–Ni3 | 0.02 | 2.88 | |
| O1–Ni2 | 0.01 | 2.88 | |
| Ni3Al(111)/Al2O3(001) | Al1(Al2O3)–Ni2 | 0.06 | 2.72 |
| Al1(Al2O3)–Ni4 | 0.05 | 2.72 | |
| Al1(Al2O3)–Ni3 | 0.05 | 2.72 | |
| O1–Ni1 | −0.01 | 2.92 | |
| O2–Ni3 | −0.01 | 2.91 | |
| O3–Ni2 | −0.01 | 2.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, J.; Cai, R.; Liu, Z.; Lei, J.; Sun, R.; Wu, N.; Zhao, N.; Tian, B.; Zhao, L. High-Temperature-Sensing Smart Bolt Based on Indium Tin Oxide/In2O3 Thin-Film Thermocouples with Nickel-Based Single-Crystal Superalloy via Screen Printing. Chemosensors 2022, 10, 347. https://doi.org/10.3390/chemosensors10090347
Zhang Z, Liu J, Cai R, Liu Z, Lei J, Sun R, Wu N, Zhao N, Tian B, Zhao L. High-Temperature-Sensing Smart Bolt Based on Indium Tin Oxide/In2O3 Thin-Film Thermocouples with Nickel-Based Single-Crystal Superalloy via Screen Printing. Chemosensors. 2022; 10(9):347. https://doi.org/10.3390/chemosensors10090347
Chicago/Turabian StyleZhang, Zhongkai, Jiangjiang Liu, Rongfu Cai, Zhaojun Liu, Jiaming Lei, Ruolin Sun, Ningning Wu, Na Zhao, Bian Tian, and Libo Zhao. 2022. "High-Temperature-Sensing Smart Bolt Based on Indium Tin Oxide/In2O3 Thin-Film Thermocouples with Nickel-Based Single-Crystal Superalloy via Screen Printing" Chemosensors 10, no. 9: 347. https://doi.org/10.3390/chemosensors10090347
APA StyleZhang, Z., Liu, J., Cai, R., Liu, Z., Lei, J., Sun, R., Wu, N., Zhao, N., Tian, B., & Zhao, L. (2022). High-Temperature-Sensing Smart Bolt Based on Indium Tin Oxide/In2O3 Thin-Film Thermocouples with Nickel-Based Single-Crystal Superalloy via Screen Printing. Chemosensors, 10(9), 347. https://doi.org/10.3390/chemosensors10090347










