Abstract
We present a combination of micromachined optofluidic platforms equipped with a fiber-optic sensing configuration based on a three-path Mach–Zehnder interferometer (MZI) for simultaneous measurement of the refractive index of liquids and the autocalibration in dynamic regime. The sensing principle is based on the low-coherence interferometry, characterized by a generation of Gaussian enveloped interferograms, for which the position of its maximum depends on the optical path difference (OPD) between the sensing and reference arm of the MZI. When liquid flows through the central microchannel of the optofluidic platform it crosses the light beam between the two optical fibers in the sensing arm causing the OPD change. An algorithm has been applied for the calculation of the refractive index of liquids out of the raw interference signals. We obtained a very good agreement between the experimental results and literature data of refractive indices of subjected fluids. The accuracy of refractive index measurement is approximately 1%, predominantly determined by the accuracy of reading the position of the mechanical scanner. The proposed sensor is attractive for the label-free biological, biochemical, and chemical sensing owing autocalibration and high sensitivity yet consuming a very small sample volume of 1 µL. It is capable to measure the refractive index of various liquids and/or gases simultaneously in the process.
1. Introduction
Refractive index is a frequently used physical parameter for material characterization in various scientific and industrial fields, including life science, biomedicine, analytical chemistry and biochemistry, material science, etc. [1,2]. Fiber-optic sensors for refractive index measurement have attracted the attention of many research groups dealing with label-free biological and biochemical sensing since they provide high sensitivity, fast response, an extremely small volume of the test sample, remote sensing, immunity against electromagnetic radiation, etc. [3]. Among them fiber-optic interferometric sensors are the most sensitive and allow different designs [4,5]. They are very convenient to combine with some other technologies, such as micro-electro-mechanical-systems (MEMS), for making high throughput analytical devices, such as Lab-on-a-Chips and micro total analyzer system (µ-TAS) [6]. These systems feature several advantages such as direct contactless detection, miniaturization, and multiplexing.
There are a number of different sensing configurations dedicated to the refractive index measurement of gases and liquids [7,8,9]. Fiber-optic surface plasmon resonance (SPR) sensors can provide high resolution by combining the metal (e.g., silver, Ag and gold, Au) and conductive metal oxides (e.g., indium tin oxide, ITO) coatings of the fiber-optic core, but their dynamic range of RI is limited between 1.33 and 1.36. Some other SPR sensor configurations are investigated as well. For example, Wang et al. [8] proposed a “T” structure SPR fiber-optic refractive index sensor to extend the dynamic range of the sensing sample refractive index from 1.3333 to 1.4 based on surface plasmon resonance wavelength shift from 965 nm to 1247 nm and the maximum sensitivity of 5673 nm/RIU (RIU-refractive index unit). Recently, Liu et al. [9] demonstrated a high sensitivity D-shaped photonic crystal fiber PCF-SPR sensor with ITO coating capable to measure the refractive index of the analyte from 1.380 to 1.405 with an average sensitivity of 8400 nm/RIU over wavelength between 1500 nm and 2800 nm.
Fiber Bragg grating (FBG) sensors have found a versatile application for the measurement of many physical and chemical parameters [10,11,12,13], including the refractive indices of gasses and liquids. For example, Hu et al. [10] proposed a fiber-optic SPR sensor based on the combination of multimode optical fibers and fiber Bragg grating aimed for a simultaneous measurement of the refractive index and temperature of NaCl liquid solution. It was experimentally proved that such a MMF-FBG-MMF (multimode fiber-fiber Brag grating-multimode fiber) sensor has claimed RI sensitivity of 2556.8 nm/RIU and the temperature sensitivity of 172 pm/°C. Qi et al. [11] demonstrated a special kind of FBG, so-called long period grating (LPG) optical fiber that was more sensitive to the external refractive index. The RI sensor was fabricated by silver coating on both surfaces of the cleaved fiber tip and the tail portion of the LPG. The long-distance sensor operation over 100 km was proved utilizing the optical time domain reflectometer (OTDR) as a light source and glycerol/water solutions as a testing analyte. The achieved RI resolution of the proposed reflective LPG sensor is 5.4 × 10−3 for 100 km length. Liu et al. [12] designed an integrated RI and temperature sensor that combines a Fabry–Perot interferometer (FPI) and a fiber Bragg grating in a common FPI-FBG sensor structure. The RI sensitivity of 1210.490 nm/RIU was achieved by measuring refractive index of sucrose solution in the range of 1.335 to 1.344. Zhang et al. [13] proposed an all-optical-fiber temperature-insensitive RI sensor also based on the LPG inscribed in a cobalt-doped optical fiber (COF). A part of the COF fiber was spliced between the two common single-mode fibers (SMF). Two FBGs were inscribed in the COF and photosensitive regions of SMF acting as two in-line temperature sensors. The LPG sensor was tested by measuring the RI of sucrose solutions of different concentrations. A maximum sensitivity of about 1100 nm/RIU was achieved over the refractive index from 1.32 to 1.45.
In-line fiber-optic RI sensors, including Fabry–Perot (FP) [14,15], Michelson [16,17], and Mach-Zehnder interferometers (MZI) [18,19,20,21,22,23], provide a relatively simple construction, which includes the splicing of two or more parts of optical fibers. Rao et al. [14] presents a fiber-optic RI sensor which is based on an intrinsic Fabry–Perot interferometer (IFPI) made of a piece of endlessly single-mode photonic crystal fiber (EPCF) and a common single-mode fiber. This sensor allows a simultaneous measurement of RI and temperature of glycerol solution with refractive-index resolution of about 2 × 10−5 and temperature sensitivity of 4.16 nm/°C. Wang et al. [15] demonstrated a high-accuracy hybrid fiber-optic FP sensor based on MEMS for the simultaneous measurement of RI and temperature of gas sample. The sensor is made of silicone FP cavity aimed for temperature measurement and a glass FP cavity for the gas RI measurement. The experimental results show the sensitivity of temperature measurement of about 80 pm/°C and sensitivity of RI measurement of 1535.8 nm/RIU over the gas refraction index from 1.0000248 to 1.0007681.
Fiber-optic Michelson interferometer (MI) is also a frequently used sensing configuration of refractive index measurement of liquid samples. The phase shift or the fringe contrast change of the interference signal corresponds to the change of the RI. Usually, it behaves as a point sensor that allows remote measurement. For example, Zhou et al. [16] reported on a high-sensitive intensity modulated RI sensor composed of an in-fiber Michelson interferometer produced by splicing a portion of a thin core fiber (TCF) to a common SMF with a lateral offset. Such a relatively simple senor reached a temperature insensitive high sensitivity of RI measurement of −202.46 dB/RIU at the refractive index of 1.42. Although, the sensor structure is simple and cost effective, the interrogation unit is more complex since it includes an expensive and large spectrum analyzer, which is a disadvantage in terms of RI measurement
A common sensing configuration of a MZI includes two independent arms, acting as the sensing and reference arm. The incident light in the interferometer is split into two arms by an input 1 × 2 fiber-optic splitter and then recombined by an output 2 × 1 coupler. In the in-line MZI sensing configurations the relative phase difference occurs due to the effective RI difference between the core and cladding mode. There are many different types of in-line MZI structures, which can be seen in literature like core-offset, air-hole, peanut-shape, open-air cavity made by laser ablation of a portion of fiber or by lateral offset splicing, tapered structure [17]. Ahsani et al. [18] made a cost-effective and simple MZI refractive index sensor based on tapered single-mode fibers (SMF). The fiber-optic MZI sensor shows a maximum sensitivity of 4234 nm/RIU for the taper waste diameter (TWD) of 35.5 µm for RI range from 1.3327 to 1.4348 of glycerol solution. The RI measured data were not influenced by temperature drift, which is measured to be 0.0097/°C. A similar configuration was used by Xia et al. [19], which demonstrated an in-line MZI for ultrasensitive measurement of RI and temperature. A tapered sensor with TWD of about 4.8 µm has achieved a RI sensitivity of 24209 nm/RIU at about 1.332 refractive index and temperature sensitivity of −2.47 nm/°C. Yao et al. [20] reported on a core offset MZI sensor aimed to simultaneous measurement of temperature and RI of solution. The sensor structure was made by core-offset splicing of a FBG sensor with SMF tail and laterally shifted SMF between the FBG and SMF tail. The sensor was tested by measurement of RI of NaCl water solution of different concentrations. The sensor demonstrated the RI sensitivity of 13.7592 nm/RIU for the refractive index range from 1.3232 to 1.3520 and temperature sensitivity of 0.046 nm/°C.
The survey above shows that the RI measurement of fluids is a vibrant field, still active in seeking a more effective sensing technology capable of fulfilling different technical requirements including high-sensitivity in a large dynamic range, high-throughput, and robustness especially in terms of industrial application, relatively simple construction of sensor device, low overall price of interrogation unit, etc. SPR sensors are usually associated with problems caused by nonuniformity of the thin metal films in terms of agglomerate formation and surface roughness [7]. It appears that FBG based RI sensors are rather simple construction but with a modest sensitivity and limited dynamic range. In addition, the relatively complex and expensive interrogation unit may appear as a big disadvantage of this RI sensor type. On the other hand, in-line FP sensors can be made relatively easily by splicing a piece of optical fiber between two additional fibers [17]. A challenge in this process is how to precisely control the thickness and flatness of the mirror deposited on the ends of the intermediate fiber and how to protect them from damage during splicing with in- and output fibers. A possible solution is to create the FP cavity by laser ablation of sensing fiber, but, unfortunately, low reflectivity of mirrors is a main reason for deterioration of the interference signal. The in-line MZI RI sensors allow a relatively easy fabrication, e.g., by fusion splicing of core-offset fiber portions although it includes difficulties how to control the polarization of input light. Tapered structures seem to be an advanced solution, but to be high-sensitive the TWD must be of small diameter that involves the problem associated with mechanical stability and sensor manipulation, increased parasitic effect of surrounding parameters like temperature and vibrations, etc.
The main motivation for our investigation is to overcome some of the aforementioned bottlenecks and even to improve the overall sensitivity and dynamic range of the RI measurement of liquids and gases by using the open cavity fiber-optic MZI configuration, which allows rather large optical path length (OPL) of interferometer above 125 µm [21]. For this purpose, we involve the concept of autocalibration of RI sensor by simultaneous in-line measurement of refraction index of liquid and air samples in dynamic regime. In this way we are able to reduce the cross-sensitivity influence of some parasitic effects as temperature drift and mechanical vibrations.
In this paper, we present a sensing configuration based on a common MZI with the open cavities in the sensing and reference arms. The sensing configuration is composed of two micromachined optofluidic platforms acting as a reference and a measuring one mutually connected in the same setup. The basic principle of operation is low-coherence Mach-Zehnder interferometer, embedded into the micromachined optofluidic platforms. The MZI is built up of two single-mode fiber-optic couplers, with coupling ratios of 1 × 3 and 3 × 3 for the input and output couplers, respectively, as shown in Figure 1. The optofluidic platforms are made of anodically bonded glass and silicon wafers that contain central microchannels, which enable the flow of a liquid sample through the measuring platform and simultaneously the air entering into the reference platform. Arrays of lateral V-grooves have been micromachined in the backside of a silicon wafer bonded on top of a glass wafer in order to hold the sensing optical fibers orthogonally directed to the central microchannels. The reference optical fiber is mechanically moved back and forth in and out of the guiding ferrule by using a micropositioner, changing the optical path difference of MZI. We applied the centroid and envelope fitting algorithm for finding out the center of the coherence zone in the low coherence interferograms simultaneously obtained by scanning procedure. We measured the refractive index of five liquids and got a very good agreement between the experimental results and literature data. We measured refractive index in the range of 1.32 to 1.38 of five liquids. The accuracy of the refractive index measurement is about 1% that is predominantly determined by the accuracy of reading the position of the mechanical scanner. The proposed sensor is attractive for the label-free biological, biochemical, and chemical sensing owing autocalibration and high sensitivity of about 0.0016 yet consuming a very small sample volume of 1 µL, high throughput of liquid analyte of about 2.3 µL/s and rather simple and low-price interrogation unit. By multiplexing of many micromachined optofluidic platforms it is possible to measure RI of various liquid and/or gas samples simultaneously in the process. Eventually, the micromachined optofluidic platform may be easily manufactured as a Lab-on-the-Chip by 3D printing, polymer injection molding, and hot embossing for the sake of cost-effective mass production, e.g., for the single-use purpose in biomedicine and clinical diagnosis [22].
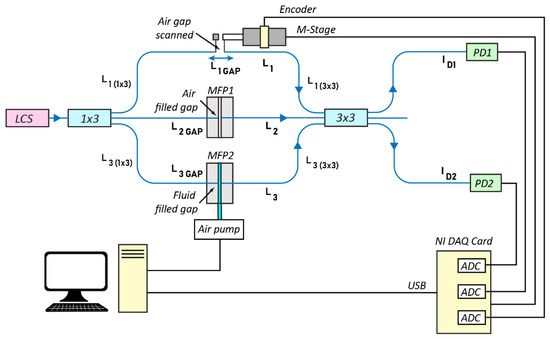
Figure 1.
Schematic presentation of fiber-optic Mach–Zehnder interferometer sensing configuration and micromachined platforms: MFP1,2—microfluidic platform; LSC—low coherence source, 1 × 3; 3 × 3—single-mode fiber-optic couplers; PD1,2—photodetectors; and ADC—analog to digital convertors.
2. Materials and Methods
2.1. Materials
In this investigation we used the following liquids: distilled water, 0.9% water solution of NaCl, methanol, ethanol, and isopropanol, all of them p.a. supplied by Sigma-Aldrich, Vienna, Austria.
2.2. Method
Figure 1 presents a sensing configuration based on single-mode “all-in-fiber” low-coherence MZI. Here, there are three completely separated light beams emitted by a low-coherence source (LCS), split by the first (1 × 3) single-mode fiber-optical coupler, and interfering at the output of the second (3 × 3) single-mode fiber-optic coupler. Coupling ratios of both fiber-optic couplers were 33:33:33, according to the specification of the producer (Optosun Technology Ltd., Shenzhen, China).
The light intensity at the output is described by the classical relation [23]:
where I1, I2, and I3 are irradiances of light beams in three interferometric arms; ΔLij = Lj − Li is the optical paths difference (OPD) between the beams in arms i and j (the indices i and j correspond to three light paths: i, j = 1, 2, 3); γ11(ΔLij) is the degree of coherence of the light source employed at the optical distance ΔLij. Optical paths L1,2,3 are obtained by integration along three separated paths, from the first fiber-optical coupler (1 × 3), throughout fibers and gaps between, defined by the micromachined platform, till the second-combining optical coupler (3 × 3):
where: ncore—is the refractive index of core of the optical fiber; nair is air index, equal to 1; nliquid—the refractive index of the examined liquid; L1,2,3(1 × 3)—lengths of 1 × 3 fiber-optic coupler arms; L1,2,3(3 × 3)—lengths of 3 × 3 fiber-optic coupler arms; and L1,2,3GAP are widths of micromachined platform channels. OPDs are Equation (3):
Since the degree of coherence γ11 has non-zero values only when the argument is close to zero, the signal on the photodetector originating from the variable interferometric terms in Equation (3) occurs if , described by (4):
where K1, K2, and K3 are constants determined by lengths of the coupler arms.
During the L1GAP scan time two zones of coherence signal appear when the 1st and 2nd conditions in Equation (4) are satisfied, in the extent of the light source coherence length. The 3rd condition in Equation (4) does not contain the scanning gap L1GAP, so it cannot give an interferometric signal. The fulfillment of the 3rd condition must be avoided, otherwise a severe spurious signal will occur. Also, the zones with satisfied 1st and 2nd conditions should not be overlapped.
The maximum of the interferometric signal defined by 1st condition in Equation (4) is at position where:
and the second maximum is at:
because nair = 1.
Using simple manipulations it can be seen that the unknown refraction index nliquid of fluid in the MFP2 microchannel is:
where the widths of the MFP microchannels are the same (L2GAP = L3GAP), ∆K = K1 − K2 is a constant value and ΔL1GAP is the difference between the two maxima of the interferometric signals described by Equation (8):
It can be seen from Equation (7) that to calculate the refractive index of an unknown liquid nliquid, it is necessary, in addition to measuring ∆, to also know two constants: the microchannel width L3GAP and ∆K, determined by the differences of the coupler arms lengths. L3GAP is the distance between the opposing tips of the optical fibers and should be equal to the width of the micromachined channel of 125 µm. However, it cannot be taken as known due to the possible pullback of the fibers, caused by curing of the glue fixing the fiber in the positions. The difference between the fiber arms ∆K is specific for one measurement set-up and does not change during the measurement. Its value, however, is unknown at the beginning of the measurement. Thus, two constants, ∆K and L3GAP should be determined firstly using two reference fluids of known refractive indices.
The constant ∆K can easily be found out from the first scanning when air is present into the microchannel on the L3 path. In this case, the ∆K is equal to the ΔL3GAP, which is the distance between the two centers of the coherence domain. Then, the actual length of the channel L3GAP can be found using a known fluid introduced into the microchannel. We were using Isopropanol (IPA) as a reference fluid, which has the refraction index 1.375 at 1298 nm and 22 °C, according to [24]. After two calibrating measurements, the index of the unknown liquid nliquid can be calculated by:
Notice that the individual position of the coherence region centers are not used to calculate the unknown index nliquid, but their difference , which is used in Equation (9). It means that there is no need to determine the exact start of the scan and resetting the gap width to zero before scanning, as it was the case in our previous experiments reported in [25], in which there was no reference microchannel.
The accuracy of the refractive index (nliquid) measurement is determined by the accuracy of the determination of distance between the two centers of the coherence area (, ) which, in turn, relates to the accuracy of determining the two positions of the center of the coherence area (L1GAP). We assume that the refractive index of the reference fluid ( is known from the literature with sufficient accuracy and precision, so it can be considered as an accurate constant.
If the accuracy of determining the center of the coherence area is described by the standard deviation in a large set of successive measurements, the accuracy of the measurement of refractive index of an unknown fluid can be calculated out from partial derivatives Equation (9):
We can reasonably assume that the standard deviation in a set of measurements of position difference is equal for all three refractive indices:
In our configuration, shown in Figure 1, a controlled change of the optical path difference in the arm 1 (L1GAP) is employed. This is done mechanically, by moving the tip of the optical fiber of the 1 × 3 coupler against the opposite optical fiber of the 3 × 3 coupler. These small-step movements were performed using a motorized stage and the position was read out using the built-in encoder.
A superluminescent diode is frequently used in low coherence interferometry due to relatively low coherence length and relatively high optical power that can be launched into a single-mode optical fiber. When such a source is employed, the interferometric term in Equation (1), which includes the degree of coherence γ11(ΔLij), decreases rapidly when ΔLij rises for several micrometers. The maximum of interferometric term is reached when γ11(ΔLij) equals one, i.e., when the interferometer OPD equals zero. Scanning the air gap in the reference arm, this position (denoted as L1GAP), where the interferometer OPD equals zero, can be found as the highest local maximum of interferometric term.
The determination of the zero OPD position is a challenging task, which includes several other assumptions and procedures. The main one is that we are scanning the OPD by moving the reference fiber with a constant, accurately measured speed. An alternative to this is to accurately measure the position of the fiber tip during the scan. The latter can be achieved using an independent (opto-) mechanical encoder, or by help of an additional high coherence laser beam sharing the same path at the same time as the low-coherence source.
Procedures for determining the zero OPD are numerous, from the simple identification of the maximal interferogram value, the envelope fitting [26], the centroid algorithm [27], to the most complex application of the FFT [28,29,30] and wavelet transformations [31]. In this work we used two techniques:
- The centroid algorithm, where the position of the center of coherence zone in the fringe pattern was calculated using the following equation [32]:where Lp is the position of local maximum point in the fringe pattern, I(Lp) is the intensity at this point, and Imax is the absolute maximum of interferometric signal; and
- The envelope fitting, where the set of local maxima of interferometric signal is fitted by Gaussian curve with its four parameters—center, width, height, and offset. Among them, the parameter center, that defines is the only one of importance.
2.3. Design of the Optofluidic Platform
Figure 2a presents the final design of the optofluidic platform that is used for the fluid flow simulation and fabrication. The platform consists of one central microchannel for testing fluid and seven orthogonal microchannels. The first one at the top of the platform serves for the reagent transportation, while the remaining six are meant for integration of different fiber-optic sensors. In this investigation we used the second one, orthogonal microchannel only, in both MFPs-reference filled with air and measuring filled with a subjected fluid-equipped with the sensing fibers of a MZI.
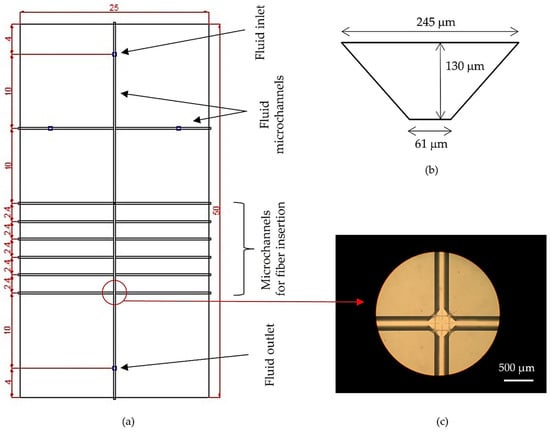
Figure 2.
(a) Overall view and dimensions (in mm) of the micromachined structure; (b) the cross-section of the microchannels for both fluid flow and fiber insertion; and (c) top view of the cross-over of the microchannels.
The platform consists of a silicon chip with overall dimensions of 50 × 25 × 0.42 mm, anodically bonded to a Pyrex glass with overall dimensions of 75 × 25 × 1.12 mm. The dimensions of the glass plate correspond to the standard microscopic glass plate and will be suitable for the inspection purposes. The width of the microchannels for both fluid flow and fiber insertion is 245 μm, measured at the channel top. The microchannels are V-shaped, determined by the (111) crystallographic planes. The cross-section of the microchannels for both fluid flow and fiber insertion is given in Figure 2b. Figure 2c shows a top view of the microchannel’s crossovers. Using the software package COMSOL (Stockholm, Sweden), we performed 3D simulation of the fluid flow through the whole structure to determine what relative pressures are needed at the inlet of the structure in order to attain a certain fluid velocity in the central microchannel. We assumed that the flow through the system is laminar. The inlet flow is fully developed laminar flow, described by the corresponding inlet boundary condition. The boundary conditions at the inlet and outlet set a constant relative pressure. All other boundaries are solid walls described by a non-slip boundary condition. The fluid used in simulation was pure water with density ρ = 1000 kg/m3 and viscosity ν = 0.001 Pa⋅s. The simulation is done for four different values of the relative pressure at the inlet [0.001, 0.005, 0.01, 0.05] bar.
The Laminar Flow (LF) user interface is primarily applied to flows of low to intermediate Reynolds numbers (R < 2000). For flow in a pipe or tube, the Reynolds number is generally defined as:
where:
- DH is the hydraulic diameter of the pipe;
- Q is the volumetric flow rate (m3/s);
- A is the pipe cross-sectional area (m2);
- u is the mean velocity of the fluid (SI units: m/s);
- μ is the dynamic viscosity of the fluid (Pa·s);
- ν is the kinematic viscosity (m2/s); and
- ρ is the density of the fluid (kg/m3).
For duct shapes, such as squares, rectangles, or annuli, where the height and width are comparable, the characteristic dimension for internal flow situations is taken to be the hydraulic diameter, DH, defined as DH = 4A/P, where A is the cross-sectional area and P is the wetted perimeter. The wetted perimeter for a channel is the total perimeter of all channel walls that are in contact with the fluid.
For our structure, and for water as a fluid, the condition that Re < 1 is fulfilled for fluid speeds below ~1 cm/s. Since the critical value of Re is about 2000, for fluid speeds of several cm/s and lower, the use of the LF user interface is justified.
The user interface solves the Navier-Stokes equation, for incompressible and weakly compressible flows:
Figure 3 gives the 3D distribution of velocity in the structure for an applied pressure at the inlet of 0.01 bar. As expected, the velocity dependence is parabolic, equal to zero at the structure walls, and its maximum value is reached in the microchannel, which is the narrowest part of the structure.
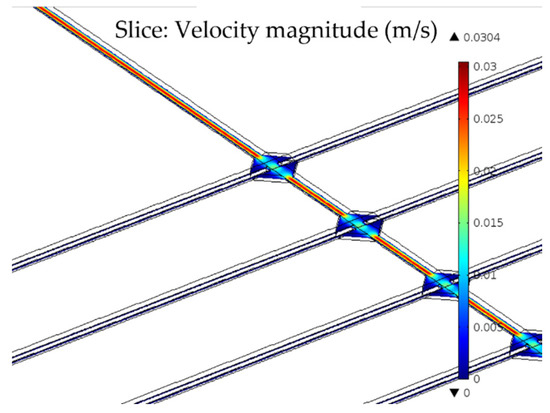
Figure 3.
3D distribution of velocity in the part of the structure given in Figure 2a for an applied pressure at the inlet of 0.01 bar.
Figure 4a shows the velocity intensity distribution along the middle line of the structure for the inlet–outlet pressure drop of 0.01 bar, while Figure 4b shows the dependence of the fluid velocity magnitude in the middle of the microchannel on different values of the relative pressure at the inlet. As seen, the velocity is the largest in the microchannel which is the narrowest part of the structure, and this velocity rises linearly with pressure applied at the inlet (pressure at the outlet = 0 bar).
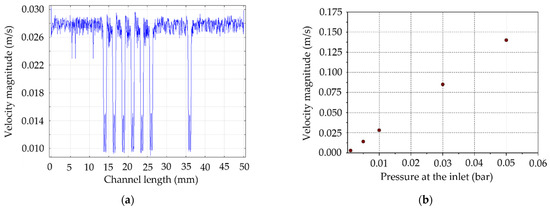
Figure 4.
(a) Velocity intensity distribution along the middle line of the channel for a relative pressure of 0.01 bar applied at the inlet; and (b) dependence of velocity intensity in a point in the middle of the channel on the pressure applied at the inlet.
Numerical simulation allows us to roughly estimate the value of pressure to be applied at the inlet of the microchannel to achieve laminar flow and required speed in the channel. Out of Figure 4a we can see a velocity drop in the microchannel in places where the channel is extended (channels crossover).
3. Experiment
An overall view of the experimental setup is schematically depicted in Figure 1. The low coherence source was a single-mode pigtailed superluminescent diode at a wavelength of 1298 nm (Superlum, Russia), with an embedded TEC for control of temperature. The optofluidic platforms MFP1 and MFP2, presented in Figure 1, are made by anodic bonding of silicone upper plate to the glass bottom plate. Central microfluidic channel and V groove lateral channels 125 µm in width are made by chemical etching of Si. The measuring platform MFP2 is placed to be just under the optical microscope, equipped with a video camera for capturing the image of the fluid streaming through the measurement microchannel. The reference optofluidic platform MFP1 and the scanning gap mechanism is placed near the measuring MFP2. The optical path differences in the sensing and the reference paths were set by cutting the 1 × 3 and 3 × 3 coupler’s arms to suitable lengths—where the zero OPD position would be inside a range of 500 µm of scanning. Mechanical scanning (M-Stage) was performed by Z600 Series Motorized Actuator (ThorLabs, Newton, NJ, USA) and SmartMove Motor Controller Software C-843 Motor (Physik Instrumente, Karlsruhe, Germany), which controls the position of the attached tip of the fiber of length L1(1 × 3) (see Figure 1). The photodetector signals from two pigtailed InGaAs photodiodes (Roithner Lasertechnik, Austria) were amplified by a pair of transimpedance amplifiers and acquired by National Instruments 16-bit/100kHz DAQ card. Simultaneously, the encoder (associated to the motorized Z600 actuators) digital signals were captured by the same card. The processing of the signals was made using the software package MATLAB (MathWorks, Natick, MA, USA).
The test fluid was fed to the microchannel of the MFP2 optofluidic platform and pushed by the air driven pump LU-FEZ-7000 (Fluigent, Le Kremlin-Bicêtre, France) at the pressure of 0.05 bar.
4. Results and Discussion
Figure 5 presents the two double Gaussian shape low-coherence interferograms (LCI), acquired using the described experimental set-up.
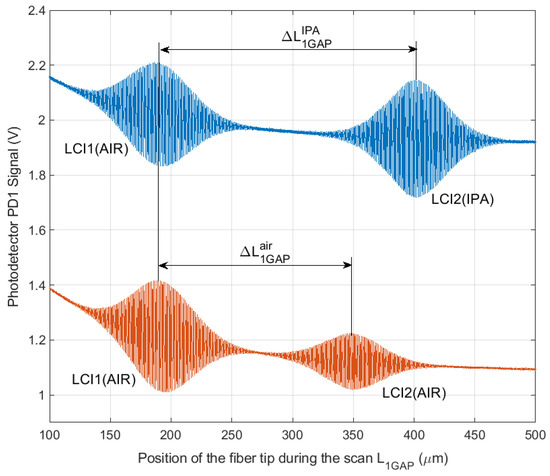
Figure 5.
Low-coherence interferograms acquired by scanning of microchannel of both optofluidic platforms. LCI1 belongs to MFP1, with air in the microchannel and LCI2 belongs to MFP2, the microchannel filled with air (lower curve) and Isopropanol (IPA) (upper curve).
The lower pair of LCIs was recorded while air was in the microcavity of both optofluidic platforms (MPF1 and MPF2). The upper pair of LCIs was obtained when Isopropanol (IPA) of known refractive index was introduced into the microchannel of the measuring optofluidic platform MPF2. In all experiments air was in the microchannel of the reference optofluidic platform MPF1. The LCIs with distilled water, ethanol, methanol, and 0.9% NaCl solutions were obtained in the same way.
The position of the scanning mirror was read out from the encoder, which generates one pulse per one motor step of 40.7 nm. The onset of the scanning was accurately and very repeatedly detected as the moment when the first interferometric fringe starts to rise, indicating the detachment of the fiber’s tips in the guiding ferrule.
The refractive index of the subjected liquids was calculated from the positions of scanning fiber , when the LCI central local maximum is reached, using Equation (9).
In order to locate central maxima of LCIs, we applied both the centroid algorithm and the envelope fitting method. The first step in signal processing was the band-pass filtration, where the quasi DC component and the high-frequency noise were removed. In the second step, the positions of all local maxima in LCI fringes were identified. An example of the interferogram at the end of the second phase is presented in Figure 6.
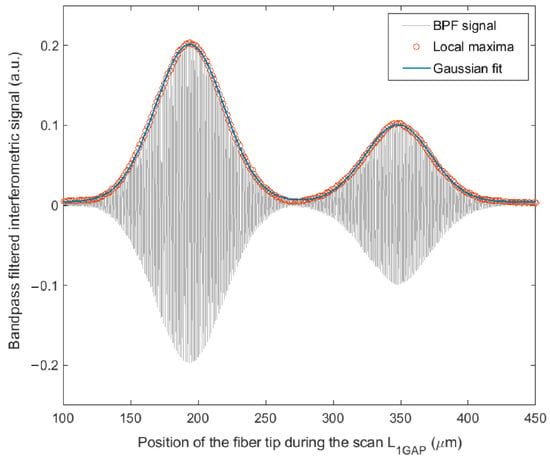
Figure 6.
Two low-coherence interferogram after band-pass filtration and local maxima detection, fitted by the double Gaussian curve.
The next steps were different for two algorithms. The centroid algorithm was realized through the direct application of the equation Equation (12), where the two coherence zones were previously separated into two sets of data. In contrast, the fitting algorithm was applied to the entire signal, using the fitting model consisted of two Gaussian functions. The nonlinear least squares fitting method and Levenberg–Marquardt algorithm were applied in MATLAB [33]. Both methods of finding the LCI center gave very similar results, with a difference deep within the error of mean value. So, only the results obtained by the fitting algorithm are shown here.
The accuracy and the precision of the method was evaluated using a set of 40 successive measurements when both channels were filled with air. The distribution of differences of two LCI center position is shown in Figure 7. The mean of 40 measurements was 149.72 µm, with the standard deviation, denoted as σΔ in Equation (11), of 0.304 µm. Applying Equation (10), the standard deviation in refraction index measurement is calculated as σn = 0.0031. This value can be considered as the precision of the index measurement.
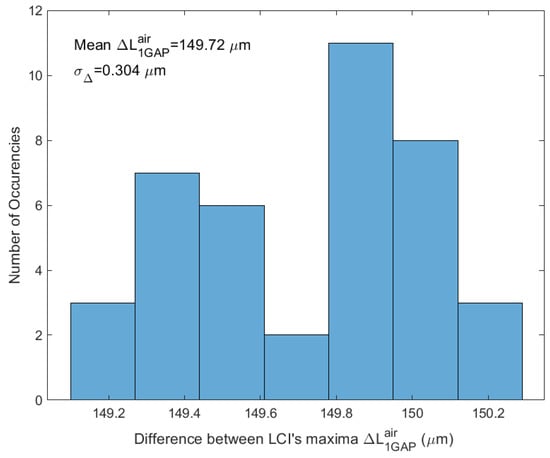
Figure 7.
The distribution of measured difference between the positions of coherence zone centers.
It is interesting to notice a non-normal distribution of the measured values of positions. The two values, around which the positions are grouped, differ from each other by about half the wavelength of the light used (0.65 µm). That corresponds to the half of the distance between two interferometric maxima, one of which is certainly central. The phenomenon suggests that the standard deviation could additionally be at least halved if an algorithm that removes this ambivalence is found.
Sensitivity and measuring range are directly related to the width of the channel in which the measured sample is located (ΔL3GAP). The sensitivity of the method increases linearly with increasing channel width, because the difference in the position of the centers of the coherence region is equal to the product of the channel width and the measured index, see Equation (6). It can be seen in Figure 7 that in our experiment it is possible to observe changes in ΔL1GAP less than 0.2 µm. This value gives a sensitivity in determining the refraction index of about 0.0016, because the channel width is 125 µm. However, the measuring range decreases with increasing channel width. The intensity of interferometric signal decreases with increasing distance between the fiber tips, due to weaker optical coupling. Experiments show that it is possible to measure the position of center of the coherence region with a declared accuracy at a distance of about 800 µm, giving an unnecessarily wide range of refractive index measurements (up to 5). If we would like to measure refractive indices up to e.g., value 2, the channel width should not exceed about 300 µm.
The position of the LCI center for the air gap L1GAP was declared as the zero, where the refractive index equals to 1. Thus, the accuracy of the measurement of L1GAP (mean value) is absolute by definition. Results of the measurement of the refractive index of the aforementioned fluids are shown in Figure 8, along with the literature data [24,34,35].
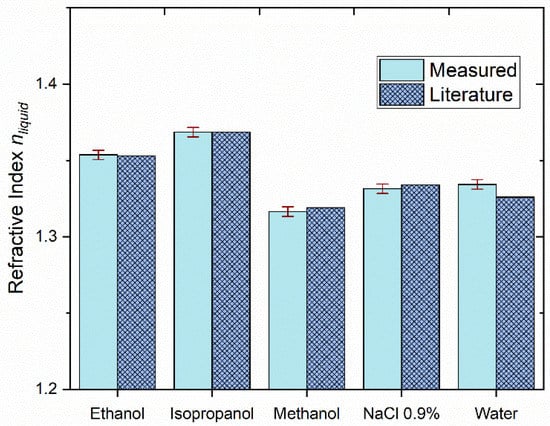
Figure 8.
Refractive index of subjected fluids obtained by our Mach–Zehnder interferometric configuration (light blue) and literature data for same fluids at 1300 nm (dark blue, patterned).
A very good agreement between our experimental results and literature data can be seen. In the fluid refractive index measurements, we obtained the mean absolute error of 0.0034. The relative measurement uncertainty calculated in respect to the value of 0.35, which was taken as the mean effectively measured index value (1.35−1), was about 1% (0.0034/0.35). One exception was the measurement of distilled water, where the refraction index is measured with the absolute error of 0.0083 (2.5%), probably caused by a contamination of the sample. The absolute error of measurement of Isopropanol is equal to zero, because its value is used for calibration (this result is omitted in calculation of the stated accuracy).
The main causes of measurement error are related to mechanical scanning and inaccuracies in determining the width of the gap during the scan. These problems can be overcome by optical interferometric measurement of the gap width. This type of measurement will be tested in the future—it can be noticed that our signal from the PD2 photodetector is not used in the measurements presented here. PD2 signal is in quasi-quadrature with the PD1 signal (shifted in the phase by about 120 degrees) and gives the same result using the algorithm described here. However, this signal can be used to perform very accurate phase measurements [36]. To realize this, a higher coherence length radiation can be passed through the configuration shown, generating continuity in phase measurement, which is here interrupted between the two coherence zones.
Another cause of inaccuracy is the error in determining the position of the center of the coherence area, which is related to the signal-to-noise ratio in the system, the isolation of fibers in the branches between the couplers from external temperature and vibro-acoustic influences, and parasitic interferences. Reducing these impacts would allow measurements with fewer averaging, which could allow real-time refractive index measurements with higher fluid flow through the microchannel plate.
5. Conclusions
We demonstrated a fiber-optic sensing technique aimed to measure refractive index of liquids and gases in dynamic regime. The technique combines an open cavity in-line Mach–Zehnder low-coherence interferometer embedded into two micromachined optofluidic platforms, one of them acting as reference (field with air) and the other as measuring (field with subjected fluid). Such a sensing configuration allows permanent autocalibration and minimization of the cross-sensitivity influences like thermal drift or mechanical vibrations on the measured interference signal. By multiplexing of many micromachined optofluidic platforms it is possible to measure refractive index of various liquids and gases simultaneously. Here, we tested five liquids with refractive indices in the range of 1.32 to 1.38. A very good agreement between the experimental and literature data was obtained. The precision and accuracy of the refractive index measurement was about 1%. The proposed sensor is suitable for the label-free sensing in biomedicine as well as in analytical chemistry, due to its high precision and accuracy and small sample volume of about 1 µL. The micromachined optofluidic platform may be easily manufactured as a Lab-on-the-Chip by 3D printing, polymer injection molding and hot embossing for the sake of cost-effective mass production.
Author Contributions
Conceptualization, Z.D. and A.K.; methodology, M.T.; validation, A.K., Z.D. and M.T.; formal analysis, Z.D. and A.K.; experimental investigation, A.K.; resources, Z.D.; writing—original draft preparation, Z.D. and M.T.; writing—review and editing, Z.D. and M.T.; project administration, Z.D.; funding acquisition, Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Gesellschaft für Forschungsförderung Niederösterreich m.b.H and ACMIT Gmbh, Austria, grant number LSC15-004.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This paper did not report any data.
Acknowledgments
The authors thank the NFB and ACMIT Gmbh, Austria, which sponsored this work in the frame of the LSC15-004 project “Immune-regulatory capacity of mesenchymal stem cells (MSCs)”. M.T. thanks the Ministry of Education, Science, and Technological Development of the Republic of Serbia, which supported him in this investigation, in the frame of the agreement 451-03-9/2021-14/ 200175, with the Institute of Technical Sciences of SASA. The authors thank Katarina Radulović, the University of Belgrade, ICTM-CMT, for the COMSOL simulation of the micromachined platforms. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Flores-Bravo, J.A.; Illarramendi, J.A.; Zubia, J.; Villatoro, J. Optical fiber interferometer for temperature-independent refractive index measuring over a broad range. Opt. Laser. Technol. 2021, 139, 106977. [Google Scholar] [CrossRef]
- Samanta, S.; Kalathimekkad, S.; Selvaraja, S.K. Fluid sensing strategies adopted in photonic devices: A review. Opt. Laser. Technol. 2021, 139, 106975. [Google Scholar] [CrossRef]
- Dong, J.T.; Cheng, C.H.; Wu, C.; Li, J.; Guan, B.O. Highly sensitive optofluidic refractive index sensor based on a seven-liquid-core Teflon-cladding fiber. Opt. Express 2020, 28, 26218–26227. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Zhao, Y.; Yang, Y.; Wang, Y.; He, X.; Yang, W.; Li, L. All-fiber Fabry–Perot interferometer for liquid refractive index measurement. J. Russ. Laser Res. 2019, 40, 370–374. [Google Scholar] [CrossRef]
- Yu, H.; Xiong, L.; Chen, Z.; Li, Q.; Yi, X.; Ding, Y.; Wang, F.; Lv, H.; Ding, Y. Ultracompact and high sensitive refractive index sensor based on Mach–Zehnder interferometer. Opt. Lasers Eng. 2014, 56, 50–53. [Google Scholar] [CrossRef]
- Rostamian, A.; Madadi-Kandjani, E.; Dalir, H.; Sorger, V.J.; Chen, R.T. Towards lab-on-chip ultrasensitive ethanol detection using photonic crystal waveguide operating in the mid-infrared. Nanophotonics 2021, 10, 1675–1682. [Google Scholar] [CrossRef]
- Mishra, A.K.; Mishra, S.K.; Gupta, B.D. SPR based fiber optic sensor for refractive index sensing with enhanced detection accuracy and figure of merit in visible region. Opt. Commun. 2021, 344, 86–91. [Google Scholar] [CrossRef]
- Wang, X.-M.; Zhao, C.-L.; Wang, Y.-R.; Jin, S. Aproposal of T-structure fiber-optic refractive index sensor based on surface plasmon resonance. Opt. Commun. 2016, 369, 189–193. [Google Scholar] [CrossRef]
- Liu, W.; Hu, C.; Zhou, L.; Yi, Z.; Liu, C.; Lv, J.; Yang, L.; Chu, P.K. A square-lattice D-shaped photonic crystal fiber sensor based on SPR to detect analytes with large refractive indexes. Phys. E 2022, 138, 115106. [Google Scholar] [CrossRef]
- Hu, T.; Zhao, Y.; Song, A. Fiber optic SPR sensor for refractive index and temperature measurement based on MMF-FBG-MMF structure. Sens. Actuators B 2016, 237, 521–525. [Google Scholar] [CrossRef]
- Qi, L.; Zhao, C.L.; Yuan, J.; Ye, M.; Wang, J.; Zhang, Z.; Jin, S. Highly reflective long period fiber grating sensor and its application in refractive index sensing. Sens. Actuators B 2014, 193, 185–189. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Zhang, T.; Zhang, W. Integrated FPI-FBG composite all-fiber sensor for simultaneous measurement of liquid refractive index and temperature. Opt. Lasers Eng. 2018, 11, 167–171. [Google Scholar] [CrossRef]
- Yebin, Z.; Gao, S.; Zhang, A.P. Optically heated long-period grating as temperature insensitive fiber-optic refractive index sensor. IEEE Photonics J. 2012, 4, 2340–2345. [Google Scholar] [CrossRef]
- Rao, Y.J.; Deng, M.; Duan, D.W.; Zhu, T. In-line Fabry-Perot refractive-index tip sensor based on endlessly photonic crystal fiber. Sens. Actuators A 2008, 148, 33–38. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Jiang, J.; Liu, K.; Zhang, P.; Wu, W.; Liu, T. High-accuracy hybrid fiber-optic Fabry-Perot sensor based on MEMS gas refractive-index and temperature sensing. Opt. Express 2019, 27, 4204–4215. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Liao, C.; Sun, B.; He, J.; Yin, G.; Liu, S.; Li, Z.; Wang, G.; Zhong, X.; et al. Intensity modulated refractive index sensor based on optical fiber Michelson interferometer. Sens. Actuators B 2015, 208, 315–319. [Google Scholar] [CrossRef]
- Zhu, T.; Wu, D.; Duan, D.W. In-line fiber optic interferometric sensors in single-mode fibers. Sensors 2012, 12, 10430–10449. [Google Scholar] [CrossRef] [Green Version]
- Ahsani, V.; Ahmed, F.; Jun, M.B.G.; Bardley, C. Tapered fiber-optic Mach-Zehnder interferometer for ultra-high sensitivity measurement of refractive index. Sensors 2019, 19, 1652. [Google Scholar] [CrossRef] [Green Version]
- Xi, F.; Zhao, Y.; Peng, Y. In-line microfiber MZI operating at two sides of the dispersion turning point for ultrasensitive RI and temperature measurement. Sens. Actuators A 2020, 301, 111754. [Google Scholar] [CrossRef]
- Yao, Q.; Meng, H.; Wang, W.; Xue, H.; Xiong, R.; Huang, B.; Tan, C.H.; Huang, X. Simultaneous measurement of refractive index and temperature based on a core-offset Mach-Zehnder interferometer combined with a fiber Bragg grating. Sens. Actuators A 2014, 209, 73–77. [Google Scholar] [CrossRef]
- Domínguez-Flores, C.E.; Valdés-Hernández, A.I.; Reyes, A.K.; David Monzón-Hernández, D.; Rodríguez-Quiroz, O.; Ochoa-Valiente, R. Ultra-long range refractive index fiber sensor. Front. Sens. 2022, 3, 855251. [Google Scholar] [CrossRef]
- Tang, J.; Qui, G.; Wang, J. Recent development of optofluidics for imaging and sensing applications. Chemosensors 2022, 10, 15. [Google Scholar] [CrossRef]
- Peng, F.; Du, J.; Du, J.; Wang, S.; Yan, W. Contrast Analysis of Polarization in Three-Beam Interference Lithography. Appl. Sci. 2021, 11, 4789. [Google Scholar] [CrossRef]
- Moutzouris, K.; Papamichael, M.; Betsis, S.C.; Stavrakas, I.; Hloupis, G.; Triantis, D. Refractive, dispersive and thermos-optic properties of twelve organic solvents in the visible and near-infrared. Appl. Phys. B 2014, 116, 617–622. [Google Scholar] [CrossRef]
- Djinovic, Z.; Kocsis, A.; Tomic, M. Fiber-optic Mach-Zehnder interferometer for refractive index measurement based on MEMS optofluidic platform. In Proceedings of the 7th International Conference on Sensors Engineering and Electronics Instrumentation Advances (SEIA’ 2021), Palma de Mallorca, Spain, 22–24 September 2021. [Google Scholar]
- Larkin, K. Efficient nonlinear algorithm for envelope detection in white light interferometry. J. Opt. Soc. Am. 1996, 13, 832–843. [Google Scholar] [CrossRef] [Green Version]
- Ai, C.; Novak, E.L. Centroid Approach for Estimating Modulation Peak in Broad-Bandwidth Interferometry. U.S. Patent 5633715A, 27 May 1997. [Google Scholar]
- Chim, S.; Kino, G. Three-dimensional image realization in interference microscopy. Appl. Opt. 1992, 31, 2550–2553. [Google Scholar] [CrossRef]
- Vo, Q.; Fang, F.; Zhang, X.; Gao, H. Surface recovery algorithm in white light interferometry based on combined white light phase shifting and fast Fourier transform algorithms. Appl. Opt. 2017, 56, 8174–8185. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, A. Fast White Light Interferometry Demodulation Algorithm for Low-Finesse Fabry–Pérot Sensors. IEEE Photon. Technol. Lett. 2015, 27, 817–820. [Google Scholar] [CrossRef]
- Sandoz, P. Wavelet transform as a processing tool in white-light interferometry. Opt. Lett. 1997, 22, 1065–1067. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Jiang, J.; Liu, K.; Wang, S.; Li, Y.; Liu, T. A Demodulation Method of Spatial Domain for Low-Coherence Interferometry with High Accuracy and Adaptability. IEEE Photonics J. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- MATLAB. 9.7.0.1190202 (R2019b); The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Kedenburg, S.; Vieweg, M.; Gissibl, T.; Giessen, H. Linear refractive index and absorption measurements of nonlinear optical liquids in the visible and near-infrared spectral region. Opt. Mater. Express 2012, 2, 1588–1611. [Google Scholar] [CrossRef]
- Li, X.; Liu, L.; Zhao, J.; Tan, J. Optical properties of sodium chloride solution within spectral range from 300 to 2500nm at room temperature. Appl. Spectrosc. 2015, 69, 635–640. [Google Scholar] [CrossRef] [PubMed]
- Tomic, M.C.; Djinovic, Z.V.; Petricevic, S.J. Demodulation of quasi-quadrature interferometric signals for use in the totally implantable hearing aid. Biomed. Opt. Express 2017, 8, 3404–3409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).