Acoustic Vibration Modes of Gold–Silver Core–Shell Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nanoparticle Synthesis
2.2. Characterization
2.3. Pump-Probe Transient Absorption Spectroscopy
2.4. Fast Fourier Transform Analysis
2.5. Numerical Simulations
3. Results
3.1. Sample Characteristics
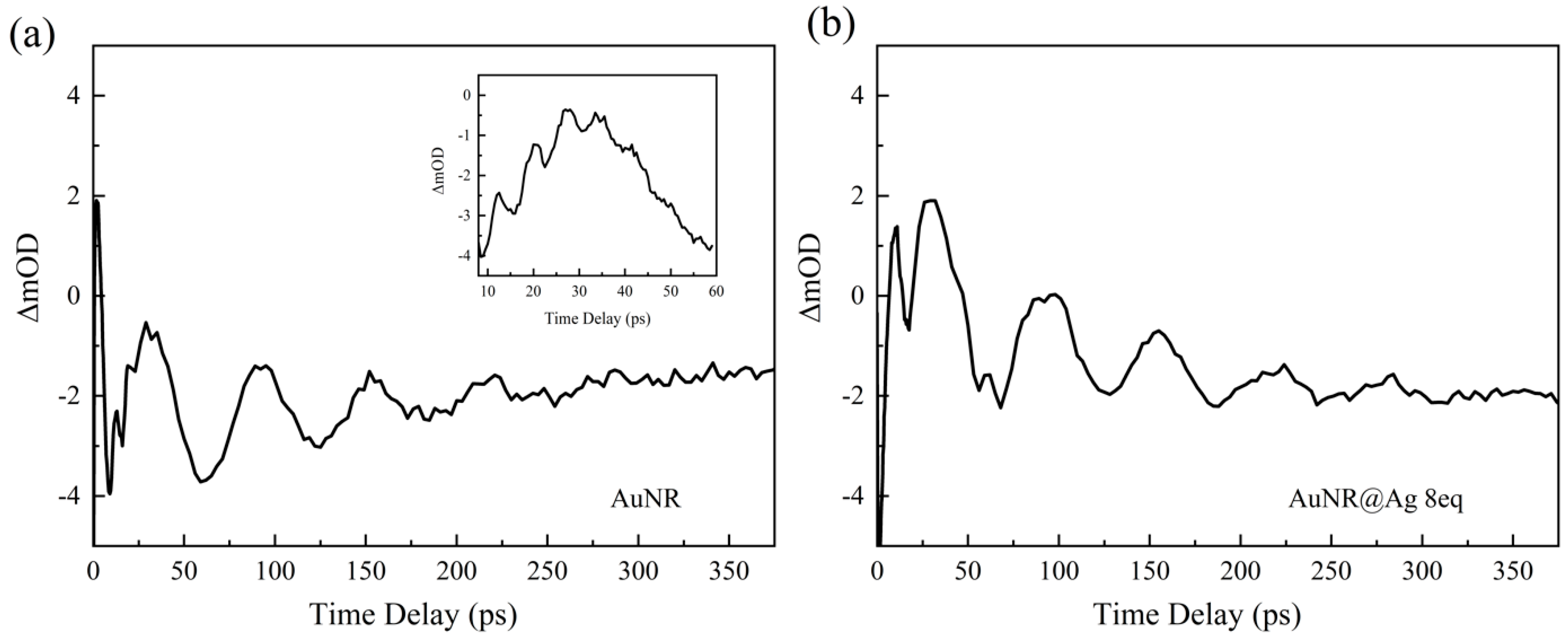
3.2. Time-Dependent TA Spectra
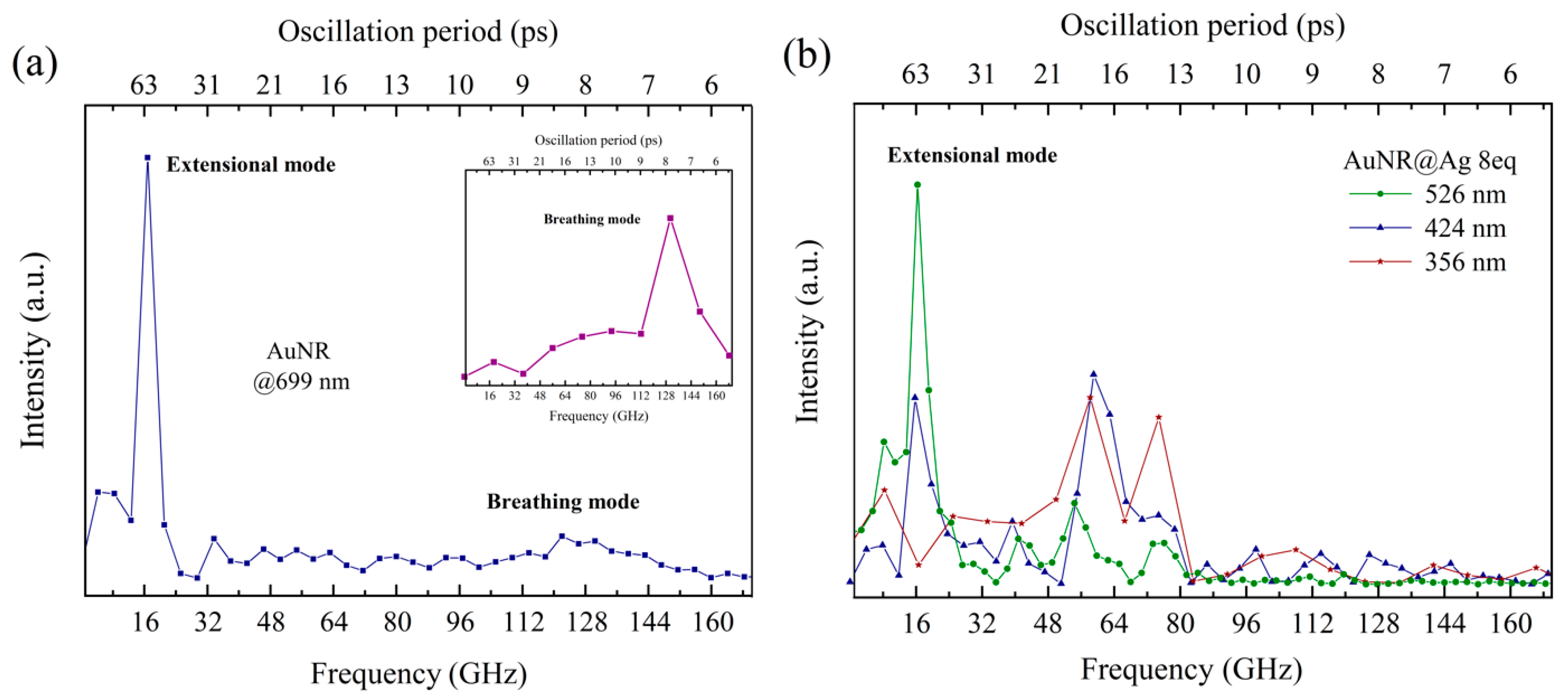
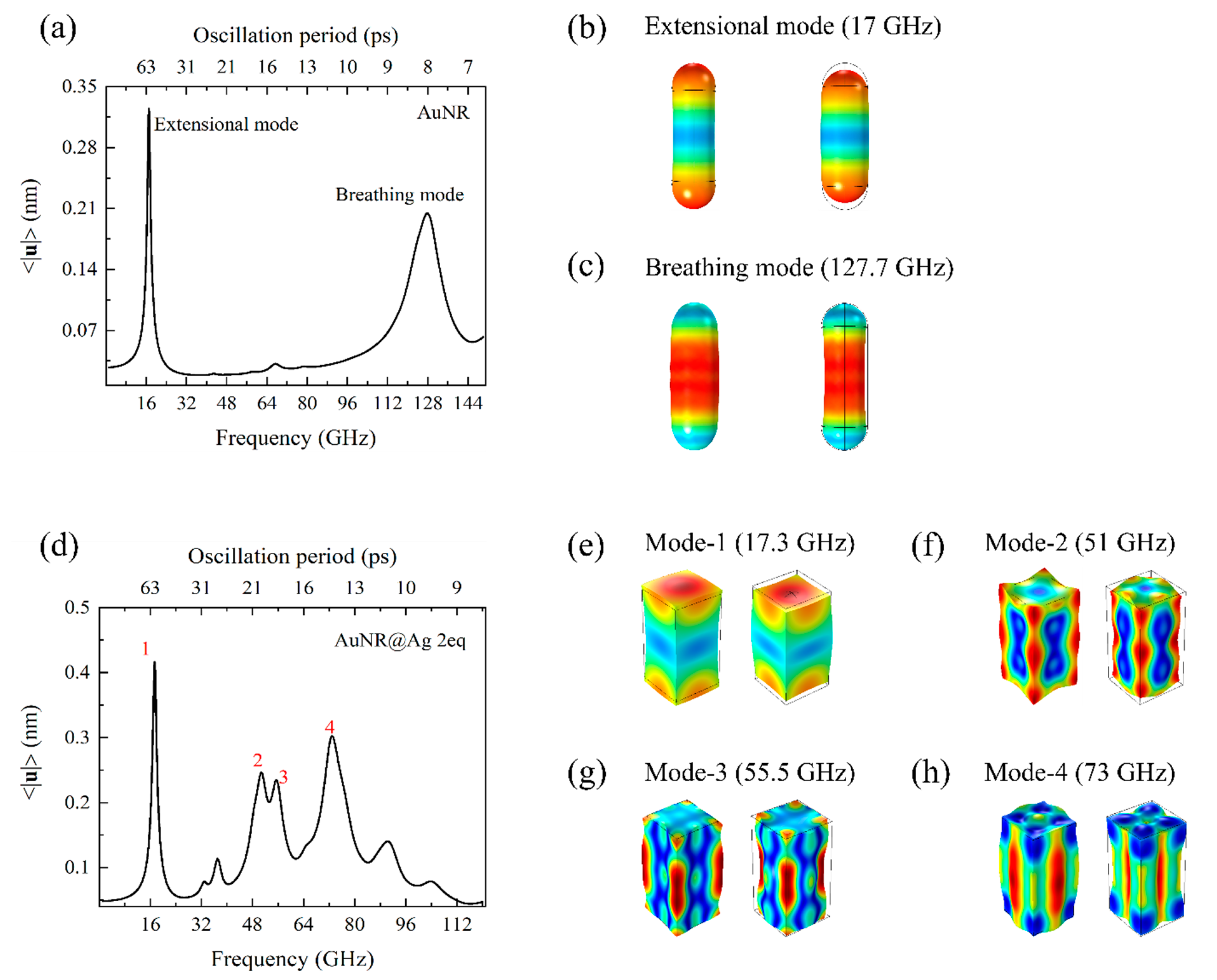
3.3. Vibration Mode Identification
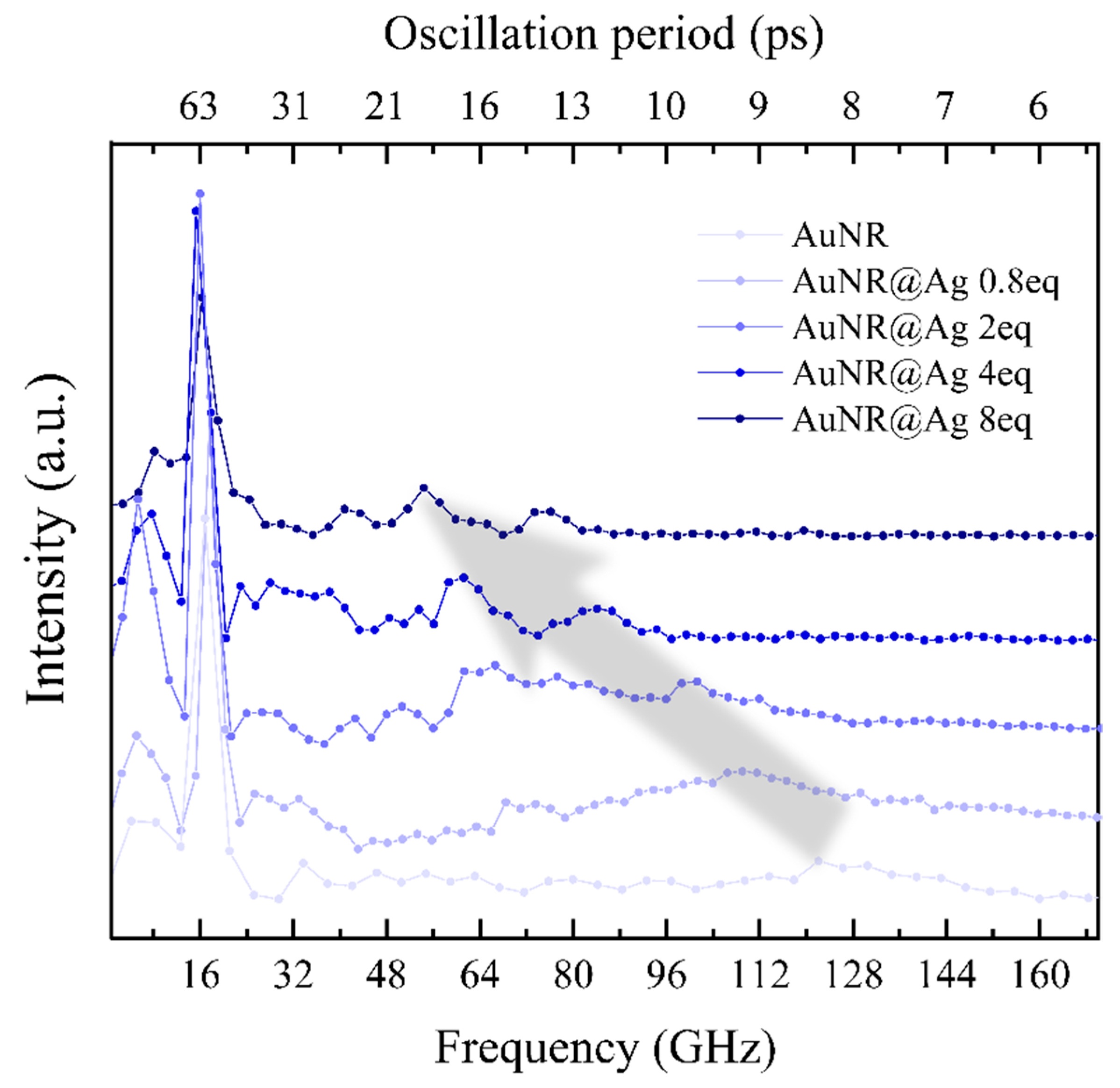
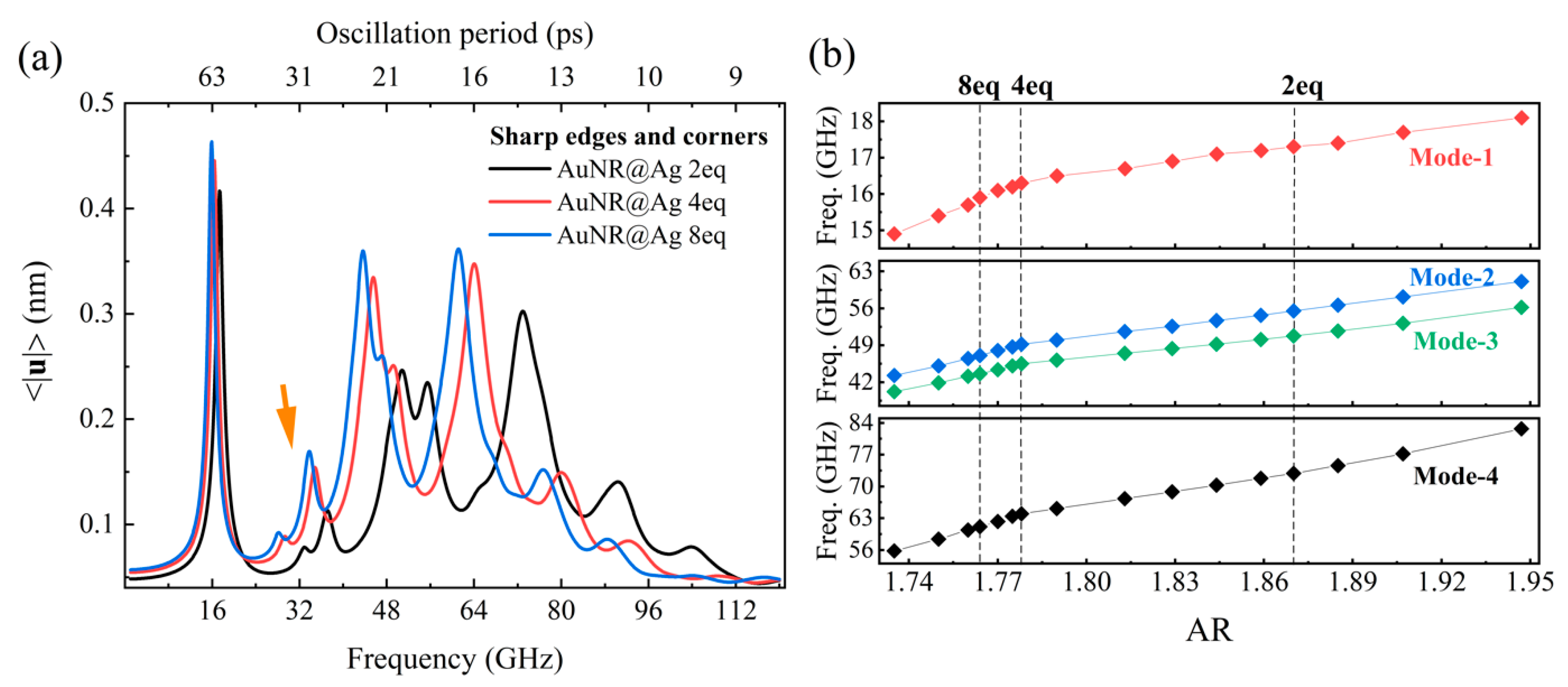
3.4. Ag-Shell Thickness Dependence of the Mode Frequency
4. Discussion
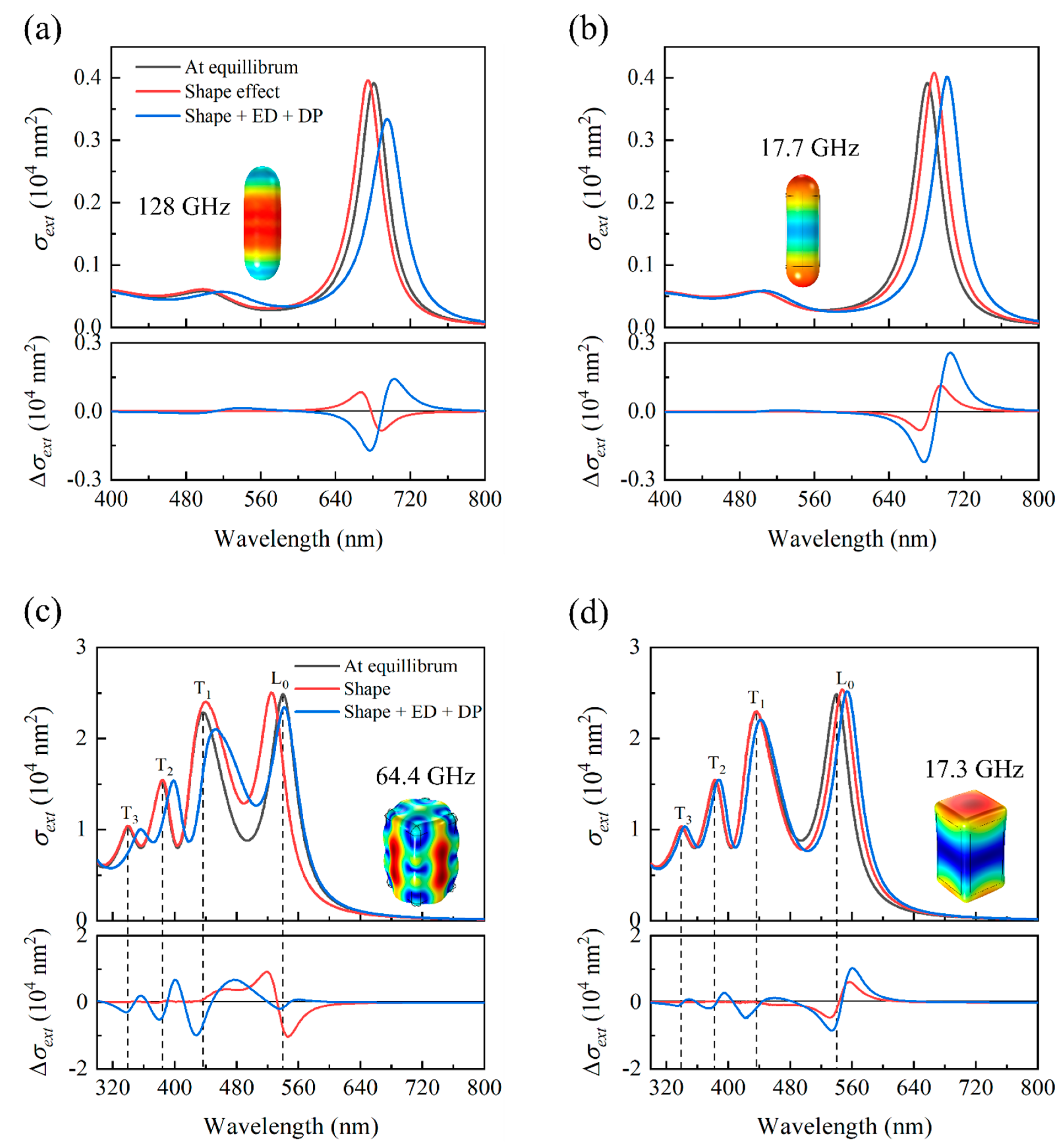
4.1. Identification of the Modes
4.2. Ag-Shell Thickness Dependence of the Spectra
4.3. Acousto-Plasmonic Coupling
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calculation of the NP Vibrational Properties
Appendix B. Calculation of the NP Optical Properties
References
- Hartland, G.V. Optical studies of dynamics in noble metal nanostructures. Chem. Rev. 2011, 111, 3858–3887. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Wang, X.; Hartland, G.V.; Mulvaney, P.; Juste, J.P.; Sader, J.E. Vibrational response of nanorods to ultrafast laser induced heating: Theoretical and experimental analysis. J. Am. Chem. Soc. 2003, 125, 14925–14933. [Google Scholar] [CrossRef] [PubMed]
- Crut, A.; Maioli, P.; Del Fatti, N.; Vallée, F. Acoustic vibrations of metal nano-objects: Time-domain investigations. Phys. Rep. 2015, 549, 1–43. [Google Scholar] [CrossRef]
- Beane, G.; Devkota, T.; Brown, B.S.; Hartland, G.V. Ultrafast measurements of the dynamics of single nanostructures: A review. Rep. Prog. Phys. 2019, 82, 16401. [Google Scholar] [CrossRef]
- Hodak, J.H.; Martini, I.; Hartland, G.V. Spectroscopy and dynamics of nanometer-sized noble metal particles. J. Phys. Chem. B 1998, 102, 6958–6967. [Google Scholar] [CrossRef]
- Del Fatti, N.; Voisin, C.; Chevy, F.; Vallée, F.; Flytzanis, C. Coherent acoustic mode oscillation and damping in silver nanoparticles. J. Chem. Phys. 1999, 110, 11484–11487. [Google Scholar] [CrossRef]
- Voisin, C.; Del Fatti, N.; Christofilos, D.; Vallee, F. Ultrafast electron dynamics and optical nonlinearities in metal nanoparticles. J. Phys. Chem. B 2001, 105, 2264–2280. [Google Scholar] [CrossRef]
- Van Dijk, M.A.; Lippitz, M.; Orrit, M. Detection of acoustic oscillations of single gold nanospheres by time-resolved interferometry. Phys. Rev. Lett. 2005, 95, 267406. [Google Scholar] [CrossRef] [Green Version]
- Perner, M.; Gresillon, S.; März, J.; von Plessen, G.; Feldmann, J.; Porstendorfer, J.; Berg, K.-J.; Berg, G. Observation of hot-electron pressure in the vibration dynamics of metal nanoparticles. Phys. Rev. Lett. 2000, 85, 792–795. [Google Scholar] [CrossRef]
- Hartland, G.V.; Hu, M.; Wilson, O.; Mulvaney, P.; Sader, J.E. Coherent excitation of vibrational modes in gold nanorods. J. Phys. Chem. B 2002, 106, 743–747. [Google Scholar] [CrossRef]
- Hu, M.; Hillyard, P.; Hartland, G.V.; Kosel, T.; Perez-Juste, J.; Mulvaney, P. Determination of the elastic constants of gold nanorods produced by seed mediated growth. Nano Lett. 2004, 4, 2493–2497. [Google Scholar] [CrossRef]
- Zijlstra, P.; Tchebotareva, A.L.; Chon, J.W.M.; Gu, M.; Orrit, M. Acoustic oscillations and elastic moduli of single gold nanorods. Nano Lett. 2008, 8, 3493–3497. [Google Scholar] [CrossRef]
- Pelton, M.; Sader, J.E.; Burgin, J.; Liu, M.; Guyot-Sionnest, P.; Gosztola, D. Damping of acoustic vibrations in gold nanoparticles. Nat. Nanotechnol. 2009, 4, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Kirschner, M.S.; Lethiec, C.M.; Lin, X.-M.; Schatz, G.C.; Chen, L.X.; Schaller, R.D. Size-dependent coherent-phonon plasmon modulation and deformation characterization in gold bipyramids and nanojavelins. ACS Photonics 2016, 3, 758–763. [Google Scholar] [CrossRef]
- Marty, R.; Arbouet, A.; Girard, C.; Mlayah, A.; Paillard, V.; Lin, V.K.; Teo, S.L.; Tripathy, S. Damping of the acoustic vibrations of individual gold nanoparticles. Nano Lett. 2011, 11, 3301–3306. [Google Scholar] [CrossRef] [PubMed]
- Su, M.-N.; Dongare, P.D.; Chakraborty, D.; Zhang, Y.; Yi, C.; Wen, F.; Chang, W.-S.; Nordlander, P.; Sader, J.E.; Halas, N.J.; et al. Optomechanics of single aluminum nanodisks. Nano Lett. 2017, 17, 2575–2583. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Takeda, S.; Sato, R.; Sakamoto, M.; Teranishi, T.; Tamai, N. Morphology-dependent coherent acoustic phonon vibrations and phonon beat of Au nanopolyhedrons. ACS Omega 2021, 6, 5485–5489. [Google Scholar] [CrossRef]
- Ruijgrok, P.V.; Zijlstra, P.; Tchebotareva, A.L.; Orrit, M. Damping of acoustic vibrations of single gold nanoparticles optically trapped in water. Nano Lett. 2012, 12, 1063–1069. [Google Scholar] [CrossRef]
- Yu, K.; Zijlstra, P.; Sader, J.E.; Xu, Q.H.; Orrit, M. Damping of acoustic vibrations of immobilized single gold nanorods in different environments. Nano Lett. 2013, 13, 2710–2716. [Google Scholar] [CrossRef] [Green Version]
- Uthe, B.; Collis, J.F.; Madadi, M.; Sader, J.E.; Pelton, M. Highly spherical nanoparticles probe gigahertz viscoelastic flows of simple liquids without the no-slip condition. J. Phys. Chem. Lett. 2021, 12, 4440–4446. [Google Scholar] [CrossRef]
- Kirakosyan, A.S.; Shahbazyan, T.V. Vibrational modes of metal nanoshells and bimetallic core-shell nanoparticles. J. Chem. Phys. 2008, 129, 34708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hodak, J.H.; Henglein, A.; Hartland, G.V. Coherent excitation of acoustic breathing modes in bimetallic core-shell nanoparticles. J. Phys. Chem. B 2000, 104, 5053–5055. [Google Scholar] [CrossRef]
- Crut, A.; Juvé, V.; Mongin, D.; Maioli, P.; Del Fatti, N.; Vallée, F. Vibrations of spherical core-shell nanoparticles. Phys. Rev. B 2011, 83, 205430. [Google Scholar] [CrossRef]
- Wang, L.; Kiya, A.; Okuno, Y.; Niidome, Y.; Tamai, N. Ultrafast spectroscopy and coherent acoustic phonons of Au/Ag core/shell nanorods. J. Chem. Phys. 2011, 134, 54501. [Google Scholar] [CrossRef] [PubMed]
- Cardinal, M.F.; Mongin, D.; Crut, A.; Maioli, P.; Rodríguez-González, B.; Pérez-Juste, J.; Liz-Marzán, L.M.; Del Fatti, N.; Vallée, F. Acoustic vibrations in bimetallic Au@Pd core-shell nanorods. J. Phys. Chem. Lett. 2012, 3, 613–619. [Google Scholar] [CrossRef]
- Yu, K.; Sader, J.E.; Zijlstra, P.; Hong, M.; Xu, Q.H.; Orrit, M. Probing silver deposition on single gold nanorods by their acoustic vibrations. Nano Lett. 2014, 14, 915–922. [Google Scholar] [CrossRef] [Green Version]
- Dacosta Fernandes, B.; Spuch-Calvar, M.; Baida, H.; Tréguer-Delapierre, M.; Oberlé, J.; Langot, P.; Burgin, J. Acoustic vibrations of Au nano-bipyramids and their modification under Ag deposition: A perspective for the development of nanobalances. ACS Nano 2013, 7, 7630–7639. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Nie, Z.; Feng, Y.; Zhao, W.; Zhang, J.; Zhang, W.; Maioli, P.; Loh, Z.-H. Ultrafast acoustic vibrations of Au/Ag nanoparticles with varying elongated structures. Phys. Chem. 2020, 22, 22728–22735. [Google Scholar] [CrossRef]
- Scarabelli, L.; Grzelczak, M.; Liz-Marzán, L.M. Tuning gold nanorod synthesis through prereduction with salicylic acid. Chem. Mater. 2013, 25, 4232–4238. [Google Scholar] [CrossRef] [Green Version]
- Tebbe, M.; Kuttner, C.; Mayer, M.; Maennel, M.; Pazos-Perez, N.; König, T.A.F.; Fery, A. Silver-overgrowth-induced changes in intrinsic optical properties of gold nanorods: From noninvasive monitoring of growth kinetics to tailoring internal mirror charges. J. Phys. Chem. C 2015, 119, 9513–9523. [Google Scholar] [CrossRef]
- Park, K.; Drummy, L.F.; Vaia, R.A. Ag shell morphology on Au nanorod core: Role of Ag precursor complex. J. Mater. Chem. 2011, 21, 15608–15618. [Google Scholar] [CrossRef]
- Otomalo, T.O.; Di Mario, L.; Hamon, C.; Constantin, D.; Do, K.; O’Keeffe, P.; Catone, D.; Paladini, A.; Palpant, B. Sharp spectral variations of the ultrafast transient light extinction by bimetallic nanoparticles in the near-UV. Adv. Opt. Mater. 2021, 9, 2001778. [Google Scholar] [CrossRef]
- Hendel, T.; Wuithschick, M.; Kettemann, F.; Birnbaum, A.; Rademann, K.; Polte, J. In Situ Determination of Colloidal Gold Concentrations with UV–Vis Spectroscopy: Limitations and Perspectives. Anal. Chem. 2014, 86, 11115–11124. [Google Scholar] [CrossRef] [PubMed]
- Scarabelli, L.; Sánchez-Iglesias, A.; Pérez-Juste, J.; Liz-Marzán, L.M. A “Tips and Tricks” Practical Guide to the Synthesis of Gold Nanorods. J. Phys. Chem. Lett. 2015, 6, 4270–4279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Mario, L.; Otomalo, T.O.; Catone, D.; O’Keeffe, P.; Tian, L.; Turchini, S.; Palpant, B.; Martelli, F. Time-dependent optical response of three-dimensional Au nanoparticle arrays formed on silica nanowires. Phys. Rev. B 2018, 97, 1–9. [Google Scholar] [CrossRef]
- Catone, D.; Di Mario, L.; Martelli, F.; O’Keeffe, P.; Paladini, A.; Cresi, J.S.P.; Sivan, A.K.; Tian, L.; Toschi, F.; Turchini, S. Ultrafast optical spectroscopy of semiconducting and plasmonic nanostructures and their hybrids. Nanotechnology 2021, 32, 025703. [Google Scholar] [CrossRef]
- Goris, B.; Bals, S.; Van Den Broek, W.; Carbó-Argibay, E.; Gómez-Graña, S.; Liz-Marzán, L.M.; Van Tendeloo, G. Atomic-scale determination of surface facets in gold nanorods. Nat. Mater. 2012, 11, 930–935. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Graña, S.; Goris, B.; Altantzis, T.; Fernández-López, C.; Carbó-Argibay, E.; Guerrero-Martínez, A.; Almora-Barrios, N.; López, N.; Pastoriza-Santos, I.; Pérez-Juste, J.; et al. Au@Ag nanoparticles: Halides stabilize {100} facets. J. Phys. Chem. Lett. 2013, 4, 2209–2216. [Google Scholar] [CrossRef]
- Petrova, H.; Lin, C.H.; De Liejer, S.; Hu, M.; McLellan, J.M.; Siekkinen, A.R.; Wiley, B.J.; Marquez, M.; Xia, Y.; Sader, J.E.; et al. Time-resolved spectroscopy of silver nanocubes: Observation and assignment of coherently excited vibrational modes. J. Chem. Phys. 2007, 126, 094709. [Google Scholar] [CrossRef]
- Ahmed, A.; Pelton, M.; Guest, J.R. Understanding how acoustic vibrations modulate the optical response of plasmonic metal nanoparticles. ACS Nano 2017, 11, 9360–9369. [Google Scholar] [CrossRef]
- Juodėnas, M.; Peckus, D.; Tamulevičius, T.; Yamauchi, Y.; Tamulevičius, S.; Henzie, J. Effect of Ag nanocube optomechanical modes on plasmonic surface lattice resonances. ACS Photonics 2020, 7, 3130–3140. [Google Scholar] [CrossRef]
- Hamon, C.; Goldmann, C.; Constantin, D. Controlling the symmetry of supercrystals formed by plasmonic core-shell nanorods with tunable cross-section. Nanoscale 2018, 10, 18362–18369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saison-Francioso, O.; Lévêque, G.; Akjouj, A. Numerical modeling of acousto-plasmonic coupling in metallic nanoparticles. J. Phys. Chem. C 2020, 124, 12120–12133. [Google Scholar] [CrossRef]
- Della Picca, F.; Berte, R.; Rahmani, M.; Albella, P.; Bujjamer, J.M.; Poblet, M.; Cortés, E.; Maier, S.A.; Bragas, A.V. Tailored Hypersound Generation in Single Plasmonic Nanoantennas. Nano Lett. 2016, 16, 1428–1434. [Google Scholar] [CrossRef] [Green Version]
- O’Brien, K.; Lanzillotti-Kimura, N.D.; Rho, J.; Suchowski, H.; Yin, X.; Zhang, X. Ultrafast acousto-plasmonic control and sensing in complex nanostructures. Nat. Commun. 2014, 5, 4042. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; O’Neil, D.; El-Sayed, M.A. Shape- and symmetry-dependent mechanical properties of metallic gold and silver on the nanoscale. Nano Lett. 2014, 14, 743–748. [Google Scholar] [CrossRef]
- Saviot, L.; Netting, C.H.; Murray, D.B. Damping by bulk and shear viscosity of confined acoustic phonons for nanostructures in aqueous solution. J. Phys. Chem. B 2007, 111, 7457–7461. [Google Scholar] [CrossRef]
- Voisin, C.; Christofilos, D.; Del Fatti, N.; Vallée, F. Environment effect on the acoustic vibration of metal nanoparticles. Proc. Phys. B Condens. Matter 2002, 316–317, 89–94. [Google Scholar] [CrossRef]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.H.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of gold. Phys. Rev. B-Condens. Matter Mater. Phys. 2012, 86, 235147. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.U.; D’Archangel, J.; Sundheimer, M.L.; Tucker, E.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of silver. Phys. Rev. B-Condens. Matter Mater. Phys. 2015, 91, 235137. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otomalo, T.O.; Di Mario, L.; Hamon, C.; Constantin, D.; Toschi, F.; Do, K.-V.; Juvé, V.; Ruello, P.; O’Keeffe, P.; Catone, D.; et al. Acoustic Vibration Modes of Gold–Silver Core–Shell Nanoparticles. Chemosensors 2022, 10, 193. https://doi.org/10.3390/chemosensors10050193
Otomalo TO, Di Mario L, Hamon C, Constantin D, Toschi F, Do K-V, Juvé V, Ruello P, O’Keeffe P, Catone D, et al. Acoustic Vibration Modes of Gold–Silver Core–Shell Nanoparticles. Chemosensors. 2022; 10(5):193. https://doi.org/10.3390/chemosensors10050193
Chicago/Turabian StyleOtomalo, Tadele Orbula, Lorenzo Di Mario, Cyrille Hamon, Doru Constantin, Francesco Toschi, Khanh-Van Do, Vincent Juvé, Pascal Ruello, Patrick O’Keeffe, Daniele Catone, and et al. 2022. "Acoustic Vibration Modes of Gold–Silver Core–Shell Nanoparticles" Chemosensors 10, no. 5: 193. https://doi.org/10.3390/chemosensors10050193
APA StyleOtomalo, T. O., Di Mario, L., Hamon, C., Constantin, D., Toschi, F., Do, K.-V., Juvé, V., Ruello, P., O’Keeffe, P., Catone, D., Paladini, A., & Palpant, B. (2022). Acoustic Vibration Modes of Gold–Silver Core–Shell Nanoparticles. Chemosensors, 10(5), 193. https://doi.org/10.3390/chemosensors10050193






