Kohonen Neural Network Investigation of the Effects of the Visual, Proprioceptive and Vestibular Systems to Balance in Young Healthy Adult Subjects
Abstract
:1. Introduction
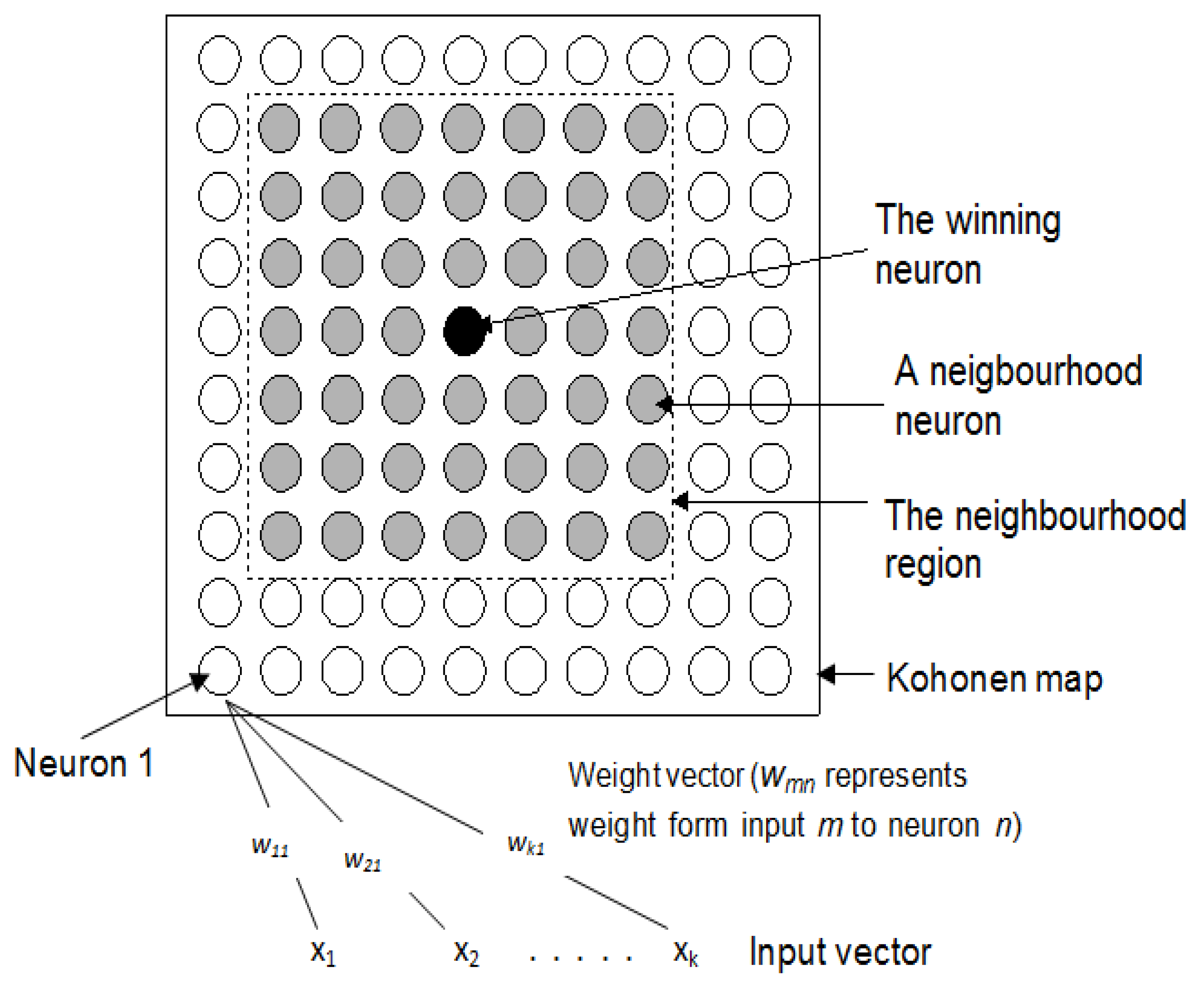
2. Kohonen Neural Network
- i.
- Initialization
- ii.
- Competition
- iii.
- Adaptation
- iv.
- Termination of iterations
3. Methodology
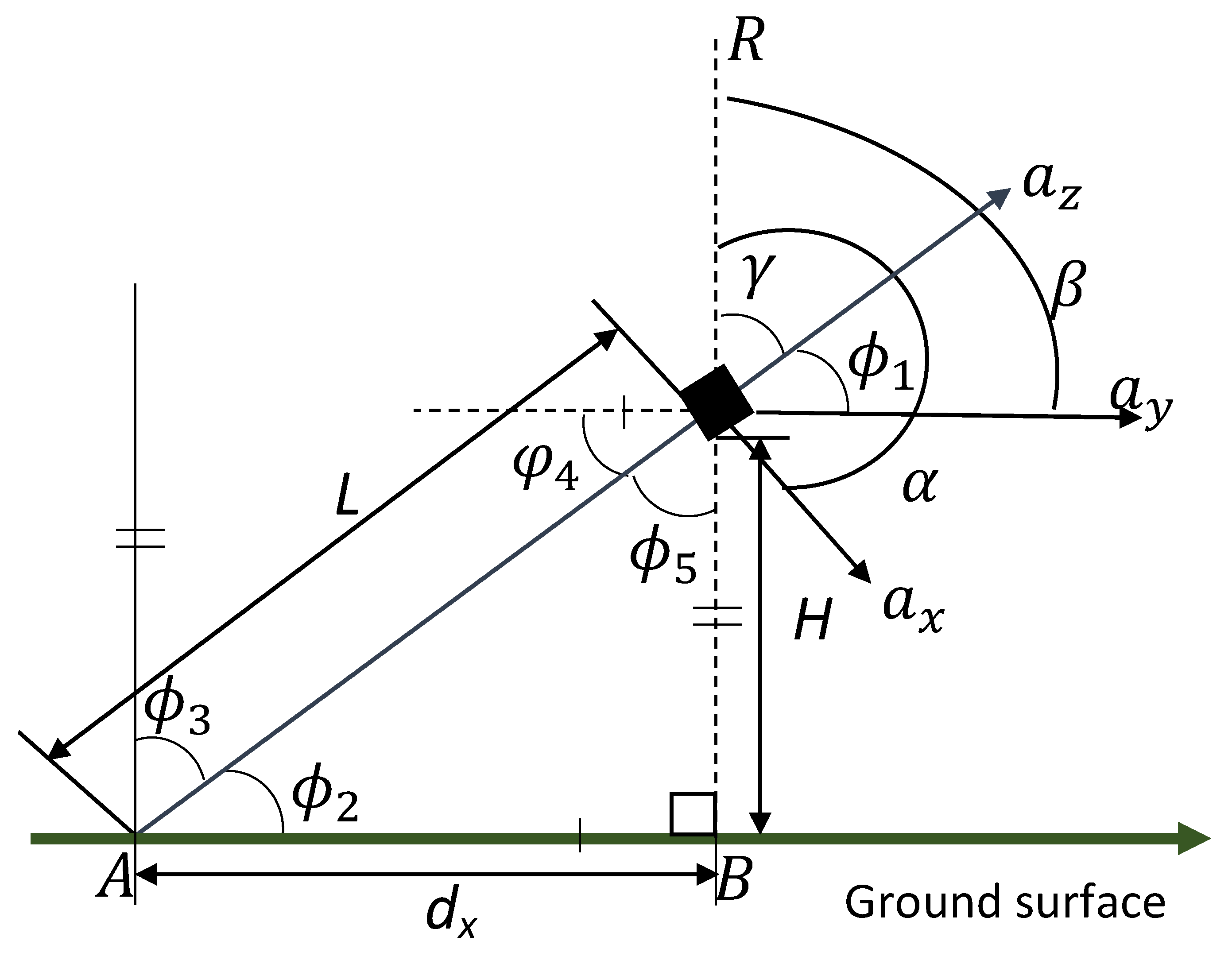
3.1. Accelerometry Algorithm to Analyse Postural Sway
3.2. Accelerometry Device Used for Data Recording
3.3. Participants’ Details and Experimental Procedure
3.4. Data Analysis
3.4.1. Conversion of the Raw Accelerometry Data into Sway Information
3.4.2. Clustering of the Postural Sway Information
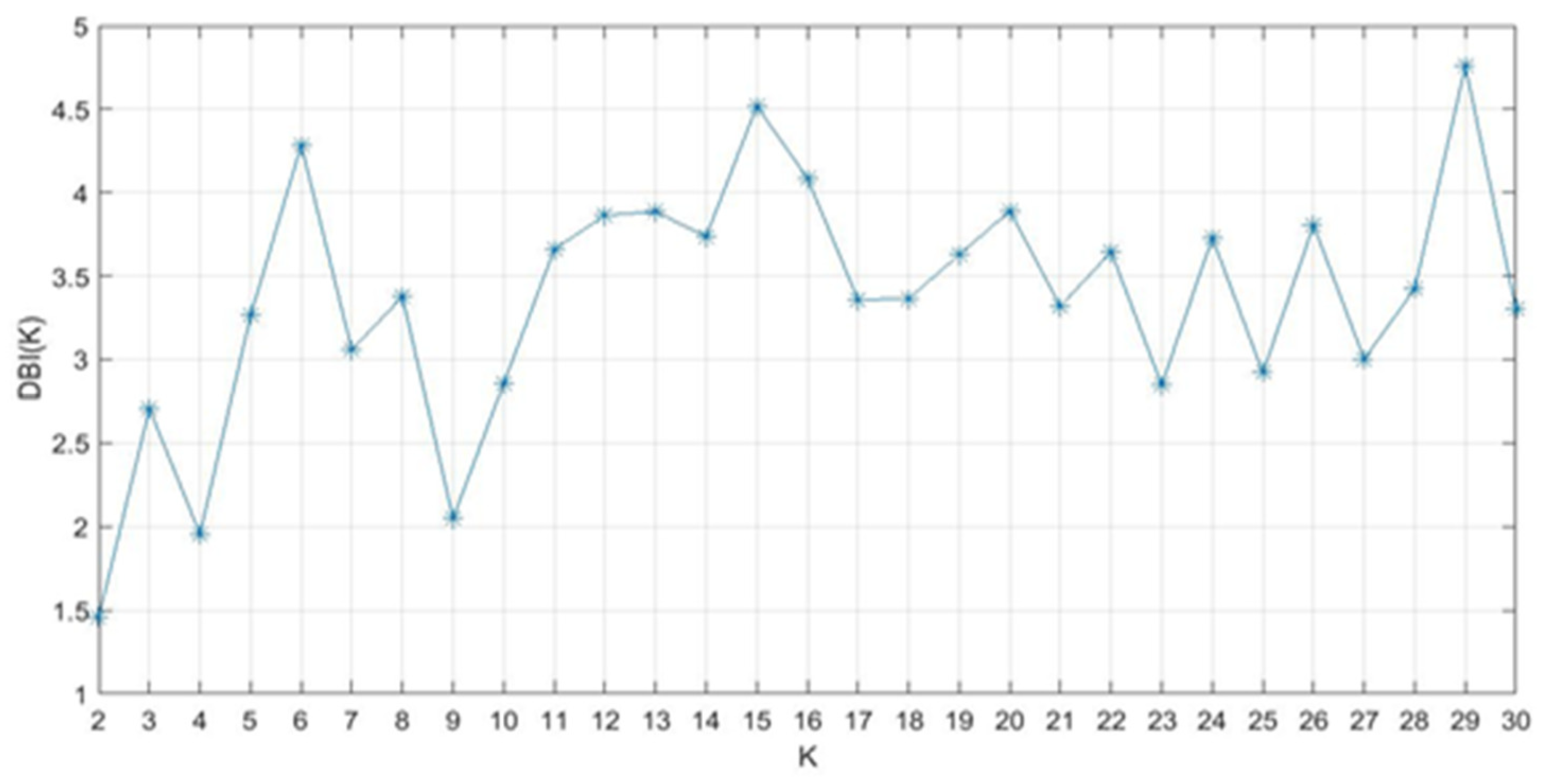
3.4.3. Clustering Performance
4. Results
4.1. Correlation Result
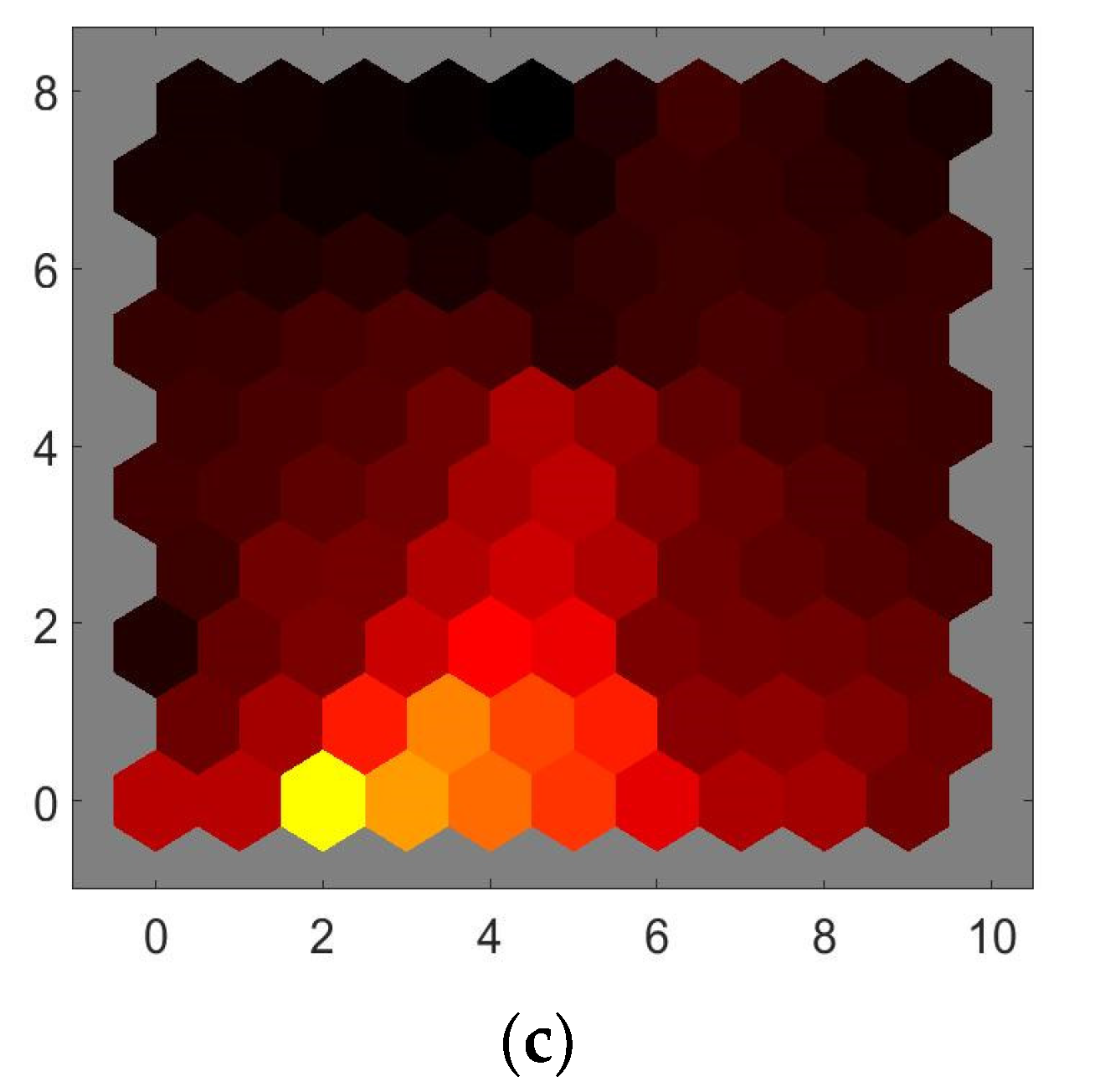
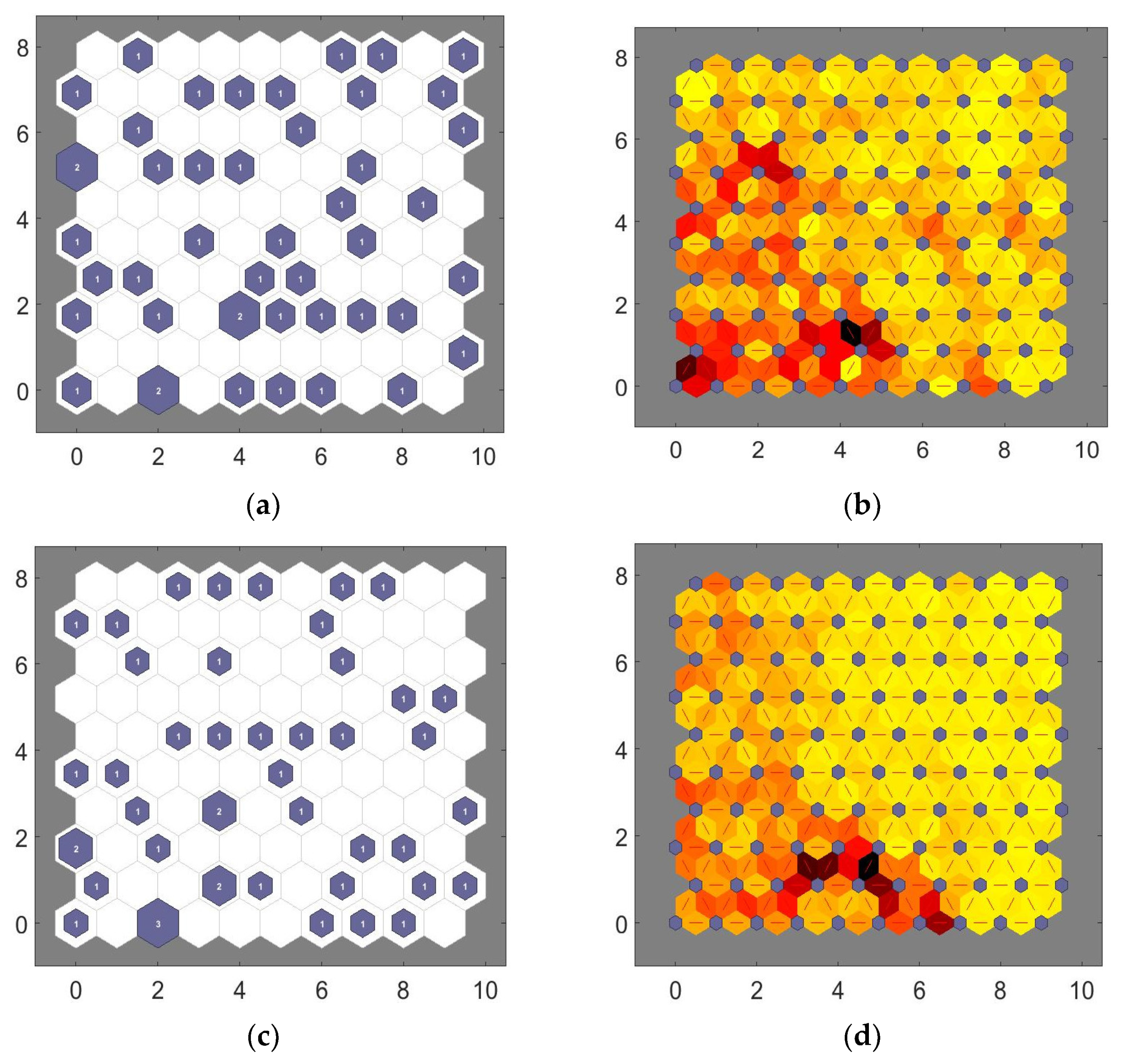
4.2. Clustering Results
5. Discussions
- i.
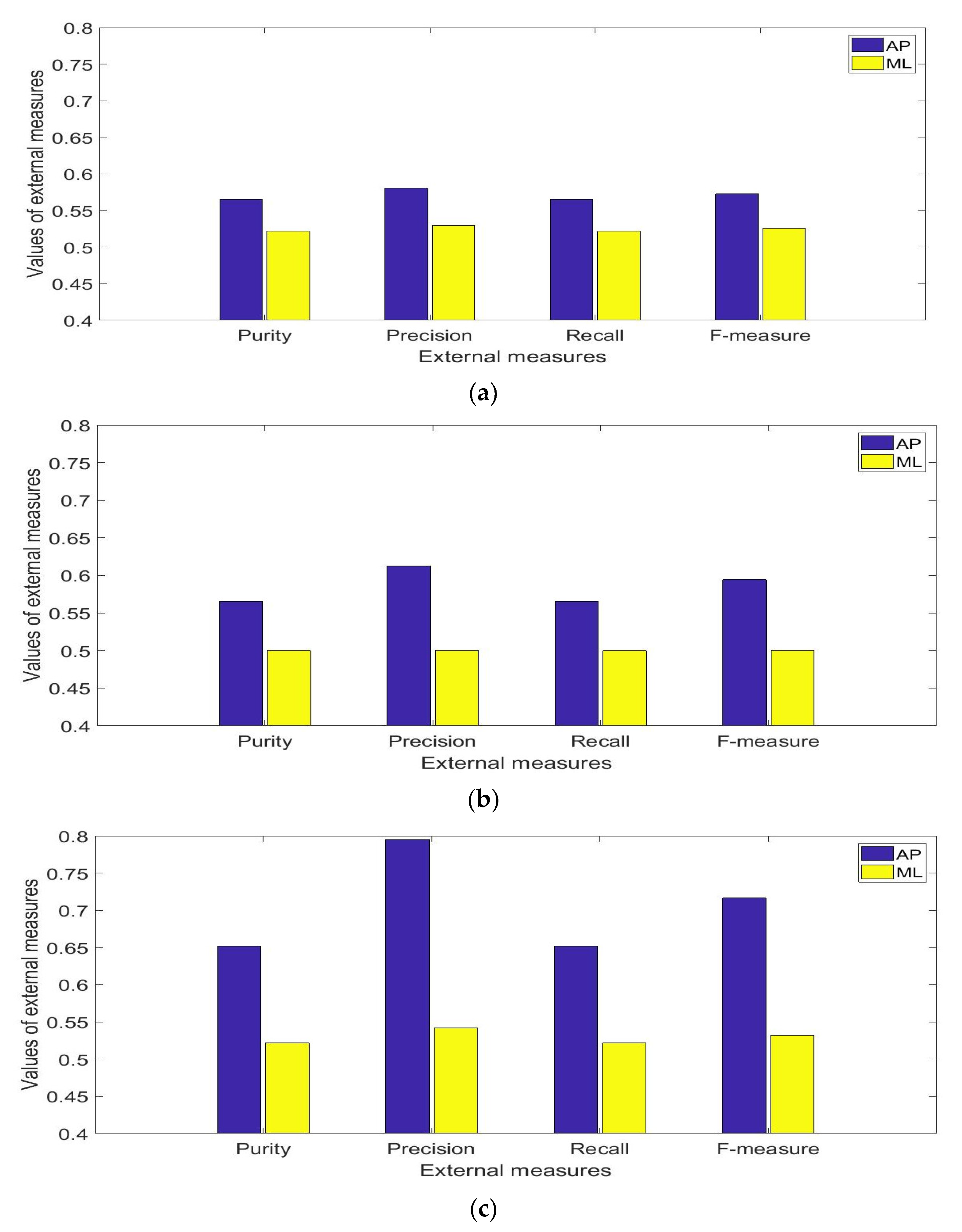
- The clustering of the postural sway, based on the RMS measures of the body’s position and velocity of the AP direction, showed larger values of external measures of the clustering performances as compared to similar variables from the ML direction. As a result, it may be inferred that the AP direction was more sensitive to the effect of the information of the sensory system as compared to the ML direction.
- ii.
- Hindrance in the operation of the visual system leads to an increase in the external performance measures of the clustering in the ML direction. In clustering between the eyes open conditions (conditions 1 and 3), the clustering evaluation measures, i.e. purity, precision, recall, and F-measure were 0.5, which was equal to the minimum value that could occur from the clustering. Thus, postural sway in the ML direction is a characteristic of the contribution of the visual system.
- iii.
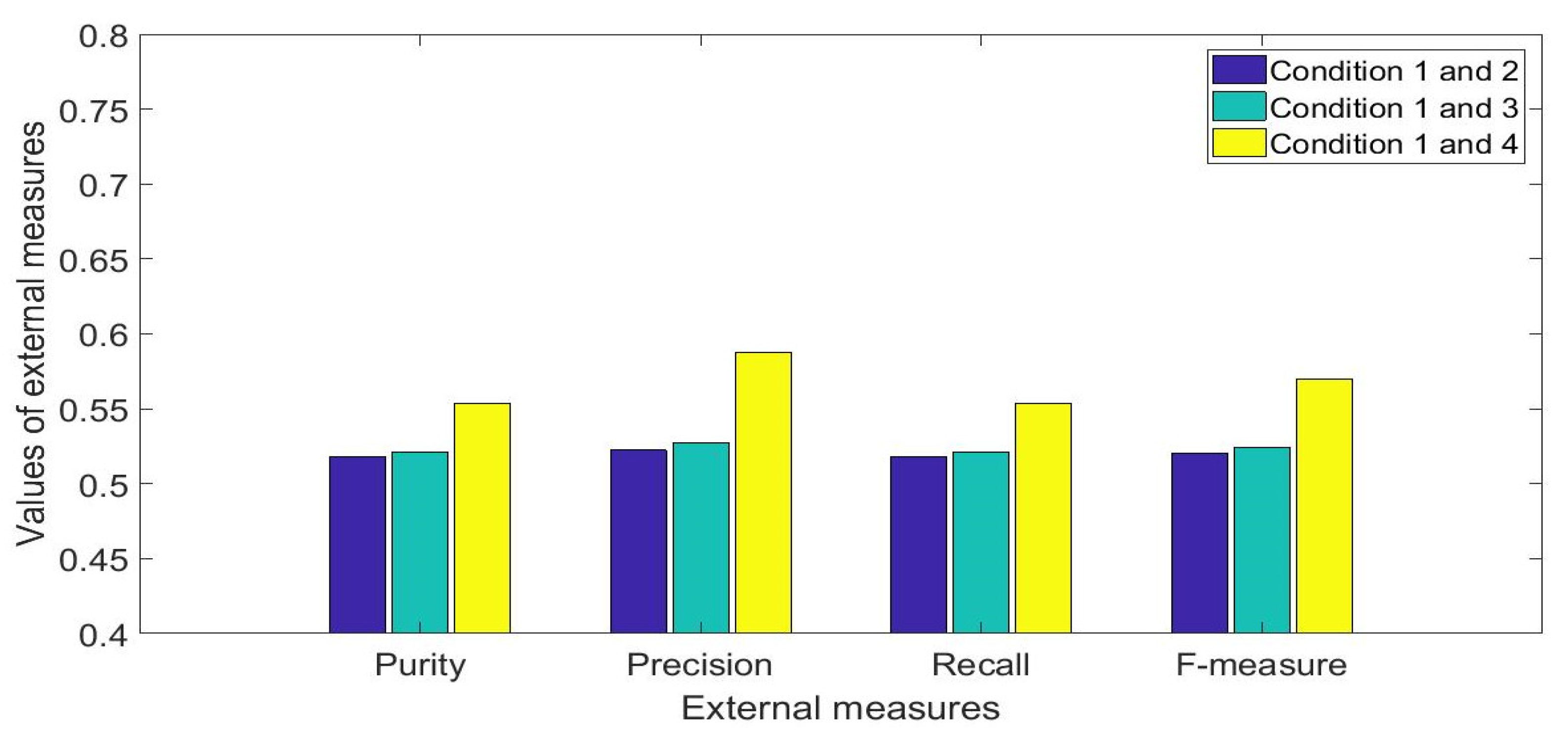
- Using separate directions resulted in differing order of similarities across the four conditions of the mCTSIB. When the clustering measures of the AP direction were used for analysis, the order of similarities of the conditions were conditions 1, 2, 3, and 4. However, when the clustering measures of the ML direction were used, the order of similarities were conditions 1, 3, 2, and 4 and the results showed less disparity across the conditions. When the measures from the AP and ML directions were combined, the external clustering performance measures were reduced. This indicated that combining the results of ML and AP directions results in closer similarities between the conditions.
- iv.
- There was not a large variation between the maximum and the minimum (0.5) values across all external measures of the clustering performance between the conditions of the mCTSIB using the RMS values of the position and velocity of the respective ML and AP directions. The maximum value of the external measures corresponded to the value of the precision measure (0.795) for the clustering between the conditions 1 and 4. In the case of clustering with two clusters, the minimum and maximum values of the external measures that can occur for two groups with an equal number of samples are 0.5 and 1 respectively. Thus, the difference of 0.295 between the precision value and the minimum i.e. 0.795 minus 0.5 is considered small. Therefore, it was concluded that for healthy young adult subjects, there is a strong interrelationship between the mCTSIB conditions and their postural sway results cannot be clustered well into two distinct groups.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peterka, R. Sensorimotor integration in human postural control. J. Neurophysiol. 2002, 88, 1097–1118. [Google Scholar] [CrossRef] [Green Version]
- Assländer, L.; Hettich, G.; Mergner, T. Visual contribution to human standing balance during support surface tilts. Hum. Mov. Sci. 2015, 41, 147–164. [Google Scholar] [CrossRef] [Green Version]
- Proske, U.; Gandevia, S.C. The proprioceptive senses: Their roles in signaling body shape, body position and movement, and muscle force. Physiol. Rev. 2012, 92, 1651–1697. [Google Scholar] [CrossRef]
- Zalewski, C. Aging of the human vestibular system. Semin. Hear. 2015, 36, 175–196. [Google Scholar] [CrossRef] [Green Version]
- Wrisley, D.; Whitney, S. The effect of foot position on the modified clinical test of sensory interaction and balance. Arch. Phys. Med. Rehabil. 2004, 85, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Cohen, H.S.; Mulavara, A.P.; Stitz, J.; Sangi-Haghpeykar, H.; Williams, S.P.; Peters, B.T.; Bloomberg, J.J. Screening for vestibular disorders using the modified Clinical Test of Sensory Interaction and Balance and Tandem Walking with eyes closed. Otol. Neurotol. 2019, 40, 658–665. [Google Scholar] [CrossRef]
- Shumway-Cook, A.; Horak, F.B. Assessing the influence of sensory interaction on balance: Suggestion from the field. Phys. Ther. 1986, 66, 1548–1550. [Google Scholar] [CrossRef]
- Cohen, H.; Blatchly, C.A.; Gombash, L.L. A study of the clinical test of sensory interaction and balance. Phys. Ther. 1993, 73, 346–354. [Google Scholar] [CrossRef]
- Goble, D.J.; Brar, H.; Brown, E.C.; Marks, C.R.; Baweja, H.S. Normative data for the balance tracking system modified Clinical Test of Sensory Integration and Balance protocol. Med. Devices 2019, 12, 183–191. [Google Scholar] [CrossRef] [Green Version]
- Boonsinsukh, R.; Khumnonchai, B.; Saengsirisuwan, V.; Chaikeeree, N. The effect of the type of foam pad used in the modified Clinical Test of Sensory Interaction and Balance (mCTSIB) on the accuracy in identifying older adults with fall history. Hong Kong Physiother. J. 2020, 40, 133–143. [Google Scholar] [CrossRef]
- Antoniadou, E.; Kalivioti, X.; Stolakis, K.; Koloniari, A.; Megas, P.; Tyllianakis, M.; Panagiotopoulos, E. Reliability and validity of the mCTSIB dynamic platform test to assess balance in a population of older women living in the community. J. Musculoskelet. Neuronal Interact. 2020, 20, 185–193. [Google Scholar]
- Porter, S.; Nantel, J. Older adults prioritize postural stability in the anterior-posterior direction to regain balance following volitional lateral step. Gait Posture 2015, 41, 666–669. [Google Scholar] [CrossRef]
- Morrison, S.; Rynders, C.; Sosnoff, J. Deficits in medio-lateral balance control and the implications for falls in individuals with multiple sclerosis. Gait Posture 2016, 49, 148–154. [Google Scholar] [CrossRef]
- Irani, J.; Pise, N.; Phatak, M. Clustering techniques and the similarity measures used in clustering: A survey. Int. J. Comput. Appl. 2016, 134, 9–14. [Google Scholar] [CrossRef]
- Parker, R.; Boyd, J.A. Comparison of a discriminant versus a clustering analysis of a patient classification for chronic disease care. Med. Care 1974, 12, 944–957. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.K.; Chandra, P. P-k-means: K-means using partition based cluster initialization method. In Proceedings of the International Conference on Advancements in Computing & Management (ICACM), Jaipur, India, 13–14 April 2019. [Google Scholar] [CrossRef]
- Samsonova, E.; Kok, J.; IJzerman, A. TreeSOM: Cluster analysis in the self-organizing map. Neural Netw. 2006, 19, 935–949. [Google Scholar] [CrossRef]
- Kim, C.; Yu, I.; Song, Y. Kohonen neural network and wavelet transform based approach to short-term load forecasting. Electr. Power Syst. Res. 2002, 63, 169–176. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef]
- Larose, D.; Larose, C. Discovering Knowledge in Data; IEEE: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Serrien, B.; Hohenauer, E.; Clijsen, R.; Taube, W.; Baeyens, J.; Küng, U. Changes in balance coordination and transfer to an unlearned balance task after slackline training: A self-organizing map analysis. Exp. Brain Res. 2017, 235, 3427–3436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodrigo, S.; Lescano, C.; Rodrigo, R. Application of Kohonen maps to kinetic analysis of human gait. Rev. Bras. Eng. Biomédica 2012, 28, 217–226. [Google Scholar] [CrossRef]
- Van Diest, M.; Stegenga, J.; Wörtche, H.; Roerdink, J.; Verkerke, G.; Lamoth, C. Quantifying postural control during exergaming using multivariate whole-body movement data: A self-organizing maps approach. PLoS ONE 2015, 10, e0134350. [Google Scholar] [CrossRef] [Green Version]
- Bação, F.; Lobo, V.; Painho, M. Self-organizing maps as substitutes for k-means clustering. Lect. Notes Comput. Sci. 2005, 476–483. [Google Scholar] [CrossRef] [Green Version]
- Pacella, M.; Grieco, A.; Blaco, M. On the use of self-organizing map for text clustering in engineering change process analysis: A case study. Comput. Intell. Neurosci. 2016, 2016, 5139574. [Google Scholar] [CrossRef]
- Lawrence, R.; Almasi, G.; Rushmeier, H. A scalable parallel algorithm for self-organizing maps with applications to sparse data mining problems. Data Min. Knowl. Discov. 1999, 3, 171–195. [Google Scholar] [CrossRef]
- Ceccarelli, M.; Petrosino, A.; Vaccaro, R. Competitive neural networks on message-passing parallel computers. Concurr. Pract. Exp. 1993, 5, 449–470. [Google Scholar] [CrossRef]
- Ojie, O.; Saatchi, R. Development and evaluation of an accelerometry system based on inverted pendulum to measure and analyze human balance. Adv. Asset Manag. Cond. Monit. 2020, 1129–1141. [Google Scholar] [CrossRef]
- Vatcheva, K.P.; Lee, M.; McCormick, J.B.; Rahbar, M.H. Multicollinearity in regression analyses conducted in epidemiologic studies. Epidemiol. Open Access 2016, 6, 227. [Google Scholar] [CrossRef] [Green Version]
- De Winter, J.C.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273–290. [Google Scholar] [CrossRef]
- Hartigan, J.; Wong, M. Algorithm AS 136: A k-means clustering algorithm. Appl. Stat. 1979, 28, 100. [Google Scholar] [CrossRef]
- Davies, D.; Bouldin, D. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Huang, A. Similarity measures for text document clustering. In Proceedings of the Sixth New Zealand Computer Science Research Student Conference, Christchurch, New Zealand, 14–18 April 2008; pp. 49–56. [Google Scholar]
- Zaki, M.; Meira, W. Data mining and machine learning. In Fundamental Concepts and Algorithms, 2nd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Horak, F.B. Postural orientation and equilibrium: What do we need to know about neural control of balance to prevent falls? Age Ageing 2006, 35, ii7–ii11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, H.; Uetake, T. Characteristics of postural sway in older adults standing on a soft surface. J. Hum. Ergol. 2005, 34, 35–40. [Google Scholar]
- Jacobson, G.P.; Calder, J.H. Self-perceived balance disability/handicap in the presence of bilateral peripheral vestibular system impairment. J. Am. Acad. Audiol. 2000, 11, 76–83. [Google Scholar]
- Murray, K.; Carroll, S.; Hill, K. Relationship between change in balance and self-reported handicap after vestibular rehabilitation therapy. Physiother. Res. Int. 2001, 6, 251–263. [Google Scholar] [CrossRef]



| mCTSIB Conditions | Purity | Precision | Recall | F-Measure | ||||
|---|---|---|---|---|---|---|---|---|
| ML | AP | ML | AP | ML | AP | ML | AP | |
| 1 and 2 | 0.522 (0.022) | 0.565 (0.065) | 0.530 (0.035) | 0.58 (0.063) | 0.522 (0.022) | 0.565 (0.065) | 0.526 (0.028) | 0.573 (0.059) |
| 1 and 3 | 0.500 (0.022) | 0.565 (0.065) | 0.500 (0.030) | 0.613 (0.070) | 0.500 (0.022) | 0.565 (0.065) | 0.500 (0.026) | 0.594 (0.061) |
| 1 and 4 | 0.522 (0.022) | 0.652 (0.044) | 0.542 (0.055) | 0.795 (0.014) | 0.522 (0.022) | 0.652 (0.044) | 0.532 (0.040) | 0.717 (0.033) |
| Averages | 0.515 (0.022) | 0.594 (0.058) | 0.524 (0.040) | 0.662 (0.049) | 0.515 (0.022) | 0.594 (0.058) | 0.519 (0.031) | 0.628 (0.051) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojie, O.D.; Saatchi, R. Kohonen Neural Network Investigation of the Effects of the Visual, Proprioceptive and Vestibular Systems to Balance in Young Healthy Adult Subjects. Healthcare 2021, 9, 1219. https://doi.org/10.3390/healthcare9091219
Ojie OD, Saatchi R. Kohonen Neural Network Investigation of the Effects of the Visual, Proprioceptive and Vestibular Systems to Balance in Young Healthy Adult Subjects. Healthcare. 2021; 9(9):1219. https://doi.org/10.3390/healthcare9091219
Chicago/Turabian StyleOjie, Oseikhuemen Davis, and Reza Saatchi. 2021. "Kohonen Neural Network Investigation of the Effects of the Visual, Proprioceptive and Vestibular Systems to Balance in Young Healthy Adult Subjects" Healthcare 9, no. 9: 1219. https://doi.org/10.3390/healthcare9091219
APA StyleOjie, O. D., & Saatchi, R. (2021). Kohonen Neural Network Investigation of the Effects of the Visual, Proprioceptive and Vestibular Systems to Balance in Young Healthy Adult Subjects. Healthcare, 9(9), 1219. https://doi.org/10.3390/healthcare9091219






