Comparison between Conventional IMRT Planning and a Novel Real-Time Adaptive Planning Strategy in Hypofractionated Regimes for Prostate Cancer: A Proof-of-Concept Planning Study
Abstract
1. Introduction
2. Results
2.1. Treatment Planning Methods Comparison
2.1.1. Standard Planning Method on Simulation CT
2.1.2. Adaptive Planning Method on Simulation CT
2.1.3. Standard Planning Method VS. Adaptive Planning Method on CBCT
3. Discussion
4. Materials and Methods
4.1. Treatment Fractions on Simulation CT
- IMRT extreme hypofractionation five-fraction scheme for a total dose of 80 Gy (16 Gy per fraction), where the five fractions were selected from the 33 available according to the following two different criteria:
- Five fractions randomly selected among the ones with small prostate motion (0–3 mm) in the set of the 33 simulated;
- Five fractions randomly selected among the ones with intermediate magnitude prostate motion (3.5–7.5 mm) in the set of the 33 simulated.
- IMRT extreme hypofractionation six-fraction scheme for a total dose of 80 Gy (~13 Gy per fraction), combining one treatment fraction with a large prostate shift (13 mm) from the 33 available with the five-fraction scheme in 1a;
- IMRT hypofractionation 15-fraction scheme for a total dose of 80 Gy (~5.33 Gy per fraction), adding to the six-fraction scheme in the previous point (2.). Eight fractions with a prostate displacement of intermediate magnitude (3–8 mm), randomly selected among the 33 available.
4.1.1. Treatment Simulation for the Standard Planning Strategy
- The prostate in the planning CT was surrounded by a minimum encompassing radius that was subsequently expanded isotropically by 2 cm. This surface enclosed the image region in which the original tissue distribution had to be adjusted to represent the new tissue configuration; while all the voxels outside this region remained as in the original image. For this reason, we refer to this surface as “zero motion barrier” (ZMB).
- A motion vector field (MVF) was determined to map the original voxel centres positions to the new configuration. The voxels of the prostate were rigidly translated according to the new position of the prostate CM. A 3D thin-plate spline interpolation was then computed between the remaining pixels in the ZMB and the pixels surrounding the ZMB.
- To generate the modified planning CT, a new grid was generated having the same dimensions as the original image. An inverse motion vector field (IMVF) was computed in MatLab to determine the relation between the new grid and the original image. The IMVF was applied to the voxels of the new grid. Whenever a voxel in the new grid corresponded to the voxel center in the original image, its voxel intensity was set as the intensity of the respective voxel in the original image. For the voxels in the new grid corresponding to “off-grid” points, their intensity values were computed performing a trilinear interpolation of the intensity values corresponding to the neighbouring voxels in the original image.
4.1.2. Treatment Simulation for the Adaptive Planning Strategy
4.2. Treatment Fractions on CBCT
4.2.1. Treatment Simulation for the Standard Planning Strategy
4.2.2. Treatment Simulation for the Adaptive Planning Strategy
5. Conclusions
6. Patents
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EBRT | External Beam Radiation Therapy |
| IMRT | Intensity-Modulated Radiation Therapy |
| PTV | Planning Target Volume |
| OAR | Organ at Risk |
| IG | Image Guidance |
| CT | Computerized Tomography |
| TPS | Treatment Planning System |
| CTV | Clinical Target Volume |
| DVH | Dose-Volume Histogram |
| CM | Centre of Mass |
References
- Webb, S. The physical basis of IMRT and inverse planning. Br. J. Radiol. 2003, 76, 678–689. [Google Scholar] [CrossRef]
- Van Herk, M. Errors and Margins in Radiotherapy. Semin. Radiat. Oncol. 2004, 14, 52–64. [Google Scholar] [CrossRef]
- Ballhausen, H.; Li, M.; Hegemann, N.-S.; Ganswindt, U.; Belka, C. Intra-fraction motion of the prostate is a random walk. Phys. Med. Biol. 2014, 60, 549. [Google Scholar] [CrossRef]
- Adamson, J.; Wu, Q. Prostate intrafraction motion assessed by simultaneous kilovoltage fluoroscopy at megavoltage delivery I: Clinical observations and pattern analysis. Int. J. Radiat. Oncol. Biol. Phys. 2010, 78, 1563–1570. [Google Scholar] [CrossRef]
- Kron, T.; Thomas, J.; Fox, C.; Thompson, A.; Owen, R.; Herschtal, A.; Haworth, A.; Tai, K.H.; Foroudi, F. Intra-fraction prostate displacement in radiotherapy estimated from pre- and post-treatment imaging of patients with implanted fiducial markers. Radiother. Oncol. 2010, 95, 191–197. [Google Scholar] [CrossRef]
- Bittner, N.; Butler, W.M.; Reed, J.L.; Murray, B.C.; Kurko, B.S.; Wallner, K.E.; Merrick, G.S. Electromagnetic Tracking of Intrafraction Prostate Displacement in Patients Externally Immobilized in the Prone Position. Int. J. Radiat. Oncol. Biol. Phys. 2010, 77, 490–495. [Google Scholar] [CrossRef]
- Wong, J.R.; Grimm, L.; Uematsu, M.; Oren, R.; Cheng, C.W.; Merrick, S.; Schiff, P. Image-guided radiotherapy for prostate cancer by CT-linear accelerator combination: Prostate movements and dosimetric considerations. Int. J. Radiat. Oncol. Biol. Phys. 2005, 61, 561–569. [Google Scholar] [CrossRef]
- Langen, K.M.; Willoughby, T.R.; Meeks, S.L.; Santhanam, A.; Cunningham, A.; Levine, L.; Kupelian, P.A. Observations on Real-Time Prostate Gland Motion Using Electromagnetic Tracking. Int. J. Radiat. Oncol. Biol. Phys. 2008, 71, 1084–1090. [Google Scholar] [CrossRef]
- Kupelian, P.; Willoughby, T.; Mahadevan, A.; Djemil, T.; Weinstein, G.; Jani, S.; Enke, C.; Solberg, T.; Flores, N.; Liu, D.; et al. Multi-institutional clinical experience with the Calypso System in localization and continuous, real-time monitoring of the prostate gland during external radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2007, 67, 1088–1098. [Google Scholar] [CrossRef]
- Wu, Q.J.J.; Thongphiew, D.; Wang, Z.; Mathayomchan, B.; Chankong, V.; Yoo, S.; Lee, W.R.R.; Yin, F.F.F.-F. On-line re-optimization of prostate IMRT plans for adaptive radiation therapy. Phys. Med. Biol. 2008, 53, 673. [Google Scholar] [CrossRef]
- Chiesa, S.; Placidi, L.; Azario, L.; Mattiucci, G.C.; Greco, F.; Damiani, A.; Mantini, G.; Frascino, V.; Piermattei, A.; Valentini, V.; et al. Adaptive optimization by 6 DOF robotic couch in prostate volumetric IMRT treatment: Rototranslational shift and dosimetric consequences. J. Appl. Clin. Med. Phys. 2015, 16, 35–45. [Google Scholar] [CrossRef]
- Antico, M.; Prinsen, P.; Cellini, F.; Fracassi, A.; Isola, A.A.; Cobben, D.; Fontanarosa, D. Real-time adaptive planning method for radiotherapy treatment delivery for prostate cancer patients, based on a library of plans accounting for possible anatomy configuration changes. PLoS ONE 2019, 14, e0213002. [Google Scholar] [CrossRef]
- Fontanarosa, D.; Isola, A.A. Radiation Therapy System Using Plural Treatment Plans. U.S. Patent Application 15/742,575, 19 July 2018. [Google Scholar]
- O’Shea, T.; Bamber, J.; Fontanarosa, D.; van der Meer, S.; Verhaegen, F.; Harris, E. Review of ultrasound image guidance in external beam radiotherapy II: intra-fraction motion management and novel applications. Phys. Med. Biol. 2016, 61, R90–R137. [Google Scholar] [CrossRef]
- Teh, B.S.; Ishiyama, H. Hypofractionated radiotherapy for prostate cancer. Lancet Oncol. 2012, 13, 5–6. [Google Scholar] [CrossRef]
- Ballhausen, H.; Reiner, M.; Kantz, S.; Belka, C.; Söhn, M. The random walk model of intrafraction movement. Phys. Med. Biol. 2013, 58, 2413–2427. [Google Scholar] [CrossRef]
- Foskey, M.; Davis, B.; Goyal, L.; Chang, S.; Chaney, E.; Strehl, N.; Tomei, S.; Rosenman, J.; Joshi, S. Large deformation three-dimensional image registration in image-guided radiation therapy. Phys. Med. Biol. 2005, 50, 5869–5892. [Google Scholar] [CrossRef]
- Kotte, A.N.T.J.; Hofman, P.; Lagendijk, J.J.W.; van Vulpen, M.; van der Heide, U.A. Intrafraction Motion of the Prostate During External-Beam Radiation Therapy: Analysis of 427 Patients with Implanted Fiducial Markers. Int. J. Radiat. Oncol. Biol. Phys. 2007, 69, 419–425. [Google Scholar] [CrossRef]
- Delobel, J.B.; Gnep, K.; Ospina, J.D.; Beckendorf, V.; Chira, C.; Zhu, J.; Bossi, A.; Messai, T.; Acosta, O.; Castelli, J.; et al. Nomogram to predict rectal toxicity following prostate cancer radiotherapy. PLoS ONE 2017, 12, 1–16. [Google Scholar] [CrossRef]
- Tomé, W.A.; Fowler, J.F. On cold spots in tumor subvolumes. Med. Phys. 2002, 29, 1590–1598. [Google Scholar] [CrossRef]
- Fuentes-Raspall, R.; Inoriza, J.M.; Rosello-Serrano, A.; Auñón-Sanz, C.; Garcia-Martin, P.; Oliu-Isern, G. Late rectal and bladder toxicity following radiation therapy for prostate cancer: Predictive factors and treatment results. Rep. Pract. Oncol. Radiother. 2013, 18, 298–303. [Google Scholar] [CrossRef][Green Version]
- Fonteyne, V.; Ost, P.; Vanpachtenbeke, F.; Colman, R.; Sadeghi, S.; Villeirs, G.; Decaestecker, K.; De Meerleer, G. Rectal toxicity after intensity modulated radiotherapy for prostate cancer: Which rectal dose volume constraints should we use? Radiother. Oncol. 2014, 113, 398–403. [Google Scholar] [CrossRef]
- Crehange, G.; Mirjolet, C.; Gauthier, M.; Martin, E.; Truc, G.; Peignaux-Casasnovas, K.; Azelie, C.; Bonnetain, F.; Naudy, S.; Maingon, P. Clinical impact of margin reduction on late toxicity and short-term biochemical control for patients treated with daily on-line image guided IMRT for prostate cancer. Radiother. Oncol. 2012, 103, 244–246. [Google Scholar] [CrossRef]
- Radiation Oncology/Toxicity/RTOG—Wikibooks, Open Books for an Open World. Available online: https://en.wikibooks.org/wiki/Radiation_Oncology/Toxicity/RTOG (accessed on 11 November 2019).
- Bey, P.; Carrie, C.; Beckendorf, V.; Ginestet, C.; Aletti, P.; Madelis, G.; Luporsi, E.; Pommier, P.; Cowen, D.; Gonzague-Casabianca, L.; et al. Dose escalation with 3D-CRT in prostate cancer: French study of dose escalation with conformal 3D radiotherapy in prostate cancer–Preliminary results. Int. J. Radiat. Oncol. Biol. Phys. 2000, 48, 513–517. [Google Scholar] [CrossRef]
- Drains, O. P^3IMRT Instructions for Use; Atrium Medical Corporation: Hudson, NH, USA, 2002; pp. 1–4. [Google Scholar]
- Smith, C. On Vertex-Vertex Systems and Their Use in Geometric and Biological Modelling; University of Calgary: Calgary, AB, Canada, 2006. [Google Scholar]
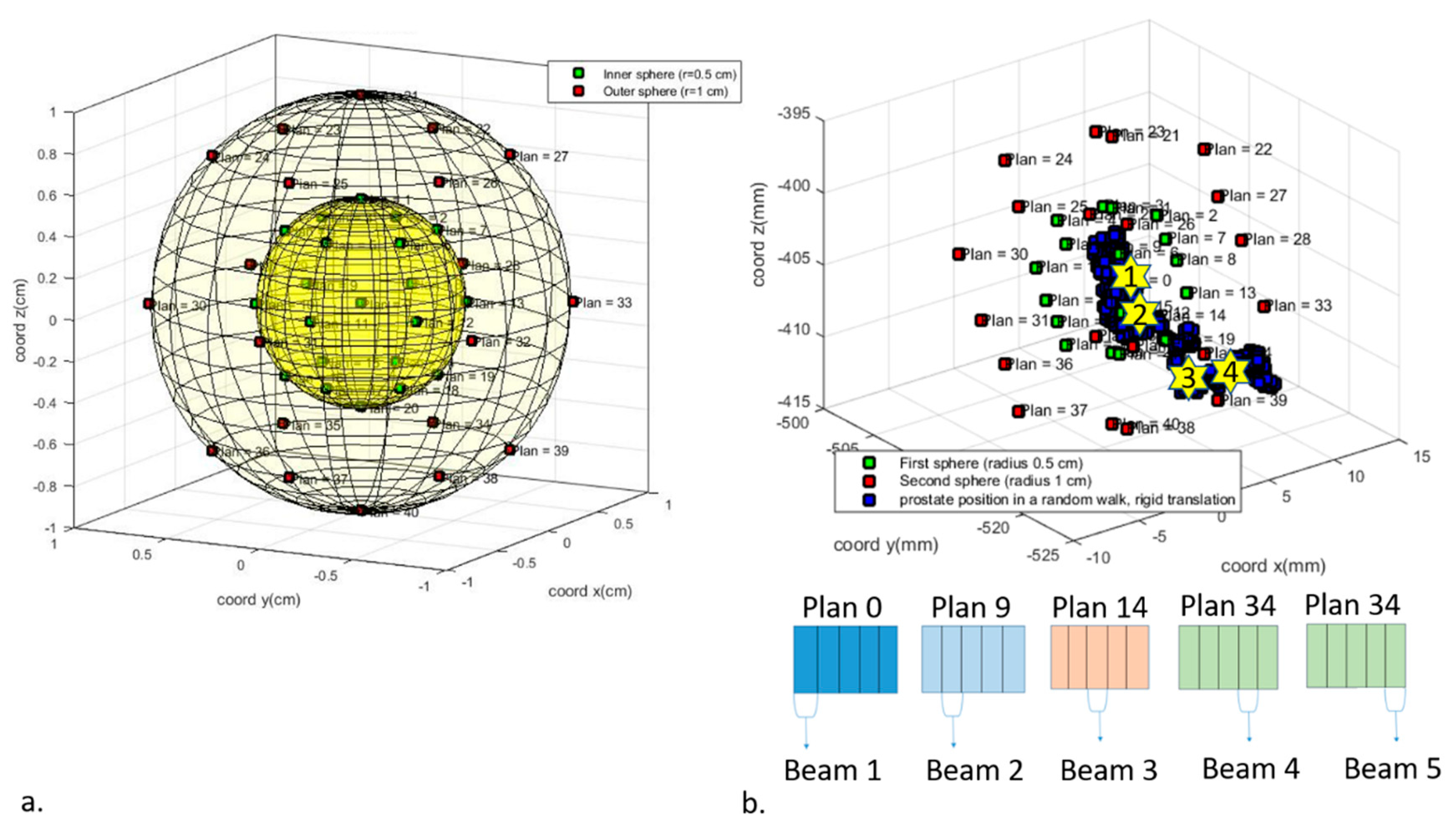
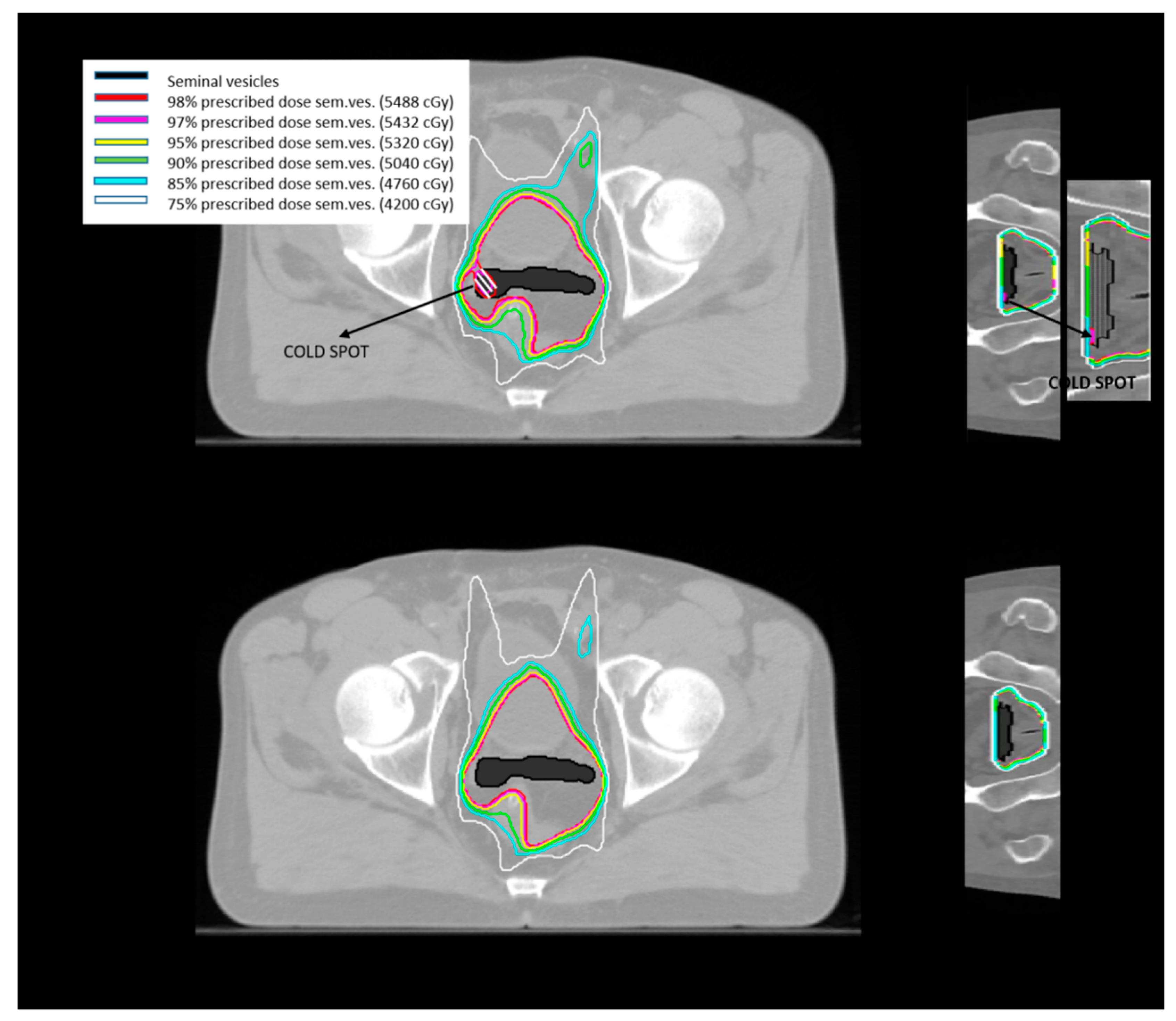
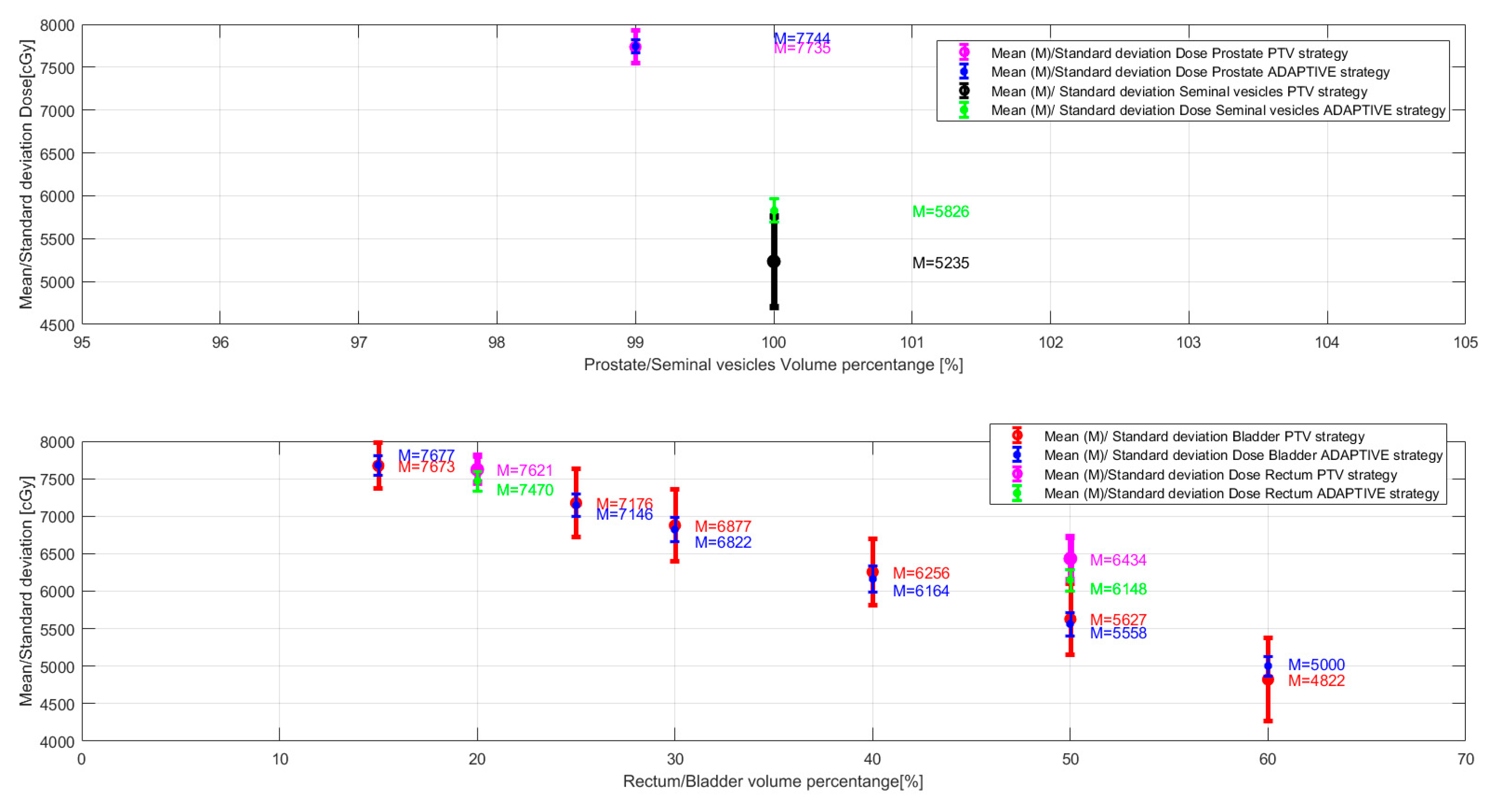

| Dose [cGy] | |||
|---|---|---|---|
| Standard Planning Method | Adaptive Planning Method | Standard Planning Method No Motion | |
| Prostate D99% > 7600 cGy | 7957 | 7809 | 7952 |
| Seminal vesicles D min > 5600 cGy | 5508 | 5777 | 5594 |
| Bladder V5000 cGy < 60% | 5154 | 5098 | 5184 |
| Bladder V6500 cGy < 50% | 5925 | 5685 | 5942 |
| Bladder V6600 cGy < 40% | 6566 | 6247 | 6595 |
| Bladder V7000 cGy < 30% | 7169 | 6910 | 7205 |
| Bladder V7500 cGy < 25% | 7508 | 7248 | 7580 |
| Bladder V8000 cGy < 15% | 7877 | 7766 | 7908 |
| Rectum V6170 cGy < 50% | 6383 | 6049 | 6382 |
| Rectum V7429 cGy < 20% | 7602 | 7397 | 7632 |
| Dose [cGy] | |||
|---|---|---|---|
| Standard Planning Method | Adaptive Method | Standard Planning Method No Motion | |
| Prostate D99% > 7600 cGy | 7940 | 7838 | 7952 |
| Seminal vesicles D100% > 5600 cGy | 5410 | 5851 | 5594 |
| Bladder V5000 cGy < 60% | 4865 | 5003 | 5184 |
| Bladder V6500 cGy < 50% | 5717 | 5587 | 5942 |
| Bladder V6600 cGy < 40% | 6265 | 6174 | 6595 |
| Bladder V7000 cGy < 30% | 6970 | 6854 | 7205 |
| Bladder V7500 cGy < 25% | 7294 | 7200 | 7580 |
| Bladder V8000 cGy < 15% | 7757 | 7736 | 7908 |
| Rectum V6170 cGy < 50% | 6448 | 6111 | 6382 |
| Rectum V7429 cGy < 20% | 7631 | 7465 | 7632 |
| Dose [cGy] | |||
|---|---|---|---|
| Standard Planning Method | Adaptive Method | Standard Planning Method No Motion | |
| Prostate D99% > 7600 cGy | 7887 | 7795 | 7952 |
| Seminal vesicles D100% > 5600 cGy | 5337 | 5804 | 5594 |
| Bladder V5000 cGy < 60% | 4908 | 5085 | 5184 |
| Bladder V6500 cGy < 50% | 5772 | 5658 | 5942 |
| Bladder V6600 cGy < 40% | 6298 | 6231 | 6595 |
| Bladder V7000 cGy < 30% | 6973 | 6879 | 7205 |
| Bladder V7500 cGy < 25% | 7256 | 7220 | 7580 |
| Bladder V8000 cGy < 15% | 7712 | 7737 | 7908 |
| Rectum V6170 cGy < 50% | 6413 | 6056 | 6382 |
| Rectum V7429 cGy < 20% | 7621 | 7386 | 7632 |
| Dose [cGy] | |||
|---|---|---|---|
| Standard Planning Method | Adaptive Method | Standard Planning Method No Motion | |
| Prostate D99% > 7600 cGy | 7823 | 7823 | 7952 |
| Seminal vesicles D100% > 5600 cGy | 5419 | 5812 | 5594 |
| Bladder V5000 cGy < 60% | 4938 | 5032 | 5184 |
| Bladder V6500 cGy < 50% | 5783 | 5607 | 5942 |
| Bladder V6600 cGy < 40% | 6356 | 6171 | 6595 |
| Bladder V7000 cGy < 30% | 6999 | 6849 | 7205 |
| Bladder V7500 cGy < 25% | 7321 | 7183 | 7580 |
| Bladder V8000 cGy < 15% | 7750 | 7717 | 7908 |
| Rectum V6170 cGy < 50% | 6423 | 6118 | 6382 |
| Rectum V7429 cGy < 20% | 7625 | 7442 | 7632 |
| Dose [cGy] | |||
|---|---|---|---|
| S | Standard Planning Method | Adaptive Method | Standard Planning Method No Motion |
| Prostate D99% > 7600 cGy | 7748 | 7666 | 7943 |
| Bladder V5000 cGy < 60% | 4970 | 904 | 5219 |
| Bladder V6500 cGy < 50% | 5784 | 1685 | 6068 |
| Bladder V6600 cGy < 40% | 6595 | 3028 | 6754 |
| Bladder V7000 cGy < 30% | 7288 | 4759 | 7393 |
| Bladder V7500 cGy < 25% | 7598 | 5549 | 7658 |
| Bladder V8000 cGy < 15% | 7888 | 7030 | 7954 |
| Rectum V6170 cGy < 50% | 5779 | 4984 | 6245 |
| Rectum V7429 cGy < 20% | 7334 | 7174 | 7441 |
| DOSIMETRIC OBJECTIVES | ||
|---|---|---|
| TREATMENT VOLUME | PTV\CTV a | D99% > 7600 cGy |
| PTV\CTV a | D3% < 8300 cGy | |
| PTV\CTV a | D uniform = 8000 cGy | |
| SEMINAL VESICLES | D min > 5600 cGy | |
| OAR | BLADDER | V5000 cGy < 60% |
| BLADDER | V6500 cGy < 50% | |
| BLADDER | V6600 cGy < 40% | |
| BLADDER | V7000 cGy < 30% | |
| BLADDER | V7500 cGy < 25% | |
| BLADDER | V8000 cGy < 15% | |
| RECTUM | V6170 cGy < 50% | |
| RECTUM | V7429 cGy < 20% | |
| LEFT FEMUR | D max < 4000 cGy | |
| RIGHT FEMUR | D max < 4000 cGy |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antico, M.; Prinsen, P.; Fracassi, A.; Isola, A.; Cobben, D.; Fontanarosa, D. Comparison between Conventional IMRT Planning and a Novel Real-Time Adaptive Planning Strategy in Hypofractionated Regimes for Prostate Cancer: A Proof-of-Concept Planning Study. Healthcare 2019, 7, 153. https://doi.org/10.3390/healthcare7040153
Antico M, Prinsen P, Fracassi A, Isola A, Cobben D, Fontanarosa D. Comparison between Conventional IMRT Planning and a Novel Real-Time Adaptive Planning Strategy in Hypofractionated Regimes for Prostate Cancer: A Proof-of-Concept Planning Study. Healthcare. 2019; 7(4):153. https://doi.org/10.3390/healthcare7040153
Chicago/Turabian StyleAntico, Maria, Peter Prinsen, Alice Fracassi, Alfonso Isola, David Cobben, and Davide Fontanarosa. 2019. "Comparison between Conventional IMRT Planning and a Novel Real-Time Adaptive Planning Strategy in Hypofractionated Regimes for Prostate Cancer: A Proof-of-Concept Planning Study" Healthcare 7, no. 4: 153. https://doi.org/10.3390/healthcare7040153
APA StyleAntico, M., Prinsen, P., Fracassi, A., Isola, A., Cobben, D., & Fontanarosa, D. (2019). Comparison between Conventional IMRT Planning and a Novel Real-Time Adaptive Planning Strategy in Hypofractionated Regimes for Prostate Cancer: A Proof-of-Concept Planning Study. Healthcare, 7(4), 153. https://doi.org/10.3390/healthcare7040153






