Miura-Reciprocal Transformation and Symmetries for the Spectral Problems of KdV and mKdV
Abstract
1. Introduction
2. Reciprocal Transformations for mKdV and its Spectral Problem
Spectral Problem of RmKdV
3. Reciprocal Transformations for KdV and Its Spectral Problem
Reciprocal Transformations for the Spectral Problem of KdV
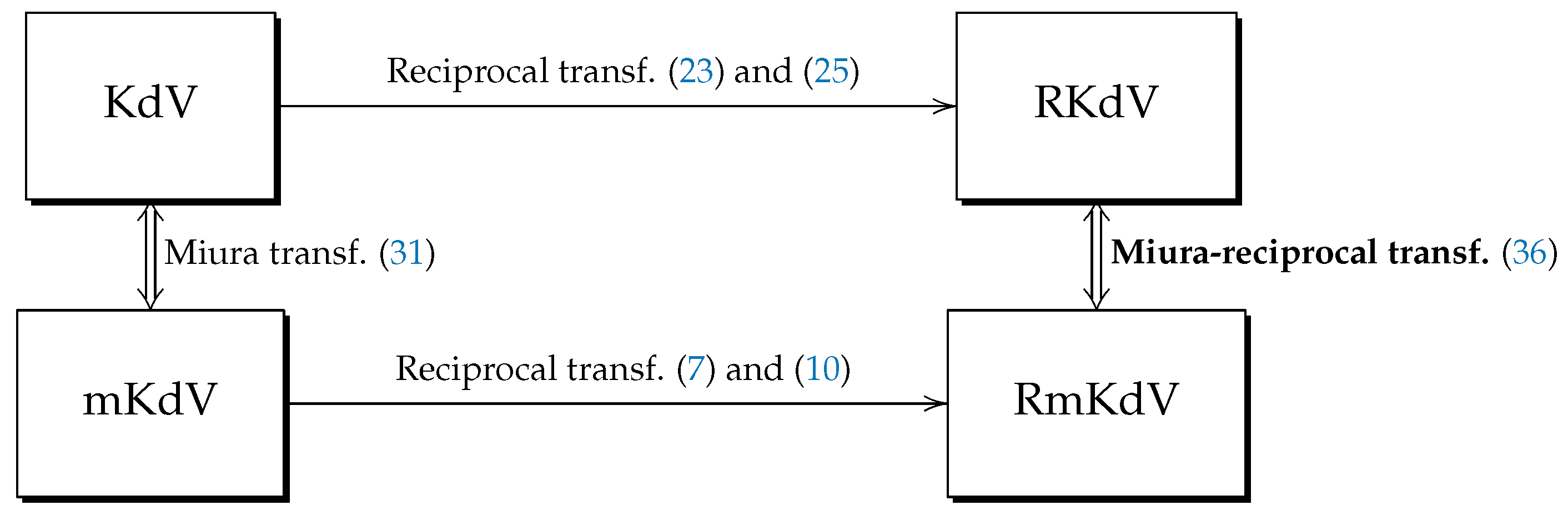
4. Reciprocal-Miura Transformations between RKdV and RmKdV
5. Lie Symmetries for the Transformed Spectral Problems
5.1. Lie Point Symmetries for RKdV
Reduction Associated to
- Reduced independent variable
- Reduced field
- Reduced spectral parameterwhere is the new spectral parameter.
- Reduced eigenfunction
- Reduced Lax pair
- Reduced ODE
5.2. Lie Point Symmetries for RmKdV
Reductions Associated to
- Reduced independent variable
- Reduced field
- Reduced spectral parameterwhere is the new spectral parameter for the reduced spectral problem.
- Reduced eigenfunctionsdenoted in the following as .
- Reduced Lax pairwhere and are the matrices
- Reduced ODE
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clarkson, P.A.; Fokas, A.S.; Ablowitz, M.J. Hodograph transformations of linearizable partial differential equations. SIAM J. Appl. Math. 1989, 49, 1188–1209. [Google Scholar] [CrossRef]
- Rogers, C.; Shadwick, W.F. Bäcklund Transformations and Their Applications; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1982; Volume 161. [Google Scholar]
- Rogers, C. Reciprocal transformations in (2 + 1) dimensions. J. Phys. A Math. Gen. 1986, 19, L491–L496. [Google Scholar] [CrossRef]
- Rogers, C. The Harry Dym equation in 2 + 1 dimensions: A reciprocal link with the Kadomtsev–Petviashvili equation. Phys. Lett. A 1987, 120, 15–18. [Google Scholar] [CrossRef]
- Estévez, P.G. Reciprocal transformations for a spectral problem in 2 + 1 dimensions. Theor. Math. Phys. 2009, 159, 763–769. [Google Scholar] [CrossRef]
- Estévez, P.G. Generalized Qiao hierarchy in 2 + 1 dimensions: Reciprocal transformations, spectral problem and non-isospectrality. Phys. Lett. A 2011, 375, 537–540. [Google Scholar] [CrossRef]
- Hone, A.N.W. Reciprocal link for 2+1-dimensional extensions of shallow water equations. Appl. Math. Lett. 2000, 13, 37–42. [Google Scholar] [CrossRef][Green Version]
- Estévez, P.G.; Prada, J. Hodograph Transformations for a Camassa–Holm hierarchy in 2 + 1 dimensions. J. Phys. A Math. Gen. 2005, 38, 1287–1297. [Google Scholar] [CrossRef][Green Version]
- Estévez, P.G.; Sardón, C. Miura reciprocal transformations for hierarchies in 2 + 1 dimensions. J. Nonlin. Math. Phys. 2013, 20, 552–564. [Google Scholar] [CrossRef]
- Degasperis, A.; Holm, D.D.; Hone, A.N. A new integral equation with peakon solutions. Theor. Math. Phys. 2002, 133, 1463–1474. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kruskal, M.; Segur, H. A note on Miura’s transformation. J. Math. Phys. 1979, 20, 999–1003. [Google Scholar] [CrossRef]
- Sakovich, S.Y. On Miura transformations of evolution equations. J. Phys. A Math. Gen. 1993, 26, L369–L373. [Google Scholar] [CrossRef]
- Weiss, J. The Painlevé property for partial differential equations. II: Bäcklund transformation, Lax pairs, and the Schwarzian derivative. J. Math. Phys. 1983, 24, 1405–1413. [Google Scholar] [CrossRef]
- Sakovich, A.; Sakovich, S. The Short Pulse Equation Is Integrable. J. Phys. Soc. Jpn. 2005, 74, 239–241. [Google Scholar] [CrossRef]
- Sakovich, S. Transformation and integrability of a generalized short pulse equation. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 21–28. [Google Scholar] [CrossRef]
- Sakovich, S. Integrability of a Generalized Short Pulse Equation Revisited. Res. Appl. Math. 2018, 2, 1–11. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; London Mathematical Society, Lecture Notes Series 149; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Levi, D.; Sym, A. Integrable systems describing surfaces of non-constant curvature. Phys. Lett. A 1990, 149, 381–387. [Google Scholar] [CrossRef]
- Cieslinski, J. Group interpretation of the spectral parameter in the case of nonhomogeneous, nonlinear Schrödinger system. J. Math. Phys. B 1993, 34, 2372–2384. [Google Scholar] [CrossRef]
- Marvan, M. On the Spectral Parameter Problem. Acta Appl. Math. 2010, 1096, 239–255. [Google Scholar] [CrossRef]
- Estévez, P.G.; Gandarias, M.L.; Prada, J. Symmetry reductions of a 2 + 1 Lax pair. Phys. Lett. A 2005, 343, 40–47. [Google Scholar] [CrossRef][Green Version]
- Camassa, R.; Holm, D.D. An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 1993, 71, 1661–1664. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Lie, S. Theorie der Transformationgruppen; B. G.Teubner: Leipzig, Germany, 1888. [Google Scholar]
- Stephani, H. Differential Equations. Their Solutions Using Symmetries; Callum, M.M., Ed.; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Snobl, L.; Winternitz, P. Classification and Identification of Lie Algebras; CRM Monograph Series; American Mathematical Society: Providence, RI, USA, 2014. [Google Scholar]
- Legare, M. Symmetry reductions of the Lax pair of the four-dimensional Euclidean self-dual Yang-Mills equations. J. Nonlinear Math. Phys. 1996, 3, 266–285. [Google Scholar] [CrossRef]
- Levi, D.; Sym, A.; Tu, G.Z. A Working Algorithm to Isolate Integrable Surfaces in E3, Preprint n. 761; Dipartimento di Fisica, Università di Roma: Roma, Italy, October 1990. [Google Scholar]
- Cieslinski, J. Nonlocal symmetries and a working algorithm to isolate integrable geometries. J. Phys. A Math. Gen. 1993, 26, L267–L271. [Google Scholar] [CrossRef]
- Cieslinski, J.; Goldstein, P.; Sym, A. On integrability of the inhomogeneous Heisenberg ferromagnet model: Examination of a new test. J. Phys. A Math. Gen. 1994, 27, 1645–1664. [Google Scholar] [CrossRef]
- Krasil’shchik, J.; Marvan, M. Coverings and Integrability of the Gauss–Mainardi–Codazzi Equation. Acta Appl. Math. 1999, 56, 217–230. [Google Scholar] [CrossRef]
- Marvan, M. On the Horizontal Gauge Cohomology and Nonremovability of the Spectral Parameter. Acta Appl. Math. 2002, 72, 51–65. [Google Scholar] [CrossRef]
- Bruzón, M.S.; Estévez, P.G.; Gandarias, M.L.; Prada, J. 1 + 1 spectral problems arising from the Manakov–Santini system. J. Phys. A Math. Theor. 2010, 43, 495204. [Google Scholar] [CrossRef]
- Albares, P.; Conde, J.M.; Estévez, P.G. Spectral problem for a two-component nonlinear Schrödinger equation in 2 + 1 dimensions: Singular manifold method and Lie point symmetries. Appl. Math. Comput. 2019, 355, 585–594. [Google Scholar] [CrossRef]
- Albares, P.; Estévez, P.G.; Lejarreta, J.D. Derivative non-linear Schrödinger equation: Singular manifold method and Lie symmetries. Appl. Math. Comput. 2021, 400, 126089. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albares, P.; Estévez, P.G. Miura-Reciprocal Transformation and Symmetries for the Spectral Problems of KdV and mKdV. Mathematics 2021, 9, 926. https://doi.org/10.3390/math9090926
Albares P, Estévez PG. Miura-Reciprocal Transformation and Symmetries for the Spectral Problems of KdV and mKdV. Mathematics. 2021; 9(9):926. https://doi.org/10.3390/math9090926
Chicago/Turabian StyleAlbares, Paz, and Pilar Garcia Estévez. 2021. "Miura-Reciprocal Transformation and Symmetries for the Spectral Problems of KdV and mKdV" Mathematics 9, no. 9: 926. https://doi.org/10.3390/math9090926
APA StyleAlbares, P., & Estévez, P. G. (2021). Miura-Reciprocal Transformation and Symmetries for the Spectral Problems of KdV and mKdV. Mathematics, 9(9), 926. https://doi.org/10.3390/math9090926





