Generalized Camassa–Holm Equations: Symmetry, Conservation Laws and Regular Pulse and Front Solutions

Abstract

In this paper, we consider a member of an integrable family of generalized Camassa–Holm (GCH) equations. We make an analysis of the point Lie symmetries of these equations by using the Lie method of infinitesimals. We derive nonclassical symmetries and we find new symmetries via the nonclassical method, which cannot be obtained by Lie symmetry method. We employ the multiplier method to construct conservation laws for this family of GCH equations. Using the conservation laws of the underlying equation, double reduction is also constructed. Finally, we investigate traveling waves of the GCH equations. We derive convergent series solutions both for the homoclinic and heteroclinic orbits of the traveling-wave equations, which correspond to pulse and front solutions of the original GCH equations, respectively.

1. Introduction

The Camassa–Holm (CH) equation, proposed in [1] as a model for the unidirectional propagation of shallow water waves, has been extensively studied in the last two decades both from analytical and numerical point of view due to its several important properties: integrability by the inverse scattering transform [2], bi-Hamiltonian structure [3], existence of peakons and multi-peakons type solutions [1,4], well-posedness and breaking waves [5,6], existence of global conservative solutions [7], infinite hierarchy of local higher symmetries [8].

More recently, Novikov in [8] classified 27 generalized Camassa–Holm equations belonging to the following class:

$$(1-D_x^2)u_t=F(u,u_x,u_{xx},u_{xxx},\cdots ).$$

(1)

The obtained equations are homogeneous polynomial generalizations of the CH equation containing quadratic and cubic nonlinearities and they are all integrable. Some of the equations considered in [8] have attracted much interest providing peakons and compactons solutions [9] and smooth multisolitons solutions [10]. Also, blow-up phenomena and local well-posedness [11] as far as the conservation laws [12] have been investigated for some of the generalized Camassa–Holm equations presented in [8].

In this paper, we will consider the following equation belonging to the class of Equation (1):

$$(1-D_x^2)u_t=(1+c{D}_x)(a{u}^2{u}_{xx}+du{u}_x^2-2b{u}^2{u}_x),$$

(2)

which explicitly reads as follows:

$$\begin{array}{c}{u}_t-u_{txx}-ac{u_{}}^2{u}_{xxx}-2c\left(a+d\right)u_{}{u}_x{u}_{xx}-\left(a-2bc\right){u_{}}^2{u}_{xx}\\ -dc{u_x}^3-\left(d-4bc\right)u_{}{u_x}^2+2b{u_{}}^2{u}_x=0.\end{array}$$

(3)

It is a Camassa–Holm type equation with cubic nonlinearities. It is a generalization of the Equation $\left(34\right)$ in [8], in fact the two equations contain the same kind of terms, but in Equation (2) all the parameter coefficients are different and not fixed; in particular, Equation (2) reduces to the one-parameter Equation $\left(34\right)$ in [8] with $a=d$ and $b=c=1$.

At first, we will study the symmetry property of Equation (2). Lie symmetries admitted by nonlinear partial differential equations (PDEs) are led to find invariant solutions and to reduce the number of independent variables of the PDE. In particular, a (1 + 1)-dimensional PDE can be reduced to an ordinary differential equation (ODE). A new method, the so-called nonclassical method of group-invariant solutions, proposed by Bluman and Cole in [13], allows the deduction of new symmetries of a PDE. Here, we will obtain symmetry reductions of Equation (2). Using the algorithm given in [13,14], based on the nonclassical method, we will obtain new reductions of (2).

Then, we will derive some conservation laws of Equation (2). A great many authors have used the conservation laws to study PDEs as they have a key role in the resolution of problems in which some physical properties do not change along the time [15,16,17,18]. We will use a general method to derive conservation laws given in [19,20,21,22]. Moreover, recalling that for PDEs in two independent variables any symmetry-invariant conservation law will reduce to a first integral for the ODE obtained by symmetry reduction, we will focus on the conservation laws invariant under translations. We will apply the multireduction method [23] to obtain first integrals and exact solutions.

Finally, we will investigate the existence of pulse and front solutions of Equation (2). Using the same method in [9,24,25], we will derive this type of solutions as convergent multi-infinite series solutions for the homoclinic and heteroclinic orbit of the traveling-wave equation corresponding to Equation (2).

The plan of the paper is the following: in Section 2 we deduce Lie symmetries and nonclassical symmetries of GCH equations, in Section 3 conservation laws have been derived by using the direct method proposed in [20]. In Section 4 the conservation laws invariant under translations are derived and a multireduction has been achieved yielding some first integrals of the reduced ODEs. In Section 5, we will first analyze the dynamics of the traveling-wave equation corresponding to Equation (2), obtaining suitable parameter regimes for the existence of homoclinic orbits to saddle equilibrium and heteroclinic orbits joining two saddle equilibria. Then, we will approximate these orbits (which are respectively pulse and front solutions of Equation (2)) via multi-series solutions, ensuring both continuity and convergence of the solutions.

2. Symmetry Analysis and Reductions

2.1. Lie Point Symmetries

At first, we apply the classical method to (3) considering the following one-parameter Lie group of infinitesimal transformations in $(x,t,u)$:

$$\begin{array}{rrr}{x}^{*}& =& x+ϵ\xi (x,t,u)+O\left({ϵ}^2\right),\hfill \end{array}$$

$$\begin{array}{rrr}{t}^{*}& =& t+ϵ\tau (x,t,u)+O\left({ϵ}^2\right),\hfill \end{array}$$

(4)

$$\begin{array}{rrr}{u}^{*}& =& u+ϵ\eta (x,t,u)+O\left({ϵ}^2\right),\hfill \end{array}$$

(5)

where $ϵ$ is the group parameter which is generated by the vector field

$$\mathbf{X}=\xi (x,t,u){\partial }_x+\tau (x,t,u){\partial }_t+\eta (x,t,u){\partial }_u.$$

(6)

By Criterion of Invariance [22] we toned to leave invariant the solution space of Equation (3). This condition is given by:

$$\begin{array}{r}{\mathrm{pr}}^{\left(3\right)}\mathbf{X}\left(u_t-u_{txx}-ac{u_{}}^2{u}_{xxx}-2c\left(a+d\right)u_{}{u}_x{u}_{xx}-\left(a-2bc\right){u_{}}^2{u}_{xx}-dc{u_x}^3\right.\end{array}$$

(7)

$$\begin{array}{rrr}\left.-\left(d-4bc\right)u_{}{u_x}^2+2b{u_{}}^2{u}_x\right)& =& 0\hfill \end{array}$$

(8)

when the equation is satisfied, where ${\mathrm{pr}}^{\left(3\right)}\mathbf{X}$ is the third-order prolongation of the vector field (6) obtained by the following prolongation formulas

$$\begin{array}{c}{\mathrm{pr}}^{\left(3\right)}\mathbf{X}=X+{\zeta }_x\frac{\partial }{\partial u_x}+{\zeta }_t\frac{\partial }{\partial u_t}+{\zeta }_{xx}\frac{\partial }{\partial u_{xx}}+{\zeta }_{tx}\frac{\partial }{\partial u_{tx}}+{\zeta }_{txx}\frac{\partial }{\partial u_{txx}}+{\zeta }_{xxx}\frac{\partial }{\partial u_{xxx}},\hfill \end{array}$$

with the coefficients

$$\begin{array}{rrr}{\zeta }_x& =& D_x\eta -u_t{D}_x\tau -u_x{D}_x\xi ,\hfill \\ {\zeta }_t& =& D_t\eta -u_t{D}_t\tau -u_x{D}_t\xi ,\hfill \\ {\zeta }_{xx}& =& D_x\left({\zeta }_x\right)-u_{tx}{D}_x\tau -u_{xx}{D}_x\xi ,\hfill \\ {\zeta }_{tx}& =& D_x\left({\zeta }_t\right)-u_{tt}{D}_x\tau -u_{tx}{D}_x\xi ,\hfill \\ {\zeta }_{txx}& =& D_x\left({\zeta }_{tx}\right)-u_{txt}{D}_x\tau -u_{txx}{D}_x\xi ,\hfill \\ {\zeta }_{xxx}& =& D_x\left({\zeta }_{xx}\right)-u_{xxt}{D}_x\tau -u_{xxx}{D}_x\xi \hfill \end{array}$$

(9)

where $D_x$ and $D_t$ are the total derivatives of x and t, respectively. The prolongation formula yields the determining equation, this splits with respect to the differential consequences of u and leads to an overdetermined system of 34 equations, generated with Maple, which depends on the parameters a, b, c and d. From this system, if $a,c\ne 0$ we obtain $\xi =\xi (x,t)$, $\tau =\tau \left(t\right)$ and $\eta =f(x,t)u+g(x,t)$ and the function $\xi ,\tau ,f,g$ are related by the conditions

$$\begin{array}{rrr}{\tau }_{t}ca{u}^2-{\xi }_{x}ca{u}^2+2cau\left(fu+g\right) - {\xi }_t& =& 0,\hfill \\ \left(f_{xtx}u+f_{xxx}ac{u}^3+g_{xtx}+g_{xxx}ac{u}^2 + \left(-2bc+a\right)u^3{f}_{xx}+u^2\left(-2bc+a\right)g_{xx}\right.& & \\ \left.-2f_{x}b{u}^3-2g_{x}b{u}^2-f_{t}u-g_t\right)ac{u}^2& =& 0,\hfill \\ ca{u}^2\left({\xi }_{xx}-2f_x\right)& =& 0,\hfill \\ -\left(-2{\xi }_{tx}ca-3{\xi }_{xx}{c}^2{a}^2{u}^2+5\left(a+2/5d\right)a{c}^2{u}^2{f}_x\right.& & \\ \left.+2a{c}^{2}u\left(a+d\right)g_x+\left(-2bc+a\right){\xi }_t+ac\left(u^2\left(-2bc+a\right){\xi }_x+f_t\right)\right)u^2& =& 0,\hfill \\ -{\tau }_{t}ca{u}^2+3{\xi }_{x}ca{u}^2-2cau\left(fu+g\right)-f_{xx}ca{u}^2+{\xi }_{t}2\left(a+d\right)\left(gacu-{\xi }_t\right)cu& =& 0,\hfill \\ cd\left(2gacu-{\xi }_t\right)& =& 0,\hfill \\ -2\left(-1/2{\xi }_{xtx}ca-1/2{\xi }_{xxx}{c}^2{a}^2{u}^2+5/2\left(a+2/5d\right)a{c}^2{u}^2{f}_{xx}+a{c}^{2}u\left(a+d\right)g_{xx}\right.& & \\ -1/2u^{2}ca\left(-2bc+a\right){\xi }_{xx}+f_{tx}ca+u^{2}ca\left(-6bc+a+d\right)f_x-4a\left(bc-d/4\right)cu{g}_x& & \\ \left.+\left(1/2ca-b\right){\xi }_t-2{\xi }_{x}ca{u}^{2}b\right)u^2& =& 0,\hfill \\ -4\left(-1/2a{c}^2{u}^2\left(a+d\right){\xi }_{xx}+a{c}^2{u}^2\left(a+7/4d\right)f_x+\left(-bc+d/4\right){\xi }_t\right.& & \\ \left.+a\left(-\left(bc-d/4\right)u{\xi }_x+3/4g_{x}cd+g\left(bc-d/4\right)\right)cu\right)u& =& 0.\hfill \end{array}$$

(10)

Solving system (11) we obtain the following result:

Theorem 1.

The classification of point symmetries admitted by the Camassa–Holm equation with four arbitrary constants (3) is given by the following cases:

(i) 

For $a\ne 0$, $b\ne 0$, $c\ne 0$ and $d\ne 0$ the admitted point symmetries are generated by:

$$\begin{array}{c}{X}_1={\partial }_x,\hfill \\ space-translation.\hfill \\ \\ X_2={\partial }_t,\hfill \\ time-translation.\hfill \\ \\ X_3=-2t{\partial }_t+u{\partial }_u,\hfill \end{array}$$

(ii) 

If $a=d$, $b=\frac{d}{c}$, $c=\pm 1$, d, arbitrary we obtain an additional point symmetries admitted by the Camassa–Holm Equation (3):

$$\begin{array}{c}{X}_4=cexp\left(2cx\right){\partial }_x+exp\left(2cx\right)u{\partial }_u,\hfill \end{array}$$

To find the solutions of the PDE (3) which are not equivalent by the group action, we must compute the one-dimensional optimal system [22], whose generators are:

$$\mu {\mathbf{X}}_1+\lambda {\mathbf{X}}_2,\mu {\mathbf{X}}_1+{\mathbf{X}}_3,\mu {\mathbf{X}}_2+{\mathbf{X}}_4.$$

From $\mu {\mathbf{X}}_1+\lambda {\mathbf{X}}_2$, by substituting into the invariant surface condition

$$\eta (t,x,u)-\tau (t,x,u)u_t-\xi (t,x,u)u_x=0.$$

(11)

we obtain the similarity variable and the similarity solution

$$\begin{array}{c}z=\mu x-\lambda t,u(x,t)=U\left(z\right).\hfill \end{array}$$

(12)

Substituting (12) into (3) we obtain

$$\begin{array}{rrr}-{\mu }^2\left(ac\mu U^2-\lambda \right)U\prime \prime \prime -2{\mu }^2\left(c\mu \left(a+d\right)U^{\prime }+1/2U\left(-2bc+a\right)\right)U\prime \prime & & \\ +4U^{\prime }\left(-1/4cd{\mu }^3{\left(U^{\prime }\right)}^2+{\mu }^{2}U\left(bc-d/4\right)U^{\prime }+1/2b\mu U^2-\lambda /4\right)& =& 0.\hfill \end{array}$$

(13)

Since Equation (3) has additional symmetries and the reductions corresponding to ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ have already been derived, we should find the similarity variables and similarity solutions corresponding to the generators $\mu {\mathbf{X}}_1+{\mathbf{X}}_3$ and $\mu {\mathbf{X}}_2+{\mathbf{X}}_4$.

• $\mu {\mathbf{X}}_1+{\mathbf{X}}_3$: We obtain the reduction

  $$\begin{array}{ccc}z=(1/2)\mu ln\left(t\right)+x,\hfill & \hfill & u=\frac{U\left(z\right)}{\sqrt{exp\left(\right(-2x+2z)/\mu )}},\hfill \end{array}$$

  (14)

  where $h\left(z\right)$ satisfies the equation

  $$\begin{array}{rrr}\left(1/2U^{2}ac+\mu /4\right)U\prime \prime \prime +\left(c{U}^{\prime }\left(a+d\right)-1/4+\left(-bc+a/2\right)U^2\right)U\prime \prime & & \\ +1/2U^{3}cd-2\left(bc-d/4\right)U{\left(U^{\prime }\right)}^2+\left(-U^{2}b-\mu /4\right)U^{\prime }+1/4U& =& 0.\hfill \end{array}$$

  (15)
• $\mu {\mathbf{X}}_2+{\mathbf{X}}_4$: The reduction is,

  $$\begin{array}{ccc}z=-t+c/2{\left({\mathrm{e}}^{cx}\right)}^2\mu ,\hfill & \hfill & u=\frac{U\left(z\right)\sqrt{2}}{\sqrt{c{\left({\mathrm{e}}^{cx}\right)}^2\mu }}.\hfill \end{array}$$

  (16)
  The reduced ODE is

  $$\begin{array}{c}2d{U}^{2}U\prime \prime \prime +8U\prime \prime U^{\prime }Ud+2{\left(U^{\prime }\right)}^{3}d+U\prime \prime \prime =0.\hfill \end{array}$$

  (17)

2.2. Nonclassical Method

Here, we will employ the nonclassical method, whose main idea is to augment the PDE (3) with the invariance surface condition (11) associated with the vector field (6). Once required that (3) and (11) are both invariant under the transformation whose infinitesimal generator is (6), we obtain an overdetermined nonlinear system of equations for the infinitesimals $\xi (x,t,u),$$\tau (x,t,u)$ and $\eta (x,t,u)$. The determining equations obtained using the nonclassical method are fewer in number than those obtained via the Lie method, therefore the set of solutions is generally larger than for the Lie symmetry method. However, the associated vector fields do not form a vector space.

Let us now apply the algorithm described in [14] to compute the determining equations. We can distinguish the two following cases:

• if $\tau \ne 0,$ we can set $\tau (x,t,u)=1$. We thus obtain a set of nine determining equations for the infinitesimals $\xi (x,t,u)$ and $\eta (x,t,u)$. Once solved this system we obtain that the nonclassical method applied to (3) yields to the Lie point symmetries.
• If $\tau =0,$ we can set $\xi =1$. We thus obtain an overdetermined nonlinear system of equations for the infinitesimal $\eta$, which is solved by making ansätze. In this way the following new infinitesimal generator is found:

  $$\begin{array}{ccccc}\xi =1,\hfill & \hfill & \tau =0,\hfill & \hfill & \eta =f(x,t),\hfill \end{array}$$

  where f is an arbitrary function. Therefore, this transformation reduces the PDE (3) into an ODE. For example, for $\eta =x{\psi }_2\left(t\right)+{\psi }_1\left(t\right)$, where ${\psi }_1\left(t\right)$ and ${\psi }_2\left(t\right)$ satisfy

  $$\frac{d^2{\psi }_2}{d{t}^2}-6{\psi }_2^2=0,$$

  (18)

  $$\frac{d^2{\psi }_1}{d{t}^2}-6{\psi }_1{\psi }_2=0,$$

  (19)

  respectively, we obtain the nonclassical symmetry reduction

  $$\begin{array}{ccc}z=t,\hfill & \hfill & u=x^2{\psi }_2\left(t\right)+x{\psi }_1\left(t\right)+{\psi }_0\left(t\right),\hfill \end{array}$$

  where ${\psi }_2\left(t\right)$ satisfies the Weierstrass elliptic function Equation (18) and ${\psi }_1\left(t\right)$ satisfies the Lamé Equation (19) [14].

3. Conservation Laws

We now look for conservation laws for Equation (3), which will provide physical, conserved quantities for all solutions $u(x,t)$.

A local conservation law for Equation (3) is a continuity equation of the following form:

$$D_{t}T+D_{x}X=0,$$

(20)

which holds for all the solutions $u(x,t)$ of Equation (3). In (20), the conserved density T and the spatial flux X are functions of t, x, u and the derivatives of u. Moreover, $D_t$ and $D_x$ are total derivatives and $(T,X)$ is the conserved current. Let $\mathsf{\Theta }$ be function of t, x, u and x-derivatives of u. If $T=D_x\mathsf{\Theta }$ and $X=-D_t\mathsf{\Theta }$ hold for all solutions $u(x,t)$, then the continuity Equation (20) reduces to an identity. These types of conservation laws are called locally trivial. Moreover, if two conservation laws differ by a locally trivial conservation law, then they are considered to be locally equivalent. The local conservation laws can be expressed in an equivalent form (an analogous of the evolutionary form for symmetries) [22] given by a divergence identity as follows:

$$\begin{array}{rr}& D_t\tilde{T}+D_x\tilde{X}=\hfill \\ & (u_t-u_{txx}-(a{u}^2{u}_{xx}-2b{u}^2{u}_x+du{u}_x^2)-c{(a{u}^2{u}_{xx}-2b{u}^2{u}_x+du{u}_x^2)}_x)Q\hfill \end{array}$$

(21)

holding off the set of solutions of the generalized Camassa Equation (3), where $\tilde{T}=T+D_x\mathsf{\Theta }$ and $\tilde{X}=X-D_t\mathsf{\Theta }$ are the conserved density and the spatial flux locally equivalent to T and X, respectively and where:

$$Q=E_u\left(\tilde{T}\right)$$

(22)

is a function of t, x, u and x-derivatives of u. The function Q is called a multiplier [21,22,26]. In (22), $E_u$ denotes the Euler operator with respect to u [22]. By the characteristic Equation (21) it follows that all non-trivial conservation laws for any regular PDE system arise from multipliers up to local equivalence [19]. We will consider the following low-order multipliers:

$$Q(t,x,u,u_t,u_x,u_{xx}).$$

(23)

The condition (21) splits with respects to the x-derivatives of u which do not appear in Q.

Proposition 1.

The low-order multipliers (23) admitted by the Camassa–Holm Equation (3) with $a\ne 0$, $b\ne 0$, $c\ne 0$ and $d\ne 0$ are given by

(i) a, b, c, d arbitrary:

$$\begin{array}{rr}& Q_1=e^{\frac{x}{c}};\hfill \end{array}$$

(24)

(ii) $c=\pm 1$, a, b, d arbitrary:

$$\begin{array}{rr}& Q_2=F\left(t\right)e^{\frac{x}{c}};\hfill \\ \end{array}$$

(25)

(iii) $a=\frac{d}{2}$, $c\ne 0$, $d\ne 0$, b, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3a}=1,\hfill \end{array}\hfill \end{array}$$

(26)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3b}=e^{\frac{x}{c}},\hfill \end{array}\hfill \end{array}$$

(27)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3c}=e^{-\frac{4bx}{d}};\hfill \end{array}\hfill \\ \end{array}$$

(28)

(iv) $a=\frac{d}{2}$, $d=\pm 4b$, c, b, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{4a}=1,\hfill \end{array}\hfill \end{array}$$

(29)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{4b}=e^{\frac{x}{c}},\hfill \end{array}\hfill \end{array}$$

(30)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{4c}=e^{-\frac{4bx}{d}};\hfill \end{array}\hfill \\ \end{array}$$

(31)

(v) $a=\frac{d}{2}$, $c=\pm 1$, d, b, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{5a}=1,\hfill \end{array}\hfill \end{array}$$

(32)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{5b}=e^{-\frac{4bx}{d}},\hfill \end{array}\hfill \end{array}$$

(33)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{5c}=F\left(t\right)e^{\pm x};\hfill \end{array}\hfill \\ \end{array}$$

(34)

(vi) $a=d$, $b=\frac{d}{c}$, c, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{6a}=u,\hfill \end{array}\hfill \end{array}$$

(35)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{6b}=e^{\frac{x}{c}},\hfill \end{array}\hfill \\ \end{array}$$

(36)

(vii) $a=d$, $b=\frac{d}{c}$, $c=\pm 1$, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{7a}=u,\hfill \end{array}\hfill \end{array}$$

(37)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{7b}=F\left(t\right)e^{\pm x}:\hfill \end{array}\hfill \\ \end{array}$$

(38)

The above given multipliers yield all non-trivial conservation laws of low order, which can be summarized as follows:

Case 1 a, b, c, d arbitrary

$$\begin{array}{rrr}{Q}_1& =& e^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& e^{\frac{x}{c}}(u+\frac{u_x}{c}),\hfill \\ {\varphi }^x& =& e^{\frac{x}{c}}(-u_{tx}-ac{u}^2{u}_{xx}+2bc{u}^2{u}_x-cdu{u}_x^2).\hfill \end{array}$$

Case 2 $c=\pm 1$a, b, d arbitrary

$$\begin{array}{rrr}{Q}_2& =& F\left(t\right)e^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& F\left(t\right)e^{\frac{x}{c}}(\frac{u_{xx}}{c}+u),\hfill \\ {\varphi }^x& =& F\left(t\right)e^{\frac{x}{c}}(-u_{tx}-ac{u}^2{u}_{xx}+2bc{u}^2{u}_x-cdu{u}_x^2)-e^{\frac{x}{c}}\frac{F^{\prime }\left(t\right)}{c}u.\hfill \end{array}$$

Case 3 $a=\frac{d}{2}$

$$\begin{array}{rrr}{Q}_{3a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}-\frac{cd}{2}{u}^2{u}_{xx}-cdu{u}_x^2+(2bc-\frac{d}{2})u^2{u}_x+\frac{2b}{3}{u}^3,\hfill \\ Q_{3b}& =& {\mathrm{e}}^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& e^{\frac{x}{c}}(\frac{u_x}{c}+u),\hfill \\ {\varphi }^x& =& -e^{\frac{x}{c}}(u_{tx}+cdu{u}_x^2+ca{u}^2{u}_{xx}-2bc{u}^2{u}_x),\hfill \\ Q_{3c}& =& {\mathrm{e}}^{-4\frac{bx}{d}},\hfill \\ {\varphi }^t& =& \left(-u_{xx}+u_{}\right)e^{-\frac{4bx}{d}},\hfill \\ {\varphi }^x& =& -\frac{1}{2}{u}_{}d\left(u_{}c{u}_{xx}+u_{}{u}_x+2c{u_x}^2\right)e^{-\frac{4bx}{d}}.\hfill \end{array}$$

Case 4$a=\frac{d}{2}$, $d=-4b$

$$\begin{array}{rrr}{Q}_{4a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}-\frac{cd}{2}{u}^2{u}_{xx}-cdu{u}_x^2+(2bc-\frac{d}{2})u^2{u}_x+\frac{2}{3}b{u}^3,\hfill \\ Q_{4b}& =& {\mathrm{e}}^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& e^{\frac{x}{c}}(\frac{u_x}{c}+u),\hfill \\ {\varphi }^x& =& e^{\frac{x}{c}}(-u_{tx}-\frac{cd}{2}{u}^2{u}_{xx}+2bc{u}^2{u}_x-cdu{u}_x^2,\hfill \\ Q_{4c}& =& e^{-\frac{4b}{d}x},\hfill \\ {\varphi }^t& =& e^{-\frac{4b}{d}x}(-\frac{4b{u}_x}{d}+u),\hfill \\ {\varphi }^x& =& -e^{-\frac{4b}{d}x}(u_{tx}+\frac{cd}{2}{u}^2{u}_{xx}+cdu{u}_x^2+\frac{d}{2}{u}^2{u}_x.\hfill \\ \end{array}$$

Case 5$a=\frac{d}{2}$, $c=\pm 1$, b, d arbitrary

$$\begin{array}{rrr}{Q}_{5a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}+\frac{d}{2}{u}^2(u_{xx}-u_x)+du{u}_x^2+\frac{2}{3}b{u}^3,\hfill \\ Q_{4b}& =& {\mathrm{e}}^{-\frac{4bx}{d}}\hfill \\ {\varphi }^t& =& e^{-\frac{4bx}{d}}(-\frac{4b{u}_x}{d}+u),\hfill \\ {\varphi }^x& =& -\frac{1}{2}{e}^{-\frac{4bx}{d}}(2u_{tx}+d{u}^2(u_x-u_{xx})-2du{u}_x^2),\hfill \\ Q_{5c}& =& F\left(t\right)e^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& F\left(t\right)e^{\frac{x}{c}}(\frac{u_x}{c}+u),\hfill \\ {\varphi }^x& =& e^{\frac{x}{c}}(-F\left(t\right)u_{tx}-\frac{cd}{2}F\left(t\right)d{u}^2{u}_{xx}+2bcF\left(t\right)u^2{u}_x-cdF\left(t\right)u{u}_x^2-\frac{F^{\prime }\left(t\right)}{c}u).\hfill \\ \end{array}$$

Case 6$a=d$$b=\frac{d}{c}$, c, d arbitrary

$$\begin{array}{rrr}{Q}_{6a}& =& u,\hfill \\ {\varphi }^t& =& \frac{1}{2}(u^2+u_x^2),\hfill \\ {\varphi }^x& =& -u{u}_{tx}-cd{u}^3{u}_{xx}-\frac{cd}{2}{u}^2{u}_x^2+d{u}^3{u}_x+\frac{d}{2c}{u}^4,\hfill \\ Q_{6b}& =& e^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& e^{\frac{x}{c}}(u+\frac{u_x}{c}),\hfill \\ {\varphi }^x& =& e^{\frac{x}{c}}(-u_{tx}-cd{u}^2{u}_{xx}-cdu{u}_x^2+2d{u}^2{u}_x).\hfill \\ \end{array}$$

Case 7$a=d$$b=\frac{d}{c}$, $c=\pm 1$, d arbitrary

$$\begin{array}{rrr}{Q}_{6a}& =& u,\hfill \\ {\varphi }^t& =& \frac{1}{2}(u^2+u_x^2),\hfill \\ {\varphi }^x& =& -u{u}_{tx}-cd{u}^3{u}_{xx}-\frac{cd}{2}{u}^2{u}_x^2+d{u}^3{u}_x+\frac{d}{2c}{u}^4,\hfill \\ Q_{6b}& =& e^{\frac{x}{c}},\hfill \\ {\varphi }^t& =& e^{\frac{x}{c}}(u+\frac{u_x}{c}),\hfill \\ {\varphi }^x& =& e^{\frac{x}{c}}(-u_{tx}-cd{u}^2{u}_{xx}-cdu{u}_x^2+2d{u}^2{u}_x).\hfill \\ \end{array}$$

4. Multireduction Method

Conservation laws that are symmetry invariant are of sure interest in applications. If a differential equation admits a Noether symmetry, then a conservation law is associated with this symmetry and a double reduction can be achieved. In particular, for PDEs depending on two independent variables, any symmetry-invariant conservation law will reduce to a first integral for the corresponding ODE obtained via symmetry reduction. In [27,28], Sjöberg introduced a new method for non-variational PDEs, which can be performed when a symmetry is associated with a conserved vector. In [29,30], the authors explored a further connection between symmetries and conservation laws which are invariant (or, more generally, homogeneous) under the action of a given set of symmetries. In [23], given a PDE with $n>2$ independent variables and a symmetry algebra of dimension at least $n>1$, an algorithmic method is described to find the symmetry-invariant conservation laws that will reduce to first integrals for the ODE describing symmetry-invariant solutions.

Given a PDE $G(t,x,u,u_t,u_x,\dots )=0$, its invariance under the translation symmetry

$$\mathrm{X}={\partial }_t+c{\partial }_x,$$

(39)

yields to traveling-wave solutions, where $\zeta =x-ct$ and $u=U$ being the invariants.

Proposition 2.

The low-order multipliers (23) invariant under the translation symmetry (39) admitted by the Camassa–Holm Equation (3) with $a\ne 0$, $b\ne 0$, $c\ne 0$$d\ne 0$ are given by

(i) $c=\pm 1$ a, b, d arbitrary:

$$\begin{array}{rr}& Q_1=e^{\frac{x-pt}{c}};\hfill \end{array}$$

(40)

(ii) $a=\frac{d}{2}$, b, c, d arbitrary:

$$\begin{array}{rr}& Q_2=1,\hfill \end{array}$$

(41)

(iii) $a=\frac{d}{2}$, $d=-4b$, b, c, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3a}=1,\hfill \end{array}\hfill \end{array}$$

(42)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3b}=e^{x-pt}\hfill \end{array}\hfill \end{array}$$

(43)

(iii) $a=\frac{d}{2}$, $d=4b$, b, c, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3a}=1,\hfill \end{array}\hfill \end{array}$$

(44)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{3b}=e^{-x+pt}\hfill \end{array}\hfill \end{array}$$

(45)

(v) $a=\frac{d}{2}$, $c=-1$, b, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{4a}=1,\hfill \end{array}\hfill \end{array}$$

(46)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{4b}=e^{-x+pt}\hfill \end{array}\hfill \end{array}$$

(47)

(vi) $a=\frac{d}{2}$, $c=1$, b, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{5a}=1,\hfill \end{array}\hfill \end{array}$$

(48)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{4b}=e^{x-pt}\hfill \end{array}\hfill \end{array}$$

(49)

(vii) $a=\frac{d}{2}$, $d=4bc$, $c=\pm 1$ b, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{6a}=1,\hfill \end{array}\hfill \end{array}$$

(50)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{6b}=e^{x-pt}\hfill \end{array}\hfill \end{array}$$

(51)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{6c}=e^{-x+pt}\hfill \end{array}\hfill \end{array}$$

(52)

(viii) $a=d$, $b=\frac{d}{c}$, c, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{7a}=u,\hfill \end{array}\hfill \end{array}$$

(53)

(ix) $a=d$, $b=d$, $c=1$, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{8a}=u,\hfill \end{array}\hfill \end{array}$$

(54)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{8b}=e^{x-pt},\hfill \end{array}\hfill \end{array}$$

(55)

(x) $a=d$, $b=d$, $c=-1$, d, arbitrary

$$\begin{array}{rr}& \begin{array}{rr}& Q_{9a}=u,\hfill \end{array}\hfill \end{array}$$

(56)

$$\begin{array}{rr}& \begin{array}{rr}& Q_{9b}=e^{-x+pt},\hfill \end{array}\hfill \end{array}$$

(57)

These multipliers yield all non-trivial conservation laws of low order invariant under the translation symmetry, summarized as follows:

Case 1 $c=\pm 1$, a, b, d arbitrary

$$\begin{array}{rrr}{Q}_1& =& e^{\frac{x-pt}{c}},\hfill \\ {\varphi }^t& =& e^{\frac{x-pt}{c}}(u+\frac{u_x}{c}),\hfill \\ {\varphi }^x& =& e^{\frac{x-pt}{c}}(-u_{tx}-ac{u}^2{u}_{xx}+2bc{u}^2{u}_x-cdu{u}_x^2).\hfill \end{array}$$

Case 2 $a=\frac{d}{2}$, b, c, d arbitrary

$$\begin{array}{rrr}{Q}_2& =& 1\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}-ac{u}^2{u}_{xx}+(2bc-a)u^2{u}_x-cdu{u}_x^2+\frac{2b}{3}{u}^3\hfill \end{array}$$

Case 3$a=\frac{d}{2}$, $d=-4b$

$$\begin{array}{rrr}{Q}_{3a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}-ac{u}^2{u}_{xx}-cdu{u}_x^2+(2bc-a)u^2{u}_x+\frac{2b}{3}{u}^3\hfill \\ Q_{3b}& =& e^{x-pt}\hfill \\ {\varphi }^t& =& e^{x-pt}(u+u_x)\hfill \\ {\varphi }^x& =& e^{x-pt}(-u_{tx}+2bc{u}^2{u}_{xx}+4bcu{u}_x^2+2b{u}^2{u}_x+pu)\hfill \\ \end{array}$$

(58)

Case 4$a=\frac{d}{2}$, $d=4b$

$$\begin{array}{rrr}{Q}_{4a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}-ac{u}^2{u}_{xx}-cdu{u}_x^2+(2bc-a)u^2{u}_x+\frac{2b}{3}{u}^3\hfill \\ Q_{4b}& =& e^{-x+pt}\hfill \\ {\varphi }^t& =& e^{-x+pt}(u-u_x)\hfill \\ {\varphi }^x& =& -e^{-x+pt}(u_{tx}+2bc{u}^2{u}_{xx}+cdu{u}_x^2+2b{u}^2{u}_x-pu)\hfill \\ \end{array}$$

(59)

Case 5$a=\frac{d}{2}$, $c=-1$, $b,d$ arbitrary

$$\begin{array}{rrr}{Q}_{5a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}+\frac{d}{2}{u}^2(u_{xx}-u_x)-2b{u}^2{u}_x+du{u}_x^2+\frac{2}{3}b{u}^3.\hfill \\ Q_{5b}& =& e^{pt-x}\hfill \\ {\varphi }^t& =& e^{pt-x}(u-u_x)\hfill \\ {\varphi }^x& =& e^{pt-x}(-u_{tx}+\frac{d}{2}{u}^2{u}_{xx}-2b{u}^2{u}_x+du{u}_x^2+pu)\hfill \\ \end{array}$$

(60)

Case 6$a=\frac{d}{2}$, $c=1$, $b,d$ arbitrary

$$\begin{array}{rrr}{Q}_{6a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}+\frac{d}{2}{u}^2(u_{xx}-u_x)-2b{u}^2{u}_x+du{u}_x^2+\frac{2}{3}b{u}^3.\hfill \\ Q_{6b}& =& e^{x-pt}\hfill \\ {\varphi }^t& =& e^x-x-pt(u+u_x)\hfill \\ {\varphi }^x& =& e^{x-pt}(-u_{tx}-\frac{d}{2}{u}^2{u}_{xx}+2b{u}^2{u}_x-du{u}_x^2+pu)\hfill \\ \end{array}$$

(61)

Case 7$a=\frac{d}{2}$, $b=\frac{d}{4c}$, $c=\pm 1$

$$\begin{array}{rrr}{Q}_{7a}& =& 1,\hfill \\ {\varphi }^t& =& u,\hfill \\ {\varphi }^x& =& -u_{tx}-ac{u}^2{u}_{xx}-cdu{u}_x^2+(2bc-a)u^2{u}_x+\frac{2b}{3}{u}^3.\hfill \\ Q_{7b}& =& e^{-x+pt}\hfill \\ {\varphi }^t& =& e^{-x+pt}(u-u_x)\hfill \\ {\varphi }^x& =& e^{-x+pt}(-u_{tx}-\frac{cd}{2}{u}^2(u_{xx}+u_x)-cdu{u}_x^2+pu\hfill \\ \end{array}$$

(62)

Case 8$a=d$$b=\frac{d}{c}$, c, d arbitrary

$$\begin{array}{rrr}{Q}_8& =& u,\hfill \\ {\varphi }^t& =& \frac{1}{2}(u^2+u_x^2),\hfill \\ {\varphi }^x& =& -u{u}_{tx}-cd{u}^3{u}_{xx}-\frac{cd}{2}{u}^2{u}_x^2+d{u}^3{u}_x+\frac{d}{2c}{u}^4.\hfill \\ \end{array}$$

(63)

Case 9$a=d$, $b=\frac{d}{c}$, $c=\pm 1$d arbitrary

$$\begin{array}{rrr}{Q}_{9a}& =& u,\hfill \\ {\varphi }^t& =& \frac{1}{2}(u^2+u_x^2),\hfill \\ {\varphi }^x& =& -u{u}_{tx}-cd{u}^3{u}_{xx}-\frac{cd}{2}{u}^2{u}_x^2+d{u}^3{u}_x+\frac{d}{2c}{u}^4.\hfill \\ \end{array}$$

(64)

$$\begin{array}{rrr}{Q}_{9b}& =& e^{x-pt},\hfill \\ {\varphi }^t& =& e^{x-pt}(u+c{u}_x),\hfill \\ {\varphi }^x& =& e^{x-pt}(-u_{tx}+c(-a{u}^2{u}_{xx}-du{u}_x^2+2b{u}^2{u}_x)+pu).\hfill \\ \end{array}$$

(65)

Substitution of the traveling-wave expression

$$u(t,x)=U(x-ct)$$

(66)

into Equation (3) yields a nonlinear third-order ODE

$$\begin{array}{c}(-ac{U}^2+p)U\prime \prime \prime -(2(c(a+d)U\prime )+(1/2)U(-2bc+a)))UU\prime \prime \hfill \\ +4U^{\prime }(-(1/4)cd{U\prime }^2+U(bc-(1/4)d)U^{\prime }+(1/2)b{U}^2-(1/4)p)=0\hfill \end{array}$$

(67)

To find the first integrals of the traveling-wave ODE (67)) the symmetry reduction of all conservation laws, invariant under the traveling-wave symmetry (39) of the PDE, should be done. The reduced conservation law is a first integral of the traveling-wave ODE (67)).

In the following we will apply the reduction method [23] so that a first integral will be obtained. Moreover, we will find two functionally independent first integrals and the ODE will be reduced to first order. Finally, in a particular case of the generalized Camassa–Holm Equation (3), the reduction will yield an additional first integral and an exact solution will be found.

• By using the Case 1 conservation law we get the first integral.

  $$e^z(Ud{U\prime }^2+(-2b{U}^2+p)U\prime +U\prime \prime a{U}^2-U\prime \prime p)=C_1$$

  (68)
• By using the Case 2 conservation law we get the first integral.

  $$(ac{U}^2-p)U\prime \prime +cdU{U\prime }^2+(a-2bc)U^{2}U\prime -\frac{2b}{3}{U}^3+pU=C_1$$

  (69)
• By using the two conservation laws of Case 3 we get the two first integrals.

  $$-4bcU{U\prime }^2-2b(c+1)U^{2}U\prime -\frac{2}{3}b{U}^3-2bc{U}^{2}U\prime \prime +pU-pU\prime \prime =C_1$$

  (70)

  $$e^z(-4bcU{U\prime }^2-2b{U}^2+pU\prime -2bc{U}^{2}U\prime \prime -pU\prime \prime )=C_2$$

  (71)
  By combining these two first integrals we get the reduced first order ODE

  $$U\prime +\frac{2b{e}^z{U}^3-3p{e}^{z}U+3e^z{C}_1-3C_2}{3e^z(2bc{U}^2+p)}$$

  (72)
• By using the two conservation laws of Case 4 we get the two first integrals.

  $$-2b{U}^{2}U\prime \prime +pU-pU\prime \prime -4bU{U\prime }^2+4b{U}^{2}U\prime -\frac{2}{3}b{U}^3=C_1$$

  (73)

  $$e^z(-4bU{U\prime }^2+(6b{U}^2+p)U^{\prime }-\frac{8}{3}b{U}^3-2b{U}^{2}U\prime \prime -pU\prime \prime )=C_2$$

  (74)
  By combining these two first integrals we get the reduced first order ODE

  $$U^{\prime }+\frac{2b{e}^z{U}^3+p{e}^{z}U-e^z{C}_1+C_2}{e^z(2b{U}^2+p)}$$

  (75)
• By using the two conservation laws of Case 5 we get the two first integrals.

  $$-dU{U\prime }^2+(2b+\frac{d}{2})U^2{U}^{\prime }-\frac{2b}{3}{U}^3-\frac{d}{2}{U}^{2}U\prime \prime +pU-pU\prime \prime =C_1$$

  (76)

  $$e^{-z}(-dU{U\prime }^2+(2b{U}^2-p)U^{\prime }-\frac{d}{2}{U}^{2}U\prime \prime -pU\prime \prime =C_2$$

  (77)
  By combining these two first integrals we get the reduced first order ODE

  $$U^{\prime }-\frac{2(2b{e}^{-z}{U}^3-3p{e}^{-z}U+3C_1{e}^{-z}-3C_2)}{3e^{-z}(d{U}^2+2p)}$$

  (78)
• By using the two conservation laws of Case 6, we get the two first integrals.

  $$dU{U\prime }^2+(-2b+\frac{d}{2})U^2{U}^{\prime }-\frac{2b}{3}{U}^3+\frac{d}{2}{U}^{2}U\prime \prime +pU-pU\prime \prime =C_1$$

  (79)

  $$e^{-z}(-dU{U\prime }^2+(2b{U}^2-p)U^{\prime }-\frac{d}{2}{U}^{2}U\prime \prime -pU\prime \prime =C_2$$

  (80)
  By combining these two first integrals we get the reduced first order ODE

  $$\begin{array}{c}\frac{24dpU{U\prime }^2+(3d^2{U}^4-48pb{U}^2+12p^2)U^{\prime }-4bd{U}^5-8p(b-\frac{3d}{4})U^3}{3d^2{U}^4-12p^2}\hfill \\ +\frac{-6d(C_2{e}^z+C_1)U^2+12p^{2}U-12p(-C_2{e}^z+C_1)}{3d^2{U}^4-12p^2}=0\hfill \end{array}$$

  (81)
• By using the three conservation laws of Case 7 we get the three first integrals.

  $$4bU{U\prime }^2-\frac{2b}{3}{U}^3+2b{U}^{2}U\prime \prime +pU-pU\prime \prime =C_1$$

  (82)

  $$e^z(4bU{U\prime }^2-2b{U}^2{U}^{\prime }+2b{U}^{2}U\prime \prime +p{U}^{\prime }-pU\prime \prime =C_2$$

  (83)

  $$2e^{-z}((b{U}^2-\frac{p}{2}U\prime \prime +U^{\prime }(b{U}^2+2U{U}^{\prime })b-\frac{p}{2})=C_3$$

  (84)
  By combining these three first integrals we get the solution

  $$2b{e}^z{U}^3-3p{e}^{z}U+3C_1{e}^z-3C_2=0$$

  (85)
• By using the Case 8 conservation laws we get the first integral.

  $$2cU(ac{U}^2-p)+(a{c}^2{U}^2+cp){U\prime }^2+2ac{U}^3{U}^{\prime }+a{U}^4-pc{U}^2+2c{C}_1)$$

  (86)
• By using the Case 9 conservation laws we get the first integrals.

  $$(\frac{a}{2}{U}^2+\frac{p}{2}){U\prime }^2+(a-2d)U^3{U}^{\prime }-\frac{d}{2}{U}^4+a{U}^{3}U\prime \prime +\frac{p}{2}{U}^2-pUU\prime \prime =C_1$$

  (87)

  $$e^z(a{U}^2-p)U\prime \prime +aU{U\prime }^2-2dU`2U^{\prime }+p{U}^{\prime })=C_2$$

  (88)
  By combining these two first integrals we get the reduced first order ODE

  $$\begin{array}{c}-a{U}^2{U\prime }^2+2a{U}^3{U}^{\prime }-d{U}^4+p{U\prime }^2-2pU{U}^{\prime }+p{U}^2-2C_1+2C_2{e}^{-z}U=0\hfill \end{array}$$

  (89)

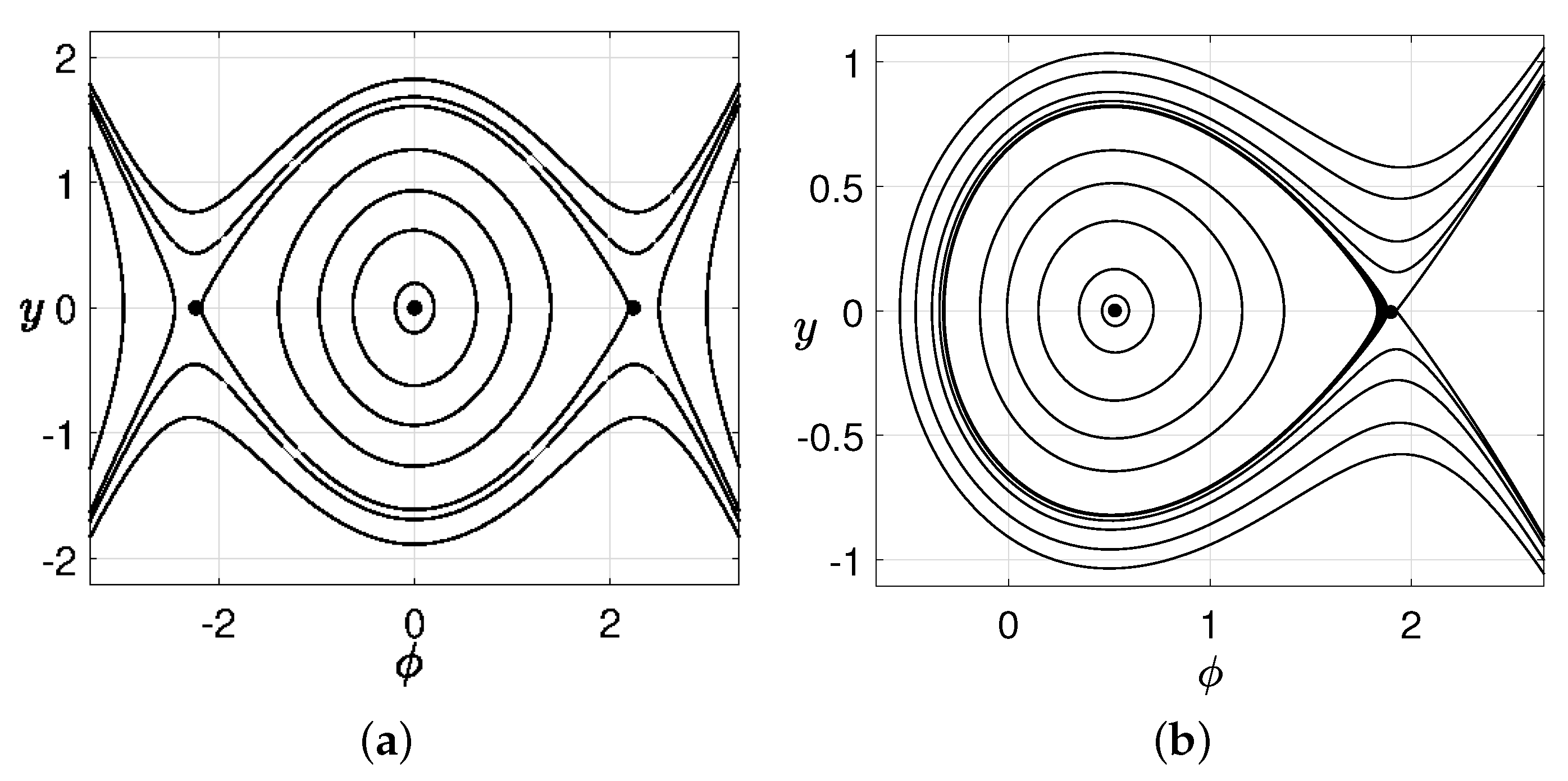
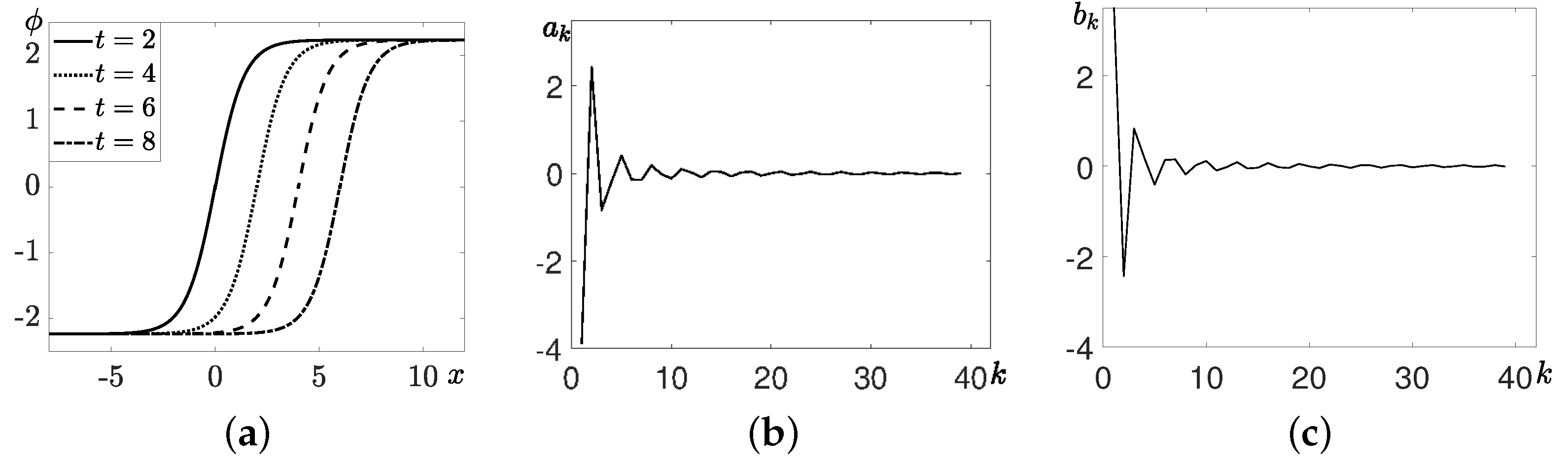
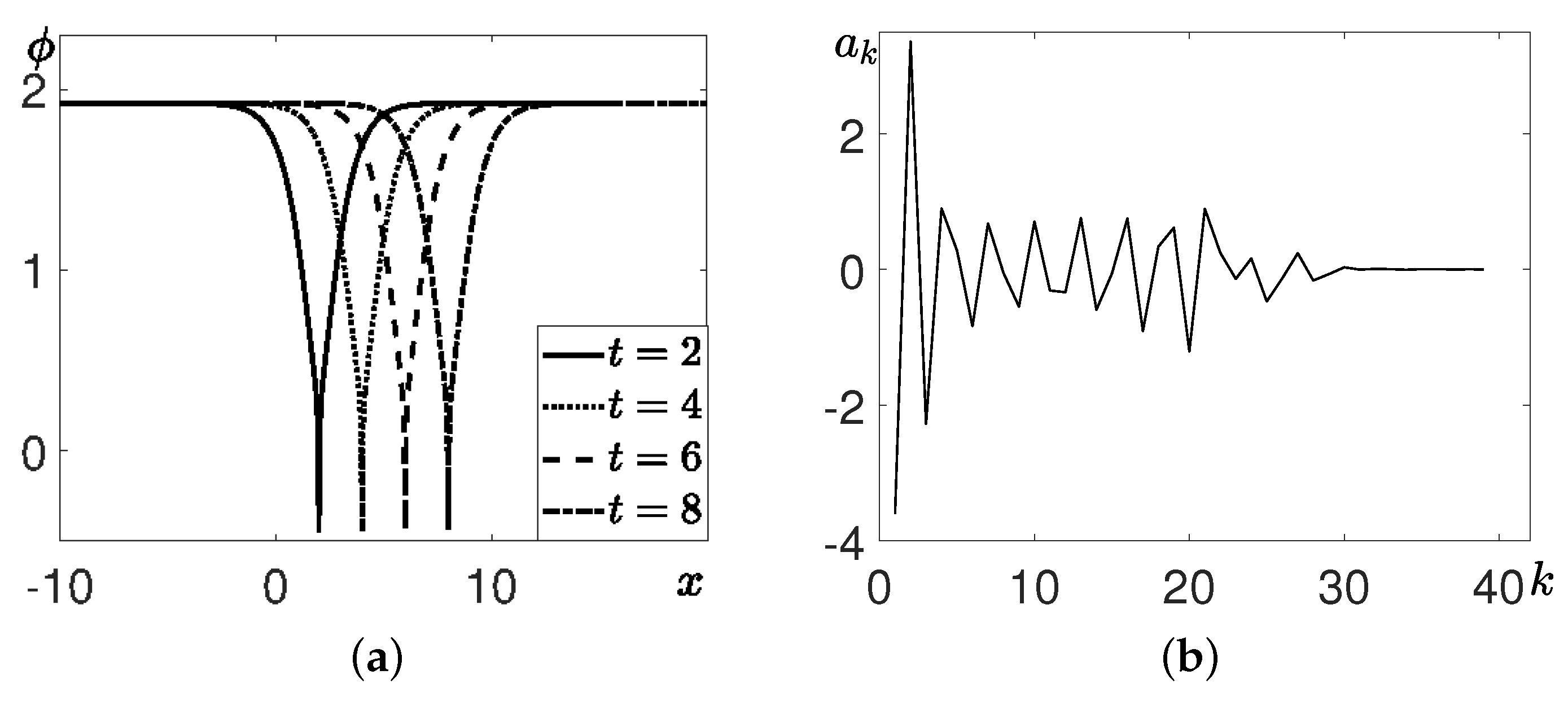
5. Analytic Solutions for Heteroclinic and Homoclinic Orbits of the Traveling-Wave Equation

To obtain regular pulse and front solutions of the GCH Equation (2), in this section we will employ the so-called method of undetermined coefficients [9,24,25] to compute multi-infinite series solutions for the possible homoclinic and heteroclinic orbits of its corresponding traveling-wave equation.

Let $\varphi (x,t)=\varphi \left(z\right)$, where $z=x-vt$ and $v>0$ is the wave speed. Once substituted $\varphi \left(z\right)$ into Equation (3), we obtain:

$$\begin{array}{rr}-v{\varphi }^{{}^{\prime }}-v\varphi \prime \prime \prime -ac{\varphi }^2\varphi \prime \prime \prime & -2c(a+d)\varphi {\varphi }^{{}^{\prime }}\varphi \prime \prime -(a-2bc){\varphi }^2\varphi \prime \prime \hfill \\ & -dc\varphi \prime \prime \prime -(d-4bc)\varphi {\varphi }^{{}^{\prime }2}+2b{\varphi }^2{\varphi }^{{}^{\prime }}=0.\hfill \end{array}$$

(90)

Choosing $d=2a$ and integrating Equation (90) once with respect to z, we get the following second-order ODE:

$$-\varphi \prime \prime (v+ac{\varphi }^2)-2ac\varphi {\varphi }^{{}^{\prime }2}-(a-2bc){\varphi }^2{\varphi }^{{}^{\prime }}-v\varphi +\frac{2}{3}b{\varphi }^3+g=0,$$

(91)

where g is the constant of integration. The ODE (91) can be equivalently written as the following first order ODE system:

$$\left\{\begin{array}{c}\frac{d\varphi }{dz}=y,\hfill \\ \frac{dy}{dz}=\frac{-2ac\varphi y^2 + (2bc - a){\varphi }^{2}y - v\varphi + \frac{2}{3}b{\varphi }^3 + g}{v + ac{\varphi }^2}.\hfill \end{array}\right.$$

(92)

Let us assume that v and $ac$ have the same sign, so that the system (92) is not singular. The ODE system (92) admits the equilibria of the form $({\varphi }^{*},0)$, where ${\varphi }^{*}$ are the roots of the following cubic equation:

$$\frac{2}{3}b{\varphi }^3-v\varphi +g=0.$$

(93)

Depending on the choice of the parameters $b,v$ and g, Equation (93) can admit one or three real solutions, whose expressions are mostly cumbersome and are not reported here. In particular, when $g=0$ the following two cases can arise:

(i)

if v and b have opposite sign, the system (92) admits only the trivial equilibrium $O\equiv (0,0)$;

(ii)

if v and b have the same sign, the system (92) admits the trivial equilibrium O and the equilibria $E_{\pm }\equiv ({\varphi }_{\pm }^{*},0)$, with:

$${\varphi }_{\pm }^{*}=\pm \sqrt{\frac{3v}{2b}}.$$

(94)

The Jacobian matrix associated with the system (92) computed at the generic equilibrium $({\varphi }^{*},0)$ reads:

$$J^{*}=\left(\begin{array}{cc}0& 1\\ \frac{2b{\varphi }^{*2}-v}{v+ac{\varphi }^{*2}}& \frac{(2bc-a){\varphi }^{*2}}{v+ac{\varphi }^{*2}}\end{array}\right),$$

(95)

and the correspondent characteristic equation is:

$${\lambda }^2+\frac{(a-2bc){\varphi }^{*2}}{v+ac{\varphi }^{*2}}\lambda +\frac{v-2b{\varphi }^{*2}}{v+ac{\varphi }^{*2}}=0.$$

(96)

We look for system parameters conditions corresponding to the existence of saddle equilibria, in such a way that homoclinic orbits to these points or heteroclinic connections between them are supported. In the case $g=0$ it can be straightforwardly checked that O is a center point and that both the equilibria $E_{\pm }$, when they exist (i.e., in the case ii)) are saddle points. The system could then support both homoclinic and heteroclinic orbit.

In Figure 1a the system parameters are chosen such that the heteroclinic orbit joining the equilibria $E_{\pm }$ forms.

Since the expressions of the solutions of the polynomial Equation (93) are complicated in terms of the parameters $a,b,c,g$ and v, the complete linear instability analysis in the general case $g\ne 0$ is almost involved. Here we report that in the particular case $a=2bc$, the generic equilibrium $({\varphi }^{*},0)$ can be a center (when $(v-2b{\varphi }^{*2})/(v+ac{\varphi }^{*2})>0$) or a saddle (when $(v-2b{\varphi }^{*2})/(v+ac{\varphi }^{*2})<0$) and homoclinic/heteroclinic orbits could exist. Notice that if $a=2bc$ Equation (91) is reversible under the standard reversibility of classical mechanical systems:

$$z\to -z,(\varphi ,{\varphi }^{\prime },\varphi \prime \prime )\to (\varphi ,-{\varphi }^{\prime },\varphi \prime \prime ).$$

(97)

Our numerical exploration has shown that homoclinic orbits to one of the equilibria $({\varphi }^{*},0)$ exist when condition (97) holds, see Figure 1b.

First, we consider the case $g=0$ and we assume to choose a parameter set such that there exist the saddle equilibria $E_{\pm }\equiv ({\varphi }_{\pm }^{*},0)$ and a heteroclinic orbit joining them arises, as in Figure 1a. Let us now proceed to construct the heteroclinic orbit looking for a solution of the following form:

$$\varphi \left(z\right)=\left\{\begin{array}{c}{\varphi }^{+}\left(z\right)z>0\hfill \\ 0z=0\hfill \\ {\varphi }^{-}\left(z\right)z<0\hfill \end{array}\right.$$

(98)

where:

$${\varphi }^{+}\left(z\right)={\varphi }_{+}^{*}+\sum _{k=1}^{\infty }{a}_k{e}^{k\alpha z},{\varphi }^{-}\left(z\right)={\varphi }_{-}^{*}+\sum _{k=1}^{\infty }{b}_k{e}^{k\beta z},$$

(99)

and ${\varphi }_{\pm }^{*}$ are given in (94), $\alpha <0$ and $\beta >0$ are undetermined constants and $a_k,b_k$, with $k\ge 1$, are arbitrary coefficients. Once substituted the series (121) for ${\varphi }^{+}\left(z\right)$ into Equation (91), for each term one has the following expressions:

$$\varphi \prime \prime =\sum _{k=1}^{\infty }{a}_k{\left(k\alpha \right)}^2{e}^{k\alpha z},$$

(100)

$$\begin{array}{lll}{\varphi }^2\varphi \prime \prime & =& {\displaystyle \sum _{k=3}^{\infty }}{\displaystyle \sum _{j=2}^{k-1}}{\displaystyle \sum _{l=1}^{j-1}}{a}_l{a}_{j-l}{a}_{k-j}{(k-j)}^2{\alpha }^2{e}^{k\alpha z}+2{\varphi }_{+}^{*}{\displaystyle \sum _{k=2}^{\infty }}{\displaystyle \sum _{j=1}^{k-1}}{a}_{k-j}{a}_j{(k-j)}^2{\alpha }^2{e}^{k\alpha z}\\ & +& {\varphi }_{+}^{*2}{\displaystyle \sum _{k=1}^{\infty }}{a}_k{\left(k\alpha \right)}^2{e}^{k\alpha z},\hfill \end{array}$$

(101)

$$\begin{array}{rrr}\varphi {\varphi }^{{}^{\prime }2}& =& {\displaystyle \sum _{k=3}^{\infty }}{\displaystyle \sum _{j=2}^{k-1}}{\displaystyle \sum _{l=1}^{j-1}}{a}_l{a}_{j-l}{a}_{k-j}(j-l)l{\alpha }^2{e}^{k\alpha z}+{\varphi }_{+}^{*}{\displaystyle \sum _{k=2}^{\infty }}{\displaystyle \sum _{j=1}^{k-1}}{a}_{k-j}{a}_j(k-j)j{\alpha }^2{e}^{k\alpha z},\hfill \end{array}$$

(102)

$$\begin{array}{rrr}{\varphi }^2{\varphi }^{\prime }& =& {\displaystyle \sum _{k=3}^{\infty }}{\displaystyle \sum _{j=2}^{k-1}}{\displaystyle \sum _{l=1}^{j-1}}{a}_l{a}_{j-l}{a}_{k-j}(k-j)\alpha e^{k\alpha z}+2{\varphi }_{+}^{*}{\displaystyle \sum _{k=2}^{\infty }}{\displaystyle \sum _{j=1}^{k-1}}{a}_{k-j}{a}_j(k-j)\alpha e^{k\alpha z}\hfill \\ & +& {\varphi }_{+}^{*}{\displaystyle \sum _{k=1}^{\infty }}{a}_k\left(k\alpha \right)e^{k\alpha z},\hfill \end{array}$$

(103)

$$\begin{array}{rrr}{\varphi }^3& =& {\varphi }_{+}^{*3}+{\displaystyle \sum _{k=3}^{\infty }}{\displaystyle \sum _{j=2}^{k-1}}{\displaystyle \sum _{l=1}^{j-1}}{a}_l{a}_{j-l}{a}_{k-j}{e}^{k\alpha z}+3{\varphi }_{+}^{*}{\displaystyle \sum _{k=2}^{\infty }}{\displaystyle \sum _{j=1}^{k-1}}{a}_{k-j}{a}_j{e}^{k\alpha z}+3{\varphi }_{+}^{*2}{\displaystyle \sum _{k=1}^{\infty }}{a}_k{e}^{k\alpha z}.\hfill \end{array}$$

(104)

Substituting the Expressions (100)–(104) into Equation (91) and taking into account that ${\varphi }_{+}^{*}$ satisfies Equation (93), we collect the coefficients of $e^{k\alpha z}$ for each k, obtaining a sequence of equations for the coefficients $a_k$. The equation at $k=1$ reads:

$$F\left(\alpha \right)a_1=0,$$

(105)

where:

$$F\left(\alpha \right)=-(v+ac{\varphi }_{+}^{*2}){\alpha }^2+(2bc-a){\varphi }_{+}^{*}\alpha +2v.$$

(106)

Imposing $a_1\ne 0$, Equation (105) is satisfied when $F\left(\alpha \right)=0$. It is easy to show that $F\left(\alpha \right)$ admits two real and opposite solutions (corresponding to the fact that $E_{+}$ is a saddle):

$$\alpha ={\alpha }_1<0\mathrm{or}\alpha ={\alpha }_2>0.$$

(107)

Since we look for a series solution ${\varphi }^{+}\left(z\right)$ convergent for $z>0$, we choose $\alpha ={\alpha }_1$ in (123). For $k=2$ we obtain the following equation:

$$F\left(2{\alpha }_1\right)a_2=2{\varphi }_{+}^{*}(b-2ac{\alpha }_1^2-(a-2bc){\alpha }_1)a_1^2,$$

(108)

where $F\left(2{\alpha }_1\right)=(-(v+ac{\varphi }_{+}^{*2}){\left(2{\alpha }_1\right)}^2+(2bc-a){\varphi }_{+}^{*}\left(2{\alpha }_1\right)+2v)$. Thus, $a_2$ can be explicitly obtained in terms of the systems coefficients and $a_1$, which is still unknown at this level:

$$a_2=\frac{2{\varphi }_{+}^{*}(b-2ac{\alpha }_1^2-(a-2bc){\alpha }_1)}{F\left(2{\alpha }_1\right)}{a}_1^2,$$

(109)

The equation for $k=3$ results:

$$F\left(3{\alpha }_1\right)a_3=2{\varphi }_{+}^{*}(9ac-2b+2(a-2bc){\alpha }_1)a_1{a}_2+\left(5ac{\alpha }_1^2-\frac{2}{3}b+(a-2bc){\alpha }_1\right)a_1^3,$$

(110)

where $F\left(3{\alpha }_1\right)=(-(v+ac{\varphi }_{+}^{*2}){\left(3{\alpha }_1\right)}^2+(2bc-a){\varphi }_{+}^{*}\left(3{\alpha }_1\right)+2v)$. Once substituted the expression (109) for $a_2$ in (110), the coefficient $a_3$ is obtained in terms of $a_1$ as follows:

$$a_3={\phi }_3{a}_1^3,$$

(111)

with:

$${\phi }_3=\frac{4{\varphi }^{*2}}{F\left(2{\alpha }_1\right)}(9ac-2b2(a-2bc){\alpha }_1)(b-2ac{\alpha }_1^2)+5ac{\alpha }_1^2-\frac{2}{3}b+(a-2bc){\alpha }_1.$$

(112)

Following the same procedure as above, at each k the coefficient $a_k$ can be computed in terms of $a_1$:

$$a_k={\phi }_k{a}_1^k,$$

(113)

where the functions ${\phi }_k$ depend on ${\alpha }_1$ and the parameters $a,b,c,g$ and v. The series solution ${\varphi }^{+}\left(z\right)$ approximating the heteroclinic orbit (98) for $z>0$ has thus the following expression:

$${\varphi }^{+}\left(z\right)={\varphi }_{+}^{*}+a_1{e}^{{\alpha }_{1}z}+\sum _{k=2}^{\infty }{\phi }_k{a}_1^k{e}^{k{\alpha }_{1}z}.$$

(114)

The computation is almost the same to compute the series ${\varphi }^{-}\left(z\right)$, which results:

$${\varphi }^{-}\left(z\right)={\varphi }_{-}^{*}+b_1{e}^{{\alpha }_{2}z}+\sum _{k=2}^{\infty }{\psi }_k{b}_1^k{e}^{k{\alpha }_{2}z},$$

(115)

where the functions ${\psi }_k$ depend on ${\alpha }_2$ and the parameters $a,b,c,g$ and v.

By imposing the continuity condition at $z=0$ leads to solve the following conditions for the unknown $a_1$ and $b_1$:

$$\begin{array}{rrr}{\varphi }_{+}^{*}+a_1+{\displaystyle \sum _{k=2}^{\infty }}{\phi }_k{a}_1^k& =& 0\hfill \end{array}$$

(116)

$$\begin{array}{rrr}{\varphi }_{-}^{*}+b_1+{\displaystyle \sum _{k=2}^{\infty }}{\psi }_k{b}_1^k& =& 0\hfill \end{array}$$

(117)

To better approximate the coefficient $a_1$ we solve the following polynomial equation for $a_1$:

$${\varphi }_{+}^{*}+a_1+{\displaystyle \sum _{k=2}^M}{\phi }_k{a}_1^k=0,$$

(118)

where M is suitably chosen. The Equation $\left(118\right)$ could admit more than one solution, therefore the solution in (98) could not be unique. We therefore choose the solution $a_1$ of (118) such that the series coefficients $a_k$ converge as k increases. We follow the same line to obtain $b_1$.

Let us consider the parameter set in Figure 1a. In this case, the equation is reversible and the solution ${\varphi }^{-}\left(z\right)$ results:

$${\varphi }^{-}\left(z\right)=-{\varphi }_{+}^{*}-a_1{e}^{{\alpha }_{2}z}-\sum _{k=2}^{\infty }{\phi }_k{a}_1^k{e}^{k{\alpha }_{2}z},$$

(119)

therefore, we must solve just the continuity condition (118) for $a_1$. In Figure 2 it is shown the traveling front obtained as the series solution (98) which approximates the heteroclinic orbit given in Figure 1a. For this parameter set there exists a unique solution $a_1=-3.9083$ of Equation (118) such that the series coefficients $a_k$ converge.

To approximate a homoclinic orbit, as obtained in Figure 1b for $g\ne 0$, we look for a series solution defined as follows:

$$\varphi \left(z\right)=\left\{\begin{array}{c}{\varphi }^{+}\left(z\right)z>0\hfill \\ 0z=0\hfill \\ {\varphi }^{-}\left(z\right)z<0\hfill \end{array}\right.$$

(120)

where:

$${\varphi }^{+}\left(z\right)={\varphi }^{*}+\sum _{k=1}^{\infty }{a}_k{e}^{k\alpha z},{\varphi }^{-}\left(z\right)={\varphi }^{*}+\sum _{k=1}^{\infty }{b}_k{e}^{k\beta z},$$

(121)

and ${\varphi }^{*}$ is solution of (93), $\alpha <0$ and $\beta >0$ are undetermined constants and $a_k,b_k$, with $k\ge 1$, are arbitrary coefficients. Repeating the same calculations as above to compute at first ${\varphi }^{+}\left(z\right)$, we obtain for $k=1$ the following equation:

$$F\left(\alpha \right)a_1=(-(v+ac{\varphi }^{*2}){\alpha }^2+(2bc-a){\varphi }^{*}\alpha +2b{\varphi }^{*2}-v)a_1=0.$$

(122)

By imposing $a_1\ne 0$ and if the parameter set is chosen such that ${\varphi }^{*}$ is a saddle (e.g., in the case $a=2bc$ it should be $v<2b{\varphi }^{*2}$) we obtain that Equation (122) is satisfied when:

$$\alpha ={\alpha }_1<0\mathrm{or}\alpha ={\alpha }_2>0,$$

(123)

where ${\alpha }_1$ and ${\alpha }_2$ are the real and opposite roots of $F\left(\alpha \right)$. Choosing $\alpha ={\alpha }_1$ and iterating the procedure at each k, the series coefficients $a_k$ have the same expression as in (113). Therefore:

$${\varphi }^{+}\left(z\right)={\varphi }^{*}+a_1{e}^{{\alpha }_{1}z}+\sum _{k=2}^{\infty }{\phi }_k{a}_1^k{e}^{k{\alpha }_{1}z}.$$

(124)

By imposing the continuity of the solution (120) at $z=0$, we obtain the same equation as in (116), which should be truncated as in (118) to find $a_1$ such that the series solution converges. Analogously, the series ${\varphi }^{-}\left(z\right)$ will have the expression as in (115) and suitably truncating the continuity Equation (117), the coefficient $b_1$ will be obtained.

Choosing the system parameters as in Figure 1b, the equation is reversible and the series ${\varphi }^{-}\left(z\right)$ results:

$${\varphi }^{-}\left(z\right)={\varphi }^{*}+a_1{e}^{{\alpha }_{2}z}+\sum _{k=2}^{\infty }{\phi }_k{a}_1^k{e}^{k{\alpha }_{2}z},$$

(125)

with ${\alpha }_2>0$ given in (123). Therefore, just the continuity condition (116) should be imposed and $a_1$ will be chosen as the solution of (118) for a suitable M such that the series solution converges.

In Figure 3 it is shown the traveling pulse obtained as the series solution (120) which approximates the homoclinic orbit given in Figure 1b. For this parameter set there exists a unique solution $a_1=-3.4558$ of Equation (118) such that the series coefficients $a_k$ converge.

6. Conclusions

In this paper, we have studied a GCH equation with variable coefficients. We have obtained the Lie-group classification for Equation (3). We have derived the optimal system of 1-dimensional subalgebras of the invariant equation and we have obtained reductions to ODE’s. By applying the nonclassical method, we have derived new reductions for Equation (3).

By using a general method to derive conservation laws we have derived low-order conservation laws for Equation (3). Moreover, we have focused on the conservation law invariant under translations, and we have derived first integrals of the reduced ODEs as well as exact solutions.

Finally, we have studied the traveling-wave equation by addressing their homoclinic and heteroclinic orbits. Once performed the linear instability analysis, we have pinpointed these orbits and they have been approximated via analytic solutions computed as convergent and continuous multi-infinite series.

Since the GCH equations support a very rich dynamics, we plan to investigate it further. In particular, the existence of regular and embedded solitary wave solution will be addresses using variational methods, as in [24,31]. Moreover, analytic solutions using the invariant Painlevé analysis and the generalized Hirota techniques could be investigated [32].