Alternative Financial Methods for Improving the Investment in Renewable Energy Companies

Abstract

Renewable energies have increased in importance in recent years due to the harm caused to the environment by fossil fuels. As a result, renewable energy companies seem to be profitable investment opportunities given their likely substantial future earnings. However, previous empirical evidence has not always agreed about this likely profitability. In addition, the methodologies employed in the existing empirical literature are complicated and not feasible for most investors to use. Therefore, it is proposed an approach which combines the use of performance measures, screening rules, devolatized returns and portfolio strategies, all of which can be implemented by investors. This approach results in high cumulative returns of more than 200% and other positive ratios, even when transaction costs are considered. This should encourage people to invest in these renewable energies and contribute to improving the environment.

1. Introduction

In the transition to sustainable finance, it is crucial to properly combine sustainable development goals with profitable investments in order to show investors the benefit of investing in these new markets and, therefore, the importance of supporting their development. Renewable energy companies are therefore a key instrument for achieving the sustainable development goals because they increase access to clean energy, reduce our reliance on fossil fuels and respect land tenure, among other benefits.

Renewable energies and, therefore, renewable energy companies, have undeniable potential and advantages. This is partly because they do not produce greenhouse-gas emissions, and therefore help improve the environment, but also because they help solve energy problems because they can be located anywhere, as highlighted by Halkos and Gkampoura [1]. However, the main disadvantages are their high initial and operating costs, the existence of policy or technology risks, the cost of storage systems and weather conditions, see [2,3] among others. Nonetheless, renewable energies are considered the best option for supplying future energy demands.

In this context, Reboredo et al. [4] argued that the universe of renewable energy company stocks is limited and that renewable energy projects may be less attractive because they offer low returns. They analyzed the performance of various alternative energy funds using linear regression models and concluded that they underperform compared to the benchmark. This outcome was corroborated, using different methodologies, by [5,6,7] and [8].

However, there are recent studies which conclude that renewable energy is a good alternative for investors. Ahmad [9] suggested that clean energy can provide a profitable hedging opportunity in combination with crude oil futures. Bai et al. [10] proposed a robust portfolio method capable of obtaining a better performance from a renewable energy stock portfolio than from a classic Markowitz approach in various market conditions. Miralles-Quirós and Miralles-Quirós [11], who employed a VAR-ADCC approach jointly with different portfolio optimization problems, provided clear evidence that Alternative Energy ETFs outperform Energy ETFs.

More recently, Marti-Ballester [12] has compared renewable-energy, black-energy and conventional investors decisions adopting a panel-data approach with Petersen’s standard errors clustered by fund and year founding that renewable-energy investors are less sensitive to past financial performance. Kazak et al. [13] have evaluated the relation between investment funds allocated for Renewable Energy Sources development and renewable energy production potential by applying the agglomeration method and k-mean method to define clusters. They found that renewable energy production should be considered for energy policy implementation. Nasreen et al. [14] have made a portfolio strategy of clean energy and technology companies after examining the dynamic connectedness between oil prices and stock returns from those companies. They have shown that there is an important connection between portfolio weights and oil prices. Finally, Dragomirescu-Gaina et al. [15] have focused on investors’ group behavior with respect to U.S. energy equities finding that it is necessary to reduce uncertainty stemming from its raising impact on investors’ portfolios.

These previous studies often employed complicated methodologies that are not feasible for a normal investor to replicate given that they normally face serious restrictions in terms of analysis and technical approaches. As a result, an appropriate way to invest in these markets is to employ a combination of performance measures, the so-called screening rule methodology (whose purpose is to rank a set of assets to select the best ones and exclude the worst ones) and portfolio strategies with simple long positions that also allow for the possibility of taking short positions.

Billio et al. [16] proposed the use of optimal combinations of performance measures where the combination of weights was derived from an optimization problem. They also showed that their proposed composite performance index provided superior results in terms of realized returns than a naïve (equally weighted) portfolio. Carneiro and Leal [17] formed equally weighted portfolios according to the lowest or highest values of different ratios, related to the Fama and French [18] factors, for a previous period and found that these portfolios frequently outperformed the benchmark. Finally, León et al. [19] analyzed whether different portfolio measures generate different subsequent returns by using a fixed one-year rolling window of past returns to estimate the measures and then selecting the assets to create an equally weighted portfolio. Their results show that the screening rule influences portfolio returns.

The spirit of [16,17,19] is followed and a contribution to this strand of the empirical literature is done by proposing a new approach to estimating performance measures and, therefore, improving an investor’s ability to determine the best assets for a portfolio. Additionally, the profitability of investing in renewable energy companies, which are the main focus of this study, is shown and which, to the best of our knowledge, have not been analyzed previously using this approach.

For this reason, a methodology is proposed in which the investor evaluates the performance measures of a group of assets until time t and uses the outcome to select the best ones to hold in time t + 1. This approach led us to construct 12 portfolios using different strategies (taking long positions, short positions and also investing in risk-free assets) and rebalancing periods (from monthly to annually) for each performance measure applied.

Additionally, the fact that asset returns, which are assumed to follow a normal distribution is considered. However, they are usually far from being normally distributed. Pesaran and Pesaran [20,21], Molnár [22] and Miralles-Quirós et al. [23] proposed the use of standardized or devolatized returns through range-based volatility estimators instead of classical returns because they show that these devolatized returns are approximately normally distributed.

Therefore, the use of these devolatized returns to estimate performance measures, to avoid these measures being misleading when the shape of the return distribution deviates from normality, is suggested and then applying the screening rules to select the assets and build the portfolio strategies.

Reality Check and Superior Predictive Ability tests are performed to check for data snooping bias while evaluating the performance of the portfolios, the aim being to test whether the proposed portfolio strategies perform better just after scanning and re-scanning to search for the objectives.

The existence of important improvements in investor profitability is reported, compared to those that could be obtained using a naïve rule, when returns standardized by range-based volatility estimators are used instead of classic returns (natural logarithm returns). Additionally, clear evidence that taking long and short positions on renewable energy companies is the best strategy for investors, even when transaction costs are considered, is provided and also that quarterly rebalancing periods are the best option for investors due to their lower turnover. Finally, the null hypothesis that the best performance of the proposed strategies compared to the rest is just based on luck is rejected. In short, we show that investing in renewable energy companies is certainly profitable for investors if they follow the approach proposed in this study.

The rest of the paper is organized as follows. Section 2, describes the theoretical background for this paper, explaining the performance measures used for selecting the assets and the portfolio strategies estimated using these selected assets. The volatility proxies used for standardizing the returns and the data snooping methodology employed for testing the validity of the results are also discussed. Section 3, analyzes the distribution of the initial returns and show the empirical results from the proposed strategies. This is followed by Section 4 which provides evidence of the robustness of the result, and finally Section 5 sets out the main conclusions.

2. Materials and Methods

This section is divided into four main sub-sections. Firstly, the different performance measures used to employ the screening rules are described. Secondly, the strategies followed to construct the portfolios and the criteria employed to evaluate the performance of the alternative framework proposed are explained. Thirdly, the volatility proxies for standardizing the returns are defined. Finally, the approaches employed to assess the effectiveness of the portfolios in the presence of data snooping bias are presented.

2.1. Performance Measures

Performance measures are ratios often used by financial analysts and investors to select a set of assets from among a group of assets or to evaluate the capability of an asset or portfolio to be profitable.

The most widely used ratio is the Sharpe ratio, which was proposed by Sharpe [24]. This ratio measures the relationship between the excess return and the standard deviation of the asset. The higher the Sharpe ratio, the better the return from the fund relative to the amount of risk taken (this statement of higher is better is valid for the rest of the performance measures that are employed in this paper). Therefore, this Sharpe ratio is calculated as follows:

$$\mathrm{S}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{{\mathsf{\sigma }}_{\mathrm{i}}}$$

(1)

where E(R_i) denotes the expected return on asset i (which is calculated as the mean return of a 252-days rolling window), R_f is the risk-free rate and σ_i is the standard deviation of the asset returns (as well as the expected return is calculated using a 252-days rolling window).

This ratio is an optimal performance measure under a normal distribution assumption. However, stock market assets, such as shares and funds, frequently generate returns that have non-normal distributions. Additionally, other ratios exist which differ from the Sharpe one in terms of the measure used to quantify risk, as was highlighted by Bacon [25] and Auer and Schuhmacher [26]. Given this, different performance measures have been considered in this study.

The first alternative is the Treynor ratio, proposed by Treynor [27], which is very similar to the Sharpe ratio. This measure is calculated as the excess return of the asset divided by its systematic risk, β_i. This beta factor is the coefficient that represents the asset return’s sensitivity to changes in the market return.

$$\mathrm{T}\mathrm{r}\mathrm{e}\mathrm{y}\mathrm{n}\mathrm{o}\mathrm{r}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{{\mathsf{\beta }}_{\mathrm{i}}}$$

(2)

In order to calculate the systematic risk, β_i, the excess return on the market downloaded from the Kenneth R. French website (http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/index.html, accessed on 10 April 2021) has been employed.

In addition to the use of standard deviation or systematic risk, there are a group of ratios that use lower partial moments, LPMs, to measure risk. This measure, which was first proposed by Bawa and Lindenberg [28], consider only negative deviations of returns from a minimal acceptable return or threshold. This is different to standard deviation which considers both positive and negative deviations from the expected return.

$$\mathrm{L}\mathrm{P}{\mathrm{M}}_{\mathrm{n}\mathrm{i}}\left(\mathsf{\tau }\right)=\frac{1}{\mathrm{T}}{{\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{T}}\max \left[\mathsf{\tau }-{\mathrm{r}}_{\mathrm{i}\mathrm{t}},0\right]}}^{\mathrm{n}}$$

(3)

where τ is the minimum acceptable return (zero in this case), n is the order of the lower partial moment which can be interpreted, in accordance with Eling and Schuhmacher [29], as the investor’s risk attitude and T is the number of returns below the minimum acceptable return. Therefore, a lower partial moment order of 0 < n < 1 is appropriate for risk-seeking investors; a lower partial moment order of 1 is the expected shortfall (for risk-neutral investors) and a lower partial moment order of 2, where τ is equal to the expected return of the asset, is the semi-variance (appropriate for risk-averse investors).

Shadwick and Keating [30] proposed the Omega ratio which is defined as:

$$\mathrm{O}\mathrm{m}\mathrm{e}\mathrm{g}\mathrm{a}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{\mathrm{L}\mathrm{P}{\mathrm{M}}_{1\mathrm{i}}\left(\mathsf{\tau }\right)}+1$$

(4)

Sortino and van der Meer [31] suggested the Sortino ratio:

$$\mathrm{S}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{o}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{\sqrt{\mathrm{L}\mathrm{P}{\mathrm{M}}_{2\mathrm{i}}\left(\mathsf{\tau }\right)}}$$

(5)

Kaplan and Knowles [32] introduced the Kappa ratio which in its general form is calculated as:

$$\mathrm{K}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{a}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{\sqrt[3]{\mathrm{L}\mathrm{P}{\mathrm{M}}_{3\mathrm{i}}\left(\mathsf{\tau }\right)}}$$

(6)

Sortino, van der Meer and Platinga [33] proposed the Upside potential ratio where instead of using the excess return in the numerator they suggest using the Higher partial moment (HPM) which measures the positive excess above the threshold.

$$\mathrm{H}\mathrm{P}{\mathrm{M}}_{\mathrm{n}\mathrm{i}}\left(\mathsf{\tau }\right)=\frac{1}{\mathrm{T}}{{\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{T}}\max \left[{\mathrm{r}}_{\mathrm{i}\mathrm{t}}-\mathsf{\tau },0\right]}}^{\mathrm{n}}$$

(7)

$$\mathrm{U}\mathrm{p}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}=\frac{\mathrm{H}\mathrm{P}{\mathrm{M}}_{1\mathrm{i}}\left(\mathsf{\tau }\right)}{\sqrt{\mathrm{L}\mathrm{P}{\mathrm{M}}_{2\mathrm{i}}\left(\mathsf{\tau }\right)}}$$

(8)

Another option for measuring risk is a drawdown-based estimator such as the Calmar ratio proposed by Young [34]:

$$\mathrm{C}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{a}\mathrm{r}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{-\mathrm{M}{\mathrm{D}}_{\mathrm{i}}}$$

(9)

where MD is the maximum drawdown, which is the greatest loss on an asset that an investor can incur over a certain investment period.

Finally, there are other alternatives for the numerator, such as Value at Risk (VaR_i), Conditional Value at Risk (CVaR_i) and Modified Value at Risk (MVaR_i), which are risk measures based on quantiles. Value at Risk (VaR_i) describes the possible loss of an investment over a given period for a given confidence interval, while Conditional Value at Risk (CVaR_i) determines the average worst-case scenario among all scenarios at or below a predetermined threshold. Finally, Modified Value at Risk (MVaR_i), which was proposed by Favre and Galeano [35], takes the high moments of the return distribution into account by using the Cornish and Fisher [36] expansion to calculate the adjusted Z value (Z_CF) as follows:

$${\mathrm{Z}}_{\mathrm{C}\mathrm{F}}={\mathrm{Z}}_{\mathrm{C}}+\frac{1}{6}\left({\mathrm{Z}}_{\mathrm{C}}^2-1\right)\mathrm{S}+\frac{1}{24}\left({\mathrm{Z}}_{\mathrm{C}}^3-3{\mathrm{Z}}_{\mathrm{C}}\right)\mathrm{K}-\frac{1}{36}\left(2{\mathrm{Z}}_{\mathrm{C}}^3-5{\mathrm{Z}}_{\mathrm{C}}\right){\mathrm{S}}^2$$

(10)

where Z_C is the critical value of the probability based on a standard normal distribution and S and K denote Fisher’s skewness and excess kurtosis of the return distribution respectively. Therefore, MVaR_i is defined as:

$$\mathrm{M}\mathrm{V}\mathrm{a}{\mathrm{R}}_{\mathrm{i}}=-\left(\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)+{\mathrm{Z}}_{\mathrm{C}\mathrm{F}}{\mathsf{\sigma }}_{\mathrm{i}}\right)$$

(11)

Based on these risk measures, the Excess return on Value at risk ratio (see [35,37,38]), the Conditional VaR Sharpe ratio (see [39,40]), and the Modified Sharpe ratio (see [41]) are calculated as:

$$\mathrm{Excess} \mathrm{return} \mathrm{on} \mathrm{VaR}\left(\mathrm{E}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{var}\right)=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{\mathrm{V}\mathrm{a}{\mathrm{R}}_{\mathrm{i}}}$$

(12)

$$\mathrm{Conditional} \mathrm{VAR} \left(\mathrm{CVaR}\right) \mathrm{Sharpe}=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{\mathrm{C}\mathrm{V}\mathrm{a}{\mathrm{R}}_{\mathrm{i}}}$$

(13)

$$\mathrm{Modified} \mathrm{Sharpe}\left(\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{p}\mathrm{e}\right)=\frac{\mathrm{E}\left({\mathrm{R}}_{\mathrm{i}}\right)-{\mathrm{R}}_{\mathrm{f}}}{\mathrm{M}\mathrm{V}\mathrm{a}{\mathrm{R}}_{\mathrm{i}}}$$

(14)

2.2. Portfolio Strategies

Once the performance measures have been calculated, for which a rolling window of 252 days (approximately one stock market year) is employed, twelve portfolios of 5, 6 or 10 assets are estimated for each measure following three strategies. Firstly, a Long-only strategy where an equally weighted portfolio is built by taking a long position in period t + 1 on the best five assets (those with the higher ratios for each performance measure) as defined in the rolling window ending in period t is used. This portfolio, as well as those following the other two strategies, is initially rebalanced monthly, but also quarterly, biannually and annually.

Secondly, a Long-only with risk free asset strategy, estimating a six-asset portfolio where 50% is invested by taking a long position in period t + 1 in the best five assets following each performance measure and the other 50% is invested in a risk free asset (one-month Treasury bill rate) is suggested. Finally, an equally weighted portfolio of ten assets is formed following a so-called Long-Short strategy where a long position in period t + 1 is taken on the best five assets and a short position on the worst five ones. Therefore, 12 portfolios are estimated for each performance measure (4 for each strategy) which gives us a total of 120 estimated portfolios.

In all cases, we opt for small portfolio sizes because we agree with Carneiro and Leal [17] who use small portfolios due to their focus on individual investors. It is not appropriate for these investors to hold a well-diversified portfolio with a large number of assets, mainly because calculating this is not feasible for them. Additionally, it is important to point out that small portfolio sizes reduce transaction costs and the burden of monitoring many stock prices.

All these portfolios are evaluated over an out-of-sample period, calculating the Cumulative return and the Sharpe, Sortino and Omega ratios. It should be noted that the cumulative returns obtained from natural logarithm returns are transformed into simple returns by using the relationship ${\mathrm{R}}_{\mathrm{p}\mathrm{t}}={\mathrm{e}}^{{\mathrm{r}}_{\mathrm{p}\mathrm{t}}}-1$ where R_pt is the simple return of the portfolio strategy and r_pt is the portfolio strategy return using natural logarithms.

2.3. Volatility Proxies and Standardized Returns

There is a significant weakness in the previous approach, namely the assumption that asset returns are normally distributed. It is widely known that asset returns are not normally distributed and usually show patterns of leptokurtosis and skewness. This could lead to risk being underestimated because loss distributions tend to exhibit heavy tails or empirical discreteness.

For that reason, we follow [42,43,44,45], and more recently [22,23], who show that standardized returns (returns divided by their standard deviations) are approximately normally distributed. More precisely, the approach suggested by Molnár [22] and Miralles Quirós et al. [23] who choose to divide the returns by the daily standard deviations of range-based volatility estimators, namely those proposed by Parkinson [46], Garman and Klass [47] and Meilijson [48] is followed.

Before explaining how the different range-based volatility estimators are calculated, we need to show how the open-to-close (c), open-to-high (h) and open-to-low (lw) returns are estimated:

$$\begin{array}{l}\mathrm{c}=\ln \left(\mathrm{C}\right)-\ln \left(\mathrm{O}\right)\\ \mathrm{h}=\ln \left(\mathrm{H}\right)-\ln \left(\mathrm{O}\right)\\ \mathrm{l}\mathrm{w}=\ln \left(\mathrm{L}\right)-\ln \left(\mathrm{O}\right)\end{array}$$

(15)

where O, H, L and C are the daily opening, high, low, and closing prices of each asset.

Parkinson [46] proposed using the daily range of high and low prices, meaning that the volatility proxy is calculated as:

$$\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{n} (\mathrm{P})={\hat{\mathsf{\sigma }}}_{\mathrm{P}}^2=\frac{{\left(\mathrm{h}-\mathrm{l}\mathrm{w}\right)}^2}{4\ln 2}$$

(16)

Garman and Klass [47] added closing prices to the equation proposed by Parkinson [46] in order to create a more precise volatility estimator. Their estimator is calculated as follows:

$$\mathrm{G}\mathrm{a}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{n}-\mathrm{K}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s} (\mathrm{G}\mathrm{K})={\widehat{\mathsf{\sigma }}}_{\mathrm{G}\mathrm{K}}^2=0.511{\left(\mathrm{h}-\mathrm{l}\mathrm{w}\right)}^2-\left(2\ln 2-1\right){\mathrm{c}}^2$$

(17)

The approach proposed by Meilijson [48] which has a smaller variance than that proposed by Garman and Klass [47] is also considered. This estimator is constructed as follows:

$$\mathrm{M}\mathrm{e}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{j}\mathrm{s}\mathrm{o}\mathrm{n} (\mathrm{M})={\widehat{\mathsf{\sigma }}}_{\mathrm{M}}^2=0.274{\mathsf{\sigma }}_1^2+0.16{\mathsf{\sigma }}_2^2+0.365{\mathsf{\sigma }}_3^2+0.2{\mathsf{\sigma }}_4^2$$

(18)

where

$$\begin{array}{l}{\mathsf{\sigma }}_1^2=2\left[{\left({\mathrm{h}}^{\prime }-{\mathrm{c}}^{\prime }\right)}^2+\mathrm{l}{\mathrm{w}}^{\prime }\right]\\ {\mathsf{\sigma }}_2^2={{\mathrm{c}}^{\prime }}^2\\ {\mathsf{\sigma }}_3^2=2\left({\mathrm{h}}^{\prime }-{\mathrm{c}}^{\prime }-\mathrm{l}{\mathrm{w}}^{\prime }\right){\mathrm{c}}^{\prime }\\ {\mathsf{\sigma }}_4^2=\frac{\left({\mathrm{h}}^{\prime }-{\mathrm{c}}^{\prime }\right)\mathrm{l}{\mathrm{w}}^{\prime }}{2\ln 2-5/4}\end{array}$$

(19)

where ${\mathrm{c}}^{\prime }=\mathrm{c},{\mathrm{h}}^{\prime }=\mathrm{h},\mathrm{l}{\mathrm{w}}^{\prime }=\mathrm{l}\mathrm{w} \mathrm{i}\mathrm{f} \mathrm{c}>0\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}{\mathrm{c}}^{\prime }=-\mathrm{c},{\mathrm{h}}^{\prime }=-\mathrm{l}\mathrm{w},\mathrm{l}{\mathrm{w}}^{\prime }=-\mathrm{h} \mathrm{i}\mathrm{f} \mathrm{c}<0$.

There are other options for calculating a volatility proxy, such as that proposed by Rogers and Satchell [49] and Yang and Zhang [50]. However, the first of these was not included in this study because, as has been highlighted by Miralles Quirós et al. [23], its value can be zero in some cases and this could result in some missing data when dividing by zero. The second approach was not included in this paper because it requires the use of the opening, high, low, and closing prices on a number of days, a procedure that goes against the spirit of this paper where only daily volatility proxies are considered.

Shu and Zhang [51], Molnar [22,52] and Miralles Quirós et al. [23] highlighted that previous volatility proxies had only considered trading day prices, that is between opening and closing, and had not taken into consideration the overnight period (that period from closing time to opening time) during which prices can change to produce a so-called opening jump. Not including that opening jump could cause an upward bias in kurtosis, particularly when the opening jump is large. For that reason, the previous volatility proxies in this study were adjusted for the presence of volatility jumps by adding the term j² to the previous equations. This term is the difference between the natural logarithms of the opening price on day t and the closing price on day t − 1.

$$\mathrm{j}=\ln \left({\mathrm{O}}_{\mathrm{t}}\right)-\ln \left({\mathrm{C}}_{\mathrm{t}-1}\right)$$

(20)

As an example, the final equation for the Parkinson volatility estimator would remain as:

$${\widehat{\mathsf{\sigma }}}_{\mathrm{P}}^2=\frac{{\left(\mathrm{h}-\mathrm{l}\mathrm{w}\right)}^2}{4\ln 2}+{\mathrm{j}}^2$$

(21)

Once these three volatility proxies have been estimated, the proposal is to standardize the asset returns, dividing them by the standard deviations of the volatility proxies, and using these returns for re-estimating the performance measures and strategies initially suggested. In this way, we can determine whether long or short positions (when necessary) are taken in each asset and, once these positions have been decided, natural logarithms are employed to calculate the performance ratios (taking also into account that the cumulative return obtained using this approach is converted into a simple return by applying the relationship previously mentioned).

2.4. Data Snooping

Different tests to demonstrate the avoidance of the typical problem faced by researchers who scan and rescan their databases in search of their objectives (an activity called data mining or data snooping) have been developed.

White [53] proposed the Reality Check framework for data snooping which is able to test the predictive ability of a set of models using bootstrapping with replacement. In this framework, the expected loss for each model is estimated and the lowest is compared to a benchmark with the null hypothesis being that there is no strategy superior to the benchmark:

$${\mathrm{H}}_{\mathrm{o}}:\underset{\mathrm{k}=1,\dots ,\mathrm{M}}{\max }\overline{{\mathrm{f}}_{\mathrm{k}}}\le 0$$

(22)

where $\overline{{\mathrm{f}}_{\mathrm{k}}}=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{t}=\mathrm{R}}^{\mathrm{T}}{\mathrm{f}}_{\mathrm{k},\mathrm{t}}}$ is the performance statistic for the portfolio strategy and f_k,t (k = 1, …, M) is the period t return for the k-th portfolio strategy out of an universe of M strategies.

Hansen [54] extended the previous model by suggesting the Superior Predictive Ability, SPA, model which analyzes whether a benchmark is outperformed by a set of alternatives. In this model, the estimated variance and p-values are simulated according to the stationary bootstrap method proposed by Politis and Romano [55]. Therefore, Hansen [54] proposed to use the following studentized test statistic:

$${\mathrm{T}}^{*}=\underset{\mathrm{k}=1,\dots ,\mathrm{M}}{\max }\left[\frac{\sqrt{\mathrm{n}} \overline{{\mathrm{Z}}_{\mathrm{k}}}}{{\widehat{\mathsf{\varpi }}}_{\mathrm{k}}},0\right]$$

(23)

where

$$\begin{gathered} \overline{{\mathrm{Z}}_{\mathrm{k}}}=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{n}}{\mathrm{Z}}_{\mathrm{k},\mathrm{t}}} \\ {\mathrm{Z}}_{\mathrm{k},\mathrm{t}}={\mathrm{f}}_{\mathrm{k},\mathrm{b}}^{*}-\overline{{\mathrm{f}}_{\mathrm{k}}}1\left(\sqrt{\mathrm{n}}\overline{{\mathrm{f}}_{\mathrm{k}}}\ge -{\widehat{\mathsf{\varpi }}}_{\mathrm{k}}\sqrt{2\ln \ln \left(\mathrm{n}\right)}\right) \left(\mathrm{b}=1,\dots ,\mathrm{B}\right) \end{gathered}$$

B = Number of replacements

Following that procedure, the bootstrap p-value could then be given as:

$$\mathrm{p}={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{B}}\frac{1\left({\mathrm{T}}_{\mathrm{i}}^{*}>\mathrm{T}\right)}{\mathrm{B}}}$$

(24)

where $\mathrm{T}=\underset{\mathrm{k}=1,\dots ,\mathrm{M}}{\max }\left[\frac{\sqrt{\mathrm{n}} \overline{{\mathrm{f}}_{\mathrm{k}}}}{{\widehat{\mathsf{\varpi }}}_{\mathrm{k}}},0\right]$ with ${\widehat{\mathsf{\varpi }}}_{\mathrm{k}}$ representing the estimator of the standard deviation of $\sqrt{\mathrm{n}} \overline{{\mathrm{f}}_{\mathrm{k}}}$. Finally, the lower, centered, and upper values for the consistent p-values are also calculated.

The data used in this paper are daily returns from 2 January 2009 through 31 December 2019 (amounting to 2768 usable observations) for ten renewable energy companies which are cited as the best investment opportunities in different reports, such as the Thomson Reuters Top 100 Global Energy Leaders. Additionally, these companies are those that provide the longer historical dataset of quotes which is difficult to find due to the early period of this economic sector.

Table 1. Renewable Energy companies.

Ticker	Name	Market	Subsector
ALB	Albemarle Corporation	NYSE	Specialty Chemicals
CQP	Cheniere Energy Partners, L.P.	NYSE AMERICAN	Oil & Gas
FSLR	First Solar, Inc.	NASDAQGS	Solar
GPRE	Green Plains Inc.	NASDAQGS	Specialty Chemicals
LEU	Centrus Energy Corp.	NYSE AMERICAN	Nuclear Power
NEE	NextEra Energy, Inc.	NYSE	Wind Power
ORA	Ormat Technologies, Inc.	NYSE	Geothermal
PEIX	Pacific Ethanol, Inc.	NASDAQGS	Oil & Gas
SPWR	SunPower Corporation	NASDAQGS	Solar
CSIQ	Canadian Solar Inc.	NASDAQGS	Solar

shows the name, market and subsector for each company.

These companies represent various subsectors such as solar, wind, geothermal and specialty chemicals, among others. The first of these, which includes First Solar, SunPower and Canadian Solar, might be the most recognizable renewable energy sector because it is affordable, efficient, and reliable. We could say the same about wind power, which is represented by NextEra Energy. This is an unsaturated industry exhibiting rapid growth. Other sectors, such as geothermal (ORA) and chemical companies (GPRE), have been attracting the attention of investors in recent years and, therefore, we consider them interesting for this study. Finally, it must be pointed out that a nuclear power company (LEU) is also included because of all the reports suggesting that nuclear power will play an increasingly important role in the near future as an environmentally benign way of producing reliable electricity on a large scale. It should also be noted that nuclear power, together with wind power, has the highest benefit-cost ratio, meaning that it should be considered by investors. All these companies are quoted on North American stock exchanges and all their prices are in US dollars.

3. Results

The summary statistics of the companies returns, which are calculated as the differences between two consecutive natural logarithms, are reported in

Table 2. Descriptive statistics.

	Mean	Std. Dev.	Skewness	Kurtosis	Jarque-Bera	p-Value
ALB	0.000429	0.020861	−0.333687	7.127706	2016.413	0.00000
CQP	0.000857	0.024491	−0.314810	24.54554	53,584.65	0.00000
FSLR	−0.000326	0.034260	0.179488	15.41668	17,796.26	0.00000
GPRE	0.000768	0.036203	1.111.078	14.55838	15,977.61	0.00000
LEU	−0.001875	0.065786	0.925393	46.40219	217,654.2	0.00000
NEE	0.000568	0.010875	−0.139638	5.274692	605.7561	0.00000
ORA	0.000307	0.019170	−0.082899	7.538235	2378.527	0.00000
PEIX	−0.001540	0.064073	0.748120	15.79248	19,132.20	0.00000
SPWR	−0.000562	0.040899	0.466874	11.98336	9408.036	0.00000
CSIQ	0.000444	0.043297	0.245409	7.350927	2211.109	0.00000
Equality Test	16.056 (0.1072)	3.540.200 (0.0000)

This table contains the descriptive statistics for the daily return series for the renewable energy companies for the sample period from 2 January 2009 through 31 December 2019. The last column reports the mean and variance equality tests using the ANOVA and Levene statistics, respectively. The p values of these tests are reported in brackets. Skewness and Kurtosis refer to the series skewness and kurtosis coefficients. The Jarque–Bera statistic tests the normality of the series. This statistic has an asymptotic $X^2\left(2\right)$ distribution under the normal distribution hypothesis.

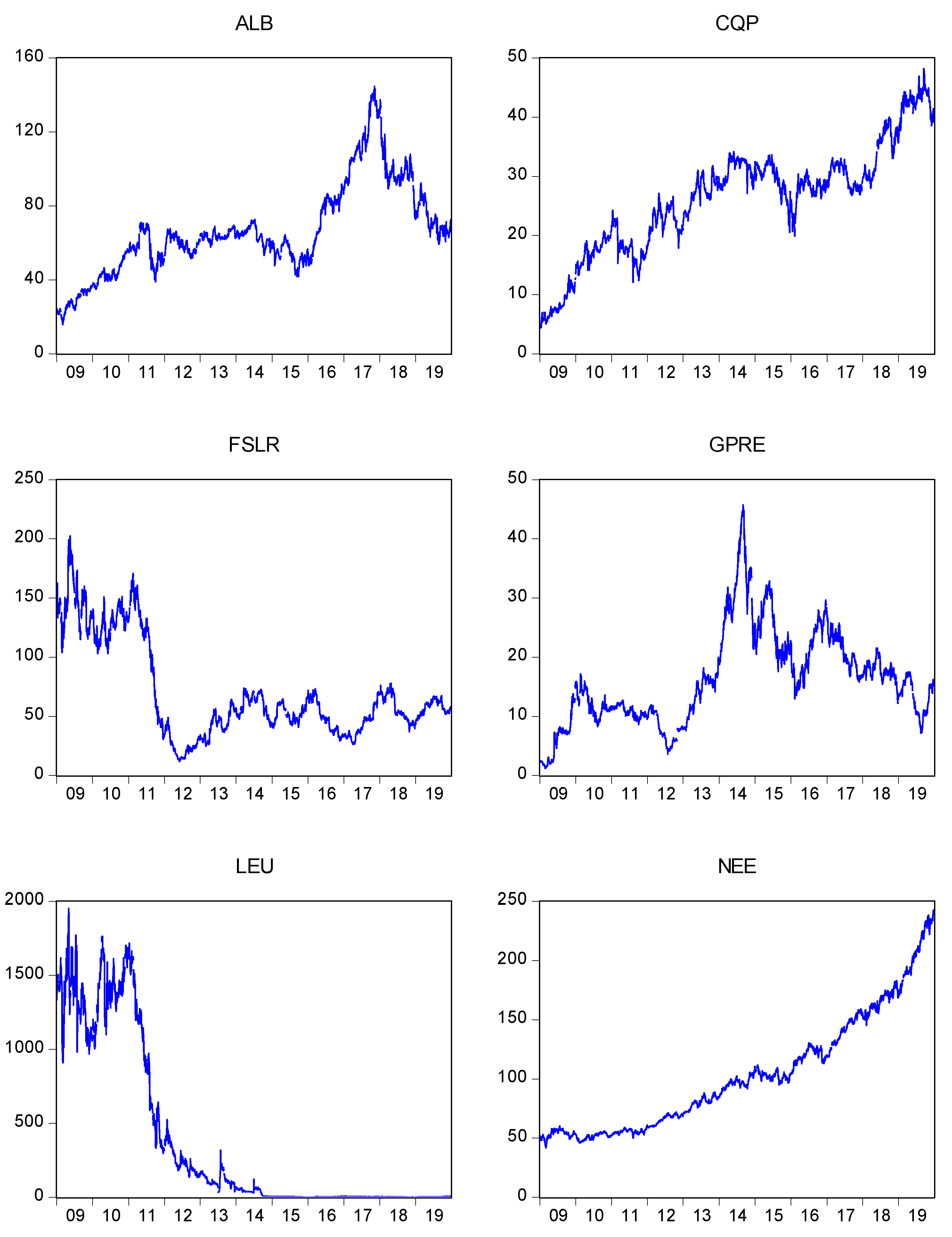
while Figure 1 shows their closing price graphs.

In order to visualize the different performances of these companies over time, in Figure 1 we set out their daily closing graphs. Sharp upward and downward trends which lead us to initially question the profitability of investing in these companies are found.

Having a rolling window to estimate the performance measures that condition portfolio composition resulted in the use of an out-of-sample period which runs from 4 January 2010 through 31 December 2019 (amounting to 2516 usable observations). All the results shown from this point refer to that period.

Table 3. Performance evaluation from the strategies.

			Long Only Strategy				Long Only Risk Free Strategy				Long-Short Strategy
		Naive	Monthly	Quarterly	Biannual	Annual	Monthly	Quarterly	Biannual	Annual	Monthly	Quarterly	Biannual	Annual
Sharpe	C. Return (%)	−54.96	44.41	−19.33	−70.70	2.01	23.32	−7.83	−44.45	−40.81	220.64	79.11	−34.94	−26.13
	Sharpe	−0.2880	0.1067	−0.0904	−0.4331	−0.0171	0.1067	−0.0904	−0.4331	−0.4039	0.5935	0.2797	−0.2593	−0.1982
	Sortino	−0.3973	0.1494	−0.1252	−0.5889	−0.0236	0.1494	−0.1252	−0.5889	−0.5419	0.8510	0.3964	−0.3541	−0.2665
	Omega	0.9524	1.0190	0.9843	0.9273	0.9969	1.0190	0.9842	0.9272	0.9324	1.1089	1.0501	0.9555	0.9656
Treynor	C. Return (%)	−54.96	36.14	16.76	−62.24	−75.99	19.73	10.88	−36.94	−49.72	202.26	159.23	−16.15	−46.69
	Sharpe	−0.2880	0.0841	0.0342	−0.3428	−0.4677	0.0841	0.0342	−0.3428	−0.4677	0.5490	0.4663	−0.1203	−0.3590
	Sortino	−0.3973	0.1188	0.0482	−0.4716	−0.6459	0.1188	0.0482	−0.4716	−0.6459	0.7943	0.6669	−0.1667	−0.4994
	Omega	0.9524	1.0150	1.0061	0.9414	0.9194	1.0151	1.0061	0.9413	0.9193	1.1007	1.0849	0.9791	0.9388
Omega	C. Return (%)	−54.96	−85.05	−72.68	−31.93	−43.96	−60.31	−46.37	−15.34	−31.08	−66.78	−39.35	51.14	0.14
	Sharpe	−0.2880	−0.4928	−0.3378	−0.1102	−0.1972	−0.4928	−0.3378	−0.1102	−0.2100	−0.6119	−0.2905	0.1939	−0.0277
	Sortino	−0.3973	−0.6886	−0.4768	−0.1585	−0.2883	−0.6886	−0.4768	−0.1585	−0.3016	−0.8506	−0.4102	0.2848	−0.0408
	Omega	0.9524	0.9169	0.9423	0.9810	0.9641	0.9168	0.9422	0.9809	0.9639	0.8990	0.9506	1.0346	0.9951
Sortino	C. Return (%)	−54.96	34.88	−18.99	−70.70	9.81	19.18	−7.64	−44.45	−40.81	199.47	79.88	−34.94	−26.13
	Sharpe	−0.2880	0.0833	−0.0881	−0.4331	0.0226	0.0833	−0.0881	−0.4331	−0.4039	0.5529	0.2798	−0.2593	−0.1982
	Sortino	−0.3973	0.1165	−0.1221	−0.5889	0.0313	0.1165	−0.1221	−0.5889	−0.5419	0.7910	0.3966	−0.3541	−0.2665
	Omega	0.9524	1.0148	0.9847	0.9273	1.0041	1.0148	0.9846	0.9272	0.9324	1.1010	1.0499	0.9555	0.9656
Kappa	C. Return (%)	−54.96	−85.51	−74.54	−27.67	−28.70	−60.94	−48.22	−12.73	−19.87	−67.84	−43.47	60.59	35.37
	Sharpe	−0.2880	−0.4995	−0.3564	−0.0952	−0.1235	−0.4995	−0.3564	−0.0952	−0.1381	−0.6266	−0.3252	0.2275	0.1404
	Sortino	−0.3973	−0.6977	−0.5025	−0.1369	−0.1828	−0.6977	−0.5025	−0.1369	−0.2001	−0.8728	−0.4579	0.3335	0.2094
	Omega	0.9524	0.9157	0.9389	0.9835	0.9774	0.9156	0.9388	0.9835	0.9761	0.8968	0.9450	1.0407	1.0251
Upside	C. Return (%)	−54.96	−63.69	−60.72	−61.69	8.04	−38.17	−35.68	−36.49	−15.17	−19.39	−12.78	−14.94	51.74
	Sharpe	−0.2880	−0.3585	−0.3263	−0.3206	0.0117	−0.3585	−0.3263	−0.3206	−0.1417	−0.1469	−0.1017	−0.1128	0.1914
	Sortino	−0.3973	−0.4923	−0.4502	−0.4449	0.0166	−0.4923	−0.4502	−0.4449	−0.1966	−0.2046	−0.1405	−0.1548	0.2678
	Omega	0.9524	0.9400	0.9449	0.9453	1.0022	0.9399	0.9448	0.9452	0.9755	0.9746	0.9823	0.9802	1.0347
Calmar	C. Return (%)	−54.96	7.99	−30.74	−74.14	1.41	6.64	−14.60	−47.82	−39.07	139.77	53.79	−42.58	−21.71
	Sharpe	−0.2880	0.0085	−0.1416	−0.4680	−0.0201	0.0085	−0.1416	−0.4680	−0.3801	0.4355	0.1999	−0.3256	−0.1659
	Sortino	−0.3973	0.0118	−0.1957	−0.6352	−0.0275	0.0118	−0.1957	−0.6352	−0.5100	0.6160	0.2817	−0.4443	−0.2237
	Omega	0.9524	1.0015	0.9755	0.9220	0.9964	1.0015	0.9755	0.9219	0.9362	1.0787	1.0355	0.9445	0.9711
Eronvar	C. Return (%)	−54.96	75.40	−7.32	−69.58	−5.15	35.90	−1.12	−43.40	−39.25	289.43	105.77	−32.45	−22.18
	Sharpe	−0.2880	0.1684	−0.0421	−0.4040	−0.0495	0.1684	−0.0421	−0.4040	−0.3642	0.6905	0.3490	−0.2363	−0.1665
	Sortino	−0.3973	0.2386	−0.0587	−0.5545	−0.0694	0.2386	−0.0587	−0.5545	−0.4975	1.0049	0.4979	−0.3260	−0.2279
	Omega	0.9524	1.0304	0.9925	0.9309	0.9906	1.0304	0.9925	0.9308	0.9378	1.1280	1.0630	0.9594	0.9710
Cvarsharpe	C. Return (%)	−54.96	31.36	−24.39	−71.95	7.43	17.61	−10.77	−45.66	−40.81	191.65	67.87	−37.73	−26.13
	Sharpe	−0.2880	0.0752	−0.1132	−0.4481	0.0108	0.0752	−0.1132	−0.4481	−0.4039	0.5435	0.2467	−0.2832	−0.1982
	Sortino	−0.3973	0.1051	−0.1564	−0.6088	0.0149	0.1051	−0.1564	−0.6088	−0.5419	0.7775	0.3482	−0.3863	−0.2665
	Omega	0.9524	1.0133	0.9803	0.9248	1.0020	1.0133	0.9803	0.9247	0.9324	1.0994	1.0440	0.9515	0.9656
Modsharpe	C. Return (%)	−54.96	44.39	−9.20	−66.18	11.35	23.31	−2.22	−40.33	−31.40	220.59	101.60	−24.92	−0.77
	Sharpe	−0.2880	0.1058	−0.0501	−0.3859	0.0295	0.1058	−0.0501	−0.3859	−0.3071	0.5788	0.3323	−0.1788	−0.0319
	Sortino	−0.3973	0.1483	−0.0695	−0.5259	0.0407	0.1483	−0.0695	−0.5259	−0.4162	0.8338	0.4740	−0.2454	−0.0434
	Omega	0.9524	1.0188	0.9912	0.9345	1.0054	1.0189	0.9912	0.9344	0.9481	1.1068	1.0597	0.9692	0.9944

This table shows the results for the different strategies considering a set of performance measures for selecting the assets in the portfolio over different rebalancing periods. Values in bold are those which outperform the naïve (benchmark) and those in red are the best for each performance measure. Sharpe, Sortino and Omega ratios are reported in annualized terms.

shows the results of the different strategies estimated in this study. The first column displays the name of the performance measures, while the second shows the different ratios estimated to evaluate the performance of each strategy. These ratios are the cumulative return (C. Return), which is expressed in percent, and the Sharpe, Sortino and Omega (with a threshold of zero) ratios, which are shown as annualized terms. The third column shows the results of the previous ratios for the naïve strategy. This strategy holds weights equal to 1/N in each of the N assets (ten in this case). This is in fact a buy and hold strategy where weights do not change over time and it is usually used by non-professional investors who base their investments on it. It is a very elementary strategy but [56,57] and [58] among others show that it is able to outperform other strategies. For that reason, we employ it as the benchmark and develop other strategies with the objective of beating it.

The previous apprehension about the profitability of investing in renewable energy companies due to the sharp rises and falls we observed in Figure 1 is confirmed when a negative cumulative return of 54.96% is obtained. With that return, negative values for the Sharpe (−0.2880) and Sortino (−0.3973) ratios and a value of less than 1 (0.9524) for the Omega ratio are obtained. This means that this strategy is not suitable for any investors who should look for better investment strategies. The following twelve columns show the results for the three strategies proposed in this study (long-only, long-only with risk free and long-short), and four rebalancing periods (monthly, quarterly, biannual, and annual). The results that outperform the naïve (benchmark) are highlighted in bold, while the best strategy in each performance measure is also highlighted in red.

It can be drawn some conclusions from these results. Firstly, the naïve strategy is clearly outperformed for most performance measures and rebalancing periods. Excess return on VaR (ERONVAR), Conditional VaR Sharpe (CVARSHARPE) and Modified Sharpe (MODSHARPE) are the performance measures with the best performing ratios when compared to the naïve ones.

More specifically, the combination of using the Excess return on VaR measure and the Long-short strategy displays a cumulative return of 289.43%, a Sharpe ratio of 0.6905, a Sortino value of 1.0049 and an Omega ratio of 1.1280, which are the best of all the approaches. In contrast, we find that the Omega, Kappa and Upside performance measures lead to poor results when they are employed to determine the assets, and then the portfolio returns, for any strategy or rebalancing period.

Secondly, it is clear that taking long and short positions is the best strategy for investors, while the long-only strategy is the worst option. Its results are similar to those obtained from a long-only with risk free strategy, but for the long-only strategy the ratios are slightly worse for all rebalancing periods. Finally, in accordance with León et al. [19] we find that most of the best results are obtained using a monthly rebalancing period. However, it must also be pointed out that using quarterly rebalancing periods leads to notable positive returns.

To reinforce understanding of the good performance of the proposed strategies, in

Table 4. Summary and outperformance percentages.

	Strategy	Cr	Sharpe	Sortino	Omega	Naive	%	ALL	%
Naive		−54.96	−0.2880	−0.3973	0.9524
Sharpe	LS-M	220.64	0.5935	0.8510	1.1089	38	79.17	17	35.42
Treynor	LS-M	202.26	0.5490	0.7943	1.1007	31	64.58	24	50.00
Omega	LS-B	51.14	0.1939	0.2848	1.0346	26	54.17	5	8.33
Sortino	LS-M	199.47	0.5529	0.7910	1.1010	38	79.17	20	40.00
Kappa	LS-B	60.59	0.2275	0.3335	1.0407	26	54.17	8	13.33
Upside	LS-A	51.74	0.1914	0.2678	1.0347	27	56.25	8	13.33
Calmar	LS-M	139.77	0.4355	0.6160	1.0787	35	72.92	17	36.67
Eronvar	LS-M	289.43	0.6905	1.0049	1.1280	38	79.17	16	33.33
Cvarsharpe	LS-M	191.65	0.5435	0.7775	1.0994	37	77.08	20	40.00
Modsharpe	LS-M	220.59	0.5788	0.8338	1.1068	38	79.17	20	40.00

This table contains a summary of the best results from each strategy where LO, LRF and LS denote Long-only, Long-only with risk free and Long-Short strategy respectively over different rebalancing periods (Monthly, M; Quarterly, Q; Biannual, B; and Annual, A). The Naïve column shows the total of performance ratios that improve those obtained with the benchmark (naïve) while the column labeled as All displays the amount of performance ratios that also have positive values (cumulative returns and Sharpe and Sortino ratios) or higher than 1 (Omega ratio). The columns labeled as % show values in percentage for each amount. Sharpe, Sortino and Omega ratios are reported in annualized terms.

we give a summary of the best results from the previous approach along with the number and percentage of ratios that outperform those obtained by the naïve strategy, with the two values being labeled “Naïve” and “%” respectively.

The last two columns in Table 4, labeled “All” and “%”, show the number of ratios that are an improvement on the naïve results but with positive values for the cumulative return, Sharpe and Sortino ratios and an Omega ratio higher than 1.

The naïve results are outperformed at least 70% when Sharpe, Sortino, Calmar, Eronvar, Cvarsharpe and Modsharpe are the performance measures determining the portfolio composition and, therefore the returns on the strategies. These percentages are reduced to 50% for Treynor and 40% for Sortino, Cvarsharpe and Modsharpe performance measures when we search for those ratios which also show positive values or values higher than 1. In contrast, ratios obtained from the strategies where Omega, Kappa and Upside performance measures condition the portfolio composition led to the worst outperforming percentages in all cases.

These results are interesting and demonstrate that performance measures are useful in outperforming the naïve strategy. However, it remains an important problem which is the non-normality of the returns. Following the methodology of Molnár [22] and Miralles Quirós et al. [23], in

Table 5. Standard deviations and kurtosis of the initial and standardized returns.

	ALB	CQP	FSLR	GPRE	LEU	NEE	ORA	PEIX	SPWR	CSIQ
Panel A: Standard deviations
Initial	0.020861	0.024491	0.034260	0.036203	0.065786	0.010875	0.019170	0.064073	0.040899	0.043297
P	0.908727	0.801400	0.897651	0.865702	0.854906	0.860285	0.891783	0.835885	0.903612	0.889834
GK	1.000866	0.877836	0.985618	0.967012	1.005566	0.939365	0.993124	0.957405	1.005182	0.978530
M	1.000196	0.875899	0.987726	0.964287	0.981749	0.941366	0.990697	0.939586	1.006803	0.980891
Panel B: Kurtosis
Initial	7.127706	24.54554	15.41668	14.55838	46.40219	5.274692	7.538235	15.79248	11.98336	7.350927
P	1.996978	2.128441	1.952674	2.074428	2.240335	2.035012	2.028354	2.153861	1.964415	1.997254
GK	2.794666	3.224822	2.668988	3.074902	3.623357	2.894969	2.842952	3.612813	2.706132	2.789992
M	2.558242	2.891464	2.476586	2.754540	3.059132	2.648927	2.614634	2.986445	2.503920	2.558183

This table contains the standard deviations and kurtosis values for the ten assets using the initial returns from the continuously compounded return and the returns standardized by the three range-based volatility estimators: Parkinson (PK), Garman–Klass (GK) and Meilijson (M).

the standard deviations and kurtosis values of the initial returns employed for each asset are shown, but also those related to the standardized returns, that is, the returns divided by the standard deviations, of the range-based volatility estimators employed in this study: Parkinson (P), Garman-Klass (GK) and Meilijson (M). The normal distribution model, which is motivated by the Central Limit Theorem developed by Polya [59], states that the mean is zero, the standard deviation is 1 and the kurtosis is 3. The use of standardized returns leads us to obtain the expected figures in all cases, as shown in Table 5, and then all errors derived from using non-normal returns should be avoided. This fact should lead us to improve the screening test results but also the performance of the strategies.

The results reported in

Table 6. Performance evaluation from the strategies using the initial and standardized returns.

Initial
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-M	220.64	0.5935	0.8510	11.089
Treynor	LS-M	202.26	0.5490	0.7943	11.007
Omega	LS-B	51.14	0.1939	0.2848	10.346
Sortino	LS-M	199.47	0.5529	0.7910	11.010
Kappa	LS-B	60.59	0.2275	0.3335	10.407
Upside	LS-A	51.74	0.1914	0.2678	10.347
Calmar	LS-M	139.77	0.4355	0.6160	10.787
Eronvar	LS-M	289.43	0.6905	10.049	11.280
Cvarsharpe	LS-M	191.65	0.5435	0.7775	10.994
Modsharpe	LS-M	220.59	0.5788	0.8338	11.068
PARKINSON
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-M	238.03	0.6209	0.8925	11.146
Treynor	LS-M	293.70	0.7059	10.192	11.314
Omega	LS-A	−42.33	−0.3335	−0.4798	0.9430
Sortino	LS-M	241.35	0.6264	0.9009	11.157
Kappa	LS-B	−30.94	−0.2374	−0.3445	0.9594
Upside	LS-M	214.99	0.5824	0.8392	11.078
Calmar	LS-M	220.48	0.5910	0.8490	11.086
Eronvar	LS-M	232.60	0.6129	0.8794	11.129
Cvarsharpe	LS-M	238.03	0.6209	0.8925	11.146
Modsharpe	LS-M	241.35	0.6264	0.9009	11.157
GARMAN-KLASS
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-M	277.70	0.6781	0.9785	11.256
Treynor	LS-M	404.68	0.8389	12.122	11.576
Omega	LS-A	−40.06	−0.3200	−0.4633	0.9453
Sortino	LS-M	286.75	0.6903	0.9964	11.280
Kappa	LS-A	−37.40	−0.2941	−0.4252	0.9496
Upside	LS-M	238.45	0.6191	0.8886	11.147
Calmar	LS-M	229.96	0.6085	0.8683	11.121
Eronvar	LS-Q	282.40	0.6873	0.9921	11.273
Cvarsharpe	LS-Q	266.68	0.6631	0.9563	11.244
Modsharpe	LS-M	270.63	0.6681	0.9640	11.237
MEILIJSON
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-M	211.16	0.5765	0.8269	11.063
Treynor	LS-M	352.36	0.7779	11.213	11.457
Omega	LS-A	−40.06	−0.3200	−0.4633	0.9453
Sortino	LS-M	255.41	0.6468	0.9298	11.201
Kappa	LS-A	−37.40	−0.2941	−0.4252	0.9496
Upside	LS-M	244.87	0.6376	0.9144	11.183
Calmar	LS-M	209.79	0.5714	0.8181	11.050
Eronvar	LS-Q	300.50	0.7176	10.387	11.352
Cvarsharpe	LS-M	239.10	0.6188	0.8885	11.145
Modsharpe	LS-Q	241.30	0.6349	0.9149	11.187

This table shows the results for the different strategies considering a set of performance measures for selecting the assets in the portfolio over different rebalancing periods (Monthly, M; Quarterly, Q; Biannual, B; and Annual, A) and where LO, LRF and LS denote Long-only, Long-only with risk free and Long-Short strategy respectively. Values in bold are those which outperform the best initial estimation and those in red are the best for each performance measure. Sharpe, Sortino and Omega ratios are reported in annualized terms.

show the performance ratios derived from re-estimating the different strategies but using the standardized results to calculate the performance measures determining the assets included in each portfolio. For the sake of brevity, from this point on only the results for the best strategy in each performance measure and volatility estimator are shown, although the other figures are available upon request. In this case, we have highlighted in bold those results showing an improvement on the previous best strategy for each performance measure, and in red those that have the best ratios.

The previous best performance ratios are clearly improved on in most cases, especially when Garman-Klass and Meilijson are the volatility measures used for standardizing the returns. Therefore, an investor using the Treynor performance measure and a long-short strategy with monthly rebalancing is able to increase the cumulative return from 202.26% to 352.36% by using the same strategy but with returns standardized through the Meilijson volatility estimator. At the same time, the Sharpe, Sortino and Omega ratios rise from 0.5490, 0.7943 and 1.1007 to 0.7779, 1.1213 and 1.1457 respectively. However, while these results are good, they are not the best that can be obtained using the approach proposed in this study. The best results are mostly provided when the Garman-Klass estimator is used. By using this volatility measure to standardize the returns plus the Treynor ratio as the performance measure and adopting a long-short strategy with monthly rebalancing, a 404.68% cumulative return, a 0.8389 Sharpe ratio, a 1.2122 Sortino ratio and a 1.1576 Omega ratio, are obtained which are clearly an improvement on any of the best performances using non-standardized returns.

Once again, it should be noted that combining a long-short strategy and monthly rebalancing provides the best results in most cases, but quarterly or even annual rebalancing periods are also serious options for investors. Finally, it should be noted that not all standardized returns lead to better results compared to the initial approach because the Omega and Kappa performance measures show negative values for all strategies and volatility measures. In keeping with the way, we previously displayed a summary, in

Table 7. Outperformance summary using standardized returns.

	Parkinson		Garman-klass		Meilijson
	All	%	All	%	All	%
Sharpe	28	58.33	44	91.67	25	52.08
Treynor	20	41.67	40	83.33	40	83.33
Omega	0	0	0	0	0	0
Sortino	28	58.33	44	91.67	44	91,67
Kappa	0	0	0	0	0	0
Upside	30	62.5	37	77.08	37	77.08
Calmar	28	58.33	36	75	44	91.67
Eronvar	12	25	38	79.17	44	91.67
Cvarsharpe	28	58.33	44	91.67	44	91.67
Modsharpe	28	58.33	44	91.67	37	77.08

This table contains a summary of the best results from each strategy where the rows labeled as All display the amount of performance ratios that outperform the naïve values but also their previous estimation using the initial returns and have positive values (cumulative returns and Sharpe and Sortino ratios) or higher than 1 (Omega ratio), while the rows labeled as % show the percentages from each amount.

the number of performance ratios that outperform the naïve ones, along with their best previous estimation using non-standardized returns is shown.

Additionally, the ones that have positive Cumulative returns or Sharpe and Sortino ratios and an Omega ratio higher than 1 are also shown. As expected, we observe an improvement in the percentages compared to those reported in Table 4. In this case, we find that more than 90% of the performance ratios are improved in several cases. This means that not only is the naïve strategy outperformed, but the initial estimation is too, so it is clear that using standardized returns results in improved ratios and, therefore, investor profitability.

4. Discussion

The previous results were shown net of transaction costs. However, it is understood that these have a significant impact on the profitability of the strategies. Not only are these costs important, but we also need to take into account the fact that shorter rebalancing periods lead to higher costs. For that reason, in

Table 8. Performance evaluation (including transaction costs).

Initial
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-M	98.40	0.3367	0.4759	10.604
Treynor	LS-Q	120.91	0.3834	0.5448	10.693
Omega	LS-B	39.52	0.1512	0.2213	10.268
Sortino	LS-M	85.31	0.2983	0.4207	10.533
Kappa	LS-B	48.25	0.1847	0.2697	10.329
Upside	LS-A	45.79	0.1704	0.2381	10.309
Calmar	LS-M	48.36	0.1811	0.2525	10.320
Eronvar	LS-M	140.97	0.4361	0.6253	10.791
Cvarsharpe	LS-M	80.47	0.2866	0.4042	10.512
Modsharpe	LS-M	98.37	0.3288	0.4668	10.593
Parkinson
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-M	109.17	0.3642	0.5167	10.657
Treynor	LS-M	143.61	0.4477	0.6380	10.815
Omega	LS-B	−41.52	−0.3266	−0.4699	0.9446
Sortino	LS-M	111.22	0.3695	0.5246	10.668
Kappa	LS-B	−36.25	−0.2828	−0.4090	0.9520
Upside	LS-B	113.94	0.3871	0.5440	10.704
Calmar	LS-M	98.31	0.3349	0.4749	10.601
Eronvar	LS-M	105.81	0.3559	0.5042	10.641
Cvarsharpe	LS-M	109.17	0.3642	0.5167	10.657
Modsharpe	LS-M	111.22	0.3695	0.5246	10.668
Garman-Klass
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-Q	179.90	0.5226	0.7484	10.966
Treynor	LS-Q	211.18	0.5855	0.8398	11.092
Omega	LS-A	−42.41	−0.3430	−0.4956	0.9415
Sortino	LS-Q	187.46	0.5363	0.7677	10.995
Kappa	LS-A	−39.86	−0.3169	−0.4574	0.9459
Upside	LS-Q	137.98	0.4351	0.6138	10.797
Calmar	LS-Q	156.62	0.4825	0.6855	10.891
Eronvar	LS-Q	212.01	0.5828	0.8367	11.085
Cvarsharpe	LS-Q	210.41	0.5764	0.8269	11.074
Modsharpe	LS-Q	176.31	0.5154	0.7376	10.953
Meilijson
	Strategy	C. Return (%)	Sharpe	Sortino	Omega
Sharpe	LS-Q	141.03	0.4480	0.6406	10.825
Treynor	LS-Q	222.63	0.6041	0.8676	11.129
Omega	LS-A	−42.41	−0.3430	−0.4956	0.9415
Sortino	LS-Q	192.36	0.5474	0.7826	11.018
Kappa	LS-A	−39.86	−0.3169	−0.4574	0.9459
Upside	LS-M	113.40	0.3785	0.5353	10.687
Calmar	LS-Q	147.28	0.4572	0.6542	10.843
Eronvar	LS-Q	241.28	0.6303	0.9075	11.179
Cvarsharpe	LS-Q	144.11	0.4500	0.6436	10.830
Modsharpe	LS-Q	190.84	0.5473	0.7845	11.016

This table shows the results for the different strategies considering a set of performance measures for selecting the assets in the portfolio over different rebalancing periods (Monthly, M; Quarterly, Q; Biannual, B; and Annual, A) and where LO, LRF and LS denote Long-only, Long-only with risk free and Long-Short strategy respectively. Values in bold are those which outperform the best initial estimation and those in red are the best for each performance measure. Sharpe, Sortino and Omega ratios are reported in annualized terms.

a summary of the best strategies considering a one-way transaction cost of 0.2% is shown.

As expected, when compared to the results shown in Table 6, the values of the ratios fall when transaction costs are taken into account. However, even when these costs are included, most of the ratios remain better than those obtained using the initial approach (which is also shown including transaction costs). There are some changes in the best strategies, mostly due to alterations in the rebalancing periods. Therefore, the quarterly rebalancing option appears to be the best in many cases as a result of its lower turnover. In this case, the combination of using Excess Return on VaR with a long-short strategy, quarterly rebalancing and standardized returns using the Meilijson volatility measure appears to be the approach reporting the best results in terms of Cumulative return (241.28%), the Sharpe ratio (0.6303), Sortino ratio (0.9075) and Omega ratio (1.1179). There are other good combinations which are also profitable, all of them using the long-short strategy, such as the combination of Meilijson volatility standardized returns and the Treynor or Modified Sharpe performance measure with quarterly rebalancing periods, but none can outperform that one previously mentioned.

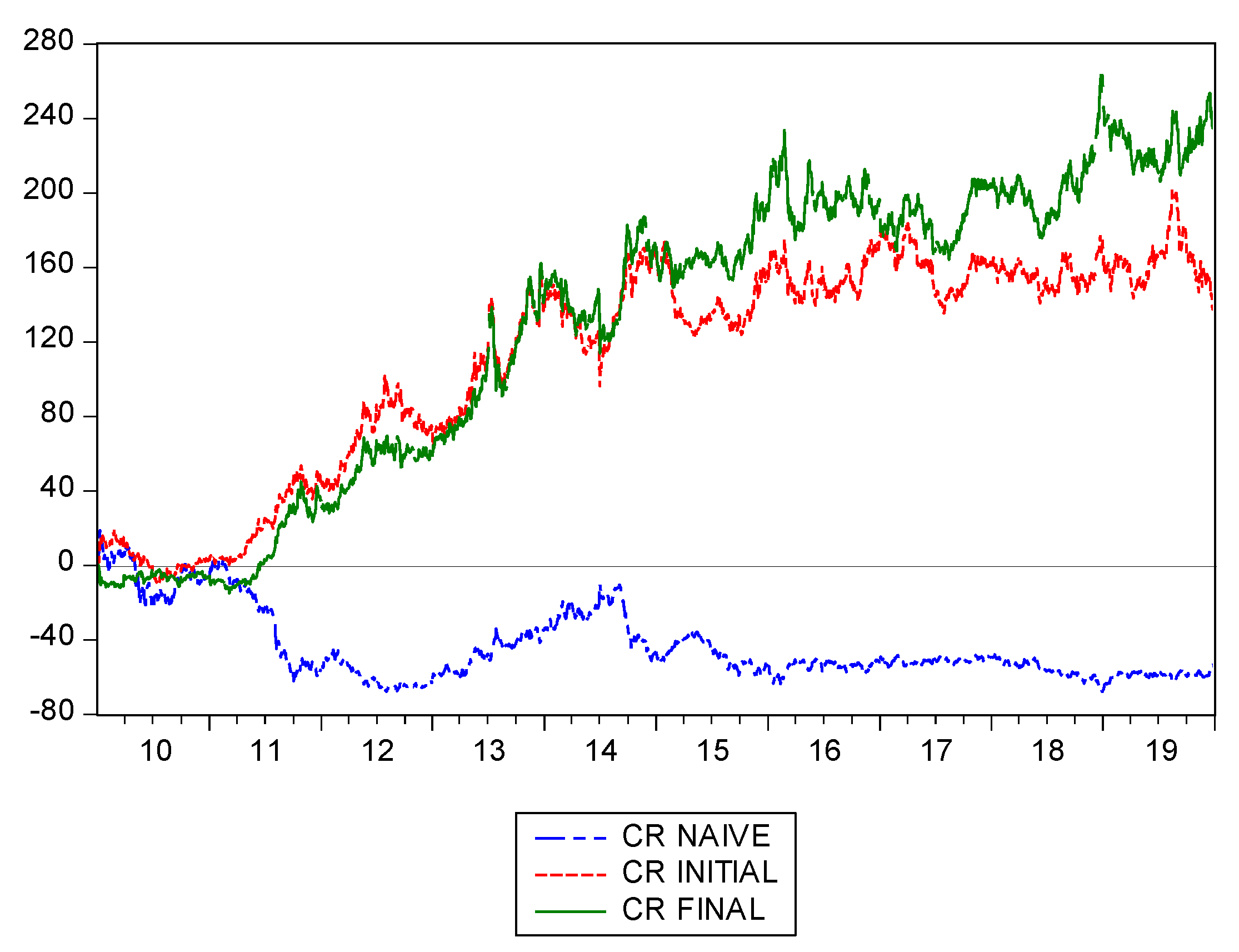
In order to reinforce the robustness of the results, in Figure 2 the cumulative returns from the naïve strategy, the best strategy using logarithm returns (Excess return on VaR, long-short and monthly rebalancing), which is labeled as initial, and the best one using standardized returns (Excess return on VaR, Meilijson volatility measure, long-short positions and quarterly rebalancing periods), which is labeled as final are shown. Values in the y-axis are shown in percent and include transaction costs. We can clearly see that the last one, where standardized returns are included, outperforms the other two over the entire out-of-sample period.

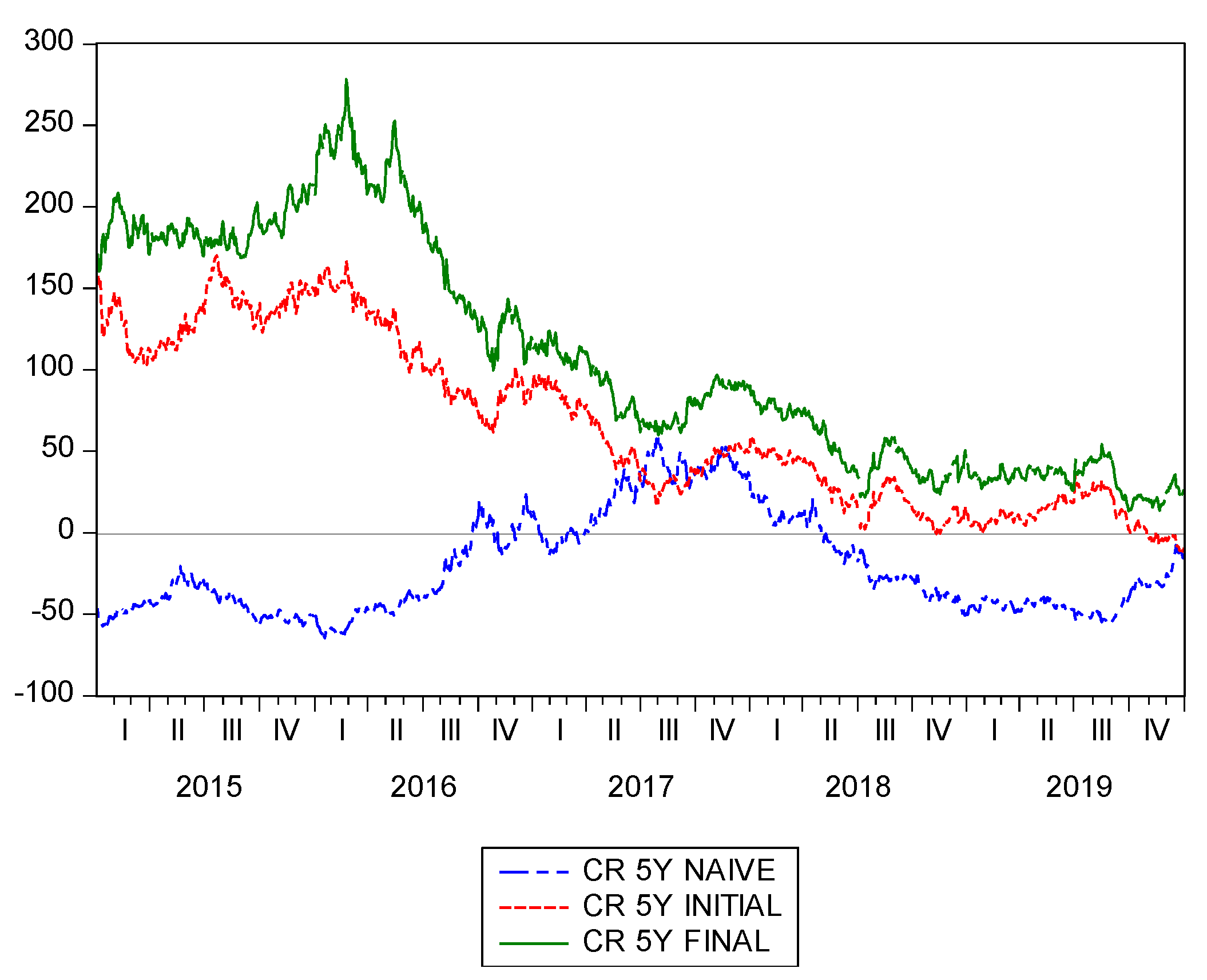
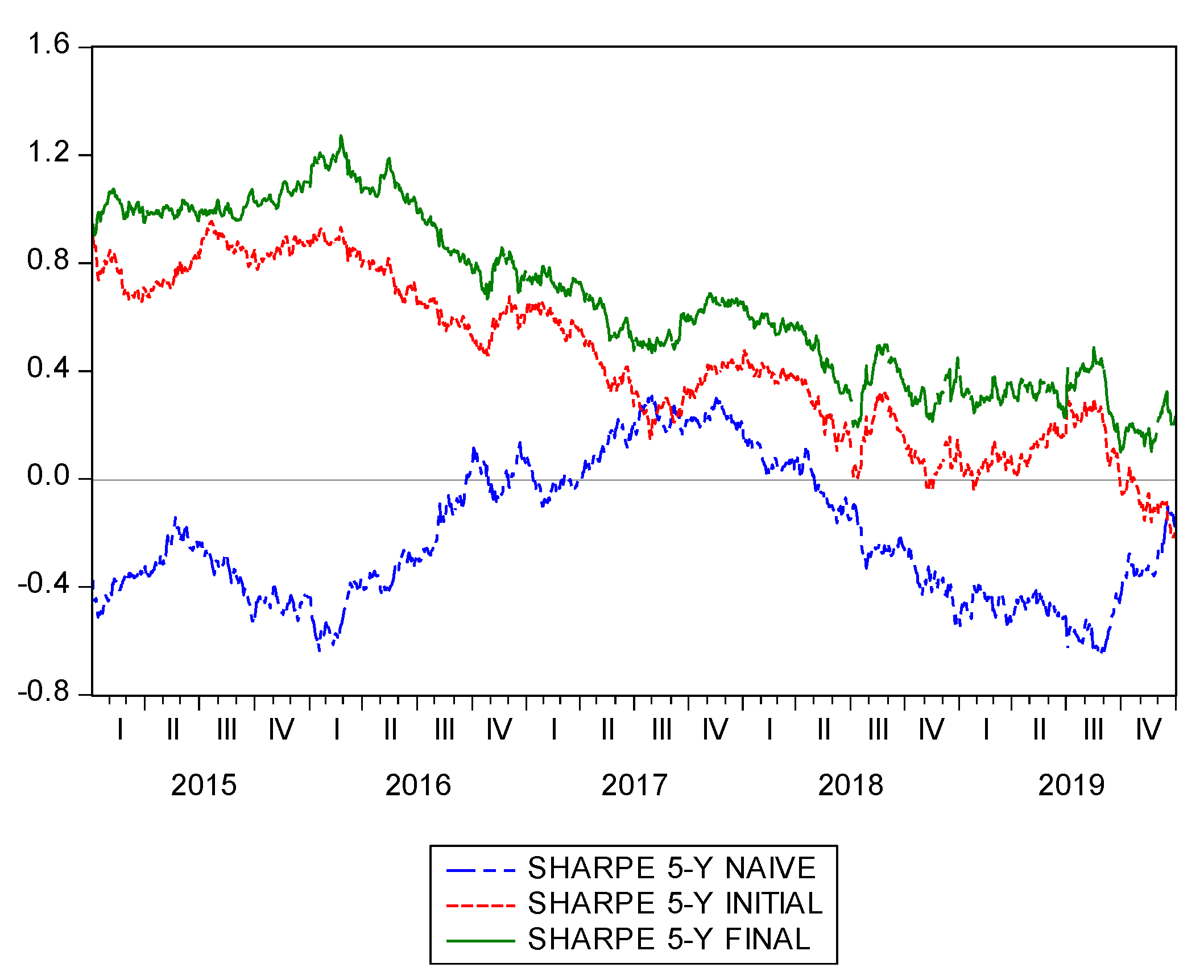
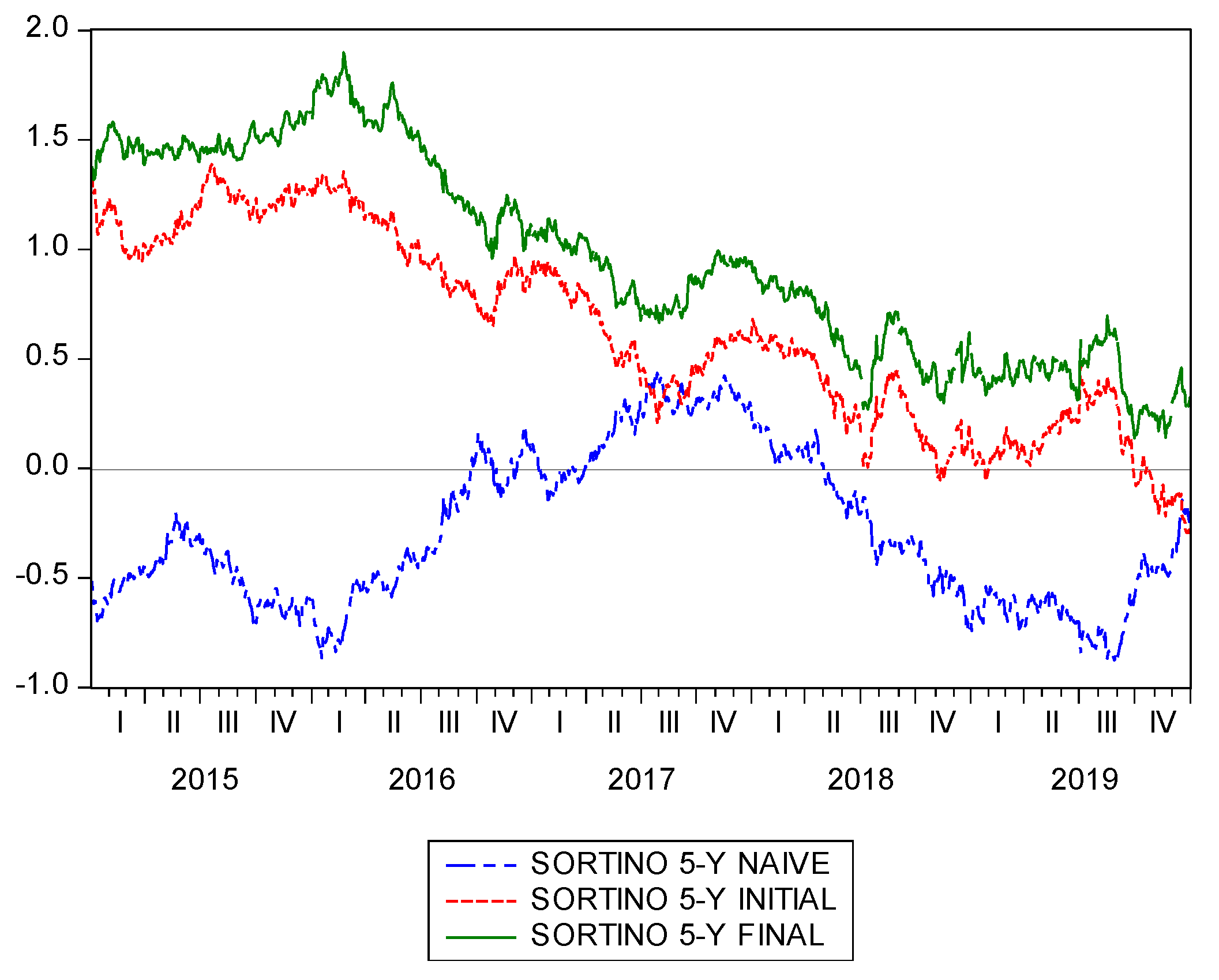
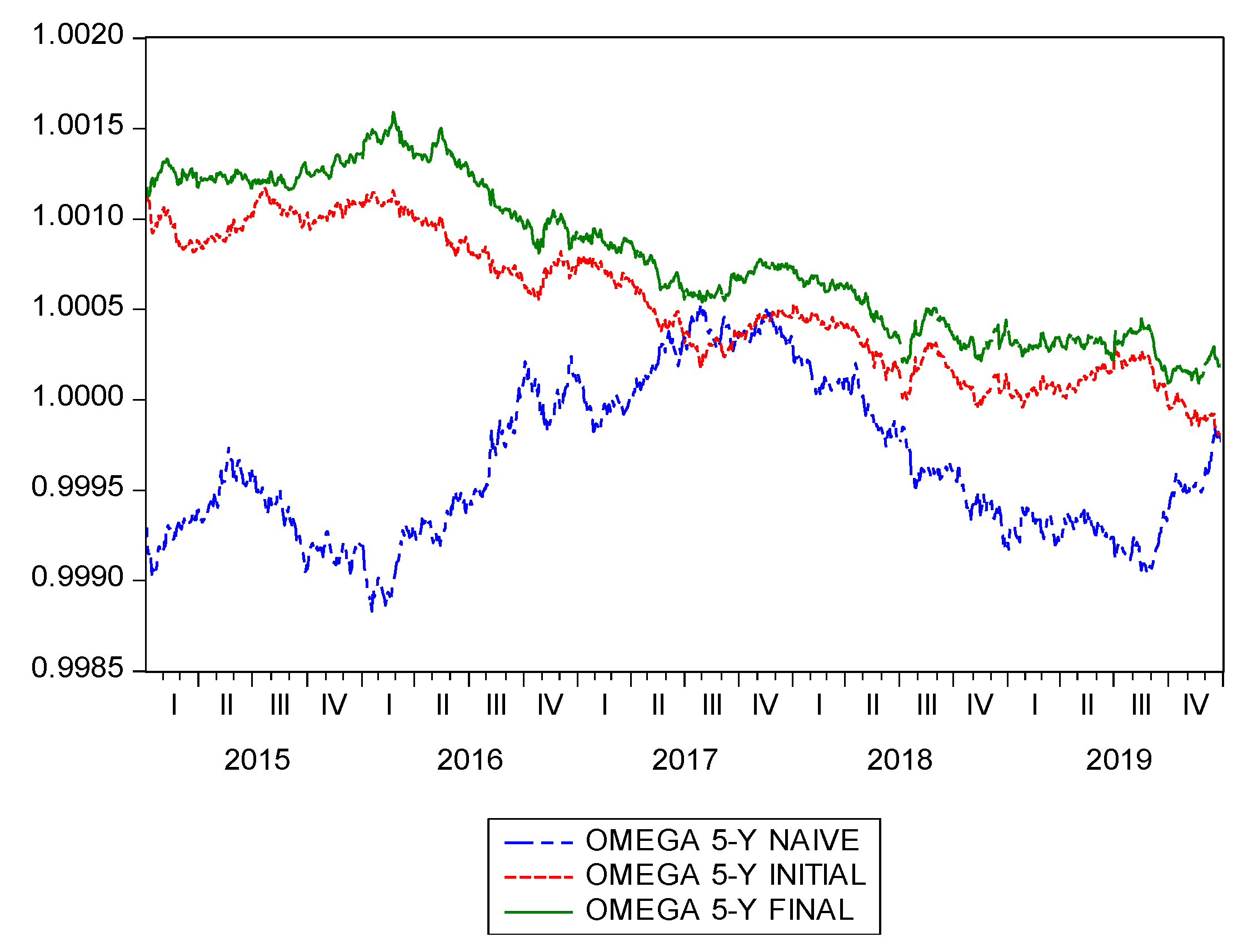
Additionally, following Bessler and Wolf [60], rolling samples with 5-year estimation windows of cumulative returns and Sharpe, Sortino and Omega ratios for the previous three strategies are shown in Figure 3, Figure 4, Figure 5 and Figure 6. As expected, it is evident that the proposal of using standardized returns leads to the best ratios over the entire sample in all cases.

Finally, some data snooping tests (Reality Check and Superior Predictive Ability) are carried out to test the null hypothesis that the better performance of the proposed strategies compared to the rest is just based on luck.

Table 9. Data snooping tests.

Index	Best Strategy	Pnom, W	Pnom, H	p-Value (RC)	p-Value (SPAl)	p-Value (SPAc)	p-Value (SPAu)
Sharpe	LS-Q-GK	0.1250	0.1050	0.1250	0.1200	0.1080	0.0990 *
Treynor	LS-Q-M	0.0680 *	0.0740 *	0.0680 *	0.0660 *	0.0660 *	0.0570 *
Omega	LS-B-P	0.5060	0.5080	0.5750	0.5150	0.5010	0.5350
Sortino	LS-Q-M	0.0720 *	0.0810 *	0.0720 *	0.0630 *	0.0800 *	0.0750 *
Kappa	LS-B-P	0.5130	0.4950	0.5890	0.5060	0.4940	0.4580
Upside	LS-Q-GK	0.1630	0.1360	0.1630	0.1460	0.1380	0.1510
Calmar	LS-Q-GK	0.1170	0.1120	0.1170	0.1080	0.1250	0.1030
Eronvar	LS-Q-M	0.0520 *	0.0620 *	0.0520 *	0.0590 *	0.0510 *	0.0440 **
Cvarsharpe	LS-Q-GK	0.0760 *	0.0780 *	0.0760 *	0.0730 *	0.0810 *	0.0800 *
Modsharpe	LS-Q-M	0.0870 *	0.0940 *	0.0870 *	0.0990 *	0.0820 *	0.0830 *

This table reports the data snooping test from the universe of 10 strategies where LO, LRF and LS denote Long-only, Long-only with risk free and Long-Short strategy respectively over different rebalancing periods (Monthly, M; Quarterly, Q; Biannual, B; and Annual, A) and the approach for standardizing the returns are denoted as Parkinson (PK), Garman–Klass (GK) and Meilijson (M). P_{nom, W} and P_{nom, H} denote White’s Reality Check and Hansen’s Superior Predictive Ability nominal p-values which are calculated by applying each methodology to the best trading rule only, thereby ignoring the effect of data snooping. p-value RC denotes White’s Reality Check p-value while p-value SPA_l, SPA_c and SPA_u denote Hansen’s Superior Predictive Ability lower, consistent, and upper p-values, respectively. Those p-values are computed by applying each methodology to the strategies and incorporate the effects of data snooping bias. * and ** represent the levels of significance of 5% and 10% respectively.

shows the p-values from the Reality Check test and the lower, centered, and upper p-values from the Superior Predictive Ability (SPA) test, but also their nominal p-values.

The results show that the null hypothesis is clearly rejected when the Treynor, Sortino, Excess Return on VaR, Conditional VaR Sharpe and Modified Sharpe performance measures are used, which are those that lead to the best results in all the estimations. Therefore, we can conclude that the good performances shown in this study were not obtained after scanning and re-scanning searching for the objective.

These results are relevant not only for investors and the CEOs of these renewable energy companies but also for policymakers and citizens. As Brunnschewiler [61] point out, nowadays one of the crucial challenges for our society is to achieve a diversified and sustainable energy supply for future generations. To that end, it is necessary to continue changing the current dependence on non-renewable and polluting hydrocarbon fuels for clean energies. Moreover, as Ntanos et al. [62] reveal, public perception of renewable energies is positive and citizens are willing to pay for the use of clean energies as they are aware of the fact that these energies can bring numerous economic, environmental and social benefits [63].

However, renewable energy projects often require high levels of financing. In addition, as noted in the introductory section, these projects often have high initial costs and long payback periods. Therefore, commercial banks are unwilling to assume those risks [64]. In this context, the role of stock markets is decisive because they can connect investors concerned about environmental and social issues to these companies. Moreover, it is essential that the academia contribute to this field by providing simple but very effective investment strategies that offer economic benefits. This is the aim of this research in which the suggested portfolio strategy allows investors to obtain substantial positive returns while contributing to accelerating the transition to a clean energy economy.

5. Conclusions

Nowadays, clean energy is one of the most urgent problems facing the world as has been explicitly exposed by the United Nations in one of the 17 Sustainable Development Goals to be achieved by 2030. Specifically, Goal 7 consists of ensuring access to affordable, reliable, sustainable and modern energy for all and the aim of one of its targets is to increase substantially the share of renewable energy in the global energy mix. In this context, not only the public sector but also the private sector is needed to make progress toward this specific goal and accelerate the transition to a clean energy economy. Particularly, investors may contribute to improving the commitment of this goal by increasing their investments in renewable energy companies.

The main objective of this paper has been to develop a feasible portfolio strategy for investors interested in renewable energy companies due to their leading role in fighting energy and climate change, but also because they are considered a lucrative investment opportunity. Given a set of candidate assets, we selected a small subset to build our strategies. We consider that this feature is useful in practice since it reduces transaction costs, execution risks and the burden of monitoring many stock prices.

From the initial results, we show that using the approach of selecting the best assets by employing different performance measures combined with taking long and short positions in the portfolios reports positive values. However, the fact that this procedure has a significant weakness, namely the assumption that asset returns are normally distributed, dead us to propose a new approach that use standardized returns with range-based volatility estimators (namely Parkinson, Garman-Klass and Meilijson). This proposed methodology not only solves the inefficiency of using non-normal distributed returns, initially present in the traditional approach, but also gives us better results.

More precisely, we observe that taking a long-short strategy, with quarterly rebalancing periods, after selecting the assets in the portfolio using the Excess Return on VaR performance measure and returns standardized by the Meilijson volatility proxy, gives us the best results from among the various options that also have high positive ratios, even when we take into account transaction costs.

To summarize, we demonstrate that there is a simple but very effective way to invest in renewable energy companies and obtain substantial positive returns. This suggested procedure has the advantage of allowing investors to contribute to a cleaner world but still obtain appreciable economic returns.

A possible limitation of this study is that a reduced number of renewable energy companies have been employed, specifically ten companies listed in the US stock markets over the 2009–2019 period. This is due to the fact that the universe of listed renewable energy companies is still limited. However, the current context is characterized by the increase in public initiatives with the aim of intensifying the change towards a green and sustainable economy. An example is the European Green Deal, an action plan to make the European Union climate neutral in 2050. This implies numerous achievements such as decarbonizing the energy sector, investing in environmental–friendly technologies and cleaner private and public transportation, among others. As a consequence of this trend all over the world, it is foreseeable that the renewable energy sector will grow exponentially in the coming years and, therefore, investors will have more opportunities to participate with their allocation decisions in the transition towards a clean energy economy.

For these reasons, future research in this field should continue analyzing the implications of renewable energy companies in stock markets as well as the profitability of investing in this specific sector. More precisely, it is necessary to increase the sample under study employing more companies not only listed in the US stock market but also on other geographical areas such as the European one. Moreover, future research in this field should extend the time period including the analysis of the effect of the current health crisis caused by the Covid-19 pandemic. Finally, more focused attention is also needed in the analysis of the attractiveness for investors of specific types of renewable energies.