Modified Hybrid Method with Four Stages for Second Order Ordinary Differential Equations
Abstract
:1. Introduction
2. Phase Lag and Stability Analysis
3. Derivation of the New Method
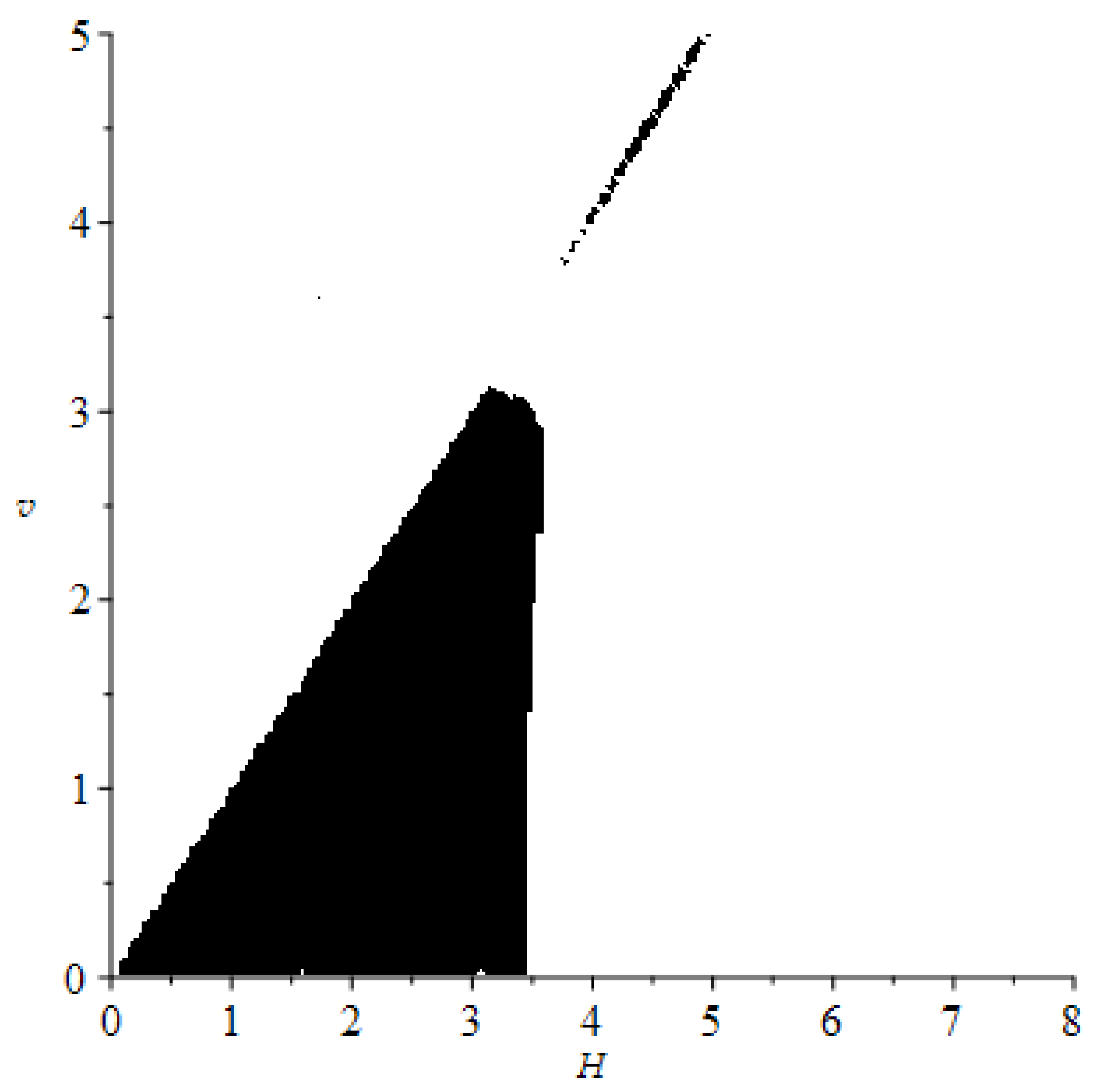
4. Results
- Problem 1 (Prothero–Robinson problem)
- Problem 2 (Duffing equation)
- Problem 3 (The well-known two-body problem)
- Problem 4 (Kramarz’s system)
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Simos, T.E.; Williams, P.S. New insights in the development of Numerov-type methods with minimal phase-lag for the numerical solution of the Schrodinger equation. Comput. Chem. 2001, 25, 77–82. [Google Scholar] [CrossRef]
- Simos, T.E.; Dimas, E.; Sideridis, A.B. A Runge-Kutta-Nystrom method for the numerical integration of special second-order periodic initial-value problem. J. Comput. Appl. Math 1994, 51, 317–326. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, X. Multi-step Runge–Kutta–Nyström methods for special second-order initial value problems. Appl. Numer. Math 2017, 113, 54–70. [Google Scholar] [CrossRef]
- Li, J.; Lu, M.; Qi, X. Trigonometrically fitted multi-step hybrid methods for oscillatory special second-order initial value problems. Int. J. Comput. Math 2018, 95, 979–997. [Google Scholar] [CrossRef]
- Kalogiratou, Z.; Monovasilis, T.; Ramos, H.; Simos, T.E. A new approach on the construction of trigonometrically fitted two step hybrid methods. J. Comput. Appl. Math 2016, 303, 146–155. [Google Scholar] [CrossRef]
- Coleman, J.P. Order conditions for a class of two-step methods for y″ = f(x,y). IMA J. Numer. Anal. 2003, 23, 197–220. [Google Scholar] [CrossRef]
- Van de Vyver, H. An explicit Numerov-type method for second-order differential equations with oscillating solutions. Comput. Math. Appl. 2007, 53, 1339–1348. [Google Scholar] [CrossRef] [Green Version]
- Samat, F.; Ismail, F.; Suleiman, M. Phase fitted and amplification fitted hybrid methods for solving second-order ordinary differential equations. IAENG Int. J. Appl. Math. 2013, 43, 99–105. [Google Scholar]
- D’Ambrosio, R.; Paternoster, B.; Santomauro, G. Revised exponentially fitted Runge-Kutta-Nystrom methods. Appl. Math. Lett. 2014, 30, 56–60. [Google Scholar] [CrossRef]
- Yusufoğlu, E. Numerical solution of Duffing equation by the Laplace decomposition algorithm. Appl. Math. Comput. 2006, 177, 572–580. [Google Scholar]
- Franco, J.M. A class of explicit two-step hybrid methods for second-order IVPs. J. Comput. Appl. Math 2006, 187, 41–57. [Google Scholar] [CrossRef] [Green Version]
- D’ Ambrosio, R.; Ferro, M.; Paternoster, B. Two step hybrid collocation methods for y″ = f(x,y). Appl. Math. Lett. 2009, 22, 1076–1080. [Google Scholar] [CrossRef] [Green Version]
- Coleman, J.P. Numerical methods for y″ = f(x,y) via rational approximations for the cosine. IMA J. Numer. Anal. 1989, 9, 145–165. [Google Scholar] [CrossRef]
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | |||
| 0 | 0 | |||||
| 0 | ||||||
| Step-Size | MEHM | EHM5IIPA |
|---|---|---|
| 0.4 | 8.12463 × 10−6 | 3.03912 × 10−5 |
| 0.2 | 4.72859 × 10−7 | 1.19831 × 10−6 |
| 0.1 | 2.80407 × 10−8 | 4.23368 × 10−8 |
| 0.05 | 1.69979 × 10−9 | 1.41116 × 10−9 |
| 0.025 | 1.04445 × 10−10 | 4.55621 × 10−11 |
| Step-Size | MEHM | EHM5IIPA |
|---|---|---|
| 0.4 | 2.48225 × 10−14 | 1.02736 |
| 0.2 | 5.51845 × 10−13 | 2.71483 × 10−1 |
| 0.1 | 2.95522 × 10−13 | 8.20955 × 10−2 |
| 0.05 | 3.76672 × 10−12 | 2.97346 × 10−3 |
| 0.025 | 4.66915 × 10−12 | 9.77418 × 10−5 |
| Step-Size | MEHM | EHM5IIPA |
|---|---|---|
| 0.4 | 1.42361 × 10−2 | 2.29762 × 10−1 |
| 0.2 | 9.29187 × 10−4 | 1.98607 × 10−3 |
| 0.1 | 6.00156 × 10−5 | 1.82083 × 10−4 |
| 0.05 | 3.81442 × 10−6 | 6.89947 × 10−6 |
| 0.025 | 2.40430 × 10−7 | 2.27004 × 10−7 |
| Step-Size | MEHM | EHM5IIPA |
|---|---|---|
| 0.05 | 1.16031 × 10−16 | 1.74602 × 10−16 |
| 0.025 | 1.72165 × 10−16 | 1.67037 × 10−15 |
| 0.0125 | 5.41637 × 10−15 | 5.97021 × 10−16 |
| 0.00625 | 7.41002 × 10−15 | 1.49427 × 10−14 |
| 0.003125 | 2.45548 × 10−14 | 5.03433 × 10−14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samat, F.; Ismail, E.S. Modified Hybrid Method with Four Stages for Second Order Ordinary Differential Equations. Mathematics 2021, 9, 1028. https://doi.org/10.3390/math9091028
Samat F, Ismail ES. Modified Hybrid Method with Four Stages for Second Order Ordinary Differential Equations. Mathematics. 2021; 9(9):1028. https://doi.org/10.3390/math9091028
Chicago/Turabian StyleSamat, Faieza, and Eddie Shahril Ismail. 2021. "Modified Hybrid Method with Four Stages for Second Order Ordinary Differential Equations" Mathematics 9, no. 9: 1028. https://doi.org/10.3390/math9091028
APA StyleSamat, F., & Ismail, E. S. (2021). Modified Hybrid Method with Four Stages for Second Order Ordinary Differential Equations. Mathematics, 9(9), 1028. https://doi.org/10.3390/math9091028






