Sixth-Order Combined Compact Finite Difference Scheme for the Numerical Solution of One-Dimensional Advection-Diffusion Equation with Variable Parameters

Abstract

A high-accuracy numerical method based on a sixth-order combined compact difference scheme and the method of lines approach is proposed for the advection–diffusion transport equation with variable parameters. In this approach, the partial differential equation representing the advection-diffusion equation is converted into many ordinary differential equations. These time-dependent ordinary differential equations are then solved using an explicit fourth order Runge–Kutta method. Three test problems are studied to demonstrate the accuracy of the present methods. Numerical solutions obtained by the proposed method are compared with the analytical solutions and the available numerical solutions given in the literature. In addition to requiring less CPU time, the proposed method produces more accurate and more stable results than the numerical methods given in the literature.

1. Introduction

The transport of solutes by water takes place in a large variety of environmental, agricultural, and industrial conditions. An accurate prediction of the pollutant transport is crucial to the effective management of these systems [1]. In the deterministic approach with constant transport parameters with respect to time and position the advection-diffusion equation (ADE) is linear and explicit closed-form solutions can generally be derived. Because of the large variability of flow and transport properties in the field, the often transient nature of the flow regime, and the non-ideal nature of applicable initial and boundary conditions, the usefulness of analytical solutions is often limited and numerical methods may be needed [2].

A variety of numerical methods have been proposed for solving ADE, such as the method of characteristics [3,4,5,6,7,8,9], the finite difference method [10,11,12,13,14,15,16,17,18,19], the finite element method [20,21,22,23], the differential quadrature method [24,25], the Lattice Boltzman method [26], and the meshless method [27,28,29,30]. In these studies, solutions of the ADE with constant parameters have been obtained. However, field and laboratory scale experiments indicate that the dispersivity in subsurface transport problems may be space- and time-dependent [31,32,33,34,35].

Several numerical solutions of the ADE with variable parameters have been proposed in the literature. A numerical solution for one-dimensional transport of conservative and non-conservative pollutants in an open channel with steady unpolluted lateral inflow uniformly distributed over the whole length of the channel was presented by Ahmad [36]. In Ahmad [36], the flow velocity was considered to be proportional to the distance and the diffusion parameter proportional to the square of velocity to account for the lateral inflow into the channel. The governing equation was converted into an equation with constant parameters using a transformation approach. The transformed equation was then solved using a cubic spline interpolation and the Crank-Nicolson finite difference scheme for advection and diffusion parts, respectively. The computed results were compared with the analytical solution for a continuous injection of the pollutant at the upstream boundary. Ahmed [37] developed a finite difference scheme based on a mathematical combination of the Siemieniuch and Gradwell approximation of time and the Dehghan’s approximation of the space variable. The author stated that the results were compared with analytical solutions and showed a good agreement. Savović and Djordjevich [38] proposed an explicit finite difference method for the numerical solution of the one-dimensional ADE with variable parameters in semi-infinite media. The continuous point source of uniform nature was considered at the origin of the medium. Savović and Djordjevich [39] then solved the same equation with a uniform pulse type input condition and the initial solute concentration that decreased with distance. In both studies, numerical solutions were obtained using the first-order explicit time integration approach and results were compared with analytical solutions reported in the literature. Gharehbaghi [40] used the differential quadrature method to obtain the numerical solution of the ADE with variable parameters in the semi-infinite domain. Numerical solutions were obtained using the first-order explicit and implicit time integration approaches. To examine the accuracy and the efficiency of the suggested explicit and implicit differential quadrature approaches, obtained solutions were compared with solutions of the finite difference method. The author stated that numerical predictions of the implicit form gave better results than the explicit one. Gharehbaghi [41] used the third- and fifth-order finite volume schemes [42] to solve a time-dependent, one-dimensional ADE with variable parameters in a semi-infinite domain. Numerical solutions were obtained using the first-order explicit time integration approach. The results of the two schemes were compared with the performance of the QUICK scheme [43]. The author stated that numerical predictions of the fifth-order finite volume scheme gave better results than the third-order finite volume and the QUICK schemes.

As can be seen from the afore-mentioned studies, low-order time integration schemes have been used in solving the ADE with variable parameters. To improve the accuracy of numerical solutions, it is required to use higher-order schemes in both time and space. The method of lines (MOL) is a well-established numerical procedure where the spatial derivatives in the partial differential equation (PDE) are approximated algebraically. Thanks to the MOL approach, a PDE system is converted into an ordinary differential equation (ODE) system. This ODE system is then integrated using standard numerical integration routines. Important variations of the MOL are possible. For example, the PDE spatial derivatives can be approximated using finite difference, finite element, finite volume, weighted residual method, and spectral method [44]. In this study, we propose another variation of the MOL approach for solving ADE with constant and variable parameters. Spatial derivatives in the proposed MOL approach are approximated using a sixth-order combined compact difference scheme. The explicit fourth order Runge–Kutta method (ERK4) is used as the numerical integration routine in the MOL approach.

2. Advection-Diffusion Equation

Solute transport through a medium is described using a PDE of the parabolic/hyperbolic type. It is derived on the principle of conservation of mass and Fick’s laws of diffusion. This equation is usually known as the ADE. The one-dimensional ADE may be written in subscript notation as [45]:

$$C_t={\left(\mathrm{D}{C}_x\right)}_x-{\left(U\mathrm{C}\right)}_x,$$

(1)

where C is the solute concentration, D is the diffusion parameter and U is the flow velocity at a position x along the longitudinal direction at time t. In Equation (1), D and U can be rewritten as:

$$\mathrm{D}=D_0{g}_1\left(x, t\right), U=U_0{g}_2\left(x,t\right),$$

(2)

In the above equation, $D_0$ and $U_0$ may be referred to as the initial diffusion parameter and the uniform velocity, respectively. $D_0$ and $U_0$ are constants whose dimensions depend upon the expressions $g_1\left(x,t\right)$ and $g_2\left(x,t\right)$. The initially solute-free state of the semi-infinite medium implies the following initial condition:

$$\mathrm{C}\left(x,0\right)=0, x\ge 0,$$

(3)

Because a continuous input concentration is introduced at the origin, whereas the concentration gradient at infinity is assumed to be zero, the following boundary conditions are obtained:

$$\mathrm{C}\left(0,t\right)=C_0, C_t\left(x_{\infty },t\right)=0, x_{\infty }\to L, t>0,$$

(4)

3. Numerical Method

The numerical solution technique that we consider in this study is based on the sixth- order combined compact finite difference and the MOL approach. Detailed information and discussions about these methods are given in the following sub-sections.

3.1. Combined Compact Finite Difference Scheme

Combined compact difference (CCD) schemes are high accuracy methods, where first and second derivatives are evaluated simultaneously utilizing the Hermitian polynomial technique, as discussed in [46,47,48,49,50]. Since these methods provide first and second derivatives simultaneously, one expects an increased accuracy and economy of operations from these methods.

The analysis of the CCD schemes by depicting scale resolution [51,52] has been augmented by properties related to phase and dispersion errors represented by numerical group velocity and phase speed, and a new CCD scheme has been proposed in Sengupta et al. [48], which has been termed as the NCCD scheme.

Consider a domain with N equidistant points with a spacing h, on which a general function $f\left(x,t\right)$ is defined. The NCCD scheme is used to simultaneously evaluate the first and second spatial derivatives, indicated by primes as $\left(f_j^{\prime }, f_j^{″}\right)$, which are evaluated at the spatial location $\left(x_j\right)$, from the following implicit equations for interior nodes, in terms of the function $\left(f_j\right)$ values [46,48,49]:

For $j=1$ and $j=2$:

$$f_1^{\prime }=\frac{1}{2h} \left(-3f_1+4f_2-f_3\right),$$

(5a)

$$f_1^{″}=\frac{1}{h^2} \left(f_1-2f_2+f_3\right),$$

(5b)

$$f_2^{\prime }=\frac{1}{h}\left[\left(\frac{2{\gamma }_1}{3}-\frac{1}{3}\right)f_1-\left(\frac{8{\gamma }_1}{3}+\frac{1}{2}\right)f_2+\left(4{\gamma }_1+1\right)f_3-\left(\frac{8{\gamma }_1}{3}+\frac{1}{6}\right)f_4+\frac{2{\gamma }_1}{3}{f}_5\right],$$

(5c)

$$f_2^{″}=\frac{1}{h^2} \left(f_1-2f_2+f_3\right),$$

(5d)

For $j=3$ to $\left(N-2\right)$:

$$\frac{7}{16}\left(f_{j+1}^{\prime }+f_{j-1}^{\prime }\right)+f_j^{\prime }-\frac{h}{16}\left(f_{j+1}^{″}+f_{j-1}^{″}\right)=\frac{15}{16h} \left(f_{j+1}+f_{j-1}\right),$$

(6)

$$\frac{9}{8h}\left(f_{j+1}^{\prime }-f_{j-1}^{\prime }\right)-\frac{1}{8}\left(f_{j+1}^{″}+f_{j-1}^{″}\right)+f_j^{″}=\frac{3}{h^2} \left(f_{j+1}-2f_j+f_{j-1}\right),$$

(7)

For $j=\left(N-1\right)$ to $N$:

$$f_{N-1}^{\prime }=-\frac{1}{h}\left[\left(\frac{2{\gamma }_2}{3}-\frac{1}{3}\right)f_N-\left(\frac{8{\gamma }_2}{3}+\frac{1}{2}\right)f_{N-1}+\left(4{\gamma }_2+1\right)f_{N-2}-\left(\frac{8{\gamma }_2}{3}+\frac{1}{6}\right)f_{N-3}+\frac{2{\gamma }_2}{3}{f}_{N-4}\right],$$

(8a)

$$f_{N-1}^{″}=\frac{1}{h^2} \left(f_N-2f_{N-1}+f_{N-2}\right),$$

(8b)

$$f_N^{\prime }=\frac{1}{2h} \left(3f_N-4f_{N-1}+f_{N-2}\right),$$

(8c)

$$f_N^{″}=\frac{1}{h^2} \left(f_N-2f_{N-1}+f_{N-2}\right),$$

(8d)

with ${\gamma }_1=-0.025$ and ${\gamma }_2=0.09$, are proposed by Sengupta [53] for better global numerical properties in the domain.

Multiplicative constants in Equations (6) and (7), are fixed by matching the Taylor series expansion coefficients up to the sixth-order. Thus, we have a complete linear algebraic system for evaluating the first and second derivatives. Equation (5) are used for $j=1$ and Equation (8) are used for $j=N$. A full-domain spectral analysis [54] for individual derivatives is performed for the CCD schemes to solve non-periodic problems. For the purpose of this analysis, we can write Equations (5)–(8) as:

$${\mathit{A}}_1{\mathit{f}}^{\prime }+{\mathit{B}}_1{\mathit{f}}^{″}={\mathit{C}}_1\mathit{f},$$

(9)

$${\mathit{A}}_2{\mathit{f}}^{\prime }+{\mathit{B}}_2{\mathit{f}}^{″}={\mathit{C}}_2\mathit{f},$$

(10)

By decoupling these two simultaneous linear algebraic equations we get [48,53]:

$${\mathit{f}}^{\prime }=\frac{1}{h}\left({\mathit{D}}_1\mathit{f}\right),$$

(11)

$${\mathit{f}}^{″}=\frac{1}{h^2}\left({\mathit{D}}_2\mathit{f}\right),$$

(12)

where

$${\mathit{D}}_1={\left({\mathit{A}}_1-{\mathit{B}}_1{\mathit{B}}_2{}^{-1}{\mathit{A}}_2\right)}^{-1}\left({\mathit{C}}_1-{\mathit{B}}_1{\mathit{B}}_2{}^{-1}{\mathit{C}}_2\right)h,$$

(13)

$${\mathit{D}}_2={\left({\mathit{B}}_2-{\mathit{A}}_2{\mathit{A}}_1{}^{-1}{\mathit{B}}_1\right)}^{-1}\left({\mathit{C}}_2-{\mathit{A}}_2{\mathit{A}}_1{}^{-1}{\mathit{C}}_1\right)h^2.$$

(14)

More details of this global spectral analysis for CCD scheme is available in Sengupta and Bhaumik [53].

3.2. Time Integration

The method of lines (MOL) is a procedure whereby one or more partial differential equations (PDEs) are reduced to a system of ordinary differential equations (ODEs) in time by approximating the spatial derivatives using standard approaches and then integrating in time using an ODE code [55]. The MOL consists of two steps. In the first step, partial differential equations are converted into a system of time-dependent ordinary differential equations by replacing spatial derivatives with any numerical schemes. In the second step, the resulting system of ODEs is numerically integrated in time using any numerical integration rule [56]. When the MOL approach is applied to Equation (1), the time-dependent initial value problem is established as follows:

$$\frac{d{C}_j}{dt}=\theta \left(t,C_j\right), 1\le j\le N,$$

(15)

The first-order system of ODEs given by Equation (22) requires N initial conditions, which are given by Equation (3). The expression $\theta \left(t,C_j\right)$ is called the right-hand side function at the location $x_j$ and $\mathbf{\theta }\left(t,\mathit{C}\right)$ can be written in the vector form as follows:

$$\mathbf{\theta }\left(t,\mathit{C}\right)=\mathbf{D}{\mathit{C}}_{\mathit{x}\mathit{x}}+\left({\mathit{D}}_{\mathit{x}}-\mathit{U}\right){\mathit{C}}_{\mathit{x}}-{\mathit{U}}_{\mathit{x}}\mathit{C},$$

(16)

As seen above, we need the boundary conditions in the calculation of derivative terms within $\mathbf{\theta }\left(t,\mathit{C}\right)$ and these are given by Equation (4). The solution of the ODE system given in Equation (22) can be easily obtained by any time-integration scheme. In the MOL approach, the differential matrices $\left({\mathit{D}}_1 \mathrm{and} {\mathit{D}}_2\right)$ and the initial and boundary conditions are first passed to the function which is needed to calculate the numerical values of $\mathbf{\theta }\left(t,\mathit{C}\right)$. Note that, the numerical derivatives in $\mathbf{\theta }\left(t,\mathit{C}\right)$ are calculated with high accuracy using the NCCD scheme. The resulting ODE system is then solved using the explicit fourth order Runge–Kutta (ERK4) scheme. The ERK4 scheme is one of the most popular general-purpose integrators as it is simple to implement and has good stability characteristics [57]. The formulation of the ERK4 scheme from time step $m$ to $m+1$ can be written as:

$${\mathit{k}}_1=\mathbf{\theta }\left(t_m,{\mathit{C}}_{\mathit{m}}\right),$$

(17a)

$${\mathit{k}}_2=\mathbf{\theta }\left(t_m+\frac{1}{2}\Delta t,{\mathit{C}}_{\mathit{m}}+\frac{1}{2}\Delta t{\mathit{k}}_1\right),$$

(17b)

$${\mathit{k}}_3=\mathbf{\theta }\left(t_m+\frac{1}{2}\Delta t,{\mathit{C}}_{\mathit{m}}+\frac{1}{2}\Delta t{\mathit{k}}_2\right),$$

(17c)

$${\mathit{k}}_4=\mathbf{\theta }\left(t_m+\Delta t,{\mathit{C}}_{\mathit{m}}+\Delta t{\mathit{k}}_3\right),$$

(17d)

$${\mathit{C}}_{\mathit{m}+1}={\mathit{C}}_{\mathit{m}}+\frac{\Delta t}{6}\left({\mathit{k}}_1+2{\mathit{k}}_2+2{\mathit{k}}_3+{\mathit{k}}_4\right),$$

(17e)

4. Numerical Applications

In this section, numerical solution of the ADE with constant and variable parameters are tested on three numerical examples. In these examples, input parameters are $C_0=1 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$, $D_0=0.0002 {\mathrm{m}}^2/\mathrm{s}$ and $U_0=0.01 \mathrm{m}/\mathrm{s}$. The transport domain is divided into intervals of a constant length $h=1 \mathrm{m}$. Calculated concentration values are presented in longitudinal region $0\le x\le L$ at different times. Since the Neumann boundary condition is valid at the right boundary point, a large enough domain length is selected in all examples, i.e., $L=100 \mathrm{m}$. The numerical examples presented in this study are closely related each other. The initial and boundary conditions, the domain lengths $\left(L\right)$, and the input parameters $\left(C_0, D_0, U_0\right)$ are the same. The parameters $m$ and $\propto$, which control only temporal and spatial change, and the total simulation times $\left(t\right)$ are different. The main goal of this approach is to observe how the behavior of the problem changes when the velocity $\left(U\right)$ and diffusion coefficients $\left(D\right)$ are selected as variables. If the velocity and diffusion coefficients are fixed, the second and the third problem is reduced to the first problem.

4.1. ADE with Constant Parameters

The advection–diffusion equation is solved for a transport domain in which the velocity and the diffusion coefficient are constant, i.e., $g_1\left(x,t\right)=1$ and $g_2\left(x,t\right)=1$. These conditions describe the propagation of a steep front, which is simultaneously subjected to the diffusion. The analytical solution of the ADE with constant parameters is given by Szymkiewicz [3]:

$$\mathrm{C}\left(x,t\right)=\frac{C_0}{2}\left[erfc\left(\frac{x-U_{0}t}{\sqrt{4D_{0}t}}\right)+exp\left(\frac{U_{0}x}{D_0}\right)erfc\left(\frac{x+U_{0}t}{\sqrt{4D_{0}t}}\right)\right],$$

(18)

In this example, a numerical solution of an ADE with constant parameters and sharp behavior was performed. The analytical solution of this example has been calculated incorrectly by various researchers [3,20,22]. Therefore, the results of these studies were not used in the comparison. Recently, Irk et al. [58] was conducted a study, by approximating the spatial derivatives with cubic B-spline collocation scheme and extended cubic B-spline collocation. They were adopted the Crank–Nicolson scheme for the time integration. These two schemes will be referred to as CN-CBSC and CN-ECBSC.

$L_{\infty }$ norm errors of the ERK4-NCCD, CN-CBSC, and CN-ECBSC schemes for different time steps at t $=3000 \mathrm{s}$ are compared in

Table 1. Comparison of the $L_{\infty }$ norm errors of several methods for different time steps $\Delta t$ at $t=3000 \mathrm{s}.$

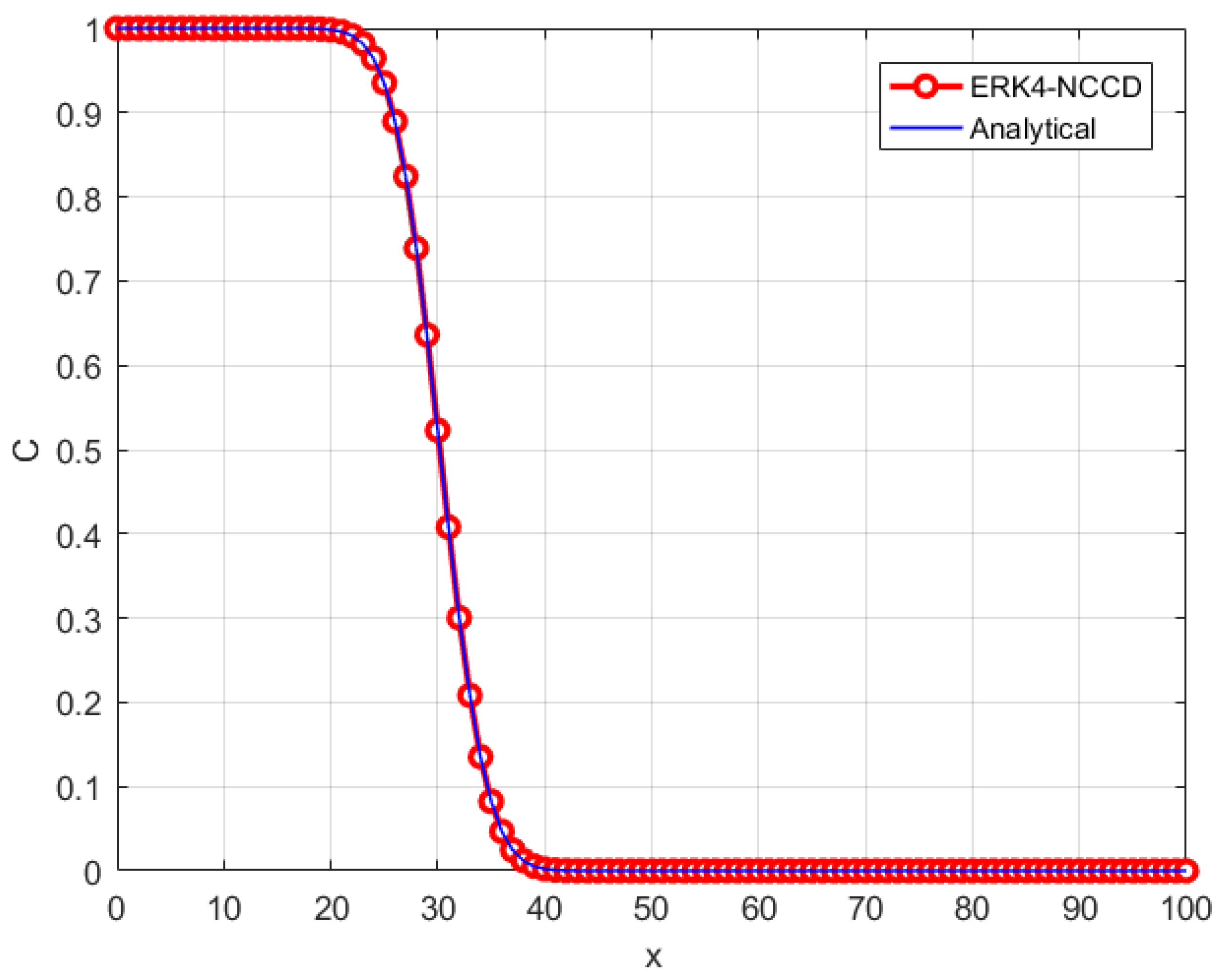
$\mathbf{\Delta }\mathit{t} \left(\mathit{s}\right)$	ERK4-NCCD (This Study)	CN-CBSC [58]	CN-ECBSC [58]
100	0.05830	NA	NA
60	0.03538	0.04330	0.0425 *
30	0.01753	0.01962	0.01961
20	0.01150	0.01270	0.01260
10	0.00543	0.00685	0.00608
5	0.00264	0.00409	0.00307
1	0.00109	0.00224	0.00127

* After a personal interview with the author of this article (Prof. Dursun Irk), it was confirmed that the correct value should be 0.0425, while the published value of 0.00425 was due to a typographic error.

. In this example, the Peclet number $\left(Pe\right)$ was selected as 5. The Courant numbers $\left(Cr\right)$ were calculated as 0.01, 0.05, 0.1, 0.2, 0.3, 0.6, and 1, respectively, when the time steps used were ordered from the smallest to the largest. As can be seen from Table 1, the ERK4-NCCD scheme is more accurate and more stable than the CN-CBSC and the CN-ECBSC schemes.

Table 2. Comparison of the analytical solution with the numerical results of the ERK4-NCCD scheme for different time steps $\Delta t$ at t$= 3000 \mathrm{s}$.

$\mathit{x} \left(\mathit{m}\right)$	$\mathbf{\Delta }\mathit{t} = 1$	$\mathbf{\Delta }\mathit{t} = 5$	$\mathbf{\Delta }\mathit{t} = 10$	$\mathbf{\Delta }\mathit{t} = 20$	$\mathbf{\Delta }\mathit{t} = 30$	$\mathbf{\Delta }\mathit{t} = 60$	$\mathbf{\Delta }\mathit{t} = 100$	Analytical
0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
…	…	…	…	…	…	…	…	…
18	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
19	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999
20	0.998	0.998	0.998	0.998	0.998	0.999	0.999	0.998
21	0.996	0.996	0.996	0.996	0.996	0.997	0.997	0.996
22	0.991	0.991	0.991	0.992	0.992	0.993	0.993	0.991
23	0.982	0.982	0.982	0.983	0.983	0.984	0.986	0.982
24	0.965	0.965	0.965	0.966	0.967	0.969	0.973	0.964
25	0.935	0.936	0.937	0.938	0.940	0.944	0.950	0.934
26	0.890	0.891	0.892	0.894	0.897	0.904	0.913	0.889
27	0.824	0.826	0.828	0.831	0.835	0.845	0.858	0.823
28	0.739	0.741	0.743	0.748	0.753	0.766	0.783	0.738
29	0.636	0.639	0.641	0.647	0.652	0.669	0.689	0.636
30	0.523	0.525	0.528	0.534	0.540	0.558	0.581	0.523
31	0.408	0.410	0.413	0.419	0.425	0.443	0.466	0.408
32	0.300	0.303	0.305	0.311	0.316	0.332	0.354	0.301
33	0.208	0.210	0.212	0.217	0.221	0.235	0.254	0.208
34	0.135	0.137	0.138	0.142	0.145	0.155	0.170	0.135
35	0.082	0.083	0.084	0.087	0.089	0.096	0.107	0.082
36	0.047	0.047	0.048	0.049	0.051	0.056	0.063	0.046
37	0.025	0.025	0.025	0.026	0.027	0.030	0.034	0.024
38	0.012	0.012	0.012	0.013	0.013	0.015	0.017	0.012
39	0.006	0.006	0.006	0.006	0.006	0.007	0.008	0.005
40	0.002	0.002	0.002	0.003	0.003	0.003	0.003	0.002
41	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001
42	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

shows the numerical results obtained with ERK4-NCCD at t = 3000 s using different time steps. It can be observed from Table 2, the ERK4-NCCD scheme it produces the more accurate solutions for $\Delta t=1 \mathrm{s}$, $5 \mathrm{s},$ and $10 \mathrm{s}$ and gives acceptable solutions for larger time steps.

Table 3. Comparison of the analytical solution with the numerical results of the ERK4-NCCD scheme for the time step $\Delta t=1 \mathrm{s}$ at times $t=2000 \mathrm{s}$, $t=4000$ s, and $t=6000$ s.

$\mathit{x} \left(\mathit{m}\right)$	$\mathit{t} = 2000 \mathbf{s}$		$\mathit{x} \left(\mathit{m}\right)$	$\mathit{t} = 4000 \mathbf{s}$		$\mathit{x} \left(\mathit{m}\right)$	$\mathit{t} = 6000 \mathbf{s}$
	Numerical	Analytical		Numerical	Analytical		Numerical	Analytical
10	1.000	1.000	26	1.000	1.000	44	1.000	1.000
11	0.999	0.999	27	0.999	1.000	45	0.999	0.999
12	0.998	0.998	28	0.999	0.999	46	0.998	0.998
13	0.995	0.995	29	0.997	0.998	47	0.997	0.997
14	0.987	0.987	30	0.995	0.995	48	0.994	0.994
15	0.969	0.968	31	0.990	0.990	49	0.989	0.989
16	0.935	0.933	32	0.980	0.980	50	0.982	0.982
17	0.875	0.873	33	0.965	0.965	51	0.970	0.970
18	0.784	0.783	34	0.941	0.940	52	0.954	0.953
19	0.665	0.665	35	0.905	0.904	53	0.930	0.930
20	0.527	0.528	36	0.855	0.854	54	0.898	0.898
21	0.387	0.388	37	0.790	0.789	55	0.857	0.856
22	0.260	0.261	38	0.710	0.709	56	0.805	0.805
23	0.159	0.159	39	0.619	0.618	57	0.744	0.744
24	0.089	0.088	40	0.520	0.520	58	0.674	0.674
25	0.044	0.044	41	0.420	0.420	59	0.597	0.597
26	0.020	0.020	42	0.326	0.326	60	0.517	0.516
27	0.008	0.008	43	0.241	0.241	61	0.435	0.435
28	0.003	0.003	44	0.170	0.170	62	0.356	0.356
29	0.001	0.001	45	0.114	0.114	63	0.283	0.283
30	0.000	0.000	46	0.073	0.073	64	0.219	0.218
			47	0.044	0.044	65	0.163	0.163
			48	0.025	0.025	66	0.118	0.118
			49	0.014	0.014	67	0.082	0.082
			50	0.007	0.007	68	0.055	0.055
			51	0.003	0.003	69	0.036	0.036
			52	0.002	0.002	70	0.023	0.022
			53	0.001	0.001	71	0.014	0.014
			54	0.000	0.000	72	0.008	0.008
						73	0.004	0.004
						74	0.002	0.002
						75	0.001	0.001
						76	0.001	0.001
						77	0.000	0.000
$L_2$	0.00390		$L_2$	0.00160		$L_2$	0.00125
$L_{\infty }$	0.00203		$L_{\infty }$	0.00073		$L_{\infty }$	0.00046

shows the numerical solutions of ERK4-NCCD at $t=2000$ s, $4000$ s, and $6000$ s using the time step $\Delta t=1 \mathrm{s}$. As seen from the Table 3, there is almost no difference between the analytical and numerical solutions.

Numerical and analytical solutions of the ADE with constant parameters for $\Delta t=1$ s is presented in Figure 1. Figure 1 shows that the numerical results obtained for $\Delta t=1$ s coincide very well with the analytical solution. Table 2 shows the numerical results obtained with ERK4-NCCD at t = 3000 s using different time steps. It can be observed from Table 2, the ERK4-NCCD scheme it produces the more accurate solutions for $\Delta t=1 \mathrm{s}$, $5 \mathrm{s},$ and $10 \mathrm{s}$ and gives acceptable solutions for larger time steps.

4.2. ADE with Spatially Variable Parameters

In this example, we assumed that the diffusion coefficient is proportional to the square of the velocity, i.e., $g_1\left(x,t\right)={\left(1+\propto x\right)}^2$ and $g_2\left(x,t\right)=1+\propto x$. Under this assumptions, the analytical solution of the ADE with spatially variable parameters is given by Kumar et al. [59] as follows:

$$\mathrm{C}\left(x,t\right)=\frac{C_0}{2}\left\{{\left(1+\propto x\right)}^{-1}erfc\left[\frac{ln\left(1+\propto x\right)}{2\propto \sqrt{D_{0}t}}-\beta \sqrt{t}\right]+{\left(1+\propto x\right)}^{\delta }erfc\left[\frac{ln\left(1+\propto x\right)}{2\propto \sqrt{D_{0}t}}+\beta \sqrt{t}\right]\right\}$$

(19)

where $\beta =\left(\left(U_0+\propto D_0\right)/\left(2\sqrt{D_0}\right)\right)$ and $\delta =U_0/\left(\propto D_0\right)$.

In this example, the velocity and the diffusion coefficient increase depending on the value of $\propto$. The numerical results at $t=3000$ s for different time steps and $\propto =0.005 {\mathrm{m}}^{-1}$ are presented in

Table 4. Comparison of the analytical solution with the numerical results of the ERK4-NCCD scheme for different time steps $\Delta t$ and $\propto = 0.005 {\mathrm{m}}^{-1}$ at $t = 3000 \mathrm{s}$.

$\mathit{x} \left(\mathit{m}\right)$	$\mathbf{\Delta }\mathit{t} = 1 \mathit{s}$	$\mathbf{\Delta }\mathit{t} = 5 \mathit{s}$	$\mathbf{\Delta }\mathit{t} = 10 \mathbf{s}$	$\mathbf{\Delta }\mathit{t} = 20 \mathit{s}$	$\mathbf{\Delta }\mathit{t} = 30 \mathit{s}$	$\mathbf{\Delta }\mathit{t} = 60 \mathit{s}$	$\mathbf{\Delta }\mathit{t} = 75 \mathit{s}$	Analytical
0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
1	0.995	0.995	0.995	0.995	0.995	0.995	0.995	0.995
2	0.990	0.990	0.990	0.990	0.990	0.990	0.990	0.990
3	0.985	0.985	0.985	0.985	0.985	0.985	0.985	0.985
4	0.980	0.980	0.980	0.980	0.980	0.980	0.980	0.980
5	0.976	0.976	0.976	0.976	0.976	0.976	0.976	0.976
6	0.971	0.971	0.971	0.971	0.971	0.971	0.971	0.971
7	0.966	0.966	0.966	0.966	0.966	0.966	0.966	0.966
8	0.962	0.962	0.962	0.962	0.962	0.962	0.962	0.962
9	0.957	0.957	0.957	0.957	0.957	0.957	0.957	0.957
10	0.952	0.952	0.952	0.952	0.952	0.952	0.952	0.952
11	0.948	0.948	0.948	0.948	0.948	0.948	0.948	0.948
12	0.943	0.943	0.943	0.943	0.943	0.943	0.943	0.943
13	0.939	0.939	0.939	0.939	0.939	0.939	0.939	0.939
14	0.935	0.935	0.935	0.935	0.935	0.935	0.935	0.935
15	0.930	0.930	0.930	0.930	0.930	0.930	0.930	0.930
16	0.926	0.926	0.926	0.926	0.926	0.926	0.926	0.926
17	0.922	0.922	0.922	0.922	0.922	0.922	0.922	0.922
18	0.917	0.917	0.917	0.917	0.917	0.917	0.917	0.917
19	0.913	0.913	0.913	0.913	0.913	0.913	0.913	0.913
20	0.908	0.908	0.908	0.908	0.908	0.909	0.909	0.909
21	0.903	0.903	0.904	0.904	0.904	0.904	0.904	0.904
22	0.898	0.898	0.898	0.898	0.898	0.898	0.898	0.898
23	0.890	0.891	0.891	0.891	0.891	0.891	0.892	0.891
24	0.880	0.881	0.881	0.881	0.881	0.882	0.883	0.880
25	0.866	0.866	0.866	0.867	0.867	0.869	0.870	0.865
26	0.844	0.845	0.845	0.846	0.847	0.850	0.851	0.844
27	0.814	0.814	0.815	0.817	0.818	0.823	0.825	0.813
28	0.772	0.772	0.774	0.776	0.778	0.785	0.788	0.771
29	0.716	0.718	0.719	0.723	0.726	0.735	0.739	0.716
30	0.649	0.650	0.652	0.656	0.660	0.672	0.678	0.648
31	0.570	0.572	0.575	0.579	0.584	0.598	0.604	0.570

. Table 4 shows that the ERK4-NCCD scheme was able to produce acceptable solutions for the maximum time step $\Delta t=75$ s. When the simulation parameters were increased, there was a slight decrease in the stability of the scheme according to the previous example. Certainly, this inference is also valid for other numerical methods. Figure 2 depicts the analytical and numerical solution of the ADE with spatially dependent parameters at $t=3000$ s for $\Delta t=1$ s and $\propto =0.02 {\mathrm{m}}^{-1}$. These results can be compared with the problem presented above for $\propto =0$ and $\Delta t=1$ s in Figure 1. When we compare Figure 1 and Figure 2, we observe that a change in $\propto$ leads to a significant change in the solution of the problem. As can be observed in

Table 5. $L_{\infty }$ norm errors of the ERK4-NCCD scheme for different time steps $\Delta t$ and $\propto$ values at $t = 3000 \mathrm{s}$. NA indicates that the solution did not converged.

$\mathbf{\Delta }\mathit{t} \left(\mathit{s}\right)$	$\propto = 0.001$	$\propto = 0.005$	$\propto = 0.01$	$\propto = 0.02$
75	0.04315	0.03812	NA	NA
60	0.03452	0.03049	NA	NA
30	0.01699	0.01498	0.01291	NA
20	0.01110	0.00978	0.00844	0.00622
10	0.00532	0.00464	0.00396	0.00291
5	0.00257	0.00219	0.00185	0.00133
1	0.00109	0.00087	0.00072	0.00050

, this change becomes more evident when we significantly increase $\propto$. The $L_{\infty }$ norm errors of the ERK4-NCCD scheme for solving ADE with different $\propto$ values at $t=3000$ s are provided in Table 5.

4.3. ADE with Spatially and Temporally Variable Parameters

In this example, we assumed that the diffusion is proportional to square of the velocity parameter as considered second example. In addition, the diffusion and velocity are supposed to vary with temporally in the same proportion as considering $g_1\left(x,t\right)=g\left(m,t\right){\left(1+\propto x\right)}^2$ and $g_2\left(x,t\right)=g\left(m,t\right)\left(1+\propto x\right)$. Under this assumptions, the analytical solution of the ADE with spatially and temporally variable parameters is given by Kumar et al. [59] as following:

$$\mathrm{C}\left(x,t\right)=\frac{C_0}{2}\left\{{\left(1+\propto x\right)}^{-1}erfc\left[\frac{ln\left(1+\propto x\right)}{2\propto \sqrt{D_{0}T}}-\beta \sqrt{T}\right]+{\left(1+\propto x\right)}^{\delta }erfc\left[\frac{ln\left(1+\propto x\right)}{2\propto \sqrt{D_{0}T}}+\beta \sqrt{T}\right]\right\}$$

(20)

where $T={{\displaystyle \int }}_0^{t}g\left(m,\vartheta \right)d\vartheta$, $\beta =\left(\left(U_0+\propto D_0\right)/\left(2\sqrt{D_0}\right)\right)$, $\delta =U_0/\left(\propto D_0\right)$, $g\left(m,t\right)=1-sin\left(mt\right)$ and $\vartheta$ is a dummy variable. In this example, the velocity and diffusion parameters are slightly increased depending on the $\mathrm{m}$ and $\propto$.

$L_{\infty }$ norm errors of the ERK4-NCCD scheme for $m=0.1 {\mathrm{s}}^{-1}$ and different $\propto$ values at $t=1500 \mathrm{s}$ can be found in

Table 6. $L_{\infty }$ norm errors of the ERK4-NCCD scheme for $m = 0.1 {\mathrm{s}}^{-1}$ with different time steps $\Delta t$ and $\propto$ values at $t = 3000 \mathrm{s}$. NA indicates that the solution did not converged.

$\mathbf{\Delta }\mathit{t} \left(\mathit{s}\right)$	$\propto = 0.001$	$\propto = 0.005$	$\propto = 0.01$	$\propto = 0.02$
100	0.08198	NA	NA	NA
75	0.06042	0.05782	NA	NA
60	0.04810	0.04577	NA	NA
30	0.02253	0.02111	0.01951	NA
20	0.01396	0.01297	0.01208	0.01029
10	0.00626	0.00567	0.00520	0.00427
5	0.00430	0.00377	0.00346	0.00270
1	0.00332	0.00305	0.00267	0.00210

. Increasing the $\propto$ value leads to increasing Courant number, $Cr=\left(U\Delta t\right)/h$. Therefore, we can face with stability problems for explicit time integration methods like ERK4. Referring to Table 6, it is seen that the stability range decreased for $\propto =0.01 {\mathrm{m}}^{-1}$ and $\propto =0.02 {\mathrm{m}}^{-1}$. The numerical results of the ERK4-NCCD scheme with $\propto =0.005 {\mathrm{m}}^{-1}$ and $\Delta t=1 \mathrm{s}$ at $t=1500 \mathrm{s}$ given in

Table 7. The numerical results of the ERK4-NCCD scheme for $\propto = 0.05 {\mathrm{m}}^{-1}$ and $\Delta t = 1 \mathrm{s}$ with different m values at $t = 1500 \mathrm{s}$.

$\mathit{x} \left(\mathit{m}\right)$	$\mathit{m} = 0.005$		$\mathit{x} \left(\mathit{m}\right)$	$\mathit{m} = 0.01$		$\mathit{x} \left(\mathit{m}\right)$	$\mathit{m} = 0.1$
	Numerical	Analytical		Numerical	Analytical		Numerical	Analytical
0	1.000	1.000	0	1.000	1.000	0	1.000	1.000
1	0.995	0.995	1	0.995	0.995	1	0.995	0.995
2	0.990	0.990	2	0.990	0.990	2	0.990	0.990
3	0.985	0.985	3	0.985	0.985	3	0.985	0.985
4	0.980	0.980	4	0.980	0.980	4	0.980	0.980
5	0.975	0.976	5	0.975	0.976	5	0.976	0.976
6	0.970	0.971	6	0.969	0.970	6	0.970	0.971
7	0.964	0.965	7	0.963	0.964	7	0.965	0.966
8	0.957	0.957	8	0.956	0.955	8	0.960	0.960
9	0.945	0.944	9	0.940	0.938	9	0.953	0.953
10	0.921	0.918	10	0.906	0.903	10	0.942	0.941
11	0.872	0.869	11	0.842	0.840	11	0.920	0.917
12	0.788	0.787	12	0.740	0.741	12	0.879	0.875
13	0.669	0.671	13	0.604	0.607	13	0.808	0.805
14	0.523	0.527	14	0.450	0.454	14	0.704	0.703
15	0.373	0.376	15	0.303	0.305	15	0.573	0.573
16	0.239	0.241	16	0.182	0.182	16	0.430	0.431
17	0.137	0.137	17	0.097	0.096	17	0.294	0.295
18	0.070	0.069	18	0.045	0.044	18	0.183	0.182
19	0.032	0.031	19	0.019	0.018	19	0.102	0.101
20	0.013	0.012	20	0.007	0.006	20	0.051	0.050
21	0.004	0.004	21	0.002	0.002	21	0.023	0.022
22	0.001	0.001	22	0.001	0.001	22	0.009	0.009
23	0.000	0.000	23	0.000	0.000	23	0.003	0.003
….	…	…	….	…	…	24	0.001	0.001
100	0.000	0.000	100	0.000	0.000	25	0.000	0.000
						….	…	…
						100	0.000	0.000
$L_2$	0.00729		$L_2$	0.00749		$L_2$	0.00590
$L_{\infty }$	0.00346		$L_{\infty }$	0.00360		$L_{\infty }$	0.00335

. As can be seen from the table, quite less $L_2$ and $L_{\infty }$ values were obtained for all $m$ values. Analytical and numerical solution of the ADE with spatially and temporally variable parameters at $t=2000 \mathrm{s}$ for $\Delta t=1 \mathrm{s}$, and $\propto =0.05 {\mathrm{m}}^{-1}$ are presented in Figure 3.

5. Conclusions

In this study, a combined compact finite difference scheme based on the method of lines is proposed for the numerical solution of the solute transport equation with variable parameters. In this approach, the partial differential equation representing the ADE is converted into many ordinary differential equations. These time-dependent ordinary differential equations are then solved using an explicit fourth order Runge–Kutta method. Numerical examples with sharp concentration fronts are presented to demonstrate the effectiveness of the method. In the first example, we compared the numerical results of the ERK4-NCCD scheme with CN-CBSC and CN-ECBSC. It is found that the ERK4-NCCD scheme is more accurate and more stable than the CN-CBSC and the CN-ECBSC schemes. It was observed that the numerical results obtained using small time steps and the analytical results coincided with each other. Moreover, acceptable results were obtained when large time steps were used as well. The ERK4-NCCD scheme gives excellent results for long time-integration, i.e., t = 2000 s, 4000 s, and 6000 s. In second example, the velocity and diffusion coefficients were slightly increased depending on the value of $\propto$. When the parameters increased, there was a slight decrease in the stability of the scheme compared to the previous example. We observe that a small change in $\propto$ leads to a significant change in the solution of the problem. This change becomes more evident when we significantly increase the $\propto$. In the third example, we observed that increasing $\propto$ value leads to increasing Courant number. Therefore, we can face with stability problems for explicit time integration methods like ERK4. As a result, the proposed method has produced more accurate and more stable results than CN-CBSC and the CN-ECBSC schemes in solving ADE with constant and variable parameters. The proposed scheme produces fairly accurate results for the $Cr\le 1$ and the $Pe\le 5$. It is recommended to use compact upwind schemes for higher Peclet numbers. When the method given in Gurarslan (2014) is followed, the proposed scheme can be easily extended to the two- and three-dimensional ADE.