Sixth-Order Combined Compact Finite Difference Scheme for the Numerical Solution of One-Dimensional Advection-Diffusion Equation with Variable Parameters
Abstract
:1. Introduction
2. Advection-Diffusion Equation
3. Numerical Method
3.1. Combined Compact Finite Difference Scheme
3.2. Time Integration
4. Numerical Applications
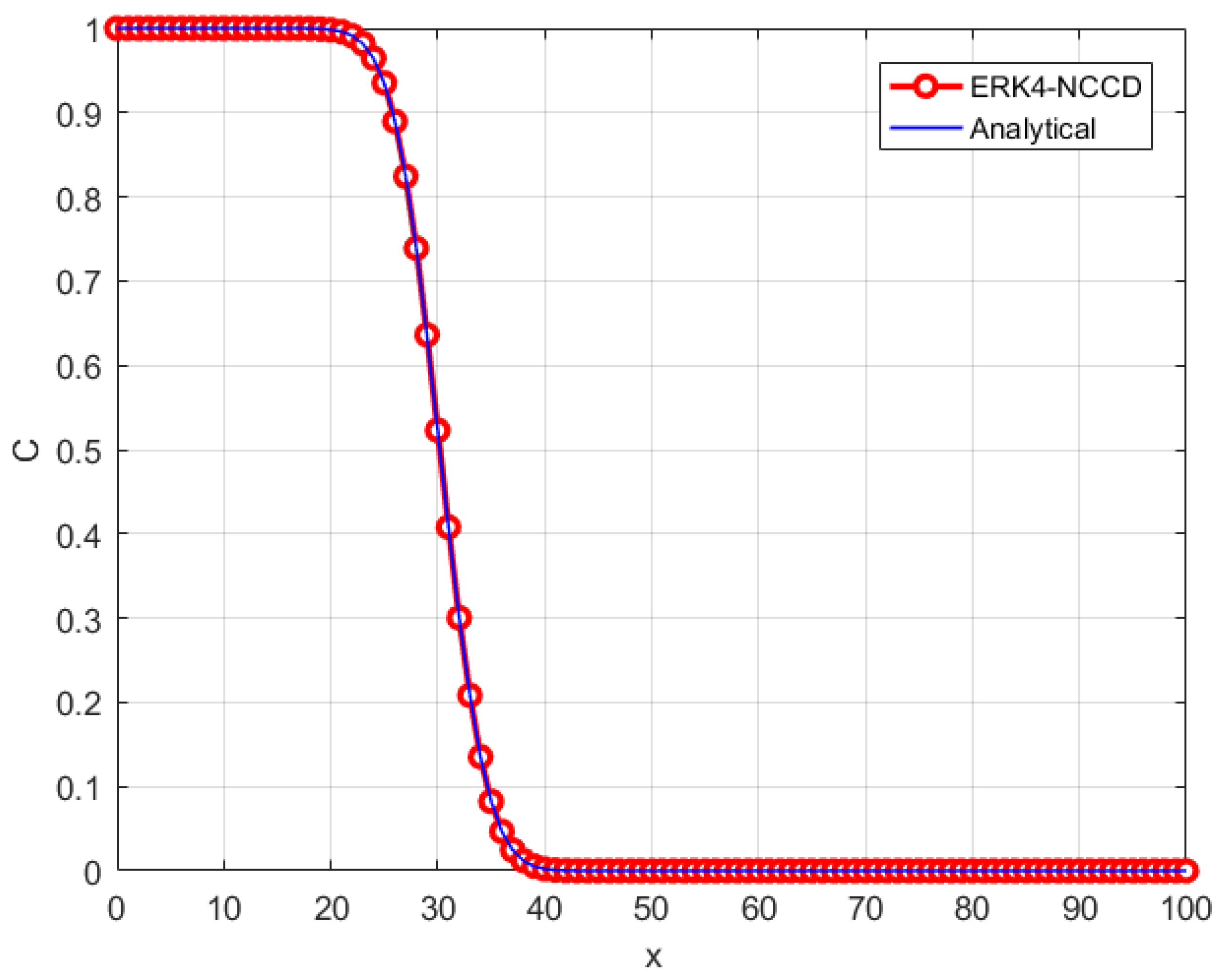
4.1. ADE with Constant Parameters
4.2. ADE with Spatially Variable Parameters
4.3. ADE with Spatially and Temporally Variable Parameters
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zoppou, C. Analytical solutions for advection and advection-diffusion equations with spatially variable coefficients. J. Hydraul. Eng. 1997, 123, 144–148. [Google Scholar] [CrossRef]
- Leij, F.J.; Skaggs, T.H.; Van Genuchten, M.T. Analytical Solutions for Solute Transport in Three-Dimensional Semi-infinite Porous Media. Water Resour. Res. 1991, 27, 2719–2733. [Google Scholar] [CrossRef]
- Szymkiewicz, R. Solution of the advection-diffusion equation using the spline function and finite elements. Commun. Numer. Methods Eng. 1993, 9, 197–206. [Google Scholar] [CrossRef]
- Holly, F.M.; Preissmann, A. Accurate calculation of transport in two dimensions. ASCE J. Hydraul. Div. 1977, 103, 1259–1277. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Yang, J.-C.; Huang, L.-H. Characteristics Method Using Cubic–Spline Interpolation for Advection–Diffusion Equation. J. Hydraul. Eng. 2004, 130, 580–585. [Google Scholar] [CrossRef] [Green Version]
- Tsai, T.L.; Chiang, S.W.; Yang, J.C. Examination of characteristics method with cubic interpolation for advection-diffusion equation. Comput. Fluids 2006, 35, 1217–1227. [Google Scholar] [CrossRef]
- Bahar, E.; Gurarslan, G. Numerical Solution of Advection-Diffusion Equation Using Operator Splitting Method. Int. J. Eng. Appl. Sci. 2017, 9, 76–88. [Google Scholar] [CrossRef] [Green Version]
- Bahar, E.; Gurarslan, G. A semi-lagrangian scheme for advection-diffusion equation. Epic Ser. Eng. 2018, 3, 162–172. [Google Scholar]
- Bahar, E.; Korkut, S.O.; Cicek, Y.; Gurarslan, G. A numerical solution for advection-diffusion equation based on a semi-Lagrangian scheme. J. BAUN Inst. Sci. Technol. 2018, 20, 36–52. [Google Scholar] [CrossRef]
- Chen, Y.; Falconer, R.A. Advection-diffusion modelling using the modified QUICK scheme. Int. J. Numer. Methods Fluids 1992, 15, 1171–1196. [Google Scholar] [CrossRef]
- Mohebbi, A.; Dehghan, M. High-order compact solution of the one-dimensional heat and advection–diffusion equations. Appl. Math. Model. 2010, 34, 3071–3084. [Google Scholar] [CrossRef]
- Dehghan, M. Weighted finite difference techniques for the one-dimensional advection-diffusion equation. Appl. Math. Comput. 2004, 147, 307–319. [Google Scholar] [CrossRef]
- Sari, M.; Gürarslan, G.; Zeytinoǧlu, A. High-order finite difference schemes for solving the advection-diffusion equation. Math. Comput. Appl. 2010, 15, 449–460. [Google Scholar] [CrossRef] [Green Version]
- Gurarslan, G.; Karahan, H.; Alkaya, D.; Sari, M.; Yasar, M. Numerical solution of advection-diffusion equation using a sixth-order compact finite difference method. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef] [Green Version]
- Gurarslan, G. Accurate Simulation of Contaminant Transport Using High-Order Compact Finite Difference Schemes. J. Appl. Math. 2014, 2014, 396738. [Google Scholar] [CrossRef]
- Mohamad, A.A. Spatially Fourth-Order-Accurate Scheme for Unsteady-Convection Problems. Numer. Heat Transf. Part B Fundam. 1997, 31, 373–385. [Google Scholar] [CrossRef]
- Rao, P.; Medina, M.A. A multiple domain algorithm for modeling two dimensional contaminant transport flows. Appl. Math. Comput. 2006, 174, 117–133. [Google Scholar] [CrossRef]
- Verma, P.; Hari Prasad, K.S.; Ojha, C.S.P. Maccormack Scheme Based Numerical Solution of Advection-Dispersion Equation. ISH J. Hydraul. Eng. 2006, 12, 27–38. [Google Scholar] [CrossRef]
- Man, C.; Tsai, C.W. A higher-order predictor–corrector scheme for two-dimensional advection–diffusion equation. Int. J. Numer. Methods Fluids 2008, 401–418. [Google Scholar] [CrossRef]
- Dag, İ.; Canivar, A.; Şahin, A. Taylor-Galerkin method for advection-diffusion equation. Kybernetes 2011, 40, 762–777. [Google Scholar] [CrossRef]
- Dhawan, S.; Kapoor, S.; Kumar, S. Numerical method for advection diffusion equation using FEM and B-splines. J. Comput. Sci. 2012, 3, 429–437. [Google Scholar] [CrossRef]
- Dag, I.; Irk, D.; Tombul, M. Least-squares finite element method for the advection-diffusion equation. Appl. Math. Comput. 2006, 173, 554–565. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Arora, P. Taylor-Galerkin B-Spline Finite Element Method for the One-Dimensional Advection-Diffusion Equation. Numer. Methods Partial. Differ. Equ. 2010, 26, 1206–1223. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Cubic B-spline differential quadrature methods for the advection-diffusion equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 1021–1036. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Quartic and quintic B-spline methods for advection-diffusion equation. Appl. Math. Comput. 2016, 274, 208–219. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Tsai, F.T.C. Lattice Boltzmann method with two relaxation times for advection-diffusion equation: Third order analysis and stability analysis. Adv. Water Resour. 2008, 31, 1113–1126. [Google Scholar] [CrossRef]
- Zerroukat, M.; Djidjeli, K.; Charafi, A. Explicit and Implicit Meshless Methods for Linear Advection-Diffusion-Type Partial Differential Equations. Int. J. Numer. Meth. Eng. 2000, 48, 19–35. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Pepper, D. Radial basis function method for 1-D and 2-D groundwater contaminant transport modeling. Comput. Mech. 2003, 32, 10–15. [Google Scholar] [CrossRef]
- Askari, M.; Adibi, H. Numerical solution of advection–diffusion equation using meshless method of lines. Iran. J. Sci. Technol. Trans. A Sci. 2017, 41, 457–464. [Google Scholar] [CrossRef]
- Ciftci, E.; Avci, C.B.; Borekci, O.S.; Sahin, A.U. Assessment of advective- dispersive contaminant transport in heterogeneous aquifers using a meshless method. Environ. Earth Sci. 2012, 67, 2399–2409. [Google Scholar] [CrossRef]
- Aral, M.M.; Liao, B. Analytical Solutions for Two-dimensional Transport Equation with Time-dependent Dispersion Coefficients. J. Hydrol. Eng. 1996, 1, 20–32. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Mantaglou, A.; Welty, C.; Rehfeldt, K.R. A Review of Field-Scale Physical Solute Transport Processes in Saturated and Unsaturated Porous Media; Electric Power Research Institute: Palo Alto, CA, USA, 1985. [Google Scholar]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Vanderborght, J.; Vereecken, H. Review of Dispersivities for Transport Modeling in Soils. Vadose Zone J. 2007, 6, 29. [Google Scholar] [CrossRef]
- Szymkiewicz, R. Numerical Modeling in Open Channel Hydraulics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 106, ISBN 978-90-481-3673-5. [Google Scholar]
- Ahmad, Z. Numerical Solution for Advection-Diffusion Equation With Spatially Variable Coefficients. ISH J. Hydraul. Eng. 2000, 6, 46–54. [Google Scholar] [CrossRef]
- Ahmed, S.G. A Numerical Algorithm for Solving Advection-Diffusion Equation with Constant and Variable Coefficients. Open Numer. Methods J. 2012, 4, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Savović, S.; Djordjevich, A. Finite difference solution of the one-dimensional advection-diffusion equation with variable coefficients in semi-infinite media. Int. J. Heat Mass Transf. 2012, 55, 4291–4294. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A. Numerical solution for temporally and spatially dependent solute dispersion of pulse type input concentration in semi-infinite media. Int. J. Heat Mass Transf. 2013, 60, 291–295. [Google Scholar] [CrossRef]
- Gharehbaghi, A. Explicit and implicit forms of differential quadrature method for advection–diffusion equation with variable coefficients in semi-infinite domain. J. Hydrol. 2016, 541, 935–940. [Google Scholar] [CrossRef]
- Gharehbaghi, A. Third- and fifth-order finite volume schemes for advection–diffusion equation with variable coefficients in semi-infinite domain. Water Environ. J. 2017, 31, 184–193. [Google Scholar] [CrossRef]
- Shu, C.-W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws; Institute for Computer Applications in Science and Engineering, NASA Langley Research Center: Hampton, VA, USA, 1997.
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Schiesser, W.E.; Griffiths, G.W. A Compendium of Partial Differential Equation Models: Method of Lines Analysis with Matlab; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Jaiswal, D.K.; Kumar, A.; Kumar, N.; Yadav, R.R. Analytical solutions for temporally and spatially dependent solute dispersion of pulse type input concentration in one-dimensional semi-infinite media. J. Hydro-Environ. Res. 2009, 2, 254–263. [Google Scholar] [CrossRef]
- Chu, P.C.; Fan, C. A Three-Point Combined Compact Difference Scheme. J. Comput. Phys. 1998, 140, 370–399. [Google Scholar] [CrossRef] [Green Version]
- Peyret, R.; Taylor, T.D. Computational Methods for Fluid Flow; Springer: New York, NY, USA, 1983. [Google Scholar]
- Sengupta, T.K.; Lakshmanan, V.; Vijay, V.V.S.N. A new combined stable and dispersion relation preserving compact scheme for non-periodic problems. J. Comput. Phys. 2009, 228, 3048–3071. [Google Scholar] [CrossRef]
- Sengupta, T.K.; Suman, V.K.; Singh, N. Solving Navier-Stokes equation for flow past cylinders using single-block structured and overset grids. J. Comput. Phys. 2010, 229, 178–199. [Google Scholar] [CrossRef]
- Zhou, Q.; Yao, Z.; He, F.; Shen, M.Y. A new family of high-order compact upwind difference schemes with good spectral resolution. J. Comput. Phys. 2007, 227, 1306–1339. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Mahesh, K. A Family of High Order Finite Difference Schemes with Good Spectral Resolution. J. Comput. Phys. 1998, 145, 332–358. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, T.K.; Vijay, V.V.S.N.; Bhaumik, S. Further improvement and analysis of CCD scheme: Dissipation discretization and de-aliasing properties. J. Comput. Phys. 2009, 228, 6150–6168. [Google Scholar] [CrossRef]
- Sengupta, T.K.; Ganeriwal, G.; De, S. Analysis of central and upwind compact schemes. J. Comput. Phys. 2003, 192, 677–694. [Google Scholar] [CrossRef]
- Tocci, M.D.; Kelley, C.T.; Miller, C.T. Accurate and economical solution of the pressure-head form of Richards’ equation by the method of lines. Adv. Water Resour. 1997, 20, 1–14. [Google Scholar] [CrossRef]
- Haq, S.; Bibi, N.; Tirmizi, S.I.A.; Usman, M. Meshless method of lines for the numerical solution of generalized Kuramoto-Sivashinsky equation. Appl. Math. Comput. 2010, 217, 2404–2413. [Google Scholar] [CrossRef]
- Griffiths, G.W. Numerical Analysis Using R: Solutions to ODEs and PDEs; Cambridge University Press: New York, NY, USA, 2016; ISBN 978-1-107-11561-3. [Google Scholar]
- Irk, D.; Dağ, İ.; Tombul, M. Extended cubic B-spline solution of the advection-diffusion equation. KSCE J. Civ. Eng. 2015, 19, 929–934. [Google Scholar] [CrossRef]
- Kumar, A.; Jaiswal, D.K.; Kumar, N. Analytical solutions to one-dimensional advection-diffusion equation with variable coefficients in semi-infinite media. J. Hydrol. 2010, 380, 330–337. [Google Scholar] [CrossRef]


| ERK4-NCCD (This Study) | CN-CBSC [58] | CN-ECBSC [58] | |
|---|---|---|---|
| 100 | 0.05830 | NA | NA |
| 60 | 0.03538 | 0.04330 | 0.0425 * |
| 30 | 0.01753 | 0.01962 | 0.01961 |
| 20 | 0.01150 | 0.01270 | 0.01260 |
| 10 | 0.00543 | 0.00685 | 0.00608 |
| 5 | 0.00264 | 0.00409 | 0.00307 |
| 1 | 0.00109 | 0.00224 | 0.00127 |
| Analytical | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| … | … | … | … | … | … | … | … | … |
| 18 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 19 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| 20 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.999 | 0.999 | 0.998 |
| 21 | 0.996 | 0.996 | 0.996 | 0.996 | 0.996 | 0.997 | 0.997 | 0.996 |
| 22 | 0.991 | 0.991 | 0.991 | 0.992 | 0.992 | 0.993 | 0.993 | 0.991 |
| 23 | 0.982 | 0.982 | 0.982 | 0.983 | 0.983 | 0.984 | 0.986 | 0.982 |
| 24 | 0.965 | 0.965 | 0.965 | 0.966 | 0.967 | 0.969 | 0.973 | 0.964 |
| 25 | 0.935 | 0.936 | 0.937 | 0.938 | 0.940 | 0.944 | 0.950 | 0.934 |
| 26 | 0.890 | 0.891 | 0.892 | 0.894 | 0.897 | 0.904 | 0.913 | 0.889 |
| 27 | 0.824 | 0.826 | 0.828 | 0.831 | 0.835 | 0.845 | 0.858 | 0.823 |
| 28 | 0.739 | 0.741 | 0.743 | 0.748 | 0.753 | 0.766 | 0.783 | 0.738 |
| 29 | 0.636 | 0.639 | 0.641 | 0.647 | 0.652 | 0.669 | 0.689 | 0.636 |
| 30 | 0.523 | 0.525 | 0.528 | 0.534 | 0.540 | 0.558 | 0.581 | 0.523 |
| 31 | 0.408 | 0.410 | 0.413 | 0.419 | 0.425 | 0.443 | 0.466 | 0.408 |
| 32 | 0.300 | 0.303 | 0.305 | 0.311 | 0.316 | 0.332 | 0.354 | 0.301 |
| 33 | 0.208 | 0.210 | 0.212 | 0.217 | 0.221 | 0.235 | 0.254 | 0.208 |
| 34 | 0.135 | 0.137 | 0.138 | 0.142 | 0.145 | 0.155 | 0.170 | 0.135 |
| 35 | 0.082 | 0.083 | 0.084 | 0.087 | 0.089 | 0.096 | 0.107 | 0.082 |
| 36 | 0.047 | 0.047 | 0.048 | 0.049 | 0.051 | 0.056 | 0.063 | 0.046 |
| 37 | 0.025 | 0.025 | 0.025 | 0.026 | 0.027 | 0.030 | 0.034 | 0.024 |
| 38 | 0.012 | 0.012 | 0.012 | 0.013 | 0.013 | 0.015 | 0.017 | 0.012 |
| 39 | 0.006 | 0.006 | 0.006 | 0.006 | 0.006 | 0.007 | 0.008 | 0.005 |
| 40 | 0.002 | 0.002 | 0.002 | 0.003 | 0.003 | 0.003 | 0.003 | 0.002 |
| 41 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| 42 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Numerical | Analytical | Numerical | Analytical | Numerical | Analytical | |||
|---|---|---|---|---|---|---|---|---|
| 10 | 1.000 | 1.000 | 26 | 1.000 | 1.000 | 44 | 1.000 | 1.000 |
| 11 | 0.999 | 0.999 | 27 | 0.999 | 1.000 | 45 | 0.999 | 0.999 |
| 12 | 0.998 | 0.998 | 28 | 0.999 | 0.999 | 46 | 0.998 | 0.998 |
| 13 | 0.995 | 0.995 | 29 | 0.997 | 0.998 | 47 | 0.997 | 0.997 |
| 14 | 0.987 | 0.987 | 30 | 0.995 | 0.995 | 48 | 0.994 | 0.994 |
| 15 | 0.969 | 0.968 | 31 | 0.990 | 0.990 | 49 | 0.989 | 0.989 |
| 16 | 0.935 | 0.933 | 32 | 0.980 | 0.980 | 50 | 0.982 | 0.982 |
| 17 | 0.875 | 0.873 | 33 | 0.965 | 0.965 | 51 | 0.970 | 0.970 |
| 18 | 0.784 | 0.783 | 34 | 0.941 | 0.940 | 52 | 0.954 | 0.953 |
| 19 | 0.665 | 0.665 | 35 | 0.905 | 0.904 | 53 | 0.930 | 0.930 |
| 20 | 0.527 | 0.528 | 36 | 0.855 | 0.854 | 54 | 0.898 | 0.898 |
| 21 | 0.387 | 0.388 | 37 | 0.790 | 0.789 | 55 | 0.857 | 0.856 |
| 22 | 0.260 | 0.261 | 38 | 0.710 | 0.709 | 56 | 0.805 | 0.805 |
| 23 | 0.159 | 0.159 | 39 | 0.619 | 0.618 | 57 | 0.744 | 0.744 |
| 24 | 0.089 | 0.088 | 40 | 0.520 | 0.520 | 58 | 0.674 | 0.674 |
| 25 | 0.044 | 0.044 | 41 | 0.420 | 0.420 | 59 | 0.597 | 0.597 |
| 26 | 0.020 | 0.020 | 42 | 0.326 | 0.326 | 60 | 0.517 | 0.516 |
| 27 | 0.008 | 0.008 | 43 | 0.241 | 0.241 | 61 | 0.435 | 0.435 |
| 28 | 0.003 | 0.003 | 44 | 0.170 | 0.170 | 62 | 0.356 | 0.356 |
| 29 | 0.001 | 0.001 | 45 | 0.114 | 0.114 | 63 | 0.283 | 0.283 |
| 30 | 0.000 | 0.000 | 46 | 0.073 | 0.073 | 64 | 0.219 | 0.218 |
| 47 | 0.044 | 0.044 | 65 | 0.163 | 0.163 | |||
| 48 | 0.025 | 0.025 | 66 | 0.118 | 0.118 | |||
| 49 | 0.014 | 0.014 | 67 | 0.082 | 0.082 | |||
| 50 | 0.007 | 0.007 | 68 | 0.055 | 0.055 | |||
| 51 | 0.003 | 0.003 | 69 | 0.036 | 0.036 | |||
| 52 | 0.002 | 0.002 | 70 | 0.023 | 0.022 | |||
| 53 | 0.001 | 0.001 | 71 | 0.014 | 0.014 | |||
| 54 | 0.000 | 0.000 | 72 | 0.008 | 0.008 | |||
| 73 | 0.004 | 0.004 | ||||||
| 74 | 0.002 | 0.002 | ||||||
| 75 | 0.001 | 0.001 | ||||||
| 76 | 0.001 | 0.001 | ||||||
| 77 | 0.000 | 0.000 | ||||||
| 0.00390 | 0.00160 | 0.00125 | ||||||
| 0.00203 | 0.00073 | 0.00046 | ||||||
| Analytical | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 1 | 0.995 | 0.995 | 0.995 | 0.995 | 0.995 | 0.995 | 0.995 | 0.995 |
| 2 | 0.990 | 0.990 | 0.990 | 0.990 | 0.990 | 0.990 | 0.990 | 0.990 |
| 3 | 0.985 | 0.985 | 0.985 | 0.985 | 0.985 | 0.985 | 0.985 | 0.985 |
| 4 | 0.980 | 0.980 | 0.980 | 0.980 | 0.980 | 0.980 | 0.980 | 0.980 |
| 5 | 0.976 | 0.976 | 0.976 | 0.976 | 0.976 | 0.976 | 0.976 | 0.976 |
| 6 | 0.971 | 0.971 | 0.971 | 0.971 | 0.971 | 0.971 | 0.971 | 0.971 |
| 7 | 0.966 | 0.966 | 0.966 | 0.966 | 0.966 | 0.966 | 0.966 | 0.966 |
| 8 | 0.962 | 0.962 | 0.962 | 0.962 | 0.962 | 0.962 | 0.962 | 0.962 |
| 9 | 0.957 | 0.957 | 0.957 | 0.957 | 0.957 | 0.957 | 0.957 | 0.957 |
| 10 | 0.952 | 0.952 | 0.952 | 0.952 | 0.952 | 0.952 | 0.952 | 0.952 |
| 11 | 0.948 | 0.948 | 0.948 | 0.948 | 0.948 | 0.948 | 0.948 | 0.948 |
| 12 | 0.943 | 0.943 | 0.943 | 0.943 | 0.943 | 0.943 | 0.943 | 0.943 |
| 13 | 0.939 | 0.939 | 0.939 | 0.939 | 0.939 | 0.939 | 0.939 | 0.939 |
| 14 | 0.935 | 0.935 | 0.935 | 0.935 | 0.935 | 0.935 | 0.935 | 0.935 |
| 15 | 0.930 | 0.930 | 0.930 | 0.930 | 0.930 | 0.930 | 0.930 | 0.930 |
| 16 | 0.926 | 0.926 | 0.926 | 0.926 | 0.926 | 0.926 | 0.926 | 0.926 |
| 17 | 0.922 | 0.922 | 0.922 | 0.922 | 0.922 | 0.922 | 0.922 | 0.922 |
| 18 | 0.917 | 0.917 | 0.917 | 0.917 | 0.917 | 0.917 | 0.917 | 0.917 |
| 19 | 0.913 | 0.913 | 0.913 | 0.913 | 0.913 | 0.913 | 0.913 | 0.913 |
| 20 | 0.908 | 0.908 | 0.908 | 0.908 | 0.908 | 0.909 | 0.909 | 0.909 |
| 21 | 0.903 | 0.903 | 0.904 | 0.904 | 0.904 | 0.904 | 0.904 | 0.904 |
| 22 | 0.898 | 0.898 | 0.898 | 0.898 | 0.898 | 0.898 | 0.898 | 0.898 |
| 23 | 0.890 | 0.891 | 0.891 | 0.891 | 0.891 | 0.891 | 0.892 | 0.891 |
| 24 | 0.880 | 0.881 | 0.881 | 0.881 | 0.881 | 0.882 | 0.883 | 0.880 |
| 25 | 0.866 | 0.866 | 0.866 | 0.867 | 0.867 | 0.869 | 0.870 | 0.865 |
| 26 | 0.844 | 0.845 | 0.845 | 0.846 | 0.847 | 0.850 | 0.851 | 0.844 |
| 27 | 0.814 | 0.814 | 0.815 | 0.817 | 0.818 | 0.823 | 0.825 | 0.813 |
| 28 | 0.772 | 0.772 | 0.774 | 0.776 | 0.778 | 0.785 | 0.788 | 0.771 |
| 29 | 0.716 | 0.718 | 0.719 | 0.723 | 0.726 | 0.735 | 0.739 | 0.716 |
| 30 | 0.649 | 0.650 | 0.652 | 0.656 | 0.660 | 0.672 | 0.678 | 0.648 |
| 31 | 0.570 | 0.572 | 0.575 | 0.579 | 0.584 | 0.598 | 0.604 | 0.570 |
| 75 | 0.04315 | 0.03812 | NA | NA |
| 60 | 0.03452 | 0.03049 | NA | NA |
| 30 | 0.01699 | 0.01498 | 0.01291 | NA |
| 20 | 0.01110 | 0.00978 | 0.00844 | 0.00622 |
| 10 | 0.00532 | 0.00464 | 0.00396 | 0.00291 |
| 5 | 0.00257 | 0.00219 | 0.00185 | 0.00133 |
| 1 | 0.00109 | 0.00087 | 0.00072 | 0.00050 |
| 100 | 0.08198 | NA | NA | NA |
| 75 | 0.06042 | 0.05782 | NA | NA |
| 60 | 0.04810 | 0.04577 | NA | NA |
| 30 | 0.02253 | 0.02111 | 0.01951 | NA |
| 20 | 0.01396 | 0.01297 | 0.01208 | 0.01029 |
| 10 | 0.00626 | 0.00567 | 0.00520 | 0.00427 |
| 5 | 0.00430 | 0.00377 | 0.00346 | 0.00270 |
| 1 | 0.00332 | 0.00305 | 0.00267 | 0.00210 |
| Numerical | Analytical | Numerical | Analytical | Numerical | Analytical | |||
|---|---|---|---|---|---|---|---|---|
| 0 | 1.000 | 1.000 | 0 | 1.000 | 1.000 | 0 | 1.000 | 1.000 |
| 1 | 0.995 | 0.995 | 1 | 0.995 | 0.995 | 1 | 0.995 | 0.995 |
| 2 | 0.990 | 0.990 | 2 | 0.990 | 0.990 | 2 | 0.990 | 0.990 |
| 3 | 0.985 | 0.985 | 3 | 0.985 | 0.985 | 3 | 0.985 | 0.985 |
| 4 | 0.980 | 0.980 | 4 | 0.980 | 0.980 | 4 | 0.980 | 0.980 |
| 5 | 0.975 | 0.976 | 5 | 0.975 | 0.976 | 5 | 0.976 | 0.976 |
| 6 | 0.970 | 0.971 | 6 | 0.969 | 0.970 | 6 | 0.970 | 0.971 |
| 7 | 0.964 | 0.965 | 7 | 0.963 | 0.964 | 7 | 0.965 | 0.966 |
| 8 | 0.957 | 0.957 | 8 | 0.956 | 0.955 | 8 | 0.960 | 0.960 |
| 9 | 0.945 | 0.944 | 9 | 0.940 | 0.938 | 9 | 0.953 | 0.953 |
| 10 | 0.921 | 0.918 | 10 | 0.906 | 0.903 | 10 | 0.942 | 0.941 |
| 11 | 0.872 | 0.869 | 11 | 0.842 | 0.840 | 11 | 0.920 | 0.917 |
| 12 | 0.788 | 0.787 | 12 | 0.740 | 0.741 | 12 | 0.879 | 0.875 |
| 13 | 0.669 | 0.671 | 13 | 0.604 | 0.607 | 13 | 0.808 | 0.805 |
| 14 | 0.523 | 0.527 | 14 | 0.450 | 0.454 | 14 | 0.704 | 0.703 |
| 15 | 0.373 | 0.376 | 15 | 0.303 | 0.305 | 15 | 0.573 | 0.573 |
| 16 | 0.239 | 0.241 | 16 | 0.182 | 0.182 | 16 | 0.430 | 0.431 |
| 17 | 0.137 | 0.137 | 17 | 0.097 | 0.096 | 17 | 0.294 | 0.295 |
| 18 | 0.070 | 0.069 | 18 | 0.045 | 0.044 | 18 | 0.183 | 0.182 |
| 19 | 0.032 | 0.031 | 19 | 0.019 | 0.018 | 19 | 0.102 | 0.101 |
| 20 | 0.013 | 0.012 | 20 | 0.007 | 0.006 | 20 | 0.051 | 0.050 |
| 21 | 0.004 | 0.004 | 21 | 0.002 | 0.002 | 21 | 0.023 | 0.022 |
| 22 | 0.001 | 0.001 | 22 | 0.001 | 0.001 | 22 | 0.009 | 0.009 |
| 23 | 0.000 | 0.000 | 23 | 0.000 | 0.000 | 23 | 0.003 | 0.003 |
| …. | … | … | …. | … | … | 24 | 0.001 | 0.001 |
| 100 | 0.000 | 0.000 | 100 | 0.000 | 0.000 | 25 | 0.000 | 0.000 |
| …. | … | … | ||||||
| 100 | 0.000 | 0.000 | ||||||
| 0.00729 | 0.00749 | 0.00590 | ||||||
| 0.00346 | 0.00360 | 0.00335 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurarslan, G. Sixth-Order Combined Compact Finite Difference Scheme for the Numerical Solution of One-Dimensional Advection-Diffusion Equation with Variable Parameters. Mathematics 2021, 9, 1027. https://doi.org/10.3390/math9091027
Gurarslan G. Sixth-Order Combined Compact Finite Difference Scheme for the Numerical Solution of One-Dimensional Advection-Diffusion Equation with Variable Parameters. Mathematics. 2021; 9(9):1027. https://doi.org/10.3390/math9091027
Chicago/Turabian StyleGurarslan, Gurhan. 2021. "Sixth-Order Combined Compact Finite Difference Scheme for the Numerical Solution of One-Dimensional Advection-Diffusion Equation with Variable Parameters" Mathematics 9, no. 9: 1027. https://doi.org/10.3390/math9091027
APA StyleGurarslan, G. (2021). Sixth-Order Combined Compact Finite Difference Scheme for the Numerical Solution of One-Dimensional Advection-Diffusion Equation with Variable Parameters. Mathematics, 9(9), 1027. https://doi.org/10.3390/math9091027






