The Influence of Latent and Chronic Infection on Pathogen Persistence
Abstract
:1. Introduction
2. Methods
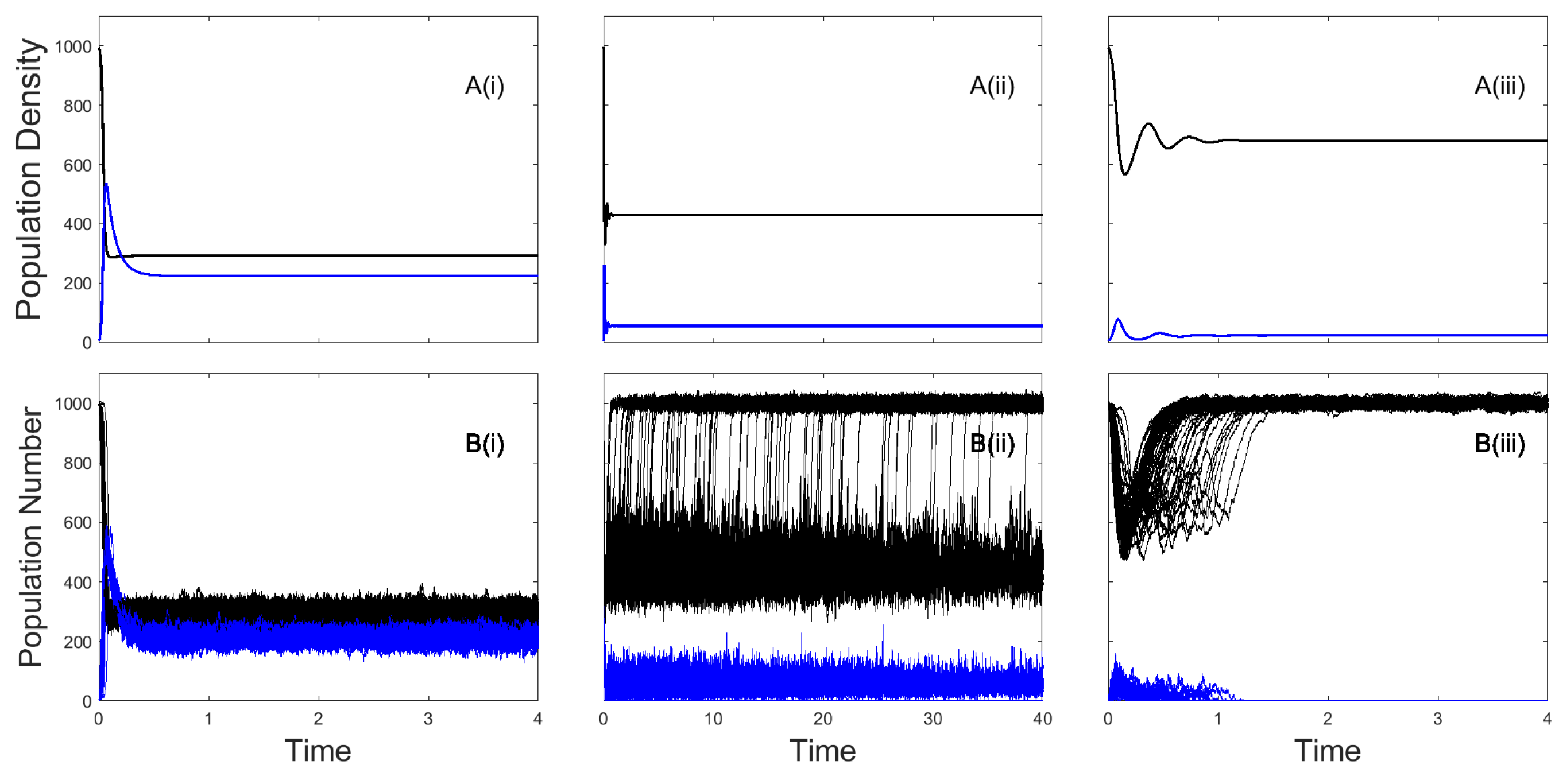
3. Results
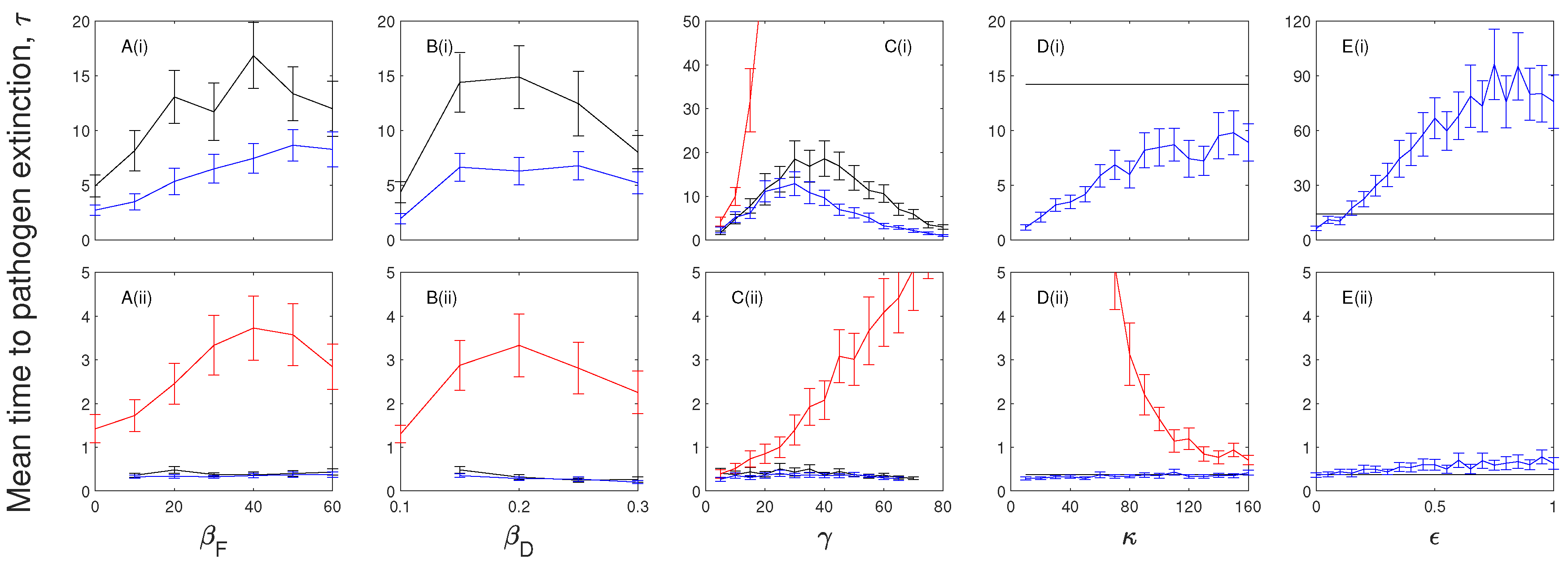
3.1. The Impacts of Exposed/Latent Infection on the Mean Time to Pathogen Extinction
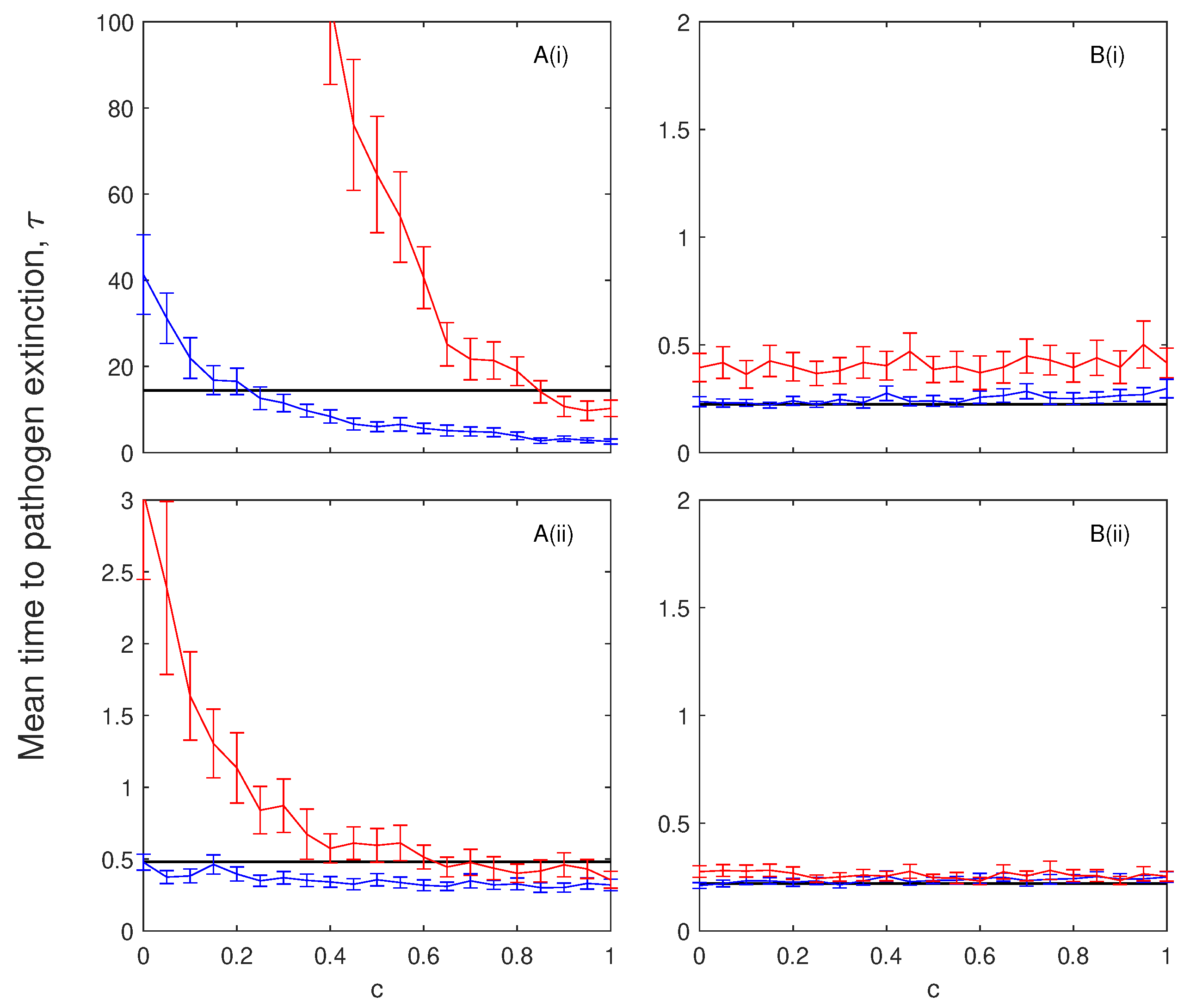
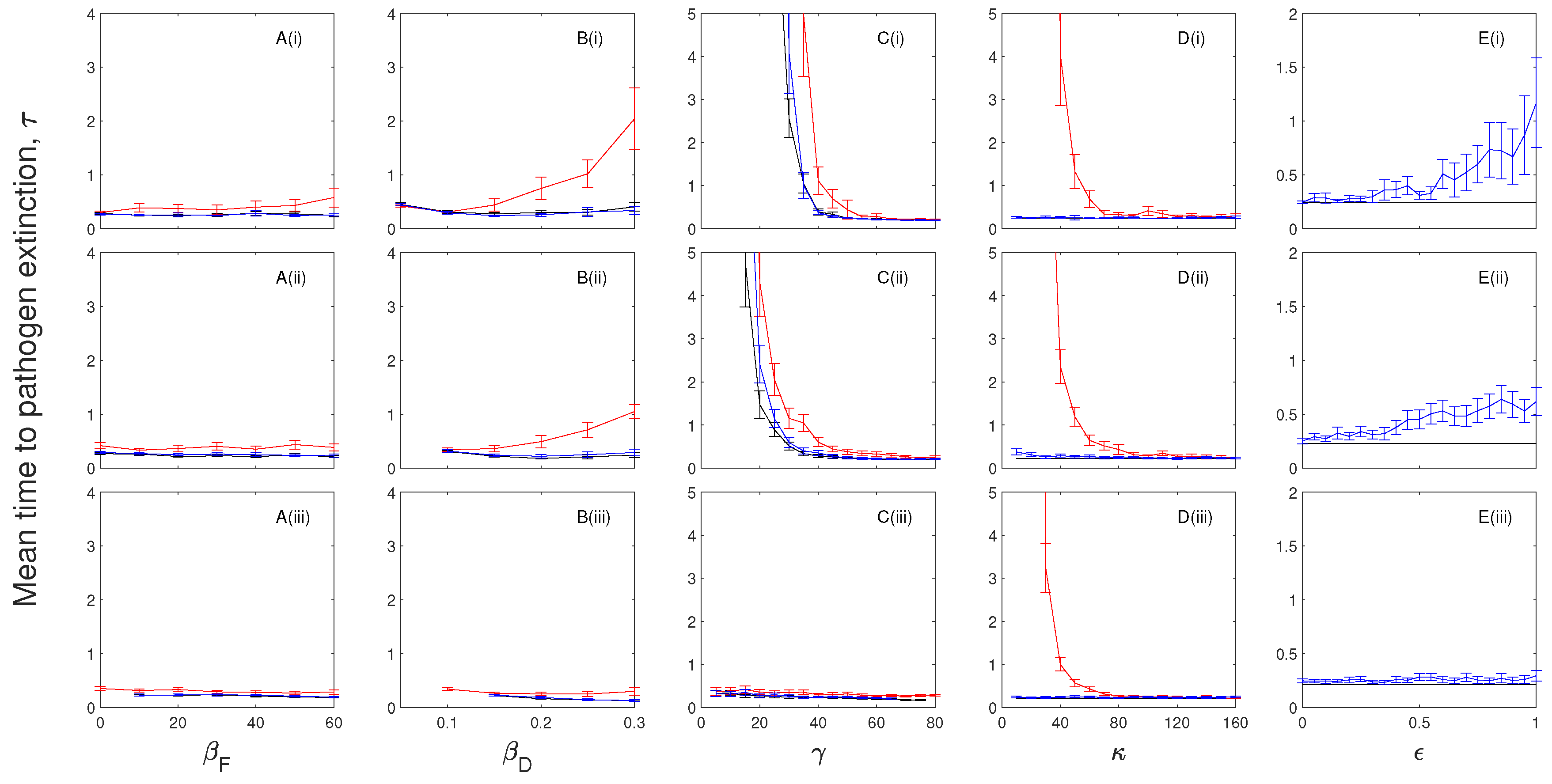
3.2. The Impacts of Chronic Infection on the Mean Time to Pathogen Extinction
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASF | African swine fever |
| TB | Tuberculosis |
References
- Anderson, R.; May, R. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Keeling, M.; Rohani, P. Modelling Infectious Diseases in Humans and Animals; Princeton Unviersity Press: Princeton, IL, USA, 2008. [Google Scholar]
- Aliee, M.; Rock, K.; Keeling, M.J. Estimating the distribution of time to extinction of infectious diseases in mean-field approaches. J. R. Soc. Interface 2020, 17, 1–7. [Google Scholar] [CrossRef]
- Lloyd-Smith, J.; Cross, P.; Briggs, C.; Daugherty, M.; Getz, W.; Latto, J.; Sanchez, M.; Smith, A.; Swei, A. Should we expect population thresholds for wildlife disease? Trends Ecol. Evol. 2005, 20, 511–519. [Google Scholar] [CrossRef]
- Nåsell, I. A new look at the critical community size for childhood infections. J. Theor. Popul. Biol. 2005, 67, 203–216. [Google Scholar] [CrossRef] [PubMed]
- Garnett, G.; Cousens, S.; Hallet, T.; Steketee, R.; Walker, N. Mathematical models in the evaluation of health programmes. Lancet 2011, 378, 515–525. [Google Scholar] [CrossRef] [Green Version]
- McCallum, H. Models for managing wildlife disease. Parasitology 2016, 143, 805–820. [Google Scholar] [CrossRef] [PubMed]
- Nåsell, I. On the time to extinction in recurrent epidemics. J. R. Stat. Soc. 1999, 61, 309–330. [Google Scholar] [CrossRef]
- Andersson, H.; Djehiche, B. A Threshold Limit Theorem for the Stochastic Logistic Epidemic. J. Appl. Probab. 1998, 35, 662–670. [Google Scholar] [CrossRef]
- Ball, F.; Britton, T.; Neal, P. On Expected Durations of Birth-Death Processes with Applications to Branching Processes and SIS Epidemics. J. Appl. Probab. 2016, 53, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Allen, L.; Burgin, A. Comparison of deterministic and stochastic SIS and SIR models in discrete time. Math. Biosci. 2000, 163, 1–33. [Google Scholar] [CrossRef]
- Clancy, D.; Mendy, S. The effect of waning immunity on long-term behaviour of stochastic models for the spread of infection. J. Math. Biol. 2010, 61, 527–544. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Texts in Applied Mathematics; Springer: New York, NY, USA, 2012; Volume 2. [Google Scholar]
- George, D.; Webb, C.; Farnsworth, M.; O’Shea, T.; Bowen, R.; Smith, D.; Stanley, T.; Ellison, L.; Rupprecht, C. Host and viral ecology determine bat rabies seasonality and maintenance. Proc. Natl. Acad. Sci. USA 2011, 108, 10208–10213. [Google Scholar] [CrossRef] [Green Version]
- Balfour, H.; Dunmire, S.; Hogquist, K. Infectious mononucleosis. Clin. Transl. Immunol. 2015, 4, e33. [Google Scholar] [CrossRef] [PubMed]
- World Health Organisation. Coronavirus Disease 2019 (COVID-19): Situation Report, 73; Technical Documents; World Health Organisation: Geneva, Switzerland, 2020. [Google Scholar]
- O’Neill, X.; White, A.; Ruiz-Fons, F.; Gortázar, C. Modelling the transmission and persistence of African swine fever in wild boar in contrasting European scenarios. Sci. Rep. 2020, 10, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ståhl, K.; Sternberg-Lewerin, S.; Blome, S.; Viltrop, A.; Penrith, M.; Chenais, E. Lack of evidence for long term carriers of African swine fever virus—A systematic review. Virus Res. 2019, 272, 197725. [Google Scholar] [CrossRef] [PubMed]
- Ebert, D.; Lipsitch, M.; Mangin, K. The Effect of parasites on host population density and extinction: Experimental epidemiology with Daphnia and six microparasites. Am. Nat. 2000, 156, 459–477. [Google Scholar] [CrossRef]
- Ryder, J.; Miller, M.; White, A.; Knell, R.; Boots, M. Host-parasite population dynamics under combined frequency- and density-dependent transmission. Oikos 2007, 116, 2017–2026. [Google Scholar] [CrossRef]
- Gillespie, D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Kamina, K.; Mwalili, S.; Wanjoya, A. The Modeling of a Stochastic SIR Model for HIV/AIDS Epidemic Using Gillespie’s Algorithm. Int. J. Data Sci. Anal. 2019, 5, 117–122. [Google Scholar] [CrossRef]
- White, A.; Bell, S.; Lurz, P.; Boots, M. Conservation management within strongholds in the face of disease-mediated invasions: Red and grey squirrels as a case study. J. Appl. Ecol. 2014, 51, 1631–1642. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.; May, R. The population dynamics of microparasites and their invertebrate hosts. Phil. Trans. R. Soc. Lond. B 1981, 291, 451–524. [Google Scholar] [CrossRef]
- Renshaw, E. Modelling Biological Populations in Space and Time; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar] [CrossRef]
- Norris, J. Markov Chains; Cambridge University Press: Cambridge, UK, 1997; Chapter 3. [Google Scholar]
- Bailey, N. The Mathematical Theory of Infectious Diseases; Charles Griffin & Company Ltd.: Glasgow, UK, 1975. [Google Scholar]
- Cross, P.; Lloyd-Smith, J.; Johnson, P.; Getz, W. Duelling timescales of host movement and disease recovery determine invasion of disease in structured populations. Ecol. Lett. 2005, 8, 587–595. [Google Scholar] [CrossRef]
- McCallum, H.; Jones, M.; Hawkins, C.; Hamede, R.; Lachish, S.; Sinn, D.; Beeton, N.; Lazenby, B. Transmission dynamics of Tasmanian devil facial tumor disease may lead to disease-induced extinction. Ecology 2009, 90, 3379–3392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gortázar, C.; Che Amat, A.; O’Brien, D. Open questions and recent advances in the control of a multi-host infectious disease: Animal tuberculosis. Mamm. Rev. 2015, 45, 160–175. [Google Scholar] [CrossRef] [Green Version]
- Díez-Delgado, I.; Sevilla, I.; Romero, B.; Tanner, E.; Barasona, J.; White, A.; Lurz, P.; Boots, M.; de la Fuente, J.; Dominguez, L.; et al. Impact of piglet oral vaccination against tuberculosis in endemic free-ranging wild boar populations. Prev. Vet. Med. 2018, 155, 11–20. [Google Scholar] [CrossRef]
- Tanner, E.; White, A.; Lurz, P.; Gortázar, C.; Díez-Delgado, I.; Boots, M. The critical role of infectious disease in compensatory population growth in response to culling. Am. Nat. 2019, 194, E1–E12. [Google Scholar] [CrossRef]
- Peng, L.; Yang, W.; Zhang, D.; Zhuge, C.; Hong, L. Epidemic analysis of COVID-19 in China by dynamical modeling. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef]



| State Transition | Transition Rate | |
|---|---|---|
| Birth of susceptible | ||
| Natural death of susceptible | ||
| Infection | ||
| Recovery of infected | ||
| Death of infected |
| Maximum birth rate of the population. | |
| Natural death rate of the population. | |
| Population carrying capacity in the absence of infection. | |
| Frequency-dependent transmission rate. | |
| Density-dependent transmission coefficient. | |
| Recovery rate of infected individuals. | |
| Disease-induced mortality rate, with representing a low, medium and high rate, respectively. | |
| Rate of progression from an exposed or chronically infected state. | |
| Exposed/latent | |
| Proportional pathogen transmission for the exposed/latent class. | |
| Chronic | |
| For models that include chronic infection we consider two baseline cases for the proportional transmission from chronically infected individuals, , and the proportion of disease-induced mortality incurred by chronic individuals, c. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Neill, X.; White, A.; Clancy, D.; Ruiz-Fons, F.; Gortázar, C. The Influence of Latent and Chronic Infection on Pathogen Persistence. Mathematics 2021, 9, 1007. https://doi.org/10.3390/math9091007
O’Neill X, White A, Clancy D, Ruiz-Fons F, Gortázar C. The Influence of Latent and Chronic Infection on Pathogen Persistence. Mathematics. 2021; 9(9):1007. https://doi.org/10.3390/math9091007
Chicago/Turabian StyleO’Neill, Xander, Andy White, Damian Clancy, Francisco Ruiz-Fons, and Christian Gortázar. 2021. "The Influence of Latent and Chronic Infection on Pathogen Persistence" Mathematics 9, no. 9: 1007. https://doi.org/10.3390/math9091007
APA StyleO’Neill, X., White, A., Clancy, D., Ruiz-Fons, F., & Gortázar, C. (2021). The Influence of Latent and Chronic Infection on Pathogen Persistence. Mathematics, 9(9), 1007. https://doi.org/10.3390/math9091007






