Advanced Metaheuristic Method for Decision-Making in a Dynamic Job Shop Scheduling Environment
Abstract
1. Introduction
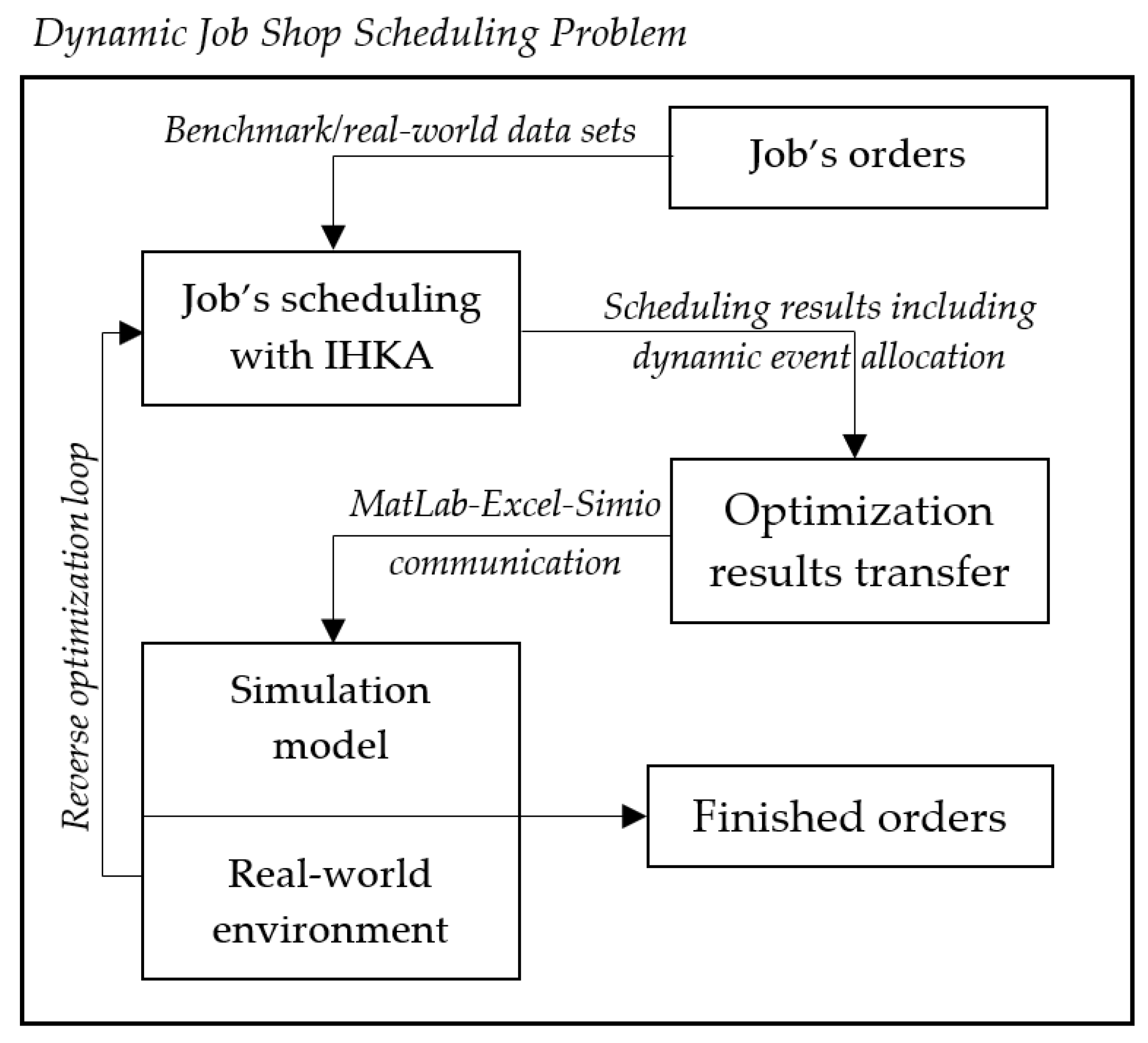
2. Dynamic Job Shop Scheduling Problem
- All machines from a set of are available at time 0;
- An individual operation can only be performed on one machine at a time;
- A single machine can only perform one operation at a time;
- The operation performed on machine can only be interrupted when there is a dynamic event of machine breakdown appearing;
- The next operation can be performed only when the previous one is completed;
- The process times of the operation and the assigned machine are known in advance. During individual operation, the processing time may change due to a dynamic event of changing the original operation processing time;
- The original operation processing time;
- Setup times do not depend on the operation execution sequence and the machine on which the operation will be performed, but are included in the processing time of the operation;
- Transport time between machines is 0.
| initial jobs | |
| new jobs | |
| machines | |
| set of routing constraints | |
| set of new jobs’ routing constraints | |
| process time of operation | |
| process time of new job operation | |
| competition time of job j on machine | |
| competition time of new job j’ on machine | |
| starting time of operation | |
| starting time of new operation | |
| the start time of the rescheduled job order | |
| the start that the machine will be idled at the start of rescheduling job order |
3. Metaheuristic Algorithm
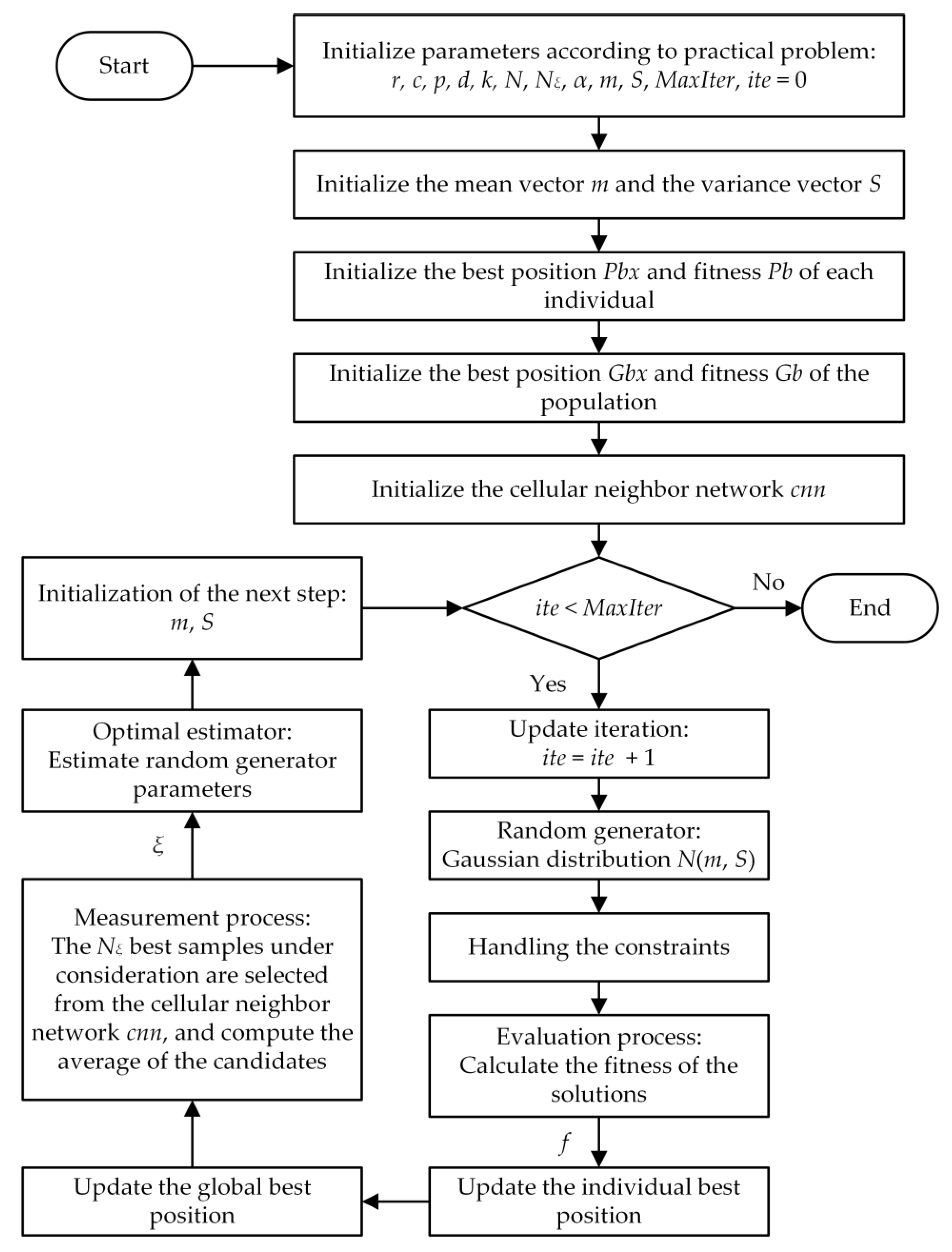
3.1. Heuristic Kalman Algorithm
3.2. Improved Heuristic Kalman Algorithm
| Algorithm 1. The general pseudo-code of the IHKA. |
|
3.2.1. Initializing the Variables
3.2.2. Handling the Constraints
3.2.3. Updating the Individual Best
3.2.4. Introducing the Cellular Neighbor Network
| Algorithm 2. The general pseudo-code for creating cellular neighbor network. |
| Input: the number of rows of the cellular neighbor network , the number of columns of the cellular neighbor network , the neighbor type of the cellular neighbor network , the rewiring probability of the cellular neighbor network , the minimum maximum depth of the cellular neighbor network , the nearest neighbors of the cellular neighbor network . Output: the cellular neighbor network.Initialize the network. Step 0: Initialize a regular cellular neighbor network based on the type of cellular neighborhood. Step 1: Create the network. Construct a cellular neighbor network based on the rewiring probability of the cellular neighbor network . After cutting, the minimum maximum depths of the two nodes selected for deletion are checked, if the requirements are not met, the disconnection is canceled. Note that this check does not affect the addition of new random connections. Step 2: Obtain nearest neighbors. Obtain the nearest neighbors (containing itself) of each node in the network. |
3.2.5. Computing the Measurement
3.2.6. Computing the Posterior Estimation
4. Experiment Design
4.1. Applying the Algorithm on DJSSP
4.2. Evaluating the Algorithm
4.2.1. Selecting the Benchmark Instance
4.2.2. Defining the Parameters
4.3. Transferring Optimization Results to Simulation Evaluation
5. Result
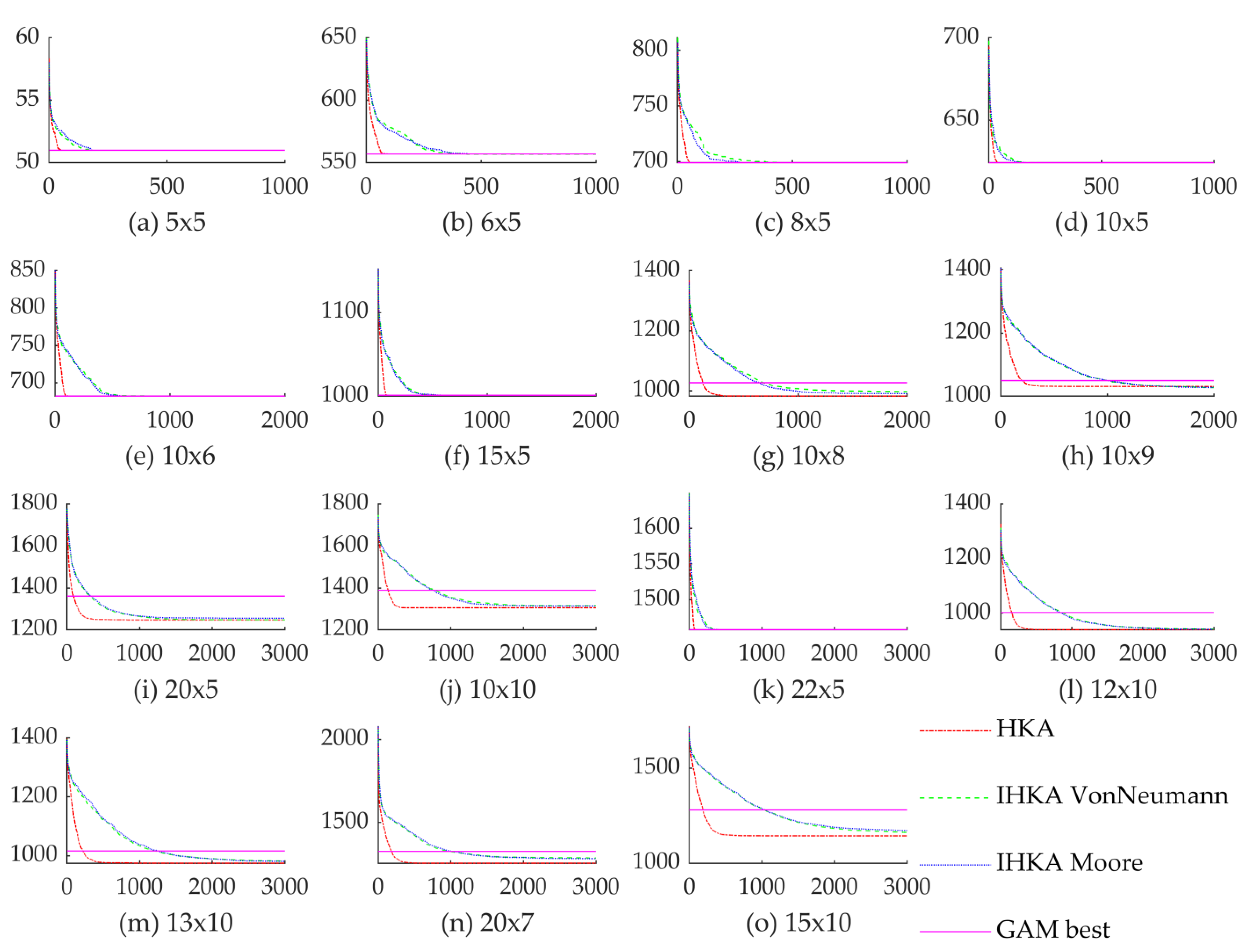
5.1. Results Comparison to Other Algorithms
5.2. Simulation Modeling Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toscano, R.; Lyonnet, P. A new heuristic approach for non-convex optimization problems. Inf. Sci. 2010, 180, 1955–1966. [Google Scholar] [CrossRef]
- Adibi, M.A.; Zandieh, M.; Amiri, M. Multi-objective scheduling of dynamic job shop using variable neighborhood search. Expert Syst. Appl. 2010, 37, 282–287. [Google Scholar] [CrossRef]
- Shahrabi, J.; Adibi, M.A.; Mahootchi, M. A reinforcement learning approach to parameter estimation in dynamic job shop scheduling. Comput. Ind. Eng. 2017, 110, 75–82. [Google Scholar] [CrossRef]
- Vinod, V.; Sridharan, R. Simulation modeling and analysis of due-date assignment methods and scheduling decision rules in a dynamic job shop production system. Int. J. Prod. Econ. 2011, 129, 127–146. [Google Scholar] [CrossRef]
- Xiong, H.; Fan, H.; Jiang, G.; Li, G. A simulation-based study of dispatching rules in a dynamic job shop scheduling problem with batch release and extended technical precedence constraints. Eur. J. Oper. Res. 2017, 257, 13–24. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, L.; Li, X. A hybrid genetic algorithm and tabu search for a multi-objective dynamic job shop scheduling problem. Int. J. Prod. Res. 2013, 51, 3516–3531. [Google Scholar] [CrossRef]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M. An investigation of ensemble combination schemes for genetic programming based hyper-heuristic approaches to dynamic job shop scheduling. Appl. Soft Comput. 2018, 63, 72–86. [Google Scholar] [CrossRef]
- Turker, A.K.; Aktepe, A.; Inal, A.F.; Ersoz, O.O.; Das, G.S.; Birgoren, B. A decision support system for dynamic job-shop scheduling using real-time data with simulation. Mathematics 2019, 7, 278. [Google Scholar] [CrossRef]
- Rajabinasab, A.; Mansour, S. Dynamic flexible job shop scheduling with alternative process plans: An agent-based approach. Int. J. Adv. Manuf. Technol. 2011, 54, 1091–1107. [Google Scholar] [CrossRef]
- Nie, L.; Gao, L.; Li, P.; Li, X. A GEP-based reactive scheduling policies constructing approach for dynamic flexible job shop scheduling problem with job release dates. J. Intell. Manuf. 2013, 24, 763–774. [Google Scholar] [CrossRef]
- Geyik, F.; Dosdogru, A.T. Process plan and part routing optimization in a dynamic flexible job shop scheduling environment: An optimization via simulation approach. Neural Comput. Appl. 2013, 23, 1631–1641. [Google Scholar] [CrossRef]
- Shen, X.-N.; Yao, X. Mathematical modeling and multi-objective evolutionary algorithms applied to dynamic flexible job shop scheduling problems. Inf. Sci. 2015, 298, 198–224. [Google Scholar] [CrossRef]
- Hosseinabadi, A.A.R.; Siar, H.; Shamshirband, S.; Shojafar, M.; Nasir, M.H.N.M. Using the gravitational emulation local search algorithm to solve the multi-objective flexible dynamic job shop scheduling problem in small and medium Enterprises. Ann. Oper. Res. 2015, 229, 451–474. [Google Scholar] [CrossRef]
- Gocken, T.; Dosdogru, A.T.; Boru, A.; Gocken, M. Integrating process plan and part routing using optimization via simulation approach. Int. J. Simul. Model. 2019, 18, 254–266. [Google Scholar] [CrossRef]
- Yu, M.R.; Yang, B.; Chen, Y. Dynamic integration of process planning and scheduling using a discrete particle swarm optimization algorithm. Adv. Prod. Eng. Manag. 2018, 13, 279–296. [Google Scholar] [CrossRef]
- Ren, T.; Zhang, Y.; Cheng, S.-R.; Wu, C.-C.; Zhang, M.; Chang, B.; Wang, X.; Zhao, P. Effective heuristic algorithms solving the jobshop scheduling problem with release dates. Mathematics 2020, 8, 1221. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.Q. A discrete job-shop scheduling algorithm based on improved genetic algorithm. Int. J. Simul. Model. 2020, 19, 517–528. [Google Scholar] [CrossRef]
- Ojstersek, R.; Zhang, H.; Liu, S.; Buchmeister, B. Improved heuristic Kalman algorithm for solving multi-objective flexible job shop scheduling problem. Procedia Manuf. 2018, 17, 895–902. [Google Scholar] [CrossRef]
- Kundakcı, N.; Kulak, O. Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem. Comput. Ind. Eng. 2016, 96, 31–51. [Google Scholar] [CrossRef]
- Toscano, R.; Lyonnet, P. A kalman optimization approach for solving some industrial electronics problems. IEEE Trans. Ind. Electron. 2012, 59, 4456–4464. [Google Scholar] [CrossRef]
- Zhang, H.; Buchmeister, B.; Liu, S.; Ojstersek, R. Use of a simulation environment and metaheuristic algorithm for human resource management in a cyber-physical system. In Simulation for Industry 4.0; Gunal, M., Ed.; Springer: Cham, Germany, 2019; pp. 219–246. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Yang, L.; Li, J. Dynamic route and departure time choice model based on self-adaptive reference point and reinforcement learning. Phys. A Stat. Mech. its Appl. 2018, 502, 77–92. [Google Scholar] [CrossRef]
- Von Neumann Neighborhood. Available online: https://en.wikipedia.org/wiki/Von_Neumann_neighborhood (accessed on 26 August 2020).
- Moore Neighborhood. Available online: https://en.wikipedia.org/wiki/Moore_neighborhood (accessed on 16 December 2020).
- Marinakis, Y.; Marinaki, M. A hybrid particle swarm optimization algorithm for the open vehicle routing problem. In Swarm Intelligence. ANTS 2012. Lecture Notes in Computer Science; Dorigo, M., Birattari, M., Blum, C., Christensen, A.L., Engelbrecht, A.P., Groß, R., Stützle, T., Eds.; Springer: Berlin, Germany, 2012; pp. 180–187. [Google Scholar] [CrossRef]
- Milgram, S. The small world problem. Psychol. Today 1967, 1, 60–67. [Google Scholar]
- Ojstersek, R.; Lalic, D.; Buchmeister, B. A new method for mathematical and simulation modelling interactivity: A case study in flexible job shop scheduling. Adv. Prod. Eng. Manag. 2019, 14, 435–448. [Google Scholar] [CrossRef]






| Size Type | No | Size n × m | Number of Operations | Number of Dynamic Operations | Total | Optimal Fitness 1 |
|---|---|---|---|---|---|---|
| small | 1 | 5 × 5 | 25 | 10 | 35 | 51 |
| 2 | 6 × 5 | 30 | 15 | 45 | 557 | |
| 3 | 8 × 5 | 40 | 5 | 45 | 699 | |
| 4 | 10 × 5 | 50 | 5 | 55 | 624 | |
| medium | 5 | 10 × 6 | 60 | 6 | 66 | 682 |
| 6 | 15 × 5 | 75 | 5 | 80 | 1001 | |
| 7 | 10 × 8 | 80 | 8 | 88 | 1027 | |
| 8 | 10 × 9 | 90 | 18 | 108 | 1049 | |
| large | 9 | 20 × 5 | 100 | 5 | 105 | 1361 |
| 10 | 10 × 10 | 100 | 10 | 110 | 1389 | |
| 11 | 22 × 5 | 110 | 15 | 125 | 1458 | |
| 12 | 12 × 10 | 120 | 10 | 130 | 1002 | |
| 13 | 13 × 10 | 130 | 10 | 140 | 1016 | |
| 14 | 20 × 7 | 140 | 14 | 154 | 1326 | |
| 15 | 15 × 10 | 150 | 20 | 170 | 1280 |
| No | Name | Value | No | Name | Value | No | Name | Value | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 20 | 4 | 5 | 7 | 10 | ||||
| 2 | 15 | 5 | 9 | 8 | 0.3 | ||||
| 3 | 0.5 | 6 | 300 | 9 | small | 1000 | |||
| medium | 2000 | ||||||||
| large | 3000 | ||||||||
| Job/Operation | Machine | Start Time (Time Unit) | End Time (Time Unit) | Process Time (Time Unit) | Dynamic Event |
|---|---|---|---|---|---|
| J3,1 | M4 | 0 | 34 + 9 = 43 | 43 | MB |
| J3,2 | M3 | 69 | 133 | 64 | / |
| J3,3 | M2 | 133 | 156 | 23 | PTC |
| J3,4 | M5 | 201 | 293 | 92 | / |
| J3,5 | M1 | 453 | 536 | 83 | / |
| J4,1 | M2 | 21 | 87 + 5 = 113 | 92 | MB |
| J4,2 | M4 | 141 | 210 | 69 | / |
| J4,3 | M3 | 318 | 405 | 87 | / |
| J4,4 | M1 | 405 | 453 | 48 | PTC |
| J4,5 | M5 | 484 | 544 | 60 | / |
| J7, 1 | M4 | 119 | 141 | 22 | NJA |
| J7,2 | M2 | 156 | 188 | 32 | NJA |
| J7,3 | M1 | 188 | 198 | 10 | NJA |
| J7,4 | M3 | 405 | 430 | 25 | NJA |
| J7,5 | M5 | 430 | 484 | 54 | NJA |
| Size n × m | GAM Best | HKA | IHKA VonNeumann | IHKA Moore | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Std. | SR | Min | Max | Mean | Std. | SR | Min | Max | Mean | Std. | SR | ||
| 5 × 5 | 51 | 51 | 51 | 51 | 0 | 100 | 51 | 51 | 51 | 0 | 100 | 51 | 51 | 51 | 0 | 100 |
| 6 × 5 | 557 | 557 | 557 | 557 | 0 | 100 | 552 | 557 | 556.83 | 0.91 | 100 | 557 | 557 | 557 | 0 | 100 |
| 8 × 5 | 699 | 699 | 699 | 699 | 0 | 100 | 699 | 699 | 699 | 0 | 100 | 699 | 699 | 699 | 0 | 100 |
| 10 × 5 | 624 | 624 | 624 | 624 | 0 | 100 | 624 | 624 | 624 | 0 | 100 | 624 | 624 | 624 | 0 | 100 |
| 10 × 6 | 682 | 682 | 682 | 682 | 0 | 100 | 682 | 682 | 682 | 0 | 100 | 682 | 682 | 682 | 0 | 100 |
| 15 × 5 | 1001 | 1001 | 1001 | 1001 | 0 | 100 | 1001 | 1001 | 1001 | 0 | 100 | 1001 | 1001 | 1001 | 0 | 100 |
| 10 × 8 | 1027 | 947 | 1009 | 982.17 | 15.11 | 100 | 953 | 1022 | 997.47 | 16.55 | 100 | 944 | 1019 | 990.77 | 19.88 | 100 |
| 10 × 9 | 1049 | 1005 | 1059 | 1030.73 | 14.17 | 86.7 | 1005 | 1043 | 1026.73 | 11.97 | 100 | 1005 | 1052 | 1027.30 | 13.28 | 96.7 |
| 20 × 5 | 1361 | 1202 | 1277 | 1245.90 | 17.49 | 100 | 1217 | 1282 | 1246.10 | 18.32 | 100 | 1218 | 1307 | 1255.20 | 18.97 | 100 |
| 10 × 10 | 1389 | 1292 | 1337 | 1304.90 | 10.84 | 100 | 1287 | 1360 | 1313.80 | 16.62 | 100 | 1289 | 1359 | 1312.60 | 18 | 100 |
| 22 × 5 | 1458 | 1458 | 1458 | 1458 | 0 | 100 | 1458 | 1458 | 1458 | 0 | 100 | 1458 | 1458 | 1458 | 0 | 100 |
| 12 × 10 | 1002 | 912 | 981 | 939.63 | 17.18 | 100 | 914 | 989 | 941.33 | 17.81 | 100 | 918 | 979 | 940.90 | 13.60 | 100 |
| 13 × 10 | 1016 | 949 | 1011 | 974.80 | 15.95 | 100 | 947 | 1016 | 981.70 | 17.95 | 100 | 952 | 1008 | 980.90 | 13.60 | 100 |
| 20 × 7 | 1326 | 1246 | 1286 | 1255.30 | 11.66 | 100 | 1260 | 1315 | 1286.40 | 15.51 | 100 | 1246 | 1324 | 1281.47 | 19.42 | 100 |
| 15 × 10 | 1280 | 1112 | 1164 | 1143.87 | 14.77 | 100 | 1130 | 1203 | 1161.77 | 20.21 | 100 | 1122 | 1246 | 1171.50 | 27.12 | 100 |
| Machine 1 | Job’s sequence | 1 | 7 | 5 | 6 | 9 | 2 | 4 | 3 | 8 |
| Start time | 69 | 188 | 231 | 275 | 370 | 393 | 405 | 453 | 536 | |
| Finish time | 122 | 198 | 275 | 370 | 393 | 405 | 453 | 536 | 545 | |
| Machine 2 | Job’s sequence | 1 | 4 | 3 | 7 | 5 | 9 | 6 | 2 | 8 |
| Start time | 0 | 21 | 133 | 156 | 275 | 324 | 370 | 405 | 447 | |
| Finish time | 21 | 113 | 156 | 188 | 324 | 334 | 377 | 447 | 496 | |
| Machine 3 | Job’s sequence | 6 | 1 | 3 | 5 | 8 | 2 | 4 | 7 | 9 |
| Start time | 0 | 35 | 69 | 133 | 231 | 287 | 318 | 405 | 430 | |
| Finish time | 35 | 69 | 133 | 231 | 287 | 318 | 405 | 430 | 477 | |
| Machine 4 | Job’s sequence | 3 | 6 | 7 | 4 | 1 | 8 | 5 | 2 | 9 |
| Start time | 0 | 43 | 119 | 141 | 210 | 320 | 420 | 447 | 486 | |
| Finish time | 43 | 119 | 141 | 210 | 265 | 352 | 437 | 486 | 513 | |
| Machine 5 | Job’s sequence | 2 | 6 | 1 | 3 | 8 | 5 | 7 | 4 | 9 |
| Start time | 0 | 119 | 180 | 201 | 293 | 324 | 430 | 484 | 544 | |
| Finish time | 55 | 180 | 201 | 293 | 320 | 420 | 484 | 544 | 552 |
| Size n × m | HKA | IHKA VonNeumann | IHKA Moore | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Std. | Min | Max | Mean | Std. | Min | Max | Mean | Std. | |
| 5 × 5 | 1.74 | 2.06 | 1.83 | 0.08 | 1.85 | 2.16 | 1.95 | 0.06 | 2.05 | 2.53 | 2.18 | 0.12 |
| 6 × 5 | 2.28 | 2.83 | 2.49 | 0.15 | 2.35 | 2.55 | 2.41 | 0.05 | 2.47 | 3.20 | 2.66 | 0.18 |
| 8 × 5 | 2.16 | 2.45 | 2.25 | 0.07 | 2.35 | 2.56 | 2.42 | 0.05 | 2.46 | 3.23 | 2.72 | 0.21 |
| 10 × 5 | 2.72 | 3.44 | 3.05 | 0.18 | 2.86 | 3.43 | 2.97 | 0.13 | 2.91 | 3.46 | 3.08 | 0.16 |
| 10 × 6 | 6.56 | 8.07 | 7.18 | 0.43 | 6.52 | 7.61 | 6.78 | 0.20 | 6.86 | 8.38 | 7.69 | 0.43 |
| 15 × 5 | 7.84 | 9.20 | 8.43 | 0.40 | 8.14 | 9.50 | 8.74 | 0.38 | 8.27 | 9.95 | 9.10 | 0.46 |
| 10 × 8 | 8.07 | 9.72 | 8.73 | 0.46 | 8.46 | 9.95 | 9.15 | 0.47 | 8.38 | 9.94 | 8.96 | 0.48 |
| 10 × 9 | 10.22 | 11.89 | 10.97 | 0.45 | 10.69 | 12.13 | 11.30 | 0.46 | 10.93 | 12.54 | 11.79 | 0.39 |
| 20 × 5 | 15.58 | 16.82 | 16.20 | 0.33 | 16.30 | 17.55 | 17.06 | 0.24 | 16.61 | 17.84 | 17.38 | 0.32 |
| 10 × 10 | 15.99 | 17.39 | 16.82 | 0.30 | 17.07 | 18.71 | 17.90 | 0.41 | 17.47 | 19.06 | 18.23 | 0.41 |
| 22 × 5 | 17.68 | 19.80 | 19.14 | 0.55 | 19.22 | 21.04 | 20.39 | 0.41 | 19.80 | 21.39 | 20.75 | 0.36 |
| 12 × 10 | 19.11 | 20.82 | 20.16 | 0.38 | 20.60 | 22.01 | 21.22 | 0.33 | 21.17 | 22.25 | 21.59 | 0.30 |
| 13 × 10 | 20.02 | 22.66 | 21.66 | 0.54 | 22.25 | 23.76 | 23.07 | 0.41 | 22.52 | 24.04 | 23.24 | 0.38 |
| 20 × 7 | 22.28 | 25.06 | 23.63 | 0.75 | 24.07 | 25.37 | 24.75 | 0.36 | 22.91 | 25.12 | 23.95 | 0.64 |
| 15 × 10 | 24.16 | 26.71 | 25.92 | 0.70 | 27.17 | 28.78 | 27.98 | 0.37 | 27.23 | 28.92 | 28.10 | 0.45 |
| Job’s Sequence | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Job priority number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Machine | M1 | J1,3 | J7,3 | J5,2 | J6,4 | J9,2 | J2,3 | J4,4 | J3,5 | J8,5 |
| M2 | J1,1 | J4,1 | J3,3 | J7,2 | J5,3 | J9,1 | J6,5 | J2,4 | J8,4 | |
| M3 | J6,1 | J1,2 | J3,2 | J5,1 | J8,1 | J2,2 | J4,3 | J7,4 | J9,3 | |
| M4 | J3,1 | J6,2 | J7,1 | J4,2 | J1,5 | J8,3 | J5,5 | J2,5 | J9,4 | |
| M5 | J2,1 | J6,3 | J1,4 | J3,4 | J8,2 | J5,4 | J7,5 | J4,5 | J9,5 | |
| Machine | M1 | M2 | M3 | M4 | M5 | Total Average |
|---|---|---|---|---|---|---|
| Machine utilization (%) | 69.2 | 65.5 | 100 | 74.1 | 85.9 | 78.9 |
| Machine process time (min) | 377 | 325 | 477 | 380 | 474 | 406.6 |
| Job | J1 | J2 | J3 | J4 | J5 | J6 | J7 | J8 | J9 | Total Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Order flow time (min) | 265 | 486 | 536 | 523 | 304 | 377 | 365 | 314 | 228 | 377 |
| Dynamic event | MB/PTC | MB/PTC | NJA | NJA | NJA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Buchmeister, B.; Li, X.; Ojstersek, R. Advanced Metaheuristic Method for Decision-Making in a Dynamic Job Shop Scheduling Environment. Mathematics 2021, 9, 909. https://doi.org/10.3390/math9080909
Zhang H, Buchmeister B, Li X, Ojstersek R. Advanced Metaheuristic Method for Decision-Making in a Dynamic Job Shop Scheduling Environment. Mathematics. 2021; 9(8):909. https://doi.org/10.3390/math9080909
Chicago/Turabian StyleZhang, Hankun, Borut Buchmeister, Xueyan Li, and Robert Ojstersek. 2021. "Advanced Metaheuristic Method for Decision-Making in a Dynamic Job Shop Scheduling Environment" Mathematics 9, no. 8: 909. https://doi.org/10.3390/math9080909
APA StyleZhang, H., Buchmeister, B., Li, X., & Ojstersek, R. (2021). Advanced Metaheuristic Method for Decision-Making in a Dynamic Job Shop Scheduling Environment. Mathematics, 9(8), 909. https://doi.org/10.3390/math9080909







