Abstract
The artificial bee colony (ABC) algorithm is a prominent swarm intelligence technique due to its simple structure and effective performance. However, the ABC algorithm has a slow convergence rate when it is used to solve complex optimization problems since its solution search equation is more of an exploration than exploitation operator. This paper presents an improved ABC algorithm for solving integer programming and minimax problems. The proposed approach employs a modified ABC search operator, which exploits the useful information of the current best solution in the onlooker phase with the intention of improving its exploitation tendency. Furthermore, the shuffle mutation operator is applied to the created solutions in both bee phases to help the search achieve a better balance between the global exploration and local exploitation abilities and to provide a valuable convergence speed. The experimental results, obtained by testing on seven integer programming problems and ten minimax problems, show that the overall performance of the proposed approach is superior to the ABC. Additionally, it obtains competitive results compared with other state-of-the-art algorithms.
1. Introduction
A wide variety of problems from different areas can be formulated as integer programming and minimax problems. Some applications in which integer programming problems appear are system-reliability design, scheduling, capital budgeting, warehouse location, portfolio analysis, automated production systems, mechanical design, transportation and cartography [1,2,3,4,5]. Furthermore, minimax optimization problems are found in many applications, such as optimal control, engineering design, game theory, signal and data processing [6,7,8,9,10].
Since integer programming is known to be NP-hard, solving these problems is considered a challenging task. Dynamic programming and branch-and-bound (BB) are well-known exact integer programming methods [11,12]. These methods divide the feasible region into smaller sub-regions or problems into sub-problems. The main drawback of dynamic programming is that the amount of computation necessary for an optimal solution exponentially grows as the number of variables rises. Branch-and-bound techniques have a high computational cost when solving large-scale problems that require the exploration of a search tree containing hundreds of nodes [11].
Metaheuristic optimization algorithms provide high-quality solutions in an acceptable amount of time. These techniques do not make any presumptions about the problem and can be used to solve a broad class of challenging optimization problems [13,14,15,16,17,18]. One of the most notable classes of metaheuristics, swarm intelligence (SI) algorithms, has foundations in imitating the collective behavior of biological agents. Particle swarm optimization (PSO) [19], artificial bee colony (ABC) [20], harmony search (HS) [21], firefly algorithm (FA) [22], gravitational search algorithm (GSA) [23], cuckoo search (CS) [24], whale optimization algorithm (WOA) [25] and bat algorithm (BA) [26] are some of the notable SI algorithms. In the last two decades, many SI algorithms were applied to solve integer programming problems. For instance, the PSO was employed to solve integer programming problems in [2]. On standard test problems, the PSO outperformed the branch-and-bound method in most cases.
Sequential quadratic programming (SQP) and smoothing techniques are common strategies for solving minimax problems [6]. These methods perform local minimization and require derivatives information for the objective function, which in most applications are not analytically available. Furthermore, SQP and smoothing techniques struggle to achieve satisfactory solutions when the objective function is discontinuous. On the other hand, metaheuristics are problem-independent optimization methods. Search operators of these methods use some randomness, which enables the algorithm to move away from a local optimum to search on a global scale [27]. Hence, metaheuristic optimization algorithms are considered an adequate alternative for minimax problems.
Since their invention, the original variants of metaheuristic algorithms have been modified to improve their performances. In [28], a memetic PSO algorithm that integrates local search methods to the basic PSO was developed. The local and global variants of the memetic PSO scheme were tested to solve minimax and integer programming problems. The experimental results showed that the memetic PSO outperformed the corresponding variants of the PSO algorithm in the majority of benchmarks. A hybrid cuckoo search algorithm with the Nelder Mead method, named HCSNM, for solving integer programming and minimax problems is proposed in [29]. In [29], it was concluded that the use of the Nelder Mead method enhances the convergence speed of the basic CS technique. A hybrid bat algorithm (HBDS) to solve integer programming is proposed in [30]. The HBDS incorporates direct search methods in the BA to enhance the intensification ability of the BA. Recently, a new hybrid harmony search algorithm with the multidirectional search method, called MDHSA, is developed to enhance the performance of the standard HS algorithm for solving integer programming and minimax problems [31].
The efficiency of the basic ABC algorithm for integer programming problems was investigated in [11]. To our knowledge, the ABC is not tested on a minimax test function in any of the studies. Therefore, investigating the performance of the standard ABC algorithm for solving minimax problems and proposing suitable modifications with the aim to further improve its performance for integer programming and minimax problems is a research problem.
Motivated by these reasons, this paper presents a shuffle-based artificial bee colony algorithm (SB-ABC) for solving integer programming and minimax problems. Although ABC has achieved success in different research fields, it was noticed that the exploitation ability of the ABC is deficient because of a randomly picked neighborhood food source in its solution search equation [32]. Therefore, the ABC algorithm has a slow convergence rate when it is applied to solve complex optimization problems. In order to enhance the exploitation ability of the ABC algorithm, the proposed approach employs a modified ABC search operator, which exploits the useful information of the current best solution in the onlooker phase. Furthermore, in certain iterations, the shuffle mutation operator is applied to the newly created solutions in both bee phases. In that way, the proposed algorithm provides useful diversity in the population, which is crucial in finding a good balance between exploitation and exploration. The SB-ABC algorithm is tested on seven integer programming problems and ten minimax problems. The obtained results for integer programming problems are compared to those of the ABC, BB method and 12 other metaheuristics. For minimax problems, the achieved results are compared to those of the ABC, SQP method and 11 other algorithms. Experimental results indicated that the SB-ABC algorithm obtained highly competitive results in comparison with the other algorithms presented in the literature.
The paper is organized as follows. In Section 2, definitions of minimax and integer programming problems are given. The standard ABC is presented in Section 3. The proposed shuffle-based artificial bee colony approach is explained in Section 4. In Section 5, the optimization results are presented and analyzed. In Section 6, the influence of the proposed modifications on the performance of the SB-ABC algorithm is discussed. Section 7 provides concluding remarks.
2. Problem Statements
An integer programming problem is a discrete optimization problem where all of the variables are limited to integer values. A general integer programming problem can be stated as [11]:
where S is the feasible region and denotes the set of integers. A problem where some variables are constrained to integers while some variables are not is a mixed integer programming problem. A special instance of the integer programming problem is that in which the variables are restricted to be either 0 or 1. This case is called the 0–1 programming problem or the binary integer programming problem.
Minimax optimization deals with a composition of an inner maximization problem and an outer minimization problem. A general form of the minimax problem can be stated as [31]:
where
with : S→, i = .
Furthermore, a nonlinear programming problem, with inequality constrains, of the form
can be transformed to minimax problems as follows:
where
for . It has been shown that when is large enough, the optimum point of the minimax problem coincides with the optimum point of the nonlinear programming problem [6].
3. Artificial Bee Colony Algorithm
Foraging behavior of a honey bee swarm motivated the development of the ABC algorithm [20]. The population of artificial bees is made of employed bees, onlooker bees and scout bees. One-half of the population consists of employed bees. Onlookers and scouts make the other half of the population. In the basic ABC, each food source represents a possible solution for the problem, and the number of the employed bees is equal to the number of food sources. All bees that are presently exploiting a food source are employed bees. The onlooker bees aim to choose promising food sources from those discovered by the employed bees according to the probability proportional to the quality of the food source. After the selection of the food source, the onlookers further seek food in the vicinity of the selected food source. The scout bees are transformed from several employed bees that abandon their unpromising food sources to seek new ones.
The control parameters of the basic ABC algorithm are the size of the population (), which is equal to the sum of employed and onlooker bees, the maximum cycle number (), and parameter , which represents the number of trials for abandoning the food source. In the initialization phase, the ABC creates randomly distributed initial population, which includes solutions. Following this step, three phases—employed, onlooker and scout—are repeated for a certain number of iterations. After each iteration, the best-discovered solution is saved.
Each employed bee seeks a better food source in the employed phase. The search operator used to create a novel food source from the old one is given by:
where j is arandomly picked index of a parameter, is a randomly selected food source that is different from and is a uniform random number between (−1, 1). Greedy selection between old and new food sources decides whether the old food source will be replaced by the new one.
In the onlooker phase, each onlooker bee chooses a food source according to the probability that is proportional to the fitness value. The same search strategy, which is given by Equation (7), is used to generate a candidate food source from the picked one. Greedy selection between old and new food sources decides whether the old food source (solution) will be updated. In the scout phase, a solution that can not be updated through a predetermined number of trials is replaced with a randomly created solution.
Many variants of ABC for solving continuous optimization problems were proposed [33,34,35,36,37,38,39,40]. For instance, an enhanced version of ABC, which introduces modifications related to elite strategy and dimension learning, is invented in [33]. The ABC variant, which uses novel search strategies in employed and onlooker bee phases, is developed in [34]. In [35], a hybrid method, which combines firefly and multi-strategy ABC, is developed for solving numerical optimization problems. An enhanced ABC based on the multi-strategy fusion is ABC variant and is proposed to improve the search ability of ABC with a small population [40].
Although the standard ABC was initially invented for continuous optimization problems, the modified variants have also been proposed for combinatorial and discrete problems [41,42,43,44,45,46]. Akay and Karaboga modified the ABC algorithm in order to solve integer programming problems. In this version of the ABC, a new control parameter called modification rate () is employed in its solution search strategy [11]. The modification rate parameter controls the possible modifications of optimization parameters. In [41], an ABC algorithm with a modified choice function for the traveling salesman problem is developed. Two novel ABC algorithms in which a multiple colonies strategy is adopted are proposed to solve the vehicle routing problem [43]. The ABC technique that integrates the initial solutions, an elitism strategy, recovery and local search schemes is a newly developed variant of ABC for solving the operating room scheduling problem [45]. An improved ABC algorithm for solving the strength–redundancy allocation problem is presented in [46]. In general, application fields of the ABC method are data mining, neural networks, image processing, cryptanalysis, data clustering and engineering [47,48,49,50,51,52,53].
4. The Proposed Approach: SB-ABC
Important characteristics of each metaheuristic algorithm are exploitation and exploration [54]. Exploitation refers to the process of visiting areas of a search space in the neighborhood of previously found satisfactory solutions. Exploration is the process of generating solutions with ample diversity and far from the current solutions. A balanced combination of these conflicting processes is essential for successful optimization performance. According to Equation (7), the new individual is generated by moving the old solution to a randomly picked solution, and the direction of the search is random. Consequently, the solution search equation given by Equation (7) has good exploration tendency, but it is not promising at exploitation. Since too much exploration tends to decrease the convergence speed of the algorithm [35], the proposed approach uses modified ABC search equations in employed and onlooker bee phases. To obtain useful diversity in the population, in each bee phase, the shuffle mutation operator is applied to new candidate solutions.
To create a new solution from the solution in the employed bee phase, the SB-ABC algorithm uses a search strategy that is described by [11]:
where j∈ and D is the number of optimization parameters or dimensions of the problem. In Equation (8), is a randomly selected food source that is different from , is a uniform random number between (−1, 1), is a randomly chosen real number in range (0, 1) and is modification rate control parameter whose value is in the range (0, 1). A higher value of the parameter will enable more parameters to be changed in the parent solution with the aim to increase the convergence speed of the basic ABC algorithm.
In the onlooker bee phase of the SB-ABC algorithm, the solutions are chosen according to the probability, which is given by [51]:
where the best fitness value in the population is denoted by maxfit, while marks the fitness value of the ith solution.
Inspired by the variant of the ABC proposed to solve numerical optimization, gbest-guided artificial bee colony (GABC) algorithm [55], we modify the search equation described by Equation (8) as follows:
where j∈ and D is the number of optimization parameters, i.e., dimension of the problem. In Equation (10), is a new candidate solution, is parent solution, is a uniform random number in range (−1, 1), is a uniform random number in the segment [0, 1.5], is a randomly selected food source that is different from , is the jth parameter of the best solution found so far, and is a randomly chosen real number within (0,1). According to Equation (10), the third term can move the new potential solution towards the global best solution. Hence, the modified search strategy given by Equation (10) can enhance the exploitation tendency of the basic ABC algorithm.
The right amount of population diversity is of great significance in achieving a proper balance between exploitation and exploration. In the SB-ABC algorithm, the exploitation is increased by using the modified search equation in the onlooker bee phase. Thus, the differences among individuals of a population are decreased since the search process is quite focused on a local region of good solutions. To promote diversity at certain stages of the search process, a new parameter called random permutation production interval () is introduced in the SB-ABC. This parameter is used as follows: after each th cycle, the shuffle mutation operator is applied to new candidate solutions at employed and onlooker bee phases. The shuffle mutation is a mutation operator where the mutated solution takes the components of the original solution, applying a permutation to them [56]. Usage of the shuffle mutation operator enables a better exploration of solutions but only every iterations.
The proposed approach computes a value for each solution during the search process. A value characterizes the non-advanced number of the solution used for the abandonment. In the scout phase of the SB-ABC algorithm, one solution with the highest value that is greater than the value of control parameter, if such solution occurs, is exchanged with a randomly generated solution.
The pseudo-code of the employed bee phase is presented in Algorithm 1, while the procedure of the onlooker bee phase is described in Algorithm 2. The input of Algorithm 1 involves the current solutions with corresponding values , , current value, values of and parameters, and the objective function f. The output of Algorithm 1 is the updated population of solutions and values, , which will be employed in the onlooker bee phase. The input of Algorithm 2 includes the current population of solutions with corresponding values , , current value, values of and parameters, and the objective function f. The output of Algorithm 2 is the updated population of solutions and values, , which will be used in the next iteration. The pseudo-code of the SB-ABC algorithm is presented in Algorithm 3. The input of Algorithm 3 includes the values of , , , and control parameters and the objective function f. The output of Algorithm 3 is the best solution found.
It is important to mention that the proposed approach SB-ABC introduces two modifications in comparison with the ABC algorithm adjusted for integer programming problems: use of the modified ABC search operator described by Equation (10) and the application of the shuffle mutation operator. The crucial difference between these two approaches consists in the different balance of exploitation and exploration. Exploitation is enhanced in the onlooker phase by applying the global best solution to guide the search process. Useful diversity of the population and better exploration of solutions is achieved on the global level by applying the shuffle mutation operator every th iteration.
The SB-ABC algorithm employs three specific control parameters to manage the search process: modification rate , and , which determines the cycles in which the shuffle mutation operator is applied to candidate solutions. It also uses standard control parameters for all population-based metaheuristics, the population size and maximum number of cycles. In order to solve the integer programming problems, the SB-ABC rounds the parameter values to the closest integer after evolution according to Equations (8) and (10). Solutions were also rounded after the initialization phase and scout phase of the algorithm. Therefore, they were considered as integer numbers for all operations.
| Algorithm 1 Employed bee phase of the SB-ABC algorithm |
|
| Algorithm 2 Onlooker bee phase of the SB-ABC algorithm |
|
| Algorithm 3 Pseudo-code of the SB-ABC algorithm |
|
5. Experimental Study
The performance of the SB-ABC algorithm is evaluated through seven integer programming problems and ten minimax problems widely used in the literature. The proposed algorithm is implemented in Java, and it was run on a PC with an Intel(R) Core(TM) i5-4460 3.2 GHz processor. In order to show the efficiency of the SB-ABC algorithm, it is compared with several algorithms that were previously applied to solve these problems. In the next subsections, brief descriptions of the used benchmark problems and results of a comparison between the SB-ABC and other state-of-the-art approaches are presented.
5.1. Benchmark Problems
In this section, the integer programming and minimax optimization test problems are described. To test the performance of the SB-ABC algorithm on integer programming problems, seven problems widely used in the literature are employed. The mathematical models of these problems can be found in [11,28,31]. These problems are presented below:
Test problem is defined in [28]:
where D is the dimension of the problem or number of optimization parameters. The global minimum is .
Test problem is defined in [28]:
where D is the dimension of the problem. The global minimum is .
Test problem is defined in [28]:
The global minimum is .
Test problem is defined in [28]:
The global minimum is .
Test problem is defined in [28]:
The global minimum is .
Test problem is defined in [28]:
The global minimum is .
Test problem is defined in [28]:
The global minimum is .
To investigate the efficiency of the SB-ABC algorithm on minimax problems, ten benchmark functions are considered [6,28,31]. These benchmarks are presented as follows:
Test problem is defined in [31,57]:
The desired error goal for this problem is = 1.9522245.
Test problem is defined in [31]:
The desired error goal for this problem is = 2.
Test problem is defined in [6,57]:
The desired error goal for this problem is = –40.1.
Test problem is defined in [31]:
The desired error goal for this problem is = .
Test problem is defined in [31]:
The desired error goal for this problem is = .
Five other test problems were selected from [57]. The name of the minimax benchmark problems, the dimension of the problem, the number of functions and desired error goal are reported in Table 1.

Table 1.
Properties of the minimax test problems –.
5.2. The General Performance of the SB-ABC for Integer Programming Problems
Because the SB-ABC is an improved variant of the ABC, in this section, a comparison between the SB-ABC and ABC algorithm adjusted to solve integer programming problems through seven integer programming problems is presented. The common traditional technique, the branch-and-bound (BB) method, is also included in the comparison with the proposed approach.
The preliminary testing of the SB-ABC was done with the aim of obtaining suitable combinations of parameter values. The SP parameter was set to 20. This value was detected to be a proper selection for all executed tests. The increasing value of this control parameter will increase the computational cost without any enhancement in the reached results. Our tests verified the previous reasoning that a value 0.8 for the parameter is a good choice for solving these optimization problems [11]. Additionally, it was experimentally determined that a value of 50 for the parameter and a value of 3 for the parameter are suitable for the SB-ABC algorithm. It was observed that significantly lower or higher values of the parameter can deteriorate the obtained results. Higher values of the parameter would lead to the less frequent use of the shuffle mutation operator and consequently weaker performance of the SB-ABC algorithm. In the SB-ABC, during the initialization step, /2 solutions are evaluated, and there are /2 employed bees, /2 onlookers and a maximum of one scout bee per iteration. Therefore, the maximum number of function evaluations for the SB-ABC is + . The maximum number of function evaluations executed by the SB-ABC for all benchmarks was set to 20,000 and the SB-ABC was terminated when the global minimum was reached.
The results of the BB method and ABC algorithm were taken from their original papers [2,11]. For these comparisons, in the BB method and ABC algorithm, the maximum number of function evaluations was set to 25,000. When an accuracy of was achieved, these methods were terminated. The BB method, ABC and SB-ABC algorithms are conducted for 30 independent runs for each benchmark problem.
The following metrics are used to estimate the performances of the BB, ABC and SB-ABC. The convergence speed of each algorithm is compared by recording the mean number of function evaluations (mean) required to reach the acceptable value. If the mean value is smaller, the convergence speed is faster. Since SI algorithms are stochastic, the obtained mean results are not the same in each run. To examine the stability of each method, standard deviation (SD) values are measured. The performance of an algorithm is more stable if the standard deviation value is lower. The success rate (SR) is used as a metric for robustness or reliability of methods. This rate is defined as the ratio of successful runs in the total number of executed runs. A run is considered successful if an algorithm obtains a solution for which the value of the objective function is less than the corresponding acceptable value. If the value of SR is greater, the reliability of the algorithm is better. In Table 2, the mean, corresponding standard deviation (SD) values and SR values of the BB method, ABC and SB-ABC for the benchmark problems with 5, 10, 15, 20, 25 and 30 variables and test problems – over 30 runs are given. The best mean results are indicated in bold.

Table 2.
Comparison results of the BB method, ABC and SB-ABC for the – integer programming problems.
As shown in Table 2, with respect to the SR results reached by these methods, the SB-ABC performs the most reliably since, for each test case, the obtained SR result of the SB-ABC is 100%. The BB method performance is less robust than the SB-ABC for problem with 30 variables, since it achieved only 14 successful runs out of 30, while in the remaining test cases, both approaches obtained the same SR results. The SB-ABC and ABC algorithms obtained the same SR results on all test problems, with the exception of problem , where the ABC performance was less robust. With respect to the mean results, from Table 2, it can be observed that the SB-ABC performs better than its rivals in the majority of cases. To be exact, the SB-ABC is better than the BB method and ABC in 12 and 11 test cases, respectively. On the other hand, the BB method has better mean results for problem , while the ABC outperformed the SB-ABC for test functions and . With respect to the standard deviation results, from Table 2, it can be seen that the SB-ABC performance is more stable than the BB and ABC methods in most cases.
5.3. Comparison against Other State-of-the-Art Algorithms for Integer Programming Problems
To further demonstrate the efficiency of the SB-ABC, it is benchmarked against 12 other metaheuristic algorithms that were previously successfully used to solve integer programming problems. These algorithms are the basic PSO and its four variants RWMPSOg, RWMPSOl, PSOg, PSOl [28], standard cuckoo search (CS), firefly algorithm (FA), gravitational search algorithm (GSA), whale optimization algorithm (WOA), hybrid cuckoo search algorithm with Nelder Mead method (HCSNM) [29], hybrid bat algorithm (HBDS) [30] and the recently proposed hybrid harmony search algorithm with multidirectional search method (MDHSA) [31].
The results obtained by the RWMPSOg, RWMPSOl, PSOg, PSOl are taken from [28], the results reached by the HCSNM are taken from [29], the results achieved by HBDS are taken from [30], while the results of the MDHSA and basic PSO, CS, FA, GSA and WOA are taken from [31]. In Table 3, the mean, corresponding standard deviation values and SR values of the RWMPSOg, RWMPSOl, PSOg, PSOl, HCSNM, MDHSA and SB-ABC for the benchmark problems with 5 variables and test problems – over 50 runs are given. Table 4 presents the mean and standard deviation values obtained by the PSO, FA, CS, GSA, WOA, HBDS and SB-ABC for problem with 5 variables and test problems – over 50 runs. The best mean results are in bold. The metaheuristics used for comparison with the SB-ABC also performed the maximum number of function evaluations of 20,000. Since the results of these 12 algorithms are achieved over 50 runs, the statistical results of the SB-ABC over 50 runs are presented in Table 3 and Table 4.

Table 3.
Comparison results of the RWMPSOg, RWMPSOl, PSOg, PSOl, MDHSA, HCSNM and SB-ABC for the – integer programming problems.

Table 4.
Comparison results of the PSO, FA, CS, GSA, WOA, HBDS and SB-ABC for the – integer programming problems.
The results from Table 3 and Table 4 show that the proposed algorithm obtained better mean results on the majority of benchmark problems in comparison with its competitors. Precisely, the SB-ABC is better than RWMPSOg, RWMPSOl, PSOg, PSOl, MDHSA, HCSNM, PSO, FA, CS, GSA, WOA and HBDS in six, six, seven, seven, five, four, seven, seven, seven, seven, seven, and six test problems, respectively. In contrast, the SB-ABC is outperformed by the RWMPSOg, RWMPSOl, PSOg, PSOl, MDHSA, HCSNM, PSO, FA, CS, GSA, WOA and HBDS in one, one, zero, zero, two, three, zero, zero, zero, zero, zero and one test problems, respectively. From the standard deviation values presented in Table 3 and Table 4, it can be observed that the proposed SB-ABC has lower standard deviation values on the majority of benchmark problems in comparison with RWMPSOg, RWMPSOl, PSOg PSOl, PSO, CS, GSA and WOA. On the other hand, the HCSNM, MDHSA, FA and HBDS have lower standard deviations compared to the SB-ABC for most of the cases. In addition, the SR results demonstrate that the SB-ABC achieved a 100% success rate on all benchmark problems.
5.4. The General Performance of the SB-ABC for Minimax Problems
In this section, the performance of the SB-ABC for solving minimax problems is investigated. The performance of the SB-ABC is compared to the performance of the SQP method and standard ABC algorithm. The fair comparison is ensured since the SQP, ABC and SB-ABC algorithms employed the maximum number of function evaluations of 20,000. The run is counted as successful when the desired error goal is reached within the maximum number of function evaluations.
The specific parameter settings of the SB-ABC are kept the same, as mentioned in Section 5.2. Since the standard ABC is not tested to solve minimax problems in any of the studies, we have tested its performance in solving problems –. The ABC employed the following parameter settings, is 20, is 0.8 and is . These values of control parameters were used in the standard ABC, adjusted to solve integer programming problems [11]. The results of the SQP method were taken from the respective paper [2].
In Table 5, the mean, corresponding standard deviation (SD) values and SR values of the SQP method, ABC and SB-ABC for the benchmark problems – over 30 runs are presented. The best mean results are in bold. The mark (-) for in the SQP method means that the results are not reported in its original paper. From Table 5, it can be noticed that the SB-ABC converges faster to the global minimum in comparison with the SQP method and ABC for the majority of test problems.

Table 5.
Comparison results of the ABC and SB-ABC for the – minimax problems.
From the obtained mean values, it can be observed that the SB-ABC has better performance than the SQP and ABC methods in 6 and 10 test problems, respectively. On the other hand, the SB-ABC is outperformed by the SQP and ABC on three and zero benchmarks, respectively. Furthermore, the SR results indicate that the SB-ABC performance is more robust in comparison with the SQP on six test problems (, , , , and ), while both methods reached the same SR results for the rest of the benchmarks. With respect to the standard deviation results, from Table 5, it can be noticed that the SB-ABC performance is more stable than the SQP and ABC methods in most cases. Furthermore, from Table 5, it can be seen that the SB-ABC performs more reliably than the ABC on four benchmark problems (, , and ), while both algorithms achieved the same SR results for the remaining problems.
5.5. Comparison against Other State-of-the-Art Algorithms for Minimax Problems
In order to further examine the efficiency of the SB-ABC for minimax problems, its performance is compared to the performance of 10 other algorithms that were previously successfully used to solve these problems. These methods are the heuristic pattern search algorithm HPS2, the basic PSO and its two variants RWMPSOg and UPSOm [58], HCSNM [29], MDHSA [31], CS, FA, GSA and WOA.
The results obtained by the RWMPSOg are taken from [28], the results reached by the HPS2 are taken from [59], the results achieved by UPSOm are taken from [58], the results obtained by the HCSNM are taken from [29], while the results of the MDHSA, PSO, FA, CS, GSA and WOA are taken from [31]. In Table 6, the mean, standard deviation values and SR values of the HPS2, UPSOm, RWMPSOg, HCSNM, MDHSA and SB-ABC for the benchmark problems – over 50 runs are given. Table 7 presents the mean and standard deviation values obtained by the PSO, FA, CS, GSA, WOA and SB-ABC for benchmark problems – over 50 runs. The best mean results are in bold. The metaheuristics used for comparison with the SB-ABC also performed the maximum number of function evaluations of 20,000. The SB-ABC was configured with the specific parameter values, as described in Section 5.2. Since the results of these 10 algorithms are achieved over 50 runs, the statistical results of the SB-ABC over 50 runs are presented in Table 6 and Table 7. In Table 6, the mark (-) indicates that the results are not presented in the corresponding paper.

Table 6.
Comparison results of the HPS2, UPSOm, RWMPSOg, HCSNM, MDHSA, HCSNM and SB-ABC for the – minimax problems.

Table 7.
Comparison results of the PSO, FA, CS, GSA, WOA and SB-ABC for the – minimax problems.
The results from Table 6 and Table 7 show that the proposed algorithm obtained better mean results on the majority of benchmark problems in comparison with its competitors. Concretely, the SB-ABC outperformed the HPS2, UPSOm, RWMPSOg, HCSNM, MDHSA, PSO, FA, CS, GSA and WOA in 5, 8, 6, 6, 7, 9, 8, 10, 9 and 10 test problems, respectively. In contrast, the SB-ABC is outperformed by the HPS2, UPSOm, RWMPSOg, HCSNM, MDHSA, PSO, FA, CS, GSA and WOA in three, one, zero, three, three, one, two, zero, one and zero benchmark problems, respectively. From standard deviation values presented in Table 6 and Table 7, it can be seen that the SB-ABC has lower standard deviation values for most of the cases in comparison with the UPSOm, RWMPSOg, CS and WOA. On the other hand, the HPS2, HCSNM, MDHSA, PSO, FA and GSA have lower standard deviations compared to the SB-ABC in most cases. With respect to the SR results reached by these methods, the SB-ABC performs the same or more reliably in comparison with the HPS2, UPSOm, RWMPSOg, HCSNM and MDHSA in these minimax problems.
6. Discussion
The impact of the introduced modifications on the SB-ABC will be examined in this section. Seven integer programming problems and ten minimax problems were solved by two diverse variants of the SB-ABC. The obtained results of each variant are compared with respect to the same of the developed SB-ABC approach. In the following text, these variants are presented:
- Variant 1: To examine the effectiveness of employing the modified ABC operator in the onlooker bee phase given by Equation (10), an SB-ABC version that uses the standard ABC search equation is tested. The label SB-ABC1 is used for this variant.
- Variant 2: To investigate the effectiveness of employing the shuffle mutation operator in employed and onlooker bee phases, an SB-ABC version that does not include this operator is tested. The label SB-ABC2 is used for this variant.
Each SB-ABC version is run 50 times for each test problem. The maximum number of function evaluations was 20,000 for each method. The tested methods were configured with specific parameter values, as described in Section 5.2. The mean, standard deviation values and SR values obtained by the SB-ABC1, SB-ABC2 and SB-ABC for seven integer programming problems and ten minimax problems are presented in Table 8 and Table 9. A result in boldface denotes the best mean result. The convergence graphs achieved by the SB-ABC1, SB-ABC2 and SB-ABC on the four picked integer programming functions and the four selected minimax optimization problems are given in Figure 1 and Figure 2, respectively.

Table 8.
Comparison results of the SB-ABC1, SB-ABC2 and SB-ABC for the – integer programming problems.

Table 9.
Comparison results of the SB-ABC1, SB-ABC2 and SB-ABC for the – minimax problems.
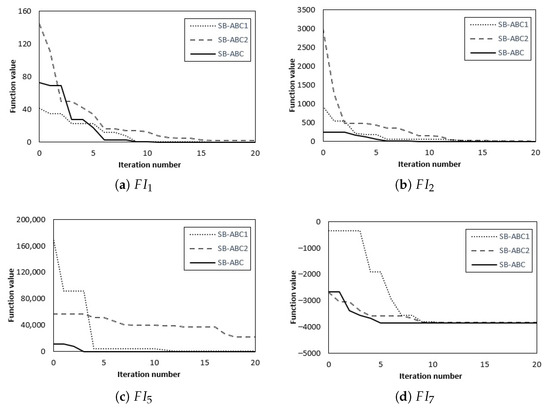
Figure 1.
Convergence graphs of SB-ABC1, SB-ABC2 and SB-ABC for the selected integer programming problems.
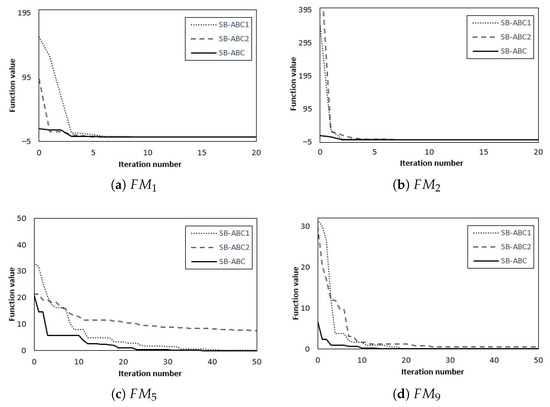
Figure 2.
Convergence graphs of SB-ABC1, SB-ABC2 and SB-ABC for the selected minimax problems.
From the mean results presented in Table 8, it can be seen that the SB-ABC results outperform SB-ABC1 and SB-ABC2 versions on all integer programming benchmark problems. With respect to the SR values, it can be noticed that each algorithm achieved a 100% success rate on all – integer programming problems. From the standard deviation values presented in Table 8, it can be observed that the SB-ABC has lower standard deviation values for most of the cases in comparison with the SB-ABC1 and SB-ABC2 versions.
Compared with the SB-ABC1, it can be seen from Table 9 that the proposed algorithm reached better mean results and the same or better SR results for all – minimax problems. When comparing the SB-ABC with respect to the SB-ABC2, it can be noticed from Table 9 that the SB-ABC obtained better mean values for eight minimax problems and slightly worse mean results for the remaining two benchmarks ( and ). From the standard deviation values presented in Table 9, it can be noticed that the SB-ABC has lower standard deviation values for most of the cases in comparison with the SB-ABC1 and SB-ABC2 variants. According to the SR results presented in Table 9, the SB-ABC outperformed the SB-ABC2 in five test problems (, , , and ), while the SB-ABC and SB-ABC2 achieved the same results in the remaining benchmarks. As shown in Figure 1 and Figure 2, SB-ABC converges faster to the optimum on the selected problems in comparison with its two variants.
These observations indicate that each introduced modification contributes to the satisfactory performance of the SB-ABC. Use of the shuffle mutation operator provides useful diversity and consequently helps the SB-ABC to locate the favorable areas within the search space. Adding the modified ABC operator enables an enhanced exploitation ability of the algorithm. Combining these modifications significantly improves the convergence speed and robustness of the SB-ABC algorithm.
7. Conclusions
In this paper, a novel shuffle-based artificial bee colony algorithm (SB-ABC) is proposed with the intention to solve integer programming and minimax problems. The proposed algorithm employs the shuffle mutation operator and modified ABC search strategy with an aim to improve the exploitation tendency of the algorithm to provide a valuable convergence speed. The proposed approach was applied to solve seven integer programming and ten minimax problems taken from the literature. The SB-ABC algorithm obtained highly competitive results in comparison with the standard ABC, BB method and 12 other metaheuristic algorithms in solving integer programming problems. Compared with the standard ABC, SQP method and 10 other state-of-the-art algorithms, the SB-ABC showed better performance for the majority of the minimax test problems.
The effects of introduced modifications related to the shuffle mutation operator and modified ABC search operator have been investigated. It is experimentally validated that the use of each introduced modification is of great importance in achieving a satisfactory performance of the SB-ABC with respect to the convergence speed and robustness. In the proposed SB-ABC method, the balance between the global exploration and local exploitation abilities is addressed by suitable configuration of control parameters. As in many other swarm intelligence techniques, the problem of discovering appropriate values for the control parameters also exists in the SB-ABC algorithm. Extending the SB-ABC method with a self-adaptive control mechanism to reach better exploration and exploitation balance during distinct search phases is a promising direction for future study. Developing a hybrid algorithm that would incorporate different operators of some other well-established metaheuristic methods in the SB-ABC algorithm for solving large scale integer programming and minimax problems will also be examined in future work. Another possible way for creating a hybrid approach is to employ certain metaheuristic methods to assume a role of a local optimizer, while the SB-ABC algorithm would perform a global search. In addition, the application of the proposed SB-ABC approach for solving some combinatorial optimization problems will be investigated.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Coit, D.W.; Zio, E. The evolution of system reliability optimization. Reliab. Eng. Syst. Saf. 2019, 192, 106259. [Google Scholar] [CrossRef]
- Laskari, E.C.; Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimization for integer programming. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; pp. 1582–1587. [Google Scholar]
- Kim, T.-H.; Cho, M.; Shin, S. Constrained Mixed-Variable Design Optimization Based on Particle Swarm Optimizer with a Diversity Classifier for Cyclically Neighboring Subpopulations. Mathematics 2020, 8, 2016. [Google Scholar] [CrossRef]
- Agarana, M.C.; Ajayi, O.O.; Akinwumi, I.I. Integer programming algorithm for public transport system in sub-saharan african cities. Wit. Trans. Built. Environ. 2019, 182, 339–350. [Google Scholar]
- Haunert, J.-H.; Wolff, A. Beyond Maximum Independent Set: An Extended Integer Programming Formulation for Point Labeling. ISPRS Int. J. Geo-Inf. 2017, 6, 342. [Google Scholar] [CrossRef]
- Laskari, E.C.; Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimization for minimax problems. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; pp. 1576–1581. [Google Scholar]
- Khakifirooz, M.; Chien, C.; Fathi, M.; Pardalos, P.M. Minimax Optimization for Recipe Management in High-Mixed Semiconductor Lithography Process. IEEE Trans. Industr. Inform. 2020, 16, 4975–4985. [Google Scholar] [CrossRef]
- Razaviyayn, M.; Huang, T.; Lu, S.; Nouiehed, M.; Sanjabi, M.; Hong, M. Nonconvex Min-Max Optimization: Applications, Challenges, and Recent Theoretical Advances. IEEE Signal Process. Mag. 2020, 37, 55–66. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Q. An Active Set Smoothing Method for Solving Unconstrained Minimax Problems. Math. Probl. Eng. 2020, 2020, 1–25. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, Y.; Liu, M. A generalized gradient projection method based on a new working set for minimax optimization problems with inequality constraints. J. Inequal Appl. 2017, 51, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Akay, B.; Karaboga, D. Solving Integer Programming Problems by Using Artificial Bee Colony Algorithm. In AI*IA 2009: Emergent Perspectives in Artificial Intelligence; Serra, R., Cucchiara, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5883, pp. 355–364. [Google Scholar]
- Tarray, T.A.; Bhat, M. A nonlinear programming problem using branch and bound method. Investig. Oper. 2017, 38, 291–298. [Google Scholar]
- Brajević, I.; Ignjatović, J. An upgraded firefly algorithm with feasibility-based rules for constrained engineering optimization problems. J. Intell. Manuf. 2019, 30, 2545–2574. [Google Scholar] [CrossRef]
- Stojanović, I.; Brajević, I.; Stanimirović, P.S.; Kazakovtsev, L.A.; Zdravev, Z. Application of Heuristic and Metaheuristic Algorithms in Solving Constrained Weber Problem with Feasible Region Bounded by Arcs. Math. Probl. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Liu, H.; Guo, Z. Multi-objective metaheuristics for discrete optimization problems: A review of the state-of-the-art. Appl. Soft Comput. 2020, 93, 106382. [Google Scholar] [CrossRef]
- Ng, K.K.H.; Lee, C.K.M.; Chan, F.T.S.; Lv, Y. Review on meta-heuristics approaches for airside operation research. Appl. Soft Comput. 2018, 66, 104–133. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Kepaptsoglou, K.; Vlahogianni, E. Metaheuristics for the transit route network design problem: A review and comparative analysis. Public Transp. 2019, 11, 487–521. [Google Scholar] [CrossRef]
- Bala, A.; Ismail, I.; Ibrahim, R.; Sait, S.M. Applications of Metaheuristics in Reservoir Computing Techniques: A Review. IEEE Access 2018, 6, 58012–58029. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications, SAGA 2009; Watanabe, O., Zeugmann, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2009; Volume 5792, pp. 169–178. [Google Scholar]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. [Google Scholar]
- Brajević, I.; Stanimirović, P. An improved chaotic firefly algorithm for global numerical optimization. Int. J. Comput. Intell. Syst. 2018, 12, 131–148. [Google Scholar] [CrossRef]
- Petalas, Y.G.; Parsopoulos, K.E.; Vrahatis, M.N. Memetic particle swarm optimization. Ann. Oper. Res. 2007, 156, 99–127. [Google Scholar] [CrossRef]
- Ali, A.F.; Tawhid, M.A. A hybrid cuckoo search algorithm with Nelder Mead method for solving global optimization problems. Springerplus 2016, 5, 1–22. [Google Scholar] [CrossRef]
- Ali, A.F.; Tawhid, M.A. Solving Integer Programming Problems by Hybrid Bat Algorithm and Direct Search Method. Trends Artif. Intell. 2018, 2, 46–59. [Google Scholar]
- Tawhid, M.A.; Ali, A.F.; Tawhid, M.A. Multidirectional harmony search algorithm for solving integer programming and minimax problems. Int. J. Bio-Inspir. Com. 2019, 13, 141–158. [Google Scholar] [CrossRef]
- Xiang, W.; Meng, X.; Li, Y.; He, R.; An, M. An improved artificial bee colony algorithm based on the gravity model. Inf. Sci. 2018, 429, 49–71. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, W.; Wang, H.; Tan, D.; Wang, Y.; Yu, X.; Wu, R. An Improved Artificial Bee Colony Algorithm Based on Elite Strategy and Dimension Learning. Mathematics 2019, 7, 289. [Google Scholar] [CrossRef]
- Lin, Q.; Zhu, M.; Li, G.; Wang, W.; Cui, L.; Chen, J.; Lu, J. A novel artificial bee colony algorithm with local and global information interaction. Appl. Soft Comput. 2018, 62, 702–735. [Google Scholar] [CrossRef]
- Brajević, I.; Stanimirović, P.S.; Li, S.; Cao, X. A Hybrid Firefly and Multi-Strategy Artificial Bee Colony Algorithm. Int. J. Comput. Intell. Syst. 2020, 13, 810–821. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B.; Karaboga, N. A survey on the studies employing machine learning (ML) for enhancing artificial bee colony (ABC) optimization algorithm. Cogent Eng. 2020, 7, 1855741. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y.; Naseem, R. Artificial bee colony algorithm: A component-wise analysis using diversity measurement. J. King Saud Univ. Comp. Inf. Sci. 2020, 32, 794–808. [Google Scholar] [CrossRef]
- Gorkemli, B.; Karaboga, D. A quick semantic artificial bee colony programming (qsABCP) for symbolic regression. Inf. Sci. 2019, 502, 346–362. [Google Scholar] [CrossRef]
- Aslan, S.; Karaboga, D.; Badem, H. A new artificial bee colony algorithm employing intelligent forager forwarding strategies. Appl. Soft Comput. 2020, 96, 106656. [Google Scholar] [CrossRef]
- Song, X.; Zhao, M.; Xing, S. A multi-strategy fusion artificial bee colony algorithm with small population. Expert Syst. Appl. 2020, 142, 112921. [Google Scholar] [CrossRef]
- Choong, S.S.; Wong, L.-P.; Lim, C.P. An artificial bee colony algorithm with a Modified Choice Function for the traveling salesman problem. Swarm Evol. Comput. 2019, 44, 622–635. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B. Solving Traveling Salesman Problem by Using Combinatorial Artificial Bee Colony Algorithms. Int. J. Artif. Intell. Tools 2019, 28, 1950004. [Google Scholar] [CrossRef]
- Ng, K.K.H.; Lee, K.M.; Zhang, S.Z.; Wu, K.; Ho, W. A multiple colonies artificial bee colony algorithm for a capacitated vehicle routing problem and re-routing strategies under time-dependent traffic congestion. Comput. Ind. Eng. 2017, 109, 151–168. [Google Scholar] [CrossRef]
- Sedighizadeh, D.; Mazaheripour, H. Optimization of multi objective vehicle routing problem using a new hybrid algorithm based on particle swarm optimization and artificial bee colony algorithm considering Precedence constraints. Alex. Eng. J. 2018, 57, 2225–2239. [Google Scholar] [CrossRef]
- Lin, Y.-K.; Li, M.-Y. Solving Operating Room Scheduling Problem Using Artificial Bee Colony Algorithm. Healthcare 2021, 9, 152. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Chen, Z. Strength–redundancy allocation problem using artificial bee colony algorithm for multi-state systems. Reliab. Eng. Syst. Saf. 2021, 209, 107494. [Google Scholar] [CrossRef]
- Hancer, E.; Karaboga, D. A comprehensive survey of traditional, merge-split and evolutionary approaches proposed for determination of cluster number. Swarm Evol. Comput. 2017, 32, 49–67. [Google Scholar] [CrossRef]
- Caliskan, A.; Çil, Z.A.; Badem, H.; Karaboga, D. Regression-Based Neuro-Fuzzy Network Trained by ABC Algorithm for High-Density Impulse Noise Elimination. IEEE Trans. Fuzzy Syst. 2020, 28, 1084–1095. [Google Scholar] [CrossRef]
- Akay, B. A Binomial Crossover Based Artificial Bee Colony Algorithm for Cryptanalysis of Polyalphabetic Cipher. Teh. Vjesn. 2020, 27, 1825–1835. [Google Scholar]
- Kumar, A.; Kumar, D.; Jarial, S.K. A Review on Artificial Bee Colony Algorithms and Their Applications to Data Clustering. Cybern. Inf. Technol. 2017, 17, 3–28. [Google Scholar] [CrossRef]
- Brajevic, I. Crossover-based artificial bee colony algorithm for constrained optimization problems. Neural. Comput. Appl. 2015, 26, 1587–1601. [Google Scholar] [CrossRef]
- Aslan, S.; Karaboga, D. A genetic Artificial Bee Colony algorithm for signal reconstruction based big data optimization. Appl. Soft Comput. 2020, 88, 106053. [Google Scholar] [CrossRef]
- Pooja, S.G. Innovative Review on Artificial Bee Colony Algorithm and Its Variants. In Advances in Computing and Intelligent Systems; Sharma, H., Govindan, K., Poonia, R., Kumar, S., El-Medany, W., Eds.; Algorithms for Intelligent Systems; Springer: Singapore, 2020; pp. 165–176. [Google Scholar]
- Črepinšek, M.; Liu, S.-H.; Mernik, M. Exploration and exploitation in evolutionary algorithms: A survey. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Canali, C.; Lancellotti, R. GASP: Genetic Algorithms for Service Placement in Fog Computing Systems. Algorithms 2019, 12, 201. [Google Scholar] [CrossRef]
- Lukšan, L.; Vlček, J. Test Problems for Non-Smooth Unconstrained and Linearly Constrained Optimization; Technical Report 798; Institute of Computer Science, Academy of Sciences of the Czech Republic: Prague, Czech Republic, 2000. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Unified particle swarm optimization for tackling operations research problems. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, SIS 2005, Pasadena, CA, USA, 8–10 June 2005; pp. 53–59. [Google Scholar]
- Santo, I.A.C.P.E.; Fernandes, E.M.G.P. Heuristics pattern search for bound constrained minimax problems. In Computational Science and Its Applications—ICCSA 2011; Murgante, B., Gervasi, O., Iglesias, A., Taniar, D., Apduhan, B.O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6784, pp. 174–184. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).