Visualizing Profiles of Large Datasets of Weighted and Mixed Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Weighted MDS
- (a)
- .
- (b)
- The squared -distances between the rows of coincide with the corresponding entries in ; that is, for each pair of individuals , we have that where is the i-th row of .
2.2. Gower’s Distance
2.3. Gower’s Interpolation Formula
3. Methodology
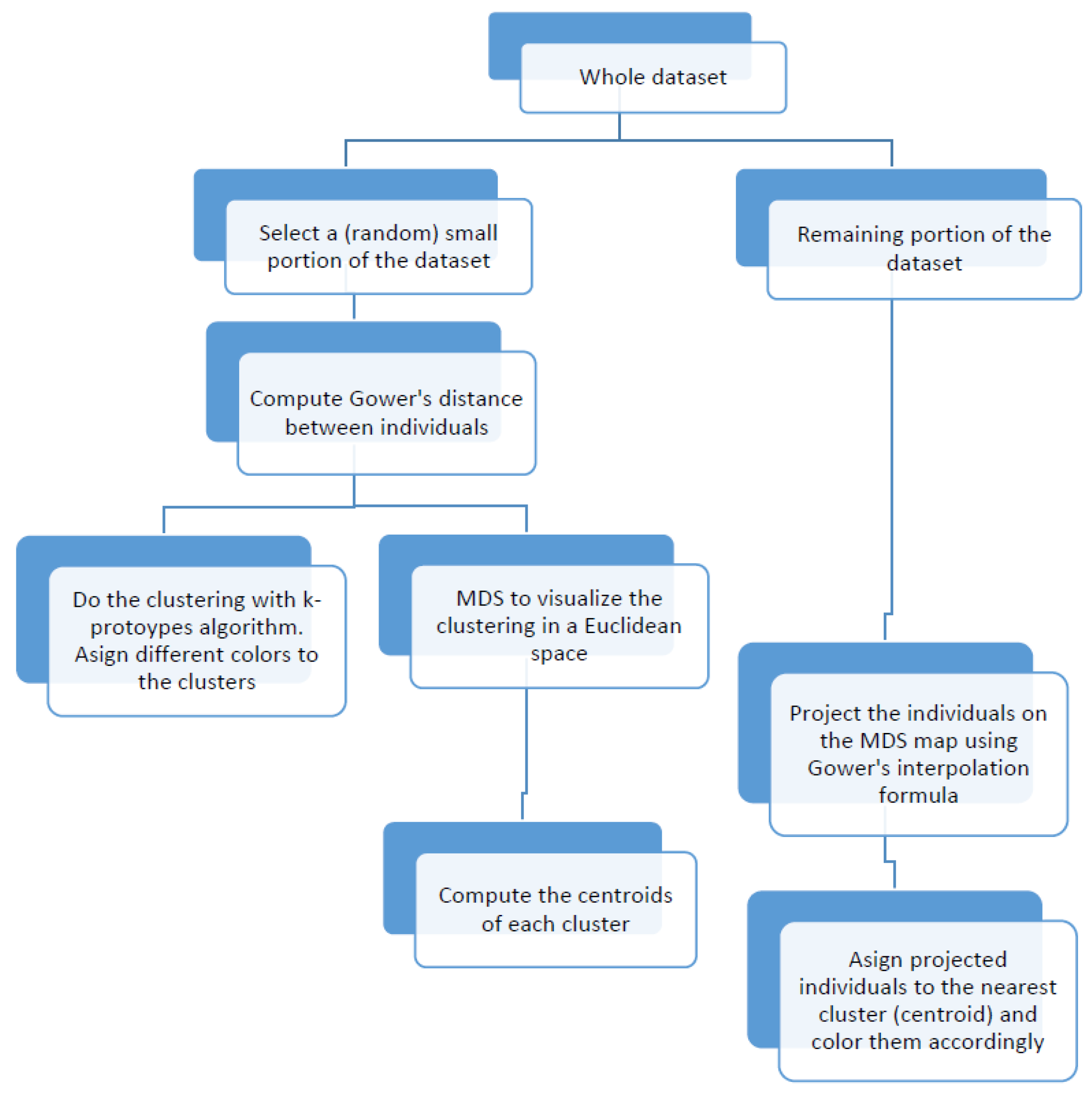
3.1. The Visualization Algorithm
- Select a small random sample, using the weights to produce a more informative sample, that is, trying to follow as much as possible the sampling scheme. Depending on the size of dataset, this selection can be 2.5, 5 or 10% of total observations. Let us denote this small sample by , where n is the number of individuals and p the number of variables.
- Compute the distance matrix between the rows of using Gower’s distance Formula (3).
- Carry out the k-prototypes clustering algorithm in order to find the different clusters and label the individuals accordingly. Determine the number of clusters in the dataset by the “elbow” rule.
- Obtain the principal coordinates of the labeled individuals through weighted MDS.
- Compute the representatives (or centroids) of the clusters. This can be done by calculating the weighted mean or weighted median of those point-coordinates belonging to the same cluster in the MDS configuration.
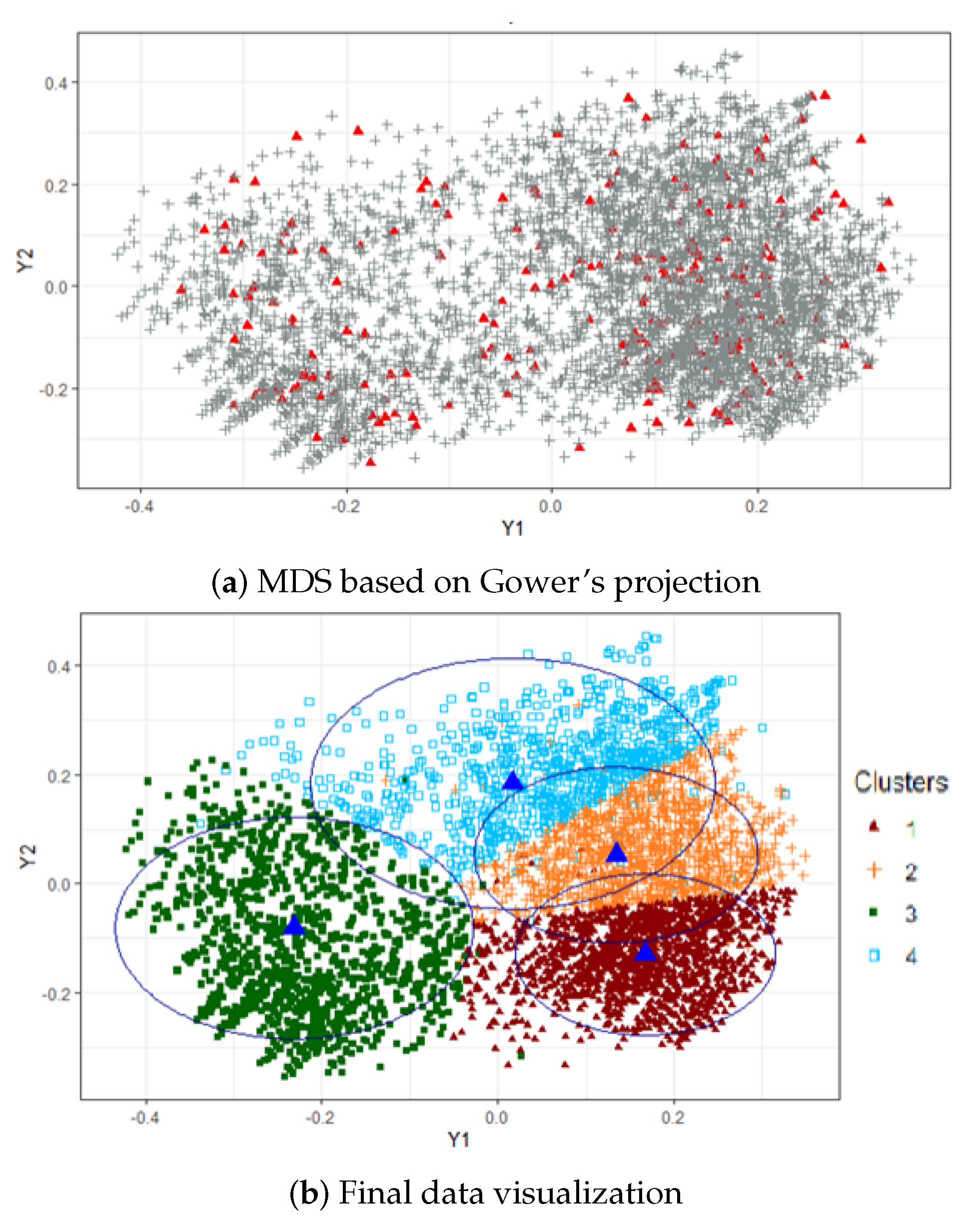
- Project the rest of the individuals (the remaining 97.5, 95 or 90%) onto the MDS configuration using Gower’s interpolation formula.
- Finally, from the MDS configuration, assign the new points to an existing cluster based on the closest centroid (according to Euclidean distance) and label/color them accordingly.
3.2. Some Important Remarks
3.2.1. On the Clustering Algorithm
- Initial prototypes selection. Select k distinct individuals from the dataset as the initial centroids.
- Initial allocation. Each individual of the dataset is assigned to the closest prototype’s cluster, according to distance (3).
- Reallocation. The prototypes for the previous and current clusters of the individuals must be updated, taking into account individual weights. This repeats until there is no reallocation of individuals.
3.2.2. On Gower’s Interpolation Formula
- Split row-wise into ℓ partitions , equally sized, with perhaps the exception of , which can be smaller. The number of partitions is set to be , where is the size of the largest distance matrix that a computer can calculate efficiently [13].
- Apply Gower’s interpolation formula to each matrix () and store the coordinates. The application of Gower’s interpolation formula to a matrix whose rows are m “new” individuals is rather straightforward from Formula (4). With the same notation as in Section 2.3, let be the matrix whose rows contain the squared distances of the “new” m individuals to the n individuals of . Then, the principal coordinates of these “new” m individuals can be computed by:where is a vector of ones.
3.3. R Functions
4. Results
4.1. Application
4.1.1. Description of the Dataset
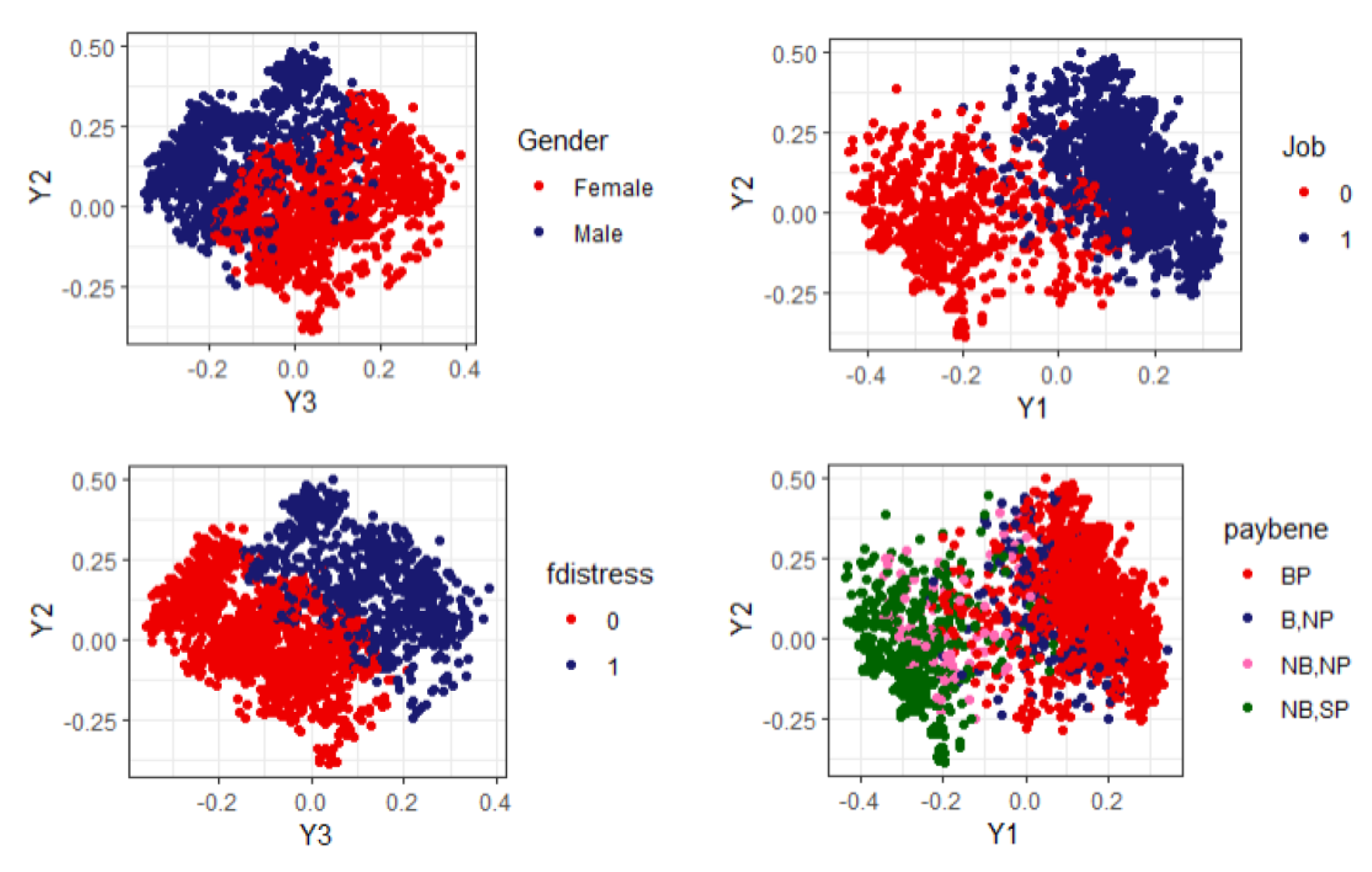
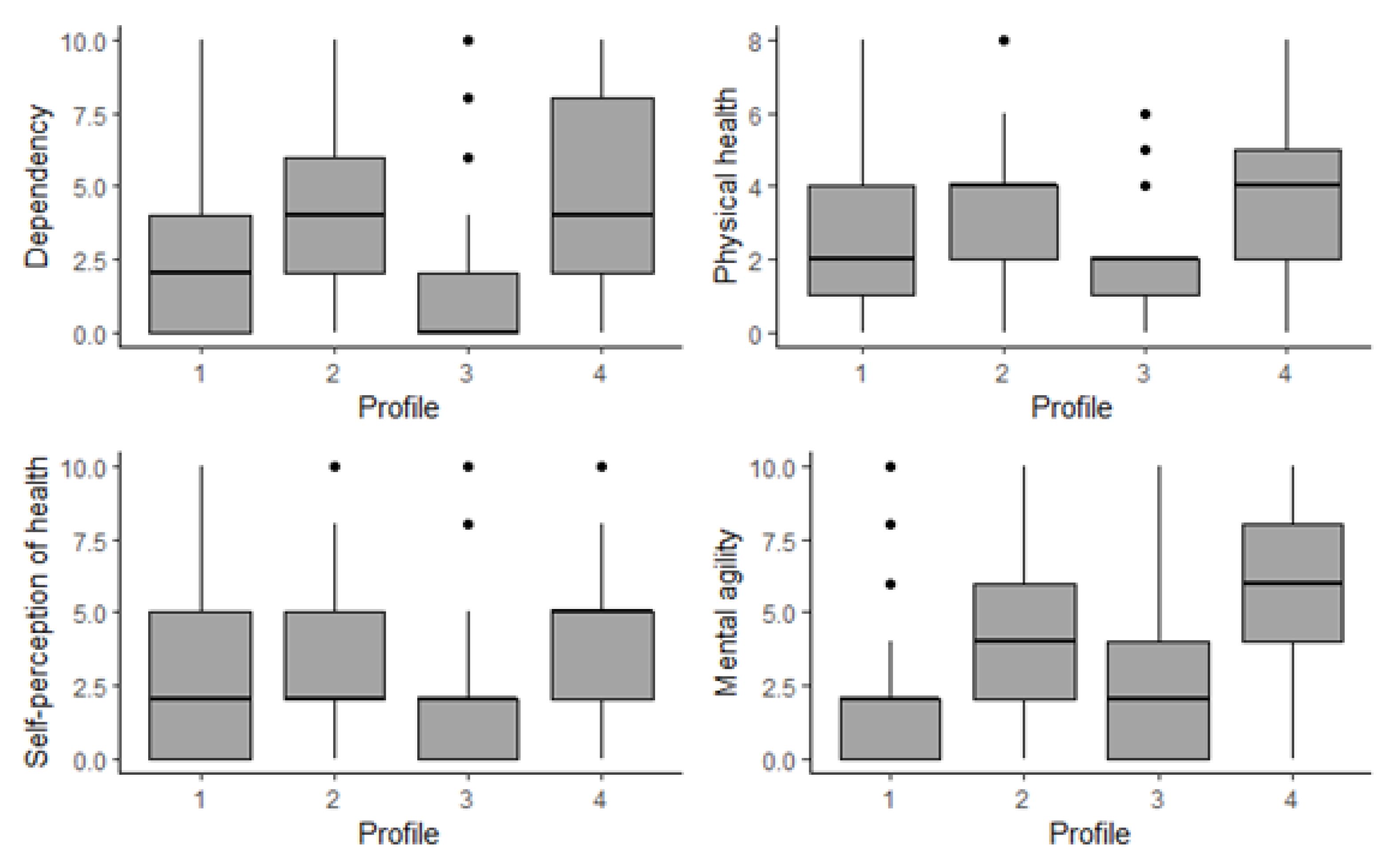
4.1.2. Visualization of Profiles and Findings
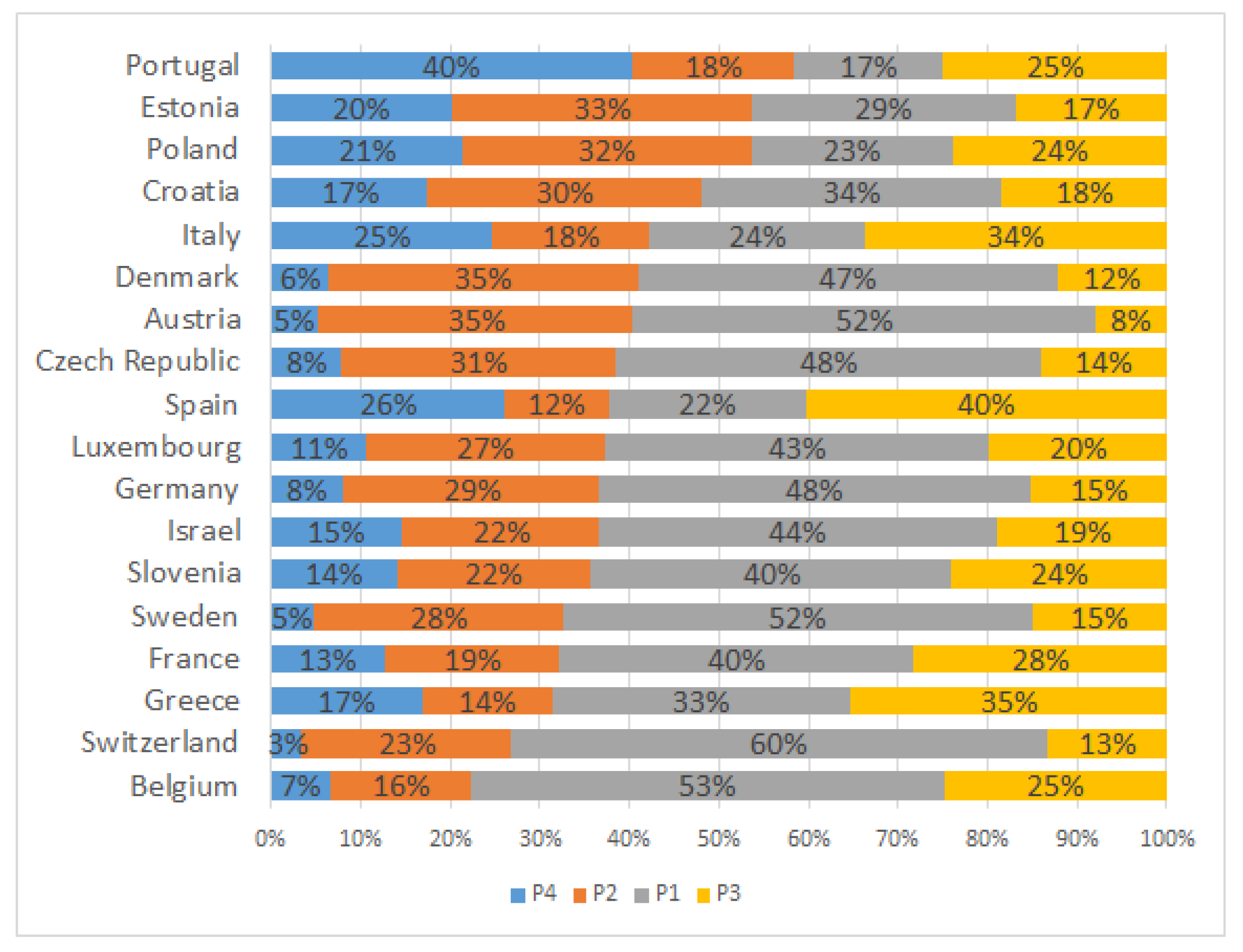
- P1:
- This included 30.48% of respondents, representing more than 37.89 million people; 56.56% of them were female, equally likely to belong to any age bracket, although more than 50% were under 71 years old; 55.18% were secondary-school-educated and more than 75% had secondary or university study behind them; not working; lived with a partner; health-related benefits and payments; wellbeing index mean values around 2–2.26 and median values of 2.
- P2:
- This included 22.76% of respondents, representing more than 28.29 million people; 50.26% of them were female; more than 50% of them were 70 years old or older; 47.80% were primary-school-educated and more than 75% were primary or secondary-school-educated; not working; lived with a partner; health-related benefits and payments; wellbeing index mean values around 3–4 and median values 2–4.
- P3:
- This included 26.82% of respondents, representing more than 33.34 million people; 57.27% female; 59.95% were between 55–65 years old and more than 80% were under 66 years old; around 70% were secondary-school-educated or university-educated; working; lived with a partner; no health-related benefits, some payments; least vulnerable group, wellbeing index mean values around 1.4–2.20, median values 0–2.
- P4:
- This included 19.94% of respondents, representing more than 24.78 million people; 51.35% female; 40.82% were 76 years old or older and more than 50% were older than 70 years old; low education (more than 75% were primary-school-educated or not at all); not working; likely lived alone or with a partner; health-related benefits and payments; 96.69% in financial distress; most vulnerable group, wellbeing index mean values around 3.4–5.4 and median values 4–6.
4.1.3. Profiles across Europe
4.2. Simulation Study
4.2.1. Design of the Simulation Study
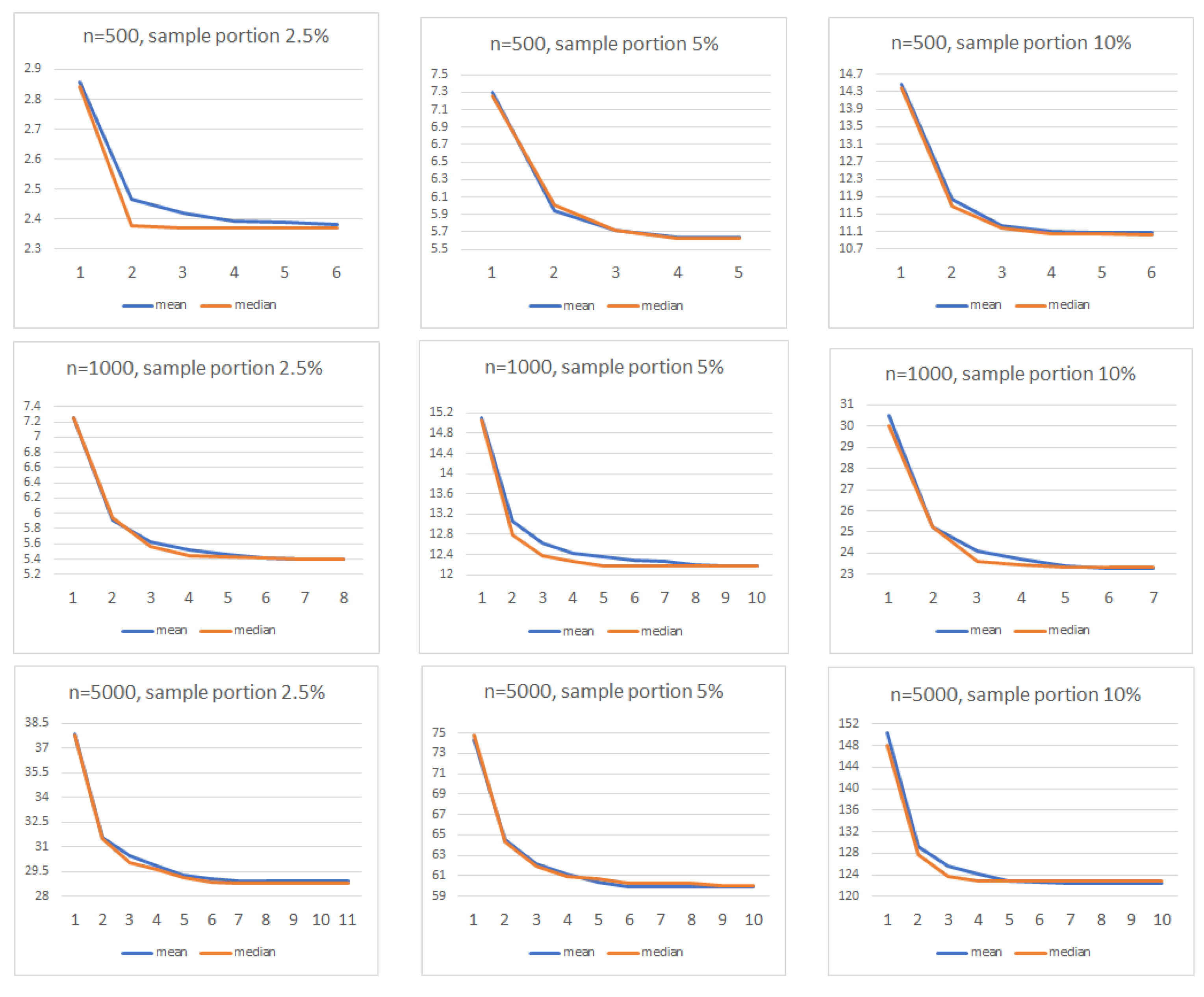
- Sample sizes. To evaluate the elapsed time, a total of nine different sample sizes were used: n = 500, 1000, 5000, 10,000, 20,000, 30,000, 40,000, 50,000 and 60,000. Discrepancies between two MDS configurations were evaluated through a total of six different sample sizes: n = 500, 1000, 2000, 3000, 4000 and 5000.
- Portion of data. Recall that the first step of the algorithm was to select a small sample from the data. We wished to see whether there exists a significant difference in using 2.5, 5 or 10% as the initial portion.
- Each scenario was the combination of a sample size and a portion of data and was repeated 100 times.
4.2.2. Time to Compute MDS
4.2.3. Discrepancies in MDS Configurations
4.2.4. Cost Function
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paradis, E. Multdimensional scaling with very large datasets. J. Comput. Graph. Stat. 2018, 27, 935–939. [Google Scholar] [CrossRef]
- Huang, Z. Clustering large data sets with mixed numeric and categorical values. In Proceedings of the First Pacific Asia Knowledge Discovery and Data Mining Conference, Singapore, 23–24 February 1997; World Scientific: Singapore, 1997; pp. 21–34. [Google Scholar]
- Van de Velden, M.; Iodice D’Enza, A.; Markos, A. Distance-based clustering of mixed data. Wires Comput. Stat. 2018, 11, e1456. [Google Scholar] [CrossRef]
- Ahmad, A.; Khan, S.S. Survey of State-of-the-Art Mixed Data Clustering Algorithms. IEEE Access 2019, 7, 31883–31902. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P.J.F. Modern Multidimensional Scaling: Theory and Applications, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Cox, T.F.; Cox, M.A.A. Multidimensional Scaling, 2nd ed.; Chapman and Hall: Boca Raton, FL, USA, 2000. [Google Scholar]
- Krzanowski, W.J.; Marriott, F.H.C. Multivariate Analysis, Part 1, Volume Distributions, Ordination and Inference; Arnold: London, UK, 1994. [Google Scholar]
- Gower, J.C.; Hand, D. Biplots; Chapman and Hall: London, UK, 1996. [Google Scholar]
- Albarrán, A.; Alonso, P.; Grané, A. Profile identification via weighted related metric scaling: An application to dependent Spanish children. J. R. Stat. Soc. Ser. Stat. Soc. 2015, 178, 1–26. [Google Scholar] [CrossRef]
- Gower, J.C. A general coefficient of similarity and some of its properties. Biometrics 1971, 27, 857–874. [Google Scholar] [CrossRef]
- Cuadras, C.M. Multidimensional Dependencies in Ordination and Classification. In Analyses Multidimensionelles des Données; Fernández, K., Morineau, A., Eds.; CISIA-CERESTA: Saint-Mandé, France, 1998; pp. 15–25. [Google Scholar]
- Boj, E.; Delicado, P.; Fortiana, J. Distance-based local linear regression for functional predictors. Comput. Stat. Data Anal. 2010, 54, 429–437. [Google Scholar] [CrossRef]
- Delicado, P.; Pachón-García, C. Multidimensional Scaling for Big Data. 2020. Available online: https://arxiv.org/abs/2007.11919 (accessed on 23 July 2020).
- Williams, M.; Munzner, T. Steerable, progressive multidimensional scaling. In Proceedings of the Information Visualization, INFOVIS 2004, IEEE Symposium, Austin, TX, USA, 10–12 October 2004; pp. 57–64. [Google Scholar]
- Basalaj, W. Incremental multidimensional scaling method for database visualization. In Proceedings of the SPIE 3643, Visual Data Exploration and Analysis VI, San Jose, CA, USA, 25 March 1999. [Google Scholar] [CrossRef]
- Naud, A.; Duch, W. Interactive data exploration using MDS mapping. In Proceedings of the Fifth Conference: Neural Networks and Soft Computing, Zakopane, Poland, 6–10 June 2000; pp. 255–260. [Google Scholar]
- Faloutsos, C.; Lin, K. FastMap: A fast algorithm for indexing, data-mining, and visualization. In Proceedings of the ACM SIGMOD, San Jose, CA, USA, 23–25 May 1995; pp. 163–174. [Google Scholar]
- Wang, J.T.-L.; Wang, X.; Lin, K.-I.; Shasa, D.; Shapiro, B.A.; Zhang, K. Evaluating a class of distance-mapping algorithms for data mining and clustering. In Proceedings of the ACM KDD, San Diego, CA, USA, 15–18 August 1999; pp. 307–311. [Google Scholar]
- De Silva, V.; Tenenbaum, J.B. Global versus local methods for nonlinear dimensionality reduction. Adv. Neural Inf. Process. Syst. 2003, 15, 721–728. [Google Scholar]
- Trosset, W.M.; Groenen, P.J. Multidimensional scaling algorithms for large data sets interactive data exploration using MDS mapping. In Proceedings of the Computing Science and Statistics, Kunming, China, 7–9 December 2005. [Google Scholar]
- McInnes, L.; Healy, J.; Saul, N.; Großberger, L. UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Chalmers, M. A linear iteration time layout algorithm for visualizing high dimensional data. Proc. IEEE Vis. 1996, 127–132. [Google Scholar] [CrossRef]
- Morrison, A.; Ross, G.; Chalmers, M. Fast Multidimensional Scaling through Sampling, Springs, and Interpolation. Inf. Vis. 2003, 2, 68–77. [Google Scholar] [CrossRef]
- Platt, J.C. FastMap, MetricMap, and Landmark MDS are all Nyström Algorithms. In Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics, Bridgetown, Barbados, 6–8 January 2005; pp. 261–268. [Google Scholar]
- Guttman, L. A general nonmetric technique for finding the smallest coordinate space for a configuration of points. Psychometrika 1968, 33, 469–506. [Google Scholar] [CrossRef]
- Bernataviciene, J.; Dzemyda, G.; Marcinkevicius, V. Diagonal Majorizarion Algorithm: Properties and efficiency. Inf. Technol. Control 2007, 36, 353–358. [Google Scholar]
- Grané, A.; Albarrán, I.; Lumley, R. Visualizing Inequality in Health and Socioeconomic Wellbeing in the EU: Findings from the SHARE Survey. Int. J. Environ. Res. Public Health 2020, 17, 7747. [Google Scholar] [CrossRef] [PubMed]
- Aschenbruck, R.; Szepannek, G. Cluster Validation for Mixed-Type Data. Achives Data Sci. Ser. A 2020. [Google Scholar] [CrossRef]
- Foss, A.H.; Markatou, M.; Ray, B. Distance Metrics and Clustering Methods for Mixed-type Data. Int. Stat. Rev. 2018, 81, 80–109. [Google Scholar] [CrossRef]
- Jia, Z.; Song, L. Weighted k-Prototypes Clustering Algorithm Based on the Hybrid Dissimilarity Coefficient. Math. Probl. Eng. 2020, 5143797. [Google Scholar] [CrossRef]
- Paradis, E.; Claude, J.; Strimmer, K. APE: Analyses of phylogenetics and evolution in R language. Bioinformatics 2004, 20, 289–290. [Google Scholar] [CrossRef]
- Dray, S.; Dufour, A.B. The ade4 Package: Implementing the Duality Diagram for Ecologists. J. Stat. Softw. 2007, 22. [Google Scholar] [CrossRef]
- De Leeuw, J.; Mair, P. Multidimensional scaling using majorization: The R package smacof. J. Stat. Softw. 2009, 31, 1–30. [Google Scholar] [CrossRef]
- Oksanen, J.; Blanchet, F.G.; Friendly, M.; Kindt, R.; Legendre, P.; McGlinn, D.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; et al. Community Ecology Package, CRAN-Package Vegan. Available online: https://cran.r-project.org; https://github.com/vegandevs/vegan (accessed on 1 March 2020).
- Roberts, D.W. Ordination and Multivariate Analysis for Ecology. CRAN-Package Labdsv. Available online: http://ecology.msu.montana.edu/labdsv/R (accessed on 1 March 2020).
- Goslee, S.; Urban, D. Dissimilarity-Based Functions for Ecological Analysis. CRAN-Package Ecodist. Available online: https://CRAN.R-project.org/package=ecodist (accessed on 1 March 2020).
- Szepannek, G. ClustMixType: User-Friendly Clustering of Mixed-Type Data in R. R J. 2018, 10, 200–208. [Google Scholar] [CrossRef]
- Ney, S. Active Aging Policy in Europe: Between Path Dependency and Path Departure. Ageing Int. 2005, 30, 325–342. [Google Scholar] [CrossRef]
- Avendano, M.; Jürges, H.; MacKenbach, J.P. Educational level and changes in health across Europe: Longitudinal results from SHARE. J. Eur. Soc. Policy 2009, 19, 301–316. [Google Scholar] [CrossRef]
- Bohácek, R.; Crespo, L.; Mira, P.; Pijoan-Mas, J. The Educational Gradient in Life Expectancy in Europe: Preliminary Evidence from SHARE. In Ageing in Europe—Supporting Policies for an Inclusive Society; Börsch-Supan, A., Kneip, T., Litwin, H., Myck, M., Weber, G., Eds.; De Gruyter: Berlin, Germany, 2015; pp. 321–330. [Google Scholar] [CrossRef][Green Version]
- Sokal, R.R.; Rohlf, F.J. The comparison of dendrograms by objective methods. Taxon 1962, 11, 33–40. [Google Scholar] [CrossRef]
- Grané, A.; Romera, R. On visualizing mixed-type data: A joint metric approach to profile construction and outlier detection. Sociol. Methods Res. 2018, 47, 207–239. [Google Scholar] [CrossRef]
- Grané, A.; Salini, S.; Verdolini, E. Robust multivariate analysis for mixed-type data: Novel algorithm and its practical application in socio-economic research. Socio-Econ. Plan. Sci. 2021, 73, 100907. [Google Scholar] [CrossRef]
- Cuadras, C.M.; Fortiana, J. Visualizing Categorical Data with Related Metric Scaling. In Visualization of Categorical Data; Blasius, J., Greenacre, M., Eds.; Academic Press: London, UK, 1998; pp. 365–376. [Google Scholar]
- Cutler, A.; Breiman, L. Archetypal analysis. Technometrics 1994, 36, 338–347. [Google Scholar] [CrossRef]
- Vinué, G.; Epifanio, I.; Alemany, S. Archetypoids: A new approach to define representative archetypal data. Comput. Statist. Data Anal. 2015, 87, 102–115. [Google Scholar] [CrossRef]

| Type | Description | Values/Categories |
|---|---|---|
| CT | Country | 19 countries |
| B | Gender | “Male”, “Female” |
| CT | Ages | “55–60”, “61–65”, “66–75”, “76+” |
| B | Employment status | “Employed”, “Not working” |
| B | Marital status | “Has no spouse”, “Has a spouse” |
| CT | Education | “No education”, “Primary”, “Secondary”, “University” |
| B | Household in financial distress | “Yes”, “No” |
| CT | Household receives benefits or has payments? | “Payments and no benefits”, “No benefits and no payments”, “Benefits and payments”, “Payments and no benefits” |
| C | Dependency index | Form 0 to 10 |
| C | Physical health and nutrition index | From 0 to 10 |
| C | Self-perception of health index | From 0 to 10 |
| C | Mental agility index | From 0 to 10 |
| Variable | 1st PC (Y1) | 2nd PC (Y2) | 3rd PC (Y3) |
|---|---|---|---|
| age | 0.4192 | 0.1829 | 0.1017 |
| gender | 0.4258 | 0.4336 | 0.6147 |
| job | 0.8589 | 0.3522 | 0.1669 |
| fdistress | 0.1196 | 0.4597 | 0.7053 |
| mstat | 0.4244 | 0.4100 | 0.4248 |
| edu | –0.0796 | –0.3448 | –0.2684 |
| paybene | 0.5372 | 0.1670 | 0.1004 |
| depend | 0.3577 | 0.3326 | 0.2047 |
| health | 0.3406 | 0.3003 | 0.1693 |
| sph | 0.2651 | 0.1473 | 0.2357 |
| mental | 0.1856 | 0.4129 | 0.3549 |
| Cluster | Count | % of Total | Age | Age Prop. | Gender | Gender Prop. | Job Status | Job Status Prop. |
|---|---|---|---|---|---|---|---|---|
| 1 | 37,890,792.42 | 30.48% | 66–70 | 33.53% | Female | 56.56% | Not working | 96.19% |
| 2 | 28,293,780.69 | 22.76% | 76+ | 39.81% | Female | 50.26% | Not working | 94.90% |
| 3 | 33,340,913.81 | 26.82% | 55–60 | 59.95% | Female | 57.27% | Working | 97.98% |
| 4 | 24,788,136.51 | 19.94% | 76+ | 40.82% | Female | 51.35% | Not working | 83.24% |
| Cluster | Financial distress | Financial distress Prop. | Marital status | Marital status Prop. | Education level | Education level Prop. | Payments or benefits? | Payments or benefits? Prop. |
| 1 | No | 98.68% | Spouse | 81.82% | Secondary | 55.18% | B & P | 85% |
| 2 | No | 63.88% | Spouse | 60.19% | Primary | 47.80% | B & P | 83% |
| 3 | No | 65.17% | Spouse | 78.22% | Secondary | 39.44% | P & No B | 70% |
| 4 | Yes | 96.69% | Spouse | 50.05% | Primary | 63.28% | B & P | 75% |
| Cluster | Dependency index | Physical health index | Self-perceived health index | Mental agility index | ||||
| mean | median | mean | median | mean | median | mean | median | |
| 1 | 2.03 | 2 | 2.24 | 2 | 2.26 | 2 | 1.92 | 2 |
| 2 | 3.74 | 4 | 3.09 | 4 | 3.26 | 2 | 4.05 | 4 |
| 3 | 1.38 | 0 | 1.82 | 2 | 1.81 | 2 | 2.20 | 2 |
| 4 | 4.60 | 4 | 3.40 | 4 | 3.94 | 5 | 5.44 | 6 |
| n | Sample Portion | Gower’s Interpolation | Complete MDS | n | Sample Portion | Gower’s Interpolation | Complete MDS | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 500 | 2.5 | 0.16 | 0.45 | 15 | 20,000 | 10 | 71.89 | - |
| 2 | 500 | 5 | 0.19 | 0.55 | 16 | 30,000 | 2.5 | 30.41 | - |
| 3 | 500 | 10 | 0.2 | 0.57 | 17 | 30,000 | 5 | 91.74 | - |
| 4 | 1000 | 2.5 | 0.18 | 2.83 | 18 | 30,000 | 10 | 190.2 | - |
| 5 | 1000 | 5 | 0.21 | 2.9 | 19 | 40,000 | 2.5 | 71.4 | - |
| 6 | 1000 | 10 | 0.25 | 2.95 | 20 | 40,000 | 5 | 165.6 | - |
| 7 | 5000 | 2.5 | 0.87 | 259.52 | 21 | 40,000 | 10 | 517.2 | - |
| 8 | 5000 | 5 | 1.71 | 271.79 | 22 | 50,000 | 2.5 | 152.52 | - |
| 9 | 5000 | 10 | 3.01 | 265.14 | 23 | 50,000 | 5 | 271.5 | - |
| 10 | 10,000 | 2.5 | 3.91 | - | 24 | 50,000 | 10 | 1125.51 | - |
| 11 | 10,000 | 5 | 9.17 | - | 25 | 60,000 | 2.5 | 195.31 | - |
| 12 | 10,000 | 10 | 19.33 | - | 26 | 60,000 | 5 | 453.78 | - |
| 13 | 20,000 | 2.5 | 19.32 | - | 27 | 60,000 | 10 | 1927.23 | - |
| 14 | 20,000 | 5 | 29.91 | - |
| n | Sample Portion | Eigenvalues | Cophenetic Correlation | |
|---|---|---|---|---|
| 1 | 500 | 2.5 | 0.079 | 0.274 |
| 2 | 500 | 5 | 0.063 | 0.749 |
| 3 | 500 | 10 | 0.043 | 0.797 |
| 4 | 1000 | 2.5 | 0.052 | 0.751 |
| 5 | 1000 | 5 | 0.053 | 0.794 |
| 6 | 1000 | 10 | 0.037 | 0.825 |
| 7 | 2000 | 2.5 | 0.047 | 0.792 |
| 8 | 2000 | 5 | 0.037 | 0.821 |
| 9 | 2000 | 10 | 0.029 | 0.844 |
| 10 | 3000 | 2.5 | 0.038 | 0.811 |
| 11 | 3000 | 5 | 0.031 | 0.836 |
| 12 | 3000 | 10 | 0.027 | 0.851 |
| 13 | 4000 | 2.5 | 0.030 | 0.821 |
| 14 | 4000 | 5 | 0.030 | 0.855 |
| 15 | 4000 | 10 | 0.022 | 0.855 |
| 16 | 5000 | 2.5 | 0.025 | 0.831 |
| 17 | 5000 | 5 | 0.025 | 0.848 |
| 18 | 5000 | 10 | 0.020 | 0.858 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grané, A.; Sow-Barry, A.A. Visualizing Profiles of Large Datasets of Weighted and Mixed Data. Mathematics 2021, 9, 891. https://doi.org/10.3390/math9080891
Grané A, Sow-Barry AA. Visualizing Profiles of Large Datasets of Weighted and Mixed Data. Mathematics. 2021; 9(8):891. https://doi.org/10.3390/math9080891
Chicago/Turabian StyleGrané, Aurea, and Alpha A. Sow-Barry. 2021. "Visualizing Profiles of Large Datasets of Weighted and Mixed Data" Mathematics 9, no. 8: 891. https://doi.org/10.3390/math9080891
APA StyleGrané, A., & Sow-Barry, A. A. (2021). Visualizing Profiles of Large Datasets of Weighted and Mixed Data. Mathematics, 9(8), 891. https://doi.org/10.3390/math9080891







