A Projected Forward-Backward Algorithm for Constrained Minimization with Applications to Image Inpainting

Abstract

In this research, we study the convex minimization problem in the form of the sum of two proper, lower-semicontinuous, and convex functions. We introduce a new projected forward-backward algorithm using linesearch and inertial techniques. We then establish a weak convergence theorem under mild conditions. It is known that image processing such as inpainting problems can be modeled as the constrained minimization problem of the sum of convex functions. In this connection, we aim to apply the suggested method for solving image inpainting. We also give some comparisons to other methods in the literature. It is shown that the proposed algorithm outperforms others in terms of iterations. Finally, we give an analysis on parameters that are assumed in our hypothesis.

1. Introduction

Let H be a real Hilbert space. The unconstrained minimization problem of the sum of two convex functions is modeled as the following form:

$$\begin{array}{c}\hfill \underset{u\in H}{min}f\left(u\right)+g\left(u\right),\end{array}$$

(1)

where f and $g:H\to \mathbb{R}\cup \{+\infty \}$ are proper, lower semi-continuous, and convex functions. If f is differentiable on H, we know that problem (1) can be described by the fixed point equation, that is,

$$\begin{array}{c}\hfill u={\mathrm{prox}}_{\alpha g}(u-\alpha \nabla f\left(u\right)),\end{array}$$

(2)

where $\alpha >0$ and ${\mathrm{prox}}_g$ is the proximal operator of g, i.e., ${\mathrm{prox}}_g={(Id+\partial g)}^{-1}$ where $Id$ is the identity operator in H and $\partial g$ is the subdifferential of g. Therefore, the forward-backward algorithm was defined in the following manner:

$$\begin{array}{c}\hfill {\displaystyle u^{k+1}=\underset{\mathrm{backward}\mathrm{step}}{\underbrace{{\mathrm{prox}}_{{\alpha }_{k}g}}}\underset{\mathrm{forward}\mathrm{step}}{\underbrace{(Id-{\alpha }_k\nabla f)}}\left(u^k\right),k\ge 0}\end{array}$$

(3)

where ${\alpha }_k>0$. Some works that relate to the forward-backward method for convex optimization problems can be investigated in [1,2,3,4,5,6]. This method covers the gradient method [7,8,9] and the proximal algorithm [10,11,12]. Combettes and Wajs [13] introduced the following relaxed forward-backward method.

Cruz and Nghia [14] suggested the forward-backward method using linesearch approach, which does not need the Lipschitz constant in implementation.

It was shown that $\left(u^k\right)$ converges weakly to a minimizer of $f+g$.

Now, inspired by Cruz and Nghia [14], we suggest a new projected forward-backward algorithm for solving the constrained convex minimization problem, which is modeled as follows:

$$\begin{array}{c}\hfill \underset{u\in \mathrm{\Omega }}{min}f\left(u\right)+g\left(u\right),\end{array}$$

(4)

where $\mathrm{\Omega }$ is a nonempty closed convex subset of H, f and g are convex functions on H that f is differentiable on H. We denote by $S_{*}$ the solution set of (4).

By the way, to obtain a nice convergence rate, Polyak [15] introduced the heavy ball method for solving smooth convex minimization problem. In case $g=0$, Nesterov [16] modified the heavy ball method as follows.

In this work, motivated by Algorithm 1 [13], Algorithm 2 [14], Algorithm 3 [16] and Algorithm 4 [17], we are interested to design a new projected forward-backward algorithm for solving the constrained convex minimization problem (4) and establishing the convergence theorem. We also apply our method to solve image inpainting and provide some comparisons and numerical results. Finally, we show the effects of each parameters in the proposed algorithm.

Algorithm 1 Ref. [13] Let $\epsilon \in (0,min\{1,\frac{1}{\alpha }\})$ and $u^0\in {\mathbb{R}}^N.$ For $k\ge 1$, define

$$\begin{array}{ccc}{v}^k\hfill & =\hfill & u^k-{\alpha }_k\nabla f\left(u^k\right),\hfill \\ u^{k+1}\hfill & =\hfill & u^k+{\lambda }_k({\mathrm{prox}}_{{\alpha }_{k}g}{v}^k-u^k),\hfill \end{array}$$ (5) where ${\alpha }_k\in [\epsilon ,\frac{2}{\alpha }-\epsilon ]$, ${\lambda }_k\in [\epsilon ,1]$ and $\alpha$ is the Lipschitz constant of the gradient of f.

Algorithm 2 Let $\sigma >0,\theta \in (0,1)$ and $\delta \in (0,\frac{1}{2})$. Let $u^0\in \mathrm{dom}g$. For $k\ge 1,$ define

$$u^{k+1}={\mathrm{prox}}_{{\alpha }_{k}g}(u^k-{\alpha }_k\nabla f\left(u^k\right)),$$ where ${\alpha }_k=\sigma {\theta }^{m_k}$ and $m_k$ is the smallest nonnegative integer satisfying $${\alpha }_k\parallel \nabla f\left(u^{k+1}\right)-\nabla f\left(u^k\right)\parallel \le \delta \parallel u^{k+1}-u^k\parallel .$$

Algorithm 3 Let $u^0,u^1\in {\mathbb{R}}^N$ and ${\theta }_k\in [0,1)$. For $k\ge 1,$ define

$$\begin{array}{ccc}\hfill v^k& =& u^k+{\theta }_k(u^k-u^{k-1}),\hfill \\ \hfill u^{k+1}& =& v^k-{\alpha }_k\nabla f\left(v^k\right),\hfill \end{array}$$ where ${\alpha }_k>0$. The term ${\theta }_k(u^k-u^{k-1})$ is called inertial term.

In 2003, Moudafi and Oliny [17] suggested the inertial forward-backward splitting as follows:

Algorithm 4 Let $u^0,u^1\in {\mathbb{R}}^N$ and ${\alpha }_k\in [0,\frac{2}{L}-\epsilon ]$. For $k\ge 1,$ define

$$\begin{array}{ccc}\hfill v^k& =& u^k+{\theta }_k(u^k-u^{k-1}),\hfill \\ \hfill u^{k+1}& =& {\mathrm{prox}}_{{\alpha }_{k}g}(v^k-{\alpha }_k\nabla f\left(u^k\right)),\hfill \end{array}$$ where ${\theta }_k\in [0,1)$. Many works explored that algorithms involving inertial term have a nice rate of convergence [3,18,19,20]. The complexity of some variants of the forward-backward algorithms can be found in the work of Cruz and Nghia [14].

This paper is organized as follows: In Section 2, we recall some preliminaries and mathemetical tools. In Section 3, we prove the weak convergence theorem of the proposed method. In Section 4, we provide numerical experiments in image inpainting to valid the convergence theorem and, finally, in Section 5, we give conclusions of this paper.

2. Preliminaries

Let us review some important definitions and lemmas for proving the convergence theorem. Let H be a real Hilbert space with inner product $⟨·,·⟩$ and norm $\parallel ·\parallel$. Let $h:H\to \overline{\mathbb{R}}$ be a proper, lower semicontinuous ($l.s.c.$), and convex function. The domain of h is defined by $\mathrm{dom}h:=\{u\in H|h\left(u\right)<+\infty \}.$ For any $u\in H$, we know that the orthogonal projection of u onto a nonempty, closed and convex subset C of H is defined by

$${\displaystyle P_{C}u:=\underset{v\in C}{\mathrm{argmin}}{\parallel u-v\parallel }^2.}$$

(6)

Lemma 1

([21]). Let C be a nonempty, closed and convex subset of a real Hilbert space H. Then, for any $u\in H$, we have

(i) 

$⟨u-P_{C}u,a-P_{C}u⟩\le 0$for all$a\in C$;

(ii) 

$\parallel P_{C}u-P_C{v\parallel }^2\le ⟨P_{C}u-P_{C}v,u-y⟩$for all$u,v\in H$;

(iii) 

$\parallel P_C{u-a\parallel }^2\le {\parallel u-a\parallel }^2-{\parallel P_{C}u-u\parallel }^2$for all$a\in C$.

The directional derivative of h at u in the direction d is

$$\begin{array}{c}\hfill {\displaystyle h^{\prime }(u;d):=\underset{t\to 0^{+}}{lim}\frac{h(u+td)-h\left(u\right)}{t}.}\end{array}$$

Definition 1.

The subdifferential of h at u is defined by

$$\partial h\left(u\right)=\{a\in H:⟨a,v-u⟩\le h(v)-h(u),y\in H\}.$$

It is known that $\partial h$ is maximal monotone and if h is differentiable, then $\partial h$ is the gradient of h denoted by $\nabla h$. Moreover, $\nabla h$ is monotone, that is, $⟨\nabla h\left(u\right)-\nabla h\left(v\right),u-v⟩\ge 0$ for all $u,v\in H$. From (4), we also know that

$$u_{*}\in \mathrm{argmin}(f+g)\iff u_{*}={\mathrm{prox}}_{cg}(Id-c\nabla f)\left(u_{*}\right),$$

where $c>0$ and ${\mathrm{prox}}_g={(Id+\partial g)}^{-1}$.

From [14], we know that

$$\begin{array}{c}\hfill \frac{a-{\mathrm{prox}}_{\alpha g}\left(a\right)}{\alpha }\in \partial g\left({\mathrm{prox}}_{\alpha g}\left(a\right)\right)\mathrm{for}\mathrm{all}a\in H,\alpha >0.\end{array}$$

(7)

Lemma 2

([22]). $\partial h,\mathrm{Gph}(\partial h)=\left\{\right(u,a)\in H\times H:a\in \partial h(u\left)\right\}$ is demiclosed, i.e., if the sequence $(u^k,a^k)\subset \mathrm{Gph}(\partial h)$ satisfies that $\left(u^k\right)$ converges weakly to u and $\left(a^k\right)$ converges strongly to a, then $(u,a)\in \mathrm{Gph}(\partial h).$

Lemma 3.

Let$\left(a^k\right)$, $\left(b^k\right)$and$\left(r_k\right)$be real positive sequences such that

$$a^{k+1}\le (1+r_k)a^k+b^k,k\in \mathbb{N}.$$

If${\displaystyle \sum _{k=1}^{\infty }{r}_k<+\infty }$and${\displaystyle \sum _{k=1}^{\infty }{b}^k<+\infty }$, then${\displaystyle \underset{k\to +\infty }{lim}{a}^k}$exists.

Lemma 4

([23]). Let $\left(a^k\right)$ and $\left({\theta }_k\right)$ be real positive sequences such that

$$a^{k+1}\le (1-{\theta }_k)a^k+{\theta }_k{a}^{k-1},k\in \mathbb{N}.$$

Then,${\displaystyle a^{k+1}\le K·\prod _{j=1}^k(1+2{\theta }_j)}$, where$K=max\{a_1,a_2\}$. Moreover, if${\displaystyle \sum _{k=1}^{\infty }{\theta }_k<+\infty }$, then$\left(a^k\right)$is bounded.

Definition 2.

Let S be a nonempty subset of H. A sequence$\left(u^k\right)$in H is said to be quasi-Fejér convergent to S if and only if for all$u\in S$there exists a positive sequence$\left({\epsilon }_k\right)$such that${\displaystyle \sum _{k=0}^{\infty }{\epsilon }_k<+\infty }$and$\parallel u^{k+1}{-u\parallel }^2\le {\parallel u^k-u\parallel }^2+{\epsilon }_k$for all$k\in \mathbb{N}.$When$\left({\epsilon }_k\right)$is a null sequence, we say that$\left(u^k\right)$is Fejér convergent to S.

Lemma 5

([21,24]). If $\left(u^k\right)$ is quasi-Fejér convergent to S, then we have:

(i) 

$\left(u^k\right)$is bounded.

(ii) 

If all weak accumulation points of$\left(u^k\right)$is in S, then$\left(u^k\right)$weakly converges to a point in S.

3. Results

In this section, we suggest a new projected forward-backward algorithm and establish the weak convergence. The following conditions are assumed:

(A1)

$f,g:H\to \mathbb{R}\cup \{+\infty \}$ are proper, $l.s.c$, convex functions on H that f is differentiable on H.

(A2)

$\nabla f$ is uniformly continuous on bounded subsets of H and is bounded on any bounded subset of H.

Next, we will prove weak convergence theorem of the proposed algorithm.

Theorem 1.

Let$\left(u^k\right)$be defined by Algorithm 5. Suppose${\displaystyle \sum _{k=1}^{\infty }{\theta }_k<+\infty }$. Then,$\left(u^k\right)$weakly converges to a point in$S_{*}$.

Algorithm 5 Let $\mathrm{\Omega }$ be a nonempty closed convex subset of H. Given $\sigma >0$, $\varphi \in (0,1)$, $\delta \in (0,\frac{1}{2})$ and ${\theta }_k\ge 0$. Let $u^0,u^1\in H$ and define

$$\begin{array}{c}\hfill w^k=u^k+{\theta }_k(u^k-u^{k-1})\end{array}$$ (8) and $$\begin{array}{c}\hfill v^k={\mathrm{prox}}_{{\alpha }_{k}g}(w^k-{\alpha }_k\nabla f\left(w^k\right))\end{array}$$ (9) where ${\alpha }_k=\sigma {\varphi }^{m_k}$ and $m_k$ is the smallest nonnegative integer such that $$\begin{array}{c}\hfill {\alpha }_k\parallel \nabla f\left(v^k\right)-\nabla f\left(w^k\right)\parallel \le \delta \parallel v^k-w^k\parallel .\end{array}$$ (10) Set $u^{k+1}$ by $$\begin{array}{c}\hfill u^{k+1}=P_{\mathrm{\Omega }}\left(v^k\right),k\ge 0.\end{array}$$ (11)

Proof. 

Let $u_{*}$ be a solution in $S_{*}$. Thus, we obtain

$$\begin{array}{ccc}\parallel u^{k+1}-u_{*}{\parallel }^2\hfill & =\hfill & \parallel P_{\mathrm{\Omega }}\left(v^k\right)-u_{*}{\parallel }^2\hfill \\ \hfill & \le \hfill & \parallel v^k-u_{*}{\parallel }^2-{\parallel P_{\mathrm{\Omega }}\left(v^k\right)-v^k\parallel }^2.\hfill \end{array}$$

(12)

By the definition of proximal operator and $v^k$, we have

$$\frac{w^k-v^k}{{\alpha }_k}-\nabla f\left(w^k\right)=\frac{w^k-{\mathrm{prox}}_{{\alpha }_{k}g}(w^k-{\alpha }_k\nabla f\left(w^k\right))}{{\alpha }_k}-\nabla f\left(w^k\right)\in \partial g\left(v^k\right).$$

By the convexity of g, we get

$$\begin{array}{c}\hfill g\left(u\right)-g\left(v^k\right)\ge ⟨\frac{w^k-v^k}{{\alpha }_k}-\nabla f\left(w^k\right),u-v^k⟩,\forall u\in H.\end{array}$$

(13)

The convexity of f gives

$$\begin{array}{c}\hfill f\left(u\right)-f\left(y\right)\ge ⟨\nabla f\left(y\right),u-y⟩,\forall u\in H,y\in H.\end{array}$$

(14)

Using (13) and (14) with any $u\in H$ and $y=w^k$, we obtain

$$\begin{array}{ccc}\hfill g\left(u\right)-g\left(v^k\right)+f\left(u\right)-f\left(w^k\right)& \ge & ⟨\frac{w^k-v^k}{{\alpha }_k}-\nabla f\left(w^k\right),u-v^k⟩+⟨\nabla f\left(w^k\right),u-w^k⟩\hfill \\ & =& \frac{1}{{\alpha }_k}⟨w^k-v^k,u-v^k⟩+⟨\nabla f\left(w^k\right),v^k-w^k⟩\hfill \\ & =& \frac{1}{{\alpha }_k}⟨w^k-v^k,u-v^k⟩+⟨\nabla f\left(v^k\right),v^k-w^k⟩\hfill \\ & & +⟨\nabla f\left(w^k\right)-\nabla f\left(v^k\right),v^k-w^k⟩\hfill \\ & \ge & \frac{1}{{\alpha }_k}⟨w^k-v^k,u-v^k⟩+⟨\nabla f\left(v^k\right),v^k-w^k⟩\hfill \\ & & -\parallel \nabla f\left(w^k\right)-\nabla f\left(v^k\right)\parallel \parallel v^k-w^k\parallel \hfill \\ & \ge & \frac{1}{{\alpha }_k}⟨w^k-v^k,u-v^k⟩+⟨\nabla f\left(v^k\right),v^k-w^k⟩\hfill \\ & & -\frac{\delta }{{\alpha }_k}{\parallel w^k-v^k\parallel }^2.\hfill \end{array}$$

This yields

$$\begin{array}{c}\hfill ⟨w^k-v^k,v^k-u⟩\ge {\alpha }_k[f\left(w^k\right)-f\left(u\right)+g\left(v^k\right)-g\left(u\right)+⟨\nabla f\left(v^k\right),v^k-w^k⟩]-\delta {\parallel w^k-v^k\parallel }^2.\end{array}$$

Since $2⟨w^k-v^k,v^k-u⟩=\parallel w^k{-u\parallel }^2-\parallel w^k-v^k{\parallel }^2-{\parallel v^k-u\parallel }^2$, it follows that

$$\begin{array}{ccc}\hfill \parallel w^k{-u\parallel }^2-{\parallel v^k-u\parallel }^2& \ge & 2{\alpha }_k[f\left(w^k\right)-f\left(u\right)+g\left(v^k\right)-g\left(u\right)+⟨\nabla f\left(v^k\right),v^k-w^k⟩]\hfill \\ & & +(1-2\delta )\parallel w^k-v^k{\parallel }^2.\hfill \end{array}$$

Since f is convex, we have $f\left(w^k\right)-f\left(v^k\right)\ge ⟨\nabla f\left(v^k\right),w^k-v^k⟩$. This implies that

$$\begin{array}{ccc}\hfill \parallel w^k{-u\parallel }^2-{\parallel v^k-u\parallel }^2& \ge & 2{\alpha }_k[f\left(w^k\right)-f\left(u\right)+g\left(v^k\right)-g\left(u\right)-f\left(w^k\right)+f\left(v^k\right)]\hfill \\ & & +(1-2\delta )\parallel w^k-v^k{\parallel }^2.\hfill \end{array}$$

Setting $u=u_{*}$, we obtain

$$\begin{array}{cc}\parallel v^k-u_{*}{\parallel }^2\hfill & \le \parallel w^k-u_{*}{\parallel }^2-2{\alpha }_k[(f+g)\left(v^k\right)-(f+g)\left(u_{*}\right)]-(1-2\delta ){\parallel w^k-v^k\parallel }^2\hfill \\ \hfill & \le \parallel w^k-u_{*}{\parallel }^2.\hfill \end{array}$$

(15)

From (12) and (15), we see that

$$\begin{array}{ccc}\hfill \parallel u^{k+1}-u_{*}{\parallel }^2& \le & \parallel w^k-u_{*}{\parallel }^2-{\parallel P_{\mathrm{\Omega }}\left(v^k\right)-v^k\parallel }^2\hfill \\ & \le & \parallel w^k-u_{*}{\parallel }^2.\hfill \end{array}$$

(16)

Hence,

$$\begin{array}{ccc}\hfill \parallel u^{k+1}-u_{*}\parallel & \le & \parallel w^k-u_{*}\parallel \hfill \\ & \le & \parallel u^k-u_{*}\parallel +{\theta }_k\parallel u^k-u^{k-1}\parallel \hfill \\ & \le & \parallel u^k-u_{*}\parallel +{\theta }_k(\parallel u^k-u_{*}\parallel +\parallel u^{k-1}-u_{*}\parallel ).\hfill \end{array}$$

This shows that $\parallel u^{k+1}-u_{*}\parallel \le (1+{\theta }_k)\parallel u^k-u_{*}\parallel +{\theta }_k\parallel u^{k-1}-u_{*}\parallel$. By Lemma 4, we have

$${\displaystyle \parallel u^{k+1}-u_{*}\parallel \le K·\prod _{j=1}^k(1+2{\theta }_j)}$$

where $K=max\{\parallel u^1-u_{*}\parallel ,\parallel u^2-u_{*}\parallel \}$. Since ${\displaystyle \sum _{k=1}^{\infty }{\theta }_k<+\infty }$, $\left(u^k\right)$ is bounded. Thus, ${\displaystyle \sum _{k=1}^{\infty }{\theta }_k\parallel u^k-u^{k-1}\parallel <+\infty }$. By Lemma 3, therefore ${\displaystyle \underset{k\to \infty }{lim}\parallel u^k-u_{*}\parallel }$ exists.

Next, we consider

$$\begin{array}{ccc}\hfill \parallel w^k-u_{*}{\parallel }^2& =& \parallel u^k+{\theta }_k(u^k-u^{k-1})-u_{*}{\parallel }^2\hfill \\ & =& \parallel u^k-u_{*}{\parallel }^2+2{\theta }_k⟨u^k-u_{*},u^k-u^{k-1}⟩+{\theta }_k^2{\parallel u^k-u^{k-1}\parallel }^2\hfill \\ & \le & \parallel u^k-u_{*}{\parallel }^2+2{\theta }_k\parallel u^k-u_{*}\parallel \parallel u^k-u^{k-1}\parallel +{\theta }_k^2{\parallel u^k-u^{k-1}\parallel }^2.\hfill \end{array}$$

(17)

By (15)–(17), we see that

$$\begin{array}{ccc}\hfill \parallel u^{k+1}-u_{*}{\parallel }^2& \le & \parallel u^k-u_{*}{\parallel }^2+2{\theta }_k\parallel u^k-u_{*}\parallel \parallel u^k-u^{k-1}\parallel +{\theta }_k^2{\parallel u^k-u^{k-1}\parallel }^2\hfill \\ & & -2{\alpha }_k[(f+g)\left(v^k\right)-(f+g)\left(u_{*}\right)]-(1-2\delta ){\parallel w^k-v^k\parallel }^2\hfill \\ & & -\parallel P_{\mathrm{\Omega }}\left(v^k\right)-v^k{\parallel }^2.\hfill \end{array}$$

This gives

$$\begin{array}{ccc}\hfill \parallel P_{\mathrm{\Omega }}\left(v^k\right)-v^k{\parallel }^2+(1-2\delta ){\parallel w^k-v^k\parallel }^2& \le & (\parallel u^k-u_{*}{\parallel }^2-\parallel u^{k+1}-u_{*}{\parallel }^2)\hfill \\ & & +2{\theta }_k\parallel u^k-u_{*}\parallel \parallel u^k-u^{k-1}\parallel \hfill \\ & & +{\theta }_k^2{\parallel u^k-u^{k-1}\parallel }^2.\hfill \end{array}$$

Since ${\displaystyle \sum _{k=1}^{\infty }{\theta }_k\parallel u^k-u^{k-1}\parallel <+\infty }$ and ${\displaystyle \underset{k\to \infty }{lim}\parallel u^k-u_{*}\parallel }$ exists, it follows that $\parallel v^k-w^k\parallel \to 0$ and $\parallel u^{k+1}-v^k\parallel \to 0$. It is easily seen that $\parallel w^k-u^k\parallel \to 0$ and hence $\parallel u^{k+1}-u^k\parallel \to 0$. On the other hand, we see that

$$\begin{array}{ccc}\hfill \parallel u^k-u_{*}{\parallel }^2-{\parallel u^{k+1}-u_{*}\parallel }^2& \ge & 2{\alpha }_k[(f+g)\left(v^k\right)-(f+g)\left(u_{*}\right)]+(1-2\delta ){\parallel w^k-v^k\parallel }^2\hfill \\ & & +\parallel P_{\mathrm{\Omega }}\left(v^k\right)-u_{*}{\parallel }^2\hfill \\ & \ge & (1-2\delta )\parallel w^k-v^k{\parallel }^2+{\parallel P_{\mathrm{\Omega }}\left(v^k\right)-u_{*}\parallel }^2\hfill \\ & \ge & 0.\hfill \end{array}$$

It follows that $\left(u^k\right)$ is Fejér convergent to $S_{*}$. Thus, we have

$$\begin{array}{ccc}\hfill 0& \le & 2{\alpha }_k[(f+g)\left(v^k\right)-(f+g)\left(u_{*}\right)]\hfill \\ & \le & \parallel u^k-u_{*}{\parallel }^2-{\parallel u^{k+1}-u_{*}\parallel }^2\hfill \\ & =& (\parallel u^k-u_{*}\parallel -\parallel u^{k+1}-u_{*}\parallel \left)\right(\parallel u^k-u_{*}\parallel +\parallel u^{k+1}-u_{*}\parallel )\hfill \\ & \le & 2M(\parallel u^k-u_{*}\parallel -\parallel u^{k+1}-u_{*}\parallel )\hfill \\ & \le & 2M\parallel u^{k+1}-u^k\parallel ,\hfill \end{array}$$

where $M=sup\{\parallel u^k-u_{*}\parallel |k\in \mathbb{N}\}<+\infty$. Since $\left(u^k\right)$ is bounded, the set of weak accumulation points is nonempty. Take any weak accumulation point $\overline{u}$ of $\left(u^k\right)$. Thus, there is a subsequence $\left(u^{k_n}\right)$ of $\left(u^k\right)$ weakly converging to $\overline{u}$. Moreover, $\left\{w^{k_n}\right\}$ also weakly converges to $\overline{u}$. Since $\left(u^{k_n}\right)$ is bounded and $\parallel w^{k_n}-v^{k_n}\parallel \to 0$, from $\left(\mathrm{A}2\right)$, we obtain

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}\parallel \nabla f\left(w^{k_n}\right)-\nabla f\left(v^{k_n}\right)\parallel =0.}\end{array}$$

Since $v^{k_n}={\mathrm{prox}}_{{\alpha }_{k_n}g}(w^{k_n}-{\alpha }_{k_n}\nabla f\left(w^{k_n}\right)),$ it follows from (7) that

$$\begin{array}{c}\hfill \frac{w^{k_n}-{\alpha }_{k_n}\nabla f\left(w^{k_n}\right)-v^{k_n}}{{\alpha }_{k_n}}\in \partial g\left(v^{k_n}\right),\end{array}$$

(18)

which yields

$$\begin{array}{c}\hfill \frac{w^{k_n}-v^{k_n}}{{\alpha }_{k_n}}+\nabla f\left(w^{k_n}\right)-\nabla f\left(v^{k_n}\right)\in \nabla f\left(v^{k_n}\right)+\partial g\left(v^{k_n}\right)\in \partial (f+g)\left(v^{k_n}\right).\end{array}$$

(19)

By passing $n\to \infty$ in (19), we get from (18) and Lemma 2 that $0\in \partial (f+g)\left(\overline{u}\right)$. Thus, $\overline{u}\in S_{*}.$ By Lemma 5 (ii), we conclude that $\left(u^k\right)$ weakly converges to a point in $S_{*}$.    □

4. Numerical Experiments

In this section, we aim to apply our result for solving an image inpainting problem which is of the following mathematical model:

$$\begin{array}{c}\hfill {\displaystyle \underset{u\in {\mathbb{R}}^{M\times N}}{min}\frac{1}{2}\parallel A(u-u^0){\parallel }_F^2+\mu {\parallel u\parallel }_{*}}\end{array}$$

(20)

where $u^0\in {\mathbb{R}}^{M\times N}(M<N)$, A is a linear map that selects a subset of the entries of an $M\times N$ matrix by setting each unknown entry in the matrix to 0, u is matrix of known entries $A\left(u^0\right)$, and $\mu >0$ is regularization parameter.

In particular, we investigate the image inpainting problem [25,26]:

$$\begin{array}{c}\hfill {\displaystyle \underset{u\in {\mathbb{R}}^{M\times N}}{min}\frac{1}{2}\parallel P_{\mathrm{\Omega }}\left(u\right)-P_{\mathrm{\Omega }}\left(u^0\right){)\parallel }_F^2+\mu {\parallel u\parallel }_{*}}\end{array}$$

(21)

where ${\parallel ·\parallel }_F$ is the Frobenius matrix norm, and ${\parallel ·\parallel }_{*}$ is the nuclear matrix norm. Here, we define $P_{\mathrm{\Omega }}$ as follows:

$$\begin{array}{c}\hfill P_{\mathrm{\Omega }}\left(u\right)=\left\{\begin{array}{c}{u}_{ij},(i,j)\in \mathrm{\Omega },\hfill \\ 0, \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(22)

The optimization problem (21) relates to (4). In fact, let $f\left(u\right)=\frac{1}{2}{\parallel P_{\mathrm{\Omega }}\left(u\right)-P_{\mathrm{\Omega }}\left(u^0\right)\parallel }_F^2$ and $g\left(u\right)={\mu \parallel u\parallel }_{*}$. Then, $\nabla f\left(u\right)=P_{\mathrm{\Omega }}\left(u\right)-P_{\mathrm{\Omega }}\left(u^0\right)$ is 1-Lipschitz continuous. Moreover, ${\mathrm{prox}}_g$ is obtained by the singular value decomposition (SVD) [27].

From Algorithm 5, we obtain the Algorithm 6 for image inpainting.

To measure the quality of images, we consider the signal-to-noise ratio (SNR) and the structural similarity index (SSIM) [28], which are given by

$$\begin{array}{c}\hfill \mathrm{SNR}=20log\frac{{\parallel u\parallel }_F}{\parallel u-u^r{\parallel }_F}\end{array}$$

(23)

and

$$\begin{array}{c}\hfill \mathrm{SSIM}=\frac{(2a_u{a}_{u^r}+c_1)(2{\sigma }_{u{u}^r}+c_2)}{(a_u^2+a_{u^r}^2+c_1)({\sigma }_u^2+{\sigma }_{u^r}^2+c_2)}\end{array}$$

(24)

where u is the original image, $u^r$ is the restored image, $a^u$ and $a_{u^r}$ are the mean values of the original image u and restored image $u^r$, respectively, ${\sigma }_u^2$ and ${\sigma }_{u^r}^2$ are the variances, ${\sigma }_{u{u}^r}^2$ is the covariance of two images, $c_1={\left(0.01L\right)}^2$ and $c_2={\left(0.03L\right)}^2$, and L is the dynamic range of pixel values. SSIM ranges from 0 to 1, and 1 means perfect recovery. Next, we analyze its convergence including its effects of the parameters $\delta ,\varphi$ and $\sigma$ that proposed in Algorithm 5. We now present the corresponding numerical results (number of iterations denoted by Iter and CPU denoted by the time of CPU).

First, we investigate the effect $\delta$. Set parameters as follows:

$$\begin{array}{c}\hfill {\theta }_k=\left\{\begin{array}{c}\frac{t_k-1}{t_{k+1}} \mathrm{if}1\le k<N,\hfill \\ \frac{1}{2^k} \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(25)

Algorithm 6 Forward-backward algorithm for image inpainting.

Step 1: Input $u^0,u^1,\sigma ,\varphi$ and $\delta$.

Step 2: Compute $$w^k=u^k+{\theta }_k(u^k-u^{k-1})$$

Step 3: (Linesearch rule) Set ${\alpha }_k=\sigma$ $$\begin{array}{ccc}\hfill A_k& =& {\alpha }_k{\parallel \nabla f\left({\mathrm{prox}}_{{\alpha }_{k}g}(u^k-{\alpha }_k\nabla f\left(u^k\right))\right)-\nabla f\left(w^k\right)\parallel }_F\hfill \\ \hfill B_k& =& \delta \parallel {\mathrm{prox}}_{{\alpha }_{k}g}(u^k-{\alpha }_k\nabla f\left(u^k\right))-w^k{\parallel }_F.\hfill \end{array}$$

While $A_k>B_k$

${\alpha }_k=\sigma {\varphi }^k$

End while.

Step 4: Compute $$v^k={\mathrm{prox}}_{{\alpha }_{k}g}(w^k-{\alpha }_k\nabla f\left(w^k\right))$$

and $$u^{k+1}=P_{\mathrm{\Omega }}\left(v^k\right),k\ge 0.$$

Set $k=k+1$ go to Step 2.

where $t_k$ is a sequence defined by $t_1=1$ and $t_{k+1}=\frac{1+\sqrt{1+4t_k^2}}{2}$.

From Table 1, we observe that SNR and SSIM of Algorithm 5 have been getting larger when the parameter $\delta$ approaches $0.5$. Moreover, the CPU of Algorithm 5 is decreasing when $\delta$ tends to $0.5$.

Table 1. The convergence results of Algorithm 5 for each $\delta$.

Set: $\mathit{\sigma }=1$ and $\mathit{\varphi }=0.4$
$\mathit{\delta }$	N = 227, M = 340 Iter = 60			N = 480, M = 360 Iter = 90
	SNR	SSIM	CPU	SNR	SSIM	CPU
0.5	22.8626	0.9476	2.2656	26.3994	0.9210	11.5229
0.1	21.8228	0.9437	4.0916	26.3982	0.9209	21.7439
0.05	14.7249	0.9165	5.0465	26.3974	0.9181	27.2411
0.01	9.9919	0.8886	6.7001	19.2859	0.8939	37.8360
0.001	−0.7012	0.3889	8.0271	5.9239	0.6228	47.7375

Figure 1, Figure 2, Figure 3 and Figure 4 show the SNR and the reconstructed images for each caseof dimensions.

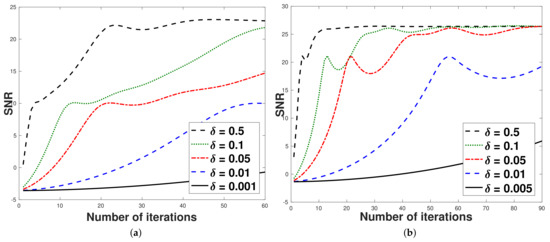
Figure 1. Graph of the number of iterations and SNR for the parameter $\delta$. (a) Number of iterations and SNR with N = 227, M = 340; (b) number of iterations and SNR with N = 480, M = 360.

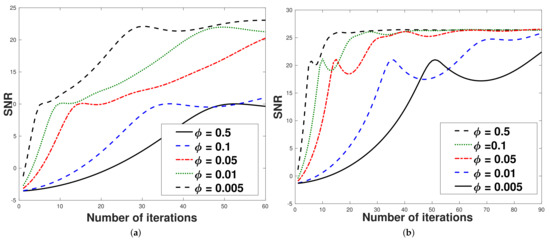
Figure 2. Graph of number of iterations and SNR for the parameter $\varphi$. (a) Number of iterations and SNR with N = 227, M = 340; (b) number of iterations and SNR with N = 480, M = 360.

Figure 3. The painted image and restored images with the real image N = 227, M = 340. (a) The painted image; (b) restored images in Table 1 for $\delta =0.5$ (SNR = 22.8626, SSIM = 0.9476); (c) restored images in Table 2 for $\varphi =0.5$ (SNR = 23.0594, SSIM = 0.9479); (d) restored images in Table 3 for $\sigma =5$ (SNR = 22.9865, SSIM = 0.9477).

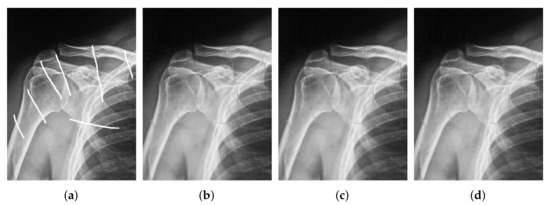
Figure 4. The painted image and restored images with the real image N = 480, M = 360. (a) The painted image; (b) restored images in Table 1 for $\delta =0.5$ (SNR = 26.3994, SSIM = 0.9210); (c) restored images in Table 2 for $\varphi =0.5$ (SNR = 26.4002, SSIM = 0.9210); (d) restored images in Table 3 for $\sigma =0.5$ (SNR = 26.4084, SSIM = 0.9210).

Next, we discuss the effect of $\varphi$. The numerical experiments are given in Table 2.

Table 2. The convergence results of Algorithm 5 for each $\varphi$.

Given: $\mathit{\delta }=0.4$ and $\mathit{\sigma }=1$
$\mathbf{\varphi }$	$\mathit{N}$ = 227, $\mathit{M}$ = 340			$\mathit{N}$ = 480, $\mathit{M}$ = 360
	Iter = 60			Iter = 90
	SNR	SSIM	CPU	SNR	SSIM	CPU
0.5	23.0594	0.9479	3.0865	26.4002	0.9210	17.0693
0.1	21.2594	0.9428	2.2104	26.3604	0.9205	11.4325
0.05	20.2735	0.9391	2.1874	26.5203	0.9207	11.5494
0.01	10.9957	0.8918	2.2586	25.8063	0.9114	11.2883
0.005	9.6387	0.8658	2.2449	22.4065	0.9095	11.3964

From Table 2, we observe that SNR, SSIM, and CPU time of Algorithm 5 have been getting larger when the parameter $\varphi$ approaches $0.5$.

Next, we discuss the effect $\sigma$. The numerical experiments are given in Table 3. From Table 3, we observe that SNR, SSIM, and the CPU time of Algorithm 5 have been getting larger if $\sigma$ increases. The SNR and the reconstructed images are shown in Figure 3, Figure 4 and Figure 5.

Table 3. The convergence results of Algorithm 5 for each $\sigma$.

Set: $\mathit{\delta }=0.4$ and $\mathit{\varphi }=0.4$
$\mathbf{\sigma }$	$\mathit{N}$ = 227, $\mathit{M}$ = 340 Iter = 60			$\mathit{N}$ = 480, $\mathit{M}$ = 360 Iter = 90
	SNR	SSIM	CPU	SNR	SSIM	CPU
5	22.9865	0.9477	3.9889	26.3946	0.9209	21.2420
1	22.8626	0.9476	2.2848	26.3994	0.9210	11.1571
0.5	22.8327	0.9474	2.3458	26.4084	0.9210	11.2728
0.05	20.2735	0.9391	1.3531	26.5230	0.9207	6.0226
0.005	9.6387	0.8638	1.3434	22.4065	0.9095	6.2738

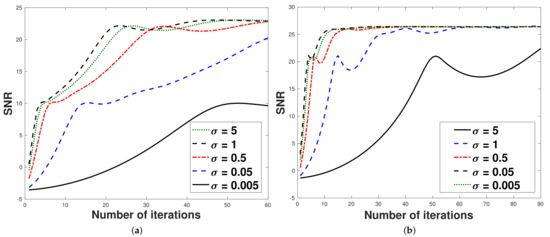
Figure 5. Graph of the number of iterations and SNR for the parameter $\sigma$. (a) Number of iterations and SNR with N = 227, M = 340; (b) number of iterations and SNR with N = 480, M = 360.

The real images are shown in Figure 6, input image, and the reconstructed images are shown in Figure 3, Figure 4 and Figure 6, respectively.

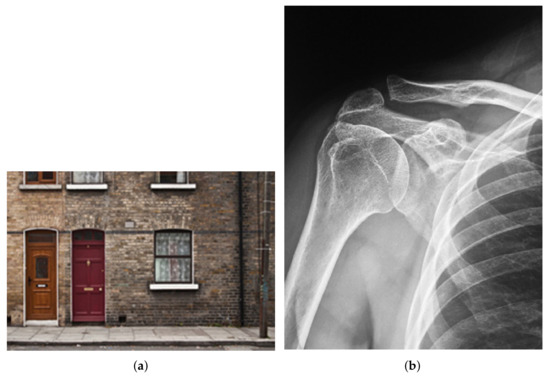
Figure 6. The original images. (a) The original image of size N = 227, M = 340; (b) the original image of size of N = 480, M = 360.

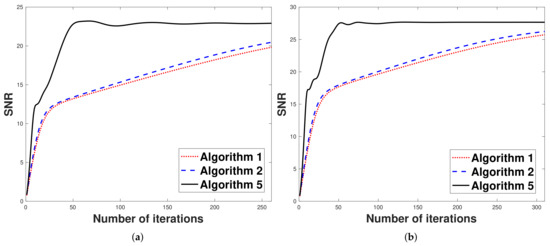
Now, we present the performance of Algorithms 5 and its comparison to the projected version of Algorithm 1 [13] and Algorithm 2 [14]. The initial point $u^0$ and $u^1$ are chosen to be zero and let ${\alpha }_k=\frac{1}{{\parallel A\parallel }^2}$ and ${\lambda }_k=0.09$ in Algorithm 1. Let $\sigma =0.1$, $\delta =0.13,\varphi =0.5$ and $\theta$ be defined by (25) in Algorithms 2 and 5, respectively. The numerical results are shown in Table 4.

Table 4. Computational results for solving (21).

	Image Size		Image Size
	SNR	SSIM	SNR	SSIM
Algorithm 1	19.8276	0.9378	25.7210	0.9363
Algorithm 2	20.4704	0.9402	26.2362	0.9373
Algorithm 5	22.9158	0.9477	27.6581	0.9400

From Table 4, we see that the experiment results of Algorithm 5 are better than Algorithms 1 and 2 in terms of SNR and SSIM in all cases.

The figure of the inpainting image for the 260th and 310th iterations are shown in Figure 7, Figure 8 and Figure 9, respectively.

Figure 7. The painted image and restored images. (a) The painted image; (b) restored images in Algorithm 1 (SNR = 19.8276, SSIM = 0.9278); (c) restored images in Algorithm 2 (SNR = 20.4704, SSIM = 0.9402); (d) restored images in Algorithm 5 (SNR = 22.9158, SSIM = 0.9477).

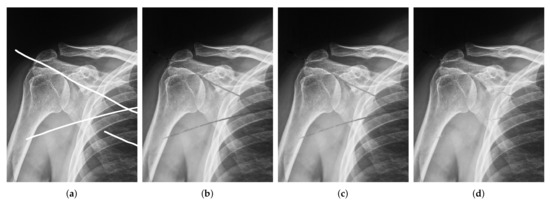
Figure 8. The painted image and restored images. (a) The painted image; (b) restored images in Algorithm 1 (SNR = 25.7210, SSIM = 0.9363); (c) restored images in Algorithm 2 (SNR = 26.2362, SSIM = 0.9373); (d) restored images in Algorithm 5 (SNR = 27.6581, SSIM = 0.9400).

Figure 9. The SNR value and number of iterations for all cases. (a) Graph of SNR value and number of iterations of Figure 7; (b) graph of SNR value and number of iterations of Figure 8.

5. Conclusions

In this research, we investigated inertial projected forward-backward algorithm using linesearches for constrained minimization problems. The weak convergence results were proved under control conditions. The proposed algorithms do not need to compute the Lipschitz constant of the gradient of functions. We applied our results to solve image inpainting. We also presented the effects of all parameters that are assumed in our method.

For our future research, we aim to find a new linesearch technique that does not require the Lipschitz continuity assumption on the gradient of the function. We note that the proposed algorithm depends on the computation of the projection which is not an easy task to find in some cases. It is interesting to construct new algorithms that do not involve the projection.